Study on the bearing capacity optimization and performance of photovoltaic support in desert sand and gravel area based on bionics

Abstract

With the continuous development and use of renewable energy, photovoltaic projects have become essential in the clean energy landscape. The bearing capacity and stability of their bracket foundations are crucial for the sustainable development of energy. Therefore, this paper aims to investigate the application of bionics principles to propose a novel type of photovoltaic bracket pile foundation designed to meet diverse bearing capacity requirements, specifically suited for desert gravel areas: the photovoltaic bracket serpentine pile foundation. This study aims to examine the factors influencing the bearing characteristics of the serpentine piles. Using a controlled variable method, we systematically analyze the effects of the serpentine pile embedment depth, width, spacing, and other factors on various aspects of the serpentine piles’ performance, including ultimate bearing capacity, unit-volume concrete bearing capacity, pile displacement, and pile body stresses. The results indicate that these parameters significantly impact the bearing performance of the serpentine piles, with burial depth and width of the snakeskin body emerging as key factors. Finally, by employing multiple linear regression analysis, we propose recommendations for optimizing the serpentine pile parameters to achieve the best balance between load-bearing performance and economic viability. These recommendations, based on experimental data and analytical results, not only provide a theoretical basis for the design and application of serpentine piles but also serve as a valuable reference for the research and development of similar foundation treatment technologies.

Introduction

With increasing global awareness of environmental protection and the deepening energy crisis, clean energy has garnered widespread attention as a crucial substitute for traditional fossil fuels^1,2. Clean energy production emits fewer or almost no harmful substances during its process and usage, with solar energy emerging as a significant component due to its high renewability and wide availability^3,4. In recent years, solar power generation technology, particularly photovoltaic power generation technology, has progressed rapidly^5,6. However, the safe and cost-effective operation of photovoltaic power plants is intricately linked to the rational design of their infrastructure, particularly the PV racking pile foundation^7,8,9.

As the primary load-bearing element of the photovoltaic power generation system, the PV racking pile foundation not only supports the system’s own weight and external loads, but also constitutes a significant portion of the total construction cost due to the extensive quantity used^10,11. Particularly in desert and gravel geological areas abundant in solar energy resources¹², the prevalent coarse-grained sandy soil with high water permeability and loose texture poses challenges^13,14. The traditional photovoltaic bracket pile foundation, while possessing high compressive strength, is susceptible to uplift forces under wind loading, leading to a host of issues¹⁵. Consequently, numerous scholars have conducted thorough studies on helical piles^16,17, PHC (Prestressed High-strength Concrete) piles^18,19, and drilled pile foundations^19,20 through on-site and model experiments, as well as numerical simulations, proposing various parameter optimization schemes to enhance their bearing capacity. For instance, Ghanbari A et al.²¹ compared the anti-corrosion effects of different PV helical pile corrosion control measures, concluding that the combined use of hot-dip galvanizing layers and sacrificial anode protection effectively mitigates corrosion under highly corrosive conditions. Furthermore, Prabowo et al.²² examined the impact of shear-to-span and axle-to-pressure ratios on the shear bearing capacity of PV PHC piles under seismic conditions. Additionally, Yang et al.²³ established a nonlinear finite element model of PHC piles, revealing that abrupt failure of PHC piles resulted from prestressing reinforcement fracture and that adjusting the number and spatial distribution of prestressing reinforcement could optimize their bearing performance. Moreover, Shalabi et al.²⁴ developed a numerical model for the joint loading of drilled piles and the bearing platforms above them, observing that under pressure loading, the contribution of pile end bearing capacity to total foundation bearing capacity increases with the rise of the length-to-diameter ratio of grouted piles. The typical foundation of commonly used PV mounts is depicted in Fig. 1.

In conclusion, numerous scholars have conducted extensive research on the use of helical piles, PHC piles, and bored pile foundations in PV power plants through field experiments, model experiments, and numerical simulations^25,26. These studies encompass corrosion prevention, construction, bearing capacity, and pile-soil interaction. However, there are limitations in the application of this research in desert gravel areas, such as the susceptibility to corrosion of helical pile foundations, inadequate pullout bearing capacity of PHC pile foundations^27,28, and challenges in controlling the quality of bored pile foundations.

Fig. 1

Schematic diagram of commonly used photovoltaic support piles.

To address these challenges, this paper introduces a new type of PV bracket pile foundation based on the principles of bionics—the precast concrete serpentine pile foundation for PV brackets, referred to as “Serpentine pile” (depicted in Fig. 2). Bionic piles imitate the structure and function of certain living organisms, providing a novel approach to pile foundation design^29,30. Snakes in nature leverage the frictional anisotropy between their transversely arranged abdominal scales and the soil to move flexibly, conferring strong pull-out resistance³¹. Building on this principle, the serpentine piles are designed to exhibit distinct friction characteristics during pile driving and pulling. This paper aims to offer innovative ideas and methods to address the challenges of PV bracket pile foundations in desert gravel areas through the design of this new type of PV bracket pile foundation. This endeavor is not only crucial for enhancing the safe and cost-effective operation of PV power stations, but also has a significant impact on advancing the PV industry in desert gravel geological regions.

Fig. 2

Concept map of snake skin-inspired pile.

Tests and methods

Ttest material

The desert gravel samples analyzed were obtained from a photovoltaic industrial park located in the desert region of Qinghai Province, as shown in Fig. 3.

Fig. 3

Desert sand and gravel soil sample.

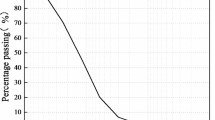
The fundamental physical properties are presented in Table 1. The desert gravel soil samples exhibit C_u ≥ 5, C_c = 1 ~ 3, and their grading curves do not display significant plateau segments, indicating well-graded soils, as shown as Fig. 4.

Table 1 Soil sample uneven coefficient and natural index table.

Fig. 4

Particle size distribution.

The pile material is C40 concrete, and the concrete material parameters are shown in Table 2.

Table 2 C40 concrete material parameters.

Straight-shear test of sand and gravel

The characterization of desert gravel specimens by particle size categorizes them as coarse-grained sand. Given the characteristics of this soil type, the direct shear experiment utilizing such soil necessitates specific dimensions^32,33: The shear box side length should range from 8 to 12 times the maximum particle size, while the total height of the upper and lower shear boxes should be within 4 to 8 times the maximum particle size. Consequently, a large direct shear instrument is required to conduct desert gravel direct shear experiments, henceforth referred to as “large-scale direct shear experiments.”

Two types of shear interface large direct shear experiments were devised using desert gravel soil samples and C40 concrete slabs³⁴. The first involves the shear interface at the contact point between desert gravel, termed as the “sand-sand interface large direct shear experiment,” to measure the angle of internal friction and cohesion of the desert gravel itself. The second type focuses on the shear interface between the desert gravel and C40 concrete slabs, labeled as the “sand-concrete interface large straight shear experiment,” to measure the friction coefficient between the desert gravel and the C40 concrete slab.

Both experiments aim to establish the shear strength parameters of the two interfaces, providing vital data for subsequent numerical simulations and offering reference points for the construction of photovoltaic support piles in the area. The concrete slab placement in the lower shear box is depicted in Fig. 5, following the preparation of soil samples based on natural density. The shear strength versus normal stress fitting curve can be found in the supplementary file.

Fig. 5

Large-straight shear instrument.

Numerical simulation of the pile foundation

The ABAQUS software is widely utilized both domestically and internationally for numerical simulations due to its robust computational capabilities, catering to both linear and nonlinear problem analyses^35,36. The variable cross-section concrete serpentine pile foundation of the PV bracket, as studied in this paper, presents complex contact setups and material structures. As a result, numerical simulation is carried out using ABAQUS software.

Bracket size

The PV bracket’s serpentine pile foundation is composed of three concrete rectangular bodies and two concrete prismatic bodies. The prismatic part, known as the serpentine pile’s variable cross-section, is referred to as the snake-skin body. The specific dimensions of the serpentine pile are illustrated in Fig. 6.

Fig. 6

Three views ( unit: mm).

Modeling assumptions

This paper adheres to the following fundamental assumptions when establishing the numerical model:

• The soil body is considered continuous and homogeneous.

• The PV bracket pile foundation undergoes no damage during the driving process.

• The driving of the PV bracket pile foundation does not impact the physical and mechanical properties of the soil surrounding the pile.

Determination of intrinsic modeling

The Mohr-Coulomb model is chosen as the soil structural model to depict the elastic-plastic characteristics of the soil. The “concrete damage plasticity” model in ABAQUS software is selected to simulate the elastic-plastic characteristics of C40 concrete^37,38,39. Notably, during the numerical simulation, the expansion angle of C40 concrete is set to 30°, the eccentricity is set to 0.1, and the cohesion coefficient is set to 0.01⁴⁰.

Mesh division

The model meshing is depicted in Fig. 7.

Fig. 7

Figure 7 Grid division of model.

Analysis step configuration

The analysis steps consist of geostress and static load steps. The geostress step simulates the initial stress conditions within the model, while the static load step applies external loads. Following the initial step, the geostress step precedes the static load step configurations, ensuring that soil settlement is solely induced by the applied loads after achieving geostress equilibrium.

Contact condition setup

The interface between the pile and soil is defined as a “surface-to-surface contact,” with the stiffer pile surface designated as the master and the soil surface as the slave. A “finite slip” formulation governs the sliding behavior.

Boundary condition specification

The boundary condition type is “displacement/rotation angle”. The bottom of the soil body is constrained from displacements in the x, y, and z directions. The sides of the soil body in the x-direction are restrained from displacements in the x-direction, while those in the y-direction are restrained from displacements in the y-direction.

Load application

The pile top is coupled to a reference point for graded loading. Tensile capacity tests apply z-axis positive loads, incremented by 2kN. Compressive capacity tests apply z-axis negative loads, incremented by 10kN. Horizontal capacity tests apply x-axis positive loads, incremented by 2kN. Stress paths are established on the pile surface using ABAQUS’s path definition feature to extract stress for direct comparisons under various loading conditions (see Fig. 8).

Fig. 8

Individual load applications and stress path extractions.

There are two stress extraction paths for each pile, and the path shown in the figure is chosen because it is prone to stress concentration phenomenon under the action of load, which is the weak part of the pile, so it is chosen to study the pile body stress. Under tension or compression, due to load and model symmetry, stress along path 1 (red lines in Fig. 8) suffices to represent pile stress distribution. For lateral loading, tension and compression sides are distinguished; path 1 represent tension-side stresses, while path 2 (yellow lines) represent compression-side stresses. Soil displacement paths are defined as orange lines in Fig. 8 for studying soil movements around the pile.

Results and discussion

The influence of burial depth on the bearing capacity of serpentine piles

Model construction

The burial depth of the serpentine pile influences the amount of concrete used and its bearing capacity. It is vital to rationally select the burial depth to ensure project quality and control costs. Based on engineering requirements, the exposed height of the serpentine pile is regulated, and only the height of the upper rectangular body is adjusted from the default serpentine pile. serpentine pile models with burial depths of h₂ = 1300 mm, 1400 mm, 1500 mm, 1600 mm, and 1700 mm are created and designated as D-1300, D-1400, D-1500, D-1600, and D-1700, respectively. The default serpentine pile is labeled D-1500. The schematic diagram depicting serpentine piles with different burial depths is presented in Fig. 9.

Fig. 9

Schematic diagram of serpentine piles with different burial depths.

Uplift bearing capacity

Figure 10 demonstrates the ultimate uplift bearing capacity of serpentine piles with varying burial depths and the uplift bearing capacity per unit volume of concrete. It is evident from Fig. 10 that as the burial depth of the serpentine pile increases:

(1)The ultimate tensile bearing capacity of the serpentine pile also increases, reaching a maximum value of 80.33 kN at a burial depth of 1700 mm and a minimum value of 51.51 kN at a burial depth of 1300 mm, both exceeding 30 kN as per engineering requirements. This increase is due to the growing soil pressure on the pile with increasing burial depth, consequently requiring a higher external force for extraction, resulting in an augmented ultimate tensile bearing capacity.

(2)The uplift bearing capacity of concrete per unit volume of the serpentine pile initially increases and then decreases, peaking at 933.29 kN/m³ with a burial depth of 1600 mm and reaching a minimum of 711.46 kN/m³ with a burial depth of 1300 mm.

Fig. 10

Diagram of uplift bearing capacity at different burial depths.

Figure 11 illustrates the displacement of the pile top for various burial depths of serpentine piles as the uplift load ranges from 0 kN to 50 kN, and it also portrays the displacement of the soil surrounding each pile under an uplift load of 50 kN.

Fig. 11

Diagram of displacement of pile top and soil around the pile at different burial depths under uplift load.

In Fig. 11a, it is evident that as the uplift load ranges from 0 to 50 kN, the displacement of the serpentine pile top decreases with an increase in burial depth under equal uplift load conditions.

In Fig. 11b, at an uplift load of 50 kN, the soil surrounding each serpentine pile undergoes upward displacement, particularly within 400 mm of the pile surface. Additionally, as the burial depth increases, the displacement of the soil at the same distance from the pile surface diminishes, while the displacement of the soil around the pile beyond 400 mm from the pile surface shows minimal variation.

To analyze the stress distribution along the pile shaft of serpentine piles with different burial depths under a 50 kN uplift load, the stress on path 1 for serpentine piles with varying burial depths is extracted, and depicted in Fig. 12.

(1)Both tensile and compressive stresses are present, and the stress distribution along the path is generally consistent: in the upper rectangular body, the tensile stress in the upper part remains relatively constant, while the tensile stress at the bottom increases suddenly, then gradually decreases at the junction with the upper snake skin body, transforming into an increasing compressive stress. Subsequently, the compressive stress gradually decreases and transforms into an increasing tensile stress until the middle rectangular body stabilizes, and a similar pattern repeats. In the lower rectangular body, the compressive stress remains around 0 MPa.

(2)The maximum tensile stress along the path increases with burial depth, occurring at the bottom of the upper rectangular solid. At a burial depth of 1700 mm, the maximum value is 1.84 MPa, and at a burial depth of 1300 mm, the minimum value is 1.73 MPa. Conversely, the maximum compressive stress initially decreases and then increases with burial depth, reaching its peak at the upper edge of the lower snake skin body. At a burial depth of 1700 mm, the maximum value is 1.76 MPa, and at a burial depth of 1500 mm, the minimum value is 1.15 MPa.

Fig. 12

Stress distribution diagram of stress path 1 of serpentine pile with different burial depths under 50 kN uplift load.

Compressive bearing performance

The ultimate compressive bearing capacity of serpentine piles with different burial depths and the compressive bearing capacity of concrete per unit volume are presented in Fig. 13. As depicted in Fig. 13, with increasing burial depth of the serpentine pile:

• (1) The ultimate compressive bearing capacity of the serpentine pile exhibits a trend of initial decrease, followed by an increase, and then another decrease, but the change is not substantial. At a depth of 1300 mm, the maximum value is 183.84 kN, and at a depth of 1500 mm, the minimum value is 168.72 kN, both exceeding 36 kN, satisfying the engineering requirements.

• (2) The compressive bearing capacity of concrete per unit volume of the serpentine pile shows a declining trend, reaching a maximum of 2539.23 kN/m3 at a burial depth of 1300 mm and a minimum of 1985.97 kN/m3 at a burial depth of 1700 mm. However, the compressive bearing capacity of concrete per unit volume of the serpentine pile at a burial depth of 1600 mm is slightly higher than that at a burial depth of 1500 mm.

Fig. 13

Limit compressive bearing capacity of serpentine pile with different burial depths and compressive bearing capacity of concrete per unit volume.

Figure 14 illustrates the displacement variation of the pile top of serpentine piles with different burial depths as the pressure load increases from 0 kN to 120 kN, along with the displacement of the soil around each pile under a pressure load of 120 kN.

As shown in Fig. 14a, within the range of 0-120 kN pressure load, the displacement of the top of each serpentine pile decreases with an increase in the burial depth of the pile under equal pressure load, albeit to a relatively small extent.

As shown in Fig. 14b, under a pressure load of 120 kN, the soil around the serpentine pile at varying burial depths all displaces downward. Additionally, as the burial depth increases, the displacement of the soil around the pile at the same distance from the pile surface diminishes.

Fig. 14

Diagram of displacement of the pile top and soil around the pile at different burial depths under pressure load.

To analyze the stress distribution along the pile shaft of the serpentine pile with varying burial depths under a pressure load of 120 kN, the stress on path 1 of the serpentine pile with different burial depths was extracted, and is presented in Fig. 15. As demonstrated in Fig. 15, under the 120 kN pressure load, on stress path 1 of serpentine piles with different burial depths:

• (1) Both tensile and compressive stresses are present and follow a consistent pattern downward along the path. In the upper rectangular body, compressive stress remains stable in the upper and middle parts, sharply increasing at the bottom and then gradually transforming into increasing tensile stress at the junction with the upper snake skin body. The tensile stress peaks at the upper edge of the upper snake skin body, then decreases and turns into increasing compressive stress. The middle rectangular body has stable compressive stress in its upper and middle parts, with a sudden increase at the bottom, followed by a decrease. There is tensile stress at the junction with the lower snake skin body, and a peak appears at the upper edge of the lower snake body. In the lower snake skin body, the tensile stress decreases and transforms into increasing compressive stress, while the compressive stress continues to increase in the lower rectangular body.

• (2) As the burial depth of the serpentine pile increases, the maximum compressive stress on its stress path remains relatively consistent at approximately 4.2 MPa, located at the bottom of the upper rectangular body. The maximum tensile stress initially increases and then decreases, but the difference is not substantial, at approximately 1.1 MPa, and occurs at the upper edge of the upper or lower snake skin body.

Fig. 15

Stress distribution diagram of stress path 1 of serpentine pile with different burial depths under a pressure load of 120 kN.

Influence of width on the bearing capacity of serpentine pile

Model construction

Modifying the default serpentine pile, the width of the upper and lower snake skin bodies was adjusted and maintained equally, resulting in serpentine pile models with upper and lower snake skin body widths of D1 = D2 = 260 mm, 290 mm, 320 mm, 350 mm, and 380 mm. Consequently, the serpentine piles with different snake skin body widths were denoted as W-260, W-290, W-320, W-350, and W-380. The default serpentine pile was labeled W-350. The schematic diagram displaying serpentine piles with different snake skin body widths is illustrated in Fig. 16.

Fig. 16

Schematic diagram of serpentine piles with different snake skin body widths.

Uplift bearing capacity

Figure 17 illustrates the ultimate uplift bearing capacity of serpentine piles with varying snake skin body widths and the uplift bearing capacity of concrete per unit volume.As depicted in Fig. 17, with the simultaneous increase in the width of the upper and lower snake skin bodies:

• (1) The ultimate uplift bearing capacity of the serpentine pile exhibits an increasing trend, with a maximum value of 74.89 kN at a snake skin width of 380 mm and a minimum value of 63.69 kN at a snake skin width of 260 mm, both exceeding 30 kN and meeting engineering requirements. This is attributed to the reinforced embedding effect of the serpentine pile in the surrounding soil when the snake skin width increases, resulting in a heightened ultimate uplift bearing capacity.

• (2) The uplift bearing capacity of concrete per unit volume of the serpentine pile initially rises, then declines, and rises again, with the difference not being substantial. At a snake skin body width of 290 mm, the maximum value is 890.64 kN/m³, while at a width of 350 mm, the minimum value is 829.62 kN/m³.

Fig. 17

Diagram of the ultimate uplift bearing capacity of serpentine piles with different snake skin body widths and the uplift bearing capacity of concrete per unit volume.

Figure 18 displays the displacement variation of the pile top for various serpentine pile widths as the uplift load increases from 0 kN to 50 kN, as well as the displacement of the surrounding soil at an uplift load of 50 kN.

In Fig. 18a, it is observed that within the 0–50 kN uplift load range, the displacement of the serpentine pile top decreases as the width of the snake skin increases under equal uplift load conditions.

From Fig. 18b, it is evident that at an uplift load of 50 kN, the soil surrounding serpentine piles of different widths undergoes upward displacement. Within the range of 0–300 mm from the pile surface, the displacement of the soil at the same distance decreases with the increase in snake skin width, while the displacement of the soil around each serpentine pile remains largely consistent beyond 300 mm from the pile surface.

Fig. 18

Diagram of displacement of pile top and soil around the pile with different snake skin body widths under uplift load.

To investigate the stress distribution along the pile shaft of serpentine piles with varying widths under a 50 kN uplift load, the stress on each serpentine pile path 1 was analyzed, and the stress distribution diagram for each serpentine pile’s stress path 1 is presented in Fig. 19.

Fig. 19

Stress distribution diagram of stress path 1 of serpentine pile with different snake skin width under 50 kN uplift load.

As per Fig. 19, under the 50 kN uplift load, the stress path 1 of serpentine piles with different widths:

• (1) Exhibits both compressive and tensile stresses, and the stress distribution pattern along the path is consistent downward.

• (2) The maximum tensile stress on the stress path remains about 1.80 MPa, located at the bottom of the upper rectangular solid. Conversely, the maximum compressive stress of serpentine piles decreases with increasing width, occurring at the upper edge of the lower snake skin body. Specifically, at a snake skin width of 260 mm, the maximum value is 1.97 MPa, while at 380 mm, the minimum value is 1.15 MPa.

Compressive bearing performance

The ultimate compressive bearing capacity of serpentine piles with varying widths and the compressive bearing capacity per unit volume of concrete are depicted in Fig. 20.

Fig. 20

Limit compressive bearing capacity of serpentine piles with different snake skin body widths and compressive bearing capacity of concrete per unit volume.

As illustrated in Fig. 20, with an increase in the width of the snake skin body:

(1) The ultimate compressive bearing capacity of the serpentine pile diminishes accordingly. At a width of 260 mm, it attains a peak value of 320 kN, while at a width of 380 mm, it descends to a minimum of 139.14 kN, both exceeding 36 kN and meeting engineering requirements. This decrease is attributed to the generation of tensile stress at the upper edge of the snake skin body due to bending moments under pressure loads. As the width of the snake skin body widens, the bending moment escalates, leading to increased tensile stress, rendering the concrete more susceptible to tensile failure, ultimately resulting in the failure of the serpentine pile. Consequently, the ultimate compressive bearing capacity of the serpentine pile decreases with an increase in the width of the snake skin body.

(2) The compressive bearing capacity of concrete per unit volume of the serpentine pile decreases, peaking at 4407.71 kN/m³ when the width of the snake skin body is 260 mm and declining to a minimum of 1556.38 kN/m³ when the width is 380 mm.

Figure 21 portrays the displacement variation of the pile top for different serpentine pile widths as the pressure load increases from 0 kN to 120 kN, and presents the displacement of the surrounding soil at a pressure load of 120 kN.

According to Fig. 21(a), within the 0-120 kN pressure load range, the displacement of the serpentine pile top decreases as the width of the snake skin increases, while the pressure load remains constant.

According to Fig. 21(b), at a pressure load of 120 kN, the soil around the serpentine pile with varying widths displaces downward. As the width of the snake skin increases, the displacement of the soil at the same distance from the pile surface also increases.

Fig. 21

Diagram of displacement of pile top and soil around the pile of different serpentine pile widths under pressure load.

To study the stress distribution along the pile shaft of serpentine piles with different widths under a 120 kN pressure load, the stress on each serpentine pile path 1 was analyzed, and the stress distribution diagram is presented in Fig. 22.

As shown in Fig. 22, under the 120 kN pressure load, the stress paths on the stress path 1 of the serpentine pile with varying widths are as follows:

• Both tensile and compressive stresses are present, and the stress distribution pattern downward along the path is consistent.

• The maximum tensile stress occurs at the upper edge of the lower snake skin body. As the width of the snake skin body increases, the maximum tensile stress initially rises and then falls. At a width of 350 mm, the maximum value is 1.53 MPa, while at 260 mm, the minimum value is 0.98 MPa. The maximum compressive stress occurs at the bottom of the upper rectangular body, and its magnitude increases with the width of the snake skin body. At a width of 380 mm, the maximum value is 4.19 MPa, and at 260 mm, the minimum value is 3.90 MPa.

Fig. 22

Stress distribution diagram of stress path 1 of serpentine pile with different snake skin width under 120 kN pressure load.

Influence of spacing on the bearing performance of serpentine pile

Model construction

To investigate the impact of the spacing between snake skin bodies on the bearing performance of serpentine piles, this study maintains the position of the lower snake skin body, while adjusting the distance between the upper and lower snake skin bodies by vertically moving the upper snake skin body along the direction of the pile body. This results in the creation of serpentine pile models with upper and lower snake skin body spacing l₂ = 250 mm, 300 mm, 350 mm, 400 mm, and 450 mm, labeled as P-250, P-300, P-350, P-400, and P-450, respectively. The default serpentine pile is designated as P-350, and the schematic diagram of serpentine piles with different snake skin body spacing is presented in Fig. 23. Notably, the volume of each serpentine pile remains constant, ensuring uniform concrete usage and consequently identical variations in the ultimate bearing capacity of the serpentine pile and the bearing capacity of concrete per unit volume.

Fig. 23

serpentine pile with different snake skin body spacing.

Uplift bearing capacity

Figure 24 illustrates the ultimate uplift bearing capacity of serpentine piles with varying snake skin body spacing, as well as the uplift bearing capacity of concrete per unit volume.

Fig. 24

The ultimate uplift bearing capacity of serpentine piles with different snake skin body spacings and the uplift bearing capacity per unit volume of concrete.

As shown in Fig. 24, as the spacing between snake skin bodies increases, the following observations can be made for serpentine piles with different spacings:

(1) The ultimate tensile bearing capacity of the serpentine pile rises, reaching a peak of 74.89 kN when the snake skin body spacing is 450 mm and a minimum of 68 kN when the spacing is 250 mm, both surpassing 30 kN and meeting engineering requirements. This increase is attributed to the effect of the snake skin body spacing on the lateral friction, where the decrease in lateral friction provided by the upper rectangular body is outweighed by the increase in lateral friction provided by the middle rectangular body, leading to an enhancement in the ultimate tensile bearing capacity of the serpentine pile.

(2) Moreover, the serpentine pile experiences an increase in its unit volume concrete tensile bearing capacity, attaining a peak of 931.47 kN/m³ at a snake skin spacing of 450 mm, and a low of 845.77 kN/m³ at a spacing of 250 mm.

Figure 25 presents the displacement variation of the pile top for serpentine piles with different snake skin body spacing as the uplift load increases from 0 kN to 50 kN, along with the displacement of the soil around each pile at an uplift load of 50 kN.

In Fig. 25a, it is evident that as the uplift load increases from 0 kN to 50 kN, the displacement of the pile top increases with the augmentation of the snake skin body spacing for varying spacings under equal uplift load conditions.

In Fig. 25b, at an uplift load of 50 kN, the soil surrounding the pile undergoes upward displacement for various serpentine pile spacings. As the spacing increases, the upward displacement of the soil around the pile intensifies within the 0–400 mm range from the pile surface, with the upward displacement at the same distance from the pile surface being essentially equal within the 300 mm range from the pile surface.

Fig. 25

Diagram of displacement of pile top and soil around the pile of different serpentine pile spacing under uplift load.

To investigate the stress distribution along the pile shaft of serpentine piles with varying snake skin body spacing under a 50 kN uplift load, the stress on each serpentine pile path 1 was analyzed, and the stress distribution diagram is presented in Fig. 26.

According to Fig. 26, under the 50 kN uplift load, the stress path 1 for the serpentine pile with different body spacing reveals:

(1) Both compressive and tensile stresses are uniformly distributed, and the stress distribution pattern along the path downward remains consistent.

(2) The maximum tensile stress on the path occurs at the bottom of the upper rectangular body. As the spacing between the snake skin bodies increases, the maximum tensile stress decreases, reaching a peak of 1.83 MPa at a spacing of 250 mm and a minimum of 1.79 MPa at a spacing of 450 mm. The maximum compressive stress on the path occurs at the upper or lower edge of the upper snake skin body and remains approximately 1.40 MPa as the spacing between the bodies increases.

Fig. 26

Stress distribution on stress path 1 of serpentine pile with different snake skin body spacing under 50 kN uplift load.

Compressive bearing performance

The ultimate compressive bearing capacity of serpentine piles with varying snake skin body spacing and the compressive bearing capacity of concrete per unit volume are presented in Fig. 27. According to the figure, for serpentine piles with different snake skin body spacing:

• (1) The ultimate compressive bearing capacity of the serpentine pile exhibits an increasing trend, with a peak value of 198.05 kN at a snake skin body spacing of 450 mm and a minimum of 148.65 kN at a spacing of 250 mm. This trend is attributed to the increase in lateral friction provided by the middle rectangular body that exceeds the decrease in lateral friction produced by the upper rectangular body when the serpentine pile is subjected to compression, leading to an augmentation in the ultimate compressive bearing capacity of the snake skin body.

• (2) Furthermore, the compressive bearing capacity of concrete per unit volume of the serpentine pile also rises, reaching a maximum value of 2463.31 kN/m³ at a snake skin spacing of 450 mm and a minimum value of 1848.88 kN/m³ at a spacing of 250 mm.

Fig. 27

The ultimate compressive bearing capacity of serpentine piles with different snake skin body spacing and the compressive bearing capacity of concrete per unit volume.

Figure 28 illustrates the displacement variation of the pile top for serpentine piles with different snake skin body spacing as the pressure load increases from 0 kN to 120 kN, and also displays the displacement of the soil around each pile at a pressure load of 120 kN.

Fig. 28

Diagram of the displacement of the pile top and the displacement of the soil around the pile of different serpentine pile spacing under pressure load.

In Fig. 28a, it is evident that for serpentine piles with various snake skin body spacings, the displacement of the pile top decreases with increasing snake skin body spacing under equal pressure loads, although the reduction is marginal, when the pressure load increases from 0 kN to 120 kN.

In Fig. 28b, at a pressure load of 120 kN, the soil surrounding the pile with different snake skin body spacing experiences downward displacement, and this downward displacement increases with the augmentation of snake skin body spacing at the same distance from the pile surface.

To investigate the stress distribution along the pile shaft of serpentine piles with varying spacing under a pressure load of 120 kN, the stress on each serpentine pile path 1 was examined, and the stress distribution diagram is depicted in Fig. 29.

As depicted in Fig. 29, under a pressure load of 120 kN, the stress path 1 for different serpentine pile spacing reveals:

• (1) Both tensile and compressive stresses are present, and the stress distribution along the path downward is consistent.

• (2) The maximum tensile stress on the stress path of each pile occurs at the upper edge of the lower snake skin body, with a magnitude around 1.55 MPa, and the maximum compressive stress on the stress path of each pile occurs at the bottom of the upper rectangular body, with a magnitude around 4.15 MPa.

Fig. 29

Stress distribution diagram of stress path 1 of serpentine pile with different snake skin body spacing under a pressure load of 120 kN.

Multivariate linear regression analysis of factors affecting the bearing capacity of serpentine piles

Analytical method

A multiple linear regression analysis model was constructed using SPSS 20.0 software⁴¹. In this model, the burial depth, width, and spacing of serpentine piles serve as independent variables, while the ultimate bearing capacity of serpentine piles and the bearing capacity per unit volume of concrete act as dependent variables. It is considered that when P < 0.05, the independent variables exert a significant impact on the dependent variables. Additionally, the absolute value of the standardized regression coefficient is utilized to gauge the degree of influence of each independent variable on the dependent variable. A larger absolute value signifies a greater impact of the independent variable on the dependent variable. Moreover, a positive regression coefficient denotes a positive correlation, whereas a negative coefficient indicates a negative correlation⁴².

Multivariate linear regression analysis of factors affecting uplift bearing capacity

The table presenting the results of the multiple linear regression analysis concerning the factors influencing the ultimate tensile bearing capacity of serpentine piles is displayed in Table 3.

Table 3 Multi-linear regression analysis of factors affecting the ultimate tensile bearing capacity of serpentine piles.

According to Table 3, the impact of each variable on the ultimate uplift bearing capacity of serpentine piles can be summarized as follows:

• (1) The P-values for the three independent variables—burial depth, width, and spacing—are all below 0.05, signifying their significant influence on the ultimate uplift bearing capacity of the serpentine pile.

• (2) The adjusted R² of the linear regression model is 0.898, indicating that the burial depth, width, and spacing can collectively account for 89.8% of the variation in the ultimate uplift bearing capacity of the serpentine pile.

• (3) Based on the absolute value of the standardized regression coefficient, the influence of independent variables on the ultimate uplift bearing capacity of serpentine piles can be ranked in descending order as follows: burial depth > width > spacing.

In conclusion, the optimal approach to enhance the ultimate uplift bearing capacity of serpentine piles involves appropriately increasing the burial depth, followed by adjusting the width or spacing of the snake skin body.

Furthermore, the multiple linear regression analysis table regarding the influencing factors of the tensile bearing capacity of concrete per unit volume of serpentine piles is presented in Table 4.

Table 4 Multiple linear regression analysis of factors affecting the uplift bearing capacity of concrete per unit volume for serpentine piles.

• (1) The P-values for both burial depth and spacing as independent variables are below 0.05, indicating their significant impact on the uplift bearing capacity per unit volume of concrete in serpentine piles. However, the P-value of width exceeds 0.05, suggesting that its effect on the uplift bearing capacity per unit volume of concrete for serpentine piles is not significant, although there is still a certain correlation between them, which holds some reference significance.

• (2) The adjusted R² of the model is 0.776, indicating that the burial depth, width, and spacing collectively account for 77.6% of the variation in the uplift bearing capacity per unit volume of concrete for serpentine piles.

• (3) Based on the absolute value of the standardized regression coefficient, the influence of independent variables on the uplift bearing capacity of concrete per unit volume of serpentine piles can be arranged in descending order of importance as follows: burial depth, spacing, and width.

In conclusion, the most effective approach to enhance the uplift bearing capacity per unit volume of concrete in serpentine piles is to appropriately increase the burial depth of the serpentine piles.

Multivariate linear regression analysis of factors affecting the compressive bearing capacity of serpentine piles

The multiple linear regression analysis table of the influencing factors of the ultimate compressive bearing capacity of serpentine piles is shown in Table 5.

Table 5 Multivariate linear regression analysis of factors affecting the ultimate compressive bearing capacity of serpentine piles.

• (1) The P-value for width is below 0.05, signifying its significant impact on the ultimate compressive bearing capacity of the serpentine pile.

• (2) Contrastingly, the P-values for both the burial depth and spacing independent variables exceed 0.05, indicating that their effects on the ultimate compressive bearing capacity of serpentine piles are not significant. However, there is still a certain correlation between them, which holds certain reference value.

• (3) The adjusted R² of the linear regression model is 0.715, suggesting that the burial depth, width, and spacing collectively account for 71.5% of the variation in the ultimate compressive bearing capacity of serpentine piles.

• (4) The influence of independent variables on the ultimate compressive bearing capacity of serpentine piles can be determined by the absolute value of the standardized regression coefficients, ranked from highest to lowest as follows: width, spacing, and burial depth.

In summary, the optimal method to improve the ultimate compressive bearing capacity of serpentine piles is to appropriately reduce the width of the snake skin body.

Furthermore, the multiple linear regression analysis table detailing the influencing factors of the compressive bearing capacity of concrete per unit volume of serpentine pile is provided in Table 6.

Table 6 Multivariate linear regression analysis of factors affecting the compressive bearing capacity of concrete per unit volume for serpentine piles.

• (1) A P-value below 0.05 for width signifies a significant impact on the compressive bearing capacity per unit volume of concrete for serpentine piles.

• (2) Conversely, the P-values for the three independent variables—burial depth and spacing—exceed 0.05, indicating that their impact on the compressive bearing capacity per unit volume of concrete for serpentine piles is not significant. Nevertheless, there is still a certain correlation between them, which holds some reference value.

• (3) The adjusted R² is 0.755, suggesting that the depth, width, and spacing collectively account for 75.5% of the variation in compressive bearing capacity per unit volume of concrete in serpentine piles.

• (4) The influence of independent variables on the compressive bearing capacity per unit volume of concrete for serpentine piles can be assessed based on the absolute value of the standardized regression coefficient, ranking from high to low as follows: width, spacing, and burial depth.

In conclusion, the preferred method to improve the compressive bearing capacity per unit volume of concrete for serpentine piles is to appropriately reduce the width of the snake skin body.

Conclusion

A numerical model was established using ABAQUS software, and the control variable method was used to study the effects of three variables: the depth of the serpentine pile, the width of the snake skin body, and the spacing between the snake skin bodies on the uplift, compression, and horizontal bearing performance of the serpentine pile. A multiple linear regression analysis was conducted using SPSS software to quantify the influence of each factor on the ultimate bearing capacity and unit volume concrete bearing capacity of the serpentine pile. The main conclusions are as follows:

• (1) The ultimate uplift bearing capacity ranged from 51.51 kN to 80.33 kN, with a maximum value achieved at a burial depth of 1700 mm. The uplift bearing capacity per unit volume of concrete peaked at 933.29 kN/m³ at a burial depth of 1600 mm.The multiple linear regression analysis indicated that burial depth had the strongest impact on the ultimate uplift bearing capacity, followed by width and spacing.

• (2) The ultimate compressive bearing capacity ranged from 139.14 kN to 198.05 kN, with the minimum value observed at a snake skin body width of 380 mm. The compressive bearing capacity per unit volume of concrete decreased from 4407.71 kN/m³ to 1556.38 kN/m³ as the snake skin body width increased. The regression analysis revealed that the width of the snake skin body had the most significant effect on the ultimate compressive bearing capacity, while burial depth and spacing had less impact.

• (3) As the burial depth increased, the displacement of the pile top decreased under both uplift and compression loads. The maximum tensile stress along the pile shaft generally increased with burial depth, while the maximum compressive stress showed more complex variations. Increasing the spacing between snake skin bodies led to higher ultimate tensile and compressive bearing capacities, but with increased displacement of the pile top and surrounding soil under uplift loads.

• (4) To enhance the uplift bearing capacity per unit volume of concrete, the burial depth should be appropriately increased. To improve the ultimate compressive bearing capacity and the compressive bearing capacity per unit volume of concrete, the width of the snake skin body should be reduced. Adjusting the spacing between snake skin bodies can also affect the bearing performance, but the optimal spacing depends on the specific loading conditions.