Study on longitudinal nonlinear deformation of adjacent existing tunnels induced by deep foundation excavation

Abstract

The simplified calculation methods for predicting the longitudinal deformation of neighboring existing tunnels caused by deep foundation excavation in engineering practice all use linear foundation model to interact with tunnel structure, and less use of nonlinear foundation model of soil body. The nonlinear Pasternak foundation model is combined with Mindlin solution to obtain the differential equations of longitudinal deformation of the tunnel, and the improved Hermite difference method and Newton iterative method are used to solve the numerical solution of the longitudinal nonlinear deformation of the neighboring tunnels induced by the excavation of the deep foundation pit. The rationality and applicability of the improved Hermite difference method for solving the nonlinear foundation model are verified by analyzing and comparing with the measured data. The calculation results of the engineering case show that the computational comparative analysis was carried out using the nonlinear Pasternak foundation model, the traditional Pasternak foundation model, the finite element model and the measured deformation data. The longitudinal deformation trends of the tunnels solved by several methods are consistent with the measured values, but the nonlinear Pasternak foundation model is closer to the measured values. The maximum bending moments of the left and right lane of the shield tunnel obtained by the nonlinear Pasternak foundation model are directly below the foundation pit; the maximum shear force values all appear at the corresponding shield tunnel position below the sidewall of the foundation pit. The research results can provide a simplified and convenient calculation method for the prediction of longitudinal deformation of the neighboring existing tunnels during the excavation and construction of the foundation pit, and guide the construction of similar projects.

Introduction

At the present time, cities with metro lines are exploring the urban public transportation-oriented development mode, i.e. TOD mode. As a result, the number of pits excavated around the metro lines is increasing, and the metro tunnels in soft soil areas such as Shanghai, Nanjing, Hangzhou, Suzhou and other cities are mainly constructed by the shield method, and the unloading of pits will cause a series of diseases such as large longitudinal uneven deformation of the neighboring metro tunnels, cracking of tube sheets, misalignments, and seepage, which will lead to a series of other disasters. Ningbo Metro Line 1, a subway interval shield tunnel by the immediate vicinity of a large area of pit construction impact, in the left tunnel near the excavation point of the part of the excavation point due to the nearby excavation and generated a considerable displacement, the left tunnel lining appeared obvious cracks and leakage.

Therefore, a reasonable safety assessment of the impact of the adjacent existing shield tunnel is required during the pit excavation construction. For the research topic of the impact of pit excavation on adjacent existing tunnels, scholars at home and abroad have carried out a large number of studies, including model tests, numerical analysis, on-site monitoring analysis and theoretical analysis methods.In terms of theoretical analysis methods, Zhang et al.^1,2,3,4 used a two-stage analysis method to calculate the longitudinal deformation of the existing tunnels in the surrounding area caused by deep foundation excavation in soft soil areas. It assumed the tunnel as an Euler-Bernoull beam model on the Winkler foundation model, but at this time, the unloading of the sidewalls of the foundation pit was not considered. Later, the longitudinal displacement of the tunnel was solved by analyzing the effect of joint unloading of the pit bottom and the sidewalls of the foundation pit, and the results obtained had the same trend with the measured values, but the results differed greatly from the actual situation because the supporting structure was not considered in the model. Jiang et al.⁵ and Wei et al.⁶ proposed a static soil pressure strength reduction factor to consider the “blocking effect” of the pit support structure, which was used as the basis for calculating the additional loads of the existing tunnel around the pit excavation. Kang et al.⁷ used the nonlinear Pasternak elastic foundation model to show that, when the longitudinal uplift of the shield tunnel caused by pit excavation is small, the simplified calculation method based on the Winkler and Pasternak elastic foundation model and the proposed method can predict the longitudinal uplift displacement of the tunnel better; whereas, when the longitudinal uplift displacement of the shield tunnel caused by pit excavation is large, the simplified calculation method based on the Winkler and Pasternak elastic foundation model can predict the longitudinal uplift displacement of the tunnel better. Winkler and Pasternak elastic foundation model, the simplified calculation method significantly underestimates the amount of shield tunnel rumble. In terms of model experiments, Huang et al.⁸ found through centrifugal model experiments that the longitudinal deformation of tunnels decreases exponentially with the excavation displacement of the foundation pit. Hu⁹ found through constant gravity model experiments that the convergence deformation of the tunnel section is in the shape of a “horizontal duck egg”. Liang et al.¹⁰ conducted a centrifugal model test on the longitudinal deformation of tunnels caused by excavation of foundation pits. The method of block control was used for excavation of foundation pits, and the model test results showed that the excavation scheme of “first large, then small” can effectively reduce the deformation of foundation pit support structures and tunnels.In terms of numerical simulation methods, Ma et al.¹¹ used the finite element method to dynamically simulate the excavation process of the foundation pit, and found that the best measure to control the deformation of the tunnel is to reduce the excavation depth, and precipitation outside the pit is carried out. Zhang et al. ¹² used finite element simulation to study the effectiveness of pit zoned excavation on the protection of neighboring trans-river tunnels, and found that the zoned excavation construction is more effective in protecting tunnels that are closer together. Renpeng et al.^13,14 suggested focusing on the protection of the center of the foundation pit corresponding to the location of the tunnel, and adopting a block excavation method to control the deformation of the tunnel. In terms of on-site monitoring and analysis methods, Tan et al.¹⁵ examined the deformation response of adjacent subway stations and shield tunnels caused by deep foundation pit excavation in a hard clay deposit. Due to the zoned construction method, the envelope deformation and ground settlement of this mega pit were insignificant and even smaller than that of the narrow subway station pit. In terms of on-site monitoring analysis methods, Gang¹⁶ statistically analyzed the measured data of multiple actual foundation pit projects, and summarized an empirical formula that can be used to predict the maximum longitudinal deformation of tunnels. Uplift deformation is a common form of maximum longitudinal deformation in tunnels. In the foundation pit engineering studied, not all tunnels have a maximum uplift within the allowable range of 10 mm, and over 60% of tunnels have deformation exceeding the allowable value. The convergence deformation of tunnels is not constant, first it is “horizontal tension, vertical compression”, and then “horizontal compression, vertical tension”. Guo et al.¹⁷ studied 39 relevant cases and provided a simplified model for predicting the maximum longitudinal deformation of tunnels. This model focuses on studying the influence of engineering geology and finds that the uplift deformation of tunnels cannot be well controlled when the engineering geological conditions are poor. Liu et al.¹⁸ conducted a 4-year on-site comprehensive monitoring of the large basement excavation construction next to the subway tunnels in the pulverized clay area of Nanjing, including lateral deflection of diaphragm walls, settlement of the tunnel roof, horizontal displacement of the starting arch line, and the tensile angle and misalignment of the tube sheet joints. The evolution of tunnel roof settlement, horizontal displacement of the starting arch line and diameter convergence can be divided into slow-growth, fast-growth and stable-growth stages, which correspond to the three stages before, during and after deep foundation pit excavation, respectively. During the process of perturbation grouting treatment, the tunnel deformation went through the correction stage and rebound stage, respectively, and the perturbation grouting well ameliorated the additional deformation of the tunnel caused by the excavation of the neighboring foundation pit.

In summary, most of the current methods for studying the deformation of the adjacent existing shield tunnel during the excavation of the foundation pit adopt a two-stage calculation method, i.e., firstly, assuming that the tunnel does not exist, the Mindlin solution is used to find out the unloading surcharge load generated by the excavation of the foundation pit at the location of the tunnel. Secondly, the tunnel is simplified as an infinite-length elastic foundation beam, and the unloading surcharge is applied to the foundation beam, and the longitudinal deformation response of the foundation beam is obtained according to the equilibrium relationship between the foundation and the foundation beam. In the two-stage method, the foundation model adopts Winkler or Pasternak model to consider the coupling effect between the beam and foundation, and the nonlinearity of the foundation model is not considered, which can not respond to the nonlinear deformation characteristics of the soil body. However, in the U.S. “Seismic Design Guidelines for Oil and Gas Pipeline Systems”, it is pointed out that it is appropriate to use nonlinear foundation models to evaluate the force and deformation characteristics of pipelines in the analysis of pipe-soil interaction. Therefore, on the basis of the existing research, it is necessary to consider the nonlinear deformation of the foundation soil and reasonably calculate the longitudinal deformation of the adjacent existing shield tunnel caused by deep foundation pit excavation.

In this paper, the nonlinear Pasternak foundation model is used to simulate the nonlinear deformation of foundation soil, and the improved Hermite difference method and Newton iterative method are used to solve the longitudinal nonlinear deformation of the neighboring existing tunnels according to the longitudinal deformation differential equations of the neighboring shield tunnels during the excavation and construction of the deep foundation pit. The rationality and applicability of the nonlinear foundation model are verified by comparing with the measured data. The research results can provide a simplified and convenient calculation method for the prediction of longitudinal deformation of the neighboring existing tunnels during the excavation of the foundation pit, which can guide the construction of similar projects.

Foundation model

Traditional Pasternak foundation model

The Pasternak foundation model considers the action between the shear layer and the spring and adds a shear term to the Winkler foundation model. It is expressed as:

$$q(x) = kw(x) - G_{c} \frac{{\partial^{2} w(x)}}{{\partial x^{2} }}$$

(1)

where $G_{{\text{c}}}$ is the shear stiffness of the shear layer; $k$ is the foundation bed coefficient.

The shear stiffness of the shear layer is determined using the empirical Eq. (2) proposed by Tanahashi¹⁹:

$$G_{c} = \frac{{E_{s} h_{t} }}{{6(1 + v_{s} )}}$$

(2)

where $E_{{\text{s}}}$ is the modulus of elasticity of the soil; $v_{s}$ is the Poisson’s ratioof the soil layer; $h_{t}$ is the depth of the elastic layer, Liang et al.²⁰ used $h_{t} = 2.5D$.

The foundation bed coefficient $k$ was adopted from Eq. (3) proposed by Attewell²¹ and others:

$$k = 1.3\left( {\frac{{E_{{\text{s}}} D^{4} }}{EI}} \right)^{\frac{1}{12}} \cdot \frac{{E_{{\text{s}}} }}{{D\left( {1 - v_{{\text{s}}}^{2} } \right)}}$$

(3)

where $E_{{\text{s}}}$ is the modulus of elasticity of the soil; $EI$ is the bending stiffness of the beam in this paper, $EI$ is taken as the equivalent bending stiffness of the tunnel; $D$ is the width of the beam or for the outer diameter of the tunnel; $v_{s}$ is the Poisson’s ratio of the soil where the beam is located in the soil layer.

Nonlinear Pasternak foundation model

The deformation of the soil body in general is characterized by nonlinearity, thus Liang²² proposed a new nonlinear foundation model: the nonlinear Pasternak foundation model, as shown in Fig. 1. The nonlinear Pasternak foundation model is to replace the linear spring of the traditional Pasternak foundation model with a nonlinear spring as follows:

$$q(x) = \frac{w(x)}{{\frac{0.3}{{k_{u} }} + \frac{w(x)}{{q_{u} }}}} - G_{c} \frac{{\partial^{2} w(x)}}{{\partial x^{2} }}$$

(4)

where for clay soils, $q_{{\text{u}}} = S_{{\text{u}}} N_{{{\text{cv}}}}$, $q_{u}$ is the foundation reaction force limit value, $S_{{\text{u}}}$ is the undrained shear strength of the soil; $N_{{{\text{cv}}}}$ is the soil vertical uplift coefficient. $k_{{\text{u}}} = q_{{\text{u}}} /\delta_{{\text{u}}}$, where $\delta_{{\text{u}}}$ is the displacement required to reach the ultimate contact pressure, which $\delta_{{\text{u}}}$ is generally taken as 0.01 to 0.02 times the embedment depth $z_{0}$ in clayey soils, and $\delta_{{\text{u}}} = 0.015z_{0}$ is taken in this paper. The calculation method of $N_{{{\text{cv}}}}$ is described in the literature²³.

Fig. 1

Nonlinear Pasternak foundation model.

The relationship between the foundation reaction force and displacement for the nonlinear Pasternak foundation model is shown in Fig. 2.The foundation reaction force has a hyperbolic relationship with displacement, and when the tunnel displacement exceeds the displacement $\delta_{{\text{u}}}$ required to reach the ultimate contact pressure, the foundation reaction force $q$ reaches its limit value $q_{{\text{u}}}$ and does not continue to grow. The nonlinear Pasternak foundation model can both consider the continuous action of soil and it can also reflect the nonlinearity of the soil.

Fig. 2

Foundation reaction force versus displacement.

Theory of longitudinal deformation in tunnels

Additional stresses at the adjacent existing tunnel due to pit excavation

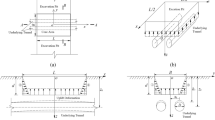
Figure 3 shows that the relative position between foundation pit and tunnel. During the construction of a deep foundation pit excavation, the additional loads generated at the bottom and side walls of the pit produce additional stresses on the surrounding soil. Different vertical soil layers are assumed to be uniform soil layers. The additional stresses at each location of the tunnel can be obtained from Mindlin’s basic stress solution²⁴.

Fig. 3

Schematic diagram of relative position between foundation pit and tunnel.

Calculation assumption: (1) Assuming the soil is a nonlinear Pasternak foundation model; (2) Assuming that the adjacent tunnel is an infinitely long Euler Bernoulli beam placed on a nonlinear Pasternak foundation model; (3) Assuming that the tunnel and surrounding soil deform together, without considering the relative displacement between the tunnel and the foundation; (4) Neglecting the temporal and spatial effects of excavation of foundation pits, and ignoring the impact of foundation pit dewatering; (5) After the excavation of the foundation pit is completed, assuming a vertically uniformly distributed load is applied on the bottom plane of the pit, simulate the unloading effect after excavation of the foundation pit; (6) After excavation of the foundation pit, it is assumed that the surrounding side walls are subjected to a triangular horizontal distributed load; (7) Calculate the additional stress of soil and ignore the influence of tunnels; (8)The influence of lateral friction resistance of the support structure on the longitudinal deformation of the tunnel was not considered.

• (1) The vertical additional stress $\sigma_{z}^{{\text{v}}}$ at the $M(x_{0} ,y_{0} ,z_{0} )$ point resulting from the vertical load from the unloading at the bottom of the pit can be solved by applying Mindlin’s basic stress solution²⁴ from Eq. (5).

  $$\begin{aligned} \sigma_{z}^{v} = & \frac{ - \gamma d}{{8\pi (1 - v_{s} )}}\iint\limits_{{\Gamma_{0} }} {\left[ {\frac{{(1 - 2v_{s} )(z_{0} - d)}}{{R_{1}^{3} }} + \frac{{3(z_{0} - d)^{3} }}{{R_{1}^{5} }} - \frac{{(1 - 2v_{s} )(z_{0} - d)}}{{R_{2}^{3} }}} \right.} \\ & \;\left. { + \frac{{3(3 - 4v_{s} )z_{0} (z_{0} + d)^{2} }}{{R_{2}^{5} }} - \frac{{3d(z_{0} + d)(5z_{0} - d)}}{{R_{2}^{5} }} - \frac{{30dz_{0} (z_{0} + d)^{3} }}{{R_{2}^{7} }}} \right]dxdy \\ \end{aligned}$$

  (5)

  where

  $$R_{1}^{2} = (x_{0} - x)^{2} + (y_{0} - y)^{2} + (z_{0} - d)^{2} ;\;R_{2}^{2} = (x_{0} - x)^{2} + (y_{0} - y)^{2} + (z_{0} + d)^{2}$$

  (6)

  $\gamma$ is the soil gravity; $v_{s}$ is the Poisson’s ratio of the soil; and $\Gamma_{0}$ is the area of the pit floor with a range of coordinates: $0 \le x \le L$, $0 \le y \le B$.

• (2) The vertical additional stress at the $M(x_{0} ,y_{0} ,z_{0} )$ point from the horizontal load generated by the unloading of the sidewalls of the pit can be solved by applying Mindlin’s basic stress solution²⁴ from Eq. (7).

  $$\begin{aligned} \sigma_{z}^{{h_{1} }} = & \frac{{K_{0} \gamma y_{0} }}{{8\pi (1 - \nu_{s} )}}\iint\limits_{{\Gamma_{1} }} {z\left\{ { - \frac{{1 - 2\nu_{s} }}{{T_{1}^{3} }} + \frac{{3(z_{0} - z)^{2} }}{{T_{1}^{5} }} + \frac{{1 - 2\nu_{s} }}{{T_{2}^{3} }} + \frac{{3(3 - 4\nu_{s} )(z_{0} + z)^{2} }}{{T_{2}^{5} }}} \right.} \\ & \left. {\; - \frac{6z}{{T_{2}^{5} }}\left[ {z + (1 - 2\nu_{s} )(z_{0} + z) + \frac{{5z_{0} (z_{0} + z)^{2} }}{{T_{2}^{2} }}} \right]} \right\}dxdy \\ \end{aligned}$$

  (7)

  where $T_{1}^{2} = (x_{0} - x)^{2} + y_{0}^{2} + (z_{0} - z)^{2} ;\;T_{2}^{2} = (x_{0} - x)^{2} + y_{0}^{2} + (z_{0} + z)^{2}$.

  $\gamma$ is the soil gravity; $v_{s}$ is the Poisson’s ratio of the soil; ${\Gamma }_{{1}}$ is the side wall of the pit (1), and its coordinate range is: $0 \le x \le L$, $0 \le z \le d$; $K_{0}$ is the static soil pressure coefficient.

Similarly, we can solve for the vertical additional stresses $\sigma_{z}^{{{\text{h}}2}}$, $\sigma_{z}^{{{\text{h}}3}}$ and $\sigma_{z}^{{{\text{h}}4}}$ at the tunnel axis caused by the unloading of others three sidewalls (2), (3), (4). Then the additional stress generated by unloading of pit excavation at any point $M(x_{0} ,y_{0} ,z_{0} )$ adjacent to the axis of the existing tunnel is:

$$\sigma_{z} = \sigma_{z}^{{\text{v}}} + \sigma_{z}^{{{\text{h}}1}} + \sigma_{z}^{{{\text{h}}2}} + \sigma_{z}^{{{\text{h}}3}} + \sigma_{z}^{{{\text{h}}4}}$$

(8)

When one side of the pit intersects the tunnel axis obliquely at an arbitrary angle, a coordinate transformation can be added on top of the parallelism of the two to solve for the additional stresses generated by the pit excavation on the neighboring tunnels when the two intersect obliquely.

Differential equations for longitudinal deformation of tunnels

After solving for the additional stresses at the location of the tunnel and simplifying the tunnel into an Euler–Bernoulli beam, the computational model for an Euler–Bernoulli beam on a nonlinear Pasternak foundation is in Fig. 4.

Fig. 4

Schematic of computational modeling of Euler–Bernoulli beams on nonlinear Pasternak foundations.

The differential equation of the tunnel longitudinal deformation on a nonlinear Pasternak foundation is obtained:

$$(EI)_{eq} \frac{{d^{4} w(x)}}{{dx^{4} }} + \frac{w(x)D}{{\frac{0.3}{{k_{u} }} + \frac{w(x)}{{q_{u} }}}} - G_{c} D\frac{{\partial^{2} w(x)}}{{\partial x^{2} }} = p(x)D$$

(9)

where $D$ is the equivalent width of the tunnel, which is taken as the outer diameter of the tunnel in this paper; $w(x)$ is the longitudinal deformation of the tunnel; $p(x)$ is the additional stress generated at the location of the tunnel during the excavation of the pit; $q_{{\text{u}}}$ is the limit value of the foundation reaction force; $k_{{\text{u}}} = q_{{\text{u}}} /\delta_{{\text{u}}}$, $\delta_{{\text{u}}}$ is the displacement required to reach the ultimate contact pressure; $G_{{\text{c}}}$ is the shear stiffness of the shear layer; $(EI)_{{{\text{eq}}}}$ is the equivalent bending stiffness of the tunnel. There are more research results on the equivalent bending stiffness of shield tunnels at the present time^{25,26,27,28,29,30,31,32,33,34}, it is solved by the equivalent continuum model proposed by the famous tunnel experts of Japan, such as Shiba³⁵in this paper, without considering factors such as lateral stiffness and bolted joints. Equation (9) can be transformed into a system of differential equations by finite difference method and solved by matrix operation.

The detailed derivation of Eq. (9) can be found in Liang et al.²⁰.

Newton’s iterative method for solving differential equations of longitudinal deformation in tunnels

Improved finite-difference format

Equation (9) is a fourth order non chi-square differential equation with nonlinear terms, which cannot be solved directly and can be solved by finite difference method and Newton iteration method. Shen et al.³⁶ proposed a seven-point finite difference format constructed according to the Hermite interpolation method:

$$\lambda_{1} w_{i - 3} + \lambda_{2} w_{i - 2} + \lambda_{3} w_{i - 1} + \lambda_{4} w_{i} + \lambda_{3} w_{i + 1} + \lambda_{2} w_{i + 2} + \lambda_{1} w_{i + 3} = p_{i}$$

(10)

where $\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,\lambda_{4}$ are the coefficients to be determined; and $w_{i}$ are the displacements at the nodes, $i = 1,2,......,n$. In this paper, the above improved seven-point difference format is applied to solve the tunnel differential equations. The specific differential formulation is presented in the literature³⁶.

Newton’s iterative method for solving the procedure

First, the tunnel is discretized in the manner of Fig. 5, and n + 7 nodes of length $l$ can be obtained, with a total of 6 imaginary nodes (− 3, − 2, − 1, n + 1, n + 2, n + 3) at both ends of the tunnel. The finite difference expression of the differential equation for the longitudinal deformation of the tunnel is obtained according to the improved Hermite interpolation method. Equation (9) can be written in the finite difference form:

$$\begin{aligned} & (EI)_{{{\text{eq}}}} \frac{{11.1899w_{i} - 7.8924\left( {w_{{i + 1}} + w_{{i - 1}} } \right) + 2.557\left( {w_{{i + 2}} + w_{{i - 2}} } \right) - 0.2595\left( {w_{{i + 3}} + w_{{i - 3}} } \right)}}{{l^{4} }} \\ & \quad + \frac{{w_{i} D}}{{\frac{{0.3}}{{k_{{\text{u}}} }} + \frac{{w_{i} }}{{q_{{\text{u}}} }}}} - G_{{\text{c}}} D\frac{{ - 2.6w_{i} + 1.4(w_{{i + 1}} + w_{{i - 1}} ) - 0.1(w_{{i + 2}} + w_{{i - 2}} )}}{{l^{2} }} = p_{i} D \\ \end{aligned}$$

(11)

Fig. 5

Tunnel discretization.

When considering the tunnel boundary conditions, the tunnel ends are far away from the foundation pit, the influence of excavation by the foundation pit can be ignored, and the tunnel is not fixed with the station. It can be assumed that both ends of the tunnel satisfy the free boundary conditions, and the shear force, bending moment, and turning angle at both ends are all zero. The relationships between bending moment $M$, shear force $Q$, turning angle ${\uptheta }$,and displacement $w$ in the Euler–Bernoulli beams are shown in Eqs. (12–14):

$$\left. {\begin{array}{*{20}l} {M_{0} = - (EI)_{eq} \frac{{d^{2} w}}{{dx^{2} }} = - (EI)_{eq} \left( {\frac{{ - 2.6w_{0} + 1.4(w_{ - 1} + w_{1} )}}{{l^{2} }} + \frac{{ - 0.1(w_{ - 2} + w_{2} )}}{{l^{2} }}} \right) = 0} \hfill \\ {M_{n} = - (EI)_{eq} \frac{{d^{2} w}}{{dx^{2} }} = - (EI)_{eq} \left( {\frac{{ - 2.6w_{n} + 1.4(w_{n - 1} + w_{n + 1} )}}{{l^{2} }} + \frac{{ - 0.1(w_{n - 2} + w_{n + 2} )}}{{l^{2} }}} \right) = 0} \hfill \\ \end{array} } \right\}$$

(12)

$$\left. {\begin{array}{*{20}l} {\theta_{0} = \frac{{{\text{d}}w}}{{{\text{d}}x}} = \frac{{w_{1} - w_{ - 1} }}{2l} = 0{\kern 1pt} {\kern 1pt} } \hfill \\ {\theta_{n} = \frac{{{\text{d}}w}}{{{\text{d}}x}} = \frac{{w_{n + 1} - w_{n - 1} }}{2l} = 0} \hfill \\ \end{array} } \right\}$$

(13)

$$\left. {\begin{array}{*{20}l} \begin{aligned} Q_{0} = & - (EI)_{{{\text{eq}}}} \frac{{{\text{d}}^{3} w}}{{{\text{d}}x^{3} }} = - (EI)_{{{\text{eq}}}} \left( {\frac{{ - 0.43255(w_{ - 3} - w_{3} ) - 0.1031(w_{ - 2} - w_{2} )}}{{l^{3} }}} \right. \\ & \;\left. { + \frac{{1.50385(w_{ - 1} - w_{1} )}}{{l^{3} }}} \right) = 0 \\ \end{aligned} \hfill \\ \begin{aligned} Q_{n} = & - (EI)_{{{\text{eq}}}} \frac{{{\text{d}}^{3} w}}{{{\text{d}}x^{3} }} = - (EI)_{{{\text{eq}}}} \left( {\frac{{ - 0.43255(w_{n - 3} - w_{n + 3} ) - 0.1031(w_{n - 2} - w_{n + 2} )}}{{l^{3} }}} \right. \\ & \;\left. { + \frac{{1.50385(w_{n - 1} - w_{n + 1} )}}{{l^{3} }}} \right) = 0 \\ \end{aligned} \hfill \\ \end{array} } \right\}$$

(14)

where $M_{0}$, $\theta_{0}$, $Q_{0}$ are the bending moment, corner and shear force at the nodes $i = 0$, respectively; $M_{n}$, $\theta_{{\text{n}}}$, $Q_{n}$ are the bending moment, corner and shear force at the nodes $i = n$; and $w_{ - 3} ,w_{ - 2} ,w_{ - 1} ,w_{0} ,w_{n + 1} ,w_{n + 2} ,w_{n + 3}$ are the longitudinal displacements of the tunnel at the imaginary nodes $i = - 3, - 2, - 1,0,n + 1,\;n + 2,\;n + 3$.

The system of Eqs. (12) to (14) can be linked to obtain Eq. (15), the expression of longitudinal displacement of the six imaginary nodes at both ends of the tunnel in Fig. 5.

$$\left. \begin{gathered} w_{ - 3} = 6.1972w_{0} - 6.6739w_{1} + 0.4767w_{2} + w_{3} \hfill \\ w_{ - 2} = - 26w_{0} + 28w_{1} - w_{2} \hfill \\ w_{ - 1} = w_{1} \hfill \\ w_{n + 1} = w_{n - 1} \hfill \\ w_{n + 2} = - 26w_{n} + 28w_{n - 1} - w_{n - 2} \hfill \\ w_{n + 3} = 6.1972w_{n} - 6.6739w_{n - 1} + 0.4767w_{n - 2} + w_{n - 3} \hfill \\ \end{gathered} \right\}$$

(15)

The finite difference Eq. (11) for the longitudinal deformation of the tunnel is actually an algebraic equation when expanded, and they can be written as Eq. (16) with the longitudinal deformation of the $w$ as the unknown vector:

$$K_{t} w + \frac{w}{{\frac{0.3}{{k_{u} }} + \frac{w}{{q_{u} }}}}D - Gw = p$$

(16)

where: $K_{t}$ is the longitudinal deformation matrix of the tunnel; $G$ is the matrix of the shear layer of the foundation soil; $w$ is the longitudinal displacement vector of the tunnel; and $p$ is the vector of the additional load caused by the excavation of the foundation pit.

Substituting Eq. (15) into Eq. (16) yields the expressions (17) to (20) for the individual vectors and matrices:

$${\mathbf{G}} = \frac{{G_{{\text{c}}} D}}{{l^{2} }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & {} & {} & 0 \\ {1.4} & { - 2.7} & {1.4} & { - 0.1} & {} & {} & {} \\ { - 0.1} & {1.4} & { - 2.6} & {1.4} & { - 0.1} & {} & {} \\ {} & \ddots & \ddots & \ddots & \ddots & \ddots & \begin{gathered} \hfill \\ \hfill \\ \end{gathered} \\ {} & {} & { - 0.1} & {1.4} & { - 2.6} & {1.4} & { - 0.1} \\ {} & {} & {} & { - 0.1} & {1.4} & { - 2.7} & {1.4} \\ 0 & {} & {} & 0 & 0 & 0 & 0 \\ \end{array} } \right]_{(n + 1) \times (n + 1)}$$

(17)

$${\mathbf{w}} = \left\{ {w_{0} ,w_{1} , \ldots w_{i} ,w_{i + 1} , \ldots ,w_{n - 1} ,w_{n} } \right\}_{(n + 1)}^{{\text{T}}}$$

(18)

$${\mathbf{p}} = D\left\{ {p_{0} ,p_{1} , \ldots p_{i} ,p_{i + 1} , \ldots ,p_{n - 1} ,p_{n} } \right\}_{(n + 1)}^{{\text{T}}}$$

(19)

$$K_{t} = \frac{{(EI)_{eq} }}{{l^{4} }}\left[ {\begin{array}{*{20}c} { - 56.9} & {57.5431} & { - 0.1237} & { - 0.519} & {} & {} & {} & {} & {} \\ { - 1.1454} & {6.4809} & { - 7.6329} & {2.557} & { - 0.2595} & {} & {} & {} & {} \\ {2.557} & { - 8.1519} & {11.1899} & { - 7.8924} & {2.557} & { - 0.2595} & {} & {} & {} \\ { - 0.2595} & {2.557} & { - 7.8924} & {11.1899} & { - 7.8924} & {2.557} & { - 0.2595} & {} & {} \\ {} & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & {} \\ {} & {} & { - 0.2595} & {2.557} & { - 7.8924} & {11.1899} & { - 7.8924} & {2.557} & { - 0.2595} \\ {} & {} & {} & { - 0.2595} & {2.557} & { - 7.8924} & {11.1899} & { - 8.1519} & {2.557} \\ {} & {} & {} & {} & { - 0.2595} & {2.557} & { - 7.6329} & {6.4809} & { - 1.1454} \\ {} & {} & {} & {} & {} & { - 0.519} & { - 0.1237} & {57.5431} & { - 56.9} \\ \end{array} } \right]_{(n + 1) \times (n + 1)}$$

(20)

Equation (16) needs to be calculated using Newton’s iterative method. Let the matrix be:

$${\mathbf{F(w}}) = {\mathbf{K}}_{{\mathbf{t}}} {\mathbf{w}} + \frac{{\mathbf{w}}}{{\frac{{{\mathbf{0}}{\mathbf{.3}}}}{{{\mathbf{k}}_{{\mathbf{u}}} }} + \frac{{\mathbf{w}}}{{{\mathbf{q}}_{{\mathbf{u}}} }}}}{\mathbf{D}} - {\mathbf{Gw}} - {\mathbf{p}}$$

(21)

The Jacobi matrix expression (22) is obtained from Eq. (21):

$${\mathbf{F^{\prime}(w)}} = {\mathbf{K}}_{{\mathbf{t}}} + {\mathbf{K}}_{{\mathbf{s}}} - {\mathbf{G}}$$

(22)

where

$${\mathbf{K}}_{{\mathbf{s}}} = \left[ {\begin{array}{*{20}c} {f_{0} } & {} & {} & {} & {} & {} & 0 \\ {} & {f_{1} } & {} & {} & {} & {} & {} \\ {} & {} & \ddots & {} & {} & {} & {} \\ {} & {} & {} & {f_{i} } & {} & {} & {} \\ {} & {} & {} & {} & \ddots & {} & {} \\ {} & {} & {} & {} & {} & {f_{n - 1} } & {} \\ 0 & {} & {} & {} & {} & {} & {f_{n} } \\ \end{array} } \right]_{(n + 1) \times (n + 1)}$$

(23)

where:

$$f_{i} = \left( {\frac{{w_{i} D}}{{\frac{0.3}{{k_{u} }} + \frac{{w_{i} }}{{q_{u} }}}}} \right)^{\prime } = \frac{1}{{\frac{0.3}{{k_{u} }} + \frac{{w_{i} }}{{q_{u} }}}}D - \frac{{w_{i} }}{{q_{u} \left( {\frac{0.3}{{k_{u} }} + \frac{{w_{i} }}{{q_{u} }}} \right)^{2} }}D,\;i = (0,1,2...,n)$$

(24)

According to Newton’s iterative method there is the iterative Eq. (25):

$$w^{(k + 1)} = w^{(k)} - \left( {F^{\prime } \left( {w^{(k)} } \right)} \right)^{ - 1} F\left( {w^{(k)} } \right)$$

(25)

where $F^{\prime} (w^{(k)} )^{ - 1}$ is the inverse matrix of the Jacobi matrix of $F(w^{(k)} )^{{}}$; $k$ is the number of iterations; $w^{(k)}$ is the longitudinal displacement vector of the tunnel at the first iteration, and $w^{(k + 1)}$ is the longitudinal displacement vector of the tunnel at the $k + 1$ iteration.

Newton’s iterative formula (25) can be further written as Eqs. (26) and (27):

$$\vartriangle {\varvec{w}}^{(k)} = - {\varvec{F}}^{\prime } \left( {{\varvec{w}}^{(k)} } \right)^{ - 1} {\varvec{F}}\left( {{\varvec{w}}^{(k)} } \right)$$

(26)

$${\varvec{w}}^{(k + 1)} = \vartriangle {\varvec{w}}^{(k)} + {\varvec{w}}^{(k)}$$

(27)

The complete procedure for solving by Newton’s iterative method is as follows⁷:

• (1) Use Eq. (8) to solve for the additional stress vectors p generated by the pit excavation at the surrounding existing tunnel;

• (2) Construct the matrix F(w) and its Jacobi matrix F(w)′;

• (3) Construct the initial value of the displacement vector $w^{(0)}$ and bring it into Eq. (26) to obtain $\vartriangle {\varvec{w}}^{(k)}$ ($k = 0$);

• (4) $\vartriangle {\mathbf{w}}^{(k)}$ is brought into Eq. (27) to obtain ${\mathbf{w}}^{(k + 1)}$;

• (5) ${\mathbf{w}}^{(k + 1)}$ will then be brought into Eq. (26), and if $\vartriangle {\varvec{w}}^{(k + 1)} < \varepsilon$ (it can be assumed for $\varepsilon = 10^{ - 6}$, $\varepsilon$ is computational accuracy), then ${\mathbf{w}}^{(k + 1)}$ is what is sought;

• (6) If $\vartriangle {\varvec{w}}^{(k + 1)} \ge \varepsilon$, then repeat steps (4), (5); until the solution accuracy is satisfied.

After the Newton iteration process described above, a numerical solution for the longitudinal displacement of the tunnel that satisfies the computational accuracy can be obtained.

Example verification and analysis

Comparison with centrifuge test data³⁷

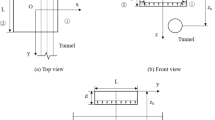
Japanese scholars Kusakabe et al.³⁸ used centrifuge tests to model the impact of pit excavation on the surrounding pipelines. Zelin et al.³⁷ conducted relevant tests and obtained corresponding data, and the model of the test is shown in Fig. 6.Cylindrical pit diameter $d_{0} = 50\;{\text{mm}}$, excavation depth $d = 100\,{\text{mm}}$; pipeline located on one side of the pit, outer diameter $D = 10{\text{mm}}$_,depth of burial $z_{0} = 35\;{\text{mm}}$,longitudinal equivalent bending stiffness $(EI)_{{{\text{eq}}}} = 20.29{\text{N}} \cdot {\text{m}}^{{2}}$, horizontal clear distance between the pit and the pipeline $s = 25{\kern 1pt} ,\;50\;{\text{mm}}$. It is used to simulate the case where the pit is close to the tunnel for $s = 25\,{\text{mm}}$, and is used to simulate the case where the pit is farther away from the tunnel $s = 50\;{\text{mm}}$. The test was conducted using Toyoura Sand standard sand taken from Japan. Toyoura Sand is an internationally renowned test standard sand and its parameters are widely used in the field of engineering tests. The density $\rho = 1.57{\text{g/cm}}^{{3}}$, Poisson’s ratio $\mu = 0.5$, modulus of elasticity of this sand $E = 15.73\;{\text{MPa}}$.

Fig. 6

Centrifuge test model.

Figure 7 is comparison of the test values and the vertical bending moment centrifuge³⁷ and the calculated values of the nonlinear Pasternak foundation model in this paper. In general, it can be seen that the distribution pattern and influence range of the theoretically calculated values and test values are approximately the same. When the pipeline is closer ($s = 25\;{\text{mm}}$) or farther ($s = 50\;{\text{mm}}$) from the foundation pit, the maximum values of positive and negative moments obtained from the calculated values are larger than the test values. Calculated values for the excavation of the pit on the surrounding pipeline to consider the scope of the influence of the larger, relatively more to ensure the safety of the project.

Fig. 7

Comparison of calculated values of vertical bending moments of pipes with test data.

Pit of Nanjing Qingliangmen tunnel crossing metro line 2 project³⁹

Nanjing Qingliangmen Tunnel pit project³⁹ is a typical pit over the existing subway tunnel project, the pit project excavation plan size $L \times B = 42\;{\text{m}} \times 28\;{\text{m}}$_, excavation depth $d = 8.5\;{\text{m}}$, the pit set up three support. Metro line 2 tunnel is located below the pit, the depth of burial $z_{0} = 16.6\;{\text{m}}$, the clear distance between the tunnel arch and the bottom of the pit is 5 m, the outer diameter of the tunnel $D = 6.2\;{\text{m}}$, the two tunnels axis is $16.2{\text{m}}$. The subway tunnel is a shield tunnel, spliced by the tube sheet, the tunnel tube sheet structural parameters are shown in Table 1, by the Shiba Yukio method³⁵ can be derived from the equivalent bending stiffness of the tunnel $(EI)_{{{\text{eq}}}} = 4.65 \times 10^{5} {\text{MN}} \cdot {\text{m}}^{{2}}$.

Table 1 Tunnel tube sheet structure parameters.

The soil parameters for the area where the project is located are detailed in Table 2. Vorster et al.⁴⁰ concluded that more accurate calculations can be obtained by using the soil modulus at burial depth for tunnels.

Table 2 Soil parameters.

In this case, the location of the tunnel is in the fourth layer of powdery clay layer, the calculation data can be taken as the soil gravity ${\upgamma } = {18}{\text{.6kN/m}}^{{3}}$, modulus of elasticity $E_{{\text{s}}} = 20.2MP{\text{a}}$, Poisson’s ratio ${\upnu }_{{\text{s}}} = {0}{\text{.33}}$. Displacement required to obtain the ultimate contact pressure $\delta_{{\text{u}}} = 0.25m$, the vertical uplift coefficient $N_{{{\text{cv}}}} = 5.35$, and the undrained shear strength of soil $S_{u} = 57kPa$.

• (1) Computational modeling

According to the results of related research, the calculated length of each tunnel is 150 m. With the corner point of the pit as the coordinate origin $O$, the axis where the long side $L$ of the pit is located is the ${\text{x - axis}}$, the axis where the short side $B$ is located is the ${\text{y - axis}}$, and the ${\text{z - axis}}$ is perpendicular to the ${\text{xoy}}$ plane downward, and the relative positions of the pit and the tunnel are shown in Fig. 8.

Fig. 8

Computational model.

• (2) Calculation process and results

The shield tunnels are first discretized according to the length of 1 m. As shown in Fig. 9, then 157 calculation points (151 real nodes and 6 imaginary nodes) are taken for each tunnel.Then the additional stresses generated at each node by the pit excavation are solved in Fig. 10. Finally, the differential equations of longitudinal displacement under different foundations are chosen to solve the longitudinal displacement of the tunnel and compared with the measured data³⁹ and finite element simulation results³⁹ in Fig. 11. The bending moment in Fig. 12 and shear force in Fig. 13 applied to the tunnel can also be solved. Leakage associated with deformation joints seriously affects tunnel structures⁴¹, so the maximum values of longitudinal displacement, bending moment and shear force of the tunnel are shown in Table 3.

Fig. 9

Discretized node graph.

Fig. 10

Value of additional stresses at the tunnel location due to pit excavation.

Fig. 11

Comparison of longitudinal displacements of tunnel.

Fig. 12

Comparison of longitudinal bending moments of tunnels.

Fig. 13

Comparison of tunnel longitudinal shear.

Table 3 Maximum longitudinal deformation and internal forces in tunnels.

• (1) Analysis of additional stresses in tunnels

In Fig. 10, it can be seen that the maximum additional stress caused by the excavation of the foundation pit occurs at the corresponding tunnel position directly below the center of the foundation pit, and the maximum additional stress on the left line of the tunnel is 118.2 kPa, and that on the right line is 96.2 kPa. The additional stress caused by the excavation of the foundation pit is decreasing along the axis of the tunnel from directly below the center of the foundation pit to the direction far away from the foundation pit, and it is decreasing to zero in the position of 75 m away from the center of the foundation pit.

• (2) Tunnel longitudinal displacement analysis

The nonlinear Pasternak foundation model, the traditional Pasternak foundation model, the finite element model and the measured longitudinal deformation data were calculated and compared, as shown in Fig. 11, the trend of longitudinal displacements of the tunnel by several analytical methods is consistent with the measured values, which indicates that it is more reasonable to use the nonlinear Pasternak foundation model for the calculation. The maximum longitudinal displacement of the tunnel occurs directly below the foundation pit, which is the location where the excavation of the foundation pit produces the largest additional stress on the tunnel. The maximum measured longitudinal displacements in the tunnel are 3.3 mm in the left line and 2.4 mm in the right line, and the maximum longitudinal displacements in the tunnel are 3.5 mm in the left line and 2.8 mm in the right line using the nonlinear Pasternak foundation model, and 3.1 mm in the left line and 2.3 mm in the right line from the conventional Pasternak foundation model. The maximum longitudinal displacements of the tunnel derived from the Pasternak foundation model are slightly larger than the measured values, while the predicted results based on the traditional Pasternak foundation model are smaller than the measured values. This is because, when the soil is unloaded in a large area, the soil body will exceed the elastic phase and enter the plastic state, and the soil deformation is no longer linearly related to the foundation reaction force. The elastic foundation model will overestimate the foundation reaction force, which leads to the prediction of the longitudinal displacement of the tunnel being lower than the actual measured value.

It can be seen that the longitudinal deformation of the existing tunnels in the vicinity caused by pit excavation can be better predicted by considering the nonlinear characteristics of the foundation soil.

• (3) Tunnel bending moment analysis

Figure 12 shows the comparison of the longitudinal bending moment $M$ of the tunnel calculated by the nonlinear Pasternak foundation model and the traditional Pasternak foundation model. The nonlinear Pasternak foundation model calculates the maximum positive bending moment of 4.23 $MN.{\text{m}}$ for the left line and 3.44 $MN.{\text{m}}$ for the right line of the tunnel, while the traditional Pasternak foundation model calculates the maximum positive bending moment of 6.15 $MN.{\text{m}}$ for the left line and 5.05 $MN.{\text{m}}$ for the right line of the tunnel, and the maximum positive bending moments of the tunnel by the two methods are the same, which are all located at the right underneath of the foundation pit. The maximum negative moment of 2.1 $MN.{\text{m}}$ in the left line and 1.8 $MN.{\text{m}}$ in the right line of the tunnel from the nonlinear Pasternak foundation model was found to be 36 m (about 1.5 B) from the center of the foundation pit. The maximum negative moments of 3.1 $MN.{\text{m}}$ in the left lane and 2.6 $MN.{\text{m}}$ in the right lane of the tunnel from the conventional Pasternak foundation model were found to occur at 26 m (approximately 1B) from the center of the pit.

Wu et al.⁴² showed that the use of Euler–Bernoulli beams to model existing tunnels significantly overestimates the internal forces in the tunnel. The results of calculating the bending moment and shear force of the tunnel using the nonlinear Pasternak foundation model in this paper are more reliable. Because the subway shield tunnel is made of tube pieces spliced together, it has a weak longitudinal bending capacity. If the shield tunnel section is subjected to bending, its neutral axis will be deflected, and the bolts at the openings of the ring joints of the tube sheets bear all the tensile stresses. Fang Yong et al.⁴⁴ calculated that the maximum longitudinal bending moment of the tunnel that can make the bolts of Nanjing shield tunnel yield is 104.5 $MN.{\text{m}}$. The maximum positive and negative bending moments of the tunnel calculated by the above method are much smaller than the bending moment that can make the bolts yield, so the bending capacity of the tunnel of this project meets the requirements of the relevant regulations.

• (4) Tunnel shear analysis.

Figure 13 shows the comparison of longitudinal shear $Q$. The maximum shear force of the tunnel is ${305}{\text{.7 k}}N$ in the left line and ${250}{\text{.8 k}}N$ in the right line from the nonlinear Pasternak foundation model, while the maximum shear force of the tunnel is ${611}{\text{.3 k}}N$ in the left line and ${509}{\text{.1 k}}N$ in the right line from the traditional Pasternak foundation model. The maximum shear force of the tunnel obtained by both methods occurs at the corresponding tunnel location below the sidewall of the foundation pit. The difference between the maximum shear force calculated by the nonlinear Pasternak foundation model and the traditional Pasternak foundation model is nearly double, mainly because the traditional Pasternak foundation model is an elastic foundation model, which is not able to take into account the nonlinear deformation of foundation soil and overestimates the tunnel shear force. Shield tunnels rely on the friction at the longitudinal joint faces of the tube sheets and the joint bolts to resist the longitudinal shear forces exerted on the tunnel, and if the shear strength is insufficient, the tube sheets of the tunnels will be misaligned and dislocated, which seriously affects the safety of the tunnels. Guo et al.⁴⁵ showed that the shear strength of shield tunnel cross-section bolts is $4.9\sim 6.4MN$. the maximum shear force of the tunnel in this project is much less than $4.9MN$, which is sufficient shear resistance.

Conclusions

• (1) The additional stress at the neighboring existing shield tunnel is obtained by applying Mindlin’s basic solution during deep foundation excavation, and then the differential equation of longitudinal deformation of the shield tunnel is derived by combining with the nonlinear Pasternak foundation model of the soil body. The improved Hermite differential method with Newton’s iterative method is used to solve the equation to obtain the solution of longitudinal nonlinear deformation of the neighboring existing tunnels caused by deep foundation excavation. Due to the adoption of the soil nonlinear Pasternak foundation model, the longitudinal deformation of the tunnel is more in line with the actual situation than that solved by the traditional elastic foundation model.

• (2) The applicability and reasonableness of the calculation method of longitudinal deformation of foundation beams on the nonlinear Pasternak foundation model based on Hermite interpolation method constructed in seven-point finite-difference format proposed in this paper are verified by two engineering examples. It can accurately predict the longitudinal deformation value of the neighboring existing shield tunnel during the excavation of the foundation pit, which provides theoretical guidance for the construction of the project.

• (3) Combined with the case of Nanjing Qingliangmen Tunnel foundation project, the maximum bending moments of the left and right tunnel alignments derived from the nonlinear Pasternak foundation model are located directly below the foundation pit; the maximum shear values of the left and right tunnel alignments are located at the corresponding tunnel positions below the sidewalls of the foundation pit. In addition, comparative computational analyses were carried out using the nonlinear Pasternak foundation model, the traditional Pasternak foundation model, the finite element model and the measured deformation data. The trends of longitudinal deformation of the tunnel solved by several analytical methods are consistent with the measured values, but the nonlinear Pasternak foundation model is closer to the measured values, which indicates that the longitudinal deformation of the existing tunnels in the surrounding area caused by the excavation of the footing can be better predicted by considering the nonlinear characteristics of the foundation soil.