Introduction

Cardiovascular disease (CVD) refers to conditions impacting the heart and blood vessels, resulting from a variety of factors, and stands as a prominent contributor to rising mortality rates on a global scale, with a 12.5% rise in CVD death rates over the past decade1. CVD’s impact spans across countries of varying income levels, specifically exerting a heavier burden on low- and middle-income countries (LMICs), where CVD contributes significantly to overall health challenges, often leading to premature mortality compared to high-income nations2. Timely identification and thorough characterization of arrhythmias play a pivotal role in precise diagnosis and risk evaluation in clinical settings3, ultimately facilitating effective patient treatment. The utilization of electrocardiogram (ECG) monitoring devices serves as a key method for the early detection and management of arrhythmias, with ECGs serving as the primary diagnostic tool for arrhythmia detection. Moreover, studies indicate that continuous ECG signal analysis and monitoring can vastly enhance the management, diagnostics, and prevention.

In recent years, artificial intelligence has emerged as a focal point in both technology and society. This prominence can largely be attributed to the exceptional capabilities demonstrated by deep neural networks in areas such as image recognition and speech processing4.The diagnosis of myocardial infarction currently necessitates skilled healthcare professionals to assess the ECG signals of patients, a process prone to human errors and observer biases. In response to these challenges, automatic arrhythmia classification has emerged. Recent years have witnessed significant advancements in the automatic detection of arrhythmias and abnormal heartbeats5, offering long-term remote cardiac monitoring to enhance patient care. Traditional methods for detecting cardiac signals mainly involve machine learning techniques such as Linear Discriminant Analysis (LDA)6, Multi-Layer Perceptron (MLP)7, Support Vector Machine (SVM)8, and K-Nearest Neighbors (KNN)9, which have proven effective in arrhythmia identification. Modern classifier architectures leverage deep learning models like Convolutional Neural Networks (CNN)10, Long Short-Term Memory (LSTM)11, Recurrent Neural Networks (RNN)12, as well as pre-trained transfer learning models such as ResNet13, VGGNet14, Inception, and Xception15. Deep learning (DL)-based technologies outperform traditional machine learning approaches by achieving superior classification performance. Their exceptional performance in ECG classification tasks is primarily attributed to the models’ hierarchical architecture, enabling the extraction of deep features crucial for classification. These models even exceed the accuracy of expert manual classification, showcasing proficiency in feature extraction from raw signals16.

In general, the processing flow of these methods begins with extracting feature vectors from cardiac segments, encompassing physiological features and diagnostic indicators (such as RR intervals and QRS complex morphology), along with statistical features (like principal component analysis and wavelet transform), and includes feature selection if needed. Subsequently, a range of machine learning algorithms, such as SVM and MLP, are utilized for classification. While many of these approaches have shown impressive results on standard electrocardiogram databases, their performance often diminishes in clinical settings17. This decline may stem from the limited scope of representative electrocardiogram records in standard databases. As a result, the derived classification models are often dataset-specific, leading to performance decay when appraised on datasets with features distinct from their training sets, with our focus on inter-patient electrocardiogram classification. Given the individual variations in electrocardiogram attributes and the intricacies of clinical data, this framework presents a formidable artificial intelligence challenge. Undoubtedly, only nonlinear models with adequate complexity are suitable for this task. Segmenting an entire electrocardiogram within patient-based heartbeats is evidently inadequate for fulfilling this requirement. To tackle these challenges for electrocardiogram analysis and diagnosis, we employed the China Cardiovascular Disease Database (CCDD)18, alongside deep learning and rule-based reasoning techniques. This approach maximizes the distinctive attributes of electrocardiogram records from diverse populations in various locations within CCDD, enhancing the clinical significance of this study. By leveraging the multivariate time-series nature of input ECG signals and the inter-lead relationships, along with utilizing multiscale features as inputs, the incorporation of multiple classifiers and logical reasoning enhances the model’s nonlinearity, further boosting detection performance. The goal of the algorithm we want to develop is to fılter out as many normal ECG records as possible accurately so that physicians only focus on interpreting the remaining abnormal ones and their workload can be reduced.

The main contributions of our work are as follows:

  1. 1.

    We propose a classification method for normal and abnormal classes based on long ECG sequence recordings within the CCDD. This method employs a multi-scale CNN architecture to extract features of varying scales from ECG signals, which is essential for understanding the entities involved in the classification task.

  2. 2.

    We propose the Lead Encoder Attention (LEA) mechanism, which leverages the multi-lead characteristics of ECG recordings to encode and locate feature information from different leads. Furthermore, we demonstrate the effectiveness of the proposed attention mechanism by comparing it with other attention mechanisms.

  3. 3.

    A novel data partitioning method is proposed within the CCDD. This method ensures that the dataset utilized during the model training phase includes all heartbeat records in the database that are labeled according to primary labels, thereby promoting comprehensive learning for the model.

  4. 4.

    Experimental results from both small-scale and large-scale datasets within the CCDD indicate that the proposed method for classifying normal and abnormal classes outperforms currently advanced networks. Furthermore, results obtained from the MIT-BIH Arrhythmia (MIT-BIH-AR) database demonstrate that the model possesses generalization capabilities, enabling it to effectively manage classification tasks for ECG sequences of varying lengths.

The subsequent sections of this paper are organized as follows: Section 2 introduces the open data set, Section 3 provides details of the experiments conducted, Section 4 presents the results, and Section 5 offers further discussion on the study.

Related work

Arrhythmia detection comprises two main stages: feature extraction and classification, with the extraction of meaningful features from ECG signals posing a significant challenge. This task is primarily accomplished through two approaches: the first involves combining manually extracted features with conventional machine learning techniques, while the second utilizes deep learning methods for automatic feature extraction and classification of ECG signals. The following sections will examine the machine learning techniques applied to ECG arrhythmia classification and deep learning methods.

Machine learning methods

The primary objective of automatic classification algorithms is to obtain characteristic information for each class through the analysis and learning of feature vectors, thereby forming a knowledge system of known categories. When confronted with unlabeled new elements, these algorithms can accurately classify them based on the learned features. Algorithms such as Decision Tree (DT)25, Support Vector Machine (SVM)26, K-Nearest Neighbor (KNN)27, Random Forest (RF)28, and Naïve Bayes Classifier29 are commonly employed. Aziz et al.30 utilized the Fractional Fourier Transform to detect waveform features and classified them using SVM; Luz et al.31 were the first to apply the Optimum-Path Forest (OPF) algorithm in ECG classification tasks and compared it with SVM, Bayesian classifiers, and Multilayer Artificial Neural Networks (MLP); Patra et al.32 implemented an ANN-based model to detect ECG signals, achieving an accuracy of 91.25% on the MIT-BIH-AR database.

Traditional ECG auxiliary diagnostic methods based on machine learning exhibit stringent requirements for signal quality and are significantly dependent on manual feature extraction, often demanding considerable time and effort. Furthermore, the accuracy attained by many of the proposed methods is frequently suboptimal.

Deep learning methods

CNN are characterized by their ability to eliminate the need for additional manual feature extraction during the feature extraction phase, they have been widely applied in ECG diagnostic tasks in recent years, with notable performance outcomes. Chen et al.33 proposed a novel hybrid method to address the challenge of imbalanced datasets and introduced a lightweight CNN framework for ECG signal classification. By modifying the amplitudes of a limited number of samples and employing a weighted loss function in the deep learning model for data augmentation, they utilized the One-Dimensional Convolutional Block Attention Module (1D_CBAM) mechanism to compress heartbeat signals and extract relevant features. Classification was subsequently performed using an enhanced one-dimensional lightweight CNN model based on the MobileNet, achieving accuracies of 98.92% and 99.72% on Dataset1 and Dataset2 of the MIT-BIH-AR database, respectively. Yang et al.34 regarded different leads as distinct views, effectively merging features from various leads using a multi-view approach, and employed a multi-scale CNN architecture to capture temporal features of ECG signals across different scales. Additionally, they captured spatial information and channel relationships of ECG features through coordinate attention to enhance the feature representation of the network. Singh et al.35 introduced a method utilizing Recurrent CNN (RCNN) optimized using the Grey Wolf Optimization (GWO) algorithm for hyperparameter tuning. Their approach was compared with several machine learning methods, including KNN, Logistic Regression, SVM, and Random Forest classifiers, with results demonstrating superior performance compared to similar machine learning and supervised methods, achieving an accuracy of 98%.

Although numerous CNN-based architectures have achieved promising results, gaps remain in feature fusion and attention to features from different leads. Our approach integrates multi-scale convolution with the LEA module to tackle these challenges and integrates rule-based reasoning to improve the classification performance of normal and abnormal cases.

Experiment setup

Environment

The model training was conducted on a workstation featuring an Intel 12700 CPU, an NVIDIA GTX 3060Ti GPU, and 16 GB of memory. The operating system is Windows 10, Python 3.7 is used as the development platform, and torch 1.8.1 is used as a deep learning framework.

Open data set

Chinese cardiovascular disease database

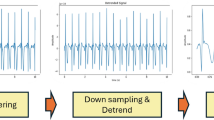
The China Cardiovascular Disease Database (CCDD) comprises 193,690 standard 12-lead electrocardiogram records gathered from various hospitals in cities like Shanghai, Suzhou, and Changsha19. Each record has a duration of approximately 10-20 seconds and is digitized at a rate of 500 samples per channel per second, following the guidelines of the National Heart, Lung, and Blood Institute (NHLBI). The establishment of CCDD has effectively addressed the issues of scale and representativeness that were observed at differing levels in previous databases20. The wavelet transform serves as an alternative to the Fourier transform and the short-time Fourier transform, as it can simultaneously provide both time and frequency components at any given instant. At high frequencies, the wavelet transform offers improved time resolution, while at low frequencies, it delivers enhanced frequency resolution21. This study utilizes wavelet transform for noise reduction in ECG records, based on the consideration of the long-term signal-to-noise ratio (SNR) in CCDD. The comparison of the records before and after denoising is presented in Fig. 1.

Fig. 1
figure 1

The ECG signals from the CCDD before and after filtering with the wavelet transform.

Full size image

To enhance the performance of electrocardiogram classification, we first shifted the starting point of the data back by 25 samples, as some of the initial 25 samples in CCDD have poor quality. Subsequently, we downsampled the raw data from 500Hz to 200Hz and then used wavelet transform to eliminate baseline drift, power frequency noise, and other noises. To increase the number of training samples, we applied random noise processing to the data, adding high-frequency noise, low-frequency noise, and white noise to each lead of a data record based on different probabilities to enhance the robustness of the model and introduce diversity among data from different leads within the same record. Finally, a segment of data with a length of 9.5 seconds was extracted as the model input. An ECG record typically contains data from 12 leads, of which 8 are orthogonal and the remaining 4 can be exported from the existing 8. Therefore, we only use these 8 orthogonal leads as our input data.

MIT-BIH-AR database

The four globally recognized standard electrocardiogram databases are the MIT-BIH Arrhythmia (MIT-BIH-AR) Database, the American Heart Association (AHA) Database, the QT Database, and the Common Standards for Electrocardiography (CSE) Database22. The MIT-BIH-AR Database comprises 48 dual-lead electrocardiogram records from 47 patients, with each record lasting 30 minutes and sampled at a frequency of 360Hz. All data in this database are freely accessible for download and utilization, rendering it the most extensively utilized database. Moreover, numerous existing studies in the realm of electrocardiography employ it as a source of experimental data and as a benchmark for testing standards23.

Due to common contaminations of original ECG signals by noise sources like baseline drift, powerline interference, and patient electrode motion artifacts, preprocessing is essential. A bandpass filter ranging from 0.5 to 50 Hz was utilized in this research to preprocess the original ECG signals for noise reduction. Heartbeat segmentation was carried out using R peak annotations extracted from the MIT-BIH-AR database. Each heartbeat, defined as 324 Hz, consisted of 144 Hz before and 180 Hz after the R peak, resulting in a total of 110,061 segmented heartbeats.

Evaluation indicators

Various metrics were employed to assess and investigate the algorithm’s performance: To assess the performance of the proposed model, this study employed four statistical performance metrics: specificity (Sp), sensitivity (Se), Accuracy (Acc), AUC and TPR95. The equations defining these metrics are presented in equations(1)−(3). Within a category, TP signifies the correctly identified beats, TN denotes the accurately unidentified beats, FP encompasses misclassified beats from different categories, and FN includes beats from a particular category falsely classified into other categories.

Sp (specificity) denotes the ratio of accurately classified negative samples, calculated per Equation 1.

$$\begin{aligned} Sp=\frac{TN}{TN+FP} \end{aligned}$$
(1)

Se (sensitivity) highlights the ratio of accurately classified positive samples, calculated as per Equation (2).

$$\begin{aligned} Se=\frac{TP}{TP+FN} \end{aligned}$$
(2)

Acc (accuracy) reflects the ratio of correctly predicted positive samples within all predicted positive samples, as computed by Equation (3)

$$\begin{aligned} Acc=\frac{TP+TN}{TP+FP+TN+FN} \end{aligned}$$
(3)

The Receiver Operating Characteristic (ROC) curve illustrates the performance of a model across various thresholds by depicting the relationship between the True Positive Rate (TPR) and the False Positive Rate (FPR), with the FPR on the x-axis and the TPR on the y-axis. The Area Under the Curve (AUC) refers to the area beneath the ROC curve. TPR, also known as sensitivity, represented as Se, is the proportion of correctly predicted positive cases to the total number of actual positive cases. In a clinical setting, a higher TPR signified that more true positives are accurately classified, which indicates better performance of the classification model. The Negative Predictive Value (NPV) is defined as the ratio of samples predicted as negative that are indeed negative, calculated as shown in Equation 4.

$$\begin{aligned} NPV=\frac{TN}{TN+FN} \end{aligned}$$
(4)

The term TPR95 denotes the NPV value corresponding to when TPR equals 95%. Specifically, TPR95 represents the proportion of truly negative samples among those classified as negative when the model correctly classifies 95% of positive samples24. This metric emphasizes the model’s capability to identify positive samples while simultaneously considering its performance in classifying negative samples, particularly in datasets where positive samples disproportionately exceed negative samples. Consequently, TPR95 provides a more accurate reflection of the model’s overall performance. By establishing a high recall threshold of 95%, the model minimizes the risk of overlooking critical records in classification tasks for both normal and abnormal classes. In contrast to the Matthews Correlation Coefficient (MCC) and Kappa metrics, TPR95 not only highlights the identification performance of positive classes but also integrates negative predictive value, thereby offering insights into the accuracy of negative predictions. This holds practical significance, as the initial step for physicians diagnosing ECG records in clinical settings is distinguishing between normal and abnormal cases. Only after categorizing a record as abnormal do they proceed to identify the specific type of disease. Thus, using the TPR95 metric can clarify the model’s accuracy in identifying normal records and quantifies the reduction in physicians’ workload, thereby enabling them to concentrate on diagnosing the disease types associated with abnormal heartbeat records.

Methodology

Experiment on CCDD-1

The dataset was partitioned into training, testing, and validation sets following the data partitioning method employed by Jin et al.36, as detailed in Table 1. Additionally, the testing set was subdivided into small-scale and large-scale testing subsets.

Table 1 Data distribution on CCDD-1.
Full size table

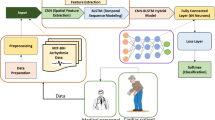
Figure 2 illustrates the experimental flowchart for the CCDD. It principally comprises convolution modules, an LEA module, and a rule inference module. After preprocessing, the ECG signal serves as the original input to the model, from which characteristic information is extracted through various convolution modules. Simultaneously, a method of progressively upsampling feature maps at different stages and merging them is employed to facilitate the integration of multi-scale feature information. The information obtained solely from the convolution is then fed into the Bidirectional LSTM (BiLSTM) module, where the acquired data and the fused feature maps are utilized as inputs for the dense layer and linear layer, respectively. After deriving category weights from the results processed through Softmax, rule inference is conducted to yield classification results for both normal and abnormal cases.

Fig. 2
figure 2

Overview of the proposed method on CCDD.

Full size image

To obtain different receptive fields, we employed convolution kernels of varying sizes in the upper and lower branches. The upper branch primarily focuses on integrating information from eight leads, where the two convolution layers in Block_1 utilize kernel sizes of (8, 12) and (8, 36). The data then undergoes batch normalization, scaling and shifting, non-linear transformations, and average pooling operations, corresponding to the BatchNorm (BN) layer, Scale (SC) layer, activation function layer (Mish), and Avgpool layer, which together can enhance the model’s accuracy37. Subsequently, the input data is processed through a (1, 1) convolution kernel via a shortcut, standardizing the number of channels before merging them as the module’s output. The Mish activation function was adopted, and the computation method is shown in Equation 5.

$$\begin{aligned} Mish=x* tanh(ln(1+{e}^{x})) \end{aligned}$$
(5)

In Block_1 of the lower branch, we employed convolution sizes of (1, 16) and (1, 32). Unlike the upper branch, which convolves across eight leads simultaneously, the objective of the lower branch is to extract feature information from each lead individually. Following Block_1, we utilized the LEA module to assign weights to the independently extracted features from the single lead in the lower branch and the multi-lead correlated features extracted from the upper branch. Detailed information regarding the LEA module will be discussed in the subsequent subsection. After processing with the attention mechanism, the data serves as the input to Block_2. Both Block_1 and Block_2 share the same overall architecture, comprising two convolution layers followed by a fusion with the input data. However, in Block_2, we replace the convolution modules with partial convolution38, which utilizes redundant information in the feature maps to conduct convolution operations on only a subset of the input channels while keeping the other channels unchanged. This approach reduces computational redundancy and memory access frequency, thereby decreasing FLOPs and improving computational speed. Subsequently, the outputs from Block_2 in both the upper and lower branches are fused to serve as inputs to the BiLSTM module. After passing through the dense layer and Softmax processing, we obtain a portion of the category weights. As illustrated in the figure, the lower branch involves extracting features from the data through the previously mentioned convolution operations, while simultaneously extracting feature maps at various stages and merging them using upsampling operations. Meanwhile, linear transformations are applied to refine these features, which preserves the information in the high-level feature space and supplements the low-level feature space with additional high-level information. This process enriches the feature data and enhances the model’s classification capability. Finally, the resultant data are fed into a linear layer, where Softmax processing is applied to derive another set of category weights39.

In the classification phase, to fully exploit the benefits of the various feature extraction methods suggested in the aforementioned model structure, we opted to employ a comprehensive approach for electrocardiogram (ECG) classification. Specifically, by utilizing two softmax functions to assess the extracted feature vectors from these methods, we adhere to the principle that if either outcome is categorized as abnormal, the heart record is marked as abnormal; conversely, if both outputs indicate normal categories, the record is classified as normal. Subsequent to the softmax evaluations, diagnostic rules were introduced to refine the categorization as normal or abnormal. Records identified as normal are directly output, while those labeled as abnormal undergo diagnostic rule verification to ascertain their abnormal status.

$$\begin{aligned} AvgRR=\frac{1}{n-1}\displaystyle \sum _{i=2}^{n}({R}_{i}-{R}_{i-1}) \end{aligned}$$
(6)

The applied rules evaluate heart rate variability and irregular rhythms to enhance classification accuracy. Considering a sampling rate of fs, where \(R(1\leqslant i\leqslant n)\) denotes the R-wave position in an ECG trace, and \(std(\cdot )\), \(min(\cdot )\), and \(max(\cdot )\) represent variance, \(min(\cdot )\), and \(max(\cdot )\) computations, respectively. The calculation formula for the average RR interval is illustrated in Equation 6. The applied disease rules, comprising bradycardia rule, locality-based arrhythmia, locally and globally based arrhythmia, and globally based arrhythmia, are defined sequentially, as illustrated in Equations (8)−(10).

$$\begin{aligned}&\quad HR=\frac{60* fs*n}{{R}_{n}-{R}_{1}} \end{aligned}$$
(7)
$$\begin{aligned}&\quad \left| \frac{{R}_{k+j}-{R}_{k+j-1}-AvgRR}{AvgRR}\right| > 0.15 \end{aligned}$$
(8)
$$\begin{aligned}&\quad {\left\{ \begin{array}{ll}{rcl} \left| \frac{{R}_{k+j}-{R}_{k+j-1}-AvgRR}{AvgRR}\right|> 0.15 \\ RC=\left\{ {RC}_{i}\right\} =\frac{{R}_{i+2}-{R}_{i+1}}{{R}_{i+1}-{R}_{i}},1\leqslant i\leqslant n-2 \\ std(RC)> 0.05 \end{array}\right. } \end{aligned}$$
(9)
$$\begin{aligned}&\quad {\left\{ \begin{array}{ll}{rcl} RA=\left\{ {RA}_{i}\right\} =\frac{{R}_{i+1}-{R}_{i}}{AvgRR},1\leqslant i\leqslant n-1 \\ std(RA)> 0.05 \end{array}\right. } \end{aligned}$$
(10)

Lead encoder attention

The Lead Encoder Attention (LEA) module integrates positional information into channel attention, enabling the network to focus on large regions while minimizing computational overhead. To address the loss of positional information resulting from two-dimensional global pooling, we decompose channel attention into N parallel one-dimensional feature encoding processes, thereby effectively integrating spatial coordinate information into the generated attention maps. The value of N is determined by either the channel dimension or height dimension of the input feature map. Specifically, our method employs N one-dimensional global pooling operations to aggregate input features separately in the vertical and horizontal directions, producing N independent direction-aware feature maps. These feature maps, which incorporate specific directional information, are subsequently encoded into two attention maps, each capturing the long-range dependencies of the input feature map in the same spatial direction. This approach allows positional information to be preserved in the generated attention maps, which are then applied to the input feature map through multiplication to highlight the relevant feature information. This operation is summarized in Fig. 3.

Fig. 3
figure 3

Overview of the proposed Attention.

Full size image

Global pooling is commonly employed to encode global spatial information across channels; however, it compresses this information into a single channel descriptor, making it difficult to retain positional information, which is crucial for capturing the spatial structure among different leads. To enable the attention module to capture long-range positional relationships, we decompose global average pooling into two one-dimensional feature encoding operations. Specifically, assuming the input is X, we use two spatial ranges of the pooling kernel, (C, 1, W) or (1, H, W), to encode the lead information either sequentially or in aggregate across the channel dimension and height dimension, respectively. Consequently, the output at height h with width w can be expressed as:

$$\begin{aligned} {z}_{w}^{h}=\frac{1}{C}\displaystyle \sum _{0\leqslant i\leqslant C} {x}_{w}(h,i) \end{aligned}$$
(11)

Similarly, the output of the c-th channel with width w can be expressed as:

$$\begin{aligned} {z}_{w}^{c}=\frac{1}{H}\displaystyle \sum _{0\leqslant J\leqslant H} {x}_{w}(j,c) \end{aligned}$$
(12)

The above two transformations aggregate features along two spatial directions, generating N direction-aware feature maps. This enables the attention module to capture long-range dependencies along one spatial direction while preserving precise positional information along the other spatial direction, which helps the network more accurately locate the objects of interest. Subsequently, we concatenate the aggregated feature maps and fuse them using a convolution kernel of size (1, 1). The resulting data undergoes batch normalization and scaling operations, denoted as the function \({f}_{0}\), yielding the following expression:

$$\begin{aligned}&f=\delta ({F}_{0}({z}^{h})) \end{aligned}$$
(13)
$$\begin{aligned}&f=\delta ({F}_{0}({z}^{c})) \end{aligned}$$
(14)

We then split f along the width dimension into two independent tensors \(f_{w1}\) and \(f_{w2}\). Additionally, two (1, 1) convolution transformations, \(F_{w1}\) and \(F_{w2}\), are employed to convert \(f_{w1}\) and \(f_{w2}\) into tensors with the same height or number of channels as the input feature map, resulting in:

$$\begin{aligned}&g=\sigma ({F}_{w1}({f}_{w1})) \end{aligned}$$
(15)
$$\begin{aligned}&g=\sigma ({F}_{w2}({f}_{w2})) \end{aligned}$$
(16)

denotes the Sigmoid activation function. Finally, by incorporating the attention weight g, the output Y of the proposed improved attention module can be expressed as

$$\begin{aligned}&{y}_{w}(i,j)={x}_{w}(i,j)*{g}_{w}^{h}(i) \end{aligned}$$
(17)
$$\begin{aligned}&{y}_{w}(i,j)={x}_{w}(i,j)*{g}_{w}^{c}(j) \end{aligned}$$
(18)

Unlike channel attention, which focuses solely on reweighting to balance the importance of different channels, our proposed improved attention mechanism also incorporates the encoding of spatial information. As described above, attention is applied to the input tensor simultaneously along the channel and height dimensions. Each element in the two attention maps reflects whether the object of interest is present in the corresponding row and column. This encoding process enables the attention module to more accurately locate the exact position of the objects of interest, thereby enhancing the model’s overall recognition performance.

Experiment on CCDD-2

Similar to the data partitioning method used in CCDD-1, Jin et al.36 did not randomize the experimental data in order to better simulate clinical situations. Instead, they naturally grouped the data based on the order in which ECG records appeared. However, this data partitioning method may prevent the training set from including all disease types in CCDD, thereby affecting ECG classification performance.

Table 2 Data distribution on CCDD-2.
Full size table

CCDD includes 12 types of diseases such as normal electrocardiograms, sinus rhythms, atrial arrhythmias, junctional arrhythmias, ventricular arrhythmias, conduction blocks, atrial enlargements, ventricular hypertrophies, myocardial infarctions, ST-T changes, other abnormalities, and invalid ECGs. In order to solve the problem of data partitioning in the CCDD-1 experiment, we adjusted the training and testing sets to include samples of each disease as much as possible, so that the classification model can learn more fully. Invalid ECGs were excluded, and 10% from each of the remaining 11 categories were allocated as the training dataset. Subsequently, 10% from each training category served as the validation set. To ensure robust experimental comparisons, the remaining dataset was consistent with the corresponding test set from CCDD-1 in terms of quantity. The proposed data partitioning approach is delineated in Table 2.

Experiment on MIT-BIH-AR database

Following the data partitioning strategy proposed by Zhou et al.40, a proportional split was applied to categorize each heart class in the MIT-BIH-AR database for training and testing sets creation. The segmented training set constituted 21.88% of all heartbeats, as detailed in Table 3. Moreover, 280 normal and 280 abnormal heartbeats, totaling 560, were randomly chosen from the training data for validation purposes.

Table 3 Data distribution on MIT-BIH-AR.
Full size table

The experimental flowchart for the MIT-BIH-AR database is illustrated in Fig. 4. Given the interrelation of information across various leads, the proposed model framework implements a dual-branch methodology, consisting of left and right branches, which integrates both synchronous and asynchronous principles. This architecture facilitates simultaneous multi-lead feature extraction in conjunction with independent feature extraction for each lead in the dual-lead heartbeat data. The left branch employs two layers of convolution, with kernel sizes of (1, 5) and (1, 12), respectively. During the convolution process, the features from the two leads are extracted sequentially. The right branch processes the two leads simultaneously using convolution kernels of (2, 2) and (2, 15) to amplify the correlation between information from different leads. Afterward, the input data is processed using a (1, 1) convolution kernel to uniformly adjust the number of channels, which is then merged through a shortcut as input to the LEA module. After the feature map has been processed by the LEA, partial convolution is employed to handle the data; this technique, originating from image restoration, remains effective for processing ECG signals, which are sequential data. The data then undergoes batch normalization, scaling and shifting, non-linearity, and average pooling to enhance the model’s classification performance. Following the combination of the outputs of the left and right branches these outputs pass through the BiLSTM module, and the subsequent results are processed through the Dense layer and Softmax to generate a portion of the classification weights. During feature extraction in the left branch, the feature maps at each stage are processed with a (1, 1) convolution kernel, unifying the number of channels to 8 and combining them one by one with the higher-level feature maps via upsampling. After processing with a (1, 3) convolution kernel, we obtain three feature maps that descend from large to small. Finally, we perform linear processing from top to bottom to consolidate the three feature maps into one, followed by further linear layers and Softmax processing to produce another portion of the classification weights. In the classification phase, we do not employ a rule inference module; instead, we combine the two classification weights to infer the classification of normal and abnormal records. During the judgment process, the criterion followed is that if either result identifies the heartbeat record as abnormal, then that heartbeat is classified as abnormal; conversely, for a heartbeat to be regarded as normal, both weights must indicate normal.

Fig. 4
figure 4

Overview of the proposed method on MIT-BIH-AR.

Full size image

Results

Result on CCDD-1

Table 4 presents the classification outcomes of our proposed ECG analysis algorithm on the small-scale testing set, which comprises 11,760 records from the CCDD. In the table, ’0’ represents the proposed model structure, while ’RF’ signifies the rule inference module. Normal ECG records account for 71.34% of the dataset. To validate the efficacy of the rule inference module, we compared the experimental results obtained with and without the use of the rule inference module. After employing the rule inference module, indicated by the results labeled as ’0+RF’ in the table, we observed a 3.1% increase in Sensitivity (Se) while Accuracy (Acc) remained unchanged. This suggests that the model is more capable of correctly identifying a greater number of normal class records, effectively reducing the number of normal records misclassified as abnormal. This outcome aligns with our objective of alleviating the workload of physicians in clinical settings. Furthermore, we conducted a pairwise comparison with the methods proposed by Zhou and Jin. Under the division scheme of the small-scale testing set, the Specificity (Sp) of our proposed method is comparable to that of Zhou’s approach, while both Se and Acc surpass those of both methods.

Table 4 Statistical results of small-scale testing set.
Full size table

Table 5 presents the classification results for 151,274 test samples in CCDD, which represent the model’s performance on the large-scale testing set. In this table, ’0’ represents the proposed model structure, ’CA’ denotes Coordinate Attention (CA)42, ’SE’ refers to the Squeeze and Excitation (SE) attention mechanism43, our proposed Lead Encoder Attention is labeled as ’LEA’, and ’RF’ indicates the rule inference module. Among all test samples, the proportion of normal class records is 58.7%.

Table 5 Statistical results of large-scale testing set.
Full size table

The algorithm prioritizes screening normal ECG records to enable healthcare professionals to concentrate on abnormal records, reducing their workload. The primary goal is to optimize the TPR9544. To validate the effectiveness of the proposed attention module, we compared LEA with the CA and SE attention mechanisms. The results presented in the table indicate that, compared to the SE attention mechanism, LEA achieves a higher TPR95 while maintaining a consistent AUC. This suggests that LEA can help alleviate the workload for physicians. In comparison to CA, LEA’s AUC is slightly lower; however, LEA demonstrates superior performance in terms of Sp, Se, Acc, and the most critical metric, TPR95. This undoubtedly confirms the effectiveness of the proposed attention module. In summary, LEA is more suitable for ECG classification tasks than the CA and SE attention mechanisms. Additionally, we verified the efficacy of the rule inference module on the large-scale testing set. Analyzing the results of the rule inference shows noticeable enhancements in various metrics, albeit at the cost of reduced sp. Notably, Se increased by 3.4%, and TPR95 improved from 49.3% to 61.3%. This advancement could reduce physicians’ workload by 34.5% (calculated as 56.3% multiplied by 61.3%), indicating significant progress. Finally, we compared the performance of our proposed method with those of currently advanced algorithms. The results indicate that, although the Sp of our method is slightly lower than that of Zhou’s approach, both the Se and Acc are significantly higher, with an improvement in Se reaching 8%, a noteworthy enhancement. When compared to Jin’s method, our approach demonstrates an improvement in Acc; however, the results for TPR95 remain unsatisfactory. To address the shortcomings in TPR95, we innovated and refined the data partitioning method, which is elaborated upon in the subsequent section regarding the CCDD-2 experiment.

Result on CCDD-2

As previously noted, we identified the potential for enhancing the data partitioning method utilized in prior CCDD research, prompting the introduction of a novel partitioning approach tailored for CCDD. Table 6 depicts the outcome of the newly proposed partitioning method, encompassing 151,274 samples within the test dataset, exhibiting a normal record ratio of 58.66%. The test set size and the normal record ratio align with those of CCDD-1. The tabulated data illustrates substantial enhancements in Se, NPV, AUC, and TPR95 following the implementation of the new segmentation method, unequivocally showcasing its superiority. We hypothesize that, compared to Jin’s data partitioning method, the novel approach presented in this section-which categorizes heartbeats into more detailed classes and incorporates them into the training process-is more advantageous for enhancing the robustness of the proposed model. This diversity in data types will allow the model to acquire a broader range of heartbeat features during the feature extraction phase, while the rule inference associated with different heartbeat categories will optimize the weight parameters during backpropagation.

Table 6 Statistical results of new segmentation on CCDD.
Full size table

Furthermore, our observations indicate that using rule inference entails a trade-off between decreased Sp and increased Se. Recognizing our model’s emphasis on accurately classifying normal records to boost TPR95, we lean towards leveraging rule inference. Through the adoption of the new partitioning strategy, we have overcome the shortfall of surpassing Jin in the CCDD-1 study, distinctly affirming the alignment of the new segmentation with the model’s learning patterns compared to the old approach. Moreover, TPR95 has notably surged to an exceptional 78.5% under the new partitioning method, resulting in a remarkable 44.2% reduction in physicians’ workload (= 56.3% \(\times\) 78.5%). This advancement not only lessens doctors’ burden by an additional 9.7% compared to that of CCDD-1 but also represents the most promising outcome achieved within the CCDD framework to date.

Result on MIT-BIH-AR database

Table 7 displays the classification outcomes of our ECG analysis algorithm on 85,980 core heartbeat records from the MIT-BIH-AR database. The achieved Acc of 99.5% stands out as the highest among the comparative literature, matching Zhou’s method. Sp also performs equally well to Shi’s method at 99.6%. However, room for improvement remains in Se compared to other approaches.

Table 7 Statistical results on MIT-BIH-AR.
Full size table

We contend that the lower Se is attributed to the model’s structure which is more suited to processing complete ECG recordings as long sequences, thus facilitating adequate temporal feature extraction. Additionally, the limited number of leads poses a challenge in determining and encoding the feature location information for different disease types across different leads. In the MIT-BIH-AR database, the data processing method segments the data according to heartbeats. Compared to the long sequence data in the CCDD, although this approach reduces the computational burden on the model, it simultaneously complicates the model to capture the temporal features of adjacent heartbeats and those occurring within specific time frames. This ultimately results in the suboptimal performance of the proposed model on the dataset.

The experiments conducted on the MIT-BIH-AR database were designed to demonstrate the generalizability of the proposed method. However, many existing methods have already achieved outstanding results in the intra-patient classification tasks based on this database, with accuracies exceeding 99%. This suggests that there is limited potential for improvement and that the advantages of our method may not be substantial. Throughout the experimental process, numerous initialization parameters, including the random seed, were fixed. As a result, after multiple rounds of experiments, the error range of the results stabilized at \(\pm 0.02\%\). Compared to the baseline, the experimental results did not show significant disadvantages or shortcomings, and we assert that these findings sufficiently demonstrate that the model can effectively manage both classification tasks when ECG input data is represented as long sequences or heartbeat lengths, thus indicating its generalizability.

Discussion

Classifying normal and abnormal ECG records presents a formidable challenge. Deep learning, a prominent research focus in recent years, has shown significant success in addressing complex artificial intelligence tasks50,51,52. The CNN-based deep learning network introduced in this study extracts features at varying scales, consolidates them through diverse methods to consider both time series and spatial features across different leads, and then employs multiple classifiers and rules to identify heart rate anomalies for comprehensive assessment. Results of the CCDD experiments underscore the efficacy of the proposed method for biomedical time-series classification. Moreover, the proposed model architecture incorporates an attention mechanism crucial for enhancing ECG classification performance. As demonstrated in Table 5, the proposed attention mechanism outperforms other attention methods in classifying normal and abnormal ECG records. Comparison with established methods for ECG classification, as presented in Table 6, reveals that the proposed approach achieves comparable or superior results, confirming its superiority. Nonetheless, the scope for refinement remains in our methodology. Data in Table 7 suggests that the model excels in analyzing complete ECG records over individual heartbeats, indicating a preference for comprehensive time series data.

First, in the experiments based on the MIT-BIH-AR database, the data was partitioned using an intra-patient approach. Specifically, after segmenting each ECG record by heartbeats, all data was shuffled and randomly divided into training and test sets. Consequently, a portion of the ECG records corresponding to one patient served as training samples, while another portion served as test samples. This partition enables the model can recognize the feature information from the same record in advance, thereby enhancing results in the testing phase. Conversely, the experiments involving the CCDD employed an inter-patient division, where the patient records in the training and test sets were mutually exclusive. In this context, each record served exclusively as either a training sample or a test sample, ensuring no data overlap. The inter-patient division method has historically posed a significant challenge in the automatic classification of ECGs. Although there remains potential for improvement in the results obtained from the CCDD relative to those from the MIT-BIH-AR database, our current findings represent the best performance among all evaluated methods.

Secondly, in the CCDD, the quality of signals collected in the CCDD was suboptimal due to various uncontrollable factors. These factors include but are not limited to, a variety of noises present for extended durations, sudden detachment of recording electrodes, which leads to signal loss, and difficulties in detecting R-peak markers within the recordings. Collectively, these issues pose significant challenges to the recognition of abnormal categories in ECG records. In future research, we aim to addess these challenges through algorithm optimization.

Furthermore, this study is limited to the one-dimensional sequence processing of ECGs. Exploring technologies like wavelet transformations, compressive sensing, and class-switching methodologies and integrating them into the proposed approach may yield enhanced combinations and elevate classification performance.

Conclusion

This study introduces a convolutional neural network that integrates mixed scales and hierarchical features for multi-lead ECG classification. To replicate real-world clinical scenarios, we conducted validation using the CCDD and testing with the MIT-BIH-AR database to demonstrate the model’s adaptability. Experimental findings indicate that our model excels in terms of Acc on CCDD achieving 87.7%, which is the highest among all methods. Although the NPV also reached 90%, it falls short in terms of TPR95, only attaining 61.3%, slightly inferior to the method proposed by Jin. To address this challenge-specifically, to reduce the workload of physicians in clinical settings-we propose a novel partitioning approach that enables the model to learn features from all ECG record types during training.

This method achieves a remarkable TPR95 of 78.5%, surpassing the performance of current methods, Meanwhile, both Acc and NPV have further improved, reaching 88.5% and 93.9%, respectively. The AUC also exceeded that of currently advanced algorithms, achieving 94.1%. Additionally, validation results on the MIT-BIH-AR database demonstrate the proposed method’s generalizability, effectively addressing both long sequences and heartbeat classification tasks. In the heartbeat classification task, the Acc reached 99.5%, while Sp attained 99.6% \(\circ\) In conclusion, our research effectively illustrates the viability of automated cardiac arrhythmia classification, enhancing the diagnosis and treatment of cardiovascular conditions while alleviating physicians’ workloads, which undoubtedly holds significant clinical application.

Although the proposed model demonstrates promising results, it may still face several challenges. First, experiments involving ECG sequences of 9.5 seconds in duration from the CCDD, calculations show that using ECG as 1D data input results in a model with 6,766,895 parameters, 745.5 million floating-point operations (FLOPs), and 27.4 million memory reads and writes (MemR+W). Although the computational complexity is not excessively high, there remains potential for optimization when compared to some lightweight models.

One of our future research directions will be identifying ways to optimize the model while maintaining performance. Secondly, our emphasis is on extracting temporal and spatial features directly from the ECG signal itself as a one-dimensional sequence; converting ECG records into two-dimensional images may facilitate breakthroughs, but it will also introduce considerable computational burdens. Finally, as the medical field continues to seek models with broad applicability, future efforts should ensure that our model demonstrates strong generalization capabilities across different datasets.