Introduction

Neural Architecture Search (NAS) automates designing neural architectures for specific tasks, surpassing manual designs in various tasks1,2,3. The original NAS method focused on improving the search for the best architecture within the search space. However, training each sampled candidate architecture from scratch during the search led to significant computational costs and time overheads1. Recent advancements in NAS algorithms have notably mitigated this cost, though many require specialized implementations4. For instance, weight sharing among neural architectures with identical operations reduces the need for training each architecture from scratch5. But while this saves resources, it adds complexity to the search process, requiring fine-tuning for optimal performance.

To mitigate search costs in NAS, predictor-based methods expedite architecture accuracy prediction using model performance predictors, rather than training all architectures to achieve accuracy6,7,8. While simple training-free predictors exhibit potential in some scenarios, their actual performance often falls short. Consequently, numerous studies concentrate on designing effective training-based predictors, typically comprising an encoder and regressor module9,10,11. These predictors are trained on surrogate datasets comprising architecture-accuracy pairs. Leveraging pre-trained predictors enables direct querying of the performance of any network structure in the same search space, thereby accelerating the search process.

During predictor training, architectures are represented with discrete encoding. Most predictor-based methods typically transform this discrete data into a continuous latent space, extracting meaningful features to model accurate architectural mappings. Among existing performance prediction methods, neural predictors8 and CTNAS7 rely on graph convolutional networks (GCN)12 to capture the feature representation of the model structure, while SemiNAS9 and GATES13 achieve the feature representation of the architecture by learning the embedding matrix of candidate operations in the search space. ReNAS14 calculates the type matrix, the FLOPs matrix, and the parameter matrix, and concatenates them to form a feature tensor to represent a specific architecture. AutoGO15employs an evolutionary strategy to perform mutations on the computational graphs of neural networks, aiming to optimize network performance and hardware compatibility. It assesses the impact of mutations using a pre-trained neural predictor and utilizes Mixed Integer Linear Programming (MILP) to ensure the validity of the resulting architectures. These methods have made some progress in performance prediction, but they still face challenges in capturing deep architectural features and optimizing the search process. There are two main issues: First, the generalizability of neural predictors is low. Predictors mainly focus on discovering how different operations at local nodes affect architecture performance, lacking attention to the entire path from input to output. Second, the efficiency of architecture search is low. Predictors only evaluate architectures and do not provide forward guidance for discovering new architectures.

Unlike previous methods, we proposed an attention-driven evolutionary neural architecture search algorithm (AE-NAS) that achieves forward evolution using an attention mechanism. We integrate the attention mechanism into the predictor model based on Transformer16 and utilize path-based architecture encoding17 as the input for the predictor. Transformer offers several advantages for training effective performance predictors. First, the self-attention module can help explore better feature representations from the graph structure data. Second, the multi-head mechanism can further help encode the different subspace information at different positions from the graph structure data. Third, the path-based architecture encoding method also helps the predictor model attention module to identify critical paths in the architecture.

Generally speaking, our contributions can be summarized as follows:

  • We propose a NAS performance predictor based on Transformer to enhance spatial topological information encoding. By incorporating the attention mechanism and combining it with path-based architecture encoding, the predictor accurately evaluates architecture performance.

  • We propose AE-NAS, a neural architecture search algorithm utilizing the attention mechanism for forward evolution. The attention-based predictor accurately evaluates architecture performance and identifies critical paths. By dynamically adjusting the search direction based on path importance, AE-NAS can prioritize exploring architectures with greater potential, guiding the search process positively to enhance efficiency.

  • Our comparative experiments on AE-NAS within the search spaces of NAS-Bench-10118 and NAS-Bench-20119 confirm that the attention-based predictor model significantly enhances both the accuracy of architectural performance prediction and search efficiency.

Related work

Due to the high search costs of traditional NAS methods like reinforcement learning1,20 and evolutionary algorithms3,21, there’s growing interest in NAS technology using network performance predictors. Most studies train predictors with limited architecture-accuracy data pairs to effectively estimate unobserved architecture performance, termed training-based network performance predictors. Additionally, some research suggests characterizing network performance by calculating specific indicators on the network structure without training, known as training-free network performance predictors.

Training-based network performance predictors

Training-based network performance predictors aim to learn the correlation between network architecture and its accuracy. Extracting useful features directly from discrete network architectures is challenging, so researchers have explored methods to map discrete representations to continuous latent spaces. These methods can be broadly categorized into sequence-based and graph-based approaches. Sequence-based schemes represent each architecture using fixed-length discrete sequences, which are then transformed into continuous representations. Techniques such as multilayer perceptrons14,22,23, embedding matrices13,24, Auto-Encoders9,25,26, or gradient boosted decision trees27 are commonly employed for this conversion. In contrast, graph-based methods treat the architecture as a graph structure and utilize graph-form data, including adjacency matrices and node features. Various graph processing technologies, such as GHN28, GCN7,8,29,30, GIN31, WL-Kernel32, etc., have been explored in this context. Like previous methods, our Transformer-based predictor is categorized as a training-based network performance predictor. However, we introduce a novel encoding scheme: the path-based architecture encoding method. This approach, combined with attention-based predictive models, enables accurate assessment of architecture performance and identification of critical paths within the architecture.

Training-free network performance predictors

Several works have explored direct metrics for evaluating network performance without relying on training processes.33 evaluated network performance during initialization by computing the correlation between binary codes across the entire mini-batch. TE-NAS34 predicts network performance by analyzing its trainability and expressiveness. Zero-Cost NAS6 evaluates network performance using six proxy metrics such as grasp35, fisher36,37, synflow38 and so on, but fails to meet expectations in the NAS-Bench-10118 architecture ranking. Zen-NAS39 evaluates network expressiveness based on expected Gaussian complexity. While these training-free methods have shown effectiveness across multiple datasets and yielded promising results, they exhibit limited robustness and significant cross-task performance fluctuations. Compared to these methods, our training-based predictor is more time-consuming, but its performance is dramatically better.

Methods

In this section, we first review the common paradigm of training-based NAS predictors in neural architecture search algorithms. Following the same paradigm, we introduce path encoding to represent architectural features, then detail the design principles and specific implementation of predictors utilizing the attention mechanism. Finally, we proposed a complete NAS algorithm: Attention-Driven Evolutionary Neural Architecture Search (AE-NAS).

Training-based network performance predictors

Previous works7,8,14,25 proposed employing an encoder \(f_{E}\) as the initial step to convert discrete architectures into continuous feature representations, as formulated below:

$$\begin{aligned} e=f_E(A,\kappa ) \end{aligned}$$
(1)

where \(A\in {\mathbb {R}}^{N\times N}\) denotes the adjacency matrix and stands for the directed acyclic connections between nodes, N denotes the number of the nodes. \(\kappa \in {\mathbb {R}}^{N\times F}\) stands for the feature matrix and represents the characteristics of the nodes, F denotes the output dimension of the embedding extractor. For NAS predictors, the adjacency matrix A shows the topology information of an architecture and \(\kappa\) usually indicates the representation of operations for nodes or edges. Among previous works, the encoder \(f_{E}\) can be a GCN or LSTM or simply an embedding matrix, and the embedding vector e can be interpreted as a latent representation of a specific architecture.

After encoding the discrete architecture into a continuous representation using an encoder, it is easier and more accurate to estimate the network accuracy \(\widehat{y}\) by a simple regressor \(f_{R}\) once the embedding vector e meaningfully represents the architecture in the latent space:

$$\begin{aligned} \widehat{y}=f_R(e) \end{aligned}$$
(2)

Architecture encodings

The majority of existing work on neural predictors use an adjacency matrix representation to encode the neural architectures. In Eq. (1), the adjacency matrix encoding A gives an arbitrary ordering to the nodes, and then gives a binary feature for an edge between node i and node j, for all \(i < j\). Then a list of the operations at each node must also be included in the encoding. This is a challenging data structure for a neural predictor to interpret because it relies on an arbitrary indexing of the nodes, and features are highly dependent on one another. For example, an edge from the input to node 2 is useless if there is no path from node 2 to the output. And if there is an edge from node 2 to the output, this edge is highly correlated with the feature that describes the operation at node 2 (\(conv 1 \times 1\), \(pool 3 \times 3\), etc.).

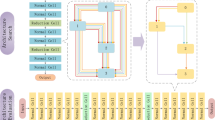
For the above reasons, we utilize an existing encoding method known as path encoding. Prior to employing a trainable encoder to convert the discrete structure into a continuous representation, we utilize a fixed transformation method to path encode the adjacency matrices A and \(\kappa\) in Eq. (1). The resulting path encoding is then utilized as input for training the Transformer-based Predictor.

The path encoding is quite simple to define: there is a binary feature for each path from the input to the output of an architecture cell, given in terms of the operations (e.g., \(input\rightarrow conv 1 \times 1 \rightarrow pool 3 \times 3\rightarrow output\)). To encode an architecture, we simply check which paths are present in the architecture, and set the corresponding features to 1s. See Fig. 1. Intuitively, the path encoding has a few strong advantages. The features are not nearly as dependent on one another as they are in the adjacency matrix encoding, since each feature represents a unique path that the data tensor can take from the input node to the output node. Furthermore, there is no longer an arbitrary node ordering, which means that each neural architecture maps to only one encoding (which is not true for the adjacency matrix encoding). On the other hand, it is possible for multiple architectures to map to the same path encoding (i.e., the encoding is welldefined, but it is not one-to-one). However,17 showed that architectures with the same path encoding also have very similar validation errors.

Fig. 1
figure 1

A neural architecture (left), is decomposed into a set of its paths from input to output (middle), which is then encoded as a one-hot vector (right).

Full size image

Attention-based predictor

The attention-based predictor we propose consists of an encoder and a regressor, as depicted in Fig. 2. The architectural encoding p of length L is first fed into a semantic embedding layer of size \(d_{e}\):

$$\begin{aligned} Emb=Embedding(p) \end{aligned}$$
(3)

The path encoding p is transformed by the embedding matrix \(W\in {\mathbb {R}}^{L\times M}\) to acquire the semantic embedding \(Emb\in {\mathbb {R}}^{L\times M}\). Next, three Transformer encoders are employed to process Emb, enabling contextualization of the embedding vector through multiple levels of abstraction. We denote the hidden state after l-th encoder layer as \(H^{l}=\left[ H_{1}^{l},...,H_{N}^{l} \right]\) of size \(d_{h}\), where \(H^{l}=T(H^{l-1})\) and T is a transformer block containing \(n_{head}\) heads. The \(l-th\) Transformer block is calculated as:

$$\begin{aligned} & Q_{k}=H^{l-1}W_{qk}^{l}, K_{k}=H^{l-1}W_{kk}^{l},V_{k}=H^{l-1}W_{vk}^{l} \end{aligned}$$
(4)
$$\begin{aligned} & \widehat{H}_{k}^{l} =softmax\left( \frac{Q_{k}{K_{k}}^T}{\sqrt{d_{h} } } \right) V_{k} \end{aligned}$$
(5)
$$\begin{aligned} & \widehat{H}^{l}=concatenate\left( \widehat{H}_{1}^{l},\widehat{H}_{2}^{l},...,\widehat{H}_{n_{head} }^{l} \right) \end{aligned}$$
(6)
$$\begin{aligned} & H^{l} =ReLU\left( \widehat{H}^{l}W_{1}+b_{1} \right) W_{2}+b_{2} \end{aligned}$$
(7)

where the initial hidden state \(H_0\) i is Emb , thus \(d_e = d_h\). \(Q_k\), \(K_k\), \(V_k\) stand for “Query”, “Key” and “Value” in the attention operation of the k-th head respectively. \(W_1\) and \(W_2\) represent the weights in the feed-forward layer, yielding a continuous representation: \(e=H^l\). Finally, a regressor is used to estimate the final accuracy \(y^{pre}\):

$$\begin{aligned} y_{pred}=MLP\left( e \right) \end{aligned}$$
(8)
Fig. 2
figure 2

Our attention-based NAS predictor mainly consists of an encoder and a regressor. We first encode the information of path into continuous representation, followed by 3 Transformer encoder layers, and the regressor uses the output feature of Transformer encoder layers to derive the final prediction.

Full size image

Attention-driven evolutionary framework

Based on the previous sections on architecture encoding and attention-based predictor design, we propose a complete NAS algorithm: Attention-based Forward Evolutionary Neural Architecture Search (AE-NAS). See algorithm 1. We leverage the self-attention mechanism in the Transformer encoder to evaluate and optimize the importance and interactions of each path in the architecture. This allows the algorithm to identify and emphasize the paths with the greatest impact on performance, while ignoring those with less influence.Specifically, algorithm 1 initially samples \(t_0\) neural network architectures uniformly at random from the given search space \(A\), and trains these architectures on the dataset \(D\) to obtain corresponding validation errors. During the iterative search process, we train an ensemble of five identical feedforward neural network predictors, using path encoding to represent each architecture, based on all architectures and their validation error data in the architecture pool up to the current iteration. The prediction accuracy and uncertainty estimation of feedforward neural networks based on path coding are superior to complex graph convolutional networks and variational autoencoders. At the same time, they have higher computational efficiency, faster training and inference speed, and are easy to implement and expand23. For the search of new architectures, we perform mutation operations based on the attention weights of each path in the architecture: discarding paths with low weights and adding paths with high weights that do not exist in the original architecture, thereby generating a new set of candidate architectures. Then, we evaluate all candidate architectures using the average of the five predictor models and select the architecture with the lowest validation error to join the architecture pool for the next round of iteration.

For the loss function in attention-based predictors, we use mean absolute percentage error (MAPE) because it gives a higher weight to architectures with lower validation losses:

$$\begin{aligned} \mathcal {L}\left( y_{pred},y_{true}\right) =\frac{1}{n}{\textstyle \sum _{i=1}^{n}}\left| \frac{y_{pred}^{\left( i\right) }-y_{LB}}{y_{true}^{\left( i\right) }-y_{LB} } -1\right| \end{aligned}$$
(9)

where \(y_{pred}^{\left( i\right) }\) and \(y_{true}^{\left( i\right) }\) are the predicted and true values of the validation error for architecture i, and \(y_{LB}\) is a global lower bound on the minimum true validation error.

figure a

Algorithm 1. AE-NAS.

Experiments

Due to the complexity of reproducing NAS algorithms, we thoroughly evaluate AE-NAS by referencing comparative experiments from existing NAS algorithm research and predictor-based NAS studies. We set two evaluation metrics to compare AE-NAS with other popular methods. The first evaluation metric is the test error of the best-searched architecture. Following the BANANAS23 experiment settings, we maintain an architecture pool in the search space and iteratively search for new architectures. Each iteration returns the architecture with the best validation error in the current pool. The test error of the final architecture with the lowest validation error is used to evaluate each algorithm. The second evaluation metric is Kendall’s Tau coefficient. Following the TNASP10 experiment settings, we use this coefficient to assess predictor performance by comparing the predicted accuracy rankings with the actual accuracy rankings of the test samples.

We compare the proposed AE-NAS with many other popular NAS algorithms on two search spaces: NAS-Bench-10118 and NAS-Bench-20119. The NAS-Bench-10118 dataset consists of over 423,000 neural architectures from a cell-based search space, and each architecture comes with precomputed validation and test accuracies on CIFAR-10. The search space consists of a DAG with 7 nodes that can each take on three different operations, and there can be at most 9 edges between the nodes. We use the open source version of the NAS-Bench-101 dataset. The NAS-Bench-20119 dataset consists of 15625 neural architectures with precomputed validation and test accuracies for 200 epochs on CIFAR-10, CIFAR-100, and ImageNet-16-120. The search space consists of a complete directed acyclic graph on 4 nodes, and each edge can take on five different operations.

Performance results on NAS-Bench-101

We compare AE-NAS to the most popular NAS algorithms from a variety of paradigms: random search40, regularized evolution3, BOHB41, NASBOT42, local search43, TPE44, BOHAMIANN45, BONAS46, REINFORCE47, GP-based BO48, AlphaX49, GCN Predictor8, DNGO50, and BANANAS23. As much as possible, we use the code directly from the open-source repositories, without changing the hyperparameters.

We maintain a sampling architecture pool during the search process, initially containing 10 architectures. In each iteration, candidate architectures are generated and evaluated. The best-performing candidate is added to the pool, and the test error of the architecture with the best validation error is recorded. The search ends when the pool size reaches T = 150. The results are shown in Table 1. To enable better parallel processing, each algorithm selects the top 10 candidate architectures in each iteration to add to the architecture pool. We conducted 200 trials for each algorithm and averaged the results. Our proposed AE-NAS algorithm and the BANANAS algorithm by White et al. tied for first place. AE-NAS shows significant advantages over traditional models and achieved the highest performance in 200 experiments. The architecture pool found the architecture with the lowest test error by iteration 60 on average, demonstrating AE-NAS’s improved search efficiency for competitive architectures guided by the attention mechanism.

Table 1 Comparison of the architectures with the lowest test error (averaged over 200 trials) returned by NAS algorithms after 150 architecture evaluations on NASBench-101. \(^{\dagger }\): results from BANANAS.
Full size table

Ranking results on NAS benchmarks

Following the data segmentation and experimental settings in TNASP, we selected 0.02%, 0.04%, 0.1%, and 1% of the whole data as training sets to train the predictor model on NAS-Bench-101. And we use all the data as a test set to calculate Kendall’s Tau to evaluate the ranking correlation between predicted and actual accuracies. The results are shown in Table 2. For NAS-Bench-201, we use 0.05%, 1%, 3%, 5%, and 10% of the data as training sets. NAS-Bench-201 provides three different results of each architecture on three different datasets and we choose CIFAR-10 results as our targets. The results are shown in Table 3.

Experimental results on two NAS benchmarks indicate that with extremely scarce training data (0.02%, 0.04%, and 0.05%), the performance of the AE-NAS method is comparable to other predictor-based NAS algorithms. As the training data increases, the attention mechanism significantly enhances the AE-NAS method’s performance, approaching state-of-the-art (STOA) levels and achieving a suboptimal effect. This demonstrates that AE-NAS is highly competitive among predictor-based NAS algorithms.

Table 2 Comparison with other methods on NAS-Bench-101. We calculate the Kendall’s Tau by predicting accuracy of all architectures in NAS-Bench-101. \(^\dagger\): results from CTNAS. \(^\ddagger\): reported by TNASP.
Full size table
Table 3 Comparison with other methods on NAS-Bench-201. We calculate the Kendall’s Tau by predicting the accuracy of all architectures in NAS-Bench-201 and comparing them with ground truths. \(^\ddagger\): reported by TNASP.
Full size table

Ablation studies

Encoder and regressor

To verify how the attention mechanism enhances the AE-NAS algorithm’s performance, we examined the impact of stacked attention modules in the AE-NAS encoder and the number of feedforward neural network layers used by the regressor. The experimental setup follows Section 4.1, with results presented in Table 4 We found that the encoder significantly impacts the AE-NAS algorithm’s effectiveness more than the regressor. Increasing the number of attention modules in the Transformer’s encoder from 0 to 1 results in the greatest improvement in search performance. Conversely, the number of layers in the regressor’s feedforward neural network has minimal impact on the final architecture’s performance, especially after incorporating the Transformer encoder. We attribute this to the encoder already containing multiple feedforward neural networks, reducing the regressor’s overall importance.

Table 4 Ablation experimental results of AE-NAS encoder and regressor on NASBench-101.
Full size table

Positive guidance of attention mechanism

Using the same predictor model, we introduced a random architecture sampling method as a benchmark in the search process of the new architecture and compared it with AE-NAS, which dynamically adjusts the search direction based on attention weights. We conducted ablation experiments according to the settings in Section 4.1. Each NAS algorithm was evaluated on the NAS-Bench-101 benchmark for approximately 150 neural architectures, repeated 200 times, with the results averaged. The results are presented in Table 5. The findings demonstrate that AE-NAS significantly improves search efficiency for competitive architectures by dynamically adjusting the search direction using the attention mechanism.

Table 5 Ablation experiment results for the architecture search process on NASBench-101.
Full size table

Conclusions

In this paper, we propose a NAS performance predictor based on Transformer to enhance spatial topological information encoding. By incorporating the attention mechanism and combining it with existing path-based architecture encoding, the predictor accurately evaluates architecture performance. Moreover, We devise a neural architecture search algorithm utilizing the attention mechanism for forward evolution. The attention-based predictor accurately evaluates architecture performance and identifies critical paths. By dynamically adjusting the search direction based on path importance, AE-NAS can prioritize exploring architectures with greater potential, guiding the search process positively to enhance efficiency.