Introduction

In recent years, the frequent occurrence of extreme temperatures has had many negative impacts on human physical and mental health as well as the development of various industries.

Extreme high temperatures are prone to induce pyrexia and cardiovascular and cerebrovascular diseases and can cause adverse effects such as dry drought in agricultural production. Persistent low temperatures can lead to icy roads, blocked transportation routes and severe interference with the normal order of life and production. Temperature data are characterized by obvious non-stationary fluctuations and are susceptible to a variety of factors, such as geographic location, limiting the application of existing temperature prediction methods. Therefore, improving the accuracy of temperature prediction has become an urgent problem. The establishment of prediction models with higher prediction accuracy and better generalizability will enable the government to issue disaster warnings in a timely manner, help people plan their production and life in advance, reduce the losses caused by meteorological disasters, and improve quality of life.

Currently, there are primarily traditional statistical analysis methods, machine learning methods and deep learning methods in the field of temperature prediction. The analysis methods used include linear regression models and time series analysis methods. Menon et al.1 used time series analysis and multiple linear regression to predict urban temperature trends by combining multiple influencing factors. Dimri et al.2 used the seasonal autoregressive integrated moving average (SARIMA) model to forecast monthly average minimum and maximum temperatures and reported that the Box–Jenkins-based SARIMA model could smooth the data and eliminate seasonal effects but exhibited a significant overprediction phenomenon during extreme temperature events. Zhang et al.3 proposed the geographically weighted regression (GWR) model, which introduces spatial distance as a weight into the linear regression model of surface air temperature and achieves better prediction results than does the ordinary linear regression model. The traditional statistical analysis method effectively predicts series with obvious temporal regularity changes but poorly fits complex and variable time series data.

Machine learning models can fully utilize the original series information without assumptions about the time series and are suitable for complex nonlinear relational time series forecasting tasks. Zhou et al.4 designed an LS-SVM model incorporating fuzzy theory to improve the computational speed and accuracy of temperature prediction. Yoo et al.5 selected the optimal set of variables on the basis of land surface temperature (LST) and atmospheric profile (AP) products from Moderate Resolution Imaging Spectroradiometer (MODIS) satellites and improved the random forest model for temperature prediction, which improved the spatial portability of the model. Martínez-Comesaña et al.6 used the NSGA-II algorithm to optimize the multilayer perceptron (MLP) for predicting the indoor air temperature. Machine learning methods are significantly better than traditional statistical methods in processing massive amounts of temperature data, but they cannot effectively capture the feature distributions in nonlinear time series data, which can lead to lower prediction accuracy to a certain extent.

Deep learning models, including recurrent neural networks (RNNs), long short-term memory (LSTM), gated recurrent units (GRUs), and convolutional neural networks (CNNs), are widely used in the field of temperature prediction. Ren et al.7 used a backpropagation (BP) neural network model to predict the winter road temperature. Zheng et al.8 used deep convolutional autoencoder to identify unauthorized broadcasting, and found it achieved a good performance. Usharani et al.9 improved the loss function in the LSTM model to predict location-specific sea surface temperatures and achieved better results than did standard prediction models. Setiawan et al.10 introduced Luong attention into LSTM and GRU models, which can significantly reduce the prediction error in indoor air temperature prediction tasks. Xiao et al.11 combined the advantages of LSTM and adaptive boosting (AdaBoost) models and proposed a combined LSTM-AdaBoost model to improve the ability to predict short- and midterm sea surface temperatures. The above studies revealed that models such as LSTM and the GRU perform well when processing time series data but consider only the time factor, ignoring the influence of the spatial geographic location between meteorological observation stations. Therefore, the temporal and spatial correlation of temperature data has become an important direction for improving prediction accuracy. Qiao et al.12 recognized the spatial correlation of sea surface temperature data and utilized 3D-CNN to capture spatial correlations among ocean observation points while employing long short-term memory (LSTM) to extract time-dependent features, successfully improving the prediction accuracy. Fu et al.13 proposed a hybrid model of the annual temperature cycle (ATC) and 3D-CNN to capture spatiotemporal information to predict surface air temperature. Zheng et al.14 proposed a hybrid model that combines CNN and LSTM which achieved success in recognizing the discharge pattern of power transformers. However, CNNs are applicable only to Euclidean data and cannot address topological structures. The GCN can obtain local features from graph structures, which compensates for the shortcomings of CNN models. Bai et al.15 introduced the attention mechanism into the T-GCN model to propose the attention temporal graph convolutional network (A3T-GCN) model for predicting traffic flow; Chen et al.16 designed the graph convolutional network (GCN) model with temporal attention (TAGCN) to capture the dynamic temporal correlations and spatial patterns in bike flow. Han et al.17 proposed a combination model of LSTM and the spatial‒temporal graph convolutional network (ST-GCN) to predict the risk of crime in communities; Gao et al.18 proposed the global spatiotemporal graph attention network (GSTGAT) model by introducing dynamic attention coefficients to the GCN model, increasing the accuracy of sea surface temperature predictions.

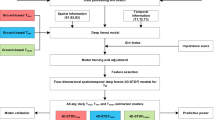
Considering the spatial and temporal correlation of the daily average temperature with previous research results, this paper proposes a combination model based on the T-GCN-Attention and GRU models. This method extracts the spatial features of the daily average temperature data through a GCN, extracts the temporal features through a GRU, uses Luong’s attention to capture the time steps that strongly correlate with the output values, and finally combines the prediction results of the T-GCN-Luong attention with the GRU through variable weights to further reduce the prediction error and the interference of redundant spatial information. This paper utilizes historical data from 15 temperature monitoring stations of the China Meteorological Administration in Jiangsu Province to conduct experiments to compare the prediction errors of the combination model with those of basic models, such as the GRU and T-GCN, and conducts ablation experiments to verify the effectiveness of each module of the combination model. A flowchart of this paper is shown in Fig. 1 :

Fig. 1
figure 1

Flowchart of this paper.

Full size image

Research methods

Temporal and Spatial information capture model

Temperature data have both spatial and temporal correlations. This paper uses the GRU model to capture temporal information and the GCN model to capture spatial information in combination with the spatial and temporal information capture model T-GCN.

GRU

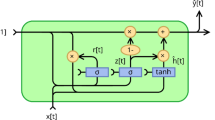
The temperature data have a strong temporal correlation, and the recurrent neural network (RNN) is the predominant model for processing sequential data. An RNN can utilize the built-in recurrent structure to transfer past information to the present, which improves the sequential data processing ability; however, as the time step increases, the internal data are repeatedly multiplied by the weight matrix, and a serious gradient explosion or vanishing problem occurs, which leads to the inability to learn. The RNN variants LSTM and GRU have been shown to solve the above problems by memorizing long-term information via control gates19. A GRU has a similar structure to an LSTM network, but a GRU has a simpler structure with fewer parameters, and the training speed is faster. Specifically, the GRU has two gates, the reset gate and the update gate. The update gate controls the combination of current information and past information, and the reset gate controls the influence of the past state on the current state. The specific calculation process of the GRU model is shown in Eqs. (1)–(4):

$$u_{t} = \upsigma \left( {W_{u} *\left[ {X_{t} ,h_{{t - 1}} } \right] + b_{u} } \right)$$
(1)
$$r_{t} = \upsigma \left( {W_{r} *\left[ {X_{t} ,h_{{t - 1}} } \right] + b_{r} } \right)$$
(2)
$$c_{t} = \tanh \left( {W_{c} \left[ {X_{t} ,\left( {r_{t} *h_{{t - 1}} } \right)} \right] + b_{c} } \right)$$
(3)
$$h_{t} = u_{t} *h_{{t - 1}} + \left( {1 - u_{t} } \right)*c_{t}$$
(4)

where \(\:{\text{h}}_{\text{t}-1}\) denotes the hidden state output at moment t-1, \(\:{\text{u}}_{\text{t}}\) denotes the update gate, \(\:{\text{r}}_{\text{t}}\) denotes the control gate, \(\:{\text{c}}_{\text{t}}\) represents the content stored at moment t, and \(\:{\text{h}}_{\text{t}}\) represents the output result of the hidden state at moment t.

GCN

Temperature data are also spatially correlated, so spatial information needs to be introduced. Traditional convolutional neural networks can capture local spatial information but are restricted to Euclidean space and lack the ability to handle topology; therefore, they are not applicable to temperature time series data. The GCN is an extension of the CNN and is essentially a spatial feature extractor that can handle topological graphs with correlations established by vertices and edges20. The principle of the GCN is as follows: for a graph with N nodes and each node with S features, an N*S-dimensional feature matrix X and an N*N adjacency matrix A are constructed on the basis of the adjacency between every two nodes; then, A and X are used as inputs. The propagation between layers is performed as shown in Eq. (5):

$$H^{{l + 1}} = \sigma \widetilde{{D^{{ - \frac{1}{2}}} }}\hat{A}\widetilde{{D^{{ - \frac{1}{2}}} }}H^{{\left( l \right)}} \uptheta ^{{\left( l \right)}}$$
(5)

where \(\:{\text{I}}_{\text{N}}\) denotes the identity matrix, \({{\hat{\text{A}}}} = {\text{A}} + {\text{I}}_{{\text{N}}}\) denotes the matrix with autocorrelated edges added to each node in the graph, \({{\tilde{\text{D}}}} = \sum\nolimits_{{\text{j}}} {\widetilde{{{\text{A}}_{{{\text{ij}}}} }}}\) is the degree matrix, which indicates the output of l, \(\:{{\uptheta\:}}^{\left(\text{l}\right)}\) includes the parameters, and \(\:{\upsigma\:}\left(\cdot\:\right)\) denotes the sigmoid function of the nonlinear model.

In this paper, the two-layer GCN model extracts spatial information, as shown in Eq. (6):

$${\text{f}}\left( {{\text{X}},{\text{A}}} \right) = \upsigma \hat{\text{A}}\text{Re} {\text{LU}}\left( {\hat{\text{A}}{\text{XW}}_{0} } \right){\text{W}}_{1}$$
(6)

where \({{\hat{\text{A}}}} = \widetilde{{{\text{D}}^{{ - 1/2}} }}{{\hat{\text{A}}}}\widetilde{{{\text{D}}^{{ - 1/2}} }}\)represents the preprocessing step, \(\:{\text{W}}_{0}\in\:{\text{R}}^{\text{P}\times\:\text{H}}\) denotes the weight matrix from the input layer to the hidden layer, \(\:{\text{W}}_{1}\in\:{\text{R}}^{\text{H}\times\:\text{T}}\) denotes the weight matrix from the hidden layer to the output layer, f(X, A)\(\:\in\:{\text{R}}^{\text{N}\times\:\text{T}}\) denotes the final output, P denotes the length of the feature matrix, H denotes the number of hidden layers, T denotes the prediction length, and \(\:\text{R}\text{e}\text{L}\text{U}\left(\:\right)\) denotes the activation layer commonly used in deep learning.

T-GCN

The T-GCN model is based on GCNs and GRUs21, in which the GCN model captures spatial information and the GRU model captures temporal information; the structure of the T-GCN is shown in Fig. 2.

Fig. 2
figure 2

Structure of the T-GCN.

Full size image

The exact calculation process is shown in Eqs. (7)–(10):

$$\:{\text{u}}_{\text{t}}={\upsigma\:}\left({\text{W}}_{\text{u}}\left[\text{f}\left(\text{A},{\text{X}}_{\text{T}}\right),{\text{h}}_{\text{t}-1}\right]+{\text{b}}_{\text{u}}\right)$$
(7)
$$\:{\text{r}}_{\text{t}}={\upsigma\:}\left({\text{W}}_{\text{r}}\left[\text{f}\left(\text{A},{\text{X}}_{\text{T}}\right),{\text{h}}_{\text{t}-1}\right]+{\text{b}}_{\text{r}}\right)$$
(8)
$$\:{\text{c}}_{\text{t}}=\text{t}\text{a}\text{n}\text{h}\left({\text{W}}_{\text{c}}\left[\text{f}\left(\text{A},{\text{X}}_{\text{T}}\right),\left({\text{r}}_{\text{t}}\text{*}{\text{h}}_{\text{t}-1}\right)\right]+{\text{b}}_{\text{c}}\right)$$
(9)
$$\:{\text{h}}_{\text{t}}={\text{u}}_{\text{t}}\text{*}{\text{h}}_{\text{t}-1}+\left(1-{\text{u}}_{\text{t}}\right)\text{*}{\text{c}}_{\text{t}}$$
(10)

where W denotes the weights and b denotes the biases in the training process.

In conclusion, the T-GCN model can address complex spatiotemporal correlation problems by using a GCN to capture spatial relationships and a GRU to capture temporal trends and ultimately complete the prediction task.

Luong attention

The Seq2Seq2 model has been widely used in time series processing in recent years. The model consists of an encoder and a decoder, which process the input sequence and the output sequence, respectively. The encoder processes the input sequences into background vectors, which contain all the information from the original sequences; however, when the amount of information is too large, the performance of the model may degrade, so an attention mechanism needs to be used. This paper introduces the Luong attention mechanism, which can assign different weights to the input data through dynamically variable intermediate variables \(\:{\text{C}}_{\text{n}}\) so that the decoder focuses on the data at different moments and improves the model’s ability to utilize effective information22. The specific calculation process of the Luong attention mechanism is shown in Eqs. (11)–(15):

$$\:{\text{h}}_{\text{n}}=\text{f}\left(\left[{\text{h}}_{\text{n}-1}\cdot\:{\text{C}}_{\text{n}-1}\right],{\text{y}}_{\text{n}-1}\right)$$
(11)
$$\:{\text{y}}_{\text{n}}^{{\prime\:}}=\text{g}\left({\text{h}}_{\text{n}},{\text{C}}_{\text{n}}\right)$$
(12)
$${\text{C}}_{{\text{n}}} = \sum\limits_{{{\text{j}} = 1}}^{{\text{T}}} {\upalpha _{{{\text{nj}}}} {\text{h}}_{{\text{j}}} }$$
(13)
$$\:{{\upalpha\:}}_{\text{n}\text{j}}=\frac{\text{e}\text{x}\text{p}\left({\text{e}}_{nj}\right)}{{\sum\:}_{\text{m}=1}^{\text{T}}{\text{e}}_{\text{n}\text{m}}}$$
(14)
$$\:{\text{e}}_{\text{n}\text{j}}=\text{S}({h}_{n},{h}_{j})$$
(15)

where \(\:{\text{h}}_{\text{n}}\) denotes the hidden state, \(\:{\text{y}}_{\text{n}}^{{\prime\:}}\) denotes the output, g is a Softmax function, \(\:\left[\cdot\:\right]\) denotes the connection of variables, f is a GRU cellular unit, \(\:{\text{C}}_{\text{n}}\) is an intermediate variable, \(\:{{\upalpha\:}}_{\text{n}\text{j}}\) is the attentional weight at time step n of the decoding layer, \(\:{\text{e}}_{\text{n}\text{m}}\) and \(\:{\text{e}}_{\text{n}\text{j}}\) are the attention values for the decoding layer output with respect to the hidden layer states of inputs at time steps n and j, respectively, and S is the alignment function that indicates the degree of correlation between the input hidden layer state and the decoding layer output.

Variable weight combination of the new attention network and the GRU model

The T-GCN-Luong attention model is able to obtain the spatial features of temperature data by capturing the temperature changes at neighboring stations while processing temporal information; therefore, it is difficult to avoid being affected by redundant spatial information. The residual weight combination model can determine the weight of the base model on the basis of the error between the predicted result and the true value; this approach is a kind of variable weight combination method. The specific calculation process is shown in Eqs. (16)–(18):

$${\text{g}}\left( {{\text{X}}_{{\text{t}}} } \right) = \mathop \sum \limits_{{{\text{k}} = 1}}^{{\text{m}}} {\text{w}}_{{{\text{k}},{\text{t}} - 1}} {\text{f}}_{{\text{k}}} \left( {x_{t} } \right)$$
(16)
$$\:{\text{w}}_{\text{k},\text{t}-1}=\frac{\frac{1}{{{\updelta\:}}_{\text{k},\text{t}-1}}}{{\sum\:}_{\text{k}=1}^{\text{m}}\frac{1}{{{\updelta\:}}_{\text{k},\text{t}-1}}}$$
(17)
$$\mathop \sum \limits_{{{\text{k}} = 1}}^{{\text{m}}} {\text{w}}_{{{\text{k}},{\text{t}} - 1}} = 1\quad {\text{w}}_{{{\text{k}},{\text{t}} - 1}} \ge 0$$
(18)

where \(\:{\text{w}}_{\text{k},\text{t}-1}\) represents the weight of the kth model at instant t-1, \(\:{\text{f}}_{\text{k}}\left({\text{x}}_{\text{t}}\right)\) represents the prediction result of the kth model at instant t, and \(\:{{\updelta\:}}_{\text{k},\text{t}-1}\) represents the sum of the squared prediction errors of the kth model at instant t-1. The variable weight method considers the variation in the residual weights over a certain time step, thus possessing a certain degree of stability.

The variable weight combination model of the T-GCN-Luong attention mechanism and the GRU is based on the residual variable weight method. The combination model is composed of five modules: data preprocessing, spatiotemporal feature extraction, attention allocation, model fusion, and temperature prediction. Specifically, T-GCN extracts the spatiotemporal features of historical temperature data from 15 monitoring stations, Luong attention captures global trends, and the final result is obtained by merging the outputs of the T-GCN-Luong attention and GRU models via the variable weight method.

Experimental analysis

Data sources and processing

The data used in this paper originate from historical daily average temperature data collected at 15 monitoring stations in the China Meteorological Administration in Jiangsu Province (http://data.cma.cn/dataService/cdcindex/datacode/A.0012.0001/show_value/normal.html). The data included the daily average temperature from January 1, 2012, to April 30, 2021, for a total of 74976 samples from 15 stations. There are 58 missing values at the Jiangsu Gaoyou temperature monitoring station and 72 missing values at the Wuxian Dongshan station. For these missing values, the linear interpolation method was used.

Moreover, to improve the convergence speed and prevent the gradient from exploding, this paper uses the min–max method to normalize the data. The data are normalized to [0, 1] in advance and then input into the prediction model to obtain the normalized prediction results; subsequently, through inverse normalization, the actual prediction results are obtained.

In this work, the combination model is used to predict the daily average temperature at 15 stations on day t + 1 on the basis of historical information from the previous t days.

Topological map construction

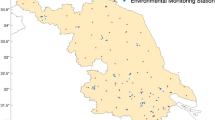
This paper takes 15 temperature monitoring stations in Jiangsu Province as an example to construct the GCN model. The latitudinal and longitudinal data of the 15 monitoring stations are shown in Table 1.

To explore the influence of spatial information on temperature prediction, this paper calculates the Pearson correlation coefficients of the temperature data from 15 stations and selects three stations, Wuxi, Kunshan, and Wuxiandongshan, to determine the correlation coefficients with the other stations, as shown in Table 1. The correlation coefficients of these three stations are very high because they are adjacent, which suggests that the introduction of spatial information is helpful for temperature prediction. Moreover, these three stations are not adjacent to Pizhou and Muyang, resulting in a lower correlation of temperature data, which indicates that whether the stations are adjacent to each other can be used as the basis for whether to introduce spatial information.

Table 1 Correlation of temperature data between selected stations.
Full size table

On the basis of the above analysis, an adjacency matrix is constructed on the basis of the adjacency of the towns in which the 15 detected stations are located. A value of 1 indicates that the two stations are adjacent to each other, and 0 indicates that they are not adjacent or are the same. For example, Muyang Station is located in Suqian and is adjacent to the Xuzhou, Pizhou and Suining stations in Xuzhou city; Guanyun Station in Lianyungang city; and Huaian Station in Huaian city; thus, the adjacency relationship between Muyang Station and the above stations is denoted as 1. Moreover, Suqian and Yangzhou are not adjacent to each other, so the adjacency relationship between Muyang station and Gaoyou station is denoted as 0. On the basis of the latitudinal and longitudinal data of the 15 monitoring stations and the adjacency relationship, the adjacency matrix is plotted in Fig. 3.

Fig. 3
figure 3

Adjacency matrix diagram.

Full size image

Experimental design

Assessment criteria

The root mean square error (RMSE) and mean absolute error (MAE) can reflect the difference between the predicted value and the real value and are easy to calculate and understand; therefore, this paper uses the RMSE and MAE as model evaluation criteria. The calculation formula is shown in Eqs. (19), (20):

$$RMSE = \sqrt {\frac{1}{m}\mathop \sum \limits_{{k = 1}}^{m} \left( {y_{k} - \widehat{{y_{k} }}} \right)^{2} }$$
(19)
$$\:MAE=\frac{1}{\text{m}}\left|{Y}_{K}-\widehat{{Y}_{K}}\right|$$
(20)

where \(\:{\text{y}}_{\text{k}}\) denotes the true value, \(\:\widehat{{\text{y}}_{\text{k}}}\:\) denotes the forecasted value, and m denotes the number of samples in the test set. The smaller the model prediction error is, the smaller the RMSE and MAE are.

Model settings and prediction results

In this work, the data are divided into a training set, a validation set and a test set at a ratio of 8:1:1. This paper uses a sliding window to construct input data via daily average temperature observations with a time step of t to predict the next day’s temperature. The main parameters of the T-GCN-Luong attention-GRU model are set as follows: the number of layers in the GCN is set to 2, the number of hidden units in each layer is 64, the size of the training batch is 20, the number of iterations is 500, and the initial learning rate is 0.001. The activation function is Relu, and the gradient descent method is Adam.

To predict the daily average temperature at 15 stations in Jiangsu Province, owing to the similarity of the average temperature changes at adjacent stations and considering the different neighboring situations of the monitoring stations, Suining, Gaoyou, Nantong, and Kunshan are selected as the four monitoring stations with different orientations to obtain the predicted and actual values of the visualization results, as shown in Fig. 4.

In this work, the daily average air temperature is predicted for 15 stations in Jiangsu Province. Owing to the similarity of the average temperature changes at adjacent stations and the different adjacent situations at the monitoring stations, the Suining, Gaoyou, Nantong, and Kunshan stations were selected to visualize the predicted and actual values, as shown in Fig. 4.

Fig. 4
figure 4

Predicted results for selected sites.

Full size image

The model effectively predicts the daily average temperature. Moreover, compared with those of the GRU, CNN-GRU-Luong attention, T-GCN, T-GCN-Self attention and T-GCN-Luong attention models, the RMSE and MAE of the combination model are the smallest, which indicates that the combination model has good predictive ability. The RMSEs of the 15-site prediction results for each model are shown in Table 2.

Table 2 RMSE values of the prediction results.
Full size table

The MAEs of the 15-site prediction results of each model are shown in Table 3.

Table 3 MAEs of the prediction results.
Full size table

The combination model is the optimal model with the lowest RMSE and MAE. Compared with those of the simple GRU and T-GCN models, the proposed TGLAG model yields average decreases of 31.949% and 13.965%, respectively, in terms of the RMSE and 26.913% and 20.259%, respectively, in terms of the MAE. These findings indicate that the introduction of a GCN to capture spatial information results in significant decreases in the RMSE and MAE of the prediction results, whereas the introduction of the Luong attention mechanism and the variable weight method also greatly affects the decrease in prediction error. Moreover, compared with the GRU model without spatial information, the combined model results in a greater reduction in prediction error at stations such as Dongtai, Gaoyou, and Nanjing. These stations are located in the middle of the adjacency matrix graph and adjacent to multiple stations. This suggests that introducing spatial information can capture the trend of climate change in surrounding areas, which is beneficial for improving prediction accuracy.

Ablation experiment

To evaluate the effectiveness of each module in the combination model, ablation experiments are performed. First, the fusion mechanism is removed from the combination model to obtain the T-GCN-Luong attention model. To examine the effectiveness of the variable weight method, the Luong attention mechanism is removed on this basis to obtain the T-GCN model. To examine whether the Luong attention mechanism is helpful for improving prediction accuracy, the GCN part of the T-GCN model is removed to obtain the simple GRU model to examine whether the prediction accuracy is significantly improved after the introduction of the GCN model, which can extract spatial information. The results of ablation experiments at four monitoring stations, Suining, Gaoyou, Nantong and Kunshan, are shown in Fig. 5.

Fig. 5
figure 5

Ablation experiment results.

Full size image

Compared with the GRU model, the T-GCN model yields average decreases of 20.903% in the RMSE and 8.344% in the MAE, indicating that the introduction of a GCN to capture the spatial features of 15-station daily average temperature data is important for improving the prediction accuracy. The T-GCN-Luong attention model shows an average decrease in the MAE of 11.854%, indicating the effectiveness of the Luong attention mechanism for daily average temperature prediction. The MAE of the combination model decreased by 9.535% compared with that of T-GCN-Luong attention, indicating that the integration of the T-GCN-Luong attention model with the GRU model can alleviate the interference of noisy data at some stations due to the large number of nodes, thus improving the model prediction accuracy.

As a result, the combination model passed through the ablation experiment, which demonstrated that each component of the model contributed significantly to enhancing the prediction accuracy for the daily average temperature at 15 monitoring stations.

Comparative analysis of models

Compared with the existing neural network prediction models that only extract temporal information, the combination model mainly introduces a GCN to extract spatial information and uses the Luong attention mechanism to weight the time step. To verify the effectiveness of the above two modules compared with that of other models, a comparison experiment is performed. By comparing the T-GCN-Luong attention model with the structurally similar CNN-GRU-Luong attention model and the T-GCN-Self attention model, this paper verifies the effectiveness of the GCN in extracting spatial information from temperature data and the advantages of the Luong attention mechanism in prediction tasks.

The experimental results of the model comparison analysis for the selected monitoring stations, Suining, Gaoyou, Nantong, and Kunshan, are shown in Fig. 6.

Fig. 6
figure 6

Comparison of the experimental results.

Full size image

Compared with that of the CNN-GRU-Luong attention model, the prediction error of the T-GCN-Luong attention model decreases by 21.798% in terms of the RMSE and 18.947% in terms of the MAE, which indicates that the addition of spatial information improves the prediction accuracy of the daily average temperature and verifies that the GCN is superior to the CNN in extracting spatial information.

Compared with that of the T-GCN-Luong attention model, the MAE of the T-GCN-Self attention model decreases by 9.948%, indicating that the Luong attention mechanism is more suitable for spatiotemporal prediction of temperature data than the self-attention mechanism is. These findings verify the correctness of the combination model for introducing the above modules.

The daily average temperatures in different regions exhibit spatiotemporal correlations, and capturing this spatiotemporal information effectively enhances the prediction efficiency. In this work, the T-GCN is employed to extract spatiotemporal information between temperature monitoring stations, Luong attention is utilized to capture and integrate global change trends, and integration with the GRU model is performed to alleviate interference from an excessive number of nodes, further improving prediction accuracy. The experimental results demonstrate that the proposed T-GCN-Luong attention-GRU combination model outperforms the other five models in terms of prediction accuracy.

Conclusion

This paper uses the daily average temperature data of Jiangsu Province to capture spatiotemporal features and establishes the TGLAG (T-GCN-Luong attention-GRU) integrated model to further improve the prediction accuracy of the daily average temperature. The method introduces a GCN to extract spatial information on the basis of time series prediction with the GRU model, obtains the spatiotemporal feature processing module T-GCN, and introduces the Luong attention mechanism to obtain the different weights of the hidden layer states. Finally, through the variable weight method, the prediction results of the T-GCN-Luong attention model are integrated with those of the GRU model to reduce interference from redundant spatial information and further improve the day-by-day prediction accuracy of the TGLAG model.

To verify the effectiveness of each module of the TGLAG model, ablation experiments are performed, and the results show that the GCN module, Luong attention mechanism, and variable weight method have significant effects on capturing spatiotemporal information. Moreover, comparison experiments of the GCN module and CNN module and comparison experiments of the Luong attention mechanism and self-attention mechanism are conducted to prove the advantages of the GCN in extracting spatial information and the superior performance of the Luong attention mechanism in the TGLAG model. The results show that (1) the daily average temperature data are spatially correlated, and the spatial information between the temperatures in different places can be effectively extracted by the GCN module. (2) Luong attention performed well in extracting the global trend of change and was more suitable for daily average temperature prediction. The weight variation method can amalgamate the advantages of the two types of models in extracting feature information while also alleviating the potential spatial information interference issue arising from an excessive number of nodes. (3) The integrated T-GCN-Luong attention-GRU model performs well at all 15 stations in Jiangsu Province, and compared with those of the base model, the RMSEs of the prediction results decrease by an average of 31.949%, and the MAEs decrease by an average of 26.913% on the daily average temperature prediction task, indicating that the combination model has good generalizability and stability.

Although the TGLAG model proposed in this paper has high accuracy in predicting daily average temperature data, several aspects deserve further research: (1) adjusting the time step and attempting to extend short-term prediction to long-term prediction to explore the stability of the combined model in the long-term prediction task; (2) Jiangsu Province has a transitional climate from temperate to subtropical, with moderate rainfall and four distinct seasons, and its climatic characteristics differ significantly from those of the tropical monsoon climate and temperate oceanic climate. It would be valuable to compare the accuracy of the combined model in terms of temperature prediction under different climatic conditions and (3) consider the introduction of other factors affecting the daily average temperature into the model, such as relative humidity, wind speed, and precipitation, to improve the prediction accuracy. In summary, the TGLAG model proposed in this paper has a simple structure and high prediction accuracy and has promising prospects for practical applications.