Introduction

The dynamics of nonlinear wave propagation in fractional media has gained significant attention in recent years due to its relevance to various complex physical systems. Among the most prominent models are nonlinear Schrödinger equations, which describe wave phenomena in a variety of fields, including fluid dynamics and nonlinear optics. This study focuses on the nonlinear time-dependent Schrödinger equation, extended to incorporate fractional derivatives via the beta derivative. This extension introduces additional complexity to wave dynamics, often leading to nontrivial bifurcations and wave patterns. The main goal of this research is to apply Kudryashov’s techniques to derive exact solutions to these equations and investigate the bifurcation behavior that emerges under specific conditions. By analyzing the stability of fixed points and exploring parameter spaces, we aim to contribute to the understanding of fractional wave systems and their applications to real-world phenomena.

The focus of this article is to deploy two novel analytical techniques, specifically Kudryashov techniques I and II (KM I and KM II), to derive solutions for nonlinear fractional equations, namely the nonlinear time-dependent Schrödinger equation and the space-time modified Benjamin-Bona-Mahony (BBM) equation using the beta derivative1 see also2,3,4,5.

The beta derivative of a function \(\Omega (\chi )\) is given by

$$\begin{aligned} ^{\alpha }D^{\beta }_{\chi }\lbrace \Omega (\chi ) \rbrace =\lim _{\sigma \longrightarrow 0}\dfrac{\Omega [\chi +\sigma (\chi +\frac{1}{\Gamma (\beta )})^{1-\beta }]-\Omega (\chi )}{\sigma },\,\,\,\chi >0,\,\,\,\beta \in (0,1].\end{aligned}$$

Some important properties for this derivative are

$$\begin{aligned} & ^{\alpha }D^{\beta }_{\chi }(\epsilon _{0}\Omega (\chi ) +\epsilon _{1}\mho (\chi ) ) =\epsilon _{0} ^{\alpha }D^{\beta }_{\chi }\Omega +\epsilon _{1} ^{\alpha }D^{\beta }_{\chi }\mho ,\,\, \forall \epsilon _{0},\epsilon _{1}\in \mathbb {R}, \\ & ^{\alpha }D^{\beta }_{\chi }(\epsilon _{0})=0,\,\,\,\forall \epsilon _{0}\in \mathbb {R},\\ & ^{\alpha }D^{\beta }_{\chi }(\Omega (\chi ) \mho (\chi ) )=\mho (\chi )^{\alpha }D^{\beta }_{\chi }(\Omega (\chi ) ) +\Omega (\chi )^{\alpha }D^{\beta }_{\chi }(\mho (\chi ) ),\\ & ^{\alpha }D^{\beta }_{\chi }(\frac{\Omega (\chi )}{ \mho (\chi ) })=\frac{\mho (\chi )^{\alpha }D^{\beta }_{\chi }(\Omega (\chi ) ) -\Omega (\chi )^{\alpha }D^{\beta }_{\chi }(\mho (\chi ) )}{[\mho (\chi )]^{2}},\,(\mho \ne 0),\\ & ^{\alpha }D^{\beta }_{\chi }(\Omega ( \mho (\chi ) ))=(\chi +\frac{1}{\Gamma (\beta )})^{1-\beta }\mho ^{\prime }(\chi )\Omega ^{\prime }(\mho (\chi )), \end{aligned}$$

where \(\Omega\) and \(\mho\) are two \(\beta\) differentiable functions and \(\beta \in (0,1].\)

History and Introduction

The study of nonlinear wave phenomena, especially in fractional systems, has become increasingly important across various scientific fields. Early work on the dynamics of nonlinear waves in media with fractional derivatives, such as the Korteweg-de Vries (KdV) and Caudrey-Dodd-Gibbon (CDG) models, has shown significant insights into soliton behavior and conservation laws2. Further optimization techniques, particularly for postblast ore boundary determination, have been applied to understand the complexities of nonlinear wave propagation in real-world systems3. In nonlinear optics, the perturbed Chen-Lee-Liu model has been utilized to derive new optical soliton solutions, paving the way for advanced applications in laser propagation4. Extending this, the modified extended Tanh technique has been successfully applied to the complex Ginzburg-Landau equation, which models nonlinear wave interactions in various physical contexts5.

The study of fractional derivatives has also led to the exploration of M-fractional optical solitons in the Gerdjikov-Ivanov equation, offering new perspectives on wave propagation in fractional media1. In recent years, significant contributions have been made to the understanding of the KdV-Caudrey-Dodd-Gibbon model through various soliton and complexiton solutions, continuing to inspire research in nonlinear wave equations6. The application of fractional calculus to ferroelectric materials has further advanced the field, particularly through studies that examine bifurcations and phase portraits in time-fractional models7. Additionally, methods like bifurcation analysis and backstepping strategies have been used to understand complex systems such as supply chain dynamics8.

Meanwhile, fractional-order nonlinear models, especially those incorporating the Atangana beta derivative, have yielded new explicit soliton solutions that enrich the theoretical understanding of wave solutions in nonlinear systems9. Solutions to generalized KdV equations with variable coefficients have also been derived, contributing to the understanding of nonlinear wave behaviors in diverse environments10. Furthermore, traveling wave solutions to space-time fractional modified equations have been studied, shedding light on the intricate behaviors of nonlinear systems with fractional derivatives11. These studies on fractional nonlinear Schrödinger equations have enhanced the diversity of optical solitonic structures and enriched our understanding of nonlinear optical wave propagation12,13.

The application of these techniques has been extended to study optical wave propagation in fiber optics, with multicomponent nonlinear fractional Schrödinger equations offering novel solutions that provide insights into the dynamics of wave solutions in fiber optics14. In addition, studies on modulation instability and optical solitons in multi-dimensional nonlinear Schrödinger systems have opened new directions for research in fiber optics and material science15. Notably, work on the dynamics of optical solitons in spinor Bose-Einstein condensates has demonstrated the potential of fractional systems to describe complex quantum phenomena16. Further contributions to the study of optical pulses in fiber optics have highlighted the significance of fractional dynamics in controlling wave propagation under nonlinear conditions17. Finally, recent research on damping effects in ferrite materials has introduced new exact solutions and solitary waves in the context of magnetic materials, contributing significantly to the broader field of nonlinear wave propagation18.

More accurately, we also have a qualitative study of optical soliton solutions conducted for the (2+1)-dimensional complex modified Korteweg-de Vries system19. Exact solutions to the complex-coupled Kuralay system were unveiled using the generalized Riccati equation mapping method20. Additionally, Lie group analysis was applied to the dual-mode nonlinear Schrödinger equation, revealing group invariant solutions and conservation laws21. Analytical soliton solutions were also derived for a fractional-order dual-mode nonlinear Schrödinger equation, incorporating time-space conformable derivatives22. Furthermore, a Caputo residual power series scheme was adapted for solving nonlinear time fractional Schrödinger equations23.

These advances collectively represent a growing body of work that continues to push the boundaries of understanding in nonlinear fractional systems, offering significant applications in fields ranging from fluid dynamics to quantum mechanics and nonlinear optics.

Novelty and contribution

This work offers a novel approach by incorporating the beta derivative in the analysis of nonlinear Schrödinger and Benjamin-Bona-Mahony equations. The primary innovation lies in the application of Kudryashov’s techniques I and II to extract exact solutions and perform bifurcation analysis in fractional contexts. Unlike previous studies, which often focus on integer-order derivatives, the introduction of fractional derivatives in this analysis provides a deeper understanding of wave behavior under fractional dynamics. This research goes beyond traditional methods, such as the Hirota method, the tanh method, and the sine-cosine method, by offering a detailed exploration of bifurcations in nonlinear systems governed by fractional derivatives. These traditional methods often struggle with the complexity introduced by fractional orders, whereas Kudryashov’s methods handle the nonlinearity and fractional derivatives more effectively. This work expands the applicability of these models in fields like nonlinear optics, quantum mechanics, and fluid dynamics.

Advantages over existing methods

The methods employed in this work, particularly Kudryashov’s techniques I and II, offer several advantages over traditional analytical approaches in nonlinear PDEs. The Hirota method and the tanh method are widely used to find soliton solutions to nonlinear equations, but they often require intricate transformations and fail to provide exact solutions for systems with fractional derivatives. Similarly, the sine-cosine method is effective for some specific nonlinear equations, but it struggles to handle the added complexity of fractional order terms in the equations.

Kudryashov’s techniques, in contrast, allow for the systematic derivation of exact solutions to nonlinear fractional equations, where other methods might fail to yield tractable results. These techniques are highly effective in handling the complex nonlinear terms and fractional derivatives, providing more accurate and efficient solutions. Additionally, the bifurcation analysis conducted in this study provides insights into the stability of solutions, which is critical for understanding the long-term behavior of the system. In contrast to numerical simulations, which may require extensive computational resources, the analytical solutions presented here provide valuable closed-form expressions for wave dynamics, making them useful for practical applications.

The basic idea of the Kudryashov techniques

Now, we present The Kudryashov’s approach for a nonlinear partial differential equation is outlined below:

  • We consider a typical nonlinear PDE of the form:

    $$\begin{aligned} \textsf{N}(\Xi , D_{\tau }^{\alpha }\Xi , D_{\chi }^{\alpha }\Xi , D_{\chi }^{\beta }\Xi , D_{\chi }^{\alpha }D_{\chi }^{\beta }\Xi , D_{\tau }^{\alpha }D_{\tau }^{\beta }\Xi , \cdots )=0, \,\,\,0<\alpha , \beta \leqslant 1, \end{aligned}$$
    (1)

    in which \(\Xi =\Xi (\chi ,\tau ).\)

  • Transform PDE (1) into an ODE by means of

    $$\begin{aligned} \kappa =\dfrac{d \chi ^{d\beta }}{\Gamma (1+\beta )}+\dfrac{c \tau ^{c\alpha }}{\Gamma (1+\alpha )}, \,\,\,\,\,\, \Xi (\chi ,\tau )=\Xi (\kappa ), \end{aligned}$$
    (2)

    where \(d, c \in \mathbb {R}\) are fixed.

  • Express Eq. (1) below nonlinear ODE format:

    $$\begin{aligned} \tilde{\textsf{N}}(\Xi , \Xi ^{\prime }, \Xi ^{\prime \prime }, \Xi ^{\prime \prime \prime }, \ldots )=0. \end{aligned}$$
    (3)

  • Assume the overall solution of (3) is represented in

    $$\begin{aligned} \Xi (\kappa )=a_{0}+a_{1}\Bbbk (\kappa )+a_{2}\Bbbk ^{2}(\kappa )+\cdots +a_{N}\Bbbk ^{N}(\kappa ). \end{aligned}$$
    (4)

    where \(\underbrace{a_{i}}_{1\le i \le N}\) are determined later, and the value of \(N\in \mathbb {N}\) is calculated using the homogeneous balance concept. In the following sections, we introduce the Kudryashov technique I (KM I) and the Kudryashov technique II (KM II).

KM I

At this point, suppose

$$\begin{aligned} \Bbbk (\kappa )=\dfrac{1}{1+dg^{\kappa }}, \end{aligned}$$
(5)

which satisfies

$$\begin{aligned} \Bbbk ^{\prime } (\kappa )=\Bbbk (\kappa )(\Bbbk (\kappa )-1)\ln (g). \end{aligned}$$
(6)

Based on Eqs. (3) and (4), a nonlinear algebraic system is formulated, and its solution provides the answers to (4).

KM II

At this point, suppose

$$\begin{aligned} \Bbbk (\kappa )=\dfrac{1}{(\varrho +\rho )\cosh (\kappa )+(\varrho -\rho )\sinh (\kappa )}, \end{aligned}$$
(7)

which satisfies

$$\begin{aligned} (\Bbbk ^{\prime } (\kappa ))^{2}=\Bbbk ^{2}(\kappa )(1-4\varrho \rho \Bbbk ^{2}(\kappa )). \end{aligned}$$
(8)

In accordance with (3) and (4), an algebraic system consists of nonlinear unkown variables is obtained, and solving it provides the solutions to (4).

Application of KM’s for the Schrödinger equation

Consider the following nonlinear time Schrödinger equation given by

$$\begin{aligned} i ^{\alpha }D^{\beta }_{\tau }\lbrace \Xi (\chi ,\tau ) \rbrace +A \Xi (\chi ,\tau )_{\chi \chi }+B\vert \Xi (\chi ,\tau ) \vert ^{2} \Xi (\chi ,\tau )=0, \,\,\,\beta \in (0,1], \end{aligned}$$
(9)

in which \(\Xi (\chi ,\tau )\) is a complex valued function.

Now, assume

$$\begin{aligned} & \Xi (\chi ,\tau )=\widehat{\Xi }(\kappa )\exp (i\varphi ),\\ & \kappa =\mu \chi -\frac{2\eta \lambda }{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta },\\ & \varphi =w\chi +\frac{\lambda }{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta }, \end{aligned}$$

where \(\eta , \lambda , \mu , w\) are fixed. Setting the above transformations in (9), we get

$$\begin{aligned} i(-2\eta \lambda \frac{d\widehat{\Xi }}{d\kappa }+2A\mu w \frac{d\widehat{\Xi }}{d\kappa }) +A\mu ^{2}\frac{d^{2}\widehat{\Xi }}{d\kappa ^{2}} -(\lambda +Aw^{2})\widehat{\Xi }(\kappa )+B\widehat{\Xi }^{3}(\kappa )=0, \end{aligned}$$
(10)

From the imaginary part of (10), we get \(\eta =\frac{A\mu w}{\lambda }.\)

Based on the real part of (10), through the balancing principle between \(\frac{d\widehat{\Xi }^{2}}{\kappa ^{2}}\) and \(\widehat{\Xi }^{3}\), we have \(N=1.\) Thus, the solution of

$$\begin{aligned} A\mu ^{2}\frac{d^{2}\widehat{\Xi }}{d\kappa ^{2}}-(\lambda +Aw^{2})\widehat{\Xi }+B\widehat{\Xi }^{3}=0 \end{aligned}$$
(11)

can be written as follows

$$\begin{aligned} \widehat{\Xi }(\mu )=a_{0}+a_{1}\Bbbk (\mu ), \end{aligned}$$
(12)

where \(a_{0},\) and \(a_{1}\) are constants to be specified later.

Bifurcation analysis of the nonlinear time Schrödinger equation

Definition 3.1

A Pickford bifurcation is a type of bifurcation that occurs in a dynamical system when a parameter variation causes a qualitative change in the system’s behavior. This bifurcation is characterized by the appearance or disappearance of stable and unstable fixed points, typically leading to a sudden change in the number or type of solutions. In mathematical terms, a Pickford bifurcation can be described by the equation:

$$\begin{aligned} \dot{x} = f(x, \mu ), \end{aligned}$$

where \(x\) represents the state of the system, \(\mu\) is the bifurcation parameter, and \(f(x, \mu )\) is the system’s dynamical function. At the bifurcation point, small changes in \(\mu\) lead to qualitative changes in the solution structure, often involving the creation or annihilation of limit cycles, fixed points, or attractors.

Now, to analysis bifurcation of the nonlinear time Schrödinger equation, Eq. (11), first we find the fixed points of Eq. (11) are found by setting the derivative terms to zero:

$$\begin{aligned} -(\lambda + A w^2) \widehat{\Xi }_0 + B \widehat{\Xi }_0^3 = 0. \end{aligned}$$

This simplifies to:

$$\begin{aligned} \widehat{\Xi }_0 \left[ B \widehat{\Xi }_0^2 - (\lambda + A w^2) \right] = 0. \end{aligned}$$

Thus, the fixed points are:

$$\begin{aligned} \widehat{\Xi }_0 = 0 \quad \text {or} \quad \widehat{\Xi }_0 = \pm \sqrt{\frac{\lambda + A w^2}{B}}. \end{aligned}$$

To analyze the stability of the fixed points, consider small perturbations around the fixed points:

$$\begin{aligned} \widehat{\Xi }(\kappa ) = \widehat{\Xi }_0 + \delta (\kappa ), \end{aligned}$$

where \(\delta (\kappa )\) is a small perturbation. Substituting this into equation (11) gives:

$$\begin{aligned} A \mu ^2 \frac{d^2 \delta }{d \kappa ^2} - (\lambda + A w^2) \delta + 3 B \widehat{\Xi }_0^2 \delta = 0. \end{aligned}$$

The equation reduces to:

$$\begin{aligned} A \mu ^2 \frac{d^2 \delta }{d \kappa ^2} - (\lambda + A w^2) \delta = 0. \end{aligned}$$

The characteristic equation is:

$$\begin{aligned} A \mu ^2 r^2 = \lambda + A w^2, \end{aligned}$$

with roots:

$$\begin{aligned} r = \pm \sqrt{\frac{\lambda + A w^2}{A \mu ^2}}. \end{aligned}$$

The stability of the perturbations depends on the sign of \(\lambda + A w^2\):

  • If \(\lambda + A w^2 > 0\), the roots are real, and the perturbations grow exponentially, indicating an unstable fixed point.

  • If \(\lambda + A w^2 < 0\), the roots are purely imaginary, leading to oscillatory behavior and a stable fixed point.

Bifurcation points occur where the stability of the fixed points changes, i.e., when \(\lambda + A w^2\) crosses zero:

$$\begin{aligned} \lambda + A w^2 = 0. \end{aligned}$$

This is the bifurcation point where the nature of the fixed points changes from stable to unstable or vice versa. As the stability of the fixed point \(\widehat{\Xi }_0 = 0\) varies when \(\lambda + A w^2 = 0\), and new nontrivial fixed points \(\widehat{\Xi }_0 = \pm \sqrt{\frac{\lambda + A w^2}{B}}\) arise, this signifies a pitchfork bifurcation. The system evolves from having a single stable fixed point to three fixed points, one of which is unstable, and the bifurcation has the following characteristics:

  • Pre-bifurcation (\(\lambda + A w^2 > 0\)): The system has a single unstable fixed point at \(\widehat{\Xi }_0 = 0\).

  • At the bifurcation point (\(\lambda + A w^2 = 0\)): The stability of the fixed point \(\widehat{\Xi }_0 = 0\) changes, and two new stable fixed points emerge.

  • Post-bifurcation (\(\lambda + A w^2 < 0\)): The system now has three fixed points: the original one at \(\widehat{\Xi }_0 = 0\) becomes stable, and two new fixed points \(\widehat{\Xi }_0 = \pm \sqrt{\frac{\lambda + A w^2}{B}}\) appear, with stability depending on the sign of the nonlinear term.

The nonlinear time Schrödinger equation exhibits a pitchfork bifurcation as the parameter \(\lambda + A w^2\) passes through zero. The stability of the solutions changes accordingly, and new stable or unstable solutions appear depending on the sign of this parameter. For more detail, we refer the reader to6,7,8,9,10.

At following two sections, we discuss the case studies of KM I and KM II.

Application of KM I

Based on Eq.(11) and Eq.(12) as well as Eq.(6), we derive a system of algebraic equations, given by:

$$\begin{aligned} & -Aw^{2}a_{0}+Ba_{0}^{3}-\lambda a_{0} =0,\\ & \ln (a)^{2}A\mu ^{2}a_{1}-Aw^{2}a_{1}+3B a_{0}^{2}a_{1}-\lambda a_{1} =0,\\ & -3\ln (A)^{2}A \mu ^{2}A_{1}+3Ba_{0}A_{1}^{2} =0,\\ & 2\ln (A)^{2}A\mu ^{2}a_{1}+Ba_{1}^{3} =0. \end{aligned}$$

By solving the above system of nonlinear algebraic equations, we obtain

$$\begin{aligned} & \lambda =-\frac{1}{2}\ln (A)^{2}A\mu ^{2}-Aw^{2}, \\ & a_{0}=\pm \frac{1}{2}\frac{\sqrt{-2BA}\mu \ln (A)}{B}, \\ & a_{1}=\pm \frac{\sqrt{-2BA}\mu \ln (A)}{B}. \end{aligned}$$

Based on the above we have

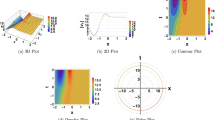
$$\begin{aligned} \Xi (\chi ,\tau )= & \bigg (\pm \frac{1}{2}\frac{\sqrt{-2BA}\mu \ln (A)}{B}\nonumber \\ & \pm \frac{\sqrt{-2BA}\mu \ln (A)}{B} \dfrac{1}{1+dg^{\mu \chi -\frac{2\eta (-\frac{1}{2}\ln (A)^{2}A\mu ^{2}-Aw^{2})}{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta }}}\bigg )e^{i(w\chi +\frac{-\frac{1}{2}\ln (A)^{2}A\mu ^{2}-Aw^{2}}{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta })}. \end{aligned}$$
(13)

Figure 1 present the real graphs of Eq. (13) for chosen values and \(\beta =0.01, 0.02, 0.03, 0.04, 0.05.\) Figure 2 present the imaginary graphs of (13), for chosen values and \(\beta =0.9, 0.99, 0.999, 0.9999, 0.99999.\)

Fig. 1
figure 1

Note [1], [5], [9], [13], [17] show the graphs of the real part of Eq. (13), and [2], [6],[10], [14], [18], and [3], [7], [11], [15], [19], and [4], [8], [12], [16], [20] display the contour graphs of z,y,x’ axis orientation, respectively, for \(\beta =0.01, 0.02, 0.03, 0.04, 0.05.\).

Full size image
Fig. 2
figure 2

Note [1], [5], [9], [13], [17] display the graphs of the imaginary part of Eq. (13), and [2], [6],[10], [14], [18], and [3], [7], [11], [15], [19], and [4], [8], [12], [16], [20] display the contour.

Full size image

Application of KM II

we derive a system of algebraic equations based on (11) and (12) as well as (8), which is described below:

$$\begin{aligned} & -Aw^{2}a_{0}+Ba_{0}^{3}-\lambda a_{0} =0,\\ & A\mu ^{2}a_{1} -Aw^{2} a_{1}+3Ba_{0}^{2}a_{1}-\lambda a_{1} =0,\\ & 3Ba_{0}a_{1}^{2} =0,\\ & -8 \rho \varrho A\mu ^{2}a_{1}+Ba_{1}^{3} =0. \end{aligned}$$

By solving the preceding system of nonlinear algebraic equations, we obtain

$$\begin{aligned} & \lambda =A\mu ^{2}-Aw^{2}, \\ & a_{0}=0,\\ & a_{1}=\pm \frac{2\sqrt{2}\sqrt{B\rho \varrho A}\mu }{B}. \end{aligned}$$

From the above, we get

$$\begin{aligned} u(\chi , \tau )=\bigg ( \pm \frac{2\sqrt{2}\sqrt{B\rho \varrho A}\mu }{B} \dfrac{1}{\varsigma } \bigg )e^{i(w\chi +\frac{A\mu ^{2}-Aw^{2} }{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta })}, \end{aligned}$$
(14)

where \(\varsigma :=(\varrho +\rho )\cosh (\mu \chi -\frac{2\eta (A\mu ^{2}-Aw^{2} )}{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta }) +(\varrho -\rho )\sinh (\mu \chi -\frac{2\eta ( A\mu ^{2}-Aw^{2})}{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta }).\)

Application of KMs for the Benjamin Bona Mahony equation

Consider the following space-time adapted Benjamin Bona Mahony equation given by

$$\begin{aligned} ^{\alpha }D^{\beta }_{\tau } \Xi (\chi ,\tau ) + ^{\alpha }D^{\beta }_{\chi } \Xi (\chi ,\tau )-A\Xi (\chi ,\tau )^{2}\, ^{\alpha }D^{\beta }_{\chi }\Xi (\chi ,\tau ) + ^{\alpha }D^{3\beta }_{\chi } \Xi (\chi ,\tau ) =0, \,\,\,\beta \in (0,1], \end{aligned}$$
(15)

in which \(\Xi (\chi ,\tau )\) is a complex value function.

Now, assume

$$\begin{aligned} & \Xi (\chi ,\tau )=\widehat{\Xi }(\kappa ),\\ & \kappa =\frac{\mu }{\beta }(\chi +\frac{1}{\Gamma (\beta )})^{\beta }-\frac{\eta }{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta }, \end{aligned}$$

where \(\eta , \mu\) are fixed. Setting the above transformations in (15), we get

$$\begin{aligned} -\eta \frac{d\widehat{\Xi }}{d\kappa }+\mu \frac{d\widehat{\Xi }}{d\kappa }-A\mu \widehat{\Xi }^{2}\frac{d\widehat{\Xi }}{d\kappa } +\mu ^{3}\frac{d^{3}\widehat{\Xi }}{d\kappa ^{3}} =0. \end{aligned}$$
(16)

Integrating (16) regarding \(\kappa\) and disregarding the constant of integration, we get

$$\begin{aligned} \mu ^{3}\frac{d^{2}\widehat{\Xi }}{d\kappa ^{2}}+(\mu -\eta )\widehat{\Xi }-\frac{A\mu }{3}\widehat{\Xi }^{3}=0. \end{aligned}$$
(17)

Through the balancing principle between \(\frac{d^{2}\widehat{\Xi }}{\kappa ^{2}}\) and \(\widehat{\Xi }^{3}\), we have \(N=1.\) Thus, the solution of (17) can be written as follows

$$\begin{aligned} \widehat{\Xi }(\mu )=a_{0}+a_{1}\Bbbk (\mu ), \end{aligned}$$
(18)

in which \(a_{0},\) and \(a_{1}\) are constants that will be defined later.

Next, In the following sections, we present the case studies of KM I and KM II.

Application of KM I

we derive a system of algebraic equations based on (17) and (18) as well as (6), which is given by:

$$\begin{aligned} & \mu a_{0}-\eta a_{0}-\frac{1}{3}A\mu a_{0}^{3} =0,\\ & \mu ^{3}a_{1} \ln (A)^{2}-A\mu a_{0}^{2}a_{1}-\eta a_{1}+\mu a_{1} =0,\\ & -3\mu ^{3} a_{1}\ln (A)^{2}-A\mu a_{0}a_{1}^{2} =0,\\ & 2\mu ^{3}a_{1}\ln (A)^{2}-\frac{1}{3}A\mu a_{1}^{3} =0. \end{aligned}$$

By solving the mentioned system of nonlinear algebraic equations, we obtain

$$\begin{aligned} & \eta = -\frac{1}{2} \ln (A)^{2}\mu ^{3}+\mu , \\ & a_{0}=\pm \frac{1}{2}\frac{\sqrt{6}\ln (A)\mu }{\sqrt{A}}, \\ & a_{1}=\pm \frac{\sqrt{6}\ln (A)\mu }{\sqrt{A}}. \end{aligned}$$

Based on the above we have

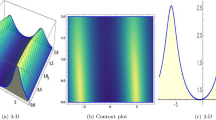
$$\begin{aligned} \Xi (\chi ,\tau )= & \pm \frac{1}{2}\frac{\sqrt{6}\ln (A)\mu }{\sqrt{A}}\nonumber \\ & \pm \frac{\sqrt{6}\ln (A)\mu }{\sqrt{A}} \dfrac{1}{1+dg^{\frac{\mu }{\beta }(\chi +\frac{1}{\Gamma (\beta )})^{\beta }-\frac{-\frac{1}{2} \ln (A)^{2}\mu ^{3}+\mu }{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta }}}. \end{aligned}$$
(19)

Figures 3 and 4 show the real and imaginary graphs of (19), for defined values and \(\beta =0.1, 0.3, 0.5, 0.7, 0.9.\)

Fig. 3
figure 3

Note [1], [6], [11], [16], [21] show the graphs of the real part of Eq. (19), and [2], [7],[12], [17], [22], and [4], [9], [14], [19], [24], and [3], [8], [13], [18], [23], and [5], [10], [15], [20], [25] show graphs of z,y-axis orientation and the contour graphs of z,y-axis orientation, respectively, for \(\beta =0.1, 0.3, 0.5, 0.7, 0.9.\).

Full size image
Fig. 4
figure 4

Note [1], [6], [11], [16], [21] show the graphs of the imaginary part of Eq. (19), and [2], [7],[12], [17], [22], and [4], [9], [14], [19], [24], and [3], [8], [13], [18], [23], and [5], [10], [15], [20], [25] show graphs of z,y-axis orientation and the contour graphs of z,y-axis orientation, respectively, for \(\beta =0.1, 0.3, 0.5, 0.7, 0.9.\).

Full size image

Application of KM II

Based on (17) and (18) as well as (8), we obtain a system of algebraic equations, given by:

$$\begin{aligned} & \mu a_{0}-\eta a_{0}-\frac{1}{3}A\mu a_{0}^{3} =0,\\ & -A\mu a_{0}^{2}a_{1}+\mu ^{3}a_{1}-\eta a_{1}+\mu a_{1} =0,\\ & -A\mu a_{0}a_{1}^{2} =0,\\ & -8\mu ^{3}a_{1}\varrho \rho -\frac{1}{3}A\mu a_{1}^{3} =0. \end{aligned}$$

By solving the mentioned system of nonlinear algebraic equations, we obtain

$$\begin{aligned} & \eta =\mu ^{3}+\mu , \\ & a_{0}=0, \\ & a_{1}=\pm \frac{2\sqrt{-6A\rho \varrho }\mu }{A}. \end{aligned}$$

Based on the above we have

$$\begin{aligned} u(\chi , \tau )=\pm \frac{2\sqrt{-6A\rho \varrho }\mu }{A}, \dfrac{1}{\iota } \end{aligned}$$
(20)

where \(\iota := (\varrho +\rho )\cosh (\frac{\mu }{\beta }(\chi +\frac{1}{\Gamma (\beta )})^{\beta }-\frac{\mu ^{3}+\mu }{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta })+(\varrho -\rho )\sinh (\frac{\mu }{\beta }(\chi +\frac{1}{\Gamma (\beta )})^{\beta }-\frac{\mu ^{3}+\mu }{\beta }(\tau +\frac{1}{\Gamma (\beta )})^{\beta }).\)

Figures 5 and 6 show the real and imaginary graphs of (20), for defined values and \(\beta =0.1, 0.3, 0.5, 0.7, 0.9.\)

Fig. 5
figure 5

Note [1], [6], [11], [16], [21] show the graphs of the real part of Eq. (20), and [2], [7],[12], [17], [22], and [4], [9], [14], [19], [24], and [3], [8], [13], [18], [23], and [5], [10], [15], [20], [25] show graphs of z,y-axis orientation and the contour graphs of z,y-axis orientation, respectively, for \(\beta =0.1, 0.3, 0.5, 0.7, 0.9.\).

Full size image
Fig. 6
figure 6

Note [1], [6], [11], [16], [21] show the graphs of the imaginary part of Eq. (20), and [2], [7],[12], [17], [22], and [4], [9], [14], [19], [24], and [3], [8], [13], [18], [23], and [5], [10], [15], [20], [25] show graphs of z,y-axis orientation and the contour graphs of z,y-axis orientation, respectively, for \(\beta =0.1, 0.3, 0.5, 0.7, 0.9.\).

Full size image

Discusion

Figure 7 displays the 2D graph of the non-negative amount of the differences between solutions (19) and (20) for defined values and \(\beta = 0.90\). Additionally, Table 1 shows the absolute amount of the solutions (19) and (20) obtained using Kudryashov techniques with distinct point locations and \(\beta = 0.90\). Also, Table 2 distinctly shows the contrasts among non-negative amount of solutions (19) and (20), denoted by \(\Delta \vert \Xi (\chi , \tau ) \vert\), for fixed \(\chi\), varying amounts of \(\tau\), and \(\beta = 0.90\). It is evident that the contrasts achieved using KM I are smaller than those from KM II, indicating that the outcomes gathered by KM I have greater precision compared to KM II.

Table 1 the non-negative amount of the solutions (19) and (20) proposed by Kudryashov techniques, with distinct point locations, and \(\beta =0.90\).
Full size table
Table 2 The contrasts within the non-negative amount of solutions (19) and (20), shown by \(\Delta \Xi (\chi ,\tau )\), with given \(\chi\) and multiple amounts of \(\tau .\).
Full size table
Fig. 7
figure 7

The 2D with the non-negative amount of the differences beyond solutions (19) and (20), for defined values, and \(\beta =0.90.\).

Full size image

Conclusion

This study provides a comprehensive bifurcation analysis of small amplitude unidirectional waves in non-local nonlinear elastic media, utilizing Kudryashov’s methods for deriving exact solutions to nonlinear equations, including the nonlinear time-dependent Schrödinger and the space-time modified Benjamin-Bona-Mahony equations. A significant contribution of this work lies in the application of the beta derivative for fractional dynamics, which introduces a novel perspective to traditional models and allows for a deeper understanding of wave propagation in fractional media.

Key findings from this research include:

  • Bifurcation Behavior: The analysis reveals the critical role of bifurcations in determining the stability of the fixed points of the system. Through parameter variations, we identify the conditions under which the system transitions from a single stable fixed point to three fixed points, one of which is unstable. This transition is indicative of a pitchfork bifurcation, a hallmark of nonlinear wave systems, where the introduction of fractional derivatives has a notable influence on the system’s behavior.

  • Exact Solutions: By deploying Kudryashov’s techniques I and II, this study successfully derives exact solutions for nonlinear fractional equations. These solutions are particularly significant for real-world applications in fields such as fluid dynamics, nonlinear optics, and quantum mechanics. The exact analytical solutions presented here are in contrast to traditional numerical methods, providing a more efficient and accurate means of solving complex nonlinear PDEs with fractional dynamics.

  • Stability Analysis: The stability of solutions is analyzed in depth, with the bifurcation analysis offering insights into the system’s long-term behavior. By examining the roots of the characteristic equation, the study demonstrates how varying the parameters can lead to either stable or unstable solutions, allowing for a more nuanced understanding of the dynamics of nonlinear waves.

  • Methodological Advantage: The Kudryashov methods applied in this work offer a significant advantage over traditional methods such as the Hirota, tanh, and sine-cosine methods. These techniques are more adept at handling the complexities introduced by fractional derivatives, providing a systematic approach to deriving exact solutions in cases where other methods might struggle.

In summary, this work not only enhances our understanding of nonlinear wave propagation in fractional systems but also demonstrates the efficacy of Kudryashov’s techniques in tackling the challenges posed by fractional differential equations. The findings from this study have potential applications in diverse areas, including materials science, optical systems, and quantum field theory, and contribute to the growing body of research in the field of fractional differential equations.