Anisotropic superconductivity in the quasi-one-dimensional superconductor V₂Ga₅

Abstract

The intermetallic quasi-one-dimensional binary superconductor V₂Ga₅ was recently found to exhibit a topologically nontrivial normal state, making it a natural candidate for a topological superconductor. By combining dc-magnetization, nuclear magnetic resonance, and muon-spin rotation (${\upmu }$SR) measurements on high-quality V₂Ga₅ single crystals, we investigate the electronic properties of its normal- and superconducting ground states. NMR measurements in the normal state indicate a strong anisotropy in both the line shifts and the relaxation rates. Such anisotropy persists also in the superconducting state, as shown by the magnetization- and ${\upmu }$SR-spectroscopy results. In the latter case, data collected at different temperatures, pressures, and directions of the magnetic field evidence a fully-gapped, strongly anisotropic superconductivity. At the same time, hydrostatic pressure is shown to only lower the $T_c$ value, but not to change the superfluid density nor its temperature dependence. Lastly, we discuss the search for topological signatures in the normal state of V₂Ga₅, as well as a peak splitting in the FFT of the ${\upmu }$SR spectrum, possibly related to an unconventional vortex lattice. Our results suggest that V₂Ga₅ is a novel system, whose anisotropy plays a key role in determining its unusual electronic properties.

Following the advent of topological insulators, the search for quantum materials with symmetry-enforced topological states has attracted widespread research interest in both the condensed-matter- and the material-science communities^1,2,3. In this new class of materials, the systems that simultaneously exhibit superconductivity and topologically nontrivial electronic bands, with Weyl- and/or Dirac nodes, are the most promising candidates for the realization of topological and/or nematic superconductivity. The potential to host Majorana fermions in their vortex cores represents a significant advantage in the pursuit of quantum computing.

V₂Ga₅, currently known as a candidate TSC material, was discovered already in the 1960s. Back then, in the search for new superconducting alloys, attempts to grow V₃Ga by cooling a gallium-rich vanadium solution resulted in a new compound, V₂Ga₅^4,5,6. V₂Ga₅ crystallizes in the form of long needles, which exhibit a unique quasi-1D structure, as confirmed by x-ray diffraction measurements and band-structure calculations on single crystals⁶. Here, one-dimensional vanadium chains along the c axis are coupled to each other by neighboring Ga ions. This pronounced 1D character makes V₂Ga₅ a natural platform to study the effects of strong crystalline anisotropy on the electronic properties and the possible occurrence of topological features. However, as its superconducting temperature is only 3.6 K, $\hbox {V}_2\hbox {Ga}_5$ was forgotten for a long time.

The increased interest in topological quantum computing has re-ignited interest in the TSCs candidate materials, including $\hbox {V}_2\hbox {Ga}_5$. Recent studies, comprising mostly bulk techniques, such as heat-capacity and transport measurements, as well as some preliminary ${\upmu }$SR results^7,8, generally agree that $\hbox {V}_2\hbox {Ga}_5$ possesses multiple nodeless superconducting gaps. However, TF-${\upmu }$SR measurements in a magnetic field orthogonal to the c-axis⁸ show a superconducting shielding fraction of only 60% and a rather weak depolarization rate (of $\sim 1$ ${\upmu }\textrm{s}^{-1}$)⁸, which casts serious doubts on the intrinsic nature of the extracted electronic properties.

In this work, we present an extensive, more detailed investigation, including bulk dc-magnetization, NMR, and ${\upmu }$SR, all performed with the applied magnetic field parallel ($H^{\parallel }$) and perpendicular ($H^{\perp }$) to the c-axis, as well as ${\upmu }$SR measurements under hydrostatic pressure on aligned single crystals. All the crystals used in our measurements possess an excellent crystalline quality, as confirmed by a shielding volume fraction of about 100% (measured via dc-susceptibility) and a superconducting volume fraction of $\sim 95$% (determined by ${\upmu }$SR spectroscopy). In particular, in the latter case, the low-T muon depolarization rate ($\sim 2.7$ ${\upmu }\textrm{s}^{-1}$ at 0.3 K) is almost three times larger than that measured on V₂Ga₅ single crystals under the same conditions⁸.

The improved quality of samples is critical for investigating their intrinsic superconducting properties, as well as for obtaining new insight on this unique compound. Our NMR and ${\upmu }$SR in the normal- and the superconducting state reveal a strong anisotropy of in-plane vs. out-of-plane electronic properties. At the same time, transverse-field ${\upmu }$SR in the superconducting state shows an unexpected peak splitting in the Fourier transform of the time-dependent asymmetry, hinting at the emergence of an unconventional vortex lattice that has never been observed in any other topological material.

Fig. 1

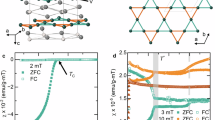
(a) Temperature-dependent magnetic susceptibility of $\hbox {V}_2\hbox {Ga}_5$, measured in an applied field of 0.5 and 14 mT, using the ZFC- and FC protocols with the magnetic field applied parallel and perpendicular to the c-axis. (b) Normal-state magnetization vs magnetic field. Note the opposite sign of the magnetic response in the two cases. Field-dependent magnetization M(H) recorded below $T_c$ (here, at 2 K) for the field applied parallel- (c) and perpendicular (d) to the c-axis. The vertical arrows indicate the estimated lower and the upper critical fields at 2 K (see text for details).

Results

Since $\hbox {V}_2\hbox {Ga}_5$ crystals are needle-shaped, all the measurements had to be carried out on groups of aligned single crystals (bundles). It is important to note that, while the whole bundle behaves as a single crystal when the applied field is parallel to the c-axis ($H^{\parallel }$ configuration), it behaves as a polycrystal when the field is perpendicular to it ($H^{\perp }$ configuration). This is due to the random orientation of the a-axis of each crystal within the bundle. Further details about the geometry of the bundles are provided in the Supplementary Information.

DC magnetization measurements

Figure 1a shows the low-field intrinsic susceptibility $\chi$ as a function of temperature, measured at 0.5 and 14 mT. Due to sample-shape demagnetization effects, the measured susceptibility $\chi _\text{meas}$ generally differs from the intrinsic one, the relation between the two being $\chi _\text{meas} = \chi /(1 + N \chi )$, where N is the demagnetization factor. Our needle-like $\hbox {V}_2\hbox {Ga}_5$ samples can be considered as long cylinders, with a length-to-diameter ratio $l/d > 10.$ In this case, the demagnetization factor is $N^{-1} = 2 + (1/\sqrt{2})\,d/l$⁹, and it can be taken equal to 0 and 0.5 for the parallel and perpendicular configuration, respectively (see also Table VI in Ref.¹⁰). DC susceptibility results indicate that: (i) the full shielding at the lowest field is suggestive of bulk superconductivity and (ii) the small difference between the zero-field cooling (ZFC) and field cooling (FC) datasets is reminiscent of a negligible vortex pinning, which is even smaller in the $H^{\parallel }$ configuration (as confirmed by our ${\upmu }$SR measurements — see below).

In Fig. 1b we show a representative set of isothermal magnetization curves recorded in the normal state. Interestingly, the field response is paramagnetic (diamagnetic) for magnetic fields applied perpendicular (parallel) to the c-axis. [TF-${\upmu }$SR results indicate the presence of an impure phase of about 5%, most likely paramagnetic. As such, it could be responsible for the slight increase in dc magnetization at low temperature, instead of the expected T-independent diamagnetic contribution. The same effect could also arise because of a slight sample misalignment during the dc susceptibility measurements.] The presence of diamagnetism in the normal state of $\hbox {V}_2\hbox {Ga}_5$ is consistent with the diamagnetism found in the normal state of elemental Ga¹¹, as well as in the binary Ga-based intermetallic superconductors, such as $\hbox {Mo}_8\hbox {Ga}_{{41}}$¹² and $\hbox {Mo}_4\hbox {Ga}_{{21}}$¹³. On the other hand, to the best of our knowledge, $\hbox {V}_2\hbox {Ga}_5$ is one of the few compounds to exhibit a significant magnetic anisotropy in the normal state: paramagnetic vs. diamagnetic for applied fields perpendicular- or parallel to the c-axis, respectively. A similar behavior has been observed in single crystals of antimony-tin alloys^14,15. Such unusual magnetic anisotropy was attributed to the Stark effect, because the crystal electric field is likely to quench the spin susceptibility¹⁵ in favor of the orbital diamagnetic contribution. This may also be the case for $\hbox {V}_2\hbox {Ga}_5$, where both Ga and V possess sizable quadrupolar moments. This picture is supported by the NMR and ${\upmu }$SR results presented in the following sections.

In Fig. 1c and d we plot the ZFC magnetization M vs. the applied magnetic field H_app at 2 K. At this temperature, we note that $\mu _{0}H_{c2}^{\parallel } \sim 0.2$ T and $\mu _{0}H_{c2}^{\perp } \sim 0.3$ T. As for the lower critical field $H_{c1}$, this is defined as the threshold value beyond which M starts to deviate from the linearity (Meissner effect). The resulting critical fields (at 2 K) are $\mu _{0}H_{c1}^{\parallel } \sim 4.5$ mT and $\mu _{0}H_{c1}^{\perp } \sim 2.5$ mT, respectively. We remark that both the lower- and the upper critical field (here measured at 2 K) are in good agreement with the values reported in literature at the same temperature^5,7,8. Finally, by taking into account that the internal magnetic field is $H_\textrm{int} = H_\textrm{app} - NM$ and the above mentioned values for N, the slopes of the linear low-field regions allow us to estimate the shielding volume fractions at 2 K. These are $\chi ^{\parallel } \sim -1.150(4)$ and $\chi ^{\perp } \sim -1.17(2)$, respectively, in good agreement with the low-T values resulting from the dc magnetic susceptibility taken at 0.5 mT (Fig. 1a).

Fig. 2

(a)$^{51}$V NMR lineshapes at 5 T. The presence of satellites (shown by arrows for the 80 K case) indicates a strong quadrupole interaction, in turn arising from the strong anisotropy of the $\hbox {V}_2\hbox {Ga}_5$ unit cell. (b) Temperature dependence of the total NMR shift in $\hbox {V}_2\hbox {Ga}_5$, which includes contributions from both the magnetic- and quadrupole interactions. While generally temperature-independent, above 90 K, it shows a slight upward shift. The solid line indicates a fit to $K = a + b\ln (T)$. (c) Temperature dependence of the Korringa product $1/T_1T$. Its practically constant value in the normal state indicates an ideal-metal behavior. (d) Anisotropy of relaxation measured via NMR (magenta) and ${\upmu }$SR (orange) (see Fig. 3). Both techniques clearly indicate that $\hbox {V}_2\hbox {Ga}_5$ relaxes much faster in the $H^{\perp }$ configuration.

NMR in the normal state

We performed NMR measurements in a magnetic field of 5 T, oriented parallel and perpendicular to the $\hbox {V}_2\hbox {Ga}_5$ c-axis. To achieve the $\textrm{H}^{\parallel }$ configuration, a special sample configuration had to be realized (see Supplementary Information). The main results, including the line shapes at selected temperatures and the evolution of the NMR shift and of $1/(T_1T)$ with temperature are shown in Fig. 2a–c, respectively. We evidence here three notable aspects.

Firstly, the $^{51}$V NMR line shapes in the $H^{\perp }$ configuration indicate that, aside from the main NMR resonance peak at 56.1 MHz, there is also clear evidence of additional peaks. At 80 K, where the signal-to-noise ratio is the highest, five equally-spaced peaks can be clearly distinguished. Since $\hbox {V}_2\hbox {Ga}_5$ has only one crystallographically unique $^{51}$V site⁶, the side peaks cannot be due to multiple $^{51}$V sites. Instead, most likely, these additional peaks arise from the quadrupolar satellite transitions, with $2\nu _Q = 274\pm 2$ kHz. Since $^{51}$V is a spin 7/2 nucleus, one would expect to observe three quadrupole satellites on each side of the main peak. However, the outermost peaks are most likely hidden in the noise floor. In any case, the presence of quadrupolar satellites in $^{51}$V NMR indicate the presence of a strong local electric-field gradient (EFG), a key signature of the anisotropy of the electronic properties of $\hbox {V}_2\hbox {Ga}_5$. Furthermore, the non-negligible quadrupole coupling observed via NMR in the normal state is consistent with our key result of anisotropic superconductivity in the superconducting state.

Secondly, the line shifts reported in Fig. 2b and the Korringa product ($1/T_{1}T$) in Fig. 2c are both largely temperature independent, except for a small increase in NMR shift above 100 K, almost negligible compared to the relevant error bars. Despite a lack of changes with temperature, the relaxation rates and line shifts are still clearly different in the $H^{\parallel }$ and $H^{\perp }$ configurations. This confirms the normal-state anisotropic behavior already revealed by the dc susceptibility results. A temperature-independent Korringa product and NMR shift indicate a temperature-independent density of states (DOS)¹⁶. This is expected, considering that the NMR measurements were conducted in the normal phase of a metal. We also note that previous calculations⁶ show that the total DOS of $\hbox {V}_2\hbox {Ga}_5$ is 8 (V) + 3 (Ga1) + 0.7 (Ga2) = 11.7 states/(eV f.u.). Considering that pure vanadium has a DOS of approximately 2 states/(eV f.u.), as calculated via different methods¹⁷, one would expect the relaxation rate (and, hence, the Korringa product) to be much faster in $\hbox {V}_2\hbox {Ga}_5$. Instead, we observe the opposite result, i.e., the Korringa product of $\hbox {V}_2\hbox {Ga}_5$ in the parallel field configuration, 1.40(6) $\textrm{sK}^{-1}$, is almost half of that measured in pure vanadium (3 $\textrm{sK}^{-1}$)¹⁸. The Korringa product measured in the perpendicular configuration is even lower, at 0.4(1) $\textrm{sK}^{-1}$. Further investigation is needed to understand the surprisingly short relaxation rate observed in $\hbox {V}_2\hbox {Ga}_5$.

Thirdly, we note that the NMR shifts reported in Fig. 2b and the relaxation rates reported in Fig. 2c are both highly anisotropic. We first consider the anisotropy in the NMR line shift. Since, in the $H^{\perp }$ configuration, the dc-magnetization is positive (paramagnetic), while, in the $H^{\parallel }$ configuration, it is negative (diamagnetic) (see Fig. 1b), we expect the NMR shift, which is a measure of spin susceptibility, to be more negative in the $H^{\parallel }$ configuration. Furthermore, it is known that the NMR frequency shift of the central transition in highly anisotropic systems includes a large second-order quadrupolar shift term. For example, in the quasi-1D compound $\beta$-$\hbox {Sr}_{0:33}$ V₂O₅¹⁹, the strong quadrupole interaction term results in an additional negative $^{51}$V NMR shift of $\approx$ 0.5$\%$. Hence, the combination of magnetic and quadrupolar effects results in a strong anisotropy in the NMR shifts measured in the $H^{\parallel }$ and $\textrm{H}^{\perp }$ configurations. In the case of the NMR relaxation rates, the temperature-independent NMR Korringa product ($1/T_{1}T$) is 1.40(6) $\textrm{sK}^{-1}$ in the $H^{\perp }$ configuration, but it drops by a factor of 3.5, i.e., to 0.4$(1)^{-1}$ $\textrm{sK}^{-1}$ in the $H^{\parallel }$ configuration. Such drop is consistent with strong decrease in the ${\upmu }$SR relaxation rate (measured at 5 K) from 0.298(3) ${\upmu }\textrm{s}^{-1}$ in the $H^{\perp }$ configuration to 0.120(7) ${\upmu }\textrm{s}^{-1}$ in the $H^{\parallel }$ configuration. This is a strong indication that the anisotropy in the NMR- and ${\upmu }$SR measurements has the same structural origin, here arising from the 1D vanadium chains.

Fig. 3

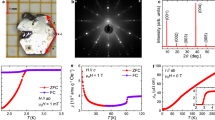
Fast Fourier transformation (FFT) of the TF-${\upmu }$SR time-dependent asymmetry below $T_c$ in a 14-mT field applied parallel- (a) and perpendicular (b) to the c-axis at ambient pressure. Representative asymmetries below and above $T_{c}$ are reported in the insets. In both cases, the increased relaxation rate below $T_c$ reflects the field modulation due to the superconducting vortices. Note the much lower relaxation rate for $T > T_c$ in the $H^{\parallel }$ case. The red lines represent the frequency-domain response of a model using the best-fit parameters of the time-dependent asymmetry. The dashed green- and black lines represent the superconducting- and normal state components, respectively. In the perpendicular configuration a further frequency component was required to resolve the tiny peak splitting (see text). Note the substantial diamagnetic shift in panel (a), attributed to an almost null pinning force in the $H^{\parallel }$ case. Diamagnetic field shift $\left(\langle B \rangle - B_\mathrm{app}\right)$ (c), $B_\mathrm{app}$ being the applied field intensity, and $1/\lambda ^{2}$ (d) vs. temperature for a magnetic field applied parallel- and perpendicular to the c-axis, as derived by assuming a conventional AVL. Continuous lines represent s-wave fitting models (see text for details).

μSR at ambient pressure

To investigate the superconducting ground-state properties of V₂Ga₅, we carried out systematic temperature-dependent TF-${\upmu }$SR measurements. A magnetic field of 14 mT, i.e., well above the $H_{c1}$ value reported in the literature^5,8 and confirmed by our measurements at 2 K (see Fig. 1), was applied parallel- and orthogonal to the c-axis by using a FC protocol. In the orthogonal configuration, we also applied a magnetic field of 50 mT. Representative TF-${\upmu }$SR spectra collected in the normal- and superconducting states of V₂Ga₅ are shown in the insets of Fig. 3a and b. In the superconducting state (i.e., $T<T_{c}$), the development of a flux-line lattice (FLL) causes an inhomogeneous field distribution and, thus, gives rise to an additional damping in the TF-${\upmu }$SR spectra²⁰. In both the parallel and perpendicular configurations the time-dependent asymmetry was modelled by the following equation²¹:

$$\begin{aligned} A_\textrm{TF}(t) = \sum \limits _{i=1}^n A_i \cos (\gamma _{\mu } B_i t + \phi ) e^{- \sigma _i^2 t^2/2} + A_\textrm{bg} \cos (\gamma _{\mu } B_\textrm{bg} t + \phi ). \end{aligned}$$

(1)

Here $A_{i}$, $A_\textrm{bg}$ and $B_{i}$, $B_\textrm{bg}$ are the initial asymmetries and local fields sensed by the muons probing the vortex state and the non superconducting part of the sample (or parts of the sample holder), respectively, $\gamma _{\mu }$/2$\pi$ = 135.53 MHz/T is the muon gyromagnetic ratio, and $\phi$ is a shared initial phase. Here, $\sigma _{i}$ represents the Gaussian relaxation rate of the ith component. This is temperature-independent in the normal state but, below $T_c$, it starts to increase due to the onset of the FLL (see insets in Fig. 3a and b). We recall that the fast Fourier transform (FFT) of the time-dependent asymmetry represents the probability distribution density of the local field p(B). In general, in the superconducting state, the p(B) distribution is material dependent. In case of a symmetric p(B), one oscillation (i.e., $n = 1$) is sufficient to describe the TF-${\upmu }$SR spectra. However, for an asymmetric p(B), two or more oscillations (i.e., $n \ge 2$) are required. Here, we find that Eq. (1) with $n = 2$ describes the experimental data quite well (see green dashed lines in the main panels of Fig. 3a and b). We evidence here four notable aspects:

Fig. 4

DFT$+\mu$ prediction of the most energetically favorable muon implantation site, which turns out to be fully anisotropic (a). Panel (b) shows the simulated asymmetries including the quadrupolar contribution (QC) vs the measured asymmetries at $T = 5$ K (i.e., above $T_{c}$) for an applied transverse field $\mu _0H^{\parallel } = 14$ mT ($\triangledown$) and $\mu _0H^{\perp } = 14$ mT ($\circ$). Panel (c) shows the simulated asymmetries without QC for a comparison.

Firstly, the muon precession is strongly damped in the superconducting state, suggesting low values of the magnetic penetration depth (see below), thus confirming the very high quality of our samples.

Secondly, in both the superconducting- and normal states, the time-dependent asymmetry is very different in the parallel vs. the perpendicular configuration (see insets in Fig. 3). The superconducting state is discussed in detail in the following sections. As to the normal state, we remark that the muon depolarization in the $H^{\perp }$ configuration is much larger than that measured in the $H^{\parallel }$ case (see also the NMR section above). Recently, Bonfà et al.²² have clarified the perturbation produced by implanted muons on the lattice and the electric field gradient at the neighboring sites. Such perturbation is more effective when the muon implantation site is close to atoms whose nuclei have non-zero quadrupole moments, as is here the case for Ga and V. Following this proposal, density functional theory (DFT) was used to calculate the most likely implantation sites for positive muons, here modeled as hydrogen impurities (DFT$+\mu$ procedure^23,24), and the (perturbed) EFG at the various nuclei. The nuclear contribution to the muon spin relaxation is finally obtained with the code developed in Ref.²⁵. In Fig. 4a we show the result of such calculation: the predicted muon implantation sites lie on the Ga planes, where the implanted muons are bounded with four Ga first-neighbour atoms, whereas the out-of-plane second and third neighbours of the muon, respectively Ga and V nuclei, are more than 3 Å apart, resulting in a less effective dipolar coupling. This scenario confirms that the coupling of the implanted muons to the environment is essentially planar, i.e. fully anisotropic. In Fig. 4b–c we show the calculated muon asymmetries with and without the quadrupolar contribution (QC) of the Ga nuclei, for both the $H^{\perp }$ and $H^{\parallel }$ configurations. [The calculation was carried out following the approach proposed by Celio²⁶, considering a Hilbert space with 4 first- and 8 second nearest-neighbor Ga nuclei.] It is worth noting that (i) the quantum entanglement with the dipolar moments of Ga nuclei is the main responsible for the large depolarization rate. (ii) The largest component of the EFG tensor at Ga nuclei is the one in the ab-plane, which makes the muon perturbation of the EFG less effective²². Thus, for $H^{\perp }$, the pure nuclear dipolar contribution can be recovered, while for $H^{\parallel }$ the anisotropy of the EFG tensor contributes significantly to reduce the muon-spin depolarization. The excellent agreement between the simulated asymmetries in the presence of QC and the corresponding experimental data sets (Fig. 4b) confirms the picture of a very large and anisotropic EFG at the Ga nuclei. As an additional check on the accuracy of our numerical calculations, we also calculated the EFG and quadrupolar coupling constants at the V nuclei. The calculated value of $2\nu _Q = 214 \pm 2$ kHz is close to the experimental value of $2\nu _Q = 274\pm 2$ kHz (see Fig. 2a). Hence, our DFT model is consistent with both the μSR and NMR data.

Thirdly, the corresponding fast Fourier transforms show a main superconducting peak and a minor peak at the applied field value. The latter is ascribed to a tiny non superconducting part of the sample (or parts of the sample holder). The resulting low-temperature lower-limit of the superconducting volume fraction is $V_\textrm{sc}(\mathrm {0.3\,K}) =1- A_\textrm{bg}/A_\textrm{tot} \simeq 95(1)$%, in agreement with the superconducting shielding fraction estimated by dc magnetization, thus further confirming the very high quality of the investigated samples.

Fourthly, in the parallel-field configuration, the normal peak is $\sim 10$ mT away from the superconducting one, thus indicating an almost null pinning force in this case. Conversely, in the perpendicular-field configuration, the shift is small, indicative of strong pinning. In Fig. 3c the temperature evolution of the superconducting field shift in both field configurations is represented. Further, for $\mu _0H^{\perp } = 14$  mT we observe also a tiny peak splitting in the superconducting component (see main panel of Fig. 3b), while it is completely absent for $\mu _0H^{\perp } = 50$  mT (not shown). We calculate the resulting depolarization rate $\sigma$ from the second moment of the internal field distribution P(B) by assuming a standard Abrikosov vortex lattice (AVL) in both configurations. The resulting effective Gaussian relaxation rate can be written as²¹:

$$\begin{aligned} \frac{\sigma ^2}{\gamma _\mu ^2} = \sum _{i=1}^2 A_i [\sigma _i^2/\gamma _{\mu }^2 - \left( B_i - \langle B \rangle \right) ^2]/(A_1 + A_2),\nonumber \\ \text { where } \quad \langle B \rangle = (A_1\,B_1 + A_2\,B_2)/(A_1 + A_2). \end{aligned}$$

(2)

By considering that, in the 0–5 K range investigated here, the nuclear relaxation rate $\sigma _\textrm{n}$ is essentially independent of temperature, the Gaussian relaxation rate in the SC state can be extracted from the total depolarization rate $\sigma$ via a quadrature subtraction:

$$\begin{aligned} \sigma _\textrm{sc} = \sqrt{\sigma ^{2} - \sigma ^{2}_\textrm{n}}. \end{aligned}$$

(3)

In $\hbox {V}_2\hbox {Ga}_5$, the upper critical fields measured in samples from the same origin $\mu _0H_\textrm{c2}^{\parallel }(0) \sim 0.49$ T and $\mu _0H_\textrm{c2}^{\perp }(0) \sim 0.57$ T⁷ are significantly larger than the applied TF field (14 and 50 mT respectively). Hence, we can ignore the effects of the overlapping vortex cores when extracting the magnetic penetration depth from the measured $\sigma _\textrm{sc}$. The effective magnetic penetration depth $\lambda _\textrm{eff}(T)$ can then be calculated by using the well-known relation^27,28:

$$\begin{aligned} \frac{\sigma _\textrm{sc}^2(T)}{\gamma ^2_{\mu }} = 0.00371\frac{\varPhi _0^2}{\lambda _\textrm{eff}^4(T)}, \end{aligned}$$

(4)

where $\varPhi _0 = 2.07 \times 10^{3}$ T $\textrm{nm}^{2}$ is the magnetic flux quantum.

Fig. 5

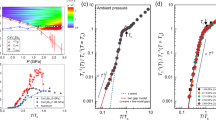
TF-${\upmu }$SR relaxation above and below $T_c$ in a 14-mT field applied perpendicular to the c-axis at zero- (a) and maximum pressure, 19.5 kbar (b). The time-domain spectra above and below $T_c$ for both pressures are given in the insets. In both cases, the ${\upmu }$SR signal is dominated by the pressure-cell contribution, here appearing as an enhanced relaxation of asymmetry (compare with insets in Fig. 3). This is reflected also in the respective FFT spectra (main panels), with the main peak due to the pressure cell and the broad hump at the left representing the sample contribution. Diamagnetic field shift (c) and $1/\lambda ^{2}$ (d) vs. temperature measured at zero- and at maximum pressure (19.5 kbar). Dashed lines in panel (b) represent a fit with a single s-wave SC pairing model. The applied pressure reduces slightly $T_c$, but it does not change the nature of the pairing nor its parameters.

Fig. 6

Critical superconducting temperature of $\hbox {V}_2\hbox {Ga}_5$ vs. applied pressure. Resistivity²⁹ and ${\upmu }$SR results (this work) suggest a linear decrease of $T_c$ with pressure, with an almost identical slope.

${\upmu }$SR under applied hydrostatic pressure

To gain further insight into the superconducting properties of $\hbox {V}_2\hbox {Ga}_5$, we performed TF-${\upmu }$SR measurements in an applied pressure up to 19.5 kbar. In Fig. 5a and b we present the time-dependent asymmetry and its fast Fourier transform at zero- and at maximum pressure, both below and above $T_c$. The pressure cell affects strongly the FFT profile by significantly broadening the superconducting peak compared with the data shown in Fig. 3a and b. For this reason, the optimal fit of the superconducting peak was obtained by assuming a skewed Gaussian (skG) field distribution³⁰. In this case, the time-dependent asymmetry was fitted by the following equation:

$$\begin{aligned} A_{{{\text{TF}}}} (t) & = A_{{\text{0}}} [\left( {1 - f_{{{\text{pc}}}} } \right) \cdot {\text{skG}}(t) \\ &\quad + f_{{{\text{pc}}}} \cos (\gamma _{\mu } B_{{{\text{pc}}}} t + \phi )e^{{ - \sigma _{{{\text{pc}}}}^{2} t^{2} /2}} e^{{ - \Lambda _{{{\text{bg}}}} t}} ]. \\ \end{aligned}$$

(5)

Here, $\textrm{skG}(t)$ is the frequency-to-time Fourier transform of the skewed Gaussian field distribution, while $A_\textrm{pc},$ $B_\textrm{pc}$ and $\sigma _\textrm{pc}$ refer to the contribution of the muons implanted in the pressure cell ($A_\textrm{pc} / A_\textrm{0} \sim$ 70%). $\sigma _\textrm{bg}$ was kept fixed at 0.26 ${\upmu }\textrm{s}^{-1}$, its known temperature-independent value in the 0.25–20 K range³¹. The additional simple exponential relaxation term $e^{-\varLambda _\textrm{bg} t}$ accounts for the fluctuating dipole moments of electronic origin. Since such relaxation increases slightly below 1 K, we had to fix $\varLambda _\textrm{bg}$ to its previously measured value at each of the corresponding temperatures, as reported in Ref. 31. Due to the overwhelming weight of the cell background, a comparison of Dolly- (no background) with the GPD results at zero pressure was essential to estimate the contribution of the pressure cell to the ${\upmu }$SR signal. In Fig. 5c and d we show the temperature evolution of the diamagnetic field shift and of $\lambda ^{-2}$, extracted from the superconducting depolarization rate by means of Eq. (4).

Superfluid density

Figures 3d and 5d summarize the temperature-dependent inverse-square of the magnetic penetration depth, which is proportional to the superfluid density, i.e., $\lambda _\textrm{eff}^{-2}(T) \propto \rho _\textrm{sc}(T)$. In the clean limit and for an s-wave pairing symmetry, this is described by the following equation:

$$\begin{aligned} \frac{\lambda ^{2}(0)}{\lambda ^{2}(T)}= \left[ 1-2 \int _{\varDelta (0)} ^{\infty } \left( - \frac{\partial f }{ \partial E} \right) \cdot \frac{E \, \textrm{d}E}{\sqrt{E^{2}-\Delta(T)^2}} \right] , \end{aligned}$$

(6)

where $f = (1+e^{E/k_\textrm{B}T})^{-1}$ is the Fermi function and $\varDelta (T) = \varDelta _0 \textrm{tanh} \left[ 1.82[1.018(T_\textrm{c}/T-1)]^{0.51} \right]$^32,33, with $\varDelta _0$ being the SC gap value at 0 K.

As shown in Figs. 3d and  5d, the constant $1/\lambda ^{2}(T)$ values at low-T clearly suggest a fully-gapped superconducting state. More interestingly, around $T_{c}/2$ an inflection point appears for $\mu _0H^{\perp } = 14$ mT in both GPD-data sets. Such an inflection point is expected to appear in superconductors with two weakly coupled superconducting bands, as for instance is the case of $\hbox {MgB}_2$³⁴. Similarly, we analyzed our datasets by assuming the superfluid density to be due to a linear combination of two independent contributions from bands with a negligible interband scattering^34,35:

$$\begin{aligned} \frac{\lambda ^{2}(0)}{\lambda ^{2}(T)}= \omega \cdot \frac{\lambda _{1}^{2}(0, \varDelta _{0,1})}{\lambda _{1}^{2}(T,\varDelta _{0,1})} + (1-\omega ) \cdot \frac{\lambda _{2}^{2}(0, \varDelta _{0,2})}{\lambda _{2}^{2}(T,\varDelta _{0,2})}, \end{aligned}$$

(7)

where $\lambda (0)$ is the zero-temperature limit of the penetration depth, $\varDelta _{0,i}$ is the value of the i-th superconducting gap ($i = 1$, 2) at $T = 0$ K and $\omega$ is a weighting factor, representing the relative contribution of each band. All the fitting parameters are summarized in Table 1. It is worth noting that, for these three datasets, a global fit was performed by assuming a negligible variation of the relative weight of the two bands up to 20 kbar. The resulting global parameter $\omega = 0.44(8)$ suggests an almost equal contribution of the two bands. We further note that, in the zero-temperature limit, both the superconducting gap and the magnetic penetration depth are almost insensitive to the applied pressure (up to $\sim 19.5$ kbar). Conversely, $T_{c}$ decreases slightly with increasing pressure, with a slope of $\textrm{d}P/\textrm{d}T =-0.020(1)$ kbar/K. Such decrease in $T_c$ is in good agreement with the resistivity data measured up to 100 kbar (see Fig. 6) on samples from the same batch²⁹ and/or reported in a recent work⁸.

We recall that for most superconductors, $T_{c}$ generally decreases with pressure^36,37. Indeed, one can write $T_{c} \sim \sqrt{k/M} \cdot \text {e}^{\frac{-k}{\eta }}$, where k is a spring constant (a lattice term), $\eta$ is a purely electronic term, and M is the atom mass. Generally, the pressure-induced lattice stiffening k dominates over small changes to the electronic term $\eta.$ When pressure is applied, the spring constant k increases. However, the increase in the prefactor is outweighed by the decrease in the exponential. The overall effect is a decrease in $T_c$.

Interestingly, no inflection points could be detected for $\mu _0H^{\parallel } = 14$ mT and $\mu _0H^{\perp } = 50$ mT. In both cases, a single s-wave gap model in the clean limit could satisfactorily fit the experimental data. In the 50-mT case, depending on the geometry of the circular motions on the Fermi surface, one of the bands may dominate the SC quasiparticle excitations, thus resulting in the vanishing of the smaller gap. As to the 14-mT case, the vanishig of the small gap could be the fingerprint of a k-space gap anisotropy due to the tetragonal structure of $\hbox {V}_2\hbox {Ga}_5$.

Table 1 Fit parameters $\lambda (0)$ and $\varDelta (0)$ at 0 K, as resulting from a fit to Eq. (6) and/or (7) as shown in Figs. 3d and 5d.

Discussion

Search for topological signatures in the normal state

It is of interest to check if the topological properties of $\hbox {V}_2\hbox {Ga}_5$ give rise to observable experimental signatures in its normal phase. We first give a brief overview of the existing theory. It is known that topological systems generally exhibit a characteristic diamagnetic response³⁸. In particular, at high temperatures, the NMR shift arising from a single (Weyl or Dirac) point node is predicted to follow a logarithmic diamagnetic temperature dependence³⁹:

$$\begin{aligned} K(\mu (T), T) \approx \frac{\mu _{0} e}{4 \pi ^{2} \hbar }\left[ \frac{g \mu _\textrm{B}}{\hbar v_\textrm{F}} \mu - \frac{e v_\textrm{F}}{3} \ln \left( \frac{W}{\max \left[ |\mu (T)|, k_\textrm{B} T\right] }\right) \right] \end{aligned}$$

Where, $W\gg \mu$ denotes a sharp high-energy cutoff regularizing the theory, $\mu _{0}$ is the chemical potential at $T=0,$ $\mu (T)$ is the temperature-dependent chemical potential away from the point node, $v_\textrm{F}$ is the Fermi velocity, and $\hbar$, e, g, $\mu _\textrm{B}$ are the usual physical constants. Likewise, at high temperatures, $1/T_{1}T$ is predicted to follow a power-law dependence given by⁴⁰:

$$\begin{aligned} \begin{aligned} \frac{\hbar }{k_{\textrm{B}} T_{1} T}&= \frac{52.7k_{\textrm{B}} \pi \mu _{0}^{2} \gamma _{\text {n}}^{2} e^{2}}{(2 \pi )^{6} \hbar v_{\textrm{F}}^{2}}\\&\times {\left\{ \begin{array}{ll}\left( \dfrac{k_{\textrm{B}} T}{\hbar }\right) ^{2} \dfrac{\pi ^{2}}{3} \ln \left( \dfrac{4 k_{\textrm{B}} T}{\hbar \omega _{0}}\right) , & \mu \ll k_{\textrm{B}} T \\ \left( \dfrac{\mu }{\hbar }\right) ^{2} \ln \left( \dfrac{2 \mu }{\hbar \omega _{0}}\right) , & \mu \gg k_{\textrm{B}}T\end{array}\right. } \end{aligned} \end{aligned}$$

In case of Kramers nodal-lines semimetals, to our knowledge, a comprehensive theory of the expected NMR behavior has not yet been developed. However, previous measurements on the nodal-line semimetal ZrSiTe⁴¹, which exhibits a single nodal line, reveal a characteristic “V-shaped” feature, with minima in both the NMR shift and relaxation rate occurring at a temperature $T_\textrm{min}$, where the temperature-dependent chemical potential $\mu (T) \propto |T - T_\textrm{min}|$ goes to 0.

Now, turning to the case of $\hbox {V}_2\hbox {Ga}_5$, our measured $1/T_{1}T$ is practically temperature-independent (see Fig. 2c). Hence, the $1/T_{1}T$ results do not exhibit any of the experimental signatures expected for a single point-node or a nodal line. The only hint of topological properties occurs in the slight logarithmic increase of the NMR Knight shift above 90 K, which corresponds to a chemical potential $\mu = k_\textrm{B}T \approx {7.76}$ meV. However, from previous calculations, the closest lying point node is at $\sim 70$ meV, hence casting doubts on the topological origin of this feature. Furthermore, the increase in K is much smaller than the NMR line width and there is no accompanying change in $1/T_{1}T$. Consequently, the increase in NMR shift above 90 K is most likely due to small changes in the quadrupole interaction caused by tiny temperature-induced changes in the crystal structure.

Fig. 7

Temperature dependence of internal fields $B_{1}$ and $B_{2}$. The continuous lines represent the temperature evolution of $B_{1}$ and $B_{2}$ obtained by fitting the time dependent asymmetry for the $\mu _0H^{\perp }=14$ mT field configuration through Eq. (1). Blue and red dots represent the temperature evolution of the peak splitting obtained by directly fitting the FFT of the time dependent asymmetry.

Anisotropic superconductivity in V₂Ga₅

V₂Ga₅ has a tetragonal structure with the c-axis being less than one third of the in-plane unit cell parameter (2.6831 Å vs. 8.936 Å⁶). This pronounced difference in the lattice parameters is most likely responsible for the highly anisotropic electronic properties we observe in the normal- and superconducting states. Yet, TF-${\upmu }$SR measurements in the superconducting state reveal a more complex picture.

Firstly, we consider the anisotropy in the superconducting state, as determined from the magnetic penetration depth and superfluid density. In the $T\rightarrow 0$ K limit, the magnetic penetration depth and, consequently, the superfluid density both show an almost negligible anisotropy [see Table 1]. On the other hand, the temperature dependence of the superfluid density shows clear differences between the in-plane $H^{\parallel }$ and out-of-plane $H^{\perp }$ configurations (Fig. 3d). These different types of behavior may explain why in the $H^{\parallel }$ case a single gap is found, while for $H^{\perp }$ a double gap provides the best fit. Angle resolved photoemission spectroscopy (ARPES) measurements evidence two discernible bands with an almost negligible dispersion along the $k_{x}$ and $k_{y}$ directions cross the Fermi level close to the Z and $\varGamma$ points⁸. Therefore, in an applied magnetic field orthogonal to the c-axis ($H^{\perp }$), the induced screening currents in the ac-plane are likely sensitive to both gaps. On the other hand, this might not be the case when the field is parallel to the c-axis and the induced currents lie in the ab-plane.

Secondly, the anisotropy of superconductivity in $\hbox {V}_2\hbox {Ga}_5$ can be observed from the anisotropy of pinning forces. The unexpectedly large diamagnetic field shift in the $H^{\parallel }$ configuration suggests a null pinning force in this case. On the other hand, the small diamagnetic field shift in the $H^{\perp }$ configuration suggests a non-negligible pinning force in this configuration. In general, the mechanism underlying the anisotropy of the pinning forces remains to be investigated.

Lastly, the anisotropy of $\hbox {V}_2\hbox {Ga}_5$ in its SC state can be evidenced from a peak splitting we observe in the $H^{\perp }$ configuration. As shown in Fig. 3, the FFT of the time-dependent ${\upmu }$SR asymmetry shows a tiny, yet distinct peak splitting at low temperatures and low magnetic fields for $\mu _0 H^{\perp } = 14$ mT, which is absent for $\mu _0 H^{\parallel } = 14$ mT. Even when including a more robust apodization, a rectangular-like peak still remains, indicative of a nontrivial spectrum, here consisting of two near-lying frequencies [see Fig. 3 in Supplementary Information]. Such splitting disappears and the two frequencies merge either above a threshold temperature $\sim T_{c}/2$ (see Fig. 7), or at a higher applied field (here, $\mu _0 H^{\perp } = 50$ mT, not shown). More importantly, in a parallel magnetic-field configuration, no splitting is found (Fig. 3a). In view of a superconducting volume fraction of $\sim 100 \%$ and of the very high quality of the investigated samples⁷, we can safely rule out any possible extrinsic origin (like inhomegeneities) of the peak splitting in the FFT of the time-dependent asymmetry and consider it an intrinsic property of $\hbox {V}_2\hbox {Ga}_5$. Whether such key feature is due to anisotropy, to topological effects, or to both remains open.

Unconventional vortex lattice in V₂Ga₅

The presence of a peak splitting in the local field distribution p(B), measured via TF-${\upmu }$SR, is suggestive of the possible presence of an unconventional vortex lattice, where two different length scales coexist in a limited region of the H-T phase diagram. In this respect, Speight et al. have shown that nematic superconductors with odd-parity pairing are expected to exhibit a non-Abrikosov-like mixed state⁴² consisting in stripes of “coreless” vortices, defined as two spatially separated half-quantum vortices. Such unconventional structures were firstly named “skyrmion” vortices, because of their additional topological properties (namely, a skyrmionic topological charge of $-1$)⁴³. This unconventional mixed state is characterized by two length scales: the separation between the chains and the inter-skyrmion separation along the same chain. Depending on the above two length scales, the local magnetic-field distribution p(B) is expected to exhibit a characteristic double-peak structure. Such feature, however, can only be observed in a small region of the mixed state, at low temperatures and low applied fields. In fact, for applied fields⁴² or temperatures⁴⁴ greater than a threshold value, the skyrmion vortices are expected to melt into a conventional Abrikosov vortex lattice.

Although the skyrmionic vortex lattices can in principle be detected by a series of techniques, such as scanning SQUID microscopy, scanning Hall probes, nuclear magnetic resonance, and small-angle neutron scattering⁴², only ${\upmu }$SR has a sufficient signal-to-noise ratio, because muons are 100% spin polarized. Furthermore, unlike NMR and neutron scattering, which require magnetic fields above $\sim 1$ T, ${\upmu }$SR can be performed at much lower fields, for which the skyrmion vortex lattice — if present — is essentially unperturbed⁴². More detailed TF-${\upmu }$SR measurements at selected $H^{\perp }$-T values are required to characterize the nature of such an unusual mixed phase. These studies are particularly relevant for $\hbox {V}_2\hbox {Ga}_5$ in view of the predicted topological nature of its normal state⁷.

Conclusion

We performed local-probe (NMR and ${\upmu }$SR) investigations of the normal- and superconducting-state properties of the binary compound $\hbox {V}_2\hbox {Ga}_5$, characterized by a topologically nontrivial normal state. Our measurements reveal that, because of its pronounced 1D character due to vanadium chains, $\hbox {V}_2\hbox {Ga}_5$ manifests a strong crystalline anisotropy on the electronic properties. In the superconducting state, we find the superfluid density to be fully-gapped, with signatures of a double s-wave gap for applied fields perpendicular to the c-axis. The vanishing of the smaller gap upon increasing the magnetic field intensity, or for applied fields parallel to the c-axis, is consistent with a marked anisotropy of the $\hbox {V}_2\hbox {Ga}_5$ superconductivity. The lack of spontaneous magnetic fields below $T_c$ (see Suppl. Material) indicates a preserved time-reversal symmetry in the superconducting state. Finally, for $H^{\perp }=14$ mT, the magnetic field distribution in the mixed state presents a double-peaked FFT structure, characteristic of the presence of an unconventional mixed phase.

In the normal state, NMR measurements reveal a strong anisotropy in the $H^{\parallel }$ and $H^{\perp }$ orientations, consistent with the 1D character of the compound. However, in the measured temperature range, we did not find signatures of topological nodes. Further measurements at higher temperatures (i.e., at $k_\textrm{B}T > \mu,$ with $\mu$ denoting the chemical potential) are needed to confirm the expected topological signatures in $\hbox {V}_2\hbox {Ga}_5$.

Methods

Sample synthesis

Needle-like single crystals of $\hbox {V}_2\hbox {Ga}_5$ were grown from elemental V in powder form in molten Ga flux. After inserting both elements into an evacuated and sealed silica ampoule, a furnace was used to heat the ampoule up to $1000^\circ$C in 12 h and to maintain it there for another 12 h. The temperature was then dropped to $85^{\circ }$C in 5 h and kept there for another 4 days. Finally, the ampoule was allowed to cool to room temperature for 4 more days (see Ref.⁷ for further details). The resulting $\hbox {V}_2\hbox {Ga}_5$ crystals adopt a tetragonal structure with a space group P4/mbm (No. 127) and unit-cell parameters $a = b = 8.9820(3)$ Å, and $c = 2.7005(2)$ Å, in agreement with previous work^6,7,45. A schematic view of the crystal structure is shown in Fig. 8.

Fig. 8

Crystal structure of $\hbox {V}_2\hbox {Ga}_5$: light-green, dark-green, and red spheres represent Ga(1), Ga(2) and V atoms, respectively. The c-direction represents the main symmetry axis along which grow the needle-like single crystals, as shown in Figure 1d in Ref.⁷. The black arrows indicate the magnetic field directions. Here, $H^{\parallel }$ and $H^{\perp }$ represent the magnetic fields applied parallel- and perpendicular to the c-axis, respectively.

DC magnetization

In recent studies, $\hbox {V}_2\hbox {Ga}_5$ was characterized by means of resistivity (as a function of temperature and applied field), as well as via heat-capacity, low-temperature thermal-conductivity measurements⁷ and ${\upmu }$SR⁸. Since our microscopic NMR and ${\upmu }$SR investigations were performed on samples of the same origin⁷, our basic sample characterization included only complementary dc magnetometry measurements performed on a MPMS2 SQUID magnetometer by Quantum Design. In our case, we covered an extended field range, up to $\mu _{0}H_{\textrm{app}} = 5$ T, with the field applied parallel and perpendicular to the c-axis ($H^{\parallel }$ and $H^{\perp }$, see Fig. 1 in the SM).

NMR experiments

To study the electronic properties of $\hbox {V}_2\hbox {Ga}_5$ with a complementary local probe, we performed nuclear magnetic resonance (NMR) experiments. The sample was oriented with the c-axis either parallel- or perpendicular to the external magnetic field, $\mu _{0}H_{\textrm{app}} = 5.007$ T [See Fig.1 in supplementary information]. In principle, both gallium and vanadium are suitable nuclei for such measurements. However, gallium has two spin-3/2 nuclei, $^{69}$Ga and $^{71}$Ga, with relatively large quadrupole moments Q. Since, in a solid, the electric-field gradients at the nucleus position can interact with the nuclear quadrupole moment, in case of a large Q, this produces a considerable spectral broadening and complex overlapping peaks. On the other hand, despite a spin of 7/2, $^{51}$V is the only naturally occurring isotope and has a large magnetogyric ratio while its quadrupole moment is relatively small, $-0.043(5) \times 10^{-28}$ $\textrm{m}^{2}$⁴⁶. Consequently, vanadium was the nucleus of choice for our NMR investigations.

Four main issues had to be overcome when performing $^{51}$V NMR. Firstly, considering the suppression of $T_c$ in an applied magnetic field (and the extensive ${\upmu }$SR study of the SC phase), we had to limit the NMR measurements to the normal state of $\hbox {V}_2\hbox {Ga}_5$. Secondly, the NMR resonance frequency of $^{51}$V (here, 56.072 MHz from the reference compound $\hbox {VOCl}_3$), is close to that of $^{63}$Cu (56.525 MHz) and $^{27}$Al (55.547 MHz). Since $^{63}$Cu and $^{27}$Al are ubiquitous among the NMR-probe materials, this leads to experimental artefacts close to the $^{51}$V resonance line. During data processing, a symmetrization procedure was performed to remove such residual artefacts that might still remain on both sides of the main $^{51}$V resonance. Thirdly, since a single $\hbox {V}_2\hbox {Ga}_5$ “needle” is too small to perform NMR measurements, numerous needles ($\sim 30$) had to be bundled together to obtain a sufficient mass for a suitable S/N ratio. Fourthly, while it is straightforward to measure NMR in the $H^{\perp }$ configuration, where the $\hbox {V}_2\hbox {Ga}_5$ “needles” are parallel to the long axis of the coil, the $H^{\parallel }$ configuration is significantly harder. To this aim a special sample bundle was realized as detailed in the SM. Due to practical problems with aligning the “needles” in the correct orientation, as well as a poorer filling factor, the S/N ratio was significantly worse in this case. A large apodization factor had to be used during post-processing, which distorts the lineshape away from the main NMR carrier frequency. This fact, together with the artefacts mentioned above, means that we could not accurately determine the complete lineshape of the NMR resonance in the $H^{\parallel }$ configuration. Nevertheless, the line shifts and the relaxation rates, where the apodization has a minimal effect, could still be reliably obtained from the central transition, here corresponding to the main NMR peak.

Muon-spin rotation and relaxation (${\upmu }$SR)

The bulk ${\upmu }$SR measurements were carried out at the multipurpose surface-muon spectrometer (Dolly) on the $\pi$E1 beamline and at the high-pressure muon facility (GPD) on the ${\upmu }$E1 beamline, both at the Swiss muon source of Paul Scherrer Institut, Villigen, Switzerland. The low $T_c$ value required the use of a He-3 refrigerator, essential for carrying out measurements in the 0.3–10 K temperature range in both facilities. For the surface-muon measurements, the samples were mounted on a 25-${\upmu }$m thick copper foil, which ensured a good thermalization at low temperatures. The needle-like samples were oriented so that the c-axis (coincident with the needle axis) was either parallel- or perpendicular to the main magnetic field. Both transverse field (TF-${\upmu }$SR) and zero field (ZF-${\upmu }$SR) muon-spin spectroscopy measurements were performed in this case.

For the studies under pressure, a suitable sample consisting of several crystals [see Fig.S2 in Supplementary Material] was inserted into a double-walled MP35N/CuBe cylinder pressure cell (PC)^31,47,48, with the c-axis parallel to the cell axis. Daphne oil 7373 was used as a pressure-transmitting medium to achieve hydrostatic conditions. Here, low-temperature TF-${\upmu }$SR measurements were performed at about 0 and 19.5 kbar, corresponding to a pressure of 2 and 22.5 kbar at room temperature, respectively. The time-differential ${\upmu }$SR data under normal- and high-pressure conditions were analyzed by means of the musrfit software package⁴⁹.