Abstract
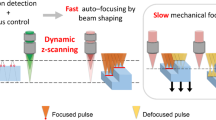
Several advanced techniques have been used for 3D micro-surface profiling, such as white light interferometry, confocal microscopy, and atomic force microscopy. However, a major technological limitation shared among these methods is the difficulty of imaging dynamic samples in real-time at high resolution. Specifically, profiling rapidly changing or moving surfaces at nanoscale 3D spatial resolution remains a challenging task. We demonstrate here a high-speed MEMS mirror-based laser differential confocal microscope for dynamic 3D micro-surface profiling. The MEMS mirror enables 2D scanning of 1200 × 650 pixels with a 140 × 90 μm field of view at 80 frames per second. Using laser differential confocal detection, the system achieves 25 nm axial resolution. The objective-space telecentric laser projection results in uniform axial response across the field of view, simplifying data acquisition and processing. These capabilities enable real-time 3D micro/nano scale profiling of dynamically changing surfaces at 80 frames per second without requiring motion stages. The system’s substantial increase in imaging throughput enables, for the first time, real-time 3D profiling of dynamic microscale surface topographies at nanometer-level axial resolutions. The high-speed 3D profiling enabled by this system provides new insights for process development and quality control in precision micro/nano fabrication.
Similar content being viewed by others

Introduction
In recent decades, integrated circuit chips and microelectromechanical systems (MEMS) have developed rapidly1,2,3. As part of quality control in producing integrated circuit chips, microelectromechanical systems (MEMS), and general micro-/nano-scale devices, 3D morphology reconstruction of microstructures has become increasingly important4,5,6,7,8,9. Among all microscopic imaging methods with 3D imaging capabilities, interferometric methods, especially white light interferometry, have become the mainstream due to its advantages such as high spatial resolution and non-contact measurement10,11,12,13,14 and has been widely commercialized, performing 3D profile scanning on various samples in laboratories or factories. In addition, research has improved it and amplified white light interferometry’s resolving power down to the tens of nanometers scale15. However, despite the advantages of non-contact measurement and high spatial resolution, the white light interferometry is generally considered to be an inefficient 3D imaging method. For example, it requires a large amount of image acquisition and processing during axial scanning16, which is computationally intensive and time-consuming. Additionally, calibrating the interferometer before measurement is complex and can significantly impact the accuracy of results. Therefore, the generally low imaging efficiency makes it unsuitable for applications involving dynamic 3D imaging. Alternative methods with higher throughput are needed to characterize microstructures in applications such as industrial process monitoring that require real-time 3D analysis.
Confocal Laser scanning microscopy (CLSM), originally designed for high precision 2D imaging, is another approach for non-contact 3D reconstruction of microstructures and has been studied in recent years17,18. It functions by using a pinhole to filter out of out-of-focus light, thereby enabling the acquisition of high-resolution, high-contrast images at specified depths within a sample18. This pinhole, when paired with a photodiode, can additionally record the intensity of light transmitted versus the axial position of the target. Through calibration of this “axial response”, the precise z-coordinate of the target can be ascertained. As a result, CLSM is capable of conducting detailed 3D surface topographic mapping of microscale targets without direct contact. Previous research has demonstrated its ability to reconstruct microstructures at exceptional optical resolution and contrast, offering information that not easily obtained through traditional microscopic methods19,20,21.
The conventional design of CLSM presents limitations that constrained its application as a 3D micro scanner. Issues exist with both axial measurement precision and the ability to conduct horizontal scanning. For example, relying solely on absolute energy values precludes distinguishing the axial positions of targets with varying reflectivity22. Additionally, the typical Gaussian-shaped axial response curve exhibited by CLSM poses additional challenges for accurate measurement. Specifically, its non-monotonic nature and zero slope in the vicinity of the peak limit reliable detection to a narrow band on a single flank of the curve. As a result, both the sensitivity and spatial resolution achievable are compromised23. Though CLSM enables rapid single-point detection by directly obtaining axial position from pre-calibrated response data without image processing or axial scanning, generating 2D mappings requires a scanning mechanism. Typically, motion stages using stepped motors or piezoelectric actuators is currently the mainstream method to provide precise 2D scanning, such as XY stage or spiral-scanning stage24. However, such approaches cannot offer the high-speed 2D scanning that matches CLSM’s fast axial response times25.
Over the years, various techniques have been developed seeking to enhance CLSM’s axial measurement capabilities. A notable advancement was multiple-pinhole differential confocal microscopy, which uses two or more pinholes to generate differential axial responses. Lee et al. employed an energy ratio approach using two pinholes of different sizes to measure height, thereby eliminating the influence of sample reflectivity26. Specifically, they determined the ratio of energy passing through the pinholes to extract topographical information while negating the effect of surface reflectivity variations. However, its axial dynamic range is still limited to one flank of the axial response curve. It was also found27,28,29 that positioning identical pinholes before and after two collecting lens focal planes, then calculating the difference between signals, greatly suppressed common-mode noise, yielding higher signal-to-noise ratios. Dividing this differential signal by either the larger individual signal or their sum further suppresses absolute light intensity effects, rendering axial detection insensitive to reflectivity and broadening applicable scenarios22,30. Additionally, this method provides a monotonic axial dynamic range concentrated near the objective focal plane, augmenting both lateral resolution and axial measurement sensitivity. When employing high-power objectives, the system’s axial resolution can reach a few nanometers31.
To enable fast 2D scanning, 2D mapping devices based on microelectromechanical systems (MEMS) technology are gradually being used in various microscope systems to achieve higher imaging efficiency. MEMS scanning mirror is one of the most commonly used method due to its fast response capabilities32,33,34,35. In recent years, MEMS mirror performance has continuously advanced, now offering high resolutions that can be maintained even at elevated refresh rates36,37. This makes it feasible to employ a single MEMS mirror to generate 2D mappings characterized by both high resolution and high refresh rate. The combination of MEMS scanning mirrors and confocal microscopes has also been studied and produced. In the work of Qiu et al.38, the 2D MEMS mirror is used for confocal 2D imaging, but it still needs to be combined with axial scanning to achieve 3D slicing and stacking, and finally an imaging rate of 3.7 Hz is achieved. However, due to the limitation of MEMS mirror performance, the image resolution is limited as 128 × 128. Another commonly used device for high-speed 2D mapping is the digital micromirror array. Some studies have combined it with confocal microscopy, using multiple micromirrors as pinholes that can be operated in parallel, without the need for point-by-point measurement, which greatly enhances the imaging speed39,40. Among them, the work of Lee et al.39 describes the use of DMD elements combined with differential confocal height measurement to achieve 50 Hz high-speed 3D imaging. However, the low-magnification objective lens cannot provide sufficient optical resolution to identify microstructures on the wafer while providing a wide measurement dynamic range. In summary, high-speed MEMS devices, namely MEMS scanning mirrors for point-by-point scanning and DMD for multi-point scanning at a time, have great potential in the field of microscopic 3D imaging. In addition, these works also emphasized the difficulty of integrating these devices into precision optical paths, which requires further optimization and design.
At the same time, higher imaging rates, such as the work of Lee et al.39 mentioned above, have essentially reached practical video-level frame rates. This makes dynamic 3D imaging of microstructures possible. Confocal-based axial detection is naturally extremely fast and when combined with high-speed 2D mapping brought by MEMS mirrors or DMDs, it achieves imaging speeds that exceed traditional microscopes. In addition, compared with other devices with similar functions, such as light field cameras41,42, it has an advantage in spatial resolution.
In this study, we demonstrate a combination of MEMS mirror scanning and laser differential confocal microscopy capable of rapid dynamic 3D reconstruction of microstructures with both high accuracy and speed. We refer to this novel system as MEMS Mirror-Integrated Laser Differential Confocal Microscopy (MLDCM). It leverages a 2D MEMS mirror for fast laser scanning combined with laser differential confocal-based axial sensing to generate full 3D maps of microstructures. It can generate 3D images with resolution of 1200 × 650 pixels at 80 frames per second and doesn’t require additional scanning mechanics. Using a 50× objective (Mitutoyo Plan APO, NA 0.42), the maximum scanning area was 140 μm × 90 μm. To validate the system’s ability, we conducted both static and dynamic 3D imaging of microfabricated structures on a commercial silicon wafer. Furthermore, the MLDCM is tested to have robustness to sample’s minor tilting up to ± 1.5°. Moreover, we exploited this tilt-tolerance by visualizing the surface angle change of a driven galvanometer mirror during the oscillation motion with MLDCM. These initial tests validate the promising performance and flexibility of MLDCM for both static and dynamic volumetric microscopy scenarios.
System design
System layout
The system layout is shown in Fig. 1.
The working principle is described as follows:
In the system, a laser beam from a 520nm continuous-wave laser diode (LD) is spatially filtered and collimated. The LD is aligned that the laser polarization matches the S axis of a polarization beam splitter (PBS). A 0.5 mm aperture (Aperture 1) then shapes the beam appropriately for the MEMS mirror dimensions. Additionally, a polarizer is used to extinguish the P polarization component of the laser beam, leaving only the desired S polarization. The collimated S-polarized laser beam is first focused by a converging lens then reflected by the PBS. It is then collimated by an eyepiece and reflected downward by the MEMS mirror (OPUS OP-7200). During reflection, the beam passes through a quarter-wave plate twice, transforming to P-polarization and passing through the PBS to a tube lens.
The laser beam is focused on the target surface upon passing through a 100mm effective focal length doublet tube lens and a switchable 50× infinity-corrected objective lens (Mitutoyo Plan APO, NA 0.42). The eyepiece and tube lens together act as a relay system, projecting the beam onto the pupil of the objective. As the objective is designed to be object space telecentric, the laser beam remains perpendicular to the target surface and retraces its path back. Upon reflection from the MEMS mirror, the beam again passes through the quarter-wave plate twice, transforming back to S-polarization and reflecting off the PBS toward a 50:50 beam splitter cube (BSC1). BSC1 directs the laser beam upward toward a second 50:50 beam splitter cube (BSC2), which divides it into two beams. A 1mm aperture (Aperture 2) placed between BSC1 and BSC2 filters stray light. The two beams then focus by two identical 50mm effective focal length singlet collecting lenses, L1 and L2. A pinhole (PH1, Φ30 μm) is placed after the focal plane of L1, the distance between the focal plane and PH1 is \(d\), another pinhole (PH2, Φ30 μm) is placed before the focal plane of L2, the distance between the focal plane and PH2 is also \(d\). Two photo diodes (PD1 and PD2, Hamamatsu C12703) are used to collect the laser beam that pass through the pinhole and output two voltage signals, which varies with the target surface axial position. The normalized differential axial response curve calculated from these signals then calibrates measured surface height.
2D mapping generation by MEMS scanning mirror
The MEMS scanning mirror is positioned at the pupil plane of the imaging system that is consisted of an eyepiece, tube lens, and objective. After the reflection by the scanning MEMS mirror, the laser beam passes through this imaging system and is focused on the target surface. During scanning, the MEMS mirror angle is determined by the superposition of simple harmonic motions in two axes. Specifically, the MEMS mirror undergoes sinusoidal scans along both a fast and slow axis. At an instant in time within a single frame time period, (i.e. the monotonic interval of a cycle of slow axis motion), the mirror angle can be described by Eqs. (1) and (2).
where \({A}_{fast}\) and \({A}_{slow}\) are scanning angle ranges of the scanning MEMS mirror’s fast and slow axis, \({f}_{fast}\) and \({f}_{slow}\) are frequencies of simple harmonic motion of fast axis and slow axis.
As the laser beam passes through the imaging system, the MEMS mirror-induced angular variations are transformed into planar scanning across the target surface. As shown in Fig. 2, the laser beam always remains perpendicular to the sample due to the imaging system being object space telecentric, this ensures the beam reflects back towards the MEMS mirror along the original path. Crucially, the use of a telecentric system means the horizontal coordinate of each sampling point is independent of its axial position. Specifically, the x and y coordinates can be determined for any point on the surface by Eqs. (3) and (4).
In the above equations, M is a calibrated scaling factor determined by the combined magnification of the eyepiece, tube lens and objective lens. M relates the angular deflection of the laser beam at the MEMS mirror to the corresponding lateral displacement on the sample plane. M requires calibration against a traceable resolution target to precisely define spatial dimensions and optical resolution in the horizontal direction.
The MLDCM system utilizes an OPUS OP-7200 MEMS scanning mirror for laser beam deflection. It is calibrated that the fast axis frequency \({f}_{fast}\) is 26,014.5 Hz, and slow axis frequency \({f}_{slow}\) is 40 Hz.
The scanning mirror performs slow axis oscillations in a sinusoidal manner. Each oscillation cycle can be divided into two monotonic intervals. Remarkably, the fast axis scanning traces out a full raster pattern across the entire field of view within each monotonic interval of slow axis oscillation, which means it can obtain two complete scans per slow axis cycle, hence the frame rate (\(F\)) of the 2D scanning system can be derived as:
The 2D scanning is achieved through the combined fast and slow axis oscillations of the MEMS mirror. This results in a grid of laser spots being generated across the sample plane during each frame. The number of rows (\(Y\)) in this spot array is calculated as:
At sampling rate of 62.5 MHz, the number of pixels (\(X\)) contained in each row is calculated as:
Therefore, at a sampling rate of 62.5 MHz, this dual-axis MEMS scanning mirror can generate a 2D mapping with a pixel resolution of 1200 × 650 at a frame rate of 80 Hz, totally 780,000 pixels in single frame of image. It is worth noting that the 2D point matrix generated by this type of MEMS scanning mirror has an uneven point arrangement due to simple harmonic motion, which is manifested in a higher point density of at the corners, thus affecting the local resolution. But overall, the point matrix is still dense enough to depict a clear picture.
Due to the fixed phase relationship between the fast and slow axis oscillations, the horizontal distribution of sample points remains constant across frames. Only the z-coordinates vary in accordance with target surface topography. Therefore, 3D image generation simply requires calculating the axial position corresponding to each sampling instant and populating the z-values into the static 2D coordinate grid. This significantly streamlines data acquisition and transmission needs. Real-time feedback of the scanning mirror angles, and recalculation of x–y positions is unnecessary. Only the voltage signals from the two photodiodes, which encode surface height information, require collection. By pre-establishing a 2D grid, 3D topographic imaging can be achieved with minimal amount of data transfer and computation through simple z-value determination at each image point.
Data collection
In MLDCM system, an oscilloscope (Tektronix MSO54) is used for signal monitoring and data acquisition. One channel is dedicated to observing the drive voltage applied to the scanning mirror’s slow axis. During one scanning process, the number of image frames \(N\) can be obtained by Eq. (8):
where \(T\) is the time period that the oscilloscope collects data.
The oscilloscope uses two other channels to simultaneously acquiring the photodiode voltage signals during scanning. After each scan, the oscilloscope waveforms are transmitted to a PC. These waveforms contain both time and voltage information. The time data provides the horizontal position coordinates, while the voltage values correspond to height details. By combining these two key data types extracted from the photodiode signals, MLDCM can efficiently reconstruct complete 3D maps of the sample surface.
Axial response curve obtaining and z coordinate calculating
The axial response of the MLDCM needs to be calibrated and determined. During this process, an aluminum-coated flat mirror (99% reflectivity) is mounted on a piezoelectric (PZT) stage capable of precision axial displacement. As the PZT stage is changing its axial position from low to high, the laser beams are focused by lenses L1 and L2. This causes the beam focal points to change location as they continuously approach, pass through, and diverge from the pinholes PH1 and PH2. As the focal points move relative to the pinholes, the amount of laser energy passing through each pinhole varies, changing the output voltages of the corresponding photodiodes. The photodiode output voltages are recorded synchronously with the PZT positions, marked as \({I}_{1}\left(z\right)\) and \({I}_{2}\left(z\right)\), and the curves are plotted in Fig. 3a.
As seen in Fig. 3a, the calibrated axial response curves \({I}_{1}\left(z\right)\) and \({I}_{2}\left(z\right)\) exhibit characteristic bell-shaped profiles that overlap partially. To relate these curves to meaningful height measurements, further calibration of the collection optics is required. In particular, the positioning of lenses L1 and L2 are adjusted such that the mirror axial position corresponding to the curves’ intersection point coincides precisely with the focal plane of the objective lens. Then use Eq. (9) to obtain the axial response of the normalized differential intensity signal \(I\left(z\right)\).
As presented in Fig. 3b, the curve of normalized differential intensity against axial position presents an S shape. The linear central region within this curve characterizes the system’s dynamic range of axial measurement. The responsivity K is defined as the slope of this linear fit. When profiling an unknown surface, the oscilloscope acquires the photodiode voltage signals during scanning. Through computation of normalized differential intensity from these signals, the sample’s current z-coordinate can be directly solved via the established calibration Eq. (10), for any height falling within the dynamic range.
By analyzing the linear region of this S-curve, the dynamic sensing range was determined to be from − 2.5 μm to + 2.5 μm, and the slope \(K\) is found to be 0.21/μm, which is the responsivity of the axial sensing.
To demonstrate the axial resolution, a resolution test was performed where a PZT stage precisely adjusted the mirror position in 25 nm height increments, corresponding to the minimum change detectable by the MLDCM based on the established calibration. Figure 4 shows the results of this test, validating the nanometer-scale resolution accessible when profiling surfaces using the normalized differential intensity quantitative model. It should be emphasized that the 25 nm axial resolution demonstrated here was obtained in a single-point test, where the MEMS mirror did not perform any scanning. Therefore, it represents a relatively simple case, where the laser beam remained stationary, resulting in a higher signal-to-noise ratio, and the 25 nm axial resolution was an ideal value. In contrast, if the MEMS mirror driving the laser beam scanning across the target surface, due to the installation and adjustment errors in the system, as well as the optical aberrations in the optical design, the return beam’s energy and optical axis become unstable. These factors cause the energy passing through the pinhole to jitter, reducing the signal-to-noise ratio, therefore, when MLDCM performs large-area scanning, the axial resolution may drop, which requires further structural and optical path optimization.
Result
Single frame static 3D image acquisition
A commercial whit light interferometer (WYKO NT9300) was used as a reference for comparison. The interferometer was configured with a 50× objective lens and 1.0× field-of-view, which provided a similar field of view and sampling resolution as the MLDCM, making it suitable for comparison. In this test, two commercial patterned silicon wafers were used as the test object. The 3D microstructure on the wafer consists of planes of different heights composed of various materials, making it suitable as an imaging object for MLDCM and white light interferometry.
The first test pattern contains four bright L-shaped blocks elevated above a darker background area. Figure 5 shows results obtained from both techniques; the test results only retain the area containing the pattern of interest to highlight the key points. Figure 5a presents the 3D topography map reconstructed from MLDCM scanning. Figure 5b displays the interferometric surface profile of the same region. Additionally, Fig. 5c shows an optical image of the pattern captured by a microscope, with Fig. 5d plotting the height profile along the dotted line indicated in Fig. 5c.
Results of Pattern 1. 3D images are displayed in CloudCompare (version 2.13. alpha, http://www.cloudcompare.org): (a) 3D image from MLDCM; (b) 3D image from white light interferometer; (c) 2D image captured by optical microscope; (d) Section profile of the location indicated by the dotted line in (c).
While both the MLDCM and interferometer techniques correctly reconstructed the general 3D structure of the pattern, some differences were observed in the surface profiles. As Fig. 5d indicates, the MLDCM data exhibited overshoots at the edges of steps, reducing its horizontal spatial resolution relative to the interferometer data. Additionally, over the 8–15 μm region highlighted by the dotted box in Fig. 5d, the interferometer measured an average height of 1.491 μm compared to 1.457 μm from MLDCM. Further, within this region, the interferometer profiled a smooth surface, while undulations were present in the MLDCM result, implying that the measurement stability of MLDCM may be limited by certain factors. One is the instability of the return beam energy and optical axis introduced by the scanning MEMS mirror. The second is the mechanical vibration from the outside. It may also be due to electrical noise inside the MLDCM system, including unstable laser diode output energy, or noise in the photodiode output circuit. At present, this undoubtedly greatly reduces the measurement accuracy of MLDCM. Overall, these comparisons to the reference interferometer results provide insights that can inform further development of MLDCM towards achieving higher resolution and stable quantification of surface topography.
Notably, the reflectivity of the dark background region was lower than that of the bright blocks. However, the MLDCM system successfully distinguished the height difference between these areas despite variations in reflectivity across the sample surface. This capability arises from the normalization process applied to the differential photodiode signals, which effectively nullifies the influence of absolute values.
The image results of another pattern are shown in Fig. 6.
Results of Pattern 2. 3D images are displayed in CloudCompare (version 2.13. alpha, http://www.cloudcompare.org): (a) 3D image from MLDCM; (b) 3D image from white light interferometer; (c) 2D image captured by optical microscope; (d) Section profile of the location indicated by the dotted line in (c).
Both the MLDCM and white light interferometer successfully resolved the raised bar patterns and texture variations across the background for this second test structure. However, as seen in Fig. 6c and d, the two techniques measured different pit depth values, with MLDCM indicating a deeper maximum depth of approximately 2000 nm compared to the interferometer’s result of 250 nm.
To provide an independent reference measurement, atomic force microscopy (AFM) was also performed on the sample. Figure 7 shows the AFM scan of a 5 μm × 5 μm area containing one representative pit feature. The pit is clearly distinguished as a quadrangular pyramidal indentation in the reconstructed 3D topography map. Quantitative analysis of this AFM data established the actual pit depth to be 700 nm.
Result from AFM, displayed in CloudCompare (version 2.13. alpha, http://www.cloudcompare.org).
The pyramidal indentation in this pattern has sidewalls sloping over 30°. Such a large tilt angle is far beyond the angular dynamic range of both the MLDCM and WLI systems. In the case interferometer, based on its principle, it is not capable of detecting such steep sidewalls. The light intensity received at these areas is also insufficient to support image processing and computations. The software and algorithm compensation makes it appear as a shallow pit with lower contrast. In the case of MLDCM, the two voltage signals received at these steep-walled locations are very small and unreliable. After normalization and the differential processing, they are converted to small values, which appear as deep depressions in the results.
While the interferometer requires over a minute of step-by-step axial scanning to generate the 3D images shown in Figs. 5 and 6, the MLDCM offers a distinct advantage in imaging speed. Although the MLDCM has not yet achieved real-time data processing and display, its high-speed data acquisition and high-speed MEMS mirror enable it to capture the 3D transient surface of the object. This level of temporal resolution is beyond the capabilities of the interferometer.
Dynamic 3D image acquisition
As mentioned above, high-speed data acquisition and high-speed MEMS mirrors bring the ability to capture 3D transients. Therefore, we tested the dynamic imaging capability of the MLDCM. To characterize the dynamic measurement capabilities of the MLDCM, a moving sample experiment was conducted. As illustrated in Fig. 8, the wafer is moving horizontally at a constant velocity during scanning, and the horizontal range of MLDCM imaging moves from the start position shown in the orange box to the end position shown in the blue box. Specifically, the oscilloscope synchronously recorded 30 frames of voltage signals from the photodiodes over a period of 365.5 ms as the pattern moved.
The starting and ending positions of the movement of the pattern. 3D images are displayed in CloudCompare (version 2.13. alpha, http://www.cloudcompare.org).
These raw data captures were then processed by a PC into 30 individual 3D topographic images and edited to a video that depicts the sample moving continuously across the field of view. The video shown in Supplementary Video 1 shows the original speed of the object’s movement, with duration of 363 ms. For improved visualization, Supplementary Video 2 renders the video played back 10 times slower.
Analyzing the distance traversed by the pattern between frames indicates a total horizontal displacement of 10.83 μm over the measurement interval. From this, the average velocity of the moving sample was calculated to be 0.02988 μm/ms. This experiment confirms the capability of MLDCM of successfully profiling dynamically moving objects in real-time.
MLDCM leverages the advantages of both differential confocal microscopy and high-speed scanning mirror implementations. MLDCM benefits from confocal microscopy’s fast single-shot axial sensing and the rapid 2D mapping afforded by the MEMS mirror. This enables MLDCM to capture dynamic 3D images of a moving sample at high frame rates. Interferometry techniques like white light interferometers generally require sequential axial scans and extensive image capturing and processing during measurement and thus prevent interferometers from achieving truly continuous and swift dynamic 3D imaging equivalent to MLDCM.
Galvanometer mirror oscillation visualization
In the work of Wang et al.43, a differential confocal microscope with a typical structure was demonstrated to be robust to tilted sample surfaces. This is obtained by using optical imaging to detect the light spot displacement at the pupil of the objective lens, combined with a series of axial response curves obtained at different angles. Therefore, we tested the response of MLDCM to tilted surfaces and it was found to be robust to minor tilting of the sample. Figure 9 shows the response curves obtained when the target aluminum mirror is tilted at − 1.5° and + 1.5° in two orthogonal directions. Overall MLDCM maintained a responsivity of about 0.21/μm over an axial range of ± 2.0 μm, which means that the axial measurement of the MLDCM is independent of the tilt angle of the sample within 1.5°. The MEMS mirror is relatively small (1 mm in diameter) as the pupil of the projection lens group, and it cannot accommodate larger beam deviations caused by object further tilting, limiting the dynamic range of angle measurement.
MLDCM’s demonstration of tolerance of tilted surface and fast dynamic imaging ability make it capable of mapping surfaces undergoing continual tilt changing over time. To demonstrate this capability, we employed MLDCM to visualize a galvanometer mirror oscillating one-dimensionally at 10 Hz over ± 1.5°. MLDCM imaged a 140 × 90 μm area near the center, and coherently recorded total 32 frames tracing 4 cycles of the mirror’s oscillation (see the video in Supplementary Video 3). For improved visualization, Supplementary Video 4 renders the video played back 10 times slower. Each oscillation cycle of the galvanometer is described by 8 3D images shown in Fig. 10.
Spatial position and tilt angle of the mirror surface within the FOV at each sampling moment, displayed in CloudCompare (version 2.13. alpha, http://www.cloudcompare.org).
As shown in Fig. 10, each frame of 3D image records the posture of the mirror surface within the FOV at the current moment, including the spatial position and tilt angle. While conventional methods provide only an averaged impression, MLDCM distinctly obtains the mirror’s posture at each instant moment. Its combination of tilt sensing and rapid 3D profiling unleashes promising applications for real-time inspection of micromechanical systems with continuous angular and axial position changes.
Conclusion
In this work, we developed and evaluated a high-speed 3D microscopy technique called MLDCM (MEMS Mirror-Integrated Laser Differential Confocal Microscopy). MLDCM integrates laser differential confocal axial sensing with rapid lateral laser scanning mediated by a MEMS mirror. Three-dimensional images acquired using the MLDCM system demonstrated its ability to successfully reconstruct detailed patterns on test silicon wafer samples. A key advantage is that MLDCM does not require specialized motion stages or complex image processing routines. Instead, the system directly converts photodiode signals to 3D topographic maps, enabling fast frame-rate 3D imaging of dynamic surfaces. To demonstrate this capability, we presented videos recorded by the MLDCM that visualizes the continuous horizontal translation of a wafer specimen and continuous angle changes of a galvanometer oscillation in real-time.
We also conducted a comparison of MLDCM with other 3D imaging methods, namely the white light interferometry. The biggest advantage of MLDCM is that its imaging rate is much higher than that of interferometer. The video-level frame rate allows MLDCM to dynamically monitor objects and gives potential for real-time monitoring in industrial-level manufacturing. On the other hand, MLDCM has low measurement accuracy and stability due to its own structural and optical design and adjustment deficiencies, as well as the influence of mechanical or electrical noise, and deficiencies in the optimization of results at the software and algorithm level. In addition, these comparisons also reveal the immaturity of MLDCM in data processing.
Compared with other works that have demonstrated high-precision dynamic microscopic imaging, such as work by Vilar et al.44 that utilized Encoded Search Focal Scan (ESFS) to achieve high accuracy and speed dynamic imaging, the MLDCM system has demonstrated capabilities in the same general performance range. However, the published results indicate that the MLDCM may be insufficient in certain indicators, like horizontal accuracy and angular characteristics. This shows that MLDCM still needs more optimization and improvement. These possible improvements include the suppression of multiple noises to achieve higher signal-to-noise ratio and enhanced spatial resolution, which requires more stable structural design and additional algorithms. In addition, the dynamic range of angular measurement is currently limited by the pupil size (objective pupil and MEMS mirror aperture), A more optimized optical path design is needed to make an improvement.
Overall, while continued refinement towards higher precision is warranted, MLDCM’s rapid scanning ability presents compelling opportunities for real-time 3D micro-scale imaging across many dynamic application scenarios. It promises an important new tool advancing precision manufacturing and microscopic study.
Data availability
The datasets generated during and/or analyzed as part of the current study is available from the corresponding author on reasonable request.
References
Marinis, T. F. The future of microelectromechanical systems (MEMS). Strain 45, 208–220 (2009).
Judy, J. W. Microelectromechanical systems (MEMS): fabrication, design and applications. Smart Mater. Struct. 10, 1115 (2001).
Varadan, V. K. & Varadan, V. V. Microsensors, microelectromechanical systems (MEMS), and electronics for smart structures and systems. Smart Mater. Struct. 9, 953 (2000).
Kammerud, C., Abidi, B., Huq, S. & Abidi, M. 3D nanovision for the inspection of micro-electro-mechanical systems. In 2005 12th IEEE International Conference on Electronics, Circuits and Systems 1–4 (2005). https://doi.org/10.1109/ICECS.2005.4633376.
Kirschmann, M. A., Pierer, J., Steinecker, A., Schmid, P. & Erdmann, A. Plenoptic inspection system for automatic quality control of MEMS and microsystems BT—smart technologies for precision assembly. In (ed. Ratchev, S.) 220–232 (Springer International Publishing, 2021).
Elkaseer, A., Salem, M., Hagenmeyer, V. & Scholz, S. Vision system-based inspection and alignment of laminated polymer films for 3D-integration of microsystems. IFAC-PapersOnLine 52, 13–18 (2019).
Blankenship, B. W. et al. Three-dimensional optical imaging of internal deformations in polymeric microscale mechanical metamaterials. Nano Lett. 24, 2735–2742 (2024).
Orji, N. G. et al. Metrology for the next generation of semiconductor devices. Nat. Electron. 1, 532–547 (2018).
Bao, J., Ferns, J. & Wen, Y. Challenges and opportunities for optical CD metrology in future lithography process. ECS Trans. 18, 315 (2009).
Gastinger, K. et al. Optical, mechanical, and electro-optical design of an interferometric test station for massive parallel inspection of MEMS and MOEMS. In Proc. SPIE, vol. 7389, 73891J (2009).
Bosseboeuf, A. & Petitgrand, S. Application of microscopic interferometry techniques in the MEMS field. In Proc. SPIE vol. 5145, 1–16 (2003).
Quan, C., Wang, S. H. & Tay, C. J. Nanoscale surface deformation inspection using FFT and phase-shifting combined interferometry. Precis. Eng. 30, 23–31 (2006).
Conroy, M. & Armstrong, J. A comparison of surface metrology techniques. Opt. Micro-Nanometrol. Microsyst. Technol. 6188, 61880B (2006).
Ingar Romero, A., Mukherjee, A. K., Fernandez Olvera, A., Mendez Aller, M. & Preu, S. Visualizing nanometric structures with sub-millimeter waves. Nat. Commun. 12, 7091 (2021).
Wang, F. et al. Three-dimensional super-resolution morphology by near-field assisted white-light interferometry. Sci. Rep. https://doi.org/10.1038/srep24703 (2016).
Deck, L. & de Groot, P. High-speed noncontact profiler based on scanning white-light interferometry. Appl. Opt. 33, 7334 (1994).
Paddock, S. W. Principles and practices of laser scanning confocal microscopy. Appl. Biochem. Biotechnol. Part B Mol. Biotechnol. 16, 127–149 (2000).
Webb, R. H. Confocal optical microscopy. Rep. Prog. Phys. 59, 427–471 (1996).
Laurent, M., Johannin, G., Le Guyader, H. & Fleury, A. Confocal scanning optical microscopy and three-dimensional imaging. Biol. Cell 76, 113–124 (1992).
Carlsson, K. et al. Three-dimensional microscopy using a confocal laser scanning microscope. Opt. Lett. 10, 53 (1985).
Lee, C.-H. & Wang, J. Noninterferometric differential confocal microscopy with 2-nm depth resolution. Opt. Commun. 135, 233–237 (1997).
Qiu, L., Liu, D., Zhao, W., Cui, H. & Sheng, Z. Real-time laser differential confocal microscopy without sample reflectivity effects. Opt. Express 22, 21626 (2014).
Zhao, W., Tan, J. & Qiu, L. Bipolar absolute differential confocal approach to higher spatial resolution. Opt. Express 12, 5013 (2004).
Ying, R., Cui, Y., Huang, J., Liang, D. & Wang, Y. Precise measurement of surface topography with microstructures based on differential confocal and spiral scanning. Meas. J. Int. Meas. Confed. 184, 110004 (2021).
Hamilton, D. K. & Wilson, T. Three-dimensional surface measurement using the confocal scanning microscope. Appl. Phys. B Photophys. Laser Chem. 27, 211–213 (1982).
Lee, D. R., Kim, Y. D., Gweon, D. G. & Yoo, H. High speed 3D surface profile without axial scanning: Dual-detection confocal reflectance microscopy. Meas. Sci. Technol. 25, 125403 (2014).
Zhao, W., Zhang, X., Wang, Y. & Qiu, L. Laser reflection differential confocal large-radius measurement. Appl. Opt. 54, 9308 (2015).
Zhao, W., Tan, J., Qiu, L. & Zou, L. A new laser heterodyne confocal probe for ultraprecision measurement of discontinuous contours. Meas. Sci. Technol. 16, 497 (2005).
Sheng, Z., Wang, Y., Zhao, W., Qiu, L. & Sun, Y. Laser differential fitting confocal microscopy with high imaging efficiency. Appl. Opt. 55, 6903–6909 (2016).
Liu, J., Tan, J., Bin, H. & Wang, Y. Improved differential confocal microscopy with ultrahigh signal-to-noise ratio and reflectance disturbance resistibility. Appl. Opt. 48, 6195–6201 (2009).
Huang, X., Tan, J. & Wang, W. Heterodyne confocal microscopy using symmetrical shifted-focus phase filters. Opt. Express 26, 30183 (2018).
Liu, L. & Xie, H. 3-D confocal laser scanning microscopy based on a full-MEMS scanning system. IEEE Photonics Technol. Lett. 25, 1478–1480 (2013).
Liu, L. et al. MEMS-based 3D confocal scanning microendoscope using MEMS scanners for both lateral and axial scan. Sens. Actuators A Phys. 215, 89–95 (2014).
Ra, H. et al. Two-dimensional MEMS scanner for dual-axes confocal microscopy. J. Microelectromech. Syst. 16, 969–976 (2007).
Pan, T. et al. A MEMS mirror-based confocal laser endomicroscope with image distortion correction. IEEE Photonics J. 15, 1–8 (2023).
Choudhury, P. K. & Lee, C.-H. Simultaneous enhancement of scanning area and imaging speed for a MEMS mirror based high resolution LiDAR. IEEE Access 8, 52113–52120 (2020).
Seo, Y.-H., Hwang, K., Kim, H. & Jeong, K.-H. Scanning MEMS mirror for high definition and high frame rate Lissajous patterns. Micromachines https://doi.org/10.3390/mi10010067 (2019).
Zhang, G. et al. Miniaturized high-resolution dual 2D MEMS mirror scanning confocal Raman microscopy for topographic and Raman mapping. Measurement 224, 113807 (2024).
Lee, D., Gweon, D. G. & Yoo, H. Multipoint scanning dual-detection confocal microscopy for fast 3D volumetric measurement. J. Microsc. 270, 200–209 (2018).
Yi, D., Liu, Z., Kong, L., Zhu, X. & Jiang, W. A parallel differential confocal method for highly precise surface height measurements. IEEE Photonics Technol. Lett. 32, 375–378 (2020).
Da Sie, Y., Lin, C.-Y. & Chen, S.-J. 3D surface morphology imaging of opaque microstructures via light-field microscopy. Sci. Rep. 8, 10505 (2018).
Kirschmann, M. A., Pierer, J., Steinecker, A., Schmid, P. & Erdmann, A. Plenoptic inspection system for automatic quality control of MEMS and microsystems BT - smart technologies for precision assembly. In (ed. Ratchev, S.) 220–232 (Springer International Publishing, 2021).
Wang, T. et al. A differential confocal sensor for simultaneous position and slope acquisitions based on a zero-crossing prediction algorithm. Sensors 23, 1453 (2023).
Vilar, N., Artigas, R., Duocastella, M. & Carles, G. Fast topographic optical imaging using encoded search focal scan. Nat. Commun. 15, 2065 (2024).
Acknowledgements
This research work was partially supported by Hong Kong Research Grants Council, General Research Fund (Project No. 11216120).
Author information
Authors and Affiliations
Contributions
Q. C and D. Y contributed equally to this work. W. J. L conceived the concept and designed the experiments. Q.C designed and built the optical setup. D. Y carried out the circuit design and MEMS mirror integration. Q. C and D. Y conducted the experiment. W. J. L supervised and guided the project. F. W and W. J. L gave technical advice. All authors contributed to the discussion and revision of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Supplementary Video 1.
Supplementary Video 2.
Supplementary Video 3.
Supplementary Video 4.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Chen, Q., Yang, D., Wang, F. et al. Dynamic 3D profiling of microscale surface using a MEMS mirror laser differential confocal microscope. Sci Rep 15, 25957 (2025). https://doi.org/10.1038/s41598-025-94711-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-94711-w