Introduction

The wavelength of terahertz signals is located between millimeter waves and infrared waves, providing a unique frequency position that offers broad application space in detection1,2,3, imaging4, and communication5. Especially the potential application of terahertz detection technology in biological sample detection6,7 has attracted widespread attention to terahertz modulation devices based on metamaterials.

As a low-profile metamaterial, metasurfaces possess the property of controlling electromagnetic waves8. In the current industry, most terahertz metasurfaces are fixed-frequency metasurfaces. However, in practical application scenarios, terahertz metamaterial absorbers based on a fixed frequency range exhibit considerable limitations. With the emergence of various adjustable metamaterial absorbers9, terahertz tunable metasurface absorbers have also received widespread attention and have the potential to play a key role in biological sample detection10,11.

Conventional adjustable metasurfaces employ controllable devices like PIN and varactor diodes. In the case of low-frequency adjustable metasurfaces, these devices are capable of fulfilling the control requirements. However, as the control frequency escalates, particularly within the terahertz range, fulfilling the requirements of radio frequency switches becomes challenging. A phase change material has the capability to alter its crystalline form in response to variations in external temperature. Concurrently, alterations in the form of crystals will lead to a notable shift in the material’s electrical conductivity properties, converting it from a non-conductive state to a conductive state. More importantly, the switching of conductivity in phase change materials results in very small parasitic parameters, allowing the switch to operate efficiently in very high frequency bands. Consequently, its suitability as a switch material is evident. With a phase transition temperature around 341 K, vanadium dioxide stands out as a phase change substance12, offering distinct benefits like a rapid and reversible phase transition, low-power consumption regulation, a wideband optical response, reduced phase transition temperature and a well-established production method. In metasurfaces, it can serve as a control switch to switch between absorption and reflection states13,14,15,16,17,18,19.

Many works focused on the adjustable terahertz metasurface based on vanadium dioxide. Li et al.20 proposed a terahertz encoded metasurface design based on vanadium dioxide, which can effectively switch between two far-field beams at 1.1 THz. This work can only operate on one single frequency point. Tang et al.21 designed a metasurface element with an adjustable phase at 0.72 THz by adjusting the size of the metasurface unit cell. In this study, they designed eight different units to generate electromagnetic vortex beams. This work involves modifying the structural dimensions to alter the electromagnetic properties of the metasurface, which does not constitute a truly dynamically controllable device. Zhong et al.22 proposed a design that operation bands can be switched through a terahertz metasurface, which allows the operating band to switch from a single frequency point of 1.15 THz to dual frequency points of 0.7 THz and 1.3 THz. Wang et al.23 also designed a metasurface that can operate in three frequency bands. By adjusting the phase change material, the operating band 1 can be switched to operating bands 2 and 3 under the control of vanadium dioxide. Although the transition from one frequency band to two operating frequency bands has been accomplished, synchronous dynamic control across multiple frequency bands remains unachievable.

Table 1 The comparison between this work and other works.
Full size table

This paper proposed a five frequencies simultaneously tunable reflective/absorptive terahertz metasurfaces. In this design, we created multiple resonance points by designing terahertz structures and make the five-frequencies tunable through the control of vanadium dioxide. This structure is similar to the chinese copper coin structure, consisting of three parts: a central circle, a central circular ring, and four strips outside. These three parts together form a multi-resonant structure, with five resonance points in 2–16 THz. The absorption and reflection performance of this structure can be adjusted through the changes in conductivity of VO2. Table 1 shows the comparison between this work and other works. This work utilizes a metasurface loaded with vanadium dioxide to achieve dynamically adjustable reflection and absorption states simultaneously across five terahertz frequencies. Biological samples are typically placed in sample trays made of PTFE material. The five operating frequency points proposed in this study effectively bypass the high absorption frequency points of PTFE material1, providing significant advantages for this adjustable metasurface design in biological sample detection.

Model

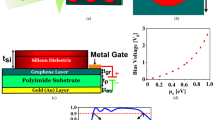
Figure 1 shows the 3D model we adopted in this work. This structure consists of three layers: vanadium dioxide at the top, silicon dioxide in the middle, a gold layer under the silicon dioxide layer, and at last the silicon substrate layer. As mentioned earlier, the design of the vanadium dioxide layer in this model is similar to that of a copper coin, consisting of a central circle with a radius of \(R_1\), a central ring with the outer radius of \(R_2\) and width of W, an outer square ring with its inner side length of \(L_1\) and width of W, and the square ring is cut by a quarter disc with radius of \(R_3\). The structural dimension parameters of the model have been clearly labeled in Fig. 1, and the specific parameter values can be found in Table 2, where all parameters are measured in micrometers. The thickness of the vanadium dioxide film is 0.5 \(\upmu\)m, represented by the symbol \(t_1\) in Table 2. The thickness of the silicon dioxide film is 4.9 \(\upmu\)m and the thickness of the gold layer is 0.05 \(\upmu\)m. The unit cell will be manufactured on a silicon substrate. The length of the outer strip line can be calculated by \(L - 2{R_3}\), and the value of L and \(R_3\) are given in Table 2.

Fig. 1
figure 1

Schematic diagram of the geometry of the metasurface.

Full size image
Table 2 The parameter of the proposed structure.
Full size table

In this design, the ground adopts a full gold film, which means that electromagnetic waves cannot penetrate the metasurface, and its transmittance rate is nearly close to 0%. Therefore, we have obtained the relationship between absorption rate A and reflection coefficient R, as shown below:

$$\begin{aligned} A = 1-R \end{aligned}$$
(1)

When conducting simulations of this model with phase change material vanadium dioxide, we chose the Drude model to discribe the material properties of vanadium dioxide, and set the following specific parameters for it27,28:

$$\begin{aligned} \varepsilon \left( \omega \right) ={\varepsilon ^{\prime }}+ {\varepsilon ^{\prime \prime }} = {\varepsilon _\infty } - \frac{{\omega _p^2\left( \sigma \right) }}{{{\omega ^2} + i\gamma \omega }} \end{aligned}$$
(2)

Wherein, \({\varepsilon _\infty }\) = 12, collision frequency \(\gamma\) = \(5.75 \times {10^{13}}\) rad/s,

$$\begin{aligned} \omega _p^2\left( \sigma \right) = \sigma \omega _p^2\left( {{\sigma _0}} \right) /{\sigma _0} \end{aligned}$$
(3)

\(\sigma _0\) = \(3 \times {10^{5}}\) S/m, \(\omega _p^2\left( \sigma _0 \right)\) = \(1.4 \times {10^{15}}\)rad/s. The conductivity curve of vanadium dioxide as a function of temperature is depicted in Fig. 2. It exhibits a non-metallic state at low temperatures and a metallic state at high temperatures. When vanadium dioxide is in a non-metallic state, its actual conductivity \(\sigma\) reaches 20 S/m, while in a metallic state, this value is nearly 80,000 S/m8,29,30.

Fig. 2
figure 2

Conductivity of phase change material VO2 under different temperature.

Full size image

Simulation and optimization

To improve the simulation accuracy of the design, we subdivided the frequency bands 2–18 THz into five sub-bands: 2–5, 5–7, 9–11, 12–15, and 16–18 THz, and conducted frequency domain full-wave simulations on this metasurface unit cell. The simulation unit cell model employs periodic boundary conditions, while both the upper and lower surfaces utilize open boundary conditions. The excitation electromagnetic waves are incident from the front side (VO2 layer side) of the model.

According to the proposed design, several key parameters affecting the resonant frequencies in the model include: the thickness of silicon dioxide substrate t, the thickness of vanadium dioxide \(t_1\), the radius of center circular vanadium dioxide patch \(R_1\) and the line width W of VO2 .

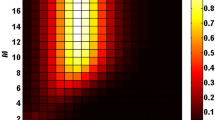
The thickness of the silicon dioxide substrate, denoted as t, was initially discussed. The simulation results are presented in Fig. 3. As t increased, the resonant frequencies gradually shifts towards lower frequencies at 3.4 THz and 6.2 THz bands, and have significant absorptive peak. At 9.9 THz and 13.3 THz bands, the trend of increasing thickness t towards lower frequencies is not significant, but when t is 4.75 \(\upmu\)m and 6 \(\upmu\)m, the absorptive peak within these two band is evident. whereas at 16.8 THz, when the thickness is 6 \(\upmu\)m, the structure has almost no resonance and does not produce absorptive peak. Therefore, considering the performance of all the five bands, t is set to near 4.7 \(\upmu\)m. Through further optimization, the thickness t is chosen as 4.9 \(\upmu\)m, which meets the requirement of producing good absorptive peaks at five frequency bands simultaneously.

Fig. 3
figure 3

Simulated reflection coefficient in five frequencies (a) 3.4 THz, (b) 6.2 THz, (c) 9.9 THz, (d) 13.3 THz, (e) 16.8 THz with different struture parameter t.

Full size image

Next, the thickness of the vanadium dioxide \(t_1\) has been discussed, as shown in Fig. 4. When vanadium dioxide is in the low conductivity state, it serves as a lossy material. When the vanadium dioxide material is in a specific state, it exhibits a constant conductivity, thereby possessing a fixed resistivity. The sheet resistance of the material varies depending on its thickness, indicating that thickness influences the lossy effect of the material. In other words, its thickness \(t_1\) directly affects the absorptive effect of the unit cell, thus directly affecting the reflection coefficient of this model. At 3.4 THz, as \(t_1\) increases, the absorption rate of the model decreases; At 6.2 THz, 9.9 THz, 13.3 THz, and 16.8 THz, the absorption rate of the model increases with the increase of thickness \(t_1\). Among them, the increase in absorption rate is not particularly significant at 13.3 THz, possibly due to the resonant mode present at that frequency. When \(t_1\) increases, the structure may undergo severe resonance, making it impossible to further enhance the absorption effect by increasing material loss.At 13.3 THz and 16.8 THz, an increase in \(t_1\) not only enhances the absorption effect but also shifts the resonant frequency towards higher frequencies. This occurs because the change in structural parameter \(t_1\) is more sensitive to the resonant mode at higher frequencies, resulting in a slight frequency deviation.

Fig. 4
figure 4

Simulated reflection coefficient in five frequencies (a) 3.4 THz, (b) 6.2 THz, (c) 9.9 THz, (d) 13.3 THz, (e) 16.8 THz with different struture parameter \(t_1\).

Full size image

The radius \(R_1\) of the central circular patch on the vanadium dioxide layer also significantly affects the absorption rate of the metasurface unit cell across various frequencies, as illustrated in Fig. 5. At frequencies of 3.4 THz, 6.2 THz, and 9.9 THz, as the value of \(R_1\) increases, the absorption rate of the unit cell gradually increases. However, at 13.3 THz, as \(R_1\) increases, the absorption rate initially increases and then decreases, reaching its peak at \(R_1 =2 \upmu\)m. At 16.8 THz, as \(R_1\) increases, the absorption rate first increases and then decreases. At \(R_1 =3 \upmu\)m, the absorption rate attains its peak. An increase in \(R_1\) can enhance the lossy efficiency of the structure, thereby explaining the rise in absorption rates at 3.4 THz, 6.2 THz, and 9.9 THz as \(R_1\) increases. However, at high frequency points, such as 13.3 THz and 16.8 THz, changes in \(R_1\) also impact the resonance strength of this structure. A decrease in resonance strength will diminish the absorption effect. Therefore, based on overall considerations, the structural parameter \(R_1\) of the metasurface model is chosen to be 2 \(\upmu\)m.

Fig. 5
figure 5

Simulated reflection coefficient in five frequencies (a) 3.4 THz, (b) 6.2 THz, (c) 9.9 THz, (d) 13.3 THz, (e) 16.8 THz with different struture parameter R1.

Full size image

The parameter W represents the line width of the vanadium dioxide strip on the unit cell. As illustrated in Fig. 6, based on the parameter scanning data from simulated results at various frequencies, it is evident that as W increases, the absorption peak shifts towards lower frequencies, and the absorption rate decreases at 3.4, 6.2, and 13.3 THz. At 9.9 THz, as W increases, the absorption peak shifts towards a lower frequency, but the trend of absorption rate change initially increases and then decreases. At 16.8 THz, as W increases, there is no significant change in frequency shifting. When W exceeds 1.5 \(\upmu\)m, the absorption rate of the unit cell does not change significantly. In summary, the optimal line width for vanadium dioxide is chosen to be 2 \(\upmu\)m.

Fig. 6
figure 6

Simulated reflection coefficient in five frequencies (a) 3.4 THz, (b) 6.2 THz, (c) 9.9 THz, (d) 13.3 THz, (e) 16.8 THz with different struture parameter W.

Full size image

Based on the optimized results, when vanadium dioxide is in its low-temperature non-metallic state, the simulation outcomes for the unit model across five frequency bands are illustrated in Fig. 7a–e. Owing to the model’s high symmetry, the simulation data for cross-polarization will align with that of the co-polarization, indicating that this design exhibits polarization insensitivity.

Fig. 7
figure 7

Simulation results in different frequencies. The reflective rate in (a) 3.4 THz, (b) 6.2 THz, (c) 9.9 THz, (d) 13.3 THz, (e) 16.8 THz.

Full size image

Operating mechanism

Due to the incorporation of the phase change material vanadium dioxide into the structure, by controlling the conductivity of vanadium dioxide, the reflectivity or absorptive performance of this model can achieve synchronous switching at five frequencies.

When vanadium dioxide is in its high-resistivity (non-metallic) state, its conductivity is fixed at 20 S/m, and all absorption peaks of this unit cell surpass − 10 dB across every sub-band. When the conductivity of vanadium dioxide attains 80,000 S/m, the metasurface unit cell demonstrates total reflection characteristics. The specific reflection coefficient curve can be referred to in Fig. 8. Simulation data indicates that when vanadium dioxide transitions from the metallic state to the non-metallic state, the metasurface unit cell successfully completes the state transition from reflection to absorption at five different frequencies.

Fig. 8
figure 8

Simulation results: the reflection coefficient of unit cell when VO2 is in different temperature.

Full size image

To elucidate the working mechanism of the five-band absorptive/reflective tunable terahertz metasurface, we analyzed the electrical field distribution of the metasurface unit cell at various frequencies, as illustrated in Fig. 9. From the field diagram, it is evident that the resonance mode of the structure varies at different frequencies. In Fig. 9, the upper figure illustrates the resonance response distribution of the surface structure in the xy-plane, while the lower figure demonstrates the electric field distribution in the yz-plane of the unit cell.

The occurrence of strong resonance in lossy materials is accompanied by the generation of absorption effect. For instance, as illustrated in Fig. 9a, strong resonance occurs on both the top and bottom sides of the central ring at 3.4 THz, resulting in the appearance of a prominent absorption peak at this frequency. The reason for the specific resonant mode can be inferred from the electric field distribution diagram within the yz-plane of unit cell. As shown in Fig. 9a, the electric field is strongest in the middle position of the structure. Therefore, in the metasurface structure, the strongest resonance point occurs at the position between the middle ring and the upper and lower strips in the middle.

Compared to 3.4 THz, although a similar resonance mode also appeared at 5 THz, as shown in Fig. 9b, the maximum electric field position has shifted, and the overall electric field resonance strength of the structure has weakened. As depicted in Fig. 9b, the electric field distribution of the unit at 5 THz resembles that at 3.4 THz, but with a generally weaker resonance, which is insufficient to produce an absorption peak.

As shown in Fig. 9c, the top and bottom positions of the left and right vertical strips form a resonant mode at 6.2 THz, and the signal excited at this frequency resonates. When VO2 transitions to the lossy state at this moment, the signal at this frequency will be absorbed. Based on the cross-sectional distribution of the electrical field within the unit cell, there are three peaks present. The resonance between the right/left strip and the central ring is stronger than that between the top/bottom strip and the central ring. Consequently, the absorption at 6.2 THz is primarily induced by the resonance between the right/left strip and the central ring.

Based on the field distribution, the absorption at 9.9 THz is triggered by the four strips featuring six circular arc structures positioned at angles of \(0^{\circ }\), \(60^{\circ }\), \(120^{\circ }\), \(180^{\circ }\), \(240^{\circ }\), and \(300^{\circ }\) on the central ring. The cross-sectional distribution aligns with the findings derived from the electric field distribution in the xy-plane.

Fig. 9
figure 9

The electrical field distribution in xy-plane and in yz cross-section at frequencies (a) 3.4 THz; (b) 5 THz; (c) 6.2 THz; (d) 9.9 THz; (e) 13.3 THz; (f) 16.8 THz;

Full size image

Application

Based on the aforementioned analysis, the unit cell in this design generates five distinct strong resonant frequencies within the range of 2–18 THz. When the phase change material VO2 transitions to its non-metallic state at these strong resonant frequencies, the energy is absorbed by the lossy materials VO2, ultimately resulting in the formation of an absorption band. This specially designed structure generates resonant modes across five frequencies, thereby creating five absorption bands. However, when vanadium dioxide transitions to its metallic state, these five absorption bands will vanish.

The tunable characteristic of metasurfaces finds excellent application in the field of biological sample detection, as shown in Fig. 10. As previously mentioned, the five frequency points of this tunable metasurface work perfectly to avoid several high absorption peak frequency points of PTFE material in the sample tray, enabling its application in biological sample detection using PTFE trays. During detection, the metasurface operates in reflection mode, whereas in absorption mode, it does not perform detection tasks. All of this depends on the scattering situation in the far field after the formation of the array of metasurface units.

Fig. 10
figure 10

The application of merasurface array in biological sample detection.

Full size image

This metasurface unit cell can be utilized to regulate the far-field beam scattering intensity across five frequencies. Arrange the unit cell into an array with a periodic spacing of 35 \(\upmu\)m, comprising 10 \(\times\) 10 units. Maintain the non-metallic state and metallic state of vanadium dioxide in the unit cell separately, and the far-field radiation patterns of the array in these two states are shown in Fig. 11.

Figure 11a–c,g,h illustrates the far-field scattering patterns of five frequencies within the 2–18 THz range when the phase change material is in a lossy state. As evident from Fig. 11a–c,g,h, the scattering intensity is relatively weak. Figure 11d–f,i,j displays the far-field scattering patterns of five frequencies in 2–18 THz band when the phase change material is in metallic state. As shown in Fig. 11d–f,i,j, compared to the non-metallic state, the scattering intensity at these five frequencies is stronger. Therefore, by switching vanadium dioxide, we can control the scattering strength of the metasurface at five terahertz frequencies simultaneously.

Fig. 11
figure 11

The far-field pattern of 10 \(\times\) 10 metasurface array when VO2 is in lossy state at (a) 3.4 THz, (b) 6.2 THz, (c) 9.9 THz, (g) 13.3 THz, (h) 16.8 THz and when VO2 is in metallic state at (d) 3.4 THz, (e) 6.2 THz, (f) 9.9 THz, (i) 13.3 THz, (j) 16.8 THz;

Full size image

Conclusion

This paper introduces a tunable metasurface capable of absorbing/reflecting across five frequencies, achieved through the design of a multi-resonant structure. Additionally, by incorporating vanadium dioxide, the design enables switching between absorption and reflection states in five frequencies. The five operating frequency points of the adjustable metasurface enable spectral detection of samples across the broadest possible frequency spectrum. Additionally, these frequency points circumvent several high absorption peaks associated with PTFE materials, thereby enabling the use of this adjustable metasurface for biological sample detection on PTFE trays.