Introduction

Recent advancements in China’s oil and gas exploration technologies have enabled significant breakthroughs in developing deep, tight, and low-permeability reservoirs. Notably, over 60% of these reservoirs exhibit abnormally high fracturing pressures (typically exceeding 80 MPa), presenting unique engineering challenges1,2,3,4,5. While hydraulic fracturing and acid stimulation remain indispensable for reservoir evaluation and production enhancement, practitioners continue to face two persistent technical bottlenecks: (1) formation breakdown failures during fracturing operations, and (2) fluid injection difficulties in acidizing treatments. These operational constraints significantly impede effective reservoir stimulation and production optimization in ultra-deep (> 6500 m) unconventional plays6,7,8,9,10.

The genesis of abnormal fracturing pressures in subsurface formations stems from a complex interplay of geological and engineering factors. Primary contributors include excessive horizontal stress anisotropy (> 1.5 stress ratio), pronounced lithological heterogeneity (variations exceeding 30% in Young’s modulus), elevated clay content (> 35% smectite-rich formations), and suboptimal perforation phasing alignment (> 15° deviation from principal stress orientation)11,12. At the core of hydraulic fracturing research lies two fundamental questions: (1) precise fracture initiation timing determination, and (2) comprehensive propagation mechanism elucidation13,14,15. Numerous scholars have committed themselves to this field and have proposed criteria for identifying fracture patterns during the hydraulic fracturing process based on various mechanical theories14,16,17. These criteria can be broadly categorized into two types: one pertaining to elastic mechanics models and the other related to fracture mechanics models18. Hubbert’s seminal work established the classical tensile failure criterion under idealized conditions of homogeneous, isotropic, impermeable elastic media19,20. This approach focuses on borehole wall tangential stresses (σ_θ) while neglecting vertical (σ_v) and radial (σ_r) stress components’ synergistic effects21,22. As a natural medium, rock mass typically contains inherent fractures; particularly in scenarios where fracture development is pronounced or artificial fractures are present, it becomes essential to analyze rock mass failure induced by hydraulic fracturing through fracture mechanics theory23,24. Essential for naturally fractured reservoirs, this paradigm addresses hydraulic fracture interaction with pre-existing discontinuities. Vallejo’s dam studies revealed that fracture propagation predominantly follows mixed-mode (I-II) mechanisms rather than pure Mode I extension23,24. Crucially, his work demonstrates that fracture advancement can occur through shear-dominated (Mode II) mechanisms without requiring normal tensile stresses, particularly in scenarios with significant pre-existing fracture networks25.

Experimental research serves as an effective and intuitive method for investigating the hydraulic fracturing mechanisms of rocks. Since the inaugural successful hydraulic fracturing test was conducted in the United States, numerous researchers have engaged in related experimental studies26,27. Nobari et al. examined the stress conditions necessary for hydraulic fracturing using a cylindrical specimen with an outer diameter of 3.56 cm, an inner diameter of 0.64 cm, and a height of 8.90 cm28. Mori et al. performed hydraulic fracturing experiments on thick-walled cylindrical specimens composed of viscous soil, featuring outer diameters of 5.00 cm, 7.50 cm, and 15.00 cm; inner diameters of 0.40 cm and 0.80 cm; and heights ranging from 1 to 2 times the outer diameter. The findings revealed that the mechanical mechanism underlying hydraulic fracturing is predominantly shear failure rather than tensile failure. Furthermore, provided that the water pressure injection rate is sufficiently high, factors such as liquid viscosity, specimen size, and local fractures near the borehole can be considered negligible regarding their influence on hydraulic fracturing pressure29.

Cheng et al. conducted field experiments that provided a comprehensive analysis of hydraulic fracturing pressure in rock masses. They asserted that the fracture surface is invariably perpendicular to the direction of the minor principal stress, regardless of whether the liquid can infiltrate the rock mass30. In various geological formations, the minor principal stress within surface rock strata may manifest as either horizontal or vertical. Fjaer conducted hydraulic fracturing experiments on rocks via drilling techniques. He asserted that in an impermeable rock mass where the direction of the minimum principal stress is orthogonal to the borehole axis, the pressure required to induce hydraulic fracturing is equivalent to the sum of the rock’s tensile strength and twice the minor principal stress19. Bjerrum et al. performed hydraulic fracturing tests on a natural clay core wall within a reservoir embankment. The experimental results indicated that when water pressure exceeded 0.40 to 0.50 times the effective self-weight of the overlying soil, there was a sudden increase in permeability, resulting in hydraulic fracturing31. A multitude of researchers have focused on numerical simulation studies related to hydraulic fracturing, developing various two-dimensional, pseudo-three-dimensional, or fully three-dimensional numerical tools for this purpose32,33,34. Presently, numerous methods exist for analyzing rock fracture behavior; from a technical standpoint regarding fracture treatment, these can be categorized into continuous deformation numerical methods and discontinuous deformation numerical methods.

Previous research has yielded a relatively comprehensive understanding of the qualitative characterization of rock fracture and the prediction of fracturing pressure. However, the influence mechanisms of various completion techniques on the fracturing pressure of reservoir rocks remain inadequately defined. Furthermore, following reservoir damage, alterations in fracturing pressure have occurred, leading to significant variability and subjectivity in selecting appropriate technologies for predicting reservoir rock fracturing pressure and optimizing fracturing operation parameters. Therefore, it is imperative to conduct further investigations into predictive methodologies for reservoir fracturing pressure under complex geological conditions and diverse completion strategies to facilitate the efficient development of deep, tight, low-permeability oil and gas reservoirs characterized by exceptionally high fracturing pressures.

By comprehensively integrating pertinent theories such as rock mechanics and elasticity theory, and based on the analysis of in-situ stress surrounding the wellbore, models for rock fracturing pressure in both open-hole and perforated wells were developed. Following the in-situ stress analysis of perforated wells, fracture initiation modes and corresponding fracturing pressure calculation models were thoroughly examined. Furthermore, a detailed investigation was conducted into the in-situ stress characteristics of open-hole and perforated wells post-reservoir damage, resulting in the formulation of formation fracturing pressure calculation models applicable to both completion methods under damaged conditions. Regarding the fracturing pressure models associated with open-hole and perforated completions, calculations for individual well fractures under varying completion scenarios were executed to validate the reliability of the formation fracturing pressure prediction model, which will facilitate advancements in optimizing techniques aimed at reducing formation fracturing pressures.

Prediction model of reservoir fracturing pressure

Geological characteristics of the oil reservoir

The reservoir in the study area is buried at a depth exceeding 6500 m, characterized by weak karstification, leading to relatively dense reservoir development. The porosity primarily ranges from 0.1 to 3.5%, with an average permeability of 0.25 × 10−3 μm2. Fracture and cavity filling is significant, with fully filled fractures comprising 34.69% and semi-filled fractures accounting for 53.99%. The average density of the reservoir rock is 2.69 g/cm3, and the overburden pressure is notably high. The primary mineral component of the reservoir rock is calcite, typically exceeding 99%, while secondary minerals such as pyrite, siliceous material, dolomite, and authigenic quartz collectively constitute less than 1%. The predominant rock types are mud microcrystalline limestone (74.3%), followed by grain limestone (17.4%) and bioclastic limestone (8.3%).

The fracturing pressure of the openhole completed reservoir

The abnormal fracturing pressure is primarily attributed to factors such as deep reservoir burial, high tectonic stress, dense lithology, and reservoir damage. Therefore, it is crucial to establish a quantitative prediction model for the fracturing pressure of the reservoir under various conditions. This model will serve as a basis for reducing stimulation risks and optimizing operations. The wellbore formation disrupts the original stress equilibrium, leading to stress redistribution in the surrounding rock and subsequent stress concentration during fracturing operations. Fractures initiate when the wellbore pressure exceeds the tensile strength of the circumferential stress in the rock. It should be noted that fracture initiation points, fracture azimuths, and fracturing pressures are all dependent on the stress state around the wellbore. To comprehensively study fracture initiation mechanisms, an analysis of the stress state surrounding the wellbore must be conducted first.

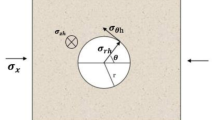
Following Biot’s poroelastic theory, the effective stress in intact media is defined as σ'ij = σij—αpδij, where α ∈ [0,1] represents the Biot coefficient (Detournay & Cheng, 1993)35. However, when evaluating shear failure through Mohr–Coulomb criteria or tensile fracturing, Terzaghi’s effective stress σ'n = σn—p is adopted (Zimmerman, 1991; Segall, 2010)36,37, consistent with standard geomechanical practice for failure analysis. By considering factors such as initial stresses, fracture fluid forces, and fluid infiltration into the formation, a comprehensive understanding of the stresses acting on the rock around the wellbore can be obtained through the superposition method38,39,40.

$$\begin{aligned} \sigma_{r} = & \frac{{\sigma_{H} + \sigma_{h} }}{2}\left( {1 - \frac{{r_{i}^{2} }}{{r^{2} }}} \right) + \left( {\frac{{\sigma_{H} - \sigma_{h} }}{2}} \right)\left( {1 - 4\frac{{r_{i}^{2} }}{{r^{2} }} + 3\frac{{r_{i}^{4} }}{{r^{4} }}} \right)\cos 2\theta + \frac{{r_{i}^{2} }}{{r^{2} }}P_{i} \\ & \quad - \alpha P_{p} + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}}\left( {1 - \frac{{r_{i}^{2} }}{{r^{2} }}} \right) - \phi } \right]\left( {P_{i} - P_{p} } \right) \\ \end{aligned}$$
(1)
$$\begin{aligned} \sigma_{\theta } & = \frac{{\sigma_{H} + \sigma_{h} }}{2}\left( {1 + \frac{{r_{i}^{2} }}{{r^{2} }}} \right) - \left( {\frac{{\sigma_{H} - \sigma_{h} }}{2}} \right)\left( {1 + 3\frac{{r_{i}^{4} }}{{r^{4} }}} \right)\cos 2\theta - \frac{{r_{i}^{2} }}{{r^{2} }}P_{i} \\ & \quad - \alpha P_{p} + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}}\left( {1 + \frac{{r_{i}^{2} }}{{r^{2} }}} \right) - \phi } \right]\left( {P_{i} - P_{p} } \right) \\ \end{aligned}$$
(2)
$${\sigma }_{z}^{ }={\sigma }_{z}-2\mu \left({\sigma }_{H}-{\sigma }_{h}\right)\frac{{r}_{i}^{2}}{{r}^{2}}\mathit{cos}2\theta +\delta \left[\frac{\alpha \left(1-2\mu \right)}{1-\mu }-\phi \right]\left({P}_{i}-{p}_{p}\right)-\alpha {P}_{p}$$
(3)
$${\tau }_{r\theta }=\frac{{\sigma }_{H}+{\sigma }_{h}}{2}\left(1-3\frac{{r}_{i}^{4}}{{r}^{4}}+2\frac{{r}_{i}^{2}}{{r}^{2}}\right)\mathit{sin}2\theta$$
(4)

The circumferential stress at the borehole is as follows.

$$\begin{aligned} \sigma_{\theta } & = - P_{i} + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{1 - \mu } - } \right]\left( {P_{i} - P_{p} } \right) + \sigma_{H} \left( {1 - 2\cos 2\theta } \right) + \sigma_{h} \left( {1 + 2\cos 2\theta } \right) - \alpha P_{p} \\ & = - P_{i} + \left( {\sigma_{H} + \sigma_{h} } \right) - 2\left( {\sigma_{H} - \sigma_{h} } \right)\cos 2\theta - \alpha P_{p} + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{1 - \mu } - } \right]\left( {P_{i} - P_{p} } \right) \\ \end{aligned}$$
(5)

where, \({\sigma }_{H}\), \({\sigma }_{h}\) are the maximum and minimum horizontal principal stresses, respectively, MPa. \(\mu\) is the Poisson’s ratio of rocks, Dimensionless. \({P}_{p}\) is the pore pressure of formation, MPa. \({P}_{i}\) is the pore pressure at point i in the formation, MPa. \(\alpha\) is the effective stress coefficient, Dimensionless. \(r\) is the radial distance, m. \(\theta\) is angle of tangential stress, °. ϕ is the rock porosity, Dimensionless. \({\sigma }_{r}\), \({\sigma }_{\theta }\), \({\sigma }_{z}\) and \({\tau }_{r\theta }\) is the effective normal stresses in radial, tangential, and vertical directions; and the shear stress, MPa. δ is the coefficient, when the borehole has seepage, δ = 1, and when the borehole has no seepage, δ = 0. \({P}_{p}\) is the pore pressure, MPa.

After extensive research and practical application, various fracture initiation criteria have been proposed for fracturing technology. Cai et al. argued that the fracturing pressure predicted by the tensile fracture criterion (maximum tensile stress principle) is more accurate than any other criterion, whether it pertains to small fractures or local stress distribution determined by fracturing test data41. Currently, the tensile failure criterion is widely employed in fracturing design to predict fracture initiation based on the rock’s tensile fracture characteristics: when subjected to circumferential tensile stress reaching its material tensile strength, new open fault chips will form perpendicular to the direction of the applied tension.

The occurrence of fracture is imminent when the maximum effective tensile stress at the borehole reaches the rock’s tensile strength σt.

$${\sigma }_{\theta }=-{\sigma }_{t}$$
(6)

From Eq. (5), as Pi increases, σθ decreases, and when Pi increases to a certain extent, σθ will become negative, meaning that the axial stress on the rock changes from compression to tension. When the tensile stress is great enough to overcome the rock’s tensile strength, the formation will undergo fracture. The fracture occurs at the specific location where the rock fractures when the stress reaches the critical value σθ, and this location is on the direction θ of 0° or 180°, and the value of σθ is as follows.

$${\sigma }_{\theta }=3{\sigma }_{h}-{\sigma }_{H}-\alpha {P}_{p}-{P}_{i}+\delta \left[\frac{\alpha \left(1-2\mu \right)}{1-\mu }-\phi \right]\left({P}_{i}-{P}_{p}\right)$$
(7)

Substitute the Eq. (7) into the Eq. (6), and the in-well pressure at which the rock undergoes tensile failure can be obtained, also known as the formation fracturing pressure.

$$P_{i} = \frac{{3\sigma_{h} - \sigma_{H} - \alpha P_{p} + \sigma_{t} - \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{1 - \mu } - \phi } \right]P_{p} }}{{\left\{ {1 - \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{1 - \mu } - \phi } \right]} \right\}}}$$
(8)

If the filtration of fracturing fluid is not taken into consideration, the fracturing of the formation can be simplified as:

$${P}_{i}=3{\sigma }_{h}-{\sigma }_{H}-\alpha {P}_{p}+{\sigma }_{t}$$
(9)

Equation (9) is a commonly used formula for predicting the fracturing pressure.

The fracture initiation model for perforated well completion

Compared to naked-eye completion, the calculation of fracturing pressure for perforated completion is more complex, as not only the casing stress on the formation but also the stress on the wellbore and the near-well area caused by the perforation hole has a significant impact.

Stress distribution around perforated well and perforated hole

If the communication between the wellbore formation and the perforation is good, and there is no perforation friction, then the bottom hole pressure is equal to the pressure within the perforation. Before the formation fractures, there is a micro fracture zone at the second interface between the formation and the cement sheath. After perforating, the wellbore can be considered as two orthogonal cylindrical holes of different diameters. The geometric model and stress redistribution model of the perforated wellbore are shown in Fig. 1.

Fig. 1
figure 1

Geometric model of perforated wellbore and redistribution of surrounding Earth stress42.

Full size image

In Fig. 1, σz is the axial stress of the wellbore, σθ is the tangential stress of the wellbore, σθ' is the tangential stress of the perforation hole, σθl is the concentrated stress that forms longitudinal fractures (vertical fractures), and σθt is the concentrated stress that forms transverse fractures (horizontal fractures). According to the principle of stress superposition, the tangential stress at the root of the hole is,

$$\begin{aligned} \sigma_{{\theta^{\prime}}} & = \left( {\sigma_{H} + \sigma_{h} + \sigma_{v} } \right) + 2\left( {\sigma_{H} + \sigma_{h} - \sigma_{v} } \right)\cos 2\theta^{\prime} - 2\left( {\sigma_{H} - \sigma_{h} } \right)\left( {\cos 2\theta + 2\cos 2\theta \cos 2\theta^{\prime}} \right) \\ & \quad - 2P_{i} \left( {1 + \cos 2\theta^{\prime}} \right) + 2\delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{1 - \mu } - } \right]\left( {P_{i} - P_{o} } \right)\left( {1 + \cos 2\theta^{\prime}} \right) \\ \end{aligned}$$
(10)

According to the stress distribution model of the open hole wellbore, the stress field distribution around the perforated wellbore can be simplified as

$$\left\{ \begin{aligned} \sigma _{{\theta ^{\prime } }} & = \left( {\sigma _{H} + \sigma _{h} + \sigma _{z} } \right) + 2\left( {\sigma _{H} + \sigma _{h} - \sigma _{z} } \right)cos2\theta ^{\prime } \\ & \quad - 2\left( {\sigma _{H} - \sigma _{h} } \right)\left( {cos2\theta + 2cos2\theta cos2\theta ^{\prime } } \right) \\ & \quad - 2P_{i} \left( {1 + cos2\theta ^{\prime } } \right) + 2\delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{{1 - \mu }} - \phi } \right]\left( {P_{i} - P_{o} } \right)\left( {1 + cos2\theta ^{\prime } } \right) \\ \sigma _{r} & = P_{i} - \delta \phi \left( {P_{i} - P_{o} } \right) \\ \sigma _{z} & = \sigma _{v} - 2\mu \left( {\sigma _{H} - \sigma _{h} } \right)cos2\theta - cP_{i} + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{{1 - \mu }} - \phi } \right]\left( {P_{i} - P_{o} } \right) \\ \end{aligned} \right.$$
(11)

Equation (11) is an approximate analytical expression for the stress distribution around perforated wells, which is widely used nowadays. It can be seen that this expression differs from the expression for open hole wells only in that σθ has been changed to σθ', emphasizing the stress distribution around the perforation and considering that the perforation is the main site of fracture initiation.

In a small range, stress near the perforation can be obtained using a stress solving method similar to that of an open hole wellbore.

$$\begin{aligned} \sigma_{pr}^{\prime} & = \frac{{\sigma_{\theta } + \sigma_{z} }}{2}\left( {1 - \frac{{r_{perf}^{2} }}{{L_{perf}^{2} }}} \right) + \frac{{\sigma_{\theta } - \sigma_{z} }}{2}\left( {1 - 4\frac{{r_{perf}^{4} }}{{L_{perf}^{4} }} + \frac{{3r_{perf}^{4} }}{{L_{perf}^{4} }}} \right)\cos 2\theta^{\prime} + \frac{{r_{perf}^{2} }}{{L_{perf}^{2} }}P_{i} - \alpha p_{p} \\ & \quad + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{1 - \mu }\left( {1 - \frac{{r_{perf}^{2} }}{{L_{perf}^{2} }}} \right) - } \right]\left( {p_{i} - p_{o} } \right){ } \\ \end{aligned}$$
(12)
$$\begin{aligned} \sigma_{p\theta }^{\prime} & = \frac{{\sigma_{\theta } + \sigma_{z} }}{2}\left( {1 + \frac{{r_{perf}^{2} }}{{L_{perf}^{2} }}} \right) - \frac{{\sigma_{\theta } - \sigma_{z} }}{2}\left( {1 + \frac{{3r_{perf}^{4} }}{{L_{perf}^{4} }}} \right)\cos 2\theta^{\prime} - \frac{{r_{perf}^{2} }}{{L_{perf}^{2} }}P_{i} \\ & \quad - \alpha p_{p} + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{1 - \mu }\left( {1 + \frac{{r_{perf}^{2} }}{{L_{perf}^{2} }}} \right) - } \right]\left( {p_{i} - p_{o} } \right) \\ \end{aligned}$$
(13)
$${\sigma }_{pz}^{\prime}={\sigma }_{r}-2\mu \left({\sigma }_{\theta }-{\sigma }_{z}\right)\frac{{{r}_{perf}}^{2}}{{{L}_{perf}}^{2}}\mathit{cos}2{\theta }^{\prime}-c{p}_{w}\frac{{{r}_{perf}}^{2}}{{{L}_{perf}}^{2}}+\delta \left[\frac{\alpha \left(1-2\mu \right)}{1-\mu }-\phi \right]\left({p}_{i}-{p}_{o}\right)-\alpha {p}_{p}$$
(14)

where, rperf represents the radius of the perforation hole; Lperf represents the distance from the perforation hole. Substituting the stresses σr, σθ, and σz around the wellbore obtained from the previous calculations into the stress formula around the borehole yields the stress distribution around the borehole.

The fracturing pressure of perforated well

In practical calculations, considering that the initiation of fractures always starts from the wellbore or perforation hole wall, it is simplified as the stress on the perforation hole wall, which is taken as rperf = Lperf. Considering that the cement sheath and formation are well consolidated, there will be no seepage of fracturing fluid into the formation. At this time, the pressure on the wellbore is 5% of the fracturing fluid pressure, and due to good consolidation, there will be no filtration of fracturing fluid43. Filtration only occurs from the perforation wall, and the pressure of the perforation hole is always equal to the fracturing fluid pressure, that is, pperf = pi. When the cement sheath and the formation are well consolidated, there is no seepage of fracturing fluid through the wellbore to the formation. Therefore, the calculation formula for the geostress around the wellbore becomes that.

$${\sigma }_{r}=\frac{{\sigma }_{H}+{\sigma }_{h}}{2}\left(1-\frac{{r}_{i}^{2}}{{r}^{2}}\right)+\left(\frac{{\sigma }_{H}-{\sigma }_{h}}{2}\right)\left(1-4\frac{{r}_{i}^{2}}{{r}^{2}}+3\frac{{r}_{i}^{4}}{{r}^{4}}\right)\mathit{cos}2\theta +\frac{{r}_{i}^{2}}{{r}^{2}}{P}_{i}-\alpha {P}_{p}$$
(15)
$${\sigma }_{\theta }=\frac{{\sigma }_{H}+{\sigma }_{h}}{2}\left(1+\frac{{r}_{i}^{2}}{{r}^{2}}\right)+\left(\frac{{\sigma }_{H}-{\sigma }_{h}}{2}\right)\left(1+3\frac{{r}_{i}^{4}}{{r}^{4}}\right)\mathit{cos}2\theta -\frac{{r}_{i}^{2}}{{r}^{2}}{P}_{i}-\alpha {P}_{p}$$
(16)
$${\sigma }_{z}={\sigma }_{z}-2\mu \left({\sigma }_{H}-{\sigma }_{h}\right)\frac{{r}_{i}^{2}}{{r}^{2}}\mathit{cos}2\theta +\delta \left[\frac{\alpha \left(1-2\mu \right)}{1-\mu }-\varphi \right]\left({P}_{i}-{p}_{p}\right)-\alpha {P}_{p}$$
(17)

Therefore, the stress on the perforation wall becomes as follows.

$$\left\{ \begin{aligned} \sigma _{{pr}}^{\prime } & = \frac{{r_{{perf}} ^{2} }}{{L_{{perf}} ^{2} }}P_{i} - \alpha p_{p} + \delta \varphi \left( {p_{i} - p_{o} } \right) \\ \sigma _{{p\theta }}^{\prime } & = \left\{ \begin{gathered} - P_{i} + \sigma _{H} \left( {1 - 2cos2\theta } \right) + \sigma _{h} \left( {1 + 2cos2\theta } \right) - \alpha P_{p} \hfill \\ + c\frac{{r_{i} ^{2} }}{{r^{2} }}P_{i} + \sigma _{v} - 2\mu \left( {\sigma _{H} - \sigma _{h} } \right)cos2\theta - \alpha P_{p} \hfill \\ \end{gathered} \right\} \\ & \quad - 2\left\{ \begin{gathered} - P_{i} + \sigma _{H} \left( {1 - 2cos2\theta } \right) + \sigma _{h} \left( {1 + 2cos2\theta } \right)_{p} \hfill \\ - c\frac{{r_{i} ^{2} }}{{r^{2} }}P_{i} - \sigma _{v} + 2\mu \left( {\sigma _{H} - \sigma _{h} } \right)cos2\theta \hfill \\ \end{gathered} \right\}cos2\theta ^{\prime } \\ & \quad - P_{i} - \alpha p_{p} + \delta \left[ {\frac{{2\alpha \left( {1 - 2\mu } \right)}}{{1 - \mu }} - \varphi } \right]\left( {p_{i} - p_{o} } \right) \\ \sigma _{{pz}}^{\prime } & = - 2\mu \left\{ \begin{gathered} - P_{i} + \sigma _{H} \left( {1 - 2cos2\theta } \right) + \sigma _{h} \left( {1 + 2cos2\theta } \right)_{p} \hfill \\ - c\frac{{r_{i} ^{2} }}{{r^{2} }}P_{i} - \sigma _{v} + 2\mu \left( {\sigma _{H} - \sigma _{h} } \right)cos2\theta \hfill \\ \end{gathered} \right\}cos2\theta ^{\prime } \\ & \quad + P_{i} + \delta \varphi \left( {P_{i} - p_{p} } \right) - \alpha P_{p} - cp_{w} \\ & \quad + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu } \right)}}{{1 - \mu }} - \varphi } \right]\left( {p_{i} - p_{o} } \right) - \alpha p_{p} \\ \end{aligned} \right.$$
(18)

Therefore, due to the good consolidation between the cement sheath and the formation, fractures cannot occur from the wellbore, but only from the perforation holes. So, take r from ri to ri + dperf (hole depth), calculate the σz and σθ at the selected point in this interval (Eqs. (16) and (17), substitute into Eq. (18) to solve for σ'pθ, and then use this parameter to determine the location of the maximum tensile stress on the hole and the fracturing pressure.

The influence of perforation parameters on the fracturing pressure

Analysis method

The analysis method of the influence of perforation parameters on rock fracture pressure mainly includes the following steps.

  1. a.

    Establish a mechanical model: Based on the principles of rock mechanics and seepage mechanics, and considering the formation conditions, rock properties and perforation operation characteristics comprehensively, a perforation in-situ stress mechanical model including fluid–solid coupling effect and dynamic effect is constructed.

  2. b.

    Solve the model using numerical methods: Use the finite element method or other applicable numerical methods, combined with rock fracture criteria, to solve the model to obtain the in-situ stress distribution state and rock fracture pressure. Analyze the fracture propagation law through the finite element model and evaluate the influence of perforation parameters on rock fracture pressure.

  3. c.

    Analyze the influence of perforation parameters: By changing perforation parameters (such as perforation density, perforation azimuth, perforation hole diameter and perforation depth, etc.), systematically observe and analyze the specific influence of these parameters on rock fracture pressure.

The analysis of the factors influencing the rock fracture pressure by perforation parameters is a comprehensive process, involving the establishment of mechanical models, the solution of numerical methods, and the detailed analysis of the impact of perforation parameters. This process is of great significance for optimizing the design of perforation parameters and improving the effect of fracturing operations.

The perforation parameters mainly include the perforation density, the phase angle and azimuth angle of the perforation eyehole, the diameter of the perforation eyehole, and the penetration depth, etc. The following is an analysis of the influencing factors based on the basic parameters of a typical well.

Result and discussion
  1. ①

    The perforation azimuth

    The angle of perforation azimuth is the angle between the perforation axis line and the direction of the maximum horizontal stress, calculated for a perforation density of 16 holes/m using the example of 16 holes/m. By changing the perforation azimuth, the impact of perforation azimuth on fracturing pressure is calculated. Simulation research shows that the stress concentration around the wellbore is a function of the perforation azimuth relative to the maximum horizontal principal stress direction, and the fracturing pressure is a function of the angle between the perforation azimuth and the maximum horizontal principal stress direction. When the perforation hole axis is parallel to the maximum horizontal principal stress direction, the fracturing pressure is lowest; when the perforation hole axis is perpendicular to the maximum horizontal principal stress direction, the fracturing pressure is highest. According to the study, the optimal perforation azimuth for effectively reducing formation fracturing pressure is within the ± 40° region of the maximum principal stress direction; beyond this range, it is easy to cause fracture deflection, and the fracturing pressure will rise rapidly (Fig. 2).

    Fig. 2
    figure 2

    The relationship between the perforation azimuth of well 1 and its formation fracturing pressure.

    Full size image

    Drilling horizontal wellbores along the maximum horizontal principal stress direction, and the lowest fracturing pressure will be achieved during the fracturing operation. This will enable the fracture to initiate and expand directly at the perforation points, with the perforation points directly communicating with the artificial fractures. The artificial fractures created by the fracturing operation can also maximize communication with natural fractures, as most reservoir natural fractures typically develop perpendicular to the maximum horizontal principal stress direction. Additionally, based on the analysis of the experimental results of the angle between the maximum horizontal principal stress and the line of perforation hole arrangement and the fracturing pressure, both tubular wells and open-hole wells show that the fracturing pressure increases as the angle between the perforation hole and the maximum horizontal principal stress increases. Moreover, the rate of increase in the open-hole well is greater than that of the tubular well.

  2. ②

    Hole spacing

    Hole spacing, defined as the number of perforations per unit depth of the wellbore, was set with a perforation azimuth of zero degrees and the perforation direction aligned with the maximum horizontal principal stress direction. According to existing experimental results, both hole spacing and the method of perforation significantly impact fracturing pressure. Specifically, spiral perforation typically exhibits a higher fracturing pressure than linear perforation by 6–8 MPa44. With the same perforation method, fracturing pressure decreases as hole spacing increases (Fig. 3).

    Fig. 3
    figure 3

    Relationship between perforation density of well 1 and its fracturing pressure.

    Full size image

    As illustrated in Fig. 3, the relationship between fracturing pressure and perforation density is not a simple linear one. The fracturing pressure decreases as the perforation density increases from 2 to 8 holes per meter and from 8 to 16 holes per meter, but remains almost unchanged beyond 16 holes per meter. Notably, the fracturing pressure shows minimal change as the perforation density increases from 4 to 8 holes per meter and from 13 to 16 holes per meter.

    This phenomenon can be attributed to the non-uniform interaction of multi-hole stress concentration effects as hole spacing decreases. Consequently, a perforation density of 16 holes per meter can be considered optimal, ensuring low fracturing pressure while mitigating potential issues related to excessive perforation on casing strength.

  3. ③

    Perforation hole diameter

    The diameter of the perforation hole is also a critical parameter in perforation design, influencing factors such as projectile selection. With a perforation density set at 16 holes per meter, research results shown in Fig. 4 indicate that the diameter of the perforation hole has a minimal effect on fracturing pressure.

  4. ④

    Perforation hole length

    Fig. 4
    figure 4

    Relationship between the perforation diameter of well 1 and its fracturing pressure.

    Full size image

    Considering the impact of perforation hole length on fracturing pressure, a perforation density of 16 holes per meter was maintained. Calculations indicate that as the length of the perforation increases, the fracturing pressure exhibits a linear decline; however, this effect is relatively minor (Fig. 5).

    Fig. 5
    figure 5

    Relationship between the perforation length of well 1 and its fracturing pressure.

    Full size image

Prediction of fracturing pressure after reservoir damage

The influence of reservoir damage on fracturing pressure is primarily evident in two aspects: Firstly, the skin effect induced by near-wellbore damage impacts the percolation capacity of fracturing fluid into the formation, leading to alterations in the circumferential stress at the wellbore and consequently affecting fracturing pressure. Secondly, following reservoir damage, changes in the mechanical properties of the rock further influence fracturing pressure.

Analysis of the impact of reservoir damage on formation stress

The changes in circumferential stress around the wellbore and the mechanical properties of rocks caused by skin effect due to reservoir damage near the wellbore can be attributed to the following factors.

  1. a.

    Drilling fluid invasion: During drilling, the invasion of drilling fluid into the surrounding reservoir alters the mechanical properties of the reservoir rock. Solid particles and filtrate from the drilling fluid can clog pore spaces, reducing permeability and modifying key mechanical parameters such as elastic modulus and Poisson’s ratio.

  2. b.

    Pressure differential effects: The pressure difference between the inside and outside of the wellbore during drilling can alter the stress state of the reservoir rock. Significant pressure differentials subject the rock near the wellbore to increased stress, potentially leading to reduced rock strength and even shear or tensile failure.

  3. c.

    Chemical reactions induced by fluid invasion: Chemical substances in the drilling fluid can react with the reservoir rock, altering its mineral composition and thereby affecting its mechanical properties. For example, certain components in the drilling fluid may interact with clay minerals, causing clay swelling and a reduction in rock strength.

  4. d.

    Temperature and pressure variations: The high-temperature and high-pressure environment near the wellbore can influence both the physical and chemical properties of the reservoir rocks. Elevated temperatures may induce phase transitions in certain minerals, while high pressures can cause plastic deformation, further impacting the mechanical properties of the rock.

  5. e.

    Formation water intrusion: During drilling, formation water may invade the reservoirs surrounding the wellbore, altering the pore structure and fluid properties of the reservoir. This intrusion can change the wettability of the reservoir rocks, thereby influencing their mechanical properties.

Stress field of open-hole completed wellbore post fracturing fluid invasion-induced damage

The presence of reservoir damage leads to an additional pressure drop as the fracturing fluid filters through the damage zone, which results in a decrease in the effective pumping pressure exerted on the formation. This reduction subsequently influences the additional stress generated by the radial infiltration of fracturing fluid into the formation. Furthermore, pore pressure also undergoes changes; thus, initial pore pressure cannot be regarded as a substitute. Consequently, conventional formulas for calculating stress induced by fracturing fluid filtration often yield certain inaccuracies due to overlooking the impact of damage.

Under the combined effect of wellbore pressure, geostress, and fracturing fluid seepage, a stress field distribution model around an open hole inclined wellbore was established based on the superposition principle using Eq. (19)

$$\begin{aligned} \sigma_{r} = & \frac{{\sigma_{H} + \sigma_{h} }}{2}\left( {1 - \frac{{r_{i}^{2} }}{{r^{2} }}} \right) + \left( {\frac{{\sigma_{H} - \sigma_{h} }}{2}} \right)\left( {1 - 4\frac{{r_{i}^{2} }}{{r^{2} }} + 3\frac{{r_{i}^{4} }}{{r^{4} }}} \right)\cos 2\theta + \frac{{r_{i}^{2} }}{{r^{2} }}P_{i} \\ & \quad + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu^{\prime}} \right)}}{{2\left( {1 - \mu^{\prime}} \right)}}\left( {1 - \frac{{r_{i}^{2} }}{{r^{2} }}} \right) - \phi^{\prime}} \right]\left( {P_{i} - p\left( {r,t} \right)} \right) \\ \end{aligned}$$
(19)
$$\begin{aligned} \sigma_{\theta } = & \frac{{\sigma_{H} + \sigma_{h} }}{2}\left( {1 + \frac{{r_{i}^{2} }}{{r^{2} }}} \right) + \left( {\frac{{\sigma_{H} - \sigma_{h} }}{2}} \right)\left( {1 + 3\frac{{r_{i}^{4} }}{{r^{4} }}} \right)\cos 2\theta - \frac{{r_{i}^{2} }}{{r^{2} }}P_{i} \\ & \quad + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu^{\prime}} \right)}}{{2\left( {1 - \mu^{\prime}} \right)}}\left( {1 + \frac{{r_{i}^{2} }}{{r^{2} }}} \right) - \phi^{\prime}} \right]\left( {P_{i} - p\left( {r,t} \right)} \right) \\ \end{aligned}$$
(20)
$${\sigma }_{z}={\sigma }_{z}-2{\mu }^{\prime}\left({\sigma }_{H}-{\sigma }_{h}\right)\frac{{r}_{i}^{2}}{{r}^{2}}\mathit{cos}2\theta +\delta \left[\frac{\alpha \left(1-2{\mu }^{\prime}\right)}{1-{\mu }^{\prime}}-{\varphi }^{\prime}\right]\left({P}_{i}-p\left(r,t\right)\right)$$
(21)
$${\tau }_{r\theta }=\frac{{\sigma }_{H}+{\sigma }_{h}}{2}\left(1-3\frac{{r}_{i}^{4}}{{r}^{4}}+2\frac{{r}_{i}^{2}}{{r}^{2}}\right)\mathit{sin}2\theta$$
(22)

When r = rw, the stress component on the wellbore can be expressed as

$${\sigma }_{r}={P}_{i}+\delta {\varphi }^{\prime}\left({P}_{i}-p\left(r,t\right)\right)$$
(23)
$${\sigma }_{\theta }=-{P}_{i}+\delta \left[\frac{\alpha \left(1-2{\mu }^{\prime}\right)}{\left(1-{\mu }^{\prime}\right)}-{\varphi }^{\prime}\right]\left({P}_{i}-p\left(r,t\right)\right)+{\sigma }_{H}\left(1-2\mathit{cos}2\theta \right)+{\sigma }_{h}\left(1+2\mathit{cos}2\theta \right)$$
(24)
$${\sigma }_{z}=c\frac{{{r}_{i}}^{2}}{{r}^{2}}{P}_{i}+{\sigma }_{v}+\delta \left[\frac{\alpha \left(1-2{\mu }^{\prime}\right)}{1-{\mu }^{\prime}}-{\varphi }^{\prime}\right]\left({P}_{i}-p\left(r,t\right)\right)-2{\mu }^{\prime}\left({\sigma }_{H}-{\sigma }_{h}\right)\mathit{cos}2\theta$$
(25)

where, p (r, t)—Pore pressure after fracturing fluid injection, MPa. pi—Inject fracturing fluid pressure, MPa. ϕ′—Porosity of mud damage zone, %. μ′—Poisson’s ratio of mud damage zone. δ—The permeability coefficient is = δ1 when the formation is permeable and = δ0 when the formation is impermeable. The original permeability, porosity, elastic modulus, and Poisson’s ratio of the reservoir are porosity (ϕ), permeability (k), Elastic modulus (E) and Poisson’s ratio (μ) respectively. The permeability, porosity, elastic modulus, and Poisson’s ratio of the damage zone within the reservoir are ϕ′, k′, E′, and μ′, respectively. Then, the additional stress field caused by the radial infiltration of fracturing fluid into the surrounding rock layers around the wellbore after reservoir damage becomes that.

The above equation represents the final stress field of the wellbore after reservoir damage in an open hole deep well.

Stress field of near wellbore in perforated wells after reservoir damage

Using a stress solution method similar to that for open-hole wellbores and considering the presence of a well-consolidated cement sheath and formation, the fracturing fluid does not influence seepage from the wellbore into the formation. The stress on the perforation wall is calculated as follows:

$$\left\{ \begin{aligned} \sigma _{{pr}}^{\prime } & = \frac{{r_{{perf}} ^{2} }}{{L_{{perf}} ^{2} }}P_{i} + \delta \varphi ^{\prime } \left( {p_{i} - p\left( {r,t} \right)} \right) \\ \sigma _{{p\theta }}^{\prime } & = \left\{ \begin{gathered} - P_{i} + \sigma _{H} \left( {1 - 2cos2\theta } \right) + \sigma _{h} \left( {1 + 2cos2\theta } \right) \hfill \\ + c\frac{{r_{i} ^{2} }}{{r^{2} }}P_{i} + \sigma _{v} - 2\mu ^{\prime } \left( {\sigma _{H} - \sigma _{h} } \right)cos2\theta \hfill \\ \end{gathered} \right\} \\ & \quad - 2\left\{ \begin{gathered} - P_{i} + \sigma _{H} \left( {1 - 2cos2\theta } \right) + \sigma _{h} \left( {1 + 2cos2\theta } \right)_{p} \hfill \\ - c\frac{{r_{i} ^{2} }}{{r^{2} }}P_{i} - \sigma _{v} + 2\mu ^{\prime } \left( {\sigma _{H} - \sigma _{h} } \right)cos2\theta \hfill \\ \end{gathered} \right\}cos2\theta ^{\prime } \\ & \quad - P_{i} + \delta \left[ {\frac{{2\alpha \left( {1 - 2\mu ^{\prime } } \right)}}{{1 - \mu ^{\prime } }} - \varphi ^{\prime } } \right]\left( {p_{i} - p\left( {r,t} \right)} \right) \\ \sigma _{{pz}}^{\prime } & = - 2\upsilon ^{\prime } \left\{ \begin{gathered} - P_{i} + \sigma _{H} \left( {1 - 2cos2\theta } \right) + \sigma _{h} \left( {1 + 2cos2\theta } \right)_{p} \hfill \\ - c\frac{{r_{i} ^{2} }}{{r^{2} }}P_{i} - \sigma _{v} + 2\mu ^{\prime } \left( {\sigma _{H} - \sigma _{h} } \right)cos2\theta \hfill \\ \end{gathered} \right\}cos2\theta ^{\prime } \\ & \quad + P_{i} + \delta \varphi \left( {p_{i} - p\left( {r,t} \right)} \right) - cp_{w} \\ & \quad + \delta \left[ {\frac{{\alpha \left( {1 - 2\mu ^{\prime } } \right)}}{{1 - \mu ^{\prime } }} - \varphi ^{\prime } } \right]\left( {p_{i} - p\left( {r,t} \right)} \right) \\ \end{aligned} \right.$$
(26)

After establishing a distribution model of the stress field around the wellbore of perforated well which formation was damaged by drilling fluid, the in-situ stress around the wellbore can be directly substituted into the formula for calculating the fracturing pressure for analysis.

Application results and analysis

Rock mechanics and geostress parameters for test wells

Rock mechanics parameter tests were conducted to obtain the rock mechanics parameters for two wells, as detailed in Tables 1, 2, 4, and 5. By substituting the parameter values from Tables 1 and 2 into Eq. (19), the fracture pressure for the open-hole completion of Well 1 was calculated and summarized in Table 3. Similarly, by substituting the parameter values from Tables 4 and 5 into Eq. (26), the fracture pressure for the perforated completion of Well 2 was determined and presented in Table 6.

Table 1 The average rock mechanics parameters of Well 1 oil reservoir.
Full size table
Table 2 Basic parameters of Well 1 oil reservoir section.
Full size table
Table 3 The calculated results of the geostress in the oil layer section of Well 1.
Full size table
Table 4 The average rock mechanics parameters of Well 2 oil reservoirs.
Full size table
Table 5 Basic parameters of Well 2 oil reservoir section.
Full size table
Table 6 The calculated results of the geostress in the oil layer section of Well 2.
Full size table

Utilizing the computed layered stress values, static rock mechanics parameters, and additional test data, the breakdown pressure corresponding to each layer position under varying conditions can be accurately determined. The basic parameters of reservoir permeability and porosity, along with rock mechanics data, were input into the model to compute the fracture pressures for the two deep wells (Well 1 and Well 2) under different completion approaches.

Results and analysis

A comprehensive comparative analysis of breakdown pressures and their gradients for reservoir rocks was conducted between perforated completions and open-hole completions, as illustrated in Figs. 6 and 7. This study aimed to evaluate the differences in fracturing pressure characteristics under different wellbore configurations, providing valuable insights into optimal completion strategies.

Fig. 6
figure 6

Calculation results of rock fracturing pressure in Well 1 with different completion.

Full size image
Fig. 7
figure 7

Calculation results of rock fracturing pressure gradient in Well 1 with different completion.

Full size image

The results derived from the reservoir rock fracturing pressure prediction model reveal significant variations between the two completion methods. For Well 1, the fracturing pressure gradient for the open-hole completion ranges from approximately 0.0182–0.0190 MPa/m. In contrast, the perforated completion exhibits a lower gradient, ranging from approximately 0.0142–0.0152 MPa/m. This difference can be attributed to the distinct hydraulic conditions and stress distributions associated with each completion method. The open-hole configuration allows for more direct interaction between the formation and the fracturing fluid, potentially leading to higher pressure gradients due to less resistance compared to the perforated completion, where the presence of casing and cement sheath may introduce additional constraints.

For Well 2, similar trends were observed. The fracturing pressure gradient for the open-hole completion ranges from approximately 0.0158–0.0165 MPa/m, while that for the perforated completion ranges from approximately 0.0130–0.0135 MPa/m. These findings highlight the importance of considering specific geological and engineering factors when selecting an appropriate completion method. The lower pressure gradients in perforated completions suggest that this method may be more suitable for formations with lower permeability or where minimizing injection pressure is a priority.

Furthermore, the analysis underscores the need for detailed modeling and site-specific data collection to accurately predict fracturing pressure gradients. Factors such as formation heterogeneity, in-situ stress conditions, and the mechanical properties of the rock play crucial roles in determining the effectiveness of each completion approach. By understanding these variations, engineers can make informed decisions to optimize fracturing operations, enhance production efficiency, and ensure well integrity.

A comparative analysis of perforated completions and open-hole completions reveals that perforated completions offer a significant advantage in reducing formation fracturing pressures. This benefit arises from the strategic placement of perforations at designated locations within the wellbore, which effectively alleviates portions of the in-situ stress, thereby diminishing the load on surrounding rock masses.

During perforation operations, specialized tools are employed to create precise holes through the casing and cement sheath into the formation. These perforations serve multiple purposes: they enhance flow channels for hydrocarbons within the reservoir and significantly mitigate instability phenomena associated with high pressure. By providing additional pathways for fluid flow, perforations help distribute pressure more evenly across the formation, thus reducing localized stress concentrations that could lead to fractures or other forms of instability.

Research indicates that following the implementation of perforation technology, a more uniform stress distribution emerges among various layers of the reservoir. This uniformity is crucial for preventing local instabilities and maintaining reservoir integrity. The even distribution of stress helps avoid excessive deformation or failure in specific areas, ensuring overall structural stability during production activities.

Based on these calculations, it is evident that perforated completions can reduce formation fracturing pressures by 10–15%. This reduction is particularly advantageous in formations characterized by exceptionally high fracturing pressures, where traditional open-hole completions may pose higher risks of inducing fractures or causing reservoir damage. By lowering the required fracturing pressure, perforated completions facilitate safer and more efficient extraction processes.

A unified fracture pressure model has been developed for both open-hole and perforated wells to enable direct mechanical comparison between the two completion methods. This model provides a quantitative basis for optimizing completion strategies. It reveals the mechanisms of stress redistribution following fracturing fluid invasion and reservoir damage, correcting errors in predicting fracture pressures in contaminated formations. According to the calculation and analysis of two wells, the error in predicting rupture pressure has been reduced by approximately 10% (Fig. 8).

Fig. 8
figure 8

Error analysis of fracture pressure value calculated by correcting the model.

Full size image

Consequently, this technology finds extensive application in challenging geological settings such as deep and ultra-deep wells, tight formations, and reservoirs with complex stress regimes. In these environments, the ability to control and manage fracturing pressures is critical for optimizing production rates while minimizing potential risks. Perforated completions not only enhance operational safety but also extend the productive life of the well by preserving reservoir integrity over time. Comparative analysis highlights the advantages of perforated completions in reducing formation fracturing pressures. By strategically creating perforations, this method effectively manages in-situ stresses, improves fluid flow, and ensures a more uniform stress distribution throughout the reservoir. These benefits make perforated completions an indispensable tool for safe and efficient hydrocarbon extraction, particularly in formations characterized by high fracturing pressures.

Conclusions

  1. (1)

    A fracturing pressure model was developed for various completion methods, specifically open-hole completions and cased perforated completions. The analysis demonstrates that cased perforated completions significantly reduce the reservoir’s fracturing pressure, with a reduction range of 10–15%. Formation damage introduces pore-scale effects, alters rock mechanical parameters, and modifies the stress distribution around the wellbore in post-damage scenarios. These changes can substantially increase the reservoir’s fracturing pressure.

  2. (2)

    The stress concentration around the wellbore is a function of the angle between the maximum horizontal principal stress direction and the perforation orientation, while the fracturing pressure depends on this angular relationship. When the perforation holes are aligned parallel to the maximum horizontal principal stress direction, the fracturing pressure reaches its minimum value. Conversely, when they are oriented perpendicular to this direction, the fracturing pressure attains its maximum value. The optimal perforation orientation for effectively reducing formation fracturing pressure lies within ± 40° of the maximum horizontal principal stress direction. Exceeding this range may cause deviations in fracture propagation, leading to a rapid increase in fracturing pressure.

  3. (3)

    Perforation density and configuration significantly influence the fracturing pressure in cased wells. For a given perforation configuration, fracturing pressure decreases progressively as perforation density increases; conversely, the diameter and length of perforation holes have relatively minor effects on the reservoir’s fracturing pressure. Understanding these relationships is essential for optimizing completion strategies to enhance hydrocarbon recovery while minimizing risks associated with fracturing operations.