Introduction

In most areas of medicine, symptoms of pathology typically originate from an identifiable common cause, an underlying disorder. For instance, in the case of COVID-19, most symptoms arise directly from the underlying viral infection, which can be identified separately from its symptomatic expression. Traditionally, psychiatric disorders have been conceptualized in a similar manner, where symptoms such as irritability, insomnia, and changes in appetite are considered direct consequences of an underlying disorder, such as Major Depressive Disorder1. However, this common-cause model encounters substantial challenges within psychopathology. Unlike somatic illnesses, many psychiatric disorders are solely defined by the presence of a specific combination of symptoms. Consequently, an asymptomatic depression is impossible, and depression cannot be identified separately from its symptoms2. This creates a circular reasoning wherein symptoms of a disorder are both the cause and the consequence of the disorder itself. Moreover, progress in identifying specific biological and environmental causes for various psychopathological conditions has been limited1,3. This suggests that the conventional model of psychiatric disorders may be insufficient1. In research, and to a lesser extent in clinical contexts, there is a prevailing focus on the presence or absence of diagnoses of entire syndromes4, even though this provides relatively limited clinical information due to the vast heterogeneity in symptom presentations that could meet criteria for diagnosis. Furthermore, individuals who do not meet the full criteria for diagnosis may still experience substantial distress5. Also, clinical diagnoses or conclusions about symptom severity are often based on single, or relatively few, measurement points, failing to consider the complex and dynamic nature of mental health conditions6. A more nuanced and comprehensive approach is needed to capture the intricate interplay between symptoms, biology, and the environment in the development and persistence of psychiatric disorders.

In recent years, the field of psychiatry has undergone a notable shift in its conceptualization of mental disorders and embraced complex dynamic systems theory7. This alternative framework posits that psychiatric disorders are constellations of interconnected symptoms that mutually influence each other, rather than a collection of symptoms that merely co-occur due to a shared origin2. Symptoms and their mutual influences can be modelled in networks, which can include dynamic feedback loops and vicious cycles. For instance, negative mood and loss of energy may contribute to concentration difficulties, increased worrying, and sleep disturbances, which, in turn, can exacerbate the loss of energy and intensify negative mood1. As a result, the disorder can become self-sustaining and persist even when any initial identifiable cause, such as a stressful experience or challenging life circumstances, has subsided2,7. This theory allows a focus on the structure and dynamics of psychological complaints, instead of focussing on classifying individuals as “cases” or “non-cases”2. This could improve our understanding of psychopathology, and facilitate personalized care8.

The dynamic interplay between symptoms or mood states can be studied and mapped in a network, using time-series data. Ecological Momentary Assessment (EMA), wherein participants complete brief questionnaires multiple times a day using a mobile device, may be an especially valuable approach. EMA provides an opportunity to capture detailed real-time information on mood states and their interactions, offering insights into subtle nuances and connections that may not be captured when relying on less frequent and retrospective assessments9. When constructing EMA networks, researchers often employ the Multi-Level Vector Autoregression (mlVAR) model. This model enables the fitting of an autoregressive model across multiple individuals, where the value of a symptom or mood state is predicted by its own value and the value of other items in time-lag analyses10. When researching psychopathology, it is common to use a lag-1 model, which regresses the values of the item scores over values from the previous time point11,12. Findings are explained in terms of Granger causality, meaning that at least the temporal sequence requirements of causal effects are met, and fluctuation in a ‘causal’ item precedes fluctuation in the ‘effect’13.

The mlVAR model, however, faces several challenges that need to be addressed14. Firstly, some assumptions connected to the model are frequently violated. For instance, the assumption of stationarity, assuming that the mean, variance, and autocorrelation of variables remain constant over time15, is violated in developmental and treatment processes16. In previous research using mlVAR in the analysis of EMA data, stationarity has been assumed due to the relatively short time span in which EMA data are captured.13 However, this is not always realistic, as developments and changes can occur in the individual in short time periods. Furthermore, it precludes the study of networks where change is expected, for instance during an intervention17. Secondly, the undirected and between-subjects mlVAR approaches rely on partial correlations, and the directed mlVAR approach relies on multivariate regression, meaning that associations between two mood items are dependent on their relationships with all other mood items. This means that when all relevant variables are included and statistical assumptions are met, causality can be inferred from the connections in the directed network. However, in psychological systems a common occurrence is the presence of colliders—items that are influenced by two or more statistically unrelated nodes. Conditioning on the relationship with these colliders in the partial correlations network introduces a negative statistical dependency between the items influencing the collider, which can show up as a negative connection in the network when no such relationship exists in the data. Therefore, in psychological systems where colliders are present, the mlVAR approach might introduce spurious connections or distort the strength of positive connections in the network, leading to misinterpretations regarding the importance of certain nodes and edges18. Previous research has indeed demonstrated instances where mlVAR models produced such spurious connections in the network, which might be the consequence of such colliders.18,19 Additionally, items in the network may have construct overlap and can be highly intercorrelated, such that relationships among items can change noticeably if such an item is added or removed from the multivariate mlVAR network.

Dynamic Time Warping (DTW) offers a promising alternative for examining the relationships between items in a dynamic network. DTW is a statistical method that identifies patterns in time-series data by optimizing alignment, even when the co-variation between symptoms is not simultaneous or linear20. This technique quantifies the shape-based similarity between variable trajectories over time, with the possibility of incorporating time lags, resulting in a DTW distance measure. Where mlVAR aims to identify causal connections, the DTW technique can be applied to study co-occurrence and synchrony between variables, with the possibility of identifying lagged and non-linear relationships. DTW has been applied to studying time-series data across various fields21,22,23. In the field of psychiatry, DTW has recently shown success in estimating symptom networks of depression8, and examining changes in depression symptom networks after electroconvulsive therapy24. It has also recently been used to map symptoms of post-traumatic stress25, bipolar disorder26,27, and eating disorder psychopathology28.

Unlike mlVAR, DTW is a non-linear technique utilized for comparing and aligning time-series data, making it less susceptible to the effects of non-stationarity. Moreover, in DTW the calculation of the relationships between items is independent of their relationships with other items in the network. This means that the choice of variables included in the network does not influence the DTW distance between other variables. Additionally, using the DTW algorithm makes it easier to incorporate time-varying lags in the model. This allows for the inclusion of lag-0, lag-1, and lag-2 co-variation within the same model29, unlike mlVAR, which requires advanced script extensions or custom equations30. However, DTW also has its potential downsides, as it cannot capture multivariate associations or autocorrelation. Therefore, under ideal conditions where assumptions are met, Granger causality may be more reliably inferred from mlVAR networks. However, the mlVAR network is more susceptible to unmeasured confounding, as this can distort the mlVAR results but not the DTW distance calculations.

The objective of this study was to assess the advantages and disadvantages of the novel DTW approach and the conventional mlVAR approach by applying both to creating mood item networks based on the same dataset. Additionally, we aimed to investigate whether the techniques were susceptible to spurious or distorted connections due to the presence of colliders and violations of the statistical assumptions of mlVAR that are common in psychological research, by repeating the analyses on simulated datasets. A script for these analyses was made available on OSF and included in the supplementary files. We hypothesized that the DTW algorithm would yield more reliable directed networks when collider variables were present, due to the potential vulnerability of the mlVAR temporal network to spurious and distorted associations under such circumstances.

Methods

Participants and procedure

The Netherlands Study of Depression and Anxiety (NESDA)31 is a multi-center cohort study that has included a wide range of psychological and biological measures, collected in seven waves thus far. The baseline data, known as the first wave (T0) were gathered from 2004 to 2007 (n = 2981). The Assessment and Actigraphy module (NESDA-EMAA) module was offered to participants in the sixth wave (T5, collected between 2010 and 2013; n = 2069 original participants and 367 siblings from the newly added sibling cohort). Participants from the sibling cohort without a current or past diagnosis of depressive and/or anxiety disorder or other severe psychiatric disorder were also eligible32. In the current study, we included participants of NESDA-EMAA with at least 35 completed time points in the final sample. The study was approved by the Medical Ethical Committee of the VUmc (reference number 2003/183) and written informed consent was obtained from all respondents. Research was conducted in accordance with the Declaration of Helsinki.

Measures

Demographics

Basic demographics and clinical characteristics were collected at each NESDA wave, including gender, age, and diagnostic status based on the Composite International Diagnostic Interview33.

Momentary affective states

The NESDA-EMAA module consisted of 30 items. For the current study, we focused on items 1 through 20. Item 1–18 assessed affect and cognition, and 19 (“I feel tired”) and 20 (“I experience physical discomfort”) aimed to capture participants’ physical condition. The module included ten negative mood items, such as “I feel irritated” and eight positive mood items, such as “I feel cheerful”. All items were rated on a seven-point Likert scale, ranging from 1 (“Not at all”) to 7 (“Very”). Participants were prompted to complete the items five times a day for a duration of 2 weeks. This resulted in a potential total of up to 70 completions per participant.

Statistical analysis

We constructed distinct undirected and directed networks of mood items using the DTW and mlVAR algorithms. To further examine the (dis)similarities in outcomes between both techniques, we replicated the directed network analyses on a simulated dataset. This simulated dataset was intentionally designed to include a small number of predetermined associations between variables, along with random error/noise. This setup allowed us to investigate the origins of the potential differences that emerged.

Prior to conducting the analyses, all mood item scores were standardized at the group level. This standardization ensured that the results were based on the relative changes in mood item scores over time, enabling a meaningful comparison of trajectories even when scores fluctuated with different mean severity levels.

Sociodemographic and clinical variables at baseline are summarized as means and standard deviations (SD) or percentages, as appropriate. Additionally, an unadjusted density plot of all the 24,422 assessments was generated to visualize the relationships between item scores in the dataset, using the R ‘corrplot’ package (version 0.92), which provided insight into the crude interdependencies.

Undirected analyses
The contemporaneous and between-subjects Multi-level Vector AutoRegression models

For the mlVAR analysis, we utilized the “mlVAR” package in R34,35. This package contains an algorithm that estimates the predictive relationships between each variable and all other included variables at the subsequent time point within a nested model. As the EMA data were collected in regular time intervals during the day, but not collected during the night, we instructed the model to account for these timing discrepancies by not regressing the first measurement point of a day over the last measurement point of the previous day. Importantly, the mlVAR model separates within-person from between-person effects to account for within-subject dependence of data points and non-ergodicity. Analysis therefore yields two separate undirected network models. The “contemporaneous” (within-subject) network estimates cross-sectional within-subject associations between mood items, while controlling for temporal relationships and all other items. The “between-subjects” network estimates associations between mean scores of the items across timepoints and across subjects35. For a more elaborate description of the mlVAR model, see Bringmann et al.10 and Epskamp et al.35

Undirected Dynamic Time Warping

The DTW networks were constructed based on the calculation of DTW distances between each pair of EMA mood items, which reflect the tendency of the items to co-vary. Each mood item’s score trajectory over time was treated as an individual time series. Unlike simple point-to-point Euclidian comparisons commonly used in longitudinal studies, the DTW technique offered a more flexible alignment by considering both the cross-sectional distance (t, lag-0) and the distance with a lagged point in time (t − 1 or t + 1). This flexibility allowed for shifts and deformations in the time axis, enabling a comprehensive analysis of dynamic patterns. For a detailed explanation and visualization of the DTW technique, see Van der Does et al.25.

The DTW distance calculation involved creating a symmetric cost matrix for each of the up to 70 × 70 item combinations. To mitigate the potential disruptive effects of starting and endpoint mismatches, we interpolated five values between time points to ensure a more accurate distance calculation. The undirected DTW algorithm was then applied to identify the optimal path that minimized the total accumulated distance, resulting in the DTW distance. The algorithm was restricted to matching time points on the first variable to time points on the second variable that were simultaneous (t) one step ahead (t + 1) and one step backwards (t − 1) through a ‘Sakoe-Chiba’ window band of 1. The Sakoe-Chiba window constrains DTW by limiting how far time points can shift. In undirected DTW, it allows time points to stretch both forward and backward, whereas in directed DTW, it restricts stretching to only forward shifts. Other methods for constraining DTW include the asymmetric Itakura parallelogram and unconstrained DTW, which lacks any restrictions36. The Sakoe-Chiba window maintains consistent constraints throughout the alignment process, making it a preferred choice in many scenarios. It is often considered superior to the Itakura parallelogram37, and unconstrained DTW can lead to overfitting by producing unnatural alignments38. The default ‘symmetric2’ step pattern was used to match the sequences, giving both time series equal priority and allowing for diagonal steps through the cost matrix, though prioritizing horizontal or vertical steps36. The resulting distance was normalized based on the number of assessments within that individual. A lower distance indicated more similar dynamics between two time-series, signaling a higher similarity of fluctuations over time.

For each pair of variables, two distances were computed: one representing the distance from mood item A to mood item B, and another representing the distance from mood item A to the inverse of mood item B. We then selected the smallest absolute value among these two distances. This approach accounted for the presence of mood items either with a positive and negative valence in the dataset (see Supplementary Fig. 1). This analysis considered the possibility of both negative and positive feedback loops existing in the network, aiming to capture the complex interplay and dynamics among the variables. This process resulted in 376 symmetrical distance matrices, each representing an individual participant. These were combined to create a single overarching distance matrix (see Supplementary Table 1). We then fit a linear model to evaluate how strongly the two variables under study influenced the DTW distance, adjusted for the variance in item-scores within each participant.

The resulting undirected network plot illustrated the dynamic interactions between the 20 mood items. Edges were included if the distance between two items was significantly smaller (p < 0.05) than the average of all remaining distances, after adjusting for the variance of the scores of both items over time for each of the participants. This adjustment accounted for the inflated clustering of scores that remained zero or constant throughout follow-up. We performed a hierarchical cluster analysis using the "Ward. D2" clustering method to identify clusters of mood items exhibiting similar dynamic patterns, reflected in the color-coding of nodes in the network. The primary objective was to group items within the same dimension while maximizing dissimilarity between items from different dimensions. The thickness and color intensity of the edges in the plot corresponded to the strength of association between two items, while thinner and lighter-colored edges represented weaker associations.

Directed analyses
The temporal Multi-Level Vector AutoRegression model

The “mlVAR” package can also yield a time series network, the “temporal” network. When using this package, one has to decide what lag to include in the model. Commonly, a lag-1 model is used, meaning that the model assesses to what extent the score on an item is predicted by other items and itself one time-lag in the past. The autoregressive effects have been removed from this model, to increase legibility of the plot, and comparability with the directed DTW network. For a figure that includes the autoregressive effect, see Supplementary Fig. 2.

Directed Dynamic Time Warping

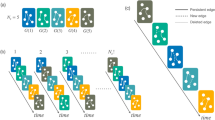
The directed analyses of variables focused on assessing the direction of fluctuations in items, or what changes in item scores tended to precede changes in other item scores. We utilized the same DTW algorithm as in the undirected analyses but with an asymmetric time window, as a variation of the Sakoe-Chiba band. This band restricted the dynamic alignment between items to the current (t) and the next time point (t + 1) (see Fig. 1).

To determine the direction of the relationship between mood item A and mood item B, we calculated the distance from item A to B (Fig. 1, panels A, C) and the distance from mood item B to mood item A [Fig. 1, panels B, D]. The difference was divided by sum of both distances which yielded the relative distances from B to A and from A to B. This procedure was repeated for the inverse of mood item B, again to account for the presence of both positive and negative valence of mood items in the dataset [see Supplementary Fig. 1]. This resulted in two distance matrices per participant, one for the positive associations between items and one for the inverse associations between items. We calculated the group-level directed network plot by testing whether the positive or inverse time-lag association was significantly different from zero. In the directed network plot, statistically significant directed edges were represented by arrows, with the arrowhead pointing in the temporal direction. If the D was not significantly different from 0, no arrow was included in the plot. A positive value of D indicated a positive feedback effect, represented by a green arrow from mood item A to mood item B. Conversely, a negative value of D indicated an inverse feedback effect (e.g., when A increases B tends to decrease one timepoint later), and a red arrow from A to B was included. To assess the centrality of each item, we utilized standardized measures of temporal lead and temporal lag. Temporal lead reflects the number and strength of outgoing arrows, with significant temporal lead indicating that fluctuations in this item tended to precede that of other items. Conversely, the temporal lag reflected the number and strengths of incoming arrows, with significant temporal lag indicating that changes in the item followed changes in other items.

Fig. 1
figure 1

The calculation of the directed DTW distance between the time-series data of two symptom items. The directed DTW distance between items “5” and “20, over 14 time points, is calculated both for the scenario where fluctuations in item 20 tend to precede fluctuations in item 5 (panel A) and the scenario where fluctuations in item 5 tend to precede fluctuations in item 20 (panel B). The first step in DTW is creating local cost matrices (LCM), which in this case have 14 × 14 dimensions (panels C and D). In the second step, the DTW algorithm finds the path that optimizes the alignment between the two time series by iteratively stepping through the LCM, starting at the lower left corner and finishing at the upper right corner, while aggregating the total distance (i.e., "cost’). At each step, the algorithm takes the step in the direction in which the cost increases the least under the chosen constraint. The constraint was the Sakoe–Chiba window of size one, meaning one time-point after the current assessment. The way in which the algorithm traverses through the LCM is dictated by the chosen step pattern, in this case the default “symmetric2” step pattern (F). Panels (E) and (F) explain the calculations of DTW distances in both directions for the symptom pair, yielding 6 and 12 as their respective distances. On the basis of this lower directed DTW distance we can conclude that fluctuations in item 20 tend to precede fluctuations in item 5, more than the other way around.

Full size image
Simulated datasets

We conducted simulations using nine datasets, each consisting of 200 participants and 200 measurement points, to identify any spurious, missing, or distorted connections introduced by the statistical models. These simulated datasets were designed to have strong predetermined associations, and included random noise with a range of [− 0.2 to 0.2] to approximate real-world measurements. No repetitions were included in the analyses, as these were not expected to yield different results. The aim of our simulation analysis was to evaluate whether the mlVAR and DTW algorithms accurately detected the known associations explicitly embedded in the data, rather than to infer or assess the underlying relationships within the dataset. The datasets each included two, three or four variables. Additionally, we manipulated the presence and number of variables with changes preceding variations in collider variables, allowing us to examine the potential bias introduced by colliders. Finally, we varied the lag in the co-variation of variables, including scenarios with a perfect lag-1, partial lag-1 (50% perfect lag-1 and 50% lag-0), or partial lag-2. By systematically manipulating the number of variables, the presence of colliders, and the lag in co-variation, we aimed to gain insights into any differences between the directed networks obtained from the mlVAR and DTW algorithms. The sample code is given in the supplementary file and on online Open Science Framework via https://osf.io/sample_code.

All statistical analyses were performed using R version 4.2.239, using the packages “dtw” (version 1.23–1), “parallelDist” (version 0.2.6), “mlVAR” (version 0.5) and “qgraph” (version 1.9.3).

Results

Sample characteristics

The final study sample consisted of 376 participants; 347 original participants and 29 from the sibling cohort. The participants’ mean age was 49.3 (SD = 12.7), and 242 were female (64.4%). 99 participants (26.3%) had a current diagnosis of anxiety and/or depression. Specifically, 29 (7.7%) participants were currently experiencing depression, 38 (10.1%) had a current anxiety disorder, and 32 (8.5%) had a current comorbid anxiety and depression diagnosis. The mean number of assessments per participant was 65.0 (SD = 5.0).

Undirected analyses

In the undirected DTW network (Fig. 2, panel A), we observed stronger positive connections among the items in the Positive Affect cluster compared to the mlVAR networks. Additionally, there were strong relationships between some negative items, for instance the relationships of the item Irritated with the items Nervous and Down, and the relationship between the items Upset and Anxious. For the undirected DTW distance matrix, see Supplementary Table 1.

Fig. 2
figure 2

The undirected DTW network, and the mlVAR contemporaneous and between-subjects networks.

Full size image

The mlVAR contemporaneous network (Fig. 2, panel B) revealed a higher number of stronger negative edges, particularly between the Positive Affect cluster and both the Negative Affect and Somatic clusters. This indicates that, within the same measurement period, stronger negative moods were associated with weaker positive mood items, as one might expect. Additionally, the strongest connections in this network were the negative associations between Tired and Energetic, Tense and Relaxed, and Tense and Calm, reflecting mood states that are intuitively indeed unlikely to occur simultaneously.

The mlVAR between-subjects network revealed several strong positive connections that were either absent or much weaker in the DTW network. These connections included associations between Physical Discomfort and Tired, Worried and Down, and Anxious and Nervous.

Directed Analyses

The mlVAR network displayed a larger total number of connections compared to the DTW network (see Fig. 3, panels A and B). However, some of the connections that were particularly important in the DTW network were weak or missing in the mlVAR network. For instance, the edges between Energetic and Satisfied and Enthusiastic and Satisfied were prominently present in the DTW network, but appeared less strong in the mlVAR network. Furthermore, some of the prominent edges of the mlVAR network were not present in the DTW network, like the edges between Physical Discomfort and Tired, and Worried and Nervous. Notably, we removed autoregressive effects from the model in the mlVAR network in Fig. 3, to enhance visual comparability to the directed DTW network. We have included an mlVAR network that includes these autoregressive effects in Supplementary Fig. 2. In this figure (Supplementary Fig. 2, panel C), the connections between mood items within the mlVAR network appear less strong than when the autoregressive effects are omitted, but the structure of the network is very similar (Supplementary Fig. 2, panel B). Therefore, the differences with the DTW network (Supplementary Fig. 2, panel A) cannot be explained by the removal of the autoregressive effects. This is to be expected, as the algorithms measure different types of relationships between mood items.

Fig. 3
figure 3

The directed DTW and temporal mlVAR mood item networks. The DTW networks’ temporal lag and temporal lead, and the mlVAR network’s in- and out-strength centrality are displayed in corresponding bar graphs. Autoregressive effects were removed from the mlVAR network to facilitate comparison.

Full size image

Centrality profiles of the mood items differed for the DTW and mlVAR networks (see Fig. 3, panels C and D). In the DTW network, we observed the highest temporal lag for the items “I feel satisfied” from the positive affect cluster and “I feel worried” and “I feel nervous” from the negatively valanced items. This indicates that fluctuations in these variables tended to follow fluctuations in other variables, for instance suggesting that changes in feelings of satisfaction may, to some extent, be influenced by the dynamics of other variables. The items for which we observed the strongest temporal lead, indicating that fluctuations in these variables tended to precede fluctuations in other variables, were “I feel tired”, and “I feel energetic”. These nodes may exert influence over other nodes within the DTW network, although this potential interdependence has not been adjusted for confounding factors. For the directed DTW distance matrix, see Supplementary Table 2.

In the mlVAR temporal network, the items with the highest in-strength were “I feel energetic” and “I feel satisfied”. As was the case in the DTW network, this indicates that satisfaction may be influenced by other mood items. The highest out-strength was observed in the item “I feel down”, reflecting the highest direct predictive value when relationships with the other variables included in the network were controlled for. When interpreted through Granger causality40, this item may play an important role in driving changes within the network.

Simulated datasets

In the simulated dataset, the results or the mlVAR and DTW analyses were identical when a complete lag-1 was simulated. This means that all fluctuations in items consistently preceded or followed fluctuations in other items with a time lag of exactly one time point. However, when a partial lag was introduced, meaning that the co-variation was not strictly lag-1 but also included instantaneous (lag-0) effects, spurious connections emerged in the mlVAR network when collider variables were present. These spurious connections indicated associations between items that were not actually present in the underlying data. Furthermore, when the algorithms were tested with a lag-window of 2, the mlVAR network no longer reflected the lag-1 associations within the network. On the other hand, using the DTW algorithm allowed for incorporating both the lag-1 and lag-2 time windows in a single analysis, still revealing the lag-1 relationship that was present in the data.

The results demonstrate that the DTW algorithm correctly identified the associations that were present in the simulated data, regardless of the lag in item fluctuations. In contrast, the mlVAR models produced spurious or distorted connections when the lag in item fluctuations was not complete (see Fig. 4). Furthermore, the standard mlVAR algorithm was not able to simultaneously reflect multiple time lag effects without mathematical extensions of the model.

Fig. 4
figure 4

Comparing the associations found between variables using the mlVAR and DTW algorithms and simulated data. Datasets were simulated with variations in the number of variables, the presence of colliders, time lag, and completeness of the time lag.

Full size image

Discussion

In this study, we aimed to compare the advantages and disadvantages of the innovative DTW technique with the more conventional mlVAR method for constructing undirected and directed mood item networks. Direct comparisons between the networks are challenging, as the mlVAR and DTW algorithms capture different underlying effects, and differences are thus to be expected. The undirected mlVAR networks aim to capture the associations between variables that occur simultaneously (contemporaneous), and associations across individuals (between-subjects). Visual inspection of the undirected DTW network and the contemporaneous mlVAR network shows that basing conclusions about connections within the networks on shape-based alignment of the time-series data, as in DTW, would lead to very different conclusions than when using the mlVAR contemporaneous network, which captures same-time associations, or the mlVAR between-subjects network, that aims to capture stable properties across subjects. Notably, even though in mlVAR networks the connections are partial correlations and could reasonably be expected to be sparser due to controlling for within-network confounding41, the DTW connections appear overall less strong. When looking at the undirected DTW network, there seems to be stronger time-lagged co-fluctuation among positive mood items, and less association between positive and negative mood items compared to the contemporaneous network. The disparities within the directed networks based on DTW and mlVAR raise more significant concerns, as interpretations regarding the directional influence and importance of symptoms or other items that would likely emerge from these networks stand in substantial contrast. Subsequent analyses conducted on simulated datasets unveiled the mlVAR technique’s susceptibility to introducing spurious and distorted connections within networks of interrelated items, especially those with complex interrelationships.

Although the connections present in the mlVAR and DTW networks could not be directly compared as they reflect different types of relationships, in certain conditions often present in real-world psychological data the mlVAR network may be more prone to reflecting spurious connections. In the evolving field of network analysis in psychopathology, there is no current consensus on how the symptom networks based on EMA data are best modelled. The use of diverse statistical techniques may yield vastly different interpretations of the importance of symptom nodes42. Therefore, clinical decisions based on these networks may be heavily influenced by the statistical decisions made in the construction of the algorithm. The directed DTW and temporal mlVAR networks exhibited numerous dissimilarities, apparent in their graphical representations and in- and out-strength profiles. For instance, the mlVAR network suggested “I feel down” as the most influential item due to its high out-strength. Interpreting this finding through Granger causality40 implies that fluctuations in this symptom may have a relatively large effect on other symptoms in the network, and therefore may be interpreted as an important target for treatment42. However, in the directed DTW network this item had low temporal lead, and energy-related items “I feel tired” and “I feel energetic” had the highest temporal lead. Therefore, the algorithm used to analyze the data and generate the network could result in significant differences in interpretation of the importance of the mood items. An important caveat of the literature on mlVAR is that it relies on Granger causality, which offers limited evidence for true causality43. Also, this form of causality cannot be inferred from DTW analyses due to the lack of conditioning on other relationships. This limitation could be addressed in the future with techniques like Convergent Cross-Mapping44, which aims to detect causality in complex systems by assessing whether one time series can reliably predict another.

To evaluate algorithm performance, we conducted analyses on simulated datasets, systematically varying the number of variables, colliders, and time lags in symptom covariation. Simulated data, in which the associations were predetermined, allowed us to reliably identify spurious or distorted connections. These simulations highlighted the mlVAR algorithm’s vulnerability to generating spurious or distorted connections when incomplete lags and colliders were present. This is an important finding, as psychological processes often involve complex relationships and items with construct overlap. Therefore, varying time lags and colliders are likely to occur. Drawing erroneous conclusions about the directionality and importance of symptom effects may be consequential in the choice of targets for treatment. On the basis of our results, we urge caution in the interpretation of temporal mlVAR networks in case of nodes with significant construct overlap and high intercorrelation. The directed DTW network could offer a promising alternative, although this technique has some significant downsides that we will also discuss in this paper.

A key distinction between the undirected DTW and mlVAR techniques lies in their approach to handling potential non-ergodicity within the data. The DTW technique initially computes within-person dynamics, and subsequently aggregates these in the network8,24,25,26,27,28. Conversely, the mlVAR method generates two separate networks – a contemporaneous (within-measurement) network and a between-subjects network12. This makes the networks based on the different algorithms difficult to directly compare. Another substantial difference between the approaches is that undirected mlVAR is based on partial correlations and the directed mlVAR on multivariate regression, while the DTW algorithm is a bivariate technique. In the mlVAR network, all connections between symptoms are conditional on all other connections within the network35. This means that the network structure changes depending on the variables measured and decisions made by the researchers on inclusion or omission of variables within the network. In contrast, because of the bivariate nature of the DTW algorithm connections in this network are independent of the absence or presence of other variables. However, this also presents some potential downsides, as the DTW algorithm’s ability to capture complex relationships between multiple variables in a network may be hampered. For example, if A leads to B and B leads to C, there will also be an edge between A and C using DTW, which may not be present in mlVAR. Although this makes the network robust against variable selection bias, it is vulnerable to associations between nodes that could be explained by associations with other variables in the network. Furthermore, the aggregate temporal lead and lag in the directed DTW analysis does not provide meaningful insights into the network. Since the relationships between variables are not conditioned on one another, the total lead or lag of a network increases as more variables are included.

A limitation of the calculation of the significance of edges in undirected DTW networks is that it is dependent on the average value of the other edges, meaning that introducing or removing variables can affect this average. Furthermore, in very unusual cases where the time lags between variables are uniform but non-zero, the network may yield no significant connections.

A limitation of the directed DTW technique is that it is not able to capture autoregressive effects, which reflect how the value of a mood item predicts its own future value12. Namely, the DTW distance between the time-series measurement of a variable and itself is always zero. In the current study, we also removed autoregressive effects from the temporal mlVAR network to enhance comparability with the directed DTW network. Including autoregressive effects may provide valuable insights into the dynamics of the network, as the persistence of certain symptoms over time may point to their clinical importance42. To address this, we included a Supplementary Fig. 2 comparing the mlVAR networks with and without these autoregressive effects. This figure shows that the differences in the networks are not artifacts of removing these autoregressive effects from the mlVAR analysis.

We believe that this study makes a substantial contribution to the existing network literature, as it is the first to compare the novel DTW technique to the more conventional mlVAR method of modelling EMA networks. It included a large and varied sample of participants with current or remitted psychopathology and healthy controls, and a high number of measurements per participant. The EMA method used in this study is especially useful in the collection of data for personalized networks, as it is able to generate a large amount of data at a low cost to the patient or participant. The high number of measurement points facilitates mapping a nuanced image of short-term interplay between mood states. Nevertheless, the DTW technique may also outperform mlVAR in analyzing sparse panel data. The mlVAR approach is not suitable for sparse data as it is susceptible to Nickell’s bias, meaning that when fewer than 20 to 60 measurement points are included, more spurious autoregressive connections could be introduced in the network12. Therefore, the DTW technique could for instance provide significant advantages for the study of serious psychiatric disorders or geriatric psychiatry, as research participants may be unable to complete extensive numbers of assessments45. Our use of simulated datasets to evaluate the DTW and mlVAR algorithms provides important insights for future research into understanding psychiatric disorders as complex dynamic systems. This study represents another step towards the clinical applicability of network theory in research, clinical practice, and personalized care.

Conclusion

We have demonstrated that the temporal mlVAR technique, while offering some theoretical advantages over the DTW algorithm, exhibits a vulnerability to introducing spurious and distorted connections in the network representation of psychological processes. The DTW network’s resilience to colliders, varying time lags and variable selection bias and non-stationarity underscore its potential as a more stable alternative to mlVAR networks.