Introduction

Various constitutive and strength models have been developed to characterize geomaterials’ mechanical and deformation behavior, ensuring safety in construction and health in health operations in geotechnical engineering1. Model parameters are essential to the constitutive model, and their scientific and reasonable determination is essential for geotechnical engineering. Laboratory tests are essential for determining model parameters and have been widely used. However, determining model parameters is challenging due to geomaterials’ complex and unclear failure mechanism. The hardening soil (HS) model is excellent for capturing the mechanical behavior and failure mechanism of soil, and it has received more attention with the development of Plaxis software. A total of 10 model parameters are required in the HS model. The performance of the HS model depends on the model parameters. Meanwhile, the laboratory test also provides an excellent way to determine the model parameters based on the soil mechanics and strength theory. Unfortunately, it is still challenging to determine the model parameters of the HS model due to the complex mechanical behavior of soil.

Various methods have been developed to determine the soil model parameters based on laboratory and in-situ tests. The back analysis provides an excellent tool to determine the constitutive parameters of geomaterial and has been widely applied in practical geotechnical engineering 2,3,4,5,6,7. Numerical simulation and field monitoring data are essential components of back analysis. Numerical simulation is time-consuming for practical geotechnical projects, and the field monitoring data is challenging to obtain and requires a lot of financial resources and workforce. Meanwhile, in-situ monitoring data contains much noise, directly affecting the precision and effect of back analysis. With the development of soil mechanics and its laboratory test instrument, much data is provided for the scientific characterization of soil mechanical behavior. The laboratory test is easy to control, has high data accuracy, and low cost. Laboratory tests provide a feasible way to scientifically determine soil mechanics parameters. A free tool has been developed to calibrate and determine the model parameters8. Qian et al.9 developed an intelligent algorithm to calibrate soil parameters by combining the neural network and Latin hypercube sampling9. Schanz et al.10 developed a procedure to determine the material parameters of the HS model10. Surarak et al.11 developed a method to determine the stiffness and strength parameters based on the HS model and the comprehensive oedometer and triaxial test data11. Wu and Tung12 presented a framework to determine the model parameters of the HS model based on the triaxial compression tests12. Sukkarak et al.13 proposed a procedure to determine the strength and stiffness parameters of rockfill materials for characterizing the behavior of rockfill materials based on triaxial and oedometer test results using the HS model13. Honkanadavar and Sharma14 predicted the HS model parameters based on uncompacted void content, uniaxial compressive strength, relative density, and material strength parameters14. The laboratory tests describe and characterize the mechanical behavior of soil well and provide sufficient data. Due to the complexity of soil mechanics behavior, traditional mechanics and mathematical methods study and determine the constitutive model and its parameters based on many assumptions. This results in complex mechanical behaviors and failure mechanisms that are difficult to characterize and describe accurately. It is essential to use and mine fully the soil mechanics model behind the test data to determine the soil mechanics model and its parameters. Recently, optimal technology has provided an excellent tool for searching the model parameters and calibrating the model in geomechanics15,16,17,18,19,20,21.

Optimal technology is essential to search the geotechnical parameters and calibrate the constitutive model in geotechnical engineering. The mathematical regression method was utilized to determine the parameters of the Hoek–Brown failure criterion22,23,24. The simplex reflection method was adopted to search the model parameters based on the laboratory test25. The multiple regression method was utilized to determine the strength parameters of the Hoek–Brown model26. Due to the complexity and nonlinearity of the soil mechanics constitutive model, the traditional optimization algorithm has problems of local optimization and premature convergence in the practical engineering field and depends on gradient information. Meanwhile, the deterministic optimization algorithm has disadvantages, such as poor solution stability, dependence on initial values, and proneness to locally minimal solutions. With the development of intelligent optimization technology, the soft computing method provides an excellent optimal method for determining the parameters of the model27. Levasseur et al.28 applied the genetic algorithm to identify the constitutive parameters of the Mohr–Coulomb model based on the field geotechnical measurements28. Zhao and Yin29 proposed a back analysis procedure to estimate the geomechanical parameters based on the support vector machine surrogated model using particle swarm optimization29. Mendez et al. 30 proposed an optimization framework to calibrate von Wolffersdorff’s constitutive law based on genetic algorithms 30. Samarajiva et al.31 applied a genetic algorithm to calibrate the soil constitutive models31. Jin et al.32 developed a novel optimization-based dynamically intelligent model selection procedure for the soil model based on the observations measured during staged excavation32. Artificial Bee Colony was applied to search the geomechanical parameters based on the support vector machine-based surrogated model 33,34. Particle swarm optimization was utilized to calibrate the soil model parameters35. Vardakos et al.36 adopted the differential evolution genetic algorithm to identify the geomechanical parameters for the geotechnical model36. In order to avoid trapping the local minimum of the optimal problem, this study employed simplicial homology global optimization (SHGO) to determine stiffness and strength parameters for the hardening soil model based on the triaxial compressive test. SHGO is a general-purpose global optimization algorithm based on applications of simplicial integral homology and combinatorial topology37.

In this study, a novel model parameters determination framework was developed by combining SHGO and triaxial compressive test. The triaxial compressive test was utilized to characterize the mechanical behavior and generated the data for SHGO. SHGO was utilized to search the model parameters by fully characterizing triaxial compressive test. The remainder of this study is organized as follows: the hardening soil model was introduced briefly in Section "Hardening soil model". The SHGO model and the developed method were presented in Section "SHGO-based endres framework for hardening soil model". A numerical example was used to verify and illustrate the developed method in Section "Verification". The developed method was applied to a triaxial compression test to determine the model parameters for the HS model in Section "Application". Finally, the conclusions of this study are summarized in Section "Conclusions".

Hardening soil model

The hardened soil (HS) model, which characterizes well the mechanical behavior of soil except for hysteretic or cyclic flow, is an elastic–plastic second-order hyperbolic isotropic model proposed by Schanz et al.10 (Fig. 1). In this model, the deformation calculation is divided into elastic strain and plastic strain. The hardened soil model consists of a set of mathematical equations describing the constitutive law of soil. The hardening is assumed to be isotropic, depending on the plastic shear and volumetric strains. A non-associated flow rule is adopted when related to frictional hardening, and an associated flow rule is assumed for the cap hardening. HS model assumes that the stress–strain relationship of the drainage triaxial test is a hyperbolic curve.

$$\varepsilon_{1} = \frac{q}{{E_{i} }}\frac{1}{{1 - {q \mathord{\left/ {\vphantom {q {q_{a} }}} \right. \kern-0pt} {q_{a} }}}}\begin{array}{*{20}c} {} & {} & {for\begin{array}{*{20}c} {} & q \\ \end{array} < q_{f} } \\ \end{array}$$
(1)

where ε1 is the axial strain, and q is the deviatoric stress. qf is the ultimate deviatoric stress. qa and Ei are the asymptotic value and the initial stiffness, respectively.

$$E_{i} = \frac{{2E_{50} }}{{2 - R_{f} }}$$
(2)
$$q_{f} = \frac{{2c\cos (\varphi ) + 2\sigma_{3} \cos (\varphi )}}{1 - \sin (\varphi )}$$
(3)
$$q_{a} = \frac{{q_{f} }}{{R_{f} }}$$
(4)

where c and φ are soil cohesion and friction angle, σ3 is the confining pressure of the triaxial test. m is the stress dependent-stiffness according to a power law. Rf is the failure ratio. E50 is the confining stress-dependent stiffness modulus for primary loading and is used instead of the initial modulus Ei for small strain. It is difficult to determine experimentally and can be determined as follows:

$$E_{50} = E_{50}^{ref} \left( {\frac{{c\cos (\varphi ) - \sigma_{s} \sin (\varphi )}}{{c\cos (\varphi ) + p^{ref} \sin (\varphi )}}} \right)^{m}$$
(5)
Fig. 1
figure 1

Stress–strain relationship of triaxial test for the hardening soil model.

Full size image

E50ref is the stiffness modulus from primary deviatoric loading. pf is the stress reference.

The model parameters of HS model can be determined based on a set of the conventional triaxial compression tests on soil specimen. In this study, the cohesion (c), friction angle of soil (φ), a power law (m). the failure ratio (Rf), and the stiffness modulus from primary deviatoric loading (E50ref) were determined based on SHGO and triaxial test.

SHGO-based endres framework for hardening soil model

The model parameters of the HS model are essential to characterize the mechanical behavior of soil based on the test data. Optimal technology provides a good way to determine it based on the HS model and test. This study developed a SHGO-based calibration framework to determine the model parameters for the hardening soil model (Fig. 2). The triaxial compressive test was leveraged to generate the strain and stress data during loading. SHGO was employed to search the model parameters based on the objective function, which describes the difference between the stress–strain relationship obtained by the experiment and the stress–strain relationship under the corresponding state.

Fig.2
figure 2

The concept of calibration HS model using optimal technology.

Full size image

SHGO

The simplicial homology global optimization (SHGO) algorithm is a general-purpose global optimization algorithm based on applications of simplicial integral homology and combinatorial topology. SHGO approximates the homology groups of a complex built on a hypersurface homeomorphic to a complex on the objective function. This provides approximations of locally convex subdomains in the search space through Sperner’s lemma and is a useful visual tool for characterizing and efficiently solving higher-dimensional black and grey box optimization problems37. In this study, SHGO was employed to solve the optimization problem of slag-desulfurization gypsum-based alkali-activated materials composition.

Objective functions

In theory, the HS model characterizes the mechanical behavior of soil based on the relationship between the strain and deviatoric stress (Eq. 1). A strain–stress relationship curve can be obtained based on the triaxial compressive test, which really reflects the mechanical behavior of soil specimen. The strain–stress curve obtained by the test should be the same as the HS model. The calibration of the HS model is to search for a set of model parameters of the HS model to minimize the discrepancy between the strain–stress curve obtained by the test and that predicted by the HS model. In order to measure the discrepancy, Eq. (1) can be rewritten into the following form.

$$q = \frac{{\varepsilon_{1} E_{i} }}{{1 + {{\varepsilon_{1} E_{i} } \mathord{\left/ {\vphantom {{\varepsilon_{1} E_{i} } {q_{a} }}} \right. \kern-0pt} {q_{a} }}}}\begin{array}{*{20}c} {} & {} & {for\begin{array}{*{20}c} {} & q \\ \end{array} < q_{f} } \\ \end{array}$$
(6)

It was necessary to construct the objective function to implement SHGO. We define it as follows:

$$HS(X) = \sqrt {\sum\limits_{i = 1}^{n} {\frac{{\left( {q(X) - q_{i} } \right)^{{2}} }}{n}} }$$
(7)

where HS(X) is the objective function, q(X) denotes the deviatoric stress predicted by the HS model (Eq. 6) under the strain X. qi is the deviatoric stress obtained by the test under the strain X. n is the discrete number of the strain–stress curve.

Procedure of the developed framework

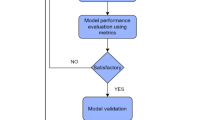
Laboratory tests have been widely used to characterize and predict soil mechanical behavior and its properties. Test data covers the critical information of the deformation and strength properties of soil. It is essential to evaluate and analyze the test data to characterize the soil properties. This study employed SHGO to determine the stiffness and strength parameters based on the triaxial test and HS model. Figure 3 shows a flowchart of the developed method for determining the model parameters, the procedure of which is as follows:

  • Step 1: Prepare the soil specimen and determine the test scheme.

  • Step 2: Implement a triaxial compressive test and record the strain and stress data.

  • Step 3: Construct the objective function for SHGO and determine the search range of the model parameters.

  • Step 4: Build the mechanical response model based on the HS model for soil.

  • Step 5: Call the SHGO algorithm to search the model parameters.

  • Step 6: Determine the HS model for engineering application.

Fig.3
figure 3

The flowchart of the developed framework.

Full size image

Verification

Results

Laboratory tests and the data obtained are widely used to analyze and characterize soil mechanical behavior, which is the basis of geotechnical engineering design, stability analysis, and safe construction. In order to verify and illustrate the developed framework, this study utilized a physical HS model (Eq. 1) to synthesize the test procedure and generate the vertical strain and deviatoric stress relationship of the triaxial compressive test. In order to generate test data, model parameters, i.e., the cohesion (c), friction angle of soil (φ), a power law (m), the failure ratio (Rf), and the stiffness modulus from primary deviatoric loading (E50ref), were listed in Table 1. The corresponding strain–stress relationship was obtained based on the HS model. Figure 4 shows the relationship between the axial strain and deviatoric stress based on the HS model.

Table 1 Comparison between the actual value and determined by SHGO.
Full size table
Fig.4
figure 4

The strain–stress relationship obtained by the HS model.

Full size image

Once the test data is obtained, the developed framework could be used to determine the stiffness and strength parameters of the HS model. Based on the strain and deviatoric stress curve in Fig. 4, the cohesion (c), friction angle of soil (φ), a power law (m), the failure ratio (Rf), and the stiffness modulus from primary deviatoric loading (E50ref) were determined based on all experimental group (all confining pressure) using the developed procedure in Sect. 3.3 and listed in Table 1. The results show that the maximum relative error is 6.16% for the failure rate Rf. The power law (m) is almost identical to the actual value. It proved that the developed framework could determine the model parameters well based on the test data. Figure 5 shows the strain–stress curve determined by the developed framework and its comparison with the actual curve obtained by the HS model. Obviously, the model parameters determined by the developed framework characterize the mechanical behavior of soil well based on the HS model. It further proved that the developed framework is feasible and scientific and can be used to determine the model parameters.

Fig.5
figure 5

The strain–stress curve determined by the developed framework and its comparison with the actual curve obtained by the HS model.

Full size image

In order to illustrate the performance of the developed framework, the deviatoric stress predicted by the model parameters obtained by the developed framework was compared with the test stress. Figure 6 shows the Taylor diagram of the deviatoric stress comparison. Obviously, the correlation coefficient is closer to 1 at different confining pressures, i.e., 20 kPa,50 kPa, and 100 kPa. The standard deviation and the root mean square error are less than 1 × 10–5 at different confining pressures. It proved again that the SHGO provides an excellent tool to search the model parameters for the constitute model, and the developed framework is feasible, helpful, and scientific in calibrating the soil model based on the laboratory test.

Fig.6
figure 6

The performance of the developed method.

Full size image

Discussions

The uniqueness of model parameter determination and performance of SHGO

In the developed framework, SHGO was selected as an optimal technology to determine the model parameters based on the HS model. Optimal technology is essential to the developed framework. In order to confirm the performance of SHGO, other optimal technologies were used to search the model parameter and compare it with the SHGO. Tables 2 and 3 lists the model parameters and the corresponding objective function value obtained by various optimal technologies. Figure 7 shows the strain–stress curve determined by the different optimal technology and their comparison with the test curve. The model parameters obtained by various methods differ significantly from the actual parameters, but the corresponding objective functions are almost close to 0. It shows that the determination of model parameters is a multi-extremum optimization problem, and the determination of model parameters is non-unique. However, multi-extremum optimization and non-uniqueness are challenging problems that hinder parameter determination and model calibration. Compared with other optimization techniques, the SHGO method can determine the model parameters well. It further proved that SHGO has good global optimization performance and has good adaptability to the complex, nonlinear, and non-unique problem of geomaterial mechanical parameter determination and model calibration.

Table 2 Comparison of the different optimal technology.
Full size table
Table 3 The objective function value based on various optimal technology.
Full size table
Fig.7
figure 7

The stress–strain curve based on the different optimal technology.

Full size image

The efficiency of the developed framework

Efficiency is another critical index essential to the developed framework for determining the model parameters based on laboratory tests. Figure 8 shows the running time at the different optimal technologies and their comparison. The gradient information is necessary for BFGS, L-BFGS-B, and the Nelder-mead method. Due to the complex and nonlinear soil mechanical behavior, it is difficult and even impossible to solve the model parameter determination and calibration using gradient-based traditional optical technology. Intelligent optimization methods, such as simulation annealing and differential evolution, etc., provide an excellent way to deal with the complex, nonlinear, and “black box” issue. This study utilized simulation annealing and differential evolution methods to determine the model parameters based on the developed framework. Figure 8 shows that simulation annealing and differential evolution methods are unable to find the correct model parameters, and the computational efficiency is far lower than that of SHGO. It once again proved the excellence of the SHGO.

Fig.8
figure 8

The running time comparison using the different optimal technology.

Full size image

The convergence

Convergence is essential to the determination of model parameters using the developed framework. In order to investigate the convergence of the developed framework, Fig. 9 shows the convergence property of the undermined model parameters and objective function. It proved that the developed framework has a good convergence. Figure 9a–e shows the variation process of the model parameters. It further proved the complexity of the strain–stress relationship. It shows that the developed framework has a good convergence.

Fig.9
figure 9

The running time comparison using the different optimal technology.

Full size image

Application

The soil specimen used in this test is the original silt in a foundation pit in Beijing, and the triaxial compression test is carried out38. The triaxial compression test adopts an automatic triaxial diagram, and the test method is a consolidation drainage shear test. Figure 10 shows the relationship between the deviational stress and axial strain with the confining pressure of 50 kPa, 100 kPa, and 200 kPa, respectively. Li et al.38 adopted the traditional method to select the model parameters based on the HS model and the corresponding parameters listed in Table 4. This study used the developed framework to determine the model parameters based on the triaxial compressive test. The model parameters obtained by the developed framework are also listed in Table 4. It shows that the model parameters obtained by the developed framework significantly differ from those obtained by traditional methods. In order to further verify the developed framework, two sets of model parameters were used to characterize the soil mechanical behavior based on the HS model. Figure 11 shows the strain-deviatoric stress relationship computed by the two sets of model parameters. The model parameters obtained by the developed framework produce a strain-deviatoric stress relationship closer to the test data than the traditional method. It concluded that the model parameters obtained by the developed framework could better characterize soil deformation and mechanical behavior based on the hardening soil model than those obtained by traditional methods. It also proved that SHGO demonstrates strong global optimization performance and merit in determining model parameters.

Fig.10
figure 10

The strain-deviatoric stress relationship of the triaxial compressive test.

Full size image
Table 4 Comparison between the actual value and determined by SHGO.
Full size table
Fig.11
figure 11

The stress–strain curve comparison between test and predicted by the developed framework.

Full size image

To further investigate the developed framework, the correlation coefficient, root square mean error, and standard deviation were utilized to evaluate the difference between the stress–strain curves of the test and the curves calculated using the HS model with the determined model parameters. Figure 12 shows the Taylor diagram of the performance of the developed framework. In each evaluation index, the developed framework outperforms the traditional one. Figures 13 and 14 show the convergence of the developed framework. Figure 13 shows that the developed framework convergences quickly. Figure 14a–d shows that the model parameters change dramatically when the objective function changes very little. It shows the complexity and nonlinear behavior of soil mechanics, and it also shows that SHGO has good global optimization performance and can avoid falling into the local optimal solution. Figure 14e displays the same pattern as the validation example in Section "Verification", providing full evidence of the proposed method’s stability and robustness. It shows that the developed framework can well mine the law and mechanism of soil mechanical behavior behind the test data. It concludes again that the developed framework is scientific, reasonable, and promising for determining the model parameter based on the laboratory test.

Fig.12
figure 12

The performance of the developed framework at the different confining pressures.

Full size image
Fig. 13
figure 13

The converge process of the developed framework.

Full size image
Fig. 14
figure 14

The running time comparison using the different optimal technologies.

Full size image

Conclusions

This study developed a SHGO-based model parameter determination framework to calibrate the HS model based on the triaxial compressive test. The triaxial compressive test generated the strain-deviatoric stress relationship, which characterizes the soil’s mechanical behavior. SHGO was utilized to determine the model parameters by minimizing the discrepancy of the strain-deviatoric stress curve between the test and that predicted based on the unknown model parameter using the HS model. A synthetic example was used to verify and illustrate the developed framework, which showed excellent performance in efficiency, global optimization ability, and solving non-uniqueness. Then, the developed was applied to an actual soil triaxial compressive test. The model parameters were determined based on the test stain-deviatoric stress curve, and soil mechanical behavior was well characterized. The following conclusions were drawn:

(1) Model parameters are essential to the corresponding soil mechanical model. This study developed an SHGO-based framework to determine the model parameter based on test data. The determined strain-deviatoric stress curve is in excellent agreement with the test curve. The developed framework provides an excellent way to calibrate the model and determine its parameters using optimal technology based on test data.

(2) Model calibration and parameter determination are complex problems with nonlinear, multi-extremum, and non-unique solutions. The developed method successfully avoids falling into local minimum solutions and can effectively solve non-unique problems. It provides a reliable way to describe and characterize the mechanical behavior of soil, offering a new way to calibrate the soil’s mechanical behavior and determine the model parameters.

(3) SHGO is an essential component of the developed framework, which shows excellent performance in terms of efficiency, global optimization performance, and convergence. Compared with traditional optimization techniques, SHGO is a scientific, reliable, and excellent optimization method that provides a new solution and tool for complex engineering problems such as geomechanics.

(4) The model parameters obtained by the developed framework can capture the mechanical behavior of soil wells. The HS model is only used to demonstrate the excellent performance of the developed framework, which has a good guiding significance and reference value for another complex model, such as stress or strain softening, which can lead to soil instability1 and similar issues. The developed framework provides a scientific, reliable, and promising method for geomaterials’ parameter determination and model calibration.