Introduction

Subjected to various geological activities, rock masses invariably comprise diverse discontinuities that divide intact rocks into segments, thereby contributing to the complexity of rock mass behaviours. Some discontinuities exhibit persistence, whereas some are intermittent. The regions of intact rocks between intermittent discontinuities, referred to as rock bridges, are widely distributed within rock masses. Therefore, a thorough understanding of rock bridges is crucial for comprehending rock mass behaviours.

Rock bridges have long been acknowledged for their pivotal roles in determining the mechanical properties of rock masses. Terzaghi1 laid the foundation for understanding rock bridges in resisting rockslides, highlighting their roles in concentrating stress and providing substantial bearing capacity. Exposed to natural events or human activities, intact rock bridges would gradually accumulate damage to rupture, interconnecting intermittent discontinuities and forming slip surfaces to trigger rockslides2,3,4,5,6. In addition to the rock slope stability analysis, rock bridges also interest researchers in other geotechnical domains, such as earthquakes7,8 and reinforcement in tunnelling9,10. With these developments, it is widely recognised that rock bridges offer crucial resistance against rock mass failure due to their considerably higher strength compared to discontinuities. For instance, Martin11 noted that the occurrence of less than 10% rock bridges could provide sufficient resistance along a potential failure surface for slopes more than 300 m high in moderately hard rock, Diederichs and Kaiser9 proved that the capacity of 1% rock bridges in hard rocks (unconfined compressive strength (UCS) > 200 MPa) matched the capacity of a single cable bolt at least.

In this context, numerous researchers have made positive contributions to understanding mechanical behaviours of rock bridges employing field investigation12,13, theoretical analysis6,14, laboratory test15,16, and numerical modelling17,18,19. Among these methods, direct shear tests have been considered a reasonable simplification benefitting from the consistency of boundary conditions with natural states20,21,22. As such, Lajtai21 carried out pioneering direct shear tests on rock bridges and found that tension gashes occurred first, followed by a connection of secondary cracks. Accordingly, fracture modes of rock bridges in direct shear were identified as tensile, shear, and crushing. Similar experimental and numerical investigations have been performed by a plethora of researchers, among them Wong et al.23 paid more attention to stress interactions between rock bridges considering stress field and superposition principles, Gehle and Kutter24 focused on rotation mechanisms of inclined rock bridges (expressed by en-échelon joints) and identified three shear phases; mechanical responses of overlapping rock bridges were experimentally and numerically characterised by Ghazvinian et al.25 and Sarfarazi et al.26, and they proved that macroscopic shear fractures were due to the accumulation of microscopic tensile breakages; Shang et al.19 numerically investigated mechanical behaviours of rock bridges, including shear stress–displacement relations, cracking processes, and influencing factors across different joint persistence (K) utilising discrete element method (DEM). It was found that the shear resistance provided by rock bridges increased with decreasing K. Moreover, recent research revealed that despite an invariant K, the mechanical properties of rock bridges deteriorated as their individual scales decreased27.

Despite prior inspirational understandings of rock bridges in direct shear, existing research primarily examines either individual or multiple rock bridges of uniform scale, leading to a poor constraint referring to diverse-scale rock bridges. Diverse-scale rock bridges are widespread in rock masses, for example, multiple diverse-scale rock bridges along the failure surface of the wedge rockslide in 1971 located in the left abutment of Libby Dam in northwestern Montana, USA (Fig. 1)28, two diverse-scale rock bridges inside Chamousset rock fall in 2007 at southern Vercors massif, French Alps29, two diverse-scale rock bridges within Staithes rock fall in the vicinity of North Yorkshire, UK30. Therefore, mechanical behaviours of diverse-scale rock bridges, such as mechanical properties, failure sequences, interaction patterns, and cracking processes, remain elusive and thus warrant further investigation. Additionally, handcrafted rock specimens containing diverse-scale rock bridges are difficult to fabricate, costly to produce, and allow for only limited experiments. Despite the prevalence of rock-like materials that may act as substitutes, their ratios of UCS to tensile strength are always significantly less than those of natural rocks31.

Fig. 1
figure 1

Schematic view of diverse-scale rock bridges in a rockslide. (a) Location of the wedge rockslide at the Libby Dam in 1971. The map was generated by QGIS 3.28.1, https://qgis.org/en/site. (b) Scar of the rockslide. (c) Conceptual model of rock bridges as inferred by Xue et al.28.

Full size image

To address this issue, herein we employed Universal Distinct Element Code (UDEC) to numerically investigate mechanical behaviours of diverse-scale rock bridges in direct shear. UDEC has been a feasible and cost-effective DEM-based software applied to the geotechnics domain, as it accommodates large displacements, rotations, sliding, and separation of elements32, enabling the simulation of progressive failure processes of rock bridges. Diverse-scale combinations of rock bridges were established and subjected to direct shear. In this process, mechanical properties, stress and displacement fields, cracking processes, and acoustic emission (AE) characteristics were monitored, focusing on interaction patterns between diverse-scale rock bridges.

The main objective of this paper is to numerically investigate mechanical behaviours of diverse-scale rock bridges in direct shear, with innovation revealing interaction patterns between rock bridges. Prototypes and modelling methodology are described first, followed by numerical results illustrating mechanical properties, stress and displacement fields, cracking processes, and AE characteristics. Accordingly, interaction patterns between rock bridges are observed, along with an examination of influencing factors and practical implications. Conclusions are given finally.

Method

Data collection

Rock mechanics tests on granites from Qingdao, Shandong Province, China, serve as prototypes. Granites were drilled as cylindrical specimens (diameter 50 mm × height 100 mm) and cut as rectangular specimens (length 200 mm × width 100 mm × height 100 mm). The cylindrical specimens were subjected to unconfined and confined compression until catastrophic failure, aiming to acquire mechanical properties of the granites, including Young's modulus, Poisson's ratio, UCS, cohesion, and internal friction angle, as shown in Table 1. The rectangular specimens were further prefabricated with two coplanar flaws with lengths of 75 mm, 50 mm, and 25 mm by a high-pressure water jet cutting machine. In other words, specimens containing rock bridges with lengths of 50 mm, 100 mm, and 150 mm were prepared (Fig. 2), corresponding to the K values of 0.75, 0.50, and 0.25, respectively. Then, these prefabricated specimens were subjected to direct shear loads to get shear strengths, as shown in Table 1. More experimental settings have been described in detail by Yang and Kulatilake31.

Table 1 Macroscopic mechanical properties acquired by laboratory tests and UDEC modelling, where K is joint persistence.
Full size table
Fig. 2
figure 2

Prototypes31 and the calibration of failure configurations between direct shear tests and simulations, where K is joint persistence. Experimental cracks are macroscopically characterised by black lines, while simulated cracks in UDEC are marked as blue (tensile) and red (shear) lines.

Full size image

UDEC modelling

Modelling algorithm

Based on discrete element method (DEM) principles, the commercial software named Universal Distinct Element Code (UDEC) has long been demonstrated as one of the most suitable approaches for modelling mechanical behaviours of rocks since it simulates a rock as an assemblage of rigid or deformable blocks connected by contacts. Forces and displacements of blocks and contacts can be calculated by specific constitutive laws. UDEC enables significant displacements along discontinuities and rotations of blocks utilising an explicit solution scheme, demonstrating its applicability for modelling mechanical behaviours of rock bridges. Therefore, UDEC 6.0 was employed to conduct simulations. Further algorithmic details about UDEC can be found in its manual (Itasca, 2014).

Parametric calibration

In accordance with the prototypes, numerical models were established with sizes of width 50 mm × height 100 mm in UDEC to reproduce the unconfined and confined compression tests. A numerical loading rate was set to 0.01 m/s, which has been proven to have less impact on failure modes and macroscopic properties33. On the other hand, three numerical models with a width of 200 mm and a height of 100 mm were generated first, followed by a cut of two coplanar flaws, according to the prototypes. In this way, numerical models containing rock bridges with lengths of 50 mm, 100 mm, and 150 mm were established. Then, consistent with the prototypes, lower boundaries were fixed, while a normal stress boundary of 4 MPa was applied to the upper boundaries until the maximum unbalanced force of numerical models was less than 10–3 N, implying that the models were statically stable. Finally, the normal stress boundary was kept constant, while a left loading rate of 0.01 m/s was added to the upper parts.

During the above processes of model establishment, division patterns applied to an initial block in UDEC determine the microscopic structure of rock models. One of the most popular division patterns is the grain-based models (GBMs), where blocks are generated as convex polygons employing a Voronoi tessellation technique, especially appropriate for modelling crystalline rocks such as granite34,35, though the determination of contact properties remains challenging. Furthermore, Gao and Stead33 integrated Voronoi tessellation into a Trigon logic framework, dividing convex polygons into triangle blocks. This approach offers a more realistic friction angle and failure modes with reduced mesh dependence. To enhance our focus on rock bridges, we refined the Trigon logic to ensure a linearly decreasing distribution of block sizes closer to the rock bridges.

After the establishment of numerical models, the next step is to calibrate modelling parameters in UDEC. We set gradient-based modelling parameters, including Young's modulus and Poisson's ratio of blocks, normal and shear stiffness of contacts, contact cohesion, contact friction angle, and contact tensile strength, which were input into the above numerical models to conduct simulations. In this way, mechanical properties, including Young's modulus, Poisson's ratio, UCS, cohesion, internal friction angle, and shear strength of numerical models with gradient-based modelling parameters, were acquired. Relationships between the mechanical properties of numerical models and modelling parameters were established. Building on this, the mechanical properties of the prototypes were input into these relationships to deduce predicted modelling parameters, which were further input into the above numerical models to conduct simulations again. Thereafter, numerical results were compared with experimental results. If discrepancies were observed, the corresponding predicted modelling parameters would be iteratively adjusted using a trial-and-error approach, and the simulations would be repeated until numerical results converge with experimental data. See Bu et al.32 for more details. In this study, experimental results from unconfined and confined compression tests and direct shear tests were used to calibrate modelling parameters, and calibrated modelling parameters are presented in Table 2. Based on the calibrated modelling parameters, numerical mechanical properties outlined in Table 1 were acquired, revealing consistency between simulations and tests in macroscopic properties.

Table 2 Calibrated modelling parameters in UDEC.
Full size table

Moreover, a comparison of failure configurations, as illustrated in Fig. 2, indicates that the roughness of failure surfaces increases with decreasing K, which is in line with the findings from the prototypes31. A minor distinction arises wherein the numerical failure configuration consists of multiple cracks, while the tested failure configuration manifests as several macroscopic cracks. This discrepancy stems from the limitations of visual resolution with the naked eye, which can only detect cracks wider than 0.05 mm normally. Therefore, microcracks in natural rocks always require auxiliary methods for observation, such as computed tomography (CT). In the numerical realm, cracks at any scale can theoretically be captured, resulting in the representation of more cracks than those visible to the naked eye. But this discrepancy would not prevent us from applying numerical models to represent rocks.

Model setup

Utilising the calibrated modelling parameters detailed in Table 2, numerical models employed to replicate prototype direct shear tests were expanded to include diverse-scale rock bridges while maintaining identical boundary conditions. Specifically, the length of rock bridge A (LA) (located near the shear loading end) was 25 mm, while the length of rock bridge B (LB) (situated away from the shear loading end) increased linearly from 5 to 75 mm in 5 mm increments. To mitigate other potential influencing factors as much as possible, distances from rock bridge A to the shear loading end, spacings between rock bridges A and B, and joint apertures were consistently set as 25 mm, 50 mm, and 3.50 mm, respectively. In this way, we designated the length ratio of rock bridge A to B (LA:LB) as the sole variable ranging from 1.0:0.2 to 1.0:3.0, as illustrated in Fig. 3.

Fig. 3
figure 3

Numerical models featuring diverse-scale rock bridges with LA:LB from 1.0:0.2 to 1.0:3.0, implemented by maintaining the length of rock bridge (A) (LA) as 25 mm while increasing the length of rock bridge (B) (LB) from 5 to 75 mm with an increment of 5 mm. Three AE monitoring points evenly distribute across each rock bridge.

Full size image

Monitoring schemes

In contrast to laboratory and field investigations, a notable advantage of numerical modelling is the visibility of the failure process of rock models. Here, we developed various FISH functions in UDEC to characterise stress and displacement fields. Stress fields can intuitively reveal stress concentrations, while displacement fields can effectively illustrate the transfer of internal displacement and cracking processes. Moreover, we calculated shear resistance by calculating reaction forces on the shear load end and determined averaged shear stress of rock bridges A and B by calculating the mean shear stress across all nodes within each respective rock bridge.

In addition to the above descriptive monitoring, a quantitative analysis is also necessary to further understand the mechanical behaviours of individual rock bridges. AE recording technique has been widely believed to be an effective method to reach this goal as it receives elastic waves radiated from fracturing events in a rock failure process and performs signal processing in the form of waveform analysis. Based on this principle, Bu et al.36 developed an AE simulation methodology by monitoring and analysing waveforms of element velocity, which performs consistency and compatibility with AE tests. We employed their methods in this research to provide simulated AE information of diverse-scale rock bridges. Three AE monitoring points were evenly distributed on each rock bridge to acquire AE parameters, including AE events and AE energy. Both parameters were normalised to facilitate a fair comparison of damage among diverse-scale rock bridges, accounting for varying distances from epicentres to receivers.

Results

Mechanical properties

Figure 4 illustrates load–displacement curves of numerical models featuring diverse-scale rock bridges. At LA:LB approaching 1.0:0.2, the load–displacement curves consistently manifest a unimodal pattern akin to that observed in laboratory tests on a solitary rock bridge, as evidenced by Lajtai37 and Luo et al.16. With increasing LB, the load–displacement curves gradually transit from unimodal to hump-shaped, concomitant with an increase in the second peak load. This transition agrees with experimental results by direct shear tests on specimens containing two equal-scale rock bridges38, attributed to the escalating shear resistance provided by the enlarged rock bridge B. Notably, there is a discernible upward trend in shear modulus as the LB increases, aligning with an observed increase in shear modulus with the extension of a solitary rock bridge, as highlighted by Zhang et al.39. This phenomenon likely stems from the decreased proportion of joint regions that do not contribute to the shear modulus40.

Fig. 4
figure 4

Load–displacement curves of numerical models featuring diverse-scale rock bridges.

Full size image

Furthermore, we conducted a statistical analysis to examine the fluctuation in peak shear resistance concerning LA:LB, as shown in Fig. 5. There is a perceptible positive correlation between peak shear resistance and LB. This correlation was anticipated, given the linear increase in the total rock bridge portion as LB increases. In other words, there is a fundamental linear correlation between peak shear resistance and joint persistence, consistent with previous investigations into a solitary rock bridge19,31.

Fig. 5
figure 5

Peak shear resistance versus LA:LB.

Full size image

Stress and displacement fields

Figure 6 illustrates shear stress (τxy) fields and displacement (d) fields at loading displacements of 0.20 mm, 0.53 mm, and 1.33 mm, corresponding to pre-peak, approximate peak, and post-peak stages, respectively, as indicated by the dotted lines in Fig. 4. It is evident that τxy and d exhibit uneven distribution at all stages, with a pronounced concentration observed particularly on rock bridges A and B.

Fig. 6
figure 6

Shear stress (τxy) and displacement (d) distribution of numerical rock models with diverse-scale rock bridges at loading displacements of 0.20 mm, 0.53 mm and 1.33 mm.

Full size image

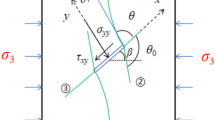
At the pre-peak stage, although the load–displacement curves (Fig. 4) indicate that the peak shear resistance of rock models has not yet been reached, there is already a significant τxy concentration at the left upper tips and right lower tips of rock bridges A and B. Additionally, negative τxy is conspicuously distributed at the left lower tips and right upper tips of rock bridge B. Previous studies on a solitary rock bridge subjected to direct shear have shown that this inclined τxy concentration distribution arises from the inclination of the major principal stress, σ1, resulting from the resultant of normal and shear stress24,41. This inclination of σ1 leads to distinct stress environments of compression and tension. Concerning the variation in τxy distribution with different LA:LB, it is noted that τxy concentration at rock bridge A exhibits negligible change, whereas that at rock bridge B diminishes with increasing LB. An intuitive explanation is the increased load-bearing area under a specific force. Some researchers have also attributed this reduction in τxy concentration to a decreased stress interaction between the joints25,39.

The irregularity in the d distribution, particularly noticeable at rock bridges A and B, signifies the suppression of displacement transmission during the pre-peak stage. Notably, the irregularity of d distribution follows an arc pattern, consistent with findings from previous research42,43. Specifically, this arc shape near rock bridge A is more prominent in the lower fixed part, while that near rock bridge B is more pronounced in the upper shear-loaded part. In addition, this arc shape is influenced by the abrupt variations of d field, which serve as clear indicators of the presence of fractures44. In this way, cracks initiating from the left tips of rock bridges and propagating along a curvilinear path are discernible. The analysis of τxy distribution indicates that these cracks occur in a tensile stress environment, known as tensile wing cracks, typically considered as the initial cracks arising from the tips of embedded joints in both unconfined compression and direct shear tests23,45. Furthermore, wing cracks near rock bridge A are more conspicuous compared to those near rock bridge B, given that the former aids in relieving the tensile stress of the rock model. Regarding the variation in d distribution with different LA:LB, d field of rock bridge A remains insensitive to LA:LB variations, while an increased scale of rock bridge B results in a smaller d field variation gradient at rock bridge B.

At a loading displacement of 0.53 mm, the irregularity in both τxy and d distribution becomes more pronounced, particularly for rock bridge B. As depicted in Fig. 4, all load–displacement curves of the 15 numerical models have surpassed their first peak, suggesting the potential rupture of one rock bridge. For rock bridge A, abrupt d field variations are evident across all 15 numerical models, with configurations extending from the left upper tips to the right lower tips of rock bridge A. In addition, τxy concentration at rock bridge A appears to be disordered due to the presence of multiple cracks, which are inclined at approximately 0° to 53° to the shearing direction. These phenomena appear to remain unaffected by alterations in LA:LB.

Furthermore, the load–displacement curves (Fig. 4) indicate that rock models with LA:LB ranging from 1.0:0.2 to 1.0:1.4 have reached their peak shear resistance, while others have not, suggesting that the former models may have already experienced macroscopic rupture, whereas the latter models remain highly resistant. For rock bridge B, abrupt variations in d field are evident for rock models with LA:LB from 1.0:0.2 to 1.0:0.8, displaying a step-path failure configuration extending from the left upper tips to the right lower tips. In the case of cracks observed in rock models with LA:LB from 1.0:1.0 to 1.0:3.0, two distinct crack sets initiating from the left tips of rock bridge B are observed: One set propagates towards the upper shear-loaded part at an angle of about 110° to the shearing direction, while the other set propagates towards the lower fixed part at an angle of approximately 30° to the shearing direction. For rock models with LA:LB of 1.0:0.2 and 1.0:0.4, τxy concentration at rock bridge B forms a continuous band. However, for rock models with LA:LB ranging from 1.0:0.6 to 1.0:3.0, τxy concentration is predominantly distributed at the left upper tips and the right lower tips of rock bridge B. The concentration at the right lower tips is notably stronger, independent of LA:LB. In addition, for rock models with LA:LB ranging from 1.0:0.2 and 1.0:1.4, several abrupt variations in the τxy field of rock bridge B are observed. In contrast, relatively smooth τxy concentration bands are evident for rock models with LA:LB from 1.0:0.6 to 1.0:3.0.

At a loading displacement of 1.33 mm, all load–displacement curves of the 15 numerical models have reached a relatively low-load and stable stage, indicative of the residual strength. d field undergoes abrupt variations at both rock bridges A and B, signalling the macroscopic rupture of both structures. A consistent failure configuration emerges from the left upper tips to the right lower tips of rock bridges.

Acoustic emission

Figure 7 illustrates the variation of averaged shear stress of the rock bridge A (\( \tau _{{{\text{xy}}}}^{{\text{A}}} \)) and B (\( \tau _{{{\text{xy}}}}^{{\text{B}}} \)), as well as AE characteristics (normalised AE events and cumulative AE energy), with loading displacements. The AE monitoring points at the centre of rock bridges serve as representative points for AE analyses. The maximum \( \tau _{{{\text{xy}}}}^{{\text{A}}} \) remains largely unchanged as LA is invariant, whereas the maximum \( \tau _{{{\text{xy}}}}^{{\text{B}}} \) generally decreases with increasing LB. This negative correlation may be attributed to the insensitivity of τxy concentration to LB, as shown in Fig. 6.

Fig. 7
figure 7

The variation of averaged shear stress of the rock bridge A (\( \tau _{{{\text{xy}}}}^{{\text{A}}} \)) and B (\( \tau _{{{\text{xy}}}}^{{\text{B}}} \)), as well as AE characteristics (normalised AE events and cumulative AE energy), with loading displacements. \( \tau _{{{\text{xy}}}}^{{\text{A}}} \)–displacement, \( \tau _{{{\text{xy}}}}^{{\text{B}}} \)–displacement, normalised AE events, and normalised cumulative AE energy are represented by red curves, blue curves, grey lines, and shaded regions, respectively.

Full size image

At the onset of shear loading, both \( \tau _{{{\text{xy}}}}^{{\text{A}}} \)– and \( \tau _{{{\text{xy}}}}^{{\text{B}}} \)–displacement curves increase in an approximately linear manner without any AE activities. Subsequently, they exhibit nonlinear increases with fluctuations corresponding to significant AE events and energy. Finally, curves reach peaks with a surge in AE activities, followed by a plunge and irregular AE parameters.

Discussion

Interaction pattern between diverse-scale rock bridges

For progressive failure of rocks, numerous studies have demonstrated a stress–strain relation consisting of five phases, namely, crack closure, elastic deformation, stable crack growth, unstable crack growth, and post-peak46,47,48, where volume-expansion point (VEP) is a division between stable and unstable crack growth, and peak-stress point (PSP) marks a moment of macroscopic rupture in rocks. Both appear essential in damage processes of rocks and are fundamental for physical predictions of rock failure6,49. For example, Xue et al.47,48,50 investigated the strain correlation between VEPs and PSPs through experimental and theoretical analysis, ultimately suggesting that VEP serves as a promising indicator for predicting lab-scale rock failure; moreover, they utilised the displacement relationship between VEPs and PSPs to analyse the accelerating creep on slopes, subsequently proposing a displacement criterion for predicting slope instability6. Specifically, rock bridges control the evolution of some rockslides, manifested as follows: Damage accumulates on rock bridges until they reach VEPs, resulting in a slope evolving to the onset of acceleration; with increasing damage, catastrophic failure occurs at rock bridges at PSPs, indicating the penetration of sliding surfaces and the initiation of rockslides. Accordingly, the clarification of relationships between VEPs and PSPs would enable the prediction of this kind of rockslide. To achieve this, one-dimension renormalisation group model and damage–constitutive model based on the Weibull distribution were employed, and the relationships between VEPs and PSPs were established.

Despite those positive contributions to the relationship between VEPs and PSPs, physical precursor patterns in progressive failure of multiple rock bridges remain elusive due to exclusive mechanical interactions among them. Several researchers have undertaken valuable investigations. For instance, Lei51 conducted experiments involving multiple asperities inserted into granite under confined compression to identify their rupture sequence. It was observed that the rupture of one asperity redistributes strain energy, accelerating stress concentration and causing damage to neighbouring asperities. Furthermore, Xue et al.6 and Chen et al.7 suggested that the rupture of one rock bridge initiated the VEP of the next rock bridge. Nevertheless, the applicability of these findings to diverse-scale rock bridges remains ambiguous.

To handle this concern, based on the numerical results, we conducted a statistical analysis of VEPs and PSPs in diverse-scale rock bridges. Previous research has discussed the feasibility of identifying VEPs and PSPs by AE characteristics, that is, a supra-exponential rise of AE activities at VEPs and a soaring of AE events at PSPs52. However, due to differences in specimen heterogeneity and the accompanying multiple clustering expansions of cracks, the number of AE events may experience multiple sharp increases. Therefore, identifying VEPs based solely on the surge in AE events is not entirely reliable. The identification of VEPs and PSPs should encompass a thorough consideration of τxy–displacement curves, AE events, and AE energy due to the following reasons: (1) τxy serves as an average index reflecting the stress state to some extent27, (2) the dense AE events observed at VEPs and PSPs may pose challenges in accurate quantification due to the inevitable deviation in waveform analysis53, and (3) AE events are often accompanied by varying levels of radiated energy54. In this context, we adopt a multi-indicator approach rather than relying on a single indicator to reduce uncertainty. VEPs were identified at the points of the maximum growth in AE events or energy during their progressive failure processes, while PSPs were determined by the plunge of τxy–displacement curves or the densest occurrence of AE activities.

Loading displacements at VEPs and PSPs of rock bridge A (\( d_{{{\text{VEP}}}}^{{\text{A}}} \) and \( d_{{{\text{PSP}}}}^{{\text{A}}} \)) and B (\( d_{{{\text{VEP}}}}^{{\text{B}}} \) and \( d_{{{\text{PSP}}}}^{{\text{B}}} \)) are depicted in Fig. 8. Both \( d_{{{\text{VEP}}}}^{{\text{A}}} \) and \( d_{{{\text{PSP}}}}^{{\text{A}}} \) exhibit minor fluctuations at 0.33 mm and 0.39 mm, respectively, attributed to the insensitivity of the mechanical behaviours of rock bridge A (\( \tau _{{{\text{xy}}}}^{{\text{A}}} \)–displacement curves, τxy fields, and d fields) to LA:LB, owing to its consistent scale and boundary conditions. For rock bridge B, both \( d_{{{\text{VEP}}}}^{{\text{B}}} \) and \( d_{{{\text{PSP}}}}^{{\text{B}}} \) display a piecewise linear relationship with LA:LB. Specifically, within the LA:LB ranging from 1.0:0.2 to 1.0:0.6, minimal changes are observed in both \( d_{{{\text{VEP}}}}^{{\text{B}}} \) and \( d_{{{\text{PSP}}}}^{{\text{B}}} \). In the range of LA:LB from 1.0:0.8 to 1.0:1.8 (shaded region in Fig. 8), \( d_{{{\text{VEP}}}}^{{\text{B}}} \) stabilises at approximately 0.44 mm, slightly lagging behind \( d_{{{\text{PSP}}}}^{{\text{A}}} \), while \( d_{{{\text{PSP}}}}^{{\text{B}}} \) exhibits a linear increase. Subsequently, within the LA:LB range of 1.0:2.0 to 1.0:3.0, both \( d_{{{\text{VEP}}}}^{{\text{B}}} \) and \( d_{{{\text{PSP}}}}^{{\text{B}}} \) demonstrate a nearly linear increase. What factors contribute to this piecewise linear relationship?

Fig. 8
figure 8

Loading displacements at volume-expansion points (VEPs) and peak-stress points (PSPs) of rock bridge A (\( d_{{{\text{VEP}}}}^{{\text{A}}} \) and \( d_{{{\text{PSP}}}}^{{\text{A}}} \)) and B (\( d_{{{\text{VEP}}}}^{{\text{B}}} \) and \( d_{{{\text{PSP}}}}^{{\text{B}}} \)). The shaded region represents an effective interaction range between rock bridges A and B.

Full size image

Within the LA:LB ranging from 1.0:0.2 to 1.0:0.6, \( d_{{{\text{VEP}}}}^{{\text{A}}} \) and \( d_{{{\text{VEP}}}}^{{\text{B}}} \) are relatively close, suggesting that the strain energy released by rock bridge A at VEPs may overwhelmingly affect the much smaller rock bridge B. In the range of LA:LB from 1.0:0.8 to 1.0:1.8, after the sequential occurrence of VEPs and PSPs of rock bridge A, the VEPs of rock bridge B occur rapidly. Specifically, the distance from \( d_{{{\text{PSP}}}}^{{\text{A}}} \) to\( d_{{{\text{PSP}}}}^{{\text{B}}} \) is relatively small, indicating that the rupture of rock bridge A at PSPs releases significant strain energy that rapidly transmits to rock bridge B, accelerating its subsequent damage to its VEPs. Subsequently, rock bridge B damages to PSPs with increasing shear load, ultimately leading to the failure of the numerical model. Within the LA:LB range of 1.0:2.0 to 1.0:3.0, rock bridge A is significantly smaller than B. Consequently, the rupture of rock bridge A does not significantly accelerate the damage of rock bridge B. In other words, rock bridge B behaves more independently in this scenario.

The observed interaction pattern in diverse-scale rock bridges can be summarised as follows: When their scales are dramatically different, mechanical behaviours of diverse-scale rock bridges are mainly dominated by the large one; on the contrary, the rupture of the rock bridge closer to the shear loading end expedites damage in the one farther away the shear loading end towards its VEPs.

Influence of rotation of confining pressure plate on the interaction pattern

The precise determination of the piecewise boundary of the grey region in Fig. 8 may have some potential error sources. Figures 6 and 7 demonstrate that rock bridge B consistently exhibits higher τxy values compared to rock bridge A during approximate peak and post-peak stages, owing to inherent characteristics of direct shear. Figure 9 depicts the variation of normal displacement (dyy) fields with loading displacements for the rock model with LA:LB of 1.0:1.0. The dyy at the upper shear-loaded part above rock bridge A significantly exceeds that above rock bridge B, particularly after the rupture of rock bridge A (loading displacement = 0.42 mm). Furthermore, dyy field exhibits an abrupt variation at rock bridge A, whereas the variation is less distinct at rock bridge B. With increasing loading displacement, the dyy field stabilises, as observed after the numerical model failure at a loading displacement of 0.54 mm. This suggests that rock bridge A fails predominantly in tension, whereas rock bridge B primarily fails in shear. Accurate determination of the number and mechanisms of cracks remains highly uncertain, attributable to multiple factors such as the uncertainty in the fractured region that is larger than rock bridges, as observed in Fig. 6, and the ambiguity of waveform analysis in defining tensile–shear boundaries55.

Fig. 9
figure 9

Normal displacement (dyy) distribution in the failure process with loading displacements from 0.07 mm to 1.26 mm.

Full size image

Numerous researchers have already noticed this non-uniform dyy distribution in direct shear56,57, despite direct shear tests being considered a viable method to study rock bridges since the 1960s21,22,23. Dang et al.58 attribute these non-uniform responses to specimen rotation and inhomogeneous stress fields, both closely linked to external boundaries. When the lower part is fixed and subjected to constant normal pressure and compressive force from one side, inevitable moments cause inclination or even rotation of the upper shear-loaded part. In our research, normal stress is maintained as a constant, while the displacement of the loading plate is allowed. With increasing shear load, the upper part would rotate clockwise, resulting in higher dyy values above rock bridge A compared to those above rock bridge B.

Limitations and future works

In this study, simulated diverse-scale rock bridges were subjected to direct shear in 2D, bringing limitations in maintaining consistency with the 3D physical prototypes, although the investigations at the 2D level might theoretically appear compatible in 3D and could save computational resources. Additionally, the main objective is to investigate diverse-scale rock bridges; thus, the scale ratio was set as the sole variable. Building on this, interaction patterns between rock bridges were found. The secondary variables, such as heterogeneity, confining pressure, loading rate, joint aperture, temperature, and saturation, have not been fully considered, but we do not exclude their potential impact on the observed interaction pattern. For example, it can be anticipated that as the loading rate increases, especially under impact loading conditions, rock bridges will behave more like a whole, and this interaction pattern will be weakened. These effects warrant further investigation, preferably through experimental studies.

Practical implications

Comprehending mechanical behaviours of rock bridges is crucial for reliably predicting rock mass failure. We consider a wide range of rock bridge scale ratios instead of limiting them to case-specific rock bridges, enhancing the generalisability of the results. Our numerical modelling provides a comprehensive explanation for the mechanical behaviours of diverse-scale rock bridges under direct shear conditions. It elucidates internal damages that are difficult to detect in laboratory and field settings. Particularly, the identified interaction modes of diverse-scale rock bridges provide compelling evidence of physical precursor patterns in the progressive failure of multiple rock bridges, essential for the prevention and management of related geological hazards such as earthquakes7 and rockslides6,20,28. Specifically, for rockslides governed by diverse-scale rock bridges, the observed interaction patterns between rock bridges contribute to inferring possible displacement evolution, thus enabling the prediction of rockslides.

Conclusions

Diverse-scale rock bridges are widespread, but their mechanical behaviours remain elusive. Employing UDEC modelling, we performed systematic analyses of mechanical properties, stress and displacement fields, cracking processes, and AE characteristics of simulated diverse-scale rock bridges in direct shear. The following conclusions can be drawn:

  1. (1)

    Load–displacement curves transition from a unimodal to a hump-shaped manner with decreasing scale differences.

  2. (2)

    There is a fundamental linear correlation between peak shear resistance and the proportion of rock bridges.

  3. (3)

    τxy concentrates at rock bridge tips, more prominently for the rock bridge farther from the shear loading end.

  4. (4)

    The irregularity of displacement distribution follows an arc-shaped configuration in proximity to rock bridges. Larger rock bridges perform lower gradients of displacement field in their vicinity.

  5. (5)

    Rock bridge ruptures in tension close to the shear loading end and in shear further away.

  6. (6)

    The rotation of confining pressure plates affects stress distribution and failure mode.

  7. (7)

    Interaction patterns between rock bridges are found. Specifically, when neighbouring rock bridges share comparable scales, the rupture of the rock bridge closer to the shear loading end expedites damage in the one farther away towards its VEPs. Conversely, in scenarios where one rock bridge significantly outweighs the other, the rupture of the larger rock bridge will overwhelmingly affect the smaller one.

These findings provide compelling evidence supporting theoretical precursor patterns crucial for the prediction of multiple rock bridge failure, which is important for the prevention and management of related geological hazards.