Introduction

Tailings are an inevitable byproduct of mineral resource extraction, and the safe management of tailings represents a critical issue confronted by the mining industry. In modern underground mines, tailings are commonly used as a primary component of CPB1. CPB serves as supplementary ground support in mining operations, improves the underground working environment, and offers significant economic, safety, and environmental benefits, thus garnering widespread attention in the mining sector2,3,4,5. As a means of controlling subsidence, the effectiveness of backfill in mining is closely related to the integrity and stability of the backfill materials. Backfill often experiences local damage, leading to the overall instability of the materials6. Therefore, studying the strain evolution and failure prediction of CPB under the load of the overlying strata in structural backfill mining has significant practical importance for the stability of the mine.

In recent years, the mechanical properties of CPB have been extensively investigated, with a particular emphasis on its strength, deformation behavior, and consolidation characteristics7,8,9,10,11,12,13,14. Investigations have been carried out to assess CPB strength using large-scale models, to develop global datasets and predictive models for UCS utilizing artificial intelligence, and to propose advanced elastoplastic and multi-physics models that have been validated through experimental data15,16,17,18,19,20. Further explorations have focused on enhancing CPB strength and microstructure through the use of construction and demolition waste, examining the effects of superplasticizers on hydration and strength development, and analyzing the influence of curing time and binder content on consolidation behavior21,22,23,24,25,26,27. Additional examinations have been conducted on one-dimensional consolidation parameters and the impact energy absorption capacity of cemented backfill materials28,29. Collectively, these investigations have significantly contributed to a deeper understanding of CPB’s mechanical properties and its applications in mining engineering.

Scholars have utilized various techniques to study the evolution characteristics of pores and micro-cracks within rocks and backfill materials. To evaluate the deformation of backfill samples, the DIC method utilizes high-speed cameras to capture the speckle field images on the surface of the samples, obtaining the corresponding local deformation and instability, which can effectively reflect the degree of damage and failure process of rocks and backfill materials30,31,32,33. Zhang et al.34 presented a novel methodology employing DIC for crack identification in jointed rock masses, revealing the mechanical properties and crack behavior of 3D-printed rock-like specimens under uniaxial compression. Gao et al.35 explored the rate dependence of fracture propagation in rocks using DIC, characterizing the dynamic fracture properties and the relationship between fracture propagation toughness and crack growth velocity in granitic rocks. Xing et al.36 combined DIC with acoustic emission technology to study rock deformation localization and developed a second-order spatial–temporal subset DIC algorithm for analyzing the deformation fields of red sandstone under uniaxial compression. Wei et al.37 analyzed the failure mechanics and energy evolution of sandstone under uniaxial loading using DIC technology to reveal the rock failure process and its associated energy changes. Sun et al.6,38 discovered that the strength of fly ash-gangue geopolymer cemented backfill is enhanced with the addition of chemically activated fly ash, and the sample’s failure characteristics, analyzed by DIC deformation field evolution, exhibited multiple shear deformation zones. Confronted with the plethora of image data, human visual recognition is impeded by high costs and a propensity for errors. Consequently, the adoption of intelligent algorithms, rooted in computer technology, has become essential for the rapid identification of images and video data. Prior research has predominantly utilized DIC data to assess the strain field evolution within specimens; however, these methods have been incapable of quantifying the specific patterns of strain value evolution39. Dong et al.40 utilized a CVR model based on DIC data to predict crack coalescence and analyze the load-bearing mechanism of defective rock specimens. This is especially pertinent in critical domains such as the prompt detection of damage in mining backfill operations.

Enhanced comprehension of the mechanical characteristics and deformation evolution of backfill materials has been achieved through these studies. However, no previous research has specifically quantified the strain field evolution and crack prediction in whole tailings cemented backfill under varying cement-to-tailings ratios, filling concentrations and curing durations using DIC. Considering the distinct composition of backfill materials from natural soil and rock, investigating the deformation behavior of backfill materials is of considerable significance. DIC is employed to monitor the fracture evolution and deformation response of CPB samples under UCS testing. The HSV-CVR model is used to analyze the strain field images derived from VIC-2D Software, quantifying the area proportions of various strain regions. Subsequently, the first derivative of these proportions is utilized for early crack prediction. The results of this research are instrumental in bolstering the stability and safety of engineering structures.

Experimental process and monitoring techniques

Material selection and sample preparation

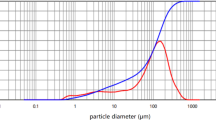
The CPB specimens were prepared by blending cement, tailings sourced from a tungsten mine in Jiangxi Province, China, and tap water. The chemical composition of the tailings is presented in Table 1, and the particle size distribution is shown in Fig. 1. The cement used is Type 42.5 OPC and a cement slurry mixer was employed for the preparation of the slurry. The mixing process involved adding water to the mixing drum, followed by a uniform blend of tailings and cement. To ensure the homogeneity of the slurry, it was first mixed at a low speed for 120 s, then at a high speed for another 120 s. The slurry was then poured into a mortar spreader (50 mm × 100 mm × 150 mm) for a slump test. Subsequently, the slurry was cast into pre-prepared standard triple mold samples (70.7 mm × 70.7 mm × 70.7 mm), wrapped with plastic wrap, and placed in a constant temperature and humidity chamber (temperature maintained at 20 ± 2 °C, humidity above 90%) for curing periods of 3 days (3d), 7 days (7d), and 28 days (28d) to prepare the CPB specimens, as illustrated in Fig. 2.

Table 1 Tailings chemical composition content.
Full size table
Fig. 1
figure 1

Particle size distribution.

Full size image
Fig. 2
figure 2

Process of CPB sample preparation and slump testing.

Full size image

Uniaxial compression testing under DIC observation

DIC methodology necessitates a digital image acquisition system and associated computation software for image correlation analysis. The digital image acquisition system comprises a UCS testing loading device, a stable light source, a high-definition digital camera, and a computer, as shown in Fig. 3. During the test, the brightness of the light source was adjusted and stabilized to ensure reliable grayscale values during the loading of the specimens. The acquisition frequency of the digital camera was then set to capture images of the artificially speckled specimens. Finally, the collected digital images were stored on a computer, and the evolution of the surface displacement field was obtained using data processing software.

Fig. 3
figure 3

Layout of the DIC experimental equipment.

Full size image

A DYE-300-10S fully automatic flexural and compressive testing machine was used to measure the UCS of CPB specimens at different curing ages. The DIC system, comprising a Charge Coupled Device (CCD) camera (4000 × 3000 pixels, 9 frames per second), a ring light source, and MV Viewer software, was employed to monitor surface deformation of the specimens. Before testing, matte white paint was applied to the specimen surface, followed by random speckles of matte black paint to create a high-contrast pattern for accurate image correlation. Subsequently, the VIC-2D software was used to process a series of continuous speckle pattern images obtained during the testing process, yielding the evolution of the specimen surface strain field40.

Computer vision recognition model

DIC methodology was first independently introduced in the early 1980s by I. Yamaguchi et al.41,42. The fundamental principle of DIC involves comparing two digital images recorded before and after deformation. By calculating the grayscale of the speckle pattern images on the surface of the specimen before and after deformation, DIC provides an optical measurement method for obtaining parameters such as displacement and deformation of the object under study. To streamline the visual recognition and segmentation process of physical images, DIC technology is leveraged to acquire strain field images. Initially, a high-definition speckle pattern image of the CPB specimen during the uniaxial compression test is captured using a camera. Subsequently, the VIC-2D software is utilized to acquire maximum principal strain (ε1) field data40. The procedures conducted include region of interest (ROI) selection, subset size suggestion, and strain calculation. Thereafter, our proprietary HSV-CVR program is applied to process the maximum principal strain field images of the CPB specimens. Ultimately, the segmentation of the strain field and the quantitative processing of visual recognition data enable a comprehensive analysis of the physical images, with the operational process shown in Fig. 4.

Fig. 4
figure 4

Workflow for the segmentation of the strain deformation field.

Full size image

The strain field images obtained through VIC-2D software processing are raster images composed of various pixel points, each containing color information. This color information is recorded using the RGB color model, which overlays a pixel’s information with red (R), green (G), and blue (B) color data. The process of color analysis for each image involves the following steps: Initially, the OpenCV library is utilized to read the image files. Subsequently, the image color space is converted from RGB to HSV to more accurately process color information. The number of hue groups and their corresponding ranges are then defined to classify pixels of different hues. For each hue group, masks are created, and the area proportion of that hue group in the entire image is determined by calculating the number of non-zero pixels within the masks. Pixels falling within the predefined intervals are retained, while those outside are substituted with white pixels to achieve image segmentation. The area proportion data are compiled into a table, and the proportion of the interval region color blocks within the entire region of interest (ROI) is calculated for corresponding frame images at different times. This results in the strain percentage change curve over time at that interval scale, which lays the foundation for subsequent data analysis and visualization. The analysis primarily focuses on the maximum principal strain ε1, with the strain scale range established between 0 and 0.03. Using the method of equal division, the strain scale is divided into eight intervals for a more detailed analysis of strain evolution patterns. These intervals are S1 (26.25 to 30.00 × 10–3), S2 (22.50 to 26.25 × 10–3), S3 (18.75 to 22.50 × 10–3), S4 (15.00 to 18.75 × 10–3), S5 (11.25 to 15.00 × 10–3), S6 (7.50 to 11.25 × 10–3), S7 (3.75 to 7.50 × 10–3), and S8 (0.00 to 3.75 × 10–3). The process not only enhances the efficiency of color analysis but also provides robust data support for a deeper understanding of color distribution characteristics within images.

Experimental results and analysis

Experimental findings

UCS and slump tests were executed on CPB specimens derived from whole tailings, with slurry filling concentration and cement-to-tailings ratios serving as the principal variables. The experimental results are presented in Table 2. The A0 group, serving as the control group, had a slurry quality concentration of 76% and a cement-to-tailings ratio of 1:8. The UCS at 3d, 7d, and 28d were 1.2 MPa, 1.7 MPa, and 2.4 MPa, respectively, with a slump of 300 mm. By adjusting the cement-to-tailings ratio to 1:4 (B1) and 1:12 (B2), significant changes in compressive strength and slump were observed for groups B1 and B2. Group B1 reached a 28d strength of 6.9 MPa, while group B2 dropped to 1.3 MPa, with slump values changing to 260 mm and 370 mm, respectively. Further adjustment of the slurry quality concentration to 74% (C1) and 78% (C2) showed that group C1 experienced a slight decrease in strength, while group C2 showed an increase in strength, with slump values changing to 380 mm and 212 mm, respectively. These results indicate that the amount of cement admixture has a significant impact on the strength and workability of the backfill. An increase in slurry filling concentration can enhance strength but may reduce slump. In practical applications, the optimal slurry filling concentration and cement-to-tailings ratio must be determined through testing, based on specific engineering requirements and construction conditions, to achieve the desired performance criteria. To ensure the reliability of the experiments, triplicate tests were performed on samples cured at 3d, 7d, and 28d, with strength variations depicted in Fig. 5.

Table 2 Experimental scheme.
Full size table
Fig. 5
figure 5

UCS test results.

Full size image

Deformation field evolution

The image captured at the start of the UCS test was used as the reference image, subsequent images captured during the experiment were regarded as deformation images. As shown in Fig. 6a–e, four points (A–D) are marked on the stress-time curve, each corresponding to a specific strain field. Based on the 28d strength values of the A0-C2 specimens, Point A, with a stress of 0.5 MPa, is selected to represent the initial loading stage for comparative analysis. Point B, the low-range strain point (LRSP), is identified as the starting point of the S7 deformation region (low-strain area), and Point C, the high-range strain point (HRSP), is identified as the starting point of the S1 deformation region (high-strain area). Point D is located at the peak stress. It should be specifically noted that, due to the absence of quantitative analysis of the strain regions in this section, Points B and C are roughly positioned as analysis points. Meanwhile, due to the inability to accurately distinguish the starting point of the S4 intermediate strain region (mid-range strain point, MRSP) with the naked eye, no observation point was set for the intermediate strain region. The specific deformation value regions will be further analyzed using the HSV-CVR algorithm and subsequent first derivatives.

Fig. 6
figure 6

Stress-time curve and deformation field for the entire loading process, (A–D) are the marker points on the stress-time curve: (a) Specimen A0 at 28d of curing. (b) Specimen B1 at 28d of curing. (c) Specimen B2 at 28d of curing. (d) Specimen C1 at 28d of curing. (e) Specimen C2 at 28d of curing. (f) Specimen A0 at 3d of curing. (g) Specimen A0 at 7d of curing.

Full size image

Figure 6a–e display the stress–strain behavior of specimens A0, B1, B2, C1, and C2 at a curing age of 28d under various filling concentrations and cement-to-tailings ratios. Figure 6a illustrates that at Point A, the A0 specimen is in the initial loading stage, where it is in the elastic phase with uniform strain distribution. At Point B, with a stress of 1.5 MPa, the strain area remains small. As stress increases, small strain concentration areas emerge within the strain field. At Point C, with a stress of 2 MPa, a distinct deformation concentration area appears in the lower right of the strain field. Point D corresponds to the peak stress of 2.4 MPa, by which time a pronounced band-like deformation concentration area has formed. The specimen fails due to rapid macro-crack growth following a sharp decrease in stress. Figure 6b shows that for the B1 specimen, the strain at Point A is minimal and difficult to discern with the naked eye. As the load is applied further to Point B with a stress value of 3 MPa, minor deformation begins in the upper left corner, though it remains small for an extended period. Until Point C, with a stress value of 6.6 MPa, the specimen begins to show a significant deformation concentration area, with the principal strain band located in the middle. At Point D, with a stress value of 6.9 MPa, the deformation concentration in the middle of the specimen intensifies, and the continuous strain band with high-stress concentration deepens further. Figure 6c indicates that for the B2 specimen, even at the initial loading stage of Point A, low-strain bands have begun to appear within the specimen. When the loading stress increases to Point C at 1.1 MPa, the principal strain field starts to show red high-strain concentration areas. At the peak stress of 1.3 MPa, cracks cover almost the entire specimen, and after reaching the peak load, the principal strain field expands, generating a large number of strain areas along existing cracks. Figure 6d shows that for the C1 specimen, deformation starts from the upper boundary towards the middle area at Point A. During the loading process from Point A to Point B, deformation exhibits a rebound phenomenon. At Point B, continuous minor deformation begins and increases with the load. At Point C, with a stress of 1.5 MPa, a continuous deformation band forms from the specimen boundary to the middle, with red high-strain concentration areas appearing. When reaching the peak stress at Point D, the specimen shows a large deformation area and high-strain concentration zones at crack locations. Figure 6e shows that for the C2 specimen, the strain field distribution at Point A is uniform, with no significant deformation concentration areas. At Point B with a stress value of 1.5 MPa, scattered deformation areas begin to appear. When the S1 strain region value emerges, Points C and D almost coincide, marking the peak stress point where red high-strain concentration areas start to appear, along with high concentrated deformation areas on both sides of the specimen.

Taking the control group specimens as an example, we analyze the strain evolution characteristics at 3d, 7d, and 28d of curing. Figure 6f and g present the stress-time curves for the A0 specimen at 3d and 7d of curing, respectively. Due to the early appearance of low-strain areas in the 3d and 7d specimens during the initial stress loading, Point B is directly used as the starting point for the analysis of the initial loading phase. Figure 6f shows that at the initial loading stage, a large area of low-strain had already begun to form at the bottom of the specimen. At Point C, with a stress of 1 MPa, a high-strain region forms as a strain band in the middle, and at Point D, significant fracture bands appear in the middle and left of the specimen, indicating failure. Figure 6g shows that at the initial loading stage, a distinct deformation concentration area had already formed on the right side of the specimen. At Point C, with a stress of 1.5 MPa, the specimen displays symmetrical strain bands with a high-strain area forming on the left. At Point D, a large high-strain area appears on the left side of the specimen, leading to its failure.

Analysis of the mean value of ε1

Figure 7 presents the variation curves of the mean value of principal strain ε1 over time for CPB specimens under different cement-to-tailings ratios, filling concentrations, and curing durations, along with strain field distribution diagrams at the peak strain points. These charts reveal the response and evolution of the CPB specimens when subjected to increasing stress.

Fig. 7
figure 7

Curve of the mean value of ε1 versus time: (a) Comparison of different cement-to-tailings ratios. (b) Comparison of different filling concentrations. (c) Comparison of different curing durations.

Full size image

In Fig. 7a, we observe the impact of different cement-to-tailings ratios on the strain behavior of CPB specimens. It can be seen that as the cement-to-tailings ratio decreases, the rate of increase in the principal strain ε1 increases. A cement-to-tailings ratio of 1:4 exhibits a slower strain increase at the early stage. This can be attributed to the fact that the higher ratio provides more cement paste, thus enhancing the material’s early strength. Specimens with a 1:8 cement-to-tailings ratio exhibit a stable strain increase, with the mean value of principal strain ε1 peaking at around 7.5 s. In contrast, specimens with a 1:12 cement-to-tailings ratio show a slower strain increase initially, but it begins to rise rapidly after about 4 s and peaks at around 6 s. This could be due to the lower ratio resulting in less cement paste, affecting the material’s strength development. Figure 7b further demonstrates the impact of different filling concentrations on the strain evolution of CPB specimens. Specimens with a 74% filling concentration show a rapid strain increase at the initial loading stage but then level off, possibly due to the higher porosity or less cement paste in the material’s internal structure, which reduces its mechanical performance. Specimens with a 78% filling concentration exhibit a slower strain increase at the initial loading stage, likely because the higher filling concentration increases the material’s density, thereby enhancing its load-bearing capacity. Figure 7c illustrates the varying strain behaviors of A0 specimens across different curing ages, with the 3d specimen showing a rapid initial strain increase, the 7d specimen exhibiting a faster initial increase followed by a rate decrease, and the 28d specimen displaying a more stable and gradual strain increase throughout the testing. This indicates that as the curing age increases, the hydration reaction within the CPB specimens becomes more complete, thereby enhancing their long-term strength and stability. Figure 7 also includes strain distribution diagrams at the peak points of the ε1 mean value-time curves, showing the strain distribution on the specimen’s surface. These strain distribution diagrams provide intuitive visual evidence for understanding the material’s deformation behavior during loading and aid in analyzing the material’s failure mechanisms.

Evolution of strain based on the HSV-CVR model

Using the HSV-CVR model, a quantitative analysis of the strain evolution characteristics of CPB specimens at different loading stages was conducted. By monitoring the percentage changes in the maximum principal strain ε1 levels (from S1 to S8) over time, we revealed the strain evolution characteristics of the samples throughout the entire experimental process.

As illustrated in Fig. 8, the strain evolution process of the control group specimen with a curing age of 28d is depicted. With the increase in stress, the percentage of the minimum strain interval S8 gradually decreases, while the percentage of other strain intervals gradually increases. These changes are not linear but are accompanied by fluctuations, reflecting the complex deformation behavior experienced by the specimen during loading. For instance, certain areas of the specimen may return to their initial state after elastic strain, while other areas may undergo plastic strain. Throughout the entire testing process, the percentages of the low-strain intervals S7 and S8 remain at a relatively high level, indicating that these intervals are more active throughout the test. Over time, the percentage of higher strain intervals increases gradually, with a sudden increase in the proportion of high-strain intervals in the later stages of the test due to irreversible plastic strain.

Fig. 8
figure 8

The evolution curve of the percentage of ε1 intervals at different levels over time for the control group A0 specimen at 28d of curing.

Full size image

Specifically, the curve of the S7 strain interval exhibits a distinct evolutionary pattern throughout the test: it starts with a rapid increase from a relatively stable state, then slightly slows down, and finally increases rapidly again as it approaches crack coalescence. This pattern indicates that the compressible deformation areas within the specimen respond quickly to the initial increase in stress, and then these areas’ deformation further increases and shifts to other strain intervals. Ultimately, during the crack coalescence phase, the strain values expand rapidly, leading to a sudden increase in the percentage of the S7 strain interval. For the A0 specimen, at the initial loading stage (Point A), the strain is mainly concentrated in the lowest strain interval S8, accounting for up to 99.95%, indicating that the specimen has undergone almost no significant deformation. As loading proceeds, the strain begins to shift to higher intervals; by Point B, the S7 interval’s percentage increases to 3.97%, while the S8 interval decreases to 96.03%. At Point C, the strain distribution becomes more dispersed, with intervals S1 to S6 beginning to show strain, the S7 interval’s percentage significantly increases to 14.23%, and the S8 interval decreases to 75.86%. Near the peak stress (Point D), the strain distribution becomes more extensive, with the percentages of intervals S1 to S6 all increasing, the S7 interval’s percentage reaching 30.26%, and the S8 interval decreasing to 29.26%.

Figure 9 presents the variation over time of different strain intervals S1-S8 for B1 and B2 specimens with a curing age of 28d, based on the HSV-CVR model. In Fig. 9a, at Point A, all strain in the B1 specimen is concentrated in the S8 interval, indicating minimal strain at the initial loading stage. At Point B, the strain begins to appear in intervals S5 to S7, with the S8 interval’s proportion dropping to 95.53%. At Point C, the proportion of intervals S1 to S6 increases, with S7’s proportion rising to 15.52% and S8’s dropping to 76.03%. At Point D, strain is significantly distributed across intervals S1 to S7, with S7’s proportion reaching 18.71% and S8’s falling to 69.16%. In Fig. 9b, for the B2 specimen at Point A, strain is primarily concentrated in intervals S7 and S8, with slight strain appearing in intervals S5 and S6. At Point B, strain significantly increases in intervals S4 to S7, reducing the S8 interval’s proportion to 73.07%. At Point C, the strain distribution further disperses, with intervals S1 to S6 all increasing in proportion, S7’s proportion reaching 27.93%, and S8’s dropping to 54.80%. At Point D, strain is significantly distributed across intervals S1 to S7, with an unusually high proportion in S1 (24.90%), indicating more pronounced strain concentration in the high-strain intervals, and S8’s proportion falling to 12.23%.

Fig. 9
figure 9

The evolution curves of the percentage of ε1 intervals at different levels over time under different cement-to-tailings ratios: (a) Specimen B1 at 28d of curing. (b) Specimen B2 at 28d of curing.

Full size image

Figure 10a depicts the C1 specimen with a filling concentration of 74%. At the initial loading stage (Point A), strain is predominantly concentrated in intervals S7 and S8, similar to the A0 specimen, indicating minimal strain at the initial stage. As loading progresses, the strain begins to shift towards lower intervals. By Point C, the proportion of intervals S1 to S6 has increased, with S7 significantly rising to 17.48% and S8 decreasing to 61.90%. Near the peak stress (Point D), the proportion of interval S1 is unusually high at 10.09%, S7 reaches 30.89%, and S8 drops to 16.43%, suggesting the presence of significant macro-cracks under high-stress. Figure 10b shows the C2 specimen with a filling concentration of 78%. At the initial loading stage (Point A), strain is mainly concentrated in interval S8, accounting for 99.79%, similar to the initial strain distribution in the C1 and A0 specimens. As loading proceeds, strain emerges in intervals S6 and S7. By Point C, the proportion of intervals S1 to S6 has increased, with S7 rising to 29.00% and S8 decreasing to 28.67%. At Point D, strain is significantly distributed across intervals S1 to S7, with S1 at 3.34%, S7 at 29.70%, and S8 at 23.98%, demonstrating a better strain distribution and crack control capability.

Fig. 10
figure 10

The evolution curves of the percentage of ε1 intervals at different levels over time under different filling concentrations: (a) SpecimenC1 at 28d of curing. (b) Specimen C2 at 28d of curing.

Full size image

Compared to the A0 specimen, the C1 and C2 specimens show similar strain distributions at the initial loading stage. However, as loading progresses, the C2 specimen exhibits a more uniform strain distribution, likely related to its higher filling concentration. The high proportion of interval S1 near peak stress for the C1 specimen may indicate the presence of significant macro-cracks, while the C2 specimen demonstrates better strain control and distribution.

Figure 11 presents the strain–time evolution diagrams for the A0 specimen at curing ages of 3d and 7d. Analysis of these data reveals significant changes in the strain evolution characteristics of the backfill specimens as the curing age increases. For the A0 specimen at a 3d curing age (Fig. 11a), at the initial loading stage (Point A), strain is predominantly concentrated in intervals S4 to S7, with S7 accounting for 19.50% and S8 for 73.38%. As loading progresses, the strain begins to shift towards higher strain intervals; by Point C, the proportion of intervals S1 to S6 has increased, particularly S6, reaching 10.77%, while S7 rises to 29.29%. Near the peak stress (Point D), the strain distribution becomes more uniform, with S1 increasing significantly to 19.13% and S7 decreasing to 11.27%. For the A0 specimen at a 7d curing age (Fig. 11b), the strain distribution at the initial loading stage (Points A and B) is similar to that of the 3d curing age specimen, but with S7 at 12.45% and S8 at 81.25%. The trend in strain distribution, as loading progresses, is consistent with the 3d curing age specimen, but at Point C, the proportion of S1 increases to 1.75% and S7 to 22.17%. Near the peak stress (Point D), the strain distribution becomes more uniform, with S1 increasing to 14.80% and S7 decreasing to 18.34%.

Fig. 11
figure 11

The evolution curves of the percentage of ε1 intervals at different levels over time under different curing durations: (a) Specimen A0 at 3d of curing. (b) Specimen A0 at 7d of curing.

Full size image

Compared to the A0 specimen at a 28d curing age, the strain evolution at 3d and 7d curing age shows earlier strain concentration phenomena, and the strain evolution curves exhibit greater fluctuations, indicating that the internal microstructure of the backfill is still developing and the strain response to stress is more sensitive and unstable at early curing ages. The A0 specimen at a 28d curing age exhibits a more uniform strain distribution, indicating that the stability and uniformity of the internal structure of CPB specimens improve with age. These results are significant for understanding the mechanical behavior of CPB specimens at different curing ages and optimizing construction processes, aiding in the prediction and control of backfill failure risks at various curing ages.

Crack prediction and early warning

Figure 12 illustrates the first derivative of the percentage curve for ε1 strain intervals S1-S8 for the A0 specimen, which can be utilized to predict the development of cracks. Analysis of the ε1 strain intervals (Fig. 8) reveals that as stress increases, strain concentration shifts from lower to higher strain intervals, with a notable increase in interval S7 indicating imminent significant strain, potentially leading to macroscopic crack coalescence. The increase in the percentage of the S7 strain interval suggests that more strain intervals below the S7 level are developing towards the S7 level, further confirming that rapid growth in low-strain intervals is a key characteristic of crack coalescence. For major mine backfilling projects with strict crack control requirements, monitoring the rate of change in the percentage of low-strain intervals is crucial. Focusing on the S7 low-strain zone is of significant reference value for predicting crack coalescence in actual mine backfilling projects. As stress increases, strain concentration progresses from low to high-strain intervals. Within the S7 to S1 range, crack coalescence is accompanied by a rapid increase in strain. Notably, the significant increase in the proportion of the S1 strain interval at Point C indicates the most pronounced strain concentration in these intervals, likely a direct result of crack coalescence and expansion. It can be determined that a rapid increase in S1 strain is caused by crack coalescence. Since the S4 strain interval reflects the behavior of CPB specimens at moderate strain levels, selecting the S4 strain interval as a key monitoring point provides important information for the early identification and prevention of cracks. Additionally, significant changes in the S4 interval may herald the intermediate stage of crack propagation, which is significant for assessing materials stability and taking timely engineering measures.

Fig. 12
figure 12

The first derivative of the ε1 strain interval percentage curve for the control group A0 specimen at 28d of curing.

Full size image

As shown in Fig. 13, taking the 28d strain interval first derivative of the A0 specimen as an example (Fig. 13a), and combining the distribution at Points B and C in Fig. 6a, by comprehensively monitoring the strain level curve rate of change for intervals S1, S4, and S7, we identify significant growth points with larger first derivative values as key monitoring points. Here, the first derivative values are defined with S1 set at 0.01 for the HRSP, S4 at 0.03 for the MRSP, and S7 at 0.2 for the LRSP. This selection is based on a detailed analysis of the strain evolution data of CPB specimens during loading to more accurately predict and assess the risk of backfill failure. Below the LRSP, the first derivative curve of the S7 strain interval percentage shows fluctuations, possibly reflecting the uneven stress distribution within the material at the initial loading stage or minor adjustments during the experiment, which are not representative of the material’s stable strain response. However, above the LRSP, the strain in the S7 interval begins to increase significantly and persistently, marking the beginning of strain concentration. Furthermore, the strain growth after the LRSP is more pronounced and sustained, indicating that the material begins to experience more significant strain concentration. The distinctness of this change makes the LRSP a suitable reference point for assessing material strain evolution and crack development, with MRSP and HRSP selected in the same manner. Since the HRSP signals that the backfill structure is about to reach its maximum load-bearing capacity, the first derivative value of the S7 region is set lower. The MRSP indicates the initiation or propagation of cracks within the backfill, and the LRSP signals that the backfill is under external pressure with a continuous increase in the strain concentration area. In practical applications, these inflection points can serve as early warning signals, helping engineers or researchers predict material failure or damage and adjust according to specific mine backfilling needs. Selecting these three key points, HRSP, MRSP, and LRSP, helps avoid interference from experimental noise and focuses on analyzing strain growth stages with engineering significance, which provides key indicators for crack identification and prediction in practical engineering applications. The research results offer a new approach to crack prediction, contributing to enhanced project stability and safety measures. When data at critical parts of the backfill structure exceed the MRSP, remedial measures should be taken to avoid potential hazards, and when exceeding the HRSP, macroscopic cracks in the mine backfill should be addressed promptly to ensure the safety and stability of the mine. Monitoring the changes in the first derivative values of these strain intervals allows for more accurate prediction and assessment of backfill failure risks, providing significant reference value for mine backfilling projects.

Fig. 13
figure 13

The first derivative of the percentage change curve for ε1 strain intervals S1, S4, and S7, along with early warning signal indicators: (a) Specimen A0 at 28d of curing. (b) Specimen B1 at 28d of curing. (c) Specimen B2 at 28d of curing. (d) Specimen C1 at 28d of curing. (e) Specimen C2 at 28d of curing. (f) Specimen A0 at 3d of curing. (g) Specimen A0 at 7d of curing.

Full size image

Conclusions

This paper presents a study on the evolution of strain fields and crack prediction in CPB samples under different cement—to—tailings ratios, filling concentrations, and curing durations. The research employs UCS tests in conjunction with DIC and the HSV-CVR model. The principal conclusions derived from this study are as follows:

Variations in the cement-to-tailings ratio, filling concentration, and curing age substantially affect the strain field evolution in CPB. Samples exhibit varying strain distributions and crack propagation paths under different conditions. After reaching peak stress, samples rapidly lose load-bearing capacity, characterized by a sharp stress decrease. Notably, the evolution rate of the principal strain field increases as the cement—to—tailings ratio, filling concentration, and curing age decrease.

The DIC and HSV-CVR models effectively reveal the deformation fields and crack propagation patterns of CPB samples under uniaxial compressive loading. The HSV-CVR model visually identifies and quantifies the area proportion of different strain intervals, providing a more accurate understanding of the strain evolution characteristics of the backfill during loading, especially the strain concentration phenomena during crack formation and propagation.

Quantitative identification of precursor features of crack extension is achieved. Crack prediction is carried out based on the values and percentage changes of different strain intervals in the sample strain fields, and early warning signals for high, medium, and low-strain levels are set. By analyzing the changes in strain intervals, the risk of backfill failure is assessed, providing a scientific basis for mine backfilling engineering and assisting engineers in making more rational design decisions before construction.