Revealing homoclinic breather waves, periodic lump waves and other waves forms of an integrable reduced spin Hirota-Maxwell-Bloch system

Abstract

In this manuscript, we investigate various wave forms of an integrable reduced spin Hirota-Maxwell-Bloch system, which accounts for the femtosecond pulses transmitted in an erbium doped fibre. We achieved this using periodic wave and logarithmic transformations. We investigated homoclinic breather waves, periodic lump waves, mixed waves, M-shaped waves interacting with kink and rogue waves and multi waves. Using carefully selected parameter values based on physical relevance, mathematical constraints, and stability analysis, we present three-dimensional plots and their accompanying contour and density maps for the homoclinic breather and periodic lump wave solutions using Mathematica. The solutions and their physical structures obtained explain the soliton phenomena and mimic the dynamic features of the travelling wave distortion front formed in the dispersive medium. It also illustrates the periodic wave and logarithmic transformations technique’s strength, applicability, and future research opportunities in finding special solutions for a variety of nonlinear equations in physical science and engineering. Finally, as far as we could verify, this is the first work in the literature in which these ansatz functions are derived for this integrable reduced spin Hirota-Maxwell-Bloch system using logarithmic transformations.

Introduction

The past few years have seen a rise in the significance of nonlinear partial differential equations (NLPDEs). Numerous fields, including physics, engineering, mechanics, chemistry, and biology, employ NLPDEs to simulate various processes^1,2,3. Understanding these models can therefore benefit from knowing the exact solutions of these NLPDEs. The solutions to these systems are found using a variety of methods and approaches, including but not limited to the neural net;work-based variational methods⁴, the modified homotopy perturbation technique⁵, the Adomian decomposition method⁶, the inverse scattering transform⁷, the Hirota bilinear approach⁸, the Backlund transform⁹, the extended auxiliary equation method¹⁰, the generalized Riccati equation mapping technique¹¹, $\frac{G^{\prime }}{G}$-expansion method¹², and the $\frac{W}{G}$-expansion direct method¹³. Additionally, other advanced analytical techniques employed to solve nonlinear wave equations and investigate soliton dynamics includes the novel modified Kudryashov (NMK) method and Simplest Equation (SE) method, which are used to obtain bright and dark bell solitons, periodic rogue waves, and connected periodic wave patterns¹⁴. The unified and advanced $exp(-\phi (\xi ))$-expansion approach are applied to the time-fractional Klein-Gordon equation, yielding kink, anti-kink, lump, and periodic rogue wave solutions¹⁴. Modified simple equation (MSE) and improved modified simple equation (EMSE) approaches are used to find kink-periodic lump waves, instanton solitons, and interaction waves in telegraph and longitudinal wave models^16,17. Bifurcation analysis is employed to study stability transitions, chaos, and soliton formation in fractional wave equations, whereas the modified Sardar sub-equation method is used to obtain trigonometric, exponential, and hyperbolic wave solutions¹⁸. Finally, the newly modified simple Equation (NMSE) approach is employed to study multi-soliton interactions, such as kink, anti-kink, and bright-dark solitons, in the Klein-Fock-Gordon equation and prove its power in nonlinear physics¹⁹. The periodic wave and logarithmic transformation technique is a powerful method, which has been employed by many researchers such as^{20,21,22,23,24,25,26,27,28}. The motivation of this piece of work is to find a series of exact solutions of the integrable reduced spin Hirota-Maxwell-Bloch (rsHMB) model using the periodic wave and logarithmic transformation technique.

One significant nonlinear optics model is the rsHMB system that accounts for the propagation of femtosecond pulses in erbium-doped optical fibers. Advances in ultrafast photonic devices have strongly fueled interest in the study of femtosecond pulse transmission through optical fibers because femtosecond pulses are central to ultrafast signal processing and high-speed fiber-optic communications^29,30,31. The rsHMB system is particularly important in describing solitons, breather waves, and rogue waves in erbium-doped media^32,33,34. Whereas the nonlinear Schrödinger equation has been established to describe how optical pulse travels in only one mode fibre at the picosecond regime³⁵. It has been discovered that a soliton called self-induced transparency (SIT), which is a different kind of optical pulse, propagates resoundingly in a two stage absorbing medium with neither loss nor distortion³⁶.The SIT soliton propagation has been described by the Maxwell-Bloch equations³⁷.

The rsHMB system given by³⁸

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{2}A_{xt}-i\omega A_{t}-2AB=0\\ \delta \vert A\vert _{t}^{2}+2B_{x}=0, \end{array}\right. } \end{aligned}$$

(1)

is used to explain how femtosecond pulses are transmits in an outer bimetallic doped fibre. A(x, t) is a complex differential function representing the complex envelope of the modulated wave. The function B(x, t) indicates the extent of the population inversion. Here, x represents the spatial distance, t denotes time, $\omega$ accounts for detuning from the transition frequency of erbium ions, and $\delta$ is a parameter controlling energy exchange between the field and the medium. The first part of the equation is optical field evolution, where the term $\frac{1}{2} i A_{xt}$ represents higher-order dispersion effects relevant for femtosecond pulses. The term $-i \omega A_t$ accounts for frequency detuning from the erbium transition frequency. The nonlinear interaction $-2 A B$ describes how the optical field exchanges energy with the erbium-doped medium. The second part of the equation is medium dynamics, where the term $\delta |A|_t^2$ shows that the pulse intensity influences the medium response, and the term $2 B_x$ represents spatial evolution of the population inversion.

To our knowledge, not much research has been done on the rsHMB system; the few that we are aware of include the publications by Cui et al.³⁸, who investigated the rsHMB equation using the N-fold Darboux transformation to produce breather solutions and bright-dark solitons and Liu et al.³⁹, who developed a generalised $(n, N-n)$-fo;ld Darboux transformation for the rsHMB model based on the N-fold Darboux transformation. They extract $N^{th}$-order hybrid wave solutions that explain how the first-order breather and the $(N-1)^{th}$-order rogue wave interact.

The logarithmic transformation technique is a systematic method for solving NLPDEs, especially those that model soliton behavior. One of the main strategies in this technique is to reduce the given NLPDE to an ODE before transforming it into a bilinear ODE. The strength of using ODEs lies in the fact that they limit the number of independent variables, which greatly simplifies the problem. This is generally done using a wave transformation, which involves the supposition that the solution is a function of one traveling wave variable in place of distinct space and time coordinates. When this transformation is used, the NLPDE is converted into an ODE, for which it is less complicated to work and analyze. After reducing the equation to the ODE, a Cole-Hopf transformation, for instance, a logarithmic transformation, is used to reform the equation into bilinear form. This method makes it possible to build exact solutions, and specifically soliton solutions. Additionally, it allows for the systematic derivation of multiple wave interactions, such as single and multi-soliton solutions, lump, periodic, M-shaped, mixed, and multi-wave solutions. This method is commonly applied in mathematical physics, fluid mechanics, nonlinear optics, and plasma physics and plays an important role in the understanding of the behavior of complex waves.

Many researchers have used this approach to various NLPDEs and found various soliton solutions and wave patterns. Alsallami et al.⁴⁰ examined stochastic-fractional Drinfel’d-Sokolov-Wilson equations and found cross-kink, homoclinic breather, and M-shaped interaction wave solutions. Seadawy et al.⁴¹ considered the perturbed nonlinear Schrödinger equation with quadratic-cubic nonlinearity and obtained homoclinic breather, multi-wave, and M-shaped solutions. Alhami and Alquran⁴² added a stochastic term to the perturbed potential-KdV equation and studied soliton dynamics in optics and plasmas by applying the Cole-Hopf logarithmic transformation to arrive at multi-soliton, lump, and breather solutions. Alquran and Alhami⁴³ used Hirota’s bilinear method in combination with the logarithmic transformation to the perturbed-KdV equation and generated lump, breather, and two-wave solutions. Zhao et al.⁴⁴ obtained lump soliton solutions to the (2+1)-dimensional asymmetrical Nizhnik-Novikov-Veselov equation based on its bilinear representation, discussing non-elastic collisions, periodic lumps, and dynamical behaviors. Ren et al.⁴⁵ put forward an extended (2+1)-dimensional Calogero-Bogoyavlenskii-Schiff-like equation and, employing generalized bilinear operators combined with logarithmic transformations, isolated lump-multi kink and lump-periodic collisions through ansatz expressions. Rizvi et al.⁴⁶ obtained multi-wave, homoclinic breather, M-shaped, and periodic cross-kink solutions of the coupled-Higgs equation using logarithmic transformations and symbolic calculations to achieve soliton and Jacobi elliptic solutions. They also discussed rational solitons of the Kraenkel-Manna-Merle system in ferromagnetic media, providing stability analyses in various dimensions. Ceesay et al.⁴⁷ performed logarithmic transformation on the nonlinear Rosenau equation and obtained homoclinic breather, periodic lump, M-shaped waves, periodic cross-kink waves, mixed waves, and multi-wave solutions. Rizvi et al.⁴⁸ also used logarithmic transformations and the sub-ODE method to obtain multi-wave, homoclinic breather, M-shaped rational solitons, and other solutions for Einstein’s vacuum field equations, such as interactions with exponential and double exponential functions. Other notable contributions are Kumar and Mohan⁴⁹ deriving a generalized fifth-order nonlinear KdV-type equation through the recursion operator and performed a Painlevé analysis to verify integrability. They utilized Hirota’s bilinear method with the logarithmic transformation to derive multi-soliton solutions, exhibiting rich dynamical behaviors. Kumar and Mohan⁵⁰ also investigated a new KP equation with time-variable coefficients by applying Hirota’s method and the logarithmic transformation and derived multiple solitons, rogue waves, breathers, and lump solutions. Kumar et al.⁵¹ examined a generalized two-mode fifth-order PDE based on Hirota’s method with the logarithmic transformation and derived multiple solitons, lump solutions, and wave interactions for magneto-sound propagation and shallow water waves. Kumar and Mohan⁵² further investigated a generalized (3+1)-dimensional KdV-type equation for rogue waves employing this method. Ultimately, Mohan and Kumar⁵³ investigated phase shifts and soliton dynamics in KdV and KP equations to demonstrate parameter-dependent soliton interactions. Also, Kumar and Mohan⁵⁴ studied a (2+1)-dimensional shallow water wave equation for ion-acoustic waves in plasma physics using Cole-Hopf and logarithmic transformations. Soliton and rogue wave solutions are derived via the N-soliton Hirota method. Finally, Mohan et al.⁵⁵ proposed a Painlevé integrable generalized (3+1)-D evolution equation. They derived third-order rogue wave and dispersive-soliton solutions using Cole-Hopf logarithmic transformations. They highlight soliton interactions across nonlinear wave systems, plasma physics, and optical fibers. This comprehensive list of studies confirms the efficacy of the logarithmic transformation method for solving a broad array of nonlinear wave equations in diverse fields of science.

Based on this findings, we suggest to investigate the rsHMB using the periodic wave and logarithmic transformation for the first time to acquire various forms of wave solutions such as the homoclinic breather waves, periodic lump waves, M-shaped wave with rogue and kink interaction, mixed and multi waves solutions.

Methodology

Steps for solving NLPDEs using the logarithmic transformation technique

step 1: We begin with an NLPDE in the form:

$$\begin{aligned} {\left\{ \begin{array}{ll} W(AB, A, A_t, A_x, A_{xx}, B_x, \dots ) =0\\ W(A_x, A_{xx}, B_x, \dots )=0 , \end{array}\right. }, \end{aligned}$$

(2)

where $A = A(x, t)$ and $B = B(x, t)$ are the dependent variables, and $x, t$ are the independent variables.

step 2: We choose the wave transformation below to reduce the NLPDE to an ODE:

$$\begin{aligned} A(x,t)=P(\varrho )e^{i\sigma },~~B(x,t)=Q(\varrho ),~~\varrho =x+\lambda t,~~\sigma =\alpha x+\beta t. \end{aligned}$$

(3)

where the wave velocity, frequency, and wave number are denoted by the parameters $\lambda$, $\alpha$, and $\beta$ respectively. Substitute Eq. (3) into the NLPDE in Eq. (2). This transformation reduces the PDE to an ODE in terms of $P(\varrho )$ and $Q(\varrho )$.

step 3: Simplify the resulting ODE by integrating and rearranging terms and substituting, if possible, to make it more tractable.

step 4: Use the Cole-Hopf logarithmic transformation to express $P(\varrho )$ in terms of a new function $\Omega (\varrho )$:

$$\begin{aligned} P(\varrho )=m(ln(\Omega (\varrho ))_{\varrho }, \end{aligned}$$

(4)

where m is a constant to be determine. Compute the derivatives of $P(\varrho )$ (e.g., $P'$, $P''$) in terms of $\Omega (\varrho )$ and its derivatives.

step 5: Substitute $P(\varrho )$, $P'(\varrho )$, $P''(\varrho )$, etc., into the ODE. Rewrite the ODE in terms of $\Omega (\varrho )$ and its derivatives.

step 6: Express the ODE in bilinear ODE form, which typically involves products of $\Omega (\varrho )$ and its derivatives.

step 7: Choose ansatz functions for $\Omega (\varrho )$ and substitute them into the bilinear ODE. Then, solve for the unknown parameters by equating coefficients of like terms to zero. (0).

step 8: Once $\Omega (\varrho )$ is determined, recover $P(\varrho )$ using the Cole-Hopf transformation logarithmic transformation in Eq. (4), and then obtain $Q(\varrho )$.

step 9: Substitute the wave transformation in Eq. (3) to obtain the solution A(x, t) and B(x, t) in terms of the original variables.

The ODE formation of the rsHMB equation

We consider the wave transformation of Eq. (3) to be a solution to Eq. (1). The NLPDEs are transformed into ODEs by the functions P and Q of $\varrho$. Equation (1) is transformed into the following ODEs by using Eq. (3).

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda P^{\prime \prime }+i\beta P^{\prime } +i\alpha \lambda P^{\prime }-\alpha \beta P-2i \omega \lambda P^{\prime }+2\beta \omega P -4PQ=0\\ 2\delta \lambda P P^{\prime }+2 Q^{\prime }=0. \end{array}\right. } \end{aligned}$$

(5)

We separate the real and imaginary parts in accordance with the first section of Eq. (5) to gain

$$\begin{aligned} \lambda P^{\prime \prime }-\beta (\alpha - 2\omega )P-4PQ =0, \end{aligned}$$

(6)

and

$$\begin{aligned} i(\beta + \alpha \lambda -2 \omega \lambda ) P^{\prime }=0. \end{aligned}$$

(7)

Integrating Eq. (7) and solve for $\lambda$ we have

$$\begin{aligned} \lambda =\dfrac{\beta }{2\omega -\alpha }. \end{aligned}$$

(8)

Integrating the second component of Eq. (5), then substitute Eq. (8) and solve for Q we have

$$\begin{aligned} Q=-\dfrac{\beta }{2(2\omega -\alpha )} \delta P^{2}. \end{aligned}$$

(9)

Substituting Eq. (9) into Eq. (6) we obtain

$$\begin{aligned} \beta P^{\prime \prime }+\beta (\alpha -2\omega )^{2}P +2\delta \beta P^{3}=0. \end{aligned}$$

(10)

Implementation of the technique

Now, we utilise Eq. (10) to determine the different wave patterns that are taken into account for Eq. (1).

First, we suppose that the solution to Eq. (10) is of the orm of Eq. (4). When we plug Eq. (4) into Eq. (10), we get

$$\begin{aligned} \beta m \left( \Omega (\varrho )^2 \left( (\alpha -2 \omega )^2 \Omega '(\varrho )+\Omega ^{(3)}(\varrho )\right) +2 \left( \delta m^2+1\right) \Omega '(\varrho )^3-3 \Omega (\varrho ) \Omega '(\varrho ) \Omega ''(\varrho )\right) =0. \end{aligned}$$

(11)

Using Mathematica, we insert the functions for the various wave types that are being studied into Eq. (11). Next, we expand, evaluate, and group similar terms together for each scenario, setting them to 0. In the end, we resolve this system of equations to derive possible classes for every case.

• 1. Homoclinic breather (HB): This pattern of waves is offered by⁵⁶

  $$\begin{aligned} \Omega =h_1 \exp \left( z \left( g_3 \varrho +g_4\right) \right) +\exp \left( -z \left( g_1 \varrho +g_2\right) \right) +h_2 \cos \left( z \left( g_5 \varrho +g_6\right) \right) . \end{aligned}$$

  (12)

  By replacing Eq. (12) and its first three derivatives into Eq. (11), we gained a simplified expression. We gather identical terms together, and equate the coefficients of each expression to zero. We have the following classes of constant values: class 1: $g_1=-\frac{\alpha -2 \omega }{\sqrt{2} z},~g_3=\frac{\alpha -2 \omega }{\sqrt{2} z},~g_5=-\frac{i (\alpha -2 \omega )}{\sqrt{2} z},~m=\frac{i}{\sqrt{\delta }}$. When we replace them in Eq. (12) and then put the result in Eq. (4), we obtain

  $$\begin{aligned} P_{1HB}(\varrho ) =\frac{i \left( \frac{h_1 (\alpha -2 \omega ) e^{z \left( g_4+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }}{\sqrt{2}}+\frac{i h_2 (\alpha -2 \omega ) \sin \left( z \left( g_6-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}+\frac{(\alpha -2 \omega ) e^{-z \left( g_2-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }}{\sqrt{2}}\right) }{\sqrt{\delta } \left( h_1 e^{z \left( g_4+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }+h_2 \cos \left( z \left( g_6-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) +e^{-z \left( g_2-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }\right) }. \end{aligned}$$

  (13)

  Inserting Eq. (13) into Eq. (9) give

  $$\begin{aligned} Q_{1HB}(\varrho ) =\frac{\beta \left( \frac{h_1 (\alpha -2 \omega ) e^{z \left( g_4+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }}{\sqrt{2}}+\frac{i h_2 (\alpha -2 \omega ) \sin \left( z \left( g_6-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}+\frac{(\alpha -2 \omega ) e^{-z \left( g_2-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }}{\sqrt{2}}\right) ^2}{2 (2 \omega -\alpha ) \left( h_1 e^{z \left( g_4+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }+h_2 \cos \left( z \left( g_6-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) +e^{-z \left( g_2-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }\right) ^2}. \end{aligned}$$

  (14)

  The necessary HB wave solutions for Eq. (1) is obtained by applying Eqs. (13) and (14) to Eq. (3).

  $$\begin{aligned} A_{1HB}(x,t) =\frac{i (\alpha -2 \omega ) e^{i (\beta t+\alpha x)} \left( -h_2 e^{g_2 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}} \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_6 z\right) +h_1 e^{\left( g_2+g_4\right) z}+1\right) }{\sqrt{2} \sqrt{\delta } \left( h_2 e^{g_2 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}} \cosh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_6 z\right) +h_1 e^{\left( g_2+g_4\right) z}+1\right) }, \end{aligned}$$

  (15)

  and

  $$\begin{aligned} B_{1HB}(x,t) =-\frac{\beta (\alpha -2 \omega ) \left( -h_2 e^{g_2 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}} \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_6 z\right) +h_1 e^{\left( g_2+g_4\right) z}+1\right) ^2}{4 \left( h_2 e^{g_2 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}} \cosh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_6 z\right) +h_1 e^{\left( g_2+g_4\right) z}+1\right) ^2}. \end{aligned}$$

  (16)

  class 2: $h_1=0,~g_1=-\frac{\alpha -2 \omega }{\sqrt{2} z},~g_5=-\frac{i (\alpha -2 \omega )}{\sqrt{2} z},~m=\frac{i}{\sqrt{\delta }}.$ Inserting these constant values into Eq. (12) and then the result in Eq. (4), we have

  $$\begin{aligned} P_{2HB}(\varrho ) =\frac{i \left( \frac{(\alpha -2 \omega ) e^{-z \left( g_2-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }}{\sqrt{2}}+\frac{i h_2 (\alpha -2 \omega ) \sin \left( z \left( g_6-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}\right) }{\sqrt{\delta } \left( e^{-z \left( g_2-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }+h_2 \cos \left( z \left( g_6-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) \right) }. \end{aligned}$$

  (17)

  Putting Eq. (17) into Eq. (9) give

  $$\begin{aligned} Q_{2HB}(\varrho ) =\frac{\beta \left( \frac{(\alpha -2 \omega ) e^{-z \left( g_2-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }}{\sqrt{2}}+\frac{i h_2 (\alpha -2 \omega ) \sin \left( z \left( g_6-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}\right) ^2}{2 (2 \omega -\alpha ) \left( e^{-z \left( g_2-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) }+h_2 \cos \left( z \left( g_6-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) \right) ^2}. \end{aligned}$$

  (18)

  The necessary HB wave solutions for Eq. (1) is obtained by applying Eqs. (17) and (18) to Eq. (3).

  $$\begin{aligned} A_{2HB}(x,t) =\frac{i (\alpha -2 \omega ) e^{i (\beta t+\alpha x)} \left( -1+h_2 e^{g_2 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}} \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_6 z\right) \right) }{\sqrt{2} \sqrt{\delta } \left( 1+h_2 e^{g_2 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}} \cosh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_6 z\right) \right) }, \end{aligned}$$

  (19)

  and

  $$\begin{aligned} B_{2HB}(x,t)=-\frac{\beta (\alpha -2 \omega ) \left( -1+h_2 e^{g_2 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}} \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_6 z\right) \right) ^2}{4 \left( 1+h_2 e^{g_2 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}} \cosh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_6 z\right) \right) ^2}. \end{aligned}$$

  (20)

• 2. Periodic Lump (PL): This wave structure is given by⁵⁶

  $$\begin{aligned} \Omega =\left( g_1 \varrho +g_2\right) ^2+\left( g_3 \varrho +g_4\right) ^2+\cos \left( g_5 \varrho +g_6\right) +g_7. \end{aligned}$$

  (21)

  By putting Eq. (21) and its first three derivatives into Eq. (11), we gained a simplified expression. We gather similar terms together, and equate the coefficients of each expression to zero. We have the following constant values:

  $$g_1=0,~g_2=0,~g_3=0,~g_4=0,~g_5=\frac{i (\alpha -2 \omega )}{\sqrt{2}},~g_7=0,~m=\frac{i}{\sqrt{\delta }}$$

  . Putting them in Eq. (21) and the result in Eq. (4), we get

  $$\begin{aligned} P_{1PL}(\varrho ) =\frac{i (\alpha -2 \omega ) \tanh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_6\right) }{\sqrt{2} \sqrt{\delta }}. \end{aligned}$$

  (22)

  Inserting Eq. (22) into Eq. (9) give

  $$\begin{aligned} Q_{1PL}(\varrho ) =\frac{\beta (\alpha -2 \omega )^2 \tanh ^2\left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_6\right) }{4 (2 \omega -\alpha )}. \end{aligned}$$

  (23)

  Equations (22) and (23) applied to Eq. (3) yield the necessary PL wave solutions for Eq. (1) as

  $$\begin{aligned} A_{1PL}(x,t) =\frac{i (\alpha -2 \omega ) e^{i (\beta t+\alpha x)} \tanh \left( \frac{x (\alpha -2 \omega )-\beta t}{\sqrt{2}}-i g_6\right) }{\sqrt{2} \sqrt{\delta }}, \end{aligned}$$

  (24)

  and

  $$\begin{aligned} B_{1PL}(x,t) =-\frac{1}{4} \beta (\alpha -2 \omega ) \tanh ^2\left( \frac{x (\alpha -2 \omega )-\beta t}{\sqrt{2}}-i g_6\right) . \end{aligned}$$

  (25)

• 3. Interaction of M-shaped with rogue and kink waves(MRK): This wave configuration is provided by⁵⁷

  $$\begin{aligned} \Omega =h_2 \exp \left( g_3 \varrho +g_4\right) +h_1 \cosh \left( g_1 \varrho +g_2\right) +\left( g_5 \varrho +g_6\right) ^2+\left( g_7 \varrho +g_8\right) ^2+g_9. \end{aligned}$$

  (26)

  By substituting Eq. (26) and its first three derivatives into Eq. (11), we obtained a simplified expression. We assemble similar terms together, and equate each expression’s coefficients zero. We obtained the following constant values: $g_1=-\frac{\alpha -2 \omega }{\sqrt{2}},~g_3=\frac{\alpha -2 \omega }{\sqrt{2}},~g_5=0,~g_7=0,~g_9=-g_6^2-g_8^2,~m=\frac{i}{\sqrt{\delta }}$. Inserting them in Eq.(26) and then the result in Eq.(4), we have

  $$\begin{aligned} P_{1MRK}(\varrho ) =\frac{i \left( \frac{h_2 (\alpha -2 \omega ) e^{\frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}+g_4}}{\sqrt{2}}+\frac{h_1 (\alpha -2 \omega ) \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_2\right) }{\sqrt{2}}\right) }{\sqrt{\delta } \left( h_2 e^{\frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}+g_4}+h_1 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_2\right) \right) }. \end{aligned}$$

  (27)

  Putting Eq. (27) into Eq. (9) give

  $$\begin{aligned} Q_{1MRK}(\varrho ) =\frac{\beta \left( \frac{h_2 (\alpha -2 \omega ) e^{\frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}+g_4}}{\sqrt{2}}+\frac{h_1 (\alpha -2 \omega ) \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_2\right) }{\sqrt{2}}\right) ^2}{2 (2 \omega -\alpha ) \left( h_2 e^{\frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}+g_4}+h_1 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_2\right) \right) ^2}. \end{aligned}$$

  (28)

  Applying Eqs. (27) and (28) in Eq. (3) gives the required MRK wave solutions for Eq. (1) as

  $$\begin{aligned} A_{1MRK}(x,t) =\frac{i (\alpha -2 \omega ) e^{i (\beta t+\alpha x)} \left( h_2 e^{g_4+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}}+h_1 \sinh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-g_2\right) \right) }{\sqrt{2} \sqrt{\delta } \left( h_2 e^{g_4+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}}+h_1 \cosh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-g_2\right) \right) }, \end{aligned}$$

  (29)

  and

  $$\begin{aligned} B_{1MRK}(x,t) =-\frac{\beta (\alpha -2 \omega ) \left( h_2 e^{g_4+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}}+h_1 \sinh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-g_2\right) \right) ^2}{4 \left( h_2 e^{g_4+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}}+h_1 \cosh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-g_2\right) \right) ^2}. \end{aligned}$$

  (30)

• 4. Multi waves (MU): This pattern of waves is offered by⁵⁸

  $$\begin{aligned} \Omega =h_2 \cos \left( z \left( g_3 \varrho +g_4\right) \right) +h_1 \cosh \left( z \left( g_1 \varrho +g_2\right) \right) +h_3 \cosh \left( z \left( g_5 \varrho +g_6\right) \right) . \end{aligned}$$

  (31)

  By replacing Eq. (31) and its first three derivatives into Eq. (11), we gained a simplified expression. We gather identical terms together, and equate the coefficients of each expression to zero. We have the following classes of constant values:

  $$\varvec{\rm class\, 1:}\,g_1=\frac{\alpha -2 \omega }{\sqrt{2} z},~g_3=\frac{i (\alpha -2 \omega )}{\sqrt{2} z},~g_5=-\frac{\alpha -2 \omega }{\sqrt{2} z},~m=\frac{i}{\sqrt{\delta }}$$

  . Inserting these constant values into Eq. (31) and then the result in Eq. (4), we have

  $$\begin{aligned} P_{1MU}(\varrho )=\frac{i (\alpha -2 \omega ) \left( h_1 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}+g_2 z\right) +h_2 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_4 z\right) +h_3 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_6 z\right) \right) }{\sqrt{2} \sqrt{\delta } \left( h_1 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}+g_2 z\right) +h_2 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_4 z\right) +h_3 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_6 z\right) \right) }. \end{aligned}$$

  (32)

  Replacing Eq. (32) in Eq. (9) give

  $$\begin{aligned} Q_{1MU}(\varrho )=-\frac{\beta (\alpha -2 \omega ) \left( h_1 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}+g_2 z\right) +h_2 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_4 z\right) +h_3 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_6 z\right) \right) ^2}{4 \left( h_1 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}+g_2 z\right) +h_2 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_4 z\right) +h_3 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_6 z\right) \right) ^2}. \end{aligned}$$

  (33)

  The necessary MU wave solutions for Eq. (1) is obtained by applying Eqs. (32) and (33) to Eq. (3)

  $$\begin{aligned} A_{1MU}(x,t)=\frac{i (\alpha -2 \omega ) e^{i (\beta t+\alpha x)} \left( h_1 \sinh \left( g_2 z+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}\right) +h_2 \sinh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-i g_4 z\right) +h_3 \sinh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-g_6 z\right) \right) }{\sqrt{2} \sqrt{\delta } \left( h_1 \cosh \left( g_2 z+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}\right) +h_2 \cosh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-i g_4 z\right) +h_3 \cosh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-g_6 z\right) \right) }, \end{aligned}$$

  (34)

  and

  $$\begin{aligned} B_{1MU}(x,t)=-\frac{\beta (\alpha -2 \omega ) \left( h_1 \sinh \left( g_2+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}\right) +h_2 \sinh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-i g_4\right) +h_3 \sinh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-g_6\right) \right) ^2}{4 \left( h_1 \cosh \left( g_2+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}\right) +h_2 \cosh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-i g_4\right) +h_3 \cosh \left( \frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}-g_6\right) \right) ^2}. \end{aligned}$$

  (35)
  $$\varvec{\rm class\, 2:}h_1=0,~g_3=-\frac{i (\alpha -2 \omega )}{\sqrt{2} z},~g_5=\frac{\alpha -2 \omega }{\sqrt{2} z},~m=\frac{i}{\sqrt{\delta }}$$

  . Inserting these constant values into Eq. (31) and then the result in Eq. (4), we have

  $$\begin{aligned} P_{2MU}(\varrho )=\frac{i \left( \frac{h_3 (\alpha -2 \omega ) \sinh \left( z \left( g_6+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}+\frac{i h_2 (\alpha -2 \omega ) \sin \left( z \left( g_4-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}\right) }{\sqrt{\delta } \left( h_3 \cosh \left( z \left( g_6+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) +h_2 \cos \left( z \left( g_4-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) \right) }. \end{aligned}$$

  (36)

  Replacing Eq. (36) in Eq. (9) give

  $$\begin{aligned} Q_{2MU}(\varrho )=\frac{\beta \left( \frac{h_3 (\alpha -2 \omega ) \sinh \left( z \left( g_6+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}+\frac{i h_2 (\alpha -2 \omega ) \sin \left( z \left( g_4-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}\right) ^2}{2 (2 \omega -\alpha ) \left( h_3 \cosh \left( z \left( g_6+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) +h_2 \cos \left( z \left( g_4-\frac{i \varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) \right) ^2}. \end{aligned}$$

  (37)

  The necessary MU wave solutions for Eq. (1) is obtained by applying Eqs. (36) and (37) to Eq. (3).

  $$\begin{aligned} A_{2MU}(x,t)=-\frac{i (\alpha -2 \omega ) e^{i (\beta t+\alpha x)} \left( h_3 \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-g_6 z\right) +h_2 \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_4 z\right) \right) }{\sqrt{2} \sqrt{\delta } \left( h_3 \cosh \left( g_6 z+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}\right) +h_2 \cosh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_4 z\right) \right) }, \end{aligned}$$

  (38)

  and

  $$\begin{aligned} B_{2MU}(x,t)=-\frac{\beta (\alpha -2 \omega ) \left( h_3 \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-g_6 z\right) +h_2 \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_4 z\right) \right) ^2}{4 \left( h_3 \cosh \left( g_6 z+\frac{-\beta t+\alpha x-2 x \omega }{\sqrt{2}}\right) +h_2 \cosh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}-i g_4 z\right) \right) ^2}. \end{aligned}$$

  (39)

• 5. Mixed waves (MI): This pattern of waves is offered by⁵⁸

  $$\begin{aligned} \Omega =h_1 \exp \left( z \left( g_1 \varrho +g_1\right) \right) +h_2 \exp \left( -z \left( g_1 \varrho +g_2\right) \right) +h_3 \sin \left( z \left( g_3 \varrho +g_4\right) \right) +h_4 \sinh \left( z \left( g_5 \varrho +g_6\right) \right) . \end{aligned}$$

  (40)

  By replacing Eq. (40) and its first three derivatives into Eq. (11), we gained a simplified expression. We gather identical terms together, and equate the coefficients of each expression to zero. We have the following classes of constant values:

  $$\varvec{\rm class\, 1:}h_2=0,~h_3=0,~g_1=\frac{\alpha -2 \omega }{\sqrt{2} z},~g_5=-\frac{\alpha -2 \omega }{\sqrt{2} z},~m=\frac{i}{\sqrt{\delta }}$$

  . Inserting these constant values into Eq. (40) and then the result in Eq. (4), we have

  $$\begin{aligned} P_{1MI}(\varrho )=\frac{i \left( \frac{h_1 (\alpha -2 \omega ) \exp \left( z \left( \frac{\alpha -2 \omega }{\sqrt{2} z}+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}-\frac{h_4 (\alpha -2 \omega ) \cosh \left( z \left( g_6-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}\right) }{\sqrt{\delta } \left( h_1 \exp \left( z \left( \frac{\alpha -2 \omega }{\sqrt{2} z}+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) +h_4 \sinh \left( z \left( g_6-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) \right) }. \end{aligned}$$

  (41)

  Replacing Eq. (41) in Eq. (9) give

  $$\begin{aligned} Q_{1MI}(\varrho ) =\frac{\beta \left( \frac{h_1 (\alpha -2 \omega ) \exp \left( z \left( \frac{\alpha -2 \omega }{\sqrt{2} z}+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}-\frac{h_4 (\alpha -2 \omega ) \cosh \left( z \left( g_6-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) }{\sqrt{2}}\right) ^2}{2 (2 \omega -\alpha ) \left( h_1 \exp \left( z \left( \frac{\alpha -2 \omega }{\sqrt{2} z}+\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) +h_4 \sinh \left( z \left( g_6-\frac{\varrho (\alpha -2 \omega )}{\sqrt{2} z}\right) \right) \right) ^2}. \end{aligned}$$

  (42)

  Executing Eqs. (41) and (42) in Eq. (3) gives the necessary MI wave solutions for Eq. (1) as

  $$\begin{aligned} A_{1MI}(x,t) =\frac{i (\alpha -2 \omega ) e^{i (\beta t+\alpha x)} \left( h_1 e^{\frac{\alpha -\beta t+\alpha x-2 (x+1) \omega }{\sqrt{2}}}-h_4 \cosh \left( g_6 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}\right) \right) }{\sqrt{2} \sqrt{\delta } \left( h_4 \sinh \left( g_6 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}\right) +h_1 e^{\frac{\alpha -\beta t+\alpha x-2 (x+1) \omega }{\sqrt{2}}}\right) }, \end{aligned}$$

  (43)

  and

  $$\begin{aligned} B_{1MI}(x,t) =-\frac{\beta (\alpha -2 \omega ) \left( h_1 e^{\frac{\alpha -\beta t+\alpha x-2 (x+1) \omega }{\sqrt{2}}}-h_4 \cosh \left( g_6 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}\right) \right) ^2}{4 \left( h_4 \sinh \left( g_6 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}\right) +h_1 e^{\frac{\alpha -\beta t+\alpha x-2 (x+1) \omega }{\sqrt{2}}}\right) ^2}. \end{aligned}$$

  (44)

  class 2: $g_1=\frac{\alpha -2 \omega }{\sqrt{2} z},~g_3=\frac{i (\alpha -2 \omega )}{\sqrt{2} z},~g_5=-\frac{\alpha -2 \omega }{\sqrt{2} z},~m=\frac{i}{\sqrt{\delta }}.$ Replacing them in Eq. (40) and then the result in Eq. (4), we have

  $$\begin{aligned} P_{2MI}(\varrho )=-\frac{i (\alpha -2 \omega ) \left( h_2+e^{g_2} \left( -h_1 e^{\frac{(2 \varrho +1) (\alpha -2 \omega )}{\sqrt{2}}}+e^{\frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}} \left( h_4 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_6\right) -i h_3 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_4\right) \right) \right) \right) }{\sqrt{2} \sqrt{\delta } \left( h_2+e^{g_2} \left( h_1 e^{\frac{(2 \varrho +1) (\alpha -2 \omega )}{\sqrt{2}}}+i e^{\frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}} \left( h_3 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_4\right) +i h_4 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_6\right) \right) \right) \right) }. \end{aligned}$$

  (45)

  Putting Eq. (45) into Eq. (4) give

  $$\begin{aligned} Q_{2MI}(\varrho ) =-\frac{\beta (\alpha -2 \omega ) \left( h_2+e^{g_2} \left( -h_1 e^{\frac{(2 \varrho +1) (\alpha -2 \omega )}{\sqrt{2}}}+e^{\frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}} \left( h_4 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_6\right) -i h_3 \cosh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_4\right) \right) \right) \right) ^2}{4 \left( h_2+e^{g_2} \left( h_1 e^{\frac{(2 \varrho +1) (\alpha -2 \omega )}{\sqrt{2}}}+i e^{\frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}} \left( h_3 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-i g_4\right) +i h_4 \sinh \left( \frac{\varrho (\alpha -2 \omega )}{\sqrt{2}}-g_6\right) \right) \right) \right) ^2}. \end{aligned}$$

  (46)

  Executing Eqs. (45) and (46) in Eq. (3) gives the needed MI wave solutions for Eq. (1) as

  $$\begin{array} {l}A_{2MI}(x,t) \\=\frac{i (\alpha -2 \omega ) e^{i (\beta t+\alpha x)} \left( -h_2+e^{g_2 z} \left( h_1 e^{\frac{\alpha -2 (\beta t+2 x \omega +\omega )+2 \alpha x}{\sqrt{2}}}+i e^{\frac{x (\alpha -2 \omega )-\beta t}{\sqrt{2}}} \left( h_3 \cosh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}+i g_4 z\right) +i h_4 \cosh \left( g_6 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}\right) \right) \right) \right) }{\sqrt{2} \sqrt{\delta } \left( h_2+e^{g_2 z} \left( h_1 e^{\frac{\alpha -2 (\beta t+2 x \omega +\omega )+2 \alpha x}{\sqrt{2}}}+e^{\frac{x (\alpha -2 \omega )-\beta t}{\sqrt{2}}} \left( h_4 \sinh \left( g_6 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}\right) -i h_3 \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}+i g_4 z\right) \right) \right) \right) }, \end{array}$$

  (47)

  and

  $$\begin{array} {l} B_{2MI}(x,t) \\=-\frac{\beta (\alpha -2 \omega ) \left( h_2+e^{g_2 z} \left( -h_1 e^{\frac{\alpha -2 (\beta t+2 x \omega +\omega )+2 \alpha x}{\sqrt{2}}}+e^{\frac{x (\alpha -2 \omega )-\beta t}{\sqrt{2}}} \left( h_4 \cosh \left( g_6 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}\right) -i h_3 \cosh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}+i g_4 z\right) \right) \right) \right) ^2}{4 \left( h_2+e^{g_2 z} \left( h_1 e^{\frac{\alpha -2 (\beta t+2 x \omega +\omega )+2 \alpha x}{\sqrt{2}}}+e^{\frac{x (\alpha -2 \omega )-\beta t}{\sqrt{2}}} \left( h_4 \sinh \left( g_6 z+\frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}\right) -i h_3 \sinh \left( \frac{\beta t+\alpha (-x)+2 x \omega }{\sqrt{2}}+i g_4 z\right) \right) \right) \right) ^2}. \end{array}$$

  (48)

Graphical presentation and results analyses

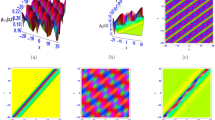
The graphical depictions of the travelling wave solutions for an integrable rsHMB model in an erbium doped fibre are shown in this section. The soliton solutions obtained in the previous section are illustrated in the graphs generated using Mathematica. Since graphical morphology affects the dynamics of traveling wave solutions, we have shown the soliton solution types in three dimensions along with their related contour and density plots.

Figure (1)(a) (3D) possesses features of a fundamental Akhmediev breather that is periodic in space and time. This breather forms through modulation instability, where a small perturbation on the background of a continuous wave grows exponentially, resulting in periodic amplification of energy. The balance between nonlinearity and group velocity dispersion (GVD) enables stable propagation. In erbium-doped fibers, this breather plays a significant role in super continuum generation and can serve as a precursor to rogue wave formation. Figure (1)(b) and (Contour Plot) shows periodic amplitude modulations, reflecting energy transfer between wave components, while Fig. (1)(d) (Density Plot) highlights peak intensity locations, essential for studying rogue wave precursors. Figure (2)(a) (3D) represents a Kuznetsov-Ma (KM) breather, which is periodic in space but localized in time. KM breathers are subject to oscillatory energy concentration in the time domain and hence are of interest for pulse compression in optical fibers. The breathers assist in controlling pulse breakup so that femtosecond pulses maintain their integrity over large distances. Figure (2)(b) (Contour Plot) captures the intensity variations and displays energy redistribution, whereas Fig. (2)(d) (Density Plot) verifies the localized energy concentration, reflecting the strong nonlinear effects. Figure (3)(a) (3D) displays a Peregrine breather, which is a localized structure and reflects an extreme energy spike that forms briefly before dissipation. It is associated with optical rogue waves, impacting high-energy optical pulse propagation and studies of optical turbulence. The Peregrine breather is central to the dynamics of instability in nonlinear fiber optics. Figure (3)(b) (Contour Plot) indicates densely populated phase lines, indicative of strong wave interactions, whereas Fig. (3)(d) (Density Plot) indicates increased energy focusing, an important characteristic of higher-order rogue waves. Figure (4)(a) (3D) displays higher-order breathers due to the nonlinear superposition of the fundamental modes. The solutions have complex interactions, resulting in higher energy localization, which is beneficial for nonlinear pulse shaping and all-optical switching. Higher-order breathers increase data transmission stability in fiber optic technology. Figure (4)(b) (Contour Plot) depicts irregular amplitude fluctuations, representing stability shifts, and Fig. (4)(d) (Density Plot) displays energy localization with some dispersion.

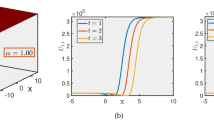
Figure (5)(a) (3D) shows a periodic lump solution, creating a stable localized oscillatory pattern. These solutions arise due to the interplay between nonlinearity and dispersion, being responsible for optical pulse stabilization and coherent optical communication. Figure (5)(b)(Contour Plot) verifies the propagation of structured waves, while Fig. (5)(d) (Density Plot) shows periodic soliton formation. Figure (6)(a) (3D) depicts another periodic lump solution with excellent spatial and temporal localization. Such structures assist in reshaping the pulse and suppressing noise to ensure reliable long-distance transmission. Figure (6)(b) (Contour Plot) is still well-organized, and Fig. (6)(c) (Density Plot) illustrates localized energy peaks crucial for soliton communications. Figure (7)(a) (3D) illustrates an M-shaped wave interacting with rogue waves and kinks solution. This configuration depicts nonlinear compression, which increases energy localization and results in extreme events. These solutions are crucial in optical switching and rogue wave generation. Figure (7)(b) (Contour Plot) illustrates asymmetric wave dynamics, whereas Fig. (7)(d) (Density Plot) displays sharp peaks showing extreme wave localization. Figure (8)(a) (3D) shows another M-shaped wave interacting with rogue waves and kinks solution with altered energy distribution, indicating the interaction between stable solitons and unstable rogue waves. These interactions are essential in high-power super continuum generation and control of optical turbulence. Figure (8)(b) (Contour Plot) reveals a transformation from rogue-wave characteristics to stable solitons, whereas Fig. (8)(d) (Density Plot) reveals secondary peaks indicative of partial dispersion.

Figures (9, 10, 11, 12) demonstrate multi-wave soliton dynamics and their interaction. Such solutions exhibit multi-soliton interaction in erbium-doped fiber, important in high-speed light wave communication and nonlinear pulse management. Figure (9)(a) (3D) is an oscillatory periodic pattern multi-wave solution important in efficient data transfer of energy. Figure (10)(a) (3D) is yet another multi-wave solution with amplitude variations and wave steepness as a result of nonlinearity induced superposition effect. Figures (11)(a) and (12)(a) (3Ds) illustrate additional multi-wave interaction, indicating coherent wave behavior pertinent to optical rogue wave management. Figures (9)(b)-(12)(b) (Contour Plots) capture rich waveform interactions, and Figs. (9)(d)C-(12)(d) (Density Plots) display localized energy hotspots and soliton stability. Figures (13, 14, 15, 16) show mixed wave dynamics with multiple nonlinear wave constituents. Figure (13)(a) (3D) displays an interaction between localized solitonic features and extended wave modes. Figure (14)(a) (3D) displays a more organized mixed profile with nonlinear resonance effects, applicable to wavelength-division multiplexing. Figure (15)(a) (3D) shows a mixed-type wave creating a solitonic wavefront, applicable to optical turbulence. Figure (16)(a) (3D) displays a complex mixed wave state with dispersive and localized wave structures occurring together. Figures (13)(b)-(16)(b) (Contour Plots) indicate nonlinear interactions, while Figs. (13)(d)-(16)(d) (Density Plots) validate localized energy bursts associated with rogue waves and instabilities.

These solitary and soliton solutions demonstrate the importance of nonlinear wave dynamics in femtosecond pulse transmission in erbium-doped fibers. Their applications are super continuum generation, pulse shaping, optical rogue wave control, and ultrafast photonic technologies, guaranteeing stable and efficient data transmission in fiber optic systems.

Remark: The 3D and 2D plots were generated using Wolfram MATHEMATICA11.1 (Wolfram Research, Inc., https://www.wolfram.com/mathematica/). Further, authors can provide the MATHEMATICA code of the simulations generated during this study. If there is any further query, can ask the corresponding author for clarification.

Fig. 1

The HB type wave function is shown by the three-dimensional, contour, and density diagrams.

Fig. 2

The HB type wave function is shown by the three-dimensional, contour, and density diagrams.

Figure (1) depicts the solution $A_{1HB}(x, t)$ corresponding to Eq. (15) for selecting parameter values $g_2=2.5,~g_4=4.2,~g_6=1.2,~h_1=0.1,~h_2=3.4,~z=1.5,~\alpha =0.1,~\beta =3.9,~\delta =9.6,~\omega =0.6.$ Figure (2)) shows the solution $B_{1HB}(x, t)$ obtained from Eq. (16) for the same choice of parameter values as Fig. (1).

Fig. 3

The HB type wave function is shown by the three-dimensional, contour, and density diagrams.

Fig. 4

The HB type wave function is shown by the three-dimensional, contour, and density diagrams.

Figure (3) shows the solution $A_{2HB}(x, t)$ representing Eq. (19) for the choice parameter values $g_2=2.5,~g_6=9.5,~h_2=3.4,~z=0.1,~\alpha =3.04,~\beta =0.8,~\delta =9.7,~\omega =3.4.$ Figure (4)) is obtained from the solution $B_{2HB}(x, t)$ corresponding to Eq. (20) for the same choice of parameter values as Fig. (3).

Fig. 5

The PL type wave function is shown by the three-dimensional, contour, and density diagrams.

Fig. 6

The PL type wave function is shown by the three-dimensional, contour, and density diagrams.

The solution $A_{1LP}(x, t)$ corresponding to Eq. (24) is depicted in Fig. (5) with the chosen parameter values $g_6=1.549,~\alpha =2.62,~\beta =9.96,~\delta =8.6,~\omega =0.6.$ Figure (6) in obtained from the solution $B_{1LP}(x, t)$ representing Eq. (25) for the same choice of parameter values as Fig. (5).

Fig. 7

The MRK type wave function is shown by the three-dimensional, contour, and density diagrams.

Fig. 8

The MRK type wave function is shown by the three-dimensional, contour, and density diagrams.

Figure (7) depicts the solution $A_{1MRK}(x, t)$ corresponding to Eq. (29) for selecting parameter values $g_2=9.95,~ g_4=5.4,~ h_1=8.6,~ h_2=4.9,~ \alpha =3.79,~ \beta =0.62,~ \delta =3.6,~ \omega =0.99.$ Figure (8)) shows the solution $B_{1MRK}(x, t)$ obtained from Eq. (30) for the same choice of parameter values as Fig. (7).

Fig. 9

The MU type wave function is shown by the three-dimensional, contour, and density diagrams.

Fig. 10

The MU type wave function is shown by the three-dimensional, contour, and density diagrams.

Figure (9) shows the solution $A_{1MU}(x, t)$ representing Eq. (34) for the choice parameter values $g_2=5.9,~ g_4=1.5,~ g_6=3.9,~ h_1=6.2,~ h_2=4.5,~ h_3=6.7,~ z=2.51,~ \alpha =3.44,~ \beta =8.2,~ \delta =7.5,~ \omega =9.9.$ Figure (10)) is obtained from the solution $B_{1MU}(x, t)$ corresponding to Eq. (35) for the same choice of parameter values as Fig. (9).

Fig. 11

The MU type wave function is shown by the three-dimensional, contour, and density diagrams.

Fig. 12

The MU type wave function is shown by the three-dimensional, contour, and density diagrams.

Figure (11) shows the solution $A_{2MU}(x, t)$ representing Eq. (38) for the choice parameter values $g_4=0.5,~ g_6=4.6,~ h_2=6.2,~ h_3=7.6,~ z=3.94,~ \alpha =4.16,~ \beta =9.1,~ \delta =0.9,~ \omega =8.9.$ Figure (12)) is obtained from the solution $B_{2MU}(x, t)$ corresponding to Eq. (39) for the same choice of parameter values as Fig. (11).

Fig. 13

The MI type wave function is shown by the three-dimensional, contour, and density diagrams.

Fig. 14

The MI type wave function is shown by the three-dimensional, contour, and density diagrams.

The solution $A_{1MI}(x, t)$ corresponding to Eq. (43) is depicted in Fig. (13) with the chosen parameter values $g_6=0.8,~ h_1=0.8,~ h_4=7.8,~ z=1.6,~ \alpha =0.76,~ \beta =0.4,~ \delta =9.3,~ \omega =0.4.$ Figure (14) in obtained from the solution $B_{1MI}(x, t)$ representing Eq. (44) for the same choice of parameter values as Fig. (13).

Fig. 15

The MI type wave function is shown by the three-dimensional, contour, and density diagrams. The plot was generated using Wolfram Mathematica 11.1 (Wolfram Research, Inc., https://www.wolfram.com/mathematica/).

Fig. 16

The MI type wave function is shown by the three-dimensional, contour, and density diagrams.

The solution $A_{2MI}(x, t)$ corresponding to Eq. (47) is depicted in Fig. (15) with the chosen parameter values $g_2=3.1~ g_4=3.6,~ g_6=0.9,~ h_1=8.6,~ h_2=2.5,~ h_3=0.7,~ h_4=0.7,~ z=1.2,~ \alpha =3.98,~ \beta =0.6,~ \delta =2.01,~ \omega =0.4.$ Figure (16) in obtained from the solution $B_{2MI}(x, t)$ representing Eq. (48) for the same choice of parameter values as Fig. (15).

Comparison

In comparison with Cui et al.³⁸ and Liu et al.³⁹, who employed Darboux transformations to investigate breather and hybrid wave solutions in the rsHMB model, the present research employs the technique of logarithmic transformation to investigate more extensive classes of nonlinear wave interactions in the rsHMB model. While Cui et al.³⁸ concentrated on breather and bright-dark solitons and Liu et al.³⁹ generalized this to higher-order hybrid waves and rogue wave interactions, we examine the complex dynamics of soliton propagation, energy localization, and nonlinear wave stability. Our results encompass basic and higher-order breathers, periodic lump solutions, interactions of M-shaped waves with rogue and kink waves, multi-wave and mixed wave dynamics, which prove their importance in femtosecond pulse transmission, pulse shaping, control of optical turbulence, and ultra-high-speed light wave communication. The MATHEMATICA 11.1 software is used for the simulations generated in this study.

Conclusion

This study examines an integrable rsHMB model in an erbium-doped fiber using periodic waves and logarithmic transformations for the first time. It focuses on lump and homoclinic breather waves, mixed wave interactions, multi-wave interactions, and M-shaped waves interacting with rogue and kink waves. Periodic lumps can shift if system conditions change, but they are stable in a moving frame. They are characterised by repeated peaks or “bumps” in space. Homoclinic breathers can show oscillations and localised patterns that cause breather splitting or fusing. They are frequently unstable and display complex interactions with their environment. The M-shaped wave has a profile with varying peaks and troughs that can become increasingly complex and unpredictable when subjected to the influence of kinks and rogue waves. These interactions cause significant distortions in the waves’ height and structure, leading to complex wave behavior. Multi waves are several wave trains or patterns that exist concurrently in various mediums, such as electromagnetic fields, sound, or water. It is possible to alter the amount of other overlapping waves by using either destructive or constructive interference. Mixed waves are created when multiple wave types, such as sinusoidal and rogue waves, combine to generate beat frequencies and other complicated patterns and behaviours.

We obtained solutions for each of these wave structures and illustrated them using three-dimensional contour and density plots generated with Mathematica software. Overall, by using the mathematical approach of the periodic wave and logarithmic transformations, this study contributes to the theoretical knowledge of wave dynamics and provides particular interpretations and applications in several scientific domains. Our findings can have ramifications for a wide range of physical phenomena and economic gains, ranging from the prediction of catastrophic wave occurrences to the optimisation of wave-based technologies. Extending these solutions to a fractional scenario is also another problem which merits attention. Another potential direction of research is the use of the exact solutions derived in this work to validate new numerical schemes to solve the rsHMB model. Indeed, exact solutions are important to verify the validity of computational methods to solve systems in physics. The solutions obtained here can be helpful to solve those problems.