Abstract
Flexible materials deform during flame propagation, altering their blockage ratio and the force exerted on the fluid due to various influencing factors. This affects gas explosion characteristics, changes the flame structure, and reduces explosion overpressure and flame speed. To determine the impact of flexible protective devices on the protection mechanism against gas explosions, this experiment used flexible obstacles (polyurethane sponge) as the protective apparatus. Employing a self-built explosion experiment platform, the research investigated methane explosion flame evolution, flame propagation speed, and explosion overpressure under various sizes of pre-positioned flexible obstacles. The study focused on observing the morphological evolution of methane explosion flames, the speed of flame spread, and the explosion overpressure in scenarios with pre-positioned obstacles of different sizes. The results showed that inserting flexible obstacles effectively reduced explosion overpressure and flame front propagation speed. Based on the working conditions set up in this experiment, the maximum rate of decrease in explosion overpressure exceeds 50% and the maximum rate of decrease in flame front velocity is around 20%. With pre-positioned flexible obstacles, as the blockage ratio of the flexible obstacle increased, the severity of deflagration also increased, with both explosion overpressure and flame front speed rising with the blockage ratio. Explosion overpressure and flame front speed also increased with the thickness of the flexible obstacle; simultaneously, the flame front position advanced with the thickness of the flexible obstacle. When constructing close-range protection devices, the height of the protection device should be lower than the protected object (H < h), and the thickness of the protection device should not be too thick.
Similar content being viewed by others
Introduction
Given global challenges such as climate change, population growth, and limited surface space, the use of underground space is increasing. More cities recognize the necessity of incorporating underground space into their construction environment management and planning strategies1. Underground space can enhance the capacity available to cities and aid recovery after acute shocks2. However, due to the enclosed nature of underground spaces and their high population density, the design of underground cities often mirrors surface cities, utilizing rigid structures like reinforced concrete to ensure stability3,4,5. This reliance on rigid structures can create explosive obstacles, which, in the event of an explosion, can cause severe damage and loss, threatening lives6,7. Natural gas, the main energy source in China, is a high-quality energy with rich reserves and high calorific value8. Whether in industrial production, or residents’ daily life, natural gas can bring convenience. However, while providing convenience, natural gas also has safety risks. In particular, because the urban underground space is closed and highly densely populated, so it is more likely to cause serious casualties and economic losses9. Therefore, the explosion of flammable gases in the urban underground space has become an important urban safety issue9.
Underground cities contain many quasi-rigid obstacles in buildings or equipment that can promote explosions. Common enclosed or semi-enclosed areas, such as tunnels and underground parking lots, often have obstacles that may accelerate flames10. The existence of rigid obstacles can easily increase the risk of explosion. Li et al.11 found that the primary function of obstacles is to generate turbulence, increasing mass and heat transfer, which accelerates flames. Similarly, G. Cicarelli12 and C. Johansen13 observed that obstacles enhance flame combustion efficiency and propagation rate. Current studies suggest that gas propagation and explosion characteristics are closely related to the number of obstacles, blockage ratio, position, and layout14,15,16,17,18,19,20. The number of obstacles and blockage ratio affect external flame size21 and flame vortex mechanisms22, increase peak gas pressure and its rate of change23,24, and lead to flame acceleration25. As the distance between the obstacle and ignition source increases, flame propagation speed first increases and then decreases26, with peak explosion pressure following a similar trend, reaching a maximum at 40 cm27. Duan et al.28 found that symmetrically distributed obstacles induce larger flame turbulence areas through vortex dynamics, increasing the flame combustion rate and explosion risk. In conclusion, the presence of rigid obstacles significantly enhances the combustion rate, explosion limit, and other characteristic parameters of methane, potentially leading to deflagration to detonation (DDT) and further complicating the explosiveness of methane gas. Therefore, the presence of quasi-rigid obstacles in underground city buildings or equipment is likely to accelerate flames and increase explosion hazards. Given the high cost or difficulty of equipping some buildings or equipment with such rigid obstacles, studying explosion control measures for these obstacles is of great significance for underground urban space safety.
Recent research has demonstrated that flexible materials alter their blockage ratio and fluid forces during explosions, influencing gas explosion characteristics, modifying flame structure, and decreasing explosion overpressure and flame speed3,29,30,31,32,33,34,35,36,37. Flexible and rigid obstacles affect gas explosions differently: flexible materials can absorb reflected waves and pressure oscillations38, deforming to reduce peak pressure and pressure rise rate, thus affecting flame speed35. The shape, blockage ratio, and thickness of flexible obstacles also impact explosion characteristics; increased thickness can raise peak pressure and flame speed39, improve impact resistance and excitation effects40, and reduce flame excitation effects41. Overall, flexible materials, with their good energy absorption, deform during flame propagation, altering flame structure and reducing explosion overpressure and flame speed, thereby inhibiting gas explosions. Duan et al.42 discovered that the presence of flexible obstacles suppresses Helmholtz oscillations and reduces explosion intensity. The experiment investigated the effects of the placement method (pre-positioned or post-positioned) and the blockage ratio of flexible obstacles. The results indicated that pre-positioning the flexible obstacles could reduce the explosion intensity to a certain extent; however, the influence on the reduction rate of explosion pressure was minimal. Based on the results of this article, this experiment will further explore, under the pre-positioned conditions of flexible protective devices, the coupled effects of blockage ratio and thickness on the changes in methane pre-mixed flame front contour, flame vortices, flame speed, and the oscillation patterns of explosion overpressure. The goal is to determine the optimal obstacle size that can best attenuate methane explosion characteristic parameters, which will serve as the morphology parameter, providing theoretical and technical support for the development of a new, scientific flexible obstacle explosion protection technology. In this experiment, flexible obstacles (polyurethane foam) were used as the flexible protective devices for the research.
Experimental methods
Experimental platform
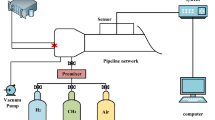
Figure 1 illustrates the self-built explosion experiment platform, comprising a gas mixing and collecting module, a pressure collection module, a high-speed imaging module, and an ignition module. The gas mixing and collecting system consist of a methane cylinder, an air compressor (providing safe air to prevent reactions between air of different humidity and methane, which could affect experimental results), a gas flow meter, and an explosion shock tube. The explosion tube, constructed of quartz glass, measures 100 cm × 10 cm × 10 cm. The pressure collection module features the NUXI-1004 pressure collection system and pressure sensors (-0.1 to 0.2 MPa), capable of effectively collecting and processing high-frequency signals. The high-speed imaging module comprises a Phantom 710 L high-speed camera and PCC graphic processing software. The ignition module consists of a homemade electric spark generator and a DC control system, utilizing a high-temperature electric spark generated by a platinum wire at the igniter to initiate the methane/air premixed gas explosion reaction. A 4-fold volume gas distribution method was used to ensure that the remaining gas in the pipeline was discharged19,20.By calculating the volume of the relevant pipeline and reading the flow meter, we estimate that the time required to fill the pipeline at ambient temperature and pressure entirely is approximately 2 min. In addition, the exhaust system located on the right side of the pipeline can effectively exhaust all gases in the exhaust pipeline, thereby promoting the air replacement process inside the pipeline, which involves using a mixture of air and fuel to replace the original air in the pipeline. This inflation phase is expected to last for 8 min.
Experimental steps and working conditions
To investigate the influence of flexible obstacles of varying sizes on the protective mechanism of methane/air explosions, the experiment employed a stoichiometric ratio of 1.0 with a methane concentration of 9.5%. The rigid obstacle was positioned 40 cm from the ignition source38, with the flexible obstacle fixed 4 cm in front of the rigid obstacle. The blockage ratio of the rigid obstacle was 0.3. To explore the optimal blockage ratio of flexible obstacles in relation to the rigid obstacles, the flexible obstacles were tested with three different blockage ratio scenarios: lower blockage ratio, same blockage ratio, and higher blockage ratio, set at 0.2, 0.3, and 0.4 respectively, with varying thicknesses of 1 and 3 cm. By comparing these scenarios with a single rigid obstacle (Case 0), the experiment assessed the impact of different sizes of flexible obstacles on methane explosions and investigated the protective role of a front-positioned flexible obstacle in complex explosion environments. The rigid obstacle was constructed of carbon fiber board, while the flexible obstacle was made of polyurethane sponge soaked in flame retardant to enhance fire resistance. Figure 2 illustrates the arrangement and installation positions for working cases 1–6 (e.g., Table 1).
Experimental analysis
Analysis of flame peak surface motion behavior
Single rigid obstacle flame propagation process
Figure 3 illustrates the flame propagation process with a rigid obstacle featuring a blockage ratio of 0.3. It can be observed that during the explosion, the flame shape transitions from spherical to finger-like, consistent with the early propagation phase of a methane explosion with a concentration of 9.5%. At 44 ms, influenced by the obstacle, the flame structure becomes partially tilted. The obstacle’s impact on the flame structure increases over time, constricting the area through which the flame can pass and distorting the flame structure. At this stage, the flame remains laminar, with heat and mass transfer occurring through molecular diffusion. In contrast, turbulent flames rely primarily on vortex mixing43. Therefore, the flame propagation process can be divided into steady state and broken state44. By 48 ms, the flame front traverses the unobstructed area below the obstacle, spreading and burning in the unburned region beneath it. This transition from laminar to turbulent flame accelerates the flame. By 52 ms, the flame front completely clears the obstacle, and the energy gained from burning in the unburned region accelerates the flame propagation speed, reaching its peak. At 55 ms, the flame surface area increases due to expansion and fluid instability. Subsequently, the flame accelerates backward, reaching the explosion vent at 60 ms, marking the end of the propagation process.
The experimental results compare the flame structures of methane explosions in scenarios 1 to 6 as the flame propagates to the explosion vent, as illustrated in Fig. 4. For a flexible obstacle thickness of 1 cm, an increased blockage ratio leads to faster arrival times of the flame front at the vent, indicating more intense explosions with a higher blockage ratio. This trend persists for a flexible obstacle thickness of 3 cm, suggesting that a slightly lower blockage ratio can mitigate the explosion severity. A comparison between scenario 1 and scenario 4 shows that the flame front reaches the vent at 68.5 ms in scenario 1 and at 63.5 ms in scenario 4, demonstrating that an increase in thickness to 0.2 blockage ratio accelerates flame propagation. This trend holds true across different blockage ratios; as the thickness of the flexible obstacle increases, the time for the flame front to reach the vent decreases, resulting in more severe explosions.
Effect of flexible obstacle with different blockage ratio on the flame structure
Figure 5 depicts the flame structure near the obstacle with a thickness of 1 cm. Due to the obstruction, unburned regions persist at both ends of the obstacle after the flame front passes through. As the flame front reaches behind the rigid obstacle, flame rollback occurs, transitioning from a laminar to a turbulent flame. Subsequently, the flame bottom is entrained into the vortex between the two obstacles, spreading and burning. By 50 ms, the flame front has completely passed through the obstacle area. By 52 ms, the flame bottom begins to spread into the unburned area between the obstacles, accelerating fuel consumption at the bottom, which promotes the acceleration of the front flame. At 54 ms, the fuel in the unburned area at the bottom is completely burned, causing the flame behind the obstacle to be immersed in a stronger vortex, leading to faster stretching and acceleration of the flame. Figure 5 also illustrates that the front end of the flexible obstacle is primarily affected by the shock wave. Furthermore, due to the different blockage ratios of the flexible obstacle, the flame structure undergoes varying degrees of deformation under its influence. This is because the different blockage ratios of the flexible obstacle result in different stretching properties, leading to varying degrees of inclination when the flame shock wave arrives. This provides channels of different sizes for the flame front to pass through, resulting in vortices of different sizes. Therefore, flexible obstacles with different blockage ratios have varying effects on the turbulence level of the flame.
Figure 6 provides a more detailed analysis of the flame at 54 ms from Fig. 5, aiming to elucidate the impact of different blockage ratios on the flame structure and turbulence level. The presence of obstacles narrows the area through which the flame can pass, hindering its progress and causing deformation in the flame structure. The impact force of the streamline generated by the shock wave as it reaches the obstacle affects the flexible obstacle at the front end, causing it to bend and bounce back. The flexibility of the obstacle leads to unpredictable changes in the flame structure. When the flame front reaches the area that is not blocked by the obstacles, the bottom of the flame spreads and burns in the unburned area between the obstacles. The brighter the flame, the higher the flame temperature45.
Figure 7 illustrates the flame structure near the obstacle with a thickness of 3 cm. The flexible obstacle, 3 cm thick, experiences the primary shockwave effect at the front. Its flexibility is influenced not only by the blockage ratio but also by the increased thickness, leading to reduced flexibility. The flame deforms and generates vortices of different sizes under its influence. As shown in Fig. 7, with the increasing thickness of the flexible obstacle, the flame front reaches the top of the obstacle in less time, resulting in a faster average speed of the flame front. By 44 ms, all flame fronts have completely passed through the obstacle area, spreading to the unburned area at the bottom by 46 ms, which accelerates the consumption of bottom fuel and is more conducive to the acceleration of the flame front. At 50 ms, the bottom fuel in the unburned area is completely burned, gaining greater gas energy. Particularly, Case 6 reaches a deflagration state at 50 ms.
Figure 8 provides a more detailed analysis of the flame at 46 ms from Fig. 7, aiming to elucidate the impact of different blockage ratios on the flame structure and turbulence level. As the flame approaches the obstacle, it inclines due to the obstruction, forming a sloping plane structure. Subsequently, as it receives kinetic energy from the burning fuel, it passes through the obstructed area from above the obstacle, causing deformation in the flame structure. When the shockwave reaches near the obstacle, the streamline impact force acts on the front end of the flexible obstacle, causing it to deform. Additionally, a flexible obstacle with a certain thickness will oscillate repeatedly when the flame front arrives, causing the flame front to vibrate back and forth, further deforming the flame structure. At this point, a flexible obstacle with a certain thickness can have a certain fire control effect.
The influence of flexible obstacle with different thicknesses on flame structure
Figure 9 captures flame images of flexible obstacles with different thicknesses but the same blockage ratio at the same moment. It is evident that as the thickness of the flexible obstacle increases, the position reached by the flame front at the same moment is farther. Therefore, the average speed of the flame front with a thickness of 3 cm is faster than that of the flame front with a thickness of 1 cm. Increasing the thickness of the flexible obstacle changes its bending characteristics; thicker obstacles are less prone to deformation and inclination. Thus, for the flame front, a thicker flexible obstacle acts more like a rigid obstacle, without producing sufficient inclination angle to expand the flame channel under the action of the shock wave, enabling smoother passage over the obstacle. However, a flexible obstacle with a certain thickness enlarges the surface area of the porous structure, effectively absorbing energy. Additionally, it can cause the flame front to oscillate repeatedly when it arrives, leading to deformation in the flame structure.
Velocity of the flame front
Figure 10(a)-(c) compares the flame front speed and position when the thickness is 1 cm, while Fig. 10(d)-(f) compares them when the thickness is 3 cm. After the insertion of the flexible obstacle, compared to the single rigid condition of Case 0, the peak flame front speed is reduced, as seen in Fig. 10(a). Additionally, the upward trend of the flame front speed around 50 ms is slowed down. Therefore, the insertion of the flexible obstacle can provide good protection by reducing the flame speed and shortening the distance the flame front reaches in the same time period. In cases 1, 2, and 3 (Fig. 10(a)-(c)), the maximum speeds are 24.821 m/s at 52 ms, 26 m/s at 52 ms, and 28.481 m/s at 54 ms, respectively. The flame front reaches positions of 815.6 mm, 826 mm, and 854.6 mm at 64 ms for cases 1, 2, and 3, respectively. Comparing these cases, with the addition of flexible obstacles with different blockage ratios, Case 3 with a blockage ratio of 0.4 has a higher peak flame front speed and reaches a farther position at the same moment. Therefore, when the thickness of the flexible obstacle is 1 cm, as the blockage ratio of the flexible obstacle increases, the peak flame front speed also increases. However, these values are smaller than when there is a single rigid obstacle. Moreover, with the increasing blockage ratio of the flexible obstacle, the distance of flame propagation in the same time period is also farther. Therefore, placing flexible obstacles in front of rigid obstacles helps protect the rigid obstacles.
Figure 10(d)-(f) illustrates that in Case 4, the maximum speed is 28.538 m/s at 48 ms, and the flame front reaches a position of 926.5 mm at 64 ms. In Case 5, the maximum speed is 28.971 m/s at 46 ms, and the flame front reaches a position of 925 mm at 64 ms. In Case 6, the maximum speed is 31.764 m/s at 44 ms, and the flame front reaches a position of 933.7 mm at 64 ms. After inserting a 3 cm thick flexible obstacle, compared to the single rigid condition of Case 0, the peak flame front speed is effectively reduced in cases 4, 5, and 6. However, at 64 ms, the flame front reaches a position greater than in Case 0, increasing the distance of flame propagation in the same time period. Among them, in Case 6 with a blockage ratio of 0.4 and a thickness of 3 cm, the peak flame front speed is not reduced, and at 64 ms, the flame front reaches the farthest position compared to all cases. Nevertheless, the 3 cm thick flexible obstacle still follows the pattern of increasing the distance of flame propagation and the peak flame front speed with the increasing blockage ratio of the pre-placed flexible obstacle in the same time period.
Figure 11 illustrates the rate of decrease in peak flame front speed and the corresponding flame structure at the peak flame front speed. It can be observed that, except for Case 6, the peak flame front speed is effectively reduced after inserting the flexible obstacle. Cases 1 and 2 exhibit a more significant decrease in peak flame front speed, with Case 2 having a peak flame front speed of 26 m/s and a decrease rate of 14.564%, and Case 1 having a peak flame front speed of 24.821 m/s and a decrease rate of 18.438%. On the right side of Fig. 11, it is evident that cases 1 and 2 have similar flame front positions at 52 ms. Compared to the single rigid condition, at the same time, the flame front reaches a shorter distance and is closer to the ignition source, further confirming the effective reduction in flame front speed. The inclusion of the flexible obstacle triggers flame turbulence earlier, as shown in the flame images on the right side. Before 52 ms, cases 1–6 already exhibit turbulent flames, while with a single rigid obstacle, the flame remains laminar until 52 ms. The addition of the flexible obstacle accelerates the transition from laminar to turbulent flames. For a flexible obstacle thickness of 3 cm, Case 4 shows the most significant decrease in peak flame front speed, with a peak flame front speed of 28.538 m/s and a decrease rate of 6.224%. The effectiveness of cases 1–6 in reducing the peak flame front speed decreases sequentially, and regardless of the thickness, the rate of decrease in peak flame front speed decreases with the increasing blockage ratio of the flexible obstacle.
Effect of different thicknesses of flexible obstacle on flame front velocity
Figure 12 compares the flame front speed and position for different thicknesses of flexible obstacles. Comparing cases with the same blockage ratio but different thicknesses to the control group, it is evident that as the thickness of the flexible obstacle increases, both the distance of flame propagation and the peak speed of the flame front increase within the same time frame. When the flame front reaches the flexible obstacle, its bending and energy-absorbing characteristics cause it to absorb some of the energy, thereby slowing down the increase in flame front speed. Simultaneously, the disturbance caused by the flexible obstacle temporarily increases the space for the flame to pass through. After passing through the obstacle, the flame front is influenced by the vortex generated behind the obstacle, further slowing down the increase in flame front speed. However, in Case 6, with the highest blockage ratio and thickest thickness, the flexibility of the flexible obstacle is not as good as in other cases, and its impact on the flame front is significantly reduced. Therefore, the flame front can pass through the obstacle area more effectively to reach the vent.
Figure 13 provides a detailed analysis of how obstacles affect the flame front and change the flame structure. It compares three scenarios: before reaching the flexible obstacle, between the flexible obstacle and the rigid obstacle, and after the rigid obstacle. Additionally, it displays the flame images at the maximum flame front speed. The overall trend of the images is consistent: the flame front speed increases with the distance of the flame front, with a brief deceleration as the flame develops incompletely, influenced by various factors. After this temporary slowdown, the flame front speed sharply increases until it approaches the obstacle, where the speed increase slows down again. Figure 13 shows that the flame front is affected by the obstacles when passing through them. The flame forms a tilted plane, with the flame tip tilting more as it gets closer to the obstacles. Near the obstacles, the flame front undergoes a turning point, resulting in an uneven flame edge. When the flame tip is above the obstacles, it forms a sharp-angled triangle. As the flame tip moves backward, the angle of the sharp angle becomes more pronounced. Only after the flame tip has completely passed through the obstacles does the flame further develop into an “M” shape.
Figure 14 illustrates the relationship between the propagation speed and position of the flame front when the obstacle thickness is 1 cm. It shows a similar trend to the curve in Fig. 13. The change in flame structure is a result of the obstacle’s influence. When the flame front reaches the flexible obstacle, the obstacle’s material properties, including good flexibility and energy absorption, partially absorb the flame, slowing down the increase in flame front speed. Additionally, the disturbance caused by the flexible obstacle temporarily increases the space for the flame to pass through. After passing through the obstacle, the flame front begins to interact with the vortices generated behind the obstacle, further slowing down the increase in flame front speed. As the flame front reaches the unburned area behind the obstacle, the fuel at the bottom burns fully, stretching the flame and accelerating it again. The initial localized turbulent combustion of the flame increases the chemical reaction area. The shear layer turbulence generated by the backward tilt of the flexible obstacle is weaker, but this mechanism is still significant during the deflagration of the flexible obstacle. The acceleration ability of the flexible obstacle is closely related to the initial explosion strength. The coupling effect of the flexible obstacle with the high-speed flow results in a lower true blockage ratio due to the faster speed. Therefore, in the turbulent acceleration mechanism caused by obstacles, the acceleration effect of the flexible obstacle is weaker than that of the rigid obstacle. Additionally, the deformation reduces the coupling effect between the hydrogen added fuel and the obstacle, decreasing the fuel’s reactivity.
Explosion overpressure change analysis
Figure 15 compares the upstream explosion overpressure under different cases. The pressure curves generally exhibit an increase followed by a sharp peak around 30 mm to 40 mm before decreasing. In cases 1 to 3, the upstream pressure curves are relatively smooth. However, in the case of the single rigid obstacle, without the protection of a flexible obstacle, there is oscillation after reaching the maximum pressure peak due to the effects of the flame and shock wave. Figure 15 shows that in cases 1, 2, and 3, where a flexible obstacle is present, the peak explosion overpressure is lower compared to the case without a rigid obstacle, indicating that the flexible obstacle effectively reduces the explosion pressure. A higher pressure peak indicates poorer suppression effects, so the flexible obstacle can effectively protect the rigid obstacle, suppressing the explosion and reducing damage. When the thickness is 1 cm, the upstream explosion pressure peak of the single rigid obstacle is higher than that with the addition of three different height flexible obstacles. Therefore, the addition of a flexible obstacle helps protect the rigid obstacle. This difference in pressure reflects the different explosion intensities guided by the two types of obstacles, with the rigid obstacle having a significantly higher explosion intensity than the flexible obstacle. Therefore, for gas explosion safety, flexible materials can better reduce the losses caused by serious accidents.
Figure 16 compares the upstream explosion overpressure. At 44ms in Case 0, the explosion overpressure rapidly increases due to the obstacle’s effect. At t = 46ms, the flame reaches above the rigid obstacle, narrowing the channel and deforming the flame structure. At t = 48ms, some flame fronts spread to the unburned area, and the energy released by the complete combustion of the fuel at the bottom rapidly increases the flame front speed, further increasing the overpressure in the space, with the final overpressure peak reaching 45.683 kPa. Case 1, 2, and 3 are restrained by the disturbance and energy absorption effects of the flexible obstacle, resulting in lower peak explosion pressures, and the upward trend of explosion pressure is also more gradual. However, in Case 2, the second wave peak reaches the peak overpressure. At this time, the blockage ratio of the flexible obstacle is the same as that of the rigid obstacle. In comparison between the effects of a single rigid obstacle and a single flexible obstacle with the same blockage ratio and thickness, under the same explosion cases, the peak explosion overpressure of the flexible obstacle is lower, and the explosion intensity of the rigid obstacle is more severe. The first wave peak is generated when the flame front passes near the flexible obstacle, and it can be clearly seen that the first wave peak is lower than the second wave peak generated when the flame front passes near the rigid obstacle. The downstream pressure curve shows two stages of increase and decrease. Figures 15 and 16 show that after adding a 3 cm-thick flexible obstacle, the time for both the upstream and downstream explosion pressure curves to reach their peaks is advanced. In Case 6, due to the large size of the flexible obstacle, it does not perform well in terms of flexibility when the flame front arrives, so the flame front speed does not decrease, and at the same time, the peak explosion overpressure downstream also increases.
Figure 17 presents a more detailed view of the downstream pressure oscillation phenomenon, showing two types of oscillations: co-frequency oscillation and oscillation separation. The co-frequency oscillation is caused by the flexible obstacle. Due to the unique material of the flexible obstacle, cases 1 to 6 exhibit similar oscillation trends. In particular, the explosion pressure oscillation curves of cases 1 and 2 overlap, reflecting the similarity in the entire explosion process after the insertion of the flexible obstacle. Furthermore, the degree of explosion pressure oscillation with the presence of the flexible obstacle is not as significant as that with a single rigid obstacle. The oscillation separation phenomenon reflects the difference in the impact of the arrangement of flexible and rigid obstacles on pressure. When the thickness of the flexible obstacle is 1 cm, the pressure oscillation separation phenomenon is significant in Case 3, while with a thickness of 3 cm, only the single rigid obstacle exhibits oscillation separation, and the other cases only exhibit co-frequency oscillation. The difference in oscillation separation is mainly caused by the flexibility of the obstacle. Helmholtz oscillation is a fluid dynamic phenomenon involving the vibration of gas in a closed or semi-closed space. The intensity of this phenomenon is directly related to the rupture response of the flexible obstacle. Rupture response is a parameter that describes the degree of inclination and curling of the obstacle when subjected to shock wave action, and different values of rupture response indicate different degrees of obstacle reaction and deformation. Oscillatory phenomena in the overpressure image during flame propagation are mainly caused by the reflection of pressure shock waves, especially in purely rigid structures. The introduction of flexible materials can change the explosion characteristics by absorbing reflected waves and pressure oscillations and deforming to reduce the peak pressure and pressure rise rate. The flexible material’s shape, obstruction rate, and thickness affect blast characteristics, with increased thickness contributing to impact resistance and increasing flame speed. Overall, flexible materials can modify the flame structure and reduce blast overpressure due to their energy-absorbing properties, effectively attenuating pressure oscillations.
Figure 18 displays the peak explosion overpressure and the corresponding decrease rate for each condition. In Case 1, the blockage ratio of the flexible obstacle is lower than that of the rigid obstacle, with a thickness of 1 cm. After inserting this type of flexible obstacle, the peak explosion overpressure rapidly decreases by 26.432 kPa to reach 19.251 kPa, a decrease of 57.86%. This reduction effectively mitigates the explosion overpressure. When the blockage ratio is the same as that of the rigid obstacle or higher, the peak overpressure is 26.829 kPa and 32.278 kPa, respectively, representing decreases of 41.271% and 29.344% compared to the single rigid obstacle. Inserting a 3 cm-thick flexible obstacle in cases 4 and 5 results in peak overpressures of 37.2 kPa and 38.325 kPa, respectively, decreasing the explosion overpressure by 18.569% and 16.107% compared to the single rigid obstacle. In Case 6, the peak overpressure is 42.715 kPa, representing a decrease of 6.497%. The addition of a certain thickness of flexible obstacles effectively reduces the explosion overpressure, but the decrease rate is lower than that of the 1 cm thickness. Therefore, increasing the thickness of the flexible obstacle will increase the explosion overpressure.
Figure 19 illustrates the peak explosion overpressure and the corresponding decrease rate for each case. In Case 1, the blockage ratio of the flexible obstacle is lower than that of the rigid obstacle. After inserting the flexible obstacle, the peak explosion overpressure decreases rapidly by 35.553 kPa to reach 48.03 kPa, a decrease of 40.397%. This reduction effectively mitigates the explosion overpressure. When the blockage ratio is the same as that of the rigid obstacle or higher, the peak overpressure is 51.468 kPa and 60.745 kPa, respectively, representing decreases of 36.12% and 24.618% compared to the single rigid obstacle. Inserting a 3 cm-thick flexible obstacle in cases 4 and 5 results in peak overpressures of 58.8896 kPa and 60.732 kPa, respectively, decreasing the explosion overpressure by 26.913% and 24.635% compared to the single rigid obstacle. In Case 6, the peak overpressure is 61.902 kPa, a decrease of 23.182%. While the addition of a certain thickness of flexible obstacles effectively reduces the explosion overpressure, the decrease rate is lower than that of the 1 cm thickness. Therefore, increasing the thickness of the flexible obstacle will increase the explosion overpressure.
Figures 20 and 21 compare the pressure rise rate (dp/dt) overpressure. The pressure rise rate is a measure of the combustion rate and also an indicator of explosion intensity46. Figure 20 shows that the upstream pressure rise rate increases with the blockage ratio of the flexible obstacle. Comparing cases 1, 2, and 3 with a thickness of 1 cm, Case 1 has the smallest pressure rise rate, reaching 19,045.4 kPa/s, while Case 3 has the largest pressure rise rate, reaching 389,696.4 kPa/s. Comparing cases 4, 5, and 6 with a thickness of 3 cm, Case 4 has the smallest pressure rise rate, reaching 31,018 kPa/s, while Case 6 has the largest pressure rise rate, reaching 46,755.8 kPa/s. Figure 21 compares cases 1, 2, and 3 with a thickness of 1 cm. Case 1 has the smallest pressure rise rate, reaching 56,976.8 kPa/s, while Case 2 has the largest pressure rise rate, reaching 65,588.8 kPa/s. In this case, Case 2 does not follow the rule that the pressure rise rate increases with the blockage ratio of the flexible obstacle. Comparing cases 4, 5, and 6 with a thickness of 3 cm, Case 4 has the smallest pressure rise rate, reaching 43,576 kPa/s, while Case 6 has the largest pressure rise rate, reaching 76,146.6 kPa/s.
Table 2 presents the standard deviation of flame front speed and explosion pressure. To ensure experimental rigor, each experiment was conducted three times. Therefore, by comprehensively analyzing all experimental data, we calculated the peak flame front speed, upstream maximum positive pressure, upstream maximum negative pressure, downstream maximum positive pressure, downstream maximum negative pressure, as well as the corresponding decrease rates of peak flame front speed and explosion pressure peak. According to Table 2, the peak flame front speed increases sequentially with the change in conditions, while the decrease rate of peak flame front speed decreases sequentially. Similarly, the maximum positive pressure upstream also follows this pattern. However, in Case 2, the maximum negative pressure upstream is higher than in Case 3, and in Case 4, the maximum negative pressure upstream is higher than in Case 5. Although the maximum positive pressure downstream does not exhibit a sequential change with the varying conditions, when the thickness is the same, the peak flame front speed increases with the increase in the blockage ratio of the flexible obstacle, and the decrease rate of peak flame front speed decreases with the increase in the blockage ratio of the flexible obstacle.
Flame acceleration mechanism
After ignition, the flame evolves from a hemispherical shape to a finger-shaped structure in a laminar flame process. Prior to encountering the obstacle, the flame front advances quickly and smoothly. However, as it interacts with the obstacle, the passage constricts, causing the flame front to tilt. Subsequently, the flame spreads and burns in the unburned area between the two obstacles. The pressure wave reflects off the wall, altering the pressure gradient at the flame’s leading edge so that it is no longer parallel to the density gradient. This creates an oblique pressure effect that induces turbulence47. The no-slip boundary condition at the wall leads to uneven flow, which, along with turbulence, distorts the flame front, increases the combustion rate, and accelerates the flame48. During the initial stages of flame development, the rapid expansion of the flame area due to turbulence ahead of the flame is predominant. When the flame traverses the obstacle, its surface area expands due to thermal expansion and fluid instability, enlarging the contact area with unburned gas and further accelerating the reaction rate. The expansion of combustion products propels the flame forward.
Front-mounted flexible obstacles are effective in reducing blast intensity. However, the propagation of the flame in the obstruction channel generates a new fuel mixture between the obstacles. The gas expansion caused by the delayed combustion of the fuel in the pockets produces a strong jet in the unobstructed part of the channel, leading to flame acceleration48. The greater the thermal expansion, the larger the blockage ratio, and the stronger the acceleration effect49. Nonetheless, the prefabricated flexible obstacle can effectively reduce the flame acceleration caused by the pocket effect. As shown in Fig. 22, the protrusion below the flame is quickly drawn into the vortex in the pocket between the two obstacles. At this point, the fuel in the pocket begins to burn and expand, accelerating the flame. Simultaneously, the flexible obstacle tilts to the left under the action of the flame front, widening the distance between the two obstacles. This allows the unburned fuel to spread and ignite prematurely, reducing the volume of unburned fuel in the pocket. Additionally, the flexible obstacle has an energy absorption effect. As the unburned fuel in the pocket burns and provides energy, the flexible obstacle absorbs some of this energy, effectively reducing the flame acceleration caused by the pocket effect. Due to the different blockage ratios of the flexible obstacles, the expansion degrees of the vortices in the pockets between the two obstacles vary. The right end is fixed with the same rigid obstacle at a distance of 40 cm from the ignition source, so the expansion degree of the vortex at the right end is similar. With an increase in the blockage ratio of the flexible obstacle, the expansion degree of the left end of the pocket increases, and the overall range of the vortex in the pocket al.so increases. For a 3 cm thick flexible obstacle, the expansion degree of the vortex in the pocket between the two obstacles increases with the blockage ratio of the flexible obstacle. Furthermore, in Case 6, the turbulence level reached that of cases 4 and 5 at 48 ms because the blockage ratio and thickness were the largest under this condition, and the flame shock wave was not sufficient to cause deformation, thus indicating an effect similar to that of two rigid obstacles.
To illustrate how a prefabricated flexible obstacle effectively reduces flame acceleration caused by the pocket effect, Fig. 23 compares two cases with the same obstacle blockage ratio. In the figure, “BR” represents the obstacle blockage ratio, “α” represents the actual blockage ratio of the flexible obstacle, “d” represents the distance between the two obstacles, and “\(\Delta {\text{d}}\)” represents the actual distance between the obstacles during the explosion process. The 1 cm thick flexible obstacle, propelled by the flow field, tilts and accelerates the contact area between the fuel and the flame inside the pocket, as depicted in the upper half of Fig. 23. As “\(\Delta {\text{d}}\)” decreases, the obstacle’s deformation leads to a slight decrease in the blockage ratio. This expands the range of vortex expansion inside the pocket of the flexible obstacle, causing the fuel to burn more rapidly and aiding in the consumption of fuel inside the pocket. For the 3 cm thick flexible obstacle, the increase in thickness reduces the range of the pocket formed between the two obstacles. Meanwhile, under the action of the explosion shock wave, there is a slight decrease in the obstacle blockage ratio, leading to the rapid combustion of the fuel accumulated inside the pocket and an expansion of the vortex range.
Figure 24 compares all cases, and through a comprehensive analysis of characteristic parameters such as flame structure, flame propagation speed, and explosion overpressure, it is evident that all cases, except for Case 6, effectively reduce these parameters. Among them, the damage level caused by Case 1 is the lowest. Therefore, the optimal arrangement when flexible and rigid facilities are in close proximity at the explosion site should have the blockage ratio (BR) of the flexible obstacle lower than that of the rigid obstacle, and the flexible obstacle should be thinner. Despite the limitations of the experimental platform, the simulated anti-explosion buildings in underground spaces to some extent reflect the strengthening effect against explosions. To ensure the operational process and environmental protection mechanism of urban underground space development, specific requirements are proposed for the layout and height setting of rigid and flexible buildings in underground spaces. As illustrated in Fig. 24, the arrangement of structures should first prioritize flexible structures, where H < h. This arrangement can weaken the structure’s resonant effect and effectively reduce oscillations and impact phenomena. However, it should be noted that the diversity and complexity of construction during the operation of underground restricted spaces are similar to those of open spaces on the ground.
The development and utilization of underground spaces are a solution to global challenges such as climate change, population growth, and surface space constraints, and are integral to the construction of urban complexes50. Ensuring the safety of urban underground space development requires effective protection of buildings or equipment, similar to rigid obstacles, and the study of explosion behavior of premixed gases in such environments. In this experiment, polyurethane sponge and carbon fiber board with varying breathability were used to simulate flexible and rigid obstacles, respectively. Methane explosion characteristic parameters, including flame structure, flame front speed, and explosion overpressure, were collected to assess the influence of these obstacles on methane combustion and explosion characteristics. The optimal obstacle size for attenuating methane explosion characteristic parameters was determined. Through a comprehensive analysis of the blockage ratio and thickness of flexible obstacles, and an investigation of changes in flame and pressure waves, it was found that the condition with a blockage ratio of 0.2 and a thickness of 1 cm had the best explosion suppression effect. Therefore, the arrangement of structures should prioritize flexible structures, where H < h, and the protective device thickness should not be excessive (e.g., Fig. 25). This arrangement can weaken the resonant effect of the structure and effectively reduce oscillations and impact phenomena. These research findings have significant implications for the safety management of underground spaces and the design of protective facilities.
Conclusion
This study investigated methane explosion characteristics in the presence of flexible obstacles (with blockage ratios of 0.2, 0.3, and 0.4) at the front. Analysis of methane explosion parameters, such as flame structure, flame front speed, and explosion overpressure collected from experiments, revealed changes in methane premixed flame front shape, flame vortex, flame speed, and explosion overpressure oscillation due to the presence of flexible obstacles at the front. The optimal obstacle size for attenuating methane explosion parameters was determined. The following conclusions were drawn from the experimental results:
-
(1)
Under the condition of front flexible obstacles, the severity of deflagration increases with the increase of flexible obstacle blockage ratio (BR), and the explosion overpressure and flame front speed increase accordingly. However, compared with the control group, the placement of flexible obstacles effectively reduced the explosion overpressure and flame front propagation speed. Based on the working conditions set up in this experiment, the maximum rate of decrease in explosion overpressure exceeds 50% and the maximum rate of decrease in flame front velocity is around 20%.
-
(2)
Under the condition of front flexible obstacles, the explosion overpressure and flame front speed increase with the increase of flexible obstacle thickness; concurrently, the flame front position increases with the increase of flexible obstacle thickness. The increase in flexible obstacle thickness alters its bending performance, with thicker obstacles being less prone to deformation and tilt, behaving more like rigid obstacles and increasing the severity of deflagration.
-
(3)
Comprehensive analysis of the flexible obstacle blockage ratio and thickness of two factors, to examine the flame wave and pressure wave change rule, we found that the BR of 0.2, thickness of 1 cm of the cases of the best effect of explosion suppression. Therefore, in the construction of the arrangement of proximity protection devices, first of all, to meet the premise of flexible structure, the height of the protective device is lower than the protected object H < h, while the thickness of the protective device should not be too thick.
Data availability
The datasets generated during and/or analysed during the current study are not publicly available due to [the research data in the article is voluminous and not easy to upload, and the data involves industry secrets not to be disclosed] but are available from the corresponding author on reasonable request.
References
Von der Tann, L., Sterling, R., Zhou, Y. & Metje, N. Systems approaches to urban underground space planning and management–A review. Undergr. Space 5 (2), 144–166. https://doi.org/10.1016/j.undsp.2019.03.003 (2020).
Admiraal, H. & Cornaro, A. Future cities, resilient cities–The role of underground space in achieving urban resilience. Undergr. Space 5 (3), 223–228. https://doi.org/10.1016/j.undsp.2019.02.001 (2020).
Bakke, J. R., van Wingerden, K., Hoorelbeke, P. & Brewerton, B. A study on the effect of trees on gas explosions. J. Loss Prev. Process Ind. 23 (6), 878–884. https://doi.org/10.1016/j.jlp.2010.08.007 (2010).
Ma, Q., Zhang, Q., Pang, L., Huang, Y. & Chen, J. Effects of hydrogen addition on the confined and vented explosion behavior of methane in air. J. Loss Prev. Process Ind. 27, 65–73. https://doi.org/10.1016/j.jlp.2013.11.007 (2014).
Chow, S. K., Cleaver, R. P., Fairweather, M. & Walker, D. G. An experimental study of vented explosions in a 3: 1 aspect ratio cylindrical vessel. Process Saf. Environ. Prot. 78 (6), 425–433. https://doi.org/10.1205/095758200530970 (2000).
Park, D. K. et al. The role of forensic anthropology in the examination of the Daegu subway disaster (2003, Korea). J. Forensic Sci. 54 (3), 513–518. https://doi.org/10.1111/j.1556-4029.2009.01027.x (2009).
Wang, L. et al. Experimental investigation of methane-oxygen detonation propagation in tubes. Appl. Therm. Eng. 123, 1300–1307. https://doi.org/10.1016/j.applthermaleng.2017.05.045 (2017).
Cao, J. et al. Suppression effects of energy-absorbing materials on natural gas explosion in utility tunnels. Energy 281, 128262. https://doi.org/10.1016/j.energy.2023.128262 (2023).
Li, Y. et al. Assessment of gas explosion risk in underground spaces adjacent to a gas pipeline. Tunn. Undergr. Space Technol. 131, 104785. https://doi.org/10.1016/j.tust.2022.104785 (2023).
Goodwin, G. B., Houim, R. W. & Oran, E. S. Effect of decreasing blockage ratio on DDT in small channels with obstacles. Combust. Flame 173, 16–26. https://doi.org/10.1016/j.combustflame.2016.07.029 (2016).
Li, Q., Wei, Z., Lv, Z., Guo, W. & Liu, X. The behaviors of supersonic combustion wave through a perforated plate in a stoichiometric mixtures of H2/CH4/O2 and H2/O2. Fuel 317, 123092. https://doi.org/10.1016/j.fuel.2021.123092 (2022).
Ciccarelli, G. Dorofeev. Flame acceleration and transition to detonation in ducts. Prog. Energy Combust. Sci. 34 (4), 499–550. https://doi.org/10.1016/j.pecs.2007.11.002 (2007).
Johansen, C. & Ciccarelli, G. Modeling the initial flame acceleration in an obstructed channel using large eddy simulation. J. Loss Prev. Process Ind. 26 (4), 571–585. https://doi.org/10.1016/j.jlp.2012.12.005 (2013).
Qiming, X., Guohua, C., Qiang, Z. & Shen, S. Numerical simulation study and dimensional analysis of hydrogen explosion characteristics in a closed rectangular duct with obstacles. Int. J. Hydrog. Energy. 47 (92), 39288–39301. https://doi.org/10.1016/j.ijhydene.2022.09.091 (2022).
Cao, W. et al. Energy output characteristics and safety design of Al-AlH3 composite dust for energetic material additive. Combust. Flame 254, 112842. https://doi.org/10.1016/j.combustflame.2023.112842 (2023).
Vyazmina, E. & Jallais, S. Validation and recommendations for FLACS CFD and engineering approaches to model hydrogen vented explosions: effects of concentration, obstruction vent area and ignition position. Int. J. Hydrog. Energy. 41 (33), 15101–15109. https://doi.org/10.1016/j.ijhydene.2016.05.189 (2016).
Zhang, T. et al. Insight into energy release characteristics of TiH2 dust explosion through ignition experiments and molecular dynamic simulations. Process Saf. Environ. Prot. 185, 853–863. https://doi.org/10.1016/j.psep.2024.03.061 (2024).
Song, X. et al. Visualization of the external flow field during a vented explosion for hydrogen-air mixtures: effects of hydrogen concentrations and vent areas. Fuel 327, 124965. https://doi.org/10.1016/j.fuel.2022.124965 (2022).
Zhang, Z., Gao, W., Jiang, H., Zheng, G. & Bai, Q. Explosion mechanism of nano-sized dust cloud in interconnected vessels. Combust. Flame 259, 113135. https://doi.org/10.1016/j.combustflame.2023.113135 (2024).
Zhang, K. et al. Effect of hydrogen concentration on the vented explosion of hydrogen–air mixtures in a 5-m-long duct. Process. Saf. Environ. Prot. 162: 978–986. https://doi.org/10.1016/j.psep.2022.05.003 (2022).
Song, X. et al. Effects of hydrogen concentration, number of obstacles, and blockage ratio on vented hydrogen-air explosions and its consequence analysis. Appl. Therm. Eng. 249, 123398. https://doi.org/10.1016/j.applthermaleng.2024.123398 (2024).
Chen, P., Li, Y., Huang, F., Guo, S. & Liu, X. Experimental and LES investigation of premixed methane/air flame propagating in a chamber for three obstacle BR configurations.. J. Loss Prev. Process Ind. 41, 48–54. https://doi.org/10.1016/j.jlp.2016.11.005 (2016).
Ahmed Alharbi, A. R., Masri, Salah, S. & Ibrahim Turbulent premixed flames of CNG, LPG, and H2 propagating past repeated obstacles. Exp. Thermal Fluid Sci. 56. https://doi.org/10.1016/j.expthermflusci.2013.11.012 (2014).
Zheng, K. et al. Explosion behavior of non-uniform methane/air mixture in an obstructed duct with different blockage ratios. Energy 255, 124603. https://doi.org/10.1016/j.energy.2022.124603 (2022).
Cai, P. et al. Effects of fuel component, airflow field and Obstacles on explosion characteristics of hydrogen/methane mixtures fuel. Energy 265, 126302. https://doi.org/10.1016/j.energy.2022.126302 (2023).
Niu, Y., Shi, B. & Jiang, B. Experimental study of overpressure evolution laws and flame propagation characteristics after methane explosion in transversal pipe networks. Appl. Therm. Eng. 154, 18–23. https://doi.org/10.1016/j.applthermaleng.2019.03.059 (2019).
Liu, L., Song, S., Ge, H., Wang, Y. & Tian, F. Study on influence of arrangement of Obstacles on characteristics of methane-air explosion. China Energy Environ. Prot. 44 (03), 55–61. https://doi.org/10.19389/j.cnki.1003-0506.2022.03.010 (2022).
Duan, Y. et al. Effects of porous materials with different thickness and obstacle layout on methane/hydrogen mixture explosion with low hydrogen ratio. Int. J. Hydrog. Energy 47 (63), 27237–27249. https://doi.org/10.1016/j.ijhydene.2022.06.065 (2022).
Johnson, D. M. The potential for vapour cloud explosions–Lessons from the Buncefield accident. J. Loss Prev. Process Ind. 23 (6), 921–927. https://doi.org/10.1016/j.jlp.2010.06.011 (2010).
Na’inna, A. M., Phylaktou, H. N. & Andrews, G. E. The acceleration of flames in tube explosions with two Obstacles as a function of the obstacle separation distance. J. Loss Prev. Process Ind. 26 (6), 1597–1603. https://doi.org/10.1016/j.jlp.2013.08.003 (2013).
Na’inna, A. M., Phylaktou, H. N., Andrews, G. E. & Andrews Explosion flame acceleration over obstacles: effects of separation distance for a range of scales. Process Saf. Environ. Prot. 107, 309–316. https://doi.org/10.1016/j.psep.2017.01.019 (2017).
Gao, K., Li, S., Liu, Y., Jia, J. & Wang, X. Effect of flexible Obstacles on gas explosion characteristic in underground coal mine. Process Saf. Environ. Prot. 149, 362–369. https://doi.org/10.1016/j.psep.2020.11.004 (2021).
Sun, W. et al. Insight into vented explosion mechanism and premixed flame dynamics in linked vessels: influence of membrane thickness and blocking rate. J. Loss Prev. Process Ind. 72, 104581. https://doi.org/10.1016/j.jlp.2021.104581 (2021).
Gamezo, V. N., Ogawa, T. & Oran, E. S. Flame acceleration and DDT in channels with obstacles: effect of obstacle spacing. Combust. Flame 155 (1), 302–315. https://doi.org/10.1016/j.combustflame.2008.06.004 (2008).
Li, Q. et al. Experimental study of flame propagation across flexible Obstacles in a square cross-section channel. Int. J. Hydrog. Energy 44 (7), 3944–3952. https://doi.org/10.1016/j.ijhydene.2018.12.085 (2019).
Quan, L., Shouxiang, L., Mingjun, X., Yanming, D. & Changjian, W. Comparison of flame propagation in a tube with a flexible/rigid Obstacle. Energy Fuels 30 (10), 8720–8726. https://doi.org/10.1021/acs.energyfuels.6b01594 (2016).
Xu, Y., Huang, Y. & Ma, G. A review on effects of different factors on gas explosions in underground structures. Undergr. Space 5 (4), 298–314. https://doi.org/10.1016/j.undsp.2019.05.002 (2020).
Yu, S. et al. The influence of flexible/rigid obstacle on flame propagation and blast injuries risk in gas explosion. Energy Sour. Part A Recover. Utilization Environ. Eff. 45 (2), 4520–4536. https://doi.org/10.1080/15567036.2023.2205357 (2023).
Chen, X. et al. Effect of different types of Obstacles on venting dynamics of methane/air premixed gas. J. Saf. Environ. 23 (04), 1101–1107. https://doi.org/10.13637/j.issn.1009-6094.2022.0073 (2023).
Liu, S. et al. Experimental study on influence of flexible obstacle thickness on methane explosion excitation effect. Coal Technol. 41 (01), 106–110. https://doi.org/10.13301/j.cnki.ct.2022.01.024 (2022).
Qiao, Z., Ma, H. & Deng, L. Research on the influence of small space flexible Obstacles on gas explosion based on Charlette model. J. Saf. Environ. 22 (05), 2420–2427. https://doi.org/10.13637/j.issn.1009-6094.2021.0754 (2022).
Duan, Y. et al. Study on flexible/rigid protection mechanism of hydrogen/methane premixed gas explosion in urban underground space. Process Saf. Environ. Prot. 182, 808–822. https://doi.org/10.1016/j.psep.2023.12.028 (2024).
Poinsot, T. J., Haworth, D. C. & Bruneaux, G. Direct simulation and modeling of flame-wall interaction for premixed turbulent combustion. Combust. Flame 95(1–2): 118–132. https://doi.org/10.1016/0010-2180(93)90056-9. (1993).
Liu, G. et al. Effect of hydrogen addition on explosion characteristics of premixed methane/air mixture under different equivalence ratio distributions. Energy 276, 127607. https://doi.org/10.1016/j.energy.2023.127607 (2023).
Yu, M. et al. Effect of Obstacles on explosion characteristics of methane/hydrogen. Explosion Shock Waves. 38 (01), 19–27. https://doi.org/10.11883/bzycj-2017-0172 (2018).
Liu, T., Li, Y. & Luo, H. Experimental study on explosion pressure variation law of coal dust with different degrees of metamorphism. Explosion Shock Waves 39 (9), 155–162. https://doi.org/10.11883/bzycj-2018-0265 (2019).
Duan, Y. et al. Mechanism of accelerating premixed hydrogen/methane flame with flexible obstacles. Int. J. Hydrog. Energy 64, 1021–1029. https://doi.org/10.1016/j.ijhydene.2024.03.279 (2024).
Valiev, D., Bychkov, V., Akkerman, V. Y., Law, C. K. & Eriksson, L. E. Flame acceleration in channels with Obstacles in the deflagration-to-detonation transition. Combust. Flame 157 (5), 1012–1021. https://doi.org/10.1016/j.combustflame.2009.12.021 (2010).
Bychkov, V., Valiev, D. & Eriksson, L. E. Physical mechanism of ultrafast flame acceleration. Phys. Rev. Lett. 101 (16), 164501. https://doi.org/10.1103/physrevlett.101.164501 (2008).
Bartel, S. & Janssen, G. Underground Spatial planning–Perspectives and current research in Germany. Tunn. Undergr. Space Technol. 55, 112–117. https://doi.org/10.1016/j.tust.2015.11.023 (2016).
Acknowledgements
This work was supported by the National Key R&D Program of China (2024YFC3013805); Key Science and Technology Project of Ministry of Emergency Management of the People’s Republic of China (2024EMST070703); Major Special Projects of Guizhou Province’s Science and Technology Plan ([2024]029); Science and Technology Research Program of Chongqing Municipal Education Commission (KJZD-K202401501). Thanks.
Author information
Authors and Affiliations
Contributions
Qinghua Zhang: Investigation, Methodology, Data curation, Funding acquisition, Writing - original draft.Yulong Duan: Carried out experiments, Investigation, Data curation, Softwar, Methodology.Xianqi Duan: Conceptualization, Resources, Funding acquisition, Writing - review & editing, Writing - original draft.Rui Lang: Conceptualization, Data curation, Methodology, Softwar, Writing - review & editing.Jun Long: Data curation, Methodology, Software, Writing - review & editing.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhang, Q., Duan, Y., Duan, X. et al. Dimensional study of flexible protection device based on methane explosion protection mechanism. Sci Rep 15, 10570 (2025). https://doi.org/10.1038/s41598-025-95341-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-95341-y