Introduction

The success of industries like automotive and aerospace depends on the productivity, quality, and accuracy of the drilled holes, as they create millions of holes per year1. According to recent surveys, manufacturers spend 50–70% of their overall manufacturing time on the hole-making process2. The use of nanocoolant particles affects machining performance and material properties. Researchers empirically investigates their impact on the corrosion rate of 316 stainless steel, ensuring durability and sustainability in manufacturing3. The process of drilling is characterized by the creation of a hole in the shape of a cylinder on the workpiece. Drilling is used extensively in various sectors. For instance, nuclear energy central heat exchangers need up to 16,000 holes for refrigeration tube construction4. Also, in the aerospace sector, millions of holes are needed to connect various components of the fuselage of an aircraft, and in the automotive sector, drilling accounts for as much as 40% of the total material removed5. With the advancement of manufacturing technologies, there has been a growing need in the aerospace, electronics, biomedical, and automotive industries for precise and small holes measuring less than 0.1 mm. These industries require such holes for many applications like turbine blades and injection nozzles6. Drilling micro-holes in difficult-to-cut materials might be difficult or impossible using conventional drilling processes. The primary issues associated with conventional drilling methods include the need for specialized machine tools, tool vibration, burrs, expensive initial investments, proper lubrication, etc7. Hence, non-conventional drilling techniques were implemented to enhance the ability to create holes in intricate shapes and difficult-to-machine materials8. An alternative to conventional drilling techniques is the use of thermal, chemical, electrical, or abrasive forces, or a combination of these, to remove material from a material rather than the applied force6.

Currently, various industries are employing AWJD because of its exceptional ability to cut various materials, generate minimal or no heat, eliminate burrs, and maintain excellent dimensional stability in drilled holes. In 1980, Dr. Hashish discovered the technique of incorporating abrasives into a regular waterjet, resulting in the invention of the first abrasive waterjet9. Since its invention over two decades ago, the Abrasive Waterjet (AWJ) process has been popular because of its many benefits over electrochemical, laser beam, and electric-discharge machining. The AWJM is particularly suited for dealing with the anisotropic and heterogeneous character of composites, which poses problems for typical machining procedures10. This method is used to drill hard-to-cut materials and applications such as deep hole drilling make excellent use of it11.

Literature review

This section deals with the AWJD performed on various materials and different optimization techniques that have been utilized to optimize the AWJD input parameters to enhance the hole characteristics. Qasem et al.12 reported that Water Pressure (WP) and Abrasive Mass Flow Rate (FR) were inversely related to Kerf Angle (KA) and Overcut (OC) on X5CrNi18-10 stainless steel, whereas Traverse Rate (TR) increased both. Chellaganesh et al.13 performed drilling on SS 316L utilizing an Abrasive Waterjet Machining (AWJM), revealing that WP and angle of contact are the primary factors affecting the erosion wear of the material. The erosive wear consistently increased with WP and decreased with an impingement angle of 60°. Llanto et al.14 performed contour cutting on AISI 304L, according to the results, decreasing the TR values that produced minimum KA. In addition, higher TR and material thickness lead to higher MRR. Karthik et al.15 conducted AWJM machining on stainless steel 304, revealing an increased FR and a reduced TR in a minimal kerf top width. Balaji et al.16 conducted a drilling experiment on ceramic-coated superalloy, revealing that the top and bottom diameters of the drilled hole and OC exhibited a linear increase with the Standoff Distance (SD). Shanmugam et al.17 investigated the influence of AWJM process parameters, focusing on reducing the taper ratio and OC. The relationship between the chosen drilling parameters and the resultant responses was examined using Analysis of Variance (ANOVA). Chen et al.18 conducted AWJ contour cutting to analyze the shape errors that occurred during the machining of various profiles. The analysis revealed that the reduced nozzle TR is the primary cause of OC. Nair and Kumaran19 conducted a hole drilling operation on Inconel 617, revealing that higher WP reduces the Top Overcut (TOC). Increased SD and FR increase the TOC. Further, increased WP increases the Bottom Overcut (BOC) and Depth Averaged Radial Overcut (DAROC). The experimental findings of Hlavac et al.20 indicated that the impacts of undercut and OC can be significantly mitigated by modifying the jet tilt angle and TR. Li et al.21 examined the hole quality of plain woven CFRP laminates and revealed that the augmented water-legging effect led to increased OC. Ramulu et al.22 experimental results showed that the OC was greater at the jet entry side than at the exit side. This can be attributed to the initial high-energy abrasive jet at the entry of the cut in the wear zone, which diminished with increasing penetration depth. The experimental findings of Popan et al.23 indicate that the OC at the cut-in and cut-out points of AWJ on CFRP is significantly reduced, but not eliminated. Wu et al.24 highlighted that the OC generated during small deep hole drilling resulted from inadequate TR of the cutting head at the cut-in/cut-out zone. Bachchha25 conducted AWJ machining on an Al-Al2O3 metal matrix composite. According to the study, the OC was significantly affected by the SD.

To obtain a hole with better features, researchers have used several optimization techniques to optimize the process parameters namely WP, FR, SD, and TR. Kumar et al.26 studied the effects of AWJM drilling variables on glass fiber-reinforced polymer. The Taguchi technique was used in the experimental design, and the data were analyzed using ANOVA. The experimental results showed that WP and TR were the two most important variables influencing the KA and OC. For AWJ cutting of AA6061, Chakraborty and Mitra27 used the grey wolf optimizer technique to evaluate MRR, KA, OC, and Surface Roughness (SR). Deaconescu et al.28 utilized response surface methodology to optimize AWJM process parameters while machining X2 CrNiMo 17-12-2 stainless steel. The proposed optimization method effectively optimized the process parameters and produced better results on AWJM responses. Nair et al.29 applied two different heuristic optimization techniques such as a genetic algorithm and simulated annealing to optimize the AWJD parameters, viz. WP, SD, and FR on the responses OC, circularity, and drill rate. Both algorithms produced almost similar results, but the genetic algorithm yielded the results in a shorter time than the simulated annealing technique. Dahiya et al.30 experimental findings indicated that higher WP and FR reduce kerf taper and improve surface quality, but increasing TR and SD increase these kerf characteristics during AWJM machining on GFRP. Wan et al.31 utilized the adaptive decreasing method multi-objective Jaya algorithm to optimize the AWJ milling settings for Ti6Al4V alloy. The operational efficiency of the devised algorithm surpasses that of the Mo-Jaya algorithm by 32%. Venkateshwar Reddy et al.32 employed two distinct multi-objective optimization techniques: weighted aggregated sum product assessment (WASPAS) and multi-objective optimization based on ratio analysis (MOORA) to minimize the KA and OC generated during the machining of Inconel 625. Dahiya et al.33 used Response Surface Methodology (RSM) and Taguchi-based Grey Relational Analysis (GRA) to evaluate their efficacy in multi-response optimization. The findings showed that increased WP, FR, reduced TR, and SD improve surface quality and dimensional accuracy. The RSM desirability technique outperformed the Taguchi-GRA method in terms of SR, kerf taper, and maximum delamination length, with percentage errors below 7.23%.

Several optimization techniques have been employed to mitigate the influence of the AWJD process parameters over various responses. Recent research has proved GHO’s excellent performance in terms of convergence speed and solution accuracy across a wide range of applications, including feature selection, engineering design, and energy optimization34. Saremi et al.35 developed the GHO, which is inspired by grasshoppers’ natural swarming behavior and allows for a dynamic balance of exploration and exploitation. This balance is critical for solving complex, high-dimensional, multi-modal optimization problems, where many traditional algorithms such as Genetic Algorithms (GA), Particle Swarm Optimization (PSO), Artificial Neural Networks (ANN), and Non-Dominated Sorting Genetic Algorithm (NSGA-II) demand a substantial amount of training data and are prone to overfitting, especially in situations where datasets are limited. Also, these techniques either converge prematurely to local optima or necessitate extensive parameter tuning36,37. GHO’s capacity to alter its search patterns based on the issue environment makes it particularly suitable for the AWJD deep hole drilling process.

Numerous studies have investigated the AWJD process, intending to increase drilling efficiency and performance. However, there is still a major gap in understanding the phenomena of overcutting, especially in precision-critical applications like automotive and biomedical sectors that demand precise deep-hole drilling. The current literature does not provide complete insights into the correlation between AWJD process parameters and the extent of overcut on top, bottom, and depth averaged levels, particularly when drilling deep holes in materials such as SS 316L, a material known for its high strength, corrosion resistance, and difficulty in machining. The difficulties associated with SS316L make this research especially important for industries such as aerospace, biomedical, and automotive, where precision machining is required. Furthermore, although several optimization techniques have been explored to mitigate overcutting, the use of swarm-based metaheuristic algorithms, such as the grasshopper optimization algorithm, has not been thoroughly examined. Therefore, this experimental investigation aims to address these knowledge gaps by systematically analyzing the influence of AWJD parameters on overcutting and utilizing advanced optimization techniques like GHO to minimize overcut and enhance drilling precision in key industrial applications.

Material and methods

Selection of material

Deep holes with small diameters and high depth-to-diameter ratios are becoming increasingly important in industries like electronics, aerospace, precision instruments, medical apparatus, and automobiles38. Multiple investigations have demonstrated the advantages of utilizing SS 316L in electronics, bio-medical, aerospace, automobile, and various other industries. The automotive industry uses boreholes like this to increase combustion efficiency and injection pressure in fuel injectors. Fuel injectors in automobiles are manufactured from SS 316L due to their favorable mechanical characteristics, including resistance to corrosion, chemical compatibility with fuels, and high temperature. A workpiece made of SS 316L measuring a dimension of 100 × 100 × 135 mm was used for this experimental work.

Selection of AWJD process parameters

The AWJD process parameters and experimental scheme were selected based on the material removal mechanism and dimensional accuracy during the drilling of SS316L and material from the most recent literature39,40,41. Previous experimental studies on AWJD indicated that WP (influencing penetration depth and cutting efficiency), FR (The volume of abrasive particles carried by the waterjet impacts the erosion rate), and SD (The distance between the nozzle and the workpiece can alter jet dispersion and energy concentration) are the most significant process parameters affecting AWJD outcomes such as the quality of the hole and surface integrity. This study identified three critical process parameters: WP, FR, and SD, to drill deep holes in the chosen material. The output parameters were chosen to thoroughly evaluate the dimensional accuracy and surface quality of the drilled holes, which are essential for SS316L applications in the automotive and biomedical industries. The experimental design evolved with the Taguchi L16 orthogonal array. The L16 orthogonal array is designed to support a maximum of 3 factors, each set at 4 levels, across a total of 16 runs. L16 facilitates the execution of more intricate experiments that require the examination of additional variables and their interactions42. In this investigation, to minimize the number of runs needed to comprehensively explore the effects of various factors and their interactions, Taguchi based orthogonal array L16 was used. The L16 orthogonal array is designed using Minitab (V18) software. The process parameters and their respective levels utilized in this study are delineated in Table 1.

Table 1 Process parameters and their levels.
Full size table

Abrasive waterjet drilling machine configuration

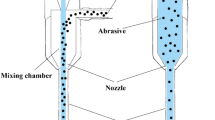
A Gantry waterjet machine tool (Model: G3020) was used to drill deep holes in the selected material. The tool had an intensifier pump, which was motorized by a 60 HP and was capable of supplying waterjet pressure as high as 400 MPa. The typical AWJD utilized for this study is depicted in Fig. 1. The clamping device shown in Fig. 1 fastens the workpiece, which has a depth of 135 mm, to the worktable. After properly securing the work material, the positions of the holes to be drilled were identified and marked. Moreover, the nozzle was located relative to the designated place.

Fig. 1
figure 1

Abrasive waterjet drilling setup.

Full size image

This study involves the use of an 80# garnet. Based on the available literature, garnet with an 80 # was utilized as an abrasive type for deep hole drilling studies43. The AWJD machine configuration and properties of garnet 80# are presented in Tables 2 and 3 respectively.

Table 2 AWJD configuration.
Full size table
Table 3 Properties of garnet 80#44.
Full size table

Measurement methods

The deep holes drilled with a nominal diameter of 3 mm into the SS 316L material through piercing mode to a depth of 135 mm using AWJD are depicted in Fig. 2. Piercing in AWJD involves a stationary jet focused on a single point to initiate the hole. A Video Measuring System (VMS) shown in Fig. 3 measured and meticulously documented the diameters at both the top and bottom of all drilled holes.

Fig. 2
figure 2

Representation of deep holes drilled on SS 316L.

Full size image
Fig. 3
figure 3

Measurement of top and bottom diameters of drilled holes using VMS.

Full size image

Top and bottom overcut

The overcut is the difference in diameter between the piercing nozzle diameter and the diameter of the top and bottom drilled holes. Equations 1 and 245 were utilized to determine the top and bottom overcut of the drilled holes.

$$\text{Top overcut }(\text{TOC}) (\text{mm})=\frac{\text{ Top Diameter of drilled hole}-\text{Nozzle Diameter }}{2}$$
(1)
$$\text{Bottom overcut }\left(\text{BOC}\right)\left(\text{mm}\right)=\frac{\text{Bottom Diameter of drilled hole}-\text{Nozzle Diameter }}{2}$$
(2)

Depth averaged radial overcut

Depth averaged radial overcut (DAROC) is a metric for quantifying the barrelling effect in drilled holes; it is defined as the mean of hole overcut along the drilled depth. The DAROC was calculated using Eq. 346. In the equation, ‘n’ is the total number of locations where the hole’s diameter has been recorded.

$$\text{DAROC }\left(\text{mm}\right)=\sum_{\text{n}-1}^{\text{n}}(\text{Hole diamter}-\text{Nozzle diameter})/2$$
(3)

To analyze the variation in diameters, the specimen was cut into nine sections of equal size, each with a thickness of 15 mm. The workpiece was laser marked to identify holes before slicing and sliced using a wire-cut EDM. The diameter of each hole available in each slice was measured using VMS. The representation of depth averaged radial overcut is shown in Fig. 4.

Fig. 4
figure 4

Representation of depth averaged radial overcut.

Full size image

The VMS system was used to measure the diameters of the top and bottom sides of each slice, and the results were documented. A hole profile was generated for each slice using Microsoft Excel, utilizing the obtained value. Figure 5a and b represent the profile of the drilled holes.

Fig. 5
figure 5

Representation of the barrelling effect on the drilled holes.

Full size image

Algorithmic approach

The main aim of this research is to determine the optimal combination of AWJD process parameters for producing high-quality holes using metaheuristic algorithms. This study included four distinct optimization algorithms: the Grasshopper Optimization Algorithm (GHO), the Whale Optimization Algorithm (WOA), the Harmony Search Algorithm (HSA), and the Multiverse Optimization Algorithm (MVO). The pseudocode for each algorithm is illustrated in Fig. 6. The algorithms were implemented utilizing the MATLAB 2020® framework.

Fig. 6
figure 6figure 6

Pseudocode of optimization algorithms.

Full size image

Results and discussion

Statistical analysis

The deep hole drilling experimental results are detailed in Table 4. Further, the statistical significance of the AWJD process parameters on the responses for TOC, BOC, and DAROC was determined through an Analysis of Variance (ANOVA) utilizing MINITAB software (V18). The regression equation and ANOVA analysis for TOC, BOC, and DAROC are given in Tables 5, 6, and 7. It is inferred that the P-value of models for TOC, BOC, and DAROC is less than 0.05.

Table 4 AWJD input variables and responses.
Full size table
Table 5 ANOVA for top overcut.
Full size table

ANOVA for top overcut

The estimated regression coefficients and ANOVA for TOC are listed in Table 5. Since the P-value is less than 0.05 for FR it has a highly significant contribution to the TOC. The residual plot displayed in Fig. 7a exhibits a uniform distribution along a linear pattern, suggesting that the constructed model had statistical significance. The projected values for R-Square, R-Square (Adj.), and R-Square (Pred.) are 93.43%, 92.88%, and 91.33%, respectively. The following regression Eq. 4 was derived for TOC by developing the relationship between TOC with the WP, SD, and FR. The linear, squared, and interactive terms of WP, SD, and FR were considered while deriving the TOC regression model.

$$\begin{aligned} {\text{TOC}} = & 1.054 - 0.00368{\text{ WP}} + 0.482{\text{SD}} + 0.00162{\text{ FR}} \\ & \quad + 0.000005{\text{ WP*WP}} - 0.0036{\text{ SD*SD}} - 0.000004{\text{ FR*FR}} \\ & \quad - 0.001328{\text{ WP*SD}} + 0.000006{\text{ WP*FR}} + 0.000163{\text{ SD*FR}} \\ \end{aligned}$$
(4)
Fig. 7
figure 7

Statistical significance of top overcut.

Full size image

Furthermore, the statistical significance of the TOC was validated by examining the model summary presented in Fig. 7b, which indicates that the p-value associated with the TOC increased beyond the threshold of 0.05. The Pareto chart depicted in Fig. 7c revealed the specific impact of the chosen drilling parameter on the TOC. The Pareto graph indicates that FR has the most impact in determining the TOC value, in comparison to WP and SD. The reason for this phenomenon is that an elevated FR value tends to decrease the TOC by enhancing the cutting capability of the waterjet. This is achieved by supplying a greater volume of abrasive particles, hence lowering the occurrence of top overcut.

ANOVA for bottom overcut

According to Table 6, which shows the BOC regression model, the control factors WP and SD contribute the most to the BOC model, although FR also makes a major contribution. Figure 8a shows a straight-line distribution of residuals, indicating that the model is statistically significant. The projected values for R-Square, R-Square (Adj.), and R-Square (Pred.) are 96.47%, 91.17%, and 89.41%, respectively. The following regression Eq. 5 was developed for BOC by considering the relationship between the BOC with WP, SD, and FR.

$$\begin{aligned} {\text{BOC}} = & 6.948 - 0.03956{\text{ WP}} + 0.570{\text{ SD}} - 0.00059{\text{ FR}} + 0.000062{\text{ WP*WP}} \\ & \quad - 0.1518{\text{ SD*SD}} - 0.000001{\text{ FR*FR}} - 0.000475{\text{ WP*SD}} + 0.000002{\text{ WP*FR}} \\ & \quad + 0.000118{\text{ SD*SR}} \\ \end{aligned}$$
(5)
Table 6 ANOVA for bottom overcut.
Full size table
Fig. 8
figure 8

Statistical significance of bottom overcut.

Full size image

In addition, the statistical significance of the BOC was confirmed by analyzing the model summary provided in Fig. 8b, which shows that the p-value linked to the BOC exceeded the threshold of 0.05. Figure 8c displays a Pareto chart that illustrates the precise influence of the selected drilling parameter on the BOC. The Pareto graph demonstrates that WP and SD exert the most influence on the BOC value, relative to FR. The uniform penetration of the waterjet throughout the depth of the workpiece is accomplished by increasing the WP and decreasing the distance between the nozzle and the workpiece. This approach effectively reduces the occurrence of bottom overcut.

ANOVA for depth averaged radial overcut

Table 7 displays the DAROC regression model, and it is clear that all the control factors significantly impact the DAROC model. Figure 9a residual plot, which shows that the constructed model is statistically significant, is also uniformly distributed over a straight line.

Table 7 ANOVA for depth averaged radial overcut.
Full size table
Fig. 9
figure 9

Statistical significance of depth averaged radial overcut.

Full size image

The R-Square, R-Square (Adj.), and R-Square (Pred.) values that were obtained are 99.44%, 98.61%, and 92.66%, respectively. A regression Eq. 6 was created specifically for DAROC, which is shown below.

$$\begin{aligned} {\text{DAROC}} = & 2.500 - 0.010846{\text{ WP}} + 0.7217{\text{ SD}} + 0.002177{\text{FR}} \\ & \quad + 0.000019{\text{ WP*WP}} - 0.06000{\text{ SD*SD}} - 0.000003{\text{ FR*FR}} \\ & \quad - 0.001191{\text{ WP*SD}} + 0.000001{\text{ WP*FR}} - 0.000222{\text{ SD*FR}} \\ \end{aligned}$$
(6)

Furthermore, the statistical significance of the DAROC was validated through an examination of the model summary shown in Fig. 9b, revealing that the p-value associated with the DAROC surpassed the predetermined threshold of 0.05. The Pareto chart in Fig. 9c clearly shows the specific impact of the chosen drilling parameter on the DAROC. The Pareto graph illustrates that the chosen drilling parameters exert a significant influence on the DAROC value. The augmentation of WP and SD enhances the cutting efficacy of the waterjet, resulting in a decreased duration required for the waterjet to penetrate the material.

Influence of AWJD parameters

Top overcut

The top overcut refers to the difference in size between the nozzle’s diameter and the hole produced on the jet entry side of the workpiece. The 3D surface plot shown in Fig. 10a–c was used to explore the influence of process parameters over TOC. Figure 10a illustrates the combined impact of WP and SD while maintaining a constant FR of 450 g/min. Increasing the WP to 360 MPa and reducing the SD to 1 mm results in a decrease in the TOC value to 1.21 mm. At a greater SD of 2.5 mm and a lower WP of 260 MPa, the TOC value rises to 1.39 mm. The trend of Fig. 10b demonstrates the relationship between WP and FR while maintaining an SD of 1.75 mm. Increasing the WP to 360 MPa and reducing the FR to 300 g/min results in a drop in the value of TOC by 1.26 mm. At a higher SD of 600 g/min and lower WP of 260 MPa, the TOC value increases to 1.39 mm. Figure 10c illustrates the correlation between the distance between the nozzle and the workpiece and the rate at which abrasive material is flowing while maintaining the WP at 316.25 MPa. Increasing the SD to 2.5 mm and reducing the FR to 300 g/min results in a decrease in the value of TOC to 1.261 mm. At a higher FR (600 g/min) and a smaller SD (1 mm), the TOC value increases to 1.264 mm.

Fig. 10
figure 10

3D Surface plots for the influence process parameter on TOC.

Full size image

The WP exerted a significant influence on TOC, as demonstrated in Fig. 10a and b. Under conditions of low WP, the TOC values appeared to be increased. A further increase in WP resulted in a significant decrease in the TOC values. Moreover, an increase in WP enhances the cutting efficacy of the waterjet, leading to rapid deterioration of materials and thus reducing the TOC. At low WP, the waterjet must wait a longer time to pierce the workpiece through depth. When the waterjet is stationary for an extended time, it causes a larger diameter to form on the top of the workpiece47.

An increase in the FR leads to a decrease in TOC. An increase in the flow rate of the abrasive reduces the quantity of excess material removed from the top surface, as illustrated in Fig. 10b and c. The graph shows that the highest TOC value initially increased up to a specific limit and subsequently decreased. This is attributed to the contribution of the abrasive flow rate volume during the drilling operation. As the waterjet pressure rises, it causes the huge volume of abrasive particles to disintegrate into smaller particles. Each particle possesses its own cutting edges, allowing it to penetrate the workpiece at a higher speed. Therefore, erosion occurs more rapidly, leading to a decrease in the diameter of the hole formed on the top surface of the workpiece48. The effect of SD was observed in Fig. 10b and c, where a bigger top diameter is formed on the workpiece when the distance between the nozzle and the target surface is increased because the water stream that leaves the nozzle is diverted and hits the target material.

Bottom overcut

The bottom overcut refers to the difference between the nozzle’s diameter and the diameter of the hole produced on the bottom side of the workpiece. The 3D surface plot shown in Fig. 11a–c was used to explore the influence of process parameters over BOC.

Fig. 11
figure 11

3D Surface plots for the influence process parameter on BOC.

Full size image

Figure 11a demonstrates the cumulative effect of WP and SD while keeping the FR constant at 450 g/min, by raising the WP to 360 MPa and decreasing the SD to 1 mm, the BOC increases to 0.93 mm. Through a higher SD of 2.5 mm and a lower WP of 260 MPa, the BOC value reduces to 0.91 mm. The trend of Fig. 11b illustrates the correlation between WP and FR, while also maintaining an SD of 1.75 mm. By raising the WP to 360 MPa and lowering the FR to 300 g/min, the value of the BOC increases by 0.93 mm. When the FR is increased to 600 g/min. and the WP is decreased to 260 MPa, the BOC value lowers to 0.91 mm. Figure 11c depicts the relationship between the SD and the FR of the abrasive material while keeping the WP constant at 316.25 MPa. By increasing the SD to 2.5 mm and reducing the FR to 300 g/min, the value of BOC increases to 0.937 mm. When the FR is increased to 600 g/min and the SD is reduced to 1 mm, the TOC value lowers to 0.930 mm.

The BOC was significantly lowered in conditions of moderate WP. The BOC value shows a decrease within the WP range of 310–335 MPa. Once again, the BOC value increases as the WP increases. Increasing the WP accelerates the erosion process, resulting in a larger hole diameter at the bottom of the target material49. This diameter exceeds the size of the nozzle. The FR also contributed positively to the reduction of BOC levels. Figure 11b and c demonstrate that an increase in FR leads to a reduction in BOC. The graph clearly shows that the increased FR contribution to drilling resulted in a progressive drop in the BOC value. The effect of SD on BOC was noticed in Fig. 11a and c. When examining the trends, the value of BOC initially rises to a particular limit and subsequently declines. A low SD results in rapid contact between the workpiece and the waterjet with significant force, resulting in increased erosion and a quicker drilling time for the hole24. An increase in SD within the range of 1.5–2.0 mm can result in a corresponding rise in BOC levels.

Depth averaged radial overcut

The 3D surface plot shown in Fig. 12 a–c was drawn to explore the influence of process parameters over DAROC. Figure 12 a demonstrates the cumulative effect of WP and SD while keeping the FR constant at 450 g/min, by raising the WP to 360 MPa and decreasing the SD to 1 mm, the DAROC decreases to 1.77 mm. With a higher SD of 2.5 mm and a lower WP of 260 MPa, the DAROC value increases to 1.85 mm. The trend of Fig. 12b illustrates the correlation between WP and FR while also maintaining an SD of 1.75 mm. By raising the WP to 360 MPa and lowering the FR to 300 g/min, the value of the DAROC decreases by 1.77 mm. When the FR is increased to 600 g/min and the WP is decreased to 260 MPa, the DAROC value increases to 1.85 mm. The diagram in 12c depicts the relationship between the SD and the FR of the abrasive material while keeping the WP constant at 316.25 MPa. By increasing the SD to 2.5 mm and reducing the FR to 300 g/min, the value of DAROC was observed as 1.77 mm. When the FR is increased to 600 g/min and the SD is reduced to 1 mm, the DAROC value lowers to 1.77 mm. For both cases, the value of DAROC was observed to be the same.

Fig. 12
figure 12

3D Surface plots for the influence process parameter on DAROC.

Full size image

The 3D surface plot 12a demonstrates that WP had a significant impact on DAROC. The DAROC values are high at both low and high WP. Under moderate waterjet pressure, the DAROC values were determined to be at their lowest. As the thickness of the workpiece increases, the waterjet must remain in contact with the workpiece for a longer duration to penetrate through its whole depth. The continued operation of the waterjet for an extended time promotes secondary erosion. The deterioration was observed to be evident in the middle of the workpiece50. Moreover, as the thickness of the workpiece decreases, this phenomenon appears to be less noticeable, particularly in the lower portion of the workpiece. The DAROC value exhibited a minimum range between 310 and 335 MPa for WP.

The DAROC was significantly impacted by the level of FR contribution during the drilling operation. As the quantity of FR rises, the quantity of cutting edges accessible to impact the workpiece also increases, resulting in a decrease in the DAROC. The DAROC values decreased as the FR increased from 400 to 600 g/min. The DAROC is inversely affected by the SD. Increasing the SD results in a greater separation between the nozzle and the workpiece. Consequently, the waterjet dissipates its kinetic energy before making full contact with the workpiece material. A decrease in kinetic energy results in the waterjet needing to remain in contact with the workpiece for a longer duration to remove the material. As the distance between the nozzle and the workpiece increases from 1.5 to 2.5 mm, the amount of DAROC also increases. Minimizing the SD value leads to improved DAROC.

Optimization of responses through algorithmic approach

The GHO algorithm, introduced by Ghumman et al.51, is a contemporary and engaging swarm intelligence framework that replicates the natural foraging and swarming behaviours of grasshoppers. Initially, a mathematical model is utilized to depict the communication among members in the group, incorporating the concepts of attraction (pull) force, repulsion (disharmony) force, and comfort (encouragement) zone. The swarming behavior of grasshoppers is mathematically represented by the following Eq. 752.

$${P}_{i}={S}_{i}+{G}_{i}+ {A}_{i}$$
(7)

The notation used in this context is as follows: Pi denotes the position of the ith grasshopper, Si denotes the social interaction between grasshoppers, Gi represents the gravity force acting on the ith grasshopper, and Ai denotes the wind advection.

Furthermore, this study assesses the efficiency of the GHO algorithm in contrast to the WOA, HSA, and MVO algorithms. All the selected algorithms were configured to execute a specified total of 15 runs, each including 100 iterations. The loop would persist for all 15 iterations, irrespective of the discovery of an optimal solution beforehand. An algorithm may discover better results early on, but further iterations may reveal even better solutions or prove that there are no better solutions. Because different iterations can produce different optimal solutions, repeating them multiple times improves the results’ robustness and reliability. Tables 8, 9, 10, and 11 show the optimum solutions developed by each algorithm.

Table 8 Optimum process parameters using GHO.
Full size table

The Evaluation Based on Distance from Average Solution (EDAS) method is used to determine the optimal combination of parameter settings from each iteration. The EDAS method is a novel distance-based measurement strategy that is similar to other recently established multi-criteria decision-making methods53. EDAS tries to identify the optimal alternative using the average solution-based normalization technique. To assess the score of each alternative and establish their relative ranking, EDAS employs two measures: Positive Distance from Average Value (PDA) and Negative Distance from Average Value (NDA). The values highlighted in bold Tables 8, 9, 10, and 11 are the optimal parameters that correspond to the highest score obtained by the EDAS approach.

Table 9 Optimum process parameters using WOA.
Full size table
Table 10 Optimum process parameters using HSA.
Full size table
Table 11 Optimum process parameters using MVO.
Full size table

The optimum parameter setting identified from each algorithm through the EDAS method is presented in Table 12. To identify the best algorithmic approach, a convergence plot produced after each iteration by the EDAS method was used.

Table 12 Optimum process parameters and its responses value.
Full size table

Convergence plot and quality metrics are the two key indicators used to identify the best optimization algorithm. The convergence plot refers to how quickly the solutions approach or converge toward the Pareto front. Steeper slopes or rapid convergence can indicate efficient optimization progress. The convergence plot of GHO and comparative algorithms are displayed in Fig. 13a–c. The convergence plots revealed that the efficacy of the GHO is superior to the other algorithms. Further, the efficacy of the GHO is confirmed through performance indicators namely Spacing (SP) and Hyper Volume (HV). The quality metrics of all the algorithms are presented in Table 13. A higher HV value indicates that the solutions are well-distributed, covering a larger portion of the Pareto front. Similarly, a smaller SP value indicates the average distance between neighboring solutions on the Pareto front. Table 13 indicates that GHO demonstrated superior performance in terms of SP and HV compared to the other methods.

Fig. 13
figure 13

Convergence plot.

Full size image
Table 13 Performance indicator.
Full size table

The validation study was conducted by applying the GHO and a set of ideal AWJD drilling parameters. Table 14 presents the outcomes of the test together with the percentage of variation for TOC, BOC, and DAROC are 1.71%, 3.03%, and 2.68% respectively associated with the GHO algorithm. In industrial practices, permissible deviation limits in dimensional accuracy and surface quality for deep hole drilling processes are determined by the individual application requirements and tolerance criteria. ISO 286 standards recommend dimensional tolerances of ± 2–3% for non-critical components and less than 1% for precision applications including aerospace and medical equipment (ISO 286-1, 2010). Furthermore, research indicates that deviations up to 3% in deep hole drilling of stainless steels are frequently deemed acceptable in industries such as automotive and general manufacturing, where functional performance is not impacted54,55. The observed deviations in our study are within or near this range, indicating that the results are acceptable for typical industrial uses of stainless steel 316L, particularly in cases where minor dimensional differences do not have a significant impact on component performance.

Table 14 Validation test results of TOC, BOC, and DAROC.
Full size table

At the outset, the parameters optimized via the GHO lead to a substantial reduction in radial overcut, thereby enhancing dimensional accuracy. The attainment of radial overcut values measuring 1.17 mm at the top, 0.66 mm at the bottom, and 1.49 mm in depth-averaged indicate a significant improvement in precision relative to traditional AWJD processes. The GHO algorithm demonstrated superior performance compared to other optimization methods, including WOA, HS, and MVO, as evaluated by quality metrics such as hyper-volume and spacing. This superior performance underscores the algorithm’s effectiveness in fine-tuning process parameters for optimal outcomes. The optimized AWJD process has significant practical implications for industries including aerospace, automotive, biomedical, and oil & gas, where accurate deep-hole drilling is essential.

Surface morphology of drilled holes

Surface morphology of drilled hole for low and high water pressure

The deep hole morphologies at the top, middle, and bottom of the drilled holes for low (260 MPa, 1 mm, and 300 g/min) and high (360 MPa, 1 mm, and 600 g/min) process parameters were analyzed using a scanning electron microscope at 50X magnification with a 500 µm scale. The SEM images reported in this study were obtained following extensive sample cleaning to eliminate surface artifacts that might interfere with proper observation. The samples were etched with an appropriate reagent, such as a nitric acid (20–40%) and hydrofluoric acid (2–5%) combination, to reveal grain boundaries while avoiding surface artifacts. The SEM images in Fig. 14a and b show that the top of the drilled holes, resulting from both low and high process parameter conditions, are smooth and uniform. However, several locations show the accumulation of small shattered abrasive particles and burrs. The middle section of the drilled hole exhibits significant jet removal, which is commonly referred to as Secondary Jet Erosion (SJE). SJE in AWJD is caused mostly by the unintended redirection of high-velocity abrasive particles and water streams within the drilled hole. The main causes include jet deflection and turbulence, rebound of abrasive particles, and inconsistent standoff distance. The first reason is that when the waterjet penetrates deeper into the material in this research it is equal to 135 mm, the interaction of the abrasive particles with the hole wall causes jet deflection and turbulence, producing secondary jets to erode undesired locations. The second reason is that abrasive particles can bounce back the hole walls, resulting in multiple erosion locations, especially in deeper holes where the jet flow is more restricted. Further, variations in the nozzle standoff distance might cause unstable jet behavior, increasing the possibility of SJE and creating hole geometry irregularities56. This effect results in the rebound of the water jet and removes a small amount of material during the water jet’s return, as observed in the middle portion of Fig. 14a and b. The presence of SJE contributes to kerf angle formation and out-of-round holes, affecting dimensional accuracy. Excessive erosion can lead to oversized holes or deviations from the intended geometry. This effect is observed to be more in the middle of the holes irrespective of the process parameters used. Moreover, as the depth of the workpiece increased, the velocity of the water jet reduced. The reduced waterjet resulted in the poor surface quality of the drilled hole at the bottom, as depicted in Fig. 14a and b bottom section.

Fig. 14
figure 14

SEM images of low and water pressure condition.

Full size image

Surface morphology of optimized hole

In order to investigate the material removal mechanism, surface quality, and potential defects in the drilled hole achieved through optimized parameters (WP 305.36 MPa, SD 1.00 mm, and FR 600 g/min as determined by the GHO algorithm), a scanning electron microscopic examination was conducted. The images displayed in Fig. 15a–c were taken at a magnification level of 12X with a 2 mm scale for the hole produced through optimized process parameters. These images indicated that the top, middle, and bottom areas were noted to be rather smooth and free from abrasive particle cohesion. Nevertheless, it was observed that there were little burrs present in the exit portion of the hole depicted in Fig. 15c. In addition, Fig. 15d–f displays images taken at a magnification of 500X with a 500 µm, illustrating the process of material removal known as primary or vertical waterjet erosion and secondary waterjet erosion in the middle and exit areas due to bouncing back of waterjet57.

Fig. 15
figure 15

Surface morphology of optimized hole.

Full size image

The experimental examination and optimization revealed that the SJE can be greatly controlled by optimizing the WP, SD, and FR values. Maintaining an optimal WP value of 305 MPa reduces turbulence and secondary jet formation; an optimal SD value of 600 g/min ensures efficient cutting while minimizing particle rebound and erosion; and a minimum SD value of 1 mm helps stabilize the jet stream, reducing deflection and secondary erosion.

Conclusions

This study comprehensively examines the AWJD, incorporating experimental analysis, regression modeling, and multi-response optimization. Furthermore, SEM has been employed to examine the deep hole surfaces to ascertain the impact of drilling process parameters on surface quality, and the mechanism of material removal. Based on the experimental results obtained during abrasive waterjet drilling of SS 316L, various conclusions are drawn as follows:

  • The statistical significance of the selected process parameters on the AWJD responses was evaluated through ANOVA. The ANOVA demonstrated that WP and SD were the two AWJD drilling parameters that had the greatest impact on the TOC and BOC values. Assessment of the DAROC values was primarily influenced by the FR and SD.

  • It is inferred from the 3D surface plot that the TOC was significantly affected by the waterjet pressure. A subsequent rise in waterjet pressure resulted in a considerable decrease in the TOC (1.21 mm) levels. The cutting efficiency of the waterjet is improved with an increase in WP, which speeds up the deterioration of materials and lowers the TOC. On the other hand, the TOC value is increased as the standoff distance from the nozzle to the target material is increased. This is because the water stream that exits the nozzle is redirected and hits the material at the target.

  • It is understood from the 3D surface plot that the BOC value was observed to be lower when the waterjet pressure was within the range of 310–335 MPa. Increased waterjet pressure intensifies the process of erosion and leads to a wider diameter of the hole at the bottom of the workpiece.

  • The degree of FR input during the drilling operation has a substantial impact on the DAROC. The increase in the quantity of FR leads to a corresponding increase in the number of cutting edges available for impacting the workpiece, thereby causing a reduction in the DAROC. As the FR ascended from 400 to 600 g/min, there was a decline in the DAROC values.

  • The GHO algorithm has demonstrated superior efficacy in achieving the ideal set of AWJD parameters when compared to the WOA, HAS, and MVO algorithms. The concurrent reduction in TOC, BOC, and DAROC values was demonstrated by performance metrics such as hyper-volume and spacing.

  • According to the GHO algorithm, the ideal process parameters for AWJD were determined to be WP 305.36 MPa, SD 1.00 mm, and FR 600 g/min. Based on the ideal parameters, the predicted values for TOC, BOC, and DAROC are 1.19 mm, 0.64 mm, and 1.53 mm, respectively.

  • The validation test yielded TOC, BOC, and DAROC values of 1.17 mm, 0.66 mm, and 1.49 mm with a percentage deviation of 1.71, 3.03, and 2.68, respectively related to GHO.

  • SEM demonstrates a more uniform surface texture across the workpiece’s top, middle, and bottom portions for the optimized process parameters (WP 305.36 MPa, SD 1.00 mm, and FR 600 g/min). Additionally, secondary jet erosion occurred in the middle portion of the workpiece due to the returning waterjet.

  • This research facilitates automobile industries drilling small-diameter deep holes in fuel injector bodies, fuel rails, and plunger pumps in high-pressure hydraulics by providing an optimal combination of abrasive waterjet drilling parameters for producing quality holes.

Limitations and future scope

The key limitations observed from this research work and future research directions are detailed below.

  • Energy dissipation and abrasive particle deflection, lead to tapered hole geometries. These inconsistencies, make it challenging to achieve uniform hole diameters throughout the depth.

  • The occurrence of secondary jet erosion leads to unintended material removal beyond the intended hole boundary. As the depth increases, the abrasive waterjet loses kinetic energy, resulting in decreasing cutting efficiency and uneven material removal. Maintaining radial overcut in deep drilling is challenging due to this restriction.

  • Further research could investigate the impact of various abrasive materials (e.g. garnet, alumina, silicon carbide) and abrasive-water mixtures to determine combinations that minimize overcut variability in SS316L deep drilling.

  • Research should concentrate on developing predictive models that incorporate the non-linear behaviour of overcut with respect to hole depth.

  • Implementing real-time monitoring techniques, such as acoustic emission sensors or machine vision systems, can offer immediate feedback on overcut progression, facilitating adaptive control of process parameters to reduce variations.