Introduction

Annually, neonatal mortality rates vary between 3 and 27% across different countries, with approximately three quarters of deaths occurring within the first week of birth. Access to life-saving neonatal interventions is crucial to ensure a steady decline in mortality rates in low- and middle-income countries1. Respiratory rates(RR) and heart rates(HR) serve as critical vital indicators during neonatal resuscitation and monitoring. Hence, the rapid and accurate acquisition of HR and RR indicators holds significant research value2.

Currently, the main devices for detecting the RR and HR of neonates include palpation, auscultation, ECG monitor, etc. ECG monitoring is the most commonly used in general hospital wards. In neonatal intensive care units (NICUs), some neonates may exhibit excessively weak HR and RR, rendering ECG signals undetectable. In such cases, manual auscultation and palpation by doctors are required to measure RR and HR. However, each of these methods has its limitations3. Among them, the accuracy of the ECG monitor is the highest, but from the initial placement of electrodes to the acquisition of data, it takes 1–2 min, which may cause the neonates missing the best rescue time4. Additionally, long-term patch application for monitoring can also cause neonatal discomfort and increase the risk of skin damage and infection. With regard to auscultation and palpation, both methodologies are susceptible to misjudgment3. Faced with these limitations, millimeter-wave radar, with its advantages of rapid measurement, millimeter-level motion capture capability, and non-contact measurement, provides a new solution for monitoring the RR and HR of neonates.

Currently, there have been studies on various radar-based vital sign monitoring systems. As early as 1975, J. Lin from the University of Florida in the United States developed a continuous wave (CW) radar system for detecting vital signs, and used this system to measure the respiratory waveforms of both humans and rabbits5. Compared to CW radar, Ultra-Wideband (UWB)radar has the ability to distinguish distances to targets, thus allowing for the acquisition of more information. Consequently, its resistance to interference and ability to distinguish multiple targets are also enhanced. In 2010, Lazaro A analyzed signal processing methods for vital sign detection using UWB radar6. In 2021, Park et al. investigated the application of IR-UWB radar for detecting stationary cardiovascular disease patients7. In comparison, Frequency Modulated Continuous Wave(FMCW) radar has been introduced into the field of vital sign monitoring due to its capability to achieve large bandwidth and higher distance resolution. In 2009, Anitori L began using FMCW radar for vital sign detection and compared frequency estimation based on fast Fourier transform and autocorrelation algorithms8. In 2021, Jinbo Chen et al. utilized FMCW radar in conjunction with deep learning networks to reconstruct ECG waveforms while monitoring adult HR9. Zhe Chen et al. achieved robust human HR monitoring under a treadmill by studying human motion10. However, most research efforts have been focused on RR and HR monitoring for adults. Although Kim et al. have preliminarily demonstrated the feasibility of using radar to monitor neonatal RR and HR11,12, the methods employed are still similar to those used in studies on adults. In terms of monitoring neonates, there are still several major unresolved issues as follows:

  1. (1)

    Existing methods still rely on measuring thoracic phase for respiration and do not account for the fact that neonates primarily use abdominal breathing13, which will lead to a decrease in the signal-to-interference ratio(SIR) of the respiratory signal, impacting RR measurement accuracy.

  2. (2)

    Neonatal monitoring scenarios are characterized by the presence of medical interfering factors. Interference caused by the movement of medical staff and instruments is common, which can result in phase mutations that overwhelm the signal of interest, as depicted in Fig. 1. These phase mutations subsequently affect measurement accuracy14.

  3. (3)

    During neonatal monitoring, the radar’s field of view is often fixed. However, the neonate’s frequent wriggling and rolling movements can lead to the radar detecting the wrong target. Therefore, it is necessary to develop a system with robust tracking capabilities to address this issue and enhance overall system robustness.

Fig. 1
figure 1

Impact of random motion.

Full size image

Some existing works have provided certain assistance or inspiration for solving the above-mentioned issues. Yang, S. et al. conducted spatial filtering by positioning a radar vertically over the thorax of a neonate15, but the fixed beam direction could not self-adapt to the potential random movements of the neonate, and this study did not consider the abdominal breathing in neonates. Mercuri, M. et al. used 2D radar imaging to distinguish multiple subjects and partially suppressed stationary clutter and multipath effects16. However, radar data often lack sufficient information. Although radar images can differentiate between different positions in adults, they cannot distinguish different body parts of a neonate, and it is also challenging to differentiate between the neonate and surrounding instruments. Gu C. et al. introduced a camera to assist the radar system, observing a black marker on the subject’s shoulder to infer random movements and correspondingly perform phase compensation in the radar17. However, this method requires placing markers on the patient’s shoulder, failing to highlight the non-contact advantage of radar and being inapplicable to neonates. A. Gharamohammadi et al. proposed a multibin breathing pattern estimation method based on the combination of dual radars for comprehensive monitoring of drivers’ breathing patterns and respiratory abnormalities18. This work provides us with an idea for separating radar beams from different body parts for spatial domain filtering. It considers adult’s abdominal breathing and presents a method to suppress random body movements by combining different range bins. However, the primary focus of this work is on adult drivers, whose respiratory patterns differ from those of neonates. Furthermore, neonates have a smaller body surface area and their position relative to the radar is less fixed compared to adults, making it impractical to directly apply the methods used in this work. A. Shokouhmand et al. were the first to combine visual information and radar beamforming in real-time to improve radar positioning accuracy19, but their system had a wide beam that could not accurately achieve spatial filtering, and they only theoretically analyzed the feasibility of adding receiving antennas in the discussion section. Wang et al. used optical results to guide radar beams, achieving tracking of subjects and adjusting the transmit-receive beams to improve the SIR, realizing RR and HR tracking measurement in adult motion scenarios20. However, their system and methods were primarily used to distinguish moving adults, so the dataset used was only for adults and did not consider the issue of beam width, making it unsuitable for clinical scenarios involving neonates. Moreover, after Digital Beam Forming(DBF), only thoracic phase extraction was performed for analysis, facing the same issues as Yang, Kim et al.11,12,14,15. In conclusion, the above-mentioned issues remain unresolved, posing ongoing difficulties for the monitoring of neonates.

In this paper, to address these issues, a method for the separation of thoracic and abdominal measurements (STAM) is proposed. Additionally, this paper designs a radar-vision fusion system (RVF) to ensure that the STAM method can be adapted to clinical applications for neonates. The main contributions of this paper are as follows:

  1. (1)

    Addressing the first issue, this paper proposes the STAM, where the thoracic phase is utilized for HR measurement and the abdominal phase is utilized for RR measurement. Compared to methods that directly extract respiration signals from thoracic beams11,15, this approach achieves higher SIR respiratory signal and yields more accurate respiratory measurements.

  2. (2)

    Considering the second issue, to accurately implement the STAM method, this paper proposes the use of a narrow-beam radar for spatial filtering. We quantitatively calculate the required beamwidth of the radar system and model the neonatal monitoring scenario. Within this model, we incorporate the dimensions of medical incubators to determine the appropriate radar illumination height, while also separately analyzing neonatal body length data in Section “System parameters analysis”. Experimental results demonstrate that the narrow beam spatial filtering of our radar effectively eliminates interference signals from medical personnel, thereby accurately isolating thoracic and abdominal beams.

  3. (3)

    To ensure the proper functioning of the STAM method when confronted with the third issue, this paper introduces a RVF system. We preliminarily created a YOLO dataset to enable the camera to guide the radar in tracking the thoracic and abdominal positions. The precision requirement for the combined camera-radar system is also calculated quantitatively. Experiments have demonstrated the robustness of the proposed RVF system.

Methods

This paper utilizes MIMO millimeter-wave radar for monitoring vital signs in neonates. The transmitted signal is a stepped-frequency continuous wave (SFCW). The briefprocessing flow is illustrated in Fig. 2: Image recognition is employed to identify the monitoring area on the neonate, assisting the radar in selecting specific beams after DBF. After pulse compression, the phase of the thorax and abdomen are extracted separately, and time-frequency analysis is performed using the continuous wavelet transform(CWT). Curve fitting and Kalman filtering are then applied to optimize the results15. These results are subsequently compared with reference values obtained from the three-lead ECG.

Fig. 2
figure 2

An overview of vital sign monitoring [Image created using Matlab R2018b and WPS Office].

Full size image

Details will be described in the method section. In Section “Radar RR and HR detection principle”, the basic principle of Radar Processing and Time-Frequency Analysis will be described. In Section “Method of separation for neonatal respiratory measurement”, we explain why STAM method suits neonates better. The visual processing and system parameters will be described in Section “Neonatal monitoring system”.

Radar RR and HR detection principle

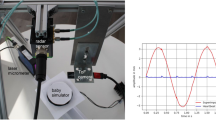
The study employs SFCW signals for detecting RR and HR. The signal waveform and the experimental setup are illustrated in Fig. 3.

Fig. 3
figure 3

SFCW signal and detection scenario (a) SFCW signal waveform (b) Neonatal monitoring scenario.

Full size image

From Fig. 3b, it can be seen that in the monitoring scenario, apart from the RR and HR signals of the neonate, there are also various interfering signals such as static target clutter and activities of medical staff. Therefore, before extracting the RR and HR, DBF can be used to select radar beams of specific positions to achieve spatial filtering and reduce clutter interference.

Assuming the radar has one transmitting antenna and M receiving antennas, and the angle of the neonate’s thorax relative to the radar is \(\theta\:\), according to Chap. 7 of “Radar principles”21, an array steering vector can be constructed:

$$\omega =\left[ {\begin{array}{*{20}{c}} 1&{\exp \left( { - j\frac{{2\pi d\sin \theta }}{\lambda }} \right)}&{.}&{\exp \left( { - j\frac{{2\pi d\left( {N - 1} \right)\sin \theta }}{\lambda }} \right)} \end{array}} \right]$$
(1)

where d is the distance between adjacent receiving antennas, and \(\lambda\:\) is the wavelength of the transmitted signal. Next, take its transpose and multiply it by the beams from the M receiving antennas of the radar, i.e.:

$$S={\omega\:}^{H}X=\sum\:_{n=1}^{M-1}{X}_{n}{e}^{-j2\pi\:\frac{(n-1)d}{\lambda\:}sin\theta\:}$$
(2)

where X is the data matrix of the received signals from the M channels:

$$X=X\left(t\right)=\left[\begin{array}{c}{X}_{1}\left(t\right)\\\:{X}_{2}\left(t\right)\\\: \vdots \\\:{X}_{M}\left(t\right)\end{array}\right]$$
(3)

If there is a target at a certain angle, S will present a larger magnitude. In DBF, the azimuth and elevation angles are artificially divided into different parts. By processing according to formula (1)–(3), a two-dimensional matrix \(S(\theta\:,\phi\:)\) will be obtained15, representing the target angle measurement results within the radar’s field of view, where each element represents a beam. Figure 4a shows the DBF schematic diagram, here each yellow cone-shaped pulse represents an element in the matrix \(S(\theta\:,\phi\:)\), specifically the echo information corresponding to a particular angle.

Fig. 4
figure 4

(a) DBF Schematic Diagram (b) Beam Tracking [Image created using Microsoft Paint].

Full size image

Generally, in RR monitoring experiments, the maximum intensity point of matrix S is often located directly beneath the radar’s vertical projection or on surrounding highly reflective medical equipment. Extracting the maximum intensity point directly11,12 would lead to beam selection errors, as depicted in Fig. 4b. In this paper, by locking onto the neonate’s thorax for HR and abdomen for RR measurement using the RVF system, the correct target beams can be directly selected from the 2D matrix S, thereby achieving accurate spatial filtering.

After selecting the angles, the SFCW signals can be used for ranging. The transmitted signal form in Fig. 3a is:

$$ s_{T} (t) = \mathop \sum \limits_{{k = 0}}^{{K - 1}} \exp \left[ {j2\pi \left( {f_{0} + k\Delta f} \right)t} \right]rect\left( {\frac{{t - k\Delta t - \Delta t/2}}{{\Delta t}}} \right) $$
(4)

When the target’s distance is \(R\left(\tau\:\right)\),the beam return is \(A\ast\:{S}_{T}(t-\frac{2R\left(\tau\:\right)}{c})\). After mixing it with the carrier frequency for down-conversion and performing pulse compression, the resulting signal is15,22:

$$ \begin{aligned} S_{b} (f) = & \frac{A}{{KT}} \cdot \exp \left( {\frac{{j4\pi f_{0} R(\tau )}}{c}} \right) \\ & \cdot \exp \left( {\frac{{j2\pi (K - 1)}}{K}\left( {f - \frac{{2K\Delta fR(\tau )}}{c}} \right)} \right) \\ & \cdot \sin c\left( {T\left( {f - \frac{{2K\Delta fR(\tau )}}{c}} \right)} \right) \\ \end{aligned} $$
(5)

Where K is the sweep frequency slope, T is the pulse repetition time(PRT), the extracted signal at \( f_{p} = \frac{{2{\text{~}}K\Delta fR\left( \tau \right)}}{c} \) is:

$${S}_{b}\left({f}_{p}\right)=\frac{A}{K}exp\left(\frac{j4\pi\:{f}_{0}R\left(\tau\:\right)}{c}\right)$$
(6)

The phase signal of (6) includes the displacement of the thorax caused by RR and HR. The function of displacement R is expressed as15,23,24,25:

$$ R\left( {t_{m} } \right) = A_{{breath}} \left( t \right)\sin \left( {2\pi f_{{breath}} t_{m} + \varphi _{b} } \right) + A_{{heart}} \left( t \right)\sin \left( {2\pi f_{{heart}} t_{m} + \varphi _{h} } \right) $$
(7)

Equation 7 is a relatively simple equation adopted in some papers. Considering that neonates have highly variable breathing patterns, we have modified \({f}_{breath}\) and \({f}_{heart}\) in Eq. (7) to make them time-varying:

$${f}_{breath}\left(t\right)={g}_{b}\left(\left[\frac{t}{T}\right]\right)$$
(8)
$${\text{f}}_{\text{h}\text{e}\text{a}\text{r}\text{t}}\left(\text{t}\right)={\text{g}}_{\text{h}}\left(\left[\frac{\text{t}}{\text{T}}\right]\right)$$
(9)

Where [] represents rounding down to the nearest integer, \({\text{g}}_{\text{b}}\) and \({g}_{h}\) are arbitrary functions representing the time-variability of RR and HR respectively. Parameter T is a constant artificially set. It represents a period during which we consider \({f}_{breath}\) and \({f}_{heart}\) to be stationary. If T tends towards an infinitesimally small value, we regard them as continuously time-varying. In the experimental processing conducted in this paper, the CWT is employed, implying that we treat \({f}_{breath}\) and \({f}_{heart}\) as continuously time-varying quantities.

By unwrapping, continuous phase signals from Eq. (6) are extracted to analyze the frequency of R. We calculate the RR and HR once using a time window of 7–8 s. CWT is applied to the phase data within a window, and curve fitting is performed to obtain one measurement of RR and HR15. The phase frequency containing HR information is relatively high, and a first-order difference filter is applied to remove non-periodic interference before CWT. RR is extract directly from the phase without the first-order difference filter since respiration is a low-frequency signal. By sliding the window at intervals of 1 s for measurement, the result is obtained every second. After Kalman filtering, continuous change curves of RR and HR is obtained. Figure 5 shows an example of the CWT result of HR extraction within one window of measured data from a neonate after curve fitting. The most continuous part with the highest intensity in the middle represents the HR, and the result obtained by averaging it represents the HR of that window.

Fig. 5
figure 5

Neonatal thoracic CWT diagram [Image created using Matlab R2018b and Microsoft Paint].

Full size image

In the processing of a fraction of windows, a phenomenon occurs where breathing harmonics overlap with the heart frequency band, as illustrated in Fig. 6. This phenomenon was infrequently observed in the experiments conducted in this paper. However, in order to provide a feasible solution, we have implemented a simple respiratory harmonic processing procedure as shown in Fig. 7.

Fig. 6
figure 6

Interference caused by Respiratory Harmonics [Image created using Matlab R2018b and Microsoft Paint].

Full size image
Fig. 7
figure 7

Simplified process for removing Respiratory Harmonics.

Full size image

Since the RVF system is capable of simultaneously measuring both RR and HR, we utilize the RR measurements as prior knowledge to extract the values of its higher harmonics when analyzing the time-frequency curve of HR. In a window where multiple continuous time-frequency curves appear in the CWT results, the curves in the vicinity of respiratory harmonic values are removed from the analysis.

Method of separation for neonatal respiratory measurement

As shown in Fig. 8a, 70% of the driving force for human respiration comes from the diaphragm, while the remaining 30% is completed by secondary respiratory muscles such as the external intercostal muscles. Therefore, most adults, especially adult females, predominantly exhibit thoracic breathing, which is characterized by the movement of thorax. However, in neonates, the intercostal muscles are very weak, and respiration relies entirely on the diaphragm, resulting in abdominal breathing13. Respiration is entirely characterized by the rising and falling of the abdomen. During neonatal resuscitation, it is necessary to perform abdominal artificial respiration, which is completely different from adult resuscitation procedures26,27.

Fig. 8
figure 8

(a) Respiratory muscles (b) Abdominal breathing.

Full size image

Therefore, the extraction of respiratory signals from neonates differs from that of adults. As shown in Fig. 8b, the rising and falling of the abdomen in neonates is most prominent. Based on Eq. (7), we extract a signal within a time period T for simulation, during which the RR and HR are constant. When the RR is \({f}_{1}\) and the HR is \({f}_{2},\) the phase variation extracted from the thorax is:

$$\varDelta\:{\varnothing\:}_{1}=\frac{4\pi\:}{\lambda\:}\left[{r}_{1}sin\right(2\pi\:{f}_{1}t+{\phi\:}_{1})+{r}_{2}sin(2\pi\:{f}_{2}t+{\phi\:}_{2})+\sigma\:]$$
(10)

Here, \({\text{r}}_{1}\) represents the fluctuations due to breathing, and \({\text{r}}_{2}\) represents the fluctuations due to the HR. The abdominal signal is given by:

$$\varDelta\:{\varnothing\:}_{2}=\frac{4\pi\:}{\lambda\:}\left[Rsin\right(2\pi\:{f}_{1}t+{\phi\:}_{3})+\sigma\:]$$
(11)

Here, \({\text{r}}_{1}<\text{R}\).

From Eq. (10), it can be observed that the neonatal thoracic signal is simultaneously mixed with fluctuations due to both RR and HR. This introduces noise in the measurement of respiration, resulting in a significant decrease in the SIR of respiratorysignal compared to the abdominal signal, as depicted in Fig. 9a. Additionally, a first-order difference operation is often applied before frequency analysis to suppress non-periodic noise when analyzing HR. This operation suppresses low-frequency signals, which may lead to weakened respiration signals. We simulated the ideal neonatal RR and HR using sinusoidal signals to demonstrate the difference in SIR when extracting signals from the thorax and abdomen for RR measurement. The results are shown in Fig. 9b: In the thoracic signal, the HR introduces significant interference to the measurement of respiration, while the respiratory signal from the abdomen exhibits a higher SIR.

Fig. 9
figure 9

(a) Selection of beams for RR measurement (b) Comparison of measurement results for neonatal thoracic and abdominal signals.

Full size image

Therefore, this paper proposes STAM based on the RVF system, utilizing first-order difference of thoracic phase to measure HR and abdominal phase to measure RR, achieving the maximum SIR for both RR and HR detection simultaneously.

Neonatal monitoring system

Visual processing

During neonatal monitoring, the positional shifts caused by the neonate’s movements can render the STAM method ineffective. For example, if the radar beam is initially set to target the neonate’s thoracic and abdominal areas, over time it may end up targeting the bed sheet or an arm instead. Therefore, it is crucial for the radar to accurately capture the beams from the thoracic and abdominal regions. Given the limited information from radar point clouds, it is extremely challenging for a single radar to track the neonatal thorax and abdomen (Fig. 10).

To address this issue, this paper proposes a RVF system as shown in Fig. 11c and has trained a YOLO dataset specifically for neonatal visual recognition, as illustrated in Fig. 11b. Figure 10 demonstrates the training process and performance, including the changes in loss values and mean average precision (map). The dataset comprises over four thousand clinical neonatal images taken at Peking University Third Hospital. To enhance recognition accuracy, the training focuses on more distinguishable features such as the armpits and navel. The midpoint between the two armpits is selected as the thorax, and the navel’s position is chosen for abdomen. After the pixel positions of the thorax and abdomen is obtained in the images, the intrinsic matrix of the camera is used to convert them into real-world positions28, thus aiding radar in DBF beam selection.

Fig. 10
figure 10

(a) Coordinate system for neonatal monitoring (b) Camera recognition example (c) The system described in this article.

Full size image
Fig. 11
figure 11

(a) Loss variation graphs for the training set and validation set (b) Changes in map with Training.

Full size image

System parameters analysis

Figure 10a depicts the 3D neonatal monitoring model we have developed. The statistical data for neonatal body length is shown in Table 129. The data presented in Table 1 represent the median values for premature infants with a gestational age of approximately 31 weeks, as reported in reference29, corresponding to the P50 percentile in medical terminology.

Table 1 Neonatal body length data.
Full size table

In Fig. 10a, the radar is required to accurately locate two areas with a size of at least 5 cm × 10 cm to ensure accurate identification of the thoracic cavity. At the same time, the beam width is less than 10 cm to ensure that the signals of the thorax and abdomen will not interfere with each other after the spatial filtering. The height of the radar in the Z direction is 60–70 cm. Therefore, according to the calculation of arc length formula, we put forward the accuracy requirements of neonatal monitoring system:

  • The beam width is less than 9° and the radar vision fusion angle error is less than 4.77°.

Based on this requirement, a 20-transmit, 16-receive 4DMIMO radar as shown in Fig. 10c is adopted, whose specific parameters are shown in the section “Results and discussion”, which meets the requirements of the monitoring system proposed in this paper.

Results and discussion

This chapter primarily discusses two sets of experiments. The Section “Radar vision calibration experiment” involves calibrating the radar and camera simultaneously using an angular reflector to validate the accuracy of unified visual coordinates for the radar. The Section “Neonatal RR and HR monitoring experiment” involves real-time measurements of RR and HR specifically for neonates to verify the effectiveness of the STAM method, the robustness of the RVF system proposed in this paper, and the performance of radar beam spatial filtering.

According to the requirements outlined in Section “System parameters analysis”, we have employed a 4D radar as shown in Fig. 10c, with its parameters listed in Table 2:

Table 2 4D radar parameters.
Full size table

Radar vision calibration experiment

To verify the fusion accuracy of the camera and radar in our system, ensuring that the radar can accurately detect small targets like the thoracic and abdominal cavities of neonates in practical applications, we conducted a calibration experiment using a corner reflector placed at various positions. The experimental setup is illustrated in Fig. 12a. Reference values for the azimuth and elevation angles of the corner reflector relative to the system were measured using a total station.

Fig. 12
figure 12

(a) Experimental scene (b) Calibration example (c) Azimuth results (d) Elevation results.

Full size image

Figure 12b is an example of calibration results from different perspectives, where the background image represents the 2D DBF results of the radar. The red cross marks indicate the results of visual angle measurement, while the black cross marks represent the reference values. It can be observed that the measurement values of these three methods are generally consistent. The results of all eight experiments are plotted as curves in Fig. 12c,d, with the horizontal axis representing the experiment number and the vertical axis representing the angle value.The radar system measures angles by comparing phase differences between different antennas. As the target angle increases, the phase difference becomes less sensitive to changes in angle. Therefore, as the target angle increases, the fusion accuracy of the system also decreases. The maximum error in azimuth reaches nearly 3°around ± 40°, while the maximum error in elevation reaches nearly 4° around ± 20°, which are still within the fusion error of 4.77° proposed in this paper. This experiment demonstrates that the system proposed in this paper has a high level of multi-sensor fusion accuracy and has potential for clinical applications in neonates.

Neonatal RR and HR monitoring experiment

To validate the STAM method and test the RVF system, we conducted clinical trials with neonates. The radio signal power emitted by the radar was less than − 10 dBm, significantly lower than that of mobile phones or WiFi devices. Data processing was implemented using MATLAB. Since Yang’s method15 and our approach both target applications for neonates and address similar issues, our method will be compared against Yang’s AMF method. The experimental subject is a neonate from Beijing Medical Third Hospital, with reference values obtained from a three-lead electrocardiogram shown in Fig. 13. The neonate under study is 33 weeks gestational age, 17 days old, and weighs 2010 g in general ward. The study was conducted according to the guidelines of the Declaration of Helsinki and approved by the Ethics Committee of Peking University Third Hospital Medical Science Research Ethics Committee (Medical Ethics Approval No.062-02(2024)).The Written Informed Consents were provided by the legal guardians of all the participants.

Fig. 13
figure 13

Three lead electrocardiogram.

Full size image

The accuracy of the system in measuring RR and HR was evaluated by the root mean square errors(RMSE) of Eq. (12), the smaller the RMSE, the more accurate the measurement.

$$ RMSE = \sqrt {\frac{1}{N}\sum {(HR_{{est}} - HR_{{ref}} )^{2} } .} $$
(12)

Figure 14 shows the experimental setup from the camera perspective in the three experiments. Each experiment is conducted for one and a half minutes, yielding approximately 60 test results. In Fig. 14a, where both the radar and camera are aligned with the neonate’s thorax, the neonate is in a state of deep sleep and immobility. This experiment aims to validate the effectiveness of the STAM method. In Fig. 14b, the neonate is awake and exhibits random limb movements.Due to the twisting movements, the radar and camera are no longer directly aligned with the thorax. This experiment aims to verify the tracking ability and robustness of the RVF system. In Fig. 14c, where hand movements are deliberately made within the radar’s field of view to simulate the interference caused by staff during rescue and monitoring scenarios. This experiment tests the spatial filtering capability of the narrow radar beam presented in this study.

Fig. 14
figure 14

Three experimental scenes.

Full size image

Figure 15a,b present the results of the first experiment. In terms of HR measurement, STAM exhibits an average error of 4.12 BPM, while AMF has an average error of 4.24 BPM. Since the experiments in this group specifically align with the thorax, there is minimal difference observed in HR measurements between the two methods. However, in the case of RR measurement, STAM, which extracts abdomen phase, shows an average measurement error of 1.51 BPM, while AMF, which still extracts thoracic phase, exhibits a higher error of 7.22 BPM. The STAM method in this study achieves superior RR measurement results due to its better alignment with the neonate’s abdominal breathing model.

Fig. 15
figure 15

Measurements align with thorax.

Full size image

Figure 16a,b shows the experimental results for the second experiment. Based on image recognition, RVF identifies the real-time positions of the thorax and abdomen and selects the phase of the corresponding beam for measurement. The average measurement error for RR is 3.35 BPM, and for HR is 3.51 BPM. In contrast, AMF lacks of tracking the neonate, which leads to phase extraction errors. As a result, the average measurement error for RR is 19.61 BPM, and for HR is 16.08 BPM. Through high-precision multi-sensor fusion, RVF achieves accurate and robust measurements of RR and HR, while also implementing spatial filtering for random limb movements in neonates.

Fig. 16
figure 16

Measurements deviation from the thorax.

Full size image

Figure 17a,b depicts the results of the third experiment. The results show that the system experiences minimal interference, with an average measurement error for RR of 1.61 BPM and for HR of 3.01 BPM. In contrast, AMF shows an average measurement error for RR of 15.68 BPM and for HR of 9.11 BPM. The results demonstrate that RVF exhibits precise spatial filtering capability with its narrow beamwidth.

Fig. 17
figure 17

Measurements With Staff Motion.

Full size image

Figures 15, 16 and 17 displays the comparative test results of a neonate across different scenarios, with the results of six experimental groups from three scenarios collectively represented using Bland-Altman plots, as depicted in Fig. 18. Figure 18a presents the comparison of RR measurements, where the limits of agreement (LoA) for the AMF method reach a width of 35 BPM, whereas the LoA for the STAM method is approximately 6 BPM. Figure 18b demonstrates the comparison of HR measurements, with the AMF method exhibiting LoA close to 60 BPM, in contrast to the STAM method’s LoA of 13 BPM. Additionally, the scatter plot for the STAM method shows a nearly uniform band-like distribution, indicating superior agreement between the STAM method and the true value.

Fig. 18
figure 18

Bland-Altman plot summarizing the results of three experimental scenarios.

Full size image
Table 3 Neonatal experimental error.
Full size table

In Table 3, we summarize the comparison of errors in three experiments between RVF and AMF. The results indicate that in different experimental scenarios, the proposed method and system achieve accurate measurement results, with errors in RR and HR both below 5 BPM. Furthermore, based on the CWT method15, the algorithm’s sensitivity to neonatal movements, rolling, and environmental disturbances is further reduced. Compared to methods using FFT7,9,11, our approach does not require the subject to remain still.

Conclusion

In this work, we have proposed a method using neonatal thoracic and abdominal radar beams for measuring HR and RR based on a radar-version fusion system. Experiments proved that the proposed method is better suited to neonatal respiratory patterns, and the developed system exhibits greater robustness in neonatal application scenarios.

This radar system and signal processing technique can be considered a useful technology for the development of neonatal resuscitation and prolonged monitoring. Future work includes expanding the dataset further, developing a more comprehensive respiratory harmonic suppression algorithm, automating the diagnosis of neonatal emergencies based on measurement results, and gathering a broader range of experimental data from different neonates.