Structural characteristics of corrugated sandwich rectangular pressure vessels

Abstract

Rectangular cross-section pressure vessels are favored for point-to-point liquid cargo transportation due to their compact structure, stability, and high volumetric efficiency. However, they suffer from insufficient local stiffness, resulting in lower load-bearing capacity compared to circular cross-section pressure vessels. The corrugated sandwich structure offers excellent bending performance, lightweight properties, and ease of forming. This paper proposes and designs a rectangular pressure vessel enhanced with a corrugated sandwich structure. Finite element analysis is employed to study its load-bearing characteristics, and the mechanical model is simplified accordingly. A deviation of 4.55% was found through theoretical calculations, confirming the accuracy of the finite element analysis results. The new pressure vessel design increases volume by 17.2% compared to traditional designs. The ratio of the moment of inertia of the circumferential reinforcement structure ($I_{z\;sq}$) to that of the external corrugated sandwich structure ($I_{z\;sd}$), denoted as Π₁. As the parameter Π₁ increases, the average displacement and maximum stress show an increasing trend, stabilizing when Π₁ ≥ 1.14. With the increase of Π₂, the average displacement rises, while the maximum stress first increases and then decreases, reaching its minimum at Π₂ = 1.55.

Introduction

Pressure vessels are enclosed containers designed to hold gases or liquids under pressure, playing a crucial role in the reaction, storage, and transportation of solid, liquid, and gaseous chemical substances. They are indispensable in various sectors of the national economy and defense industry. As vital components in refineries, petrochemical plants, and other industrial facilities, pressure vessels occupy significant land areas and present substantial opportunities for optimization. To achieve greater volume efficiency, researchers have developed numerous non-circular cross-section pressure vessels. These vessels typically feature regular and plane-symmetric cross-sections, such as rectangular, rounded rectangular, oblong, and elliptical shapes^1,2,3. Compared with conventional cylindrical pressure vessels, rectangular cross-section pressure vessels exhibit higher volumetric efficiency. They provide greater storage capacity under limited spatial constraints. However, the manufacturing process is challenged by the complex forming of large flat plates and three-dimensional transition regions at the corners. In addition, the dense distribution of weld seams and severe stress concentrations increase the risk of welding defects and deformation. These issues critically affect the sealing integrity and pressure-bearing capacity of the vessel⁴. Rectangular pressure vessels with flat bottoms are considered more convenient for transportation and installation compared to circular pressure vessels with curved bottoms⁵. Consequently, they are extensively employed in pressure storage tanks, desalination systems, fuel tanks, wind tunnel test sections, and various other applications^6,7,8.

To address the strength deficiencies of non-circular cross-section pressure vessels, researchers have proposed pressure vessels with reinforced structures, which can be generally categorized into two types based on the location of the reinforcement: internal reinforcement^9,10 and external reinforcement¹¹. The theoretical analysis and structural forms of non-circular pressure vessels are highly interrelated, resulting in significantly different stress derivation methods for various cross-sectional shapes. Thus, the research methods can be classified into three categories based on cross-sectional shapes: elliptical, rectangular, and other forms. Guo and Zeng^12,13 proposed an analytical method for cuboid pressure vessels, analyzing the interactions between four and six side plates, respectively, and validated their model against FEM results. Choi et al.¹⁴ designed a rectangular pressure vessel that uses internal plates to bear the load, offering greater volume compared to circular cross-sections. They analyzed ultimate strength, dynamic acceleration, buckling, and thermal/fatigue performance according to ASME and IGC standards. Choi also designed a truck liquid hydrogen fuel storage tank with an irregular structure and analyzed its structural strength and thermal stress using FEM, calculating strength under eight load conditions to ensure compliance with regulations. Tapeinos¹⁵ conducted simulations using FEM on a multi-chamber pressure vessel composed of shells, analyzing the impact of critical points on the structural integrity of the tank. Lokhande et al.¹⁶ investigated the influence of structural parameters on the strength of rectangular containers, analyzing the effects of corner radius, thickness, and length using FEM. Additionally, they examined the impact of stiffeners on the mechanical performance of rectangular containers, finding that stiffeners significantly improved stress distribution, with mid-position stiffeners providing the best reinforcement.

Non-circular cross-section pressure vessels, due to their complex reinforcement structures and varied cross-sectional shape parameters, require optimized design to achieve optimal structural parameters while ensuring safety. Zhang et al.¹⁷ proposed using plates of uniform thickness to fabricate stiffeners for increasing the stiffness of rectangular plates and provided an optimization method to determine the dimensions and arrangement of the stiffeners, meeting regulatory and manufacturing requirements for the best design solution. Kumar et al.¹⁸ utilized ANSYS finite element software to analyze the mechanical response of various stiffened pressure vessel structures and optimized the stiffener configuration based on total deformation and Mises stress. Xu¹⁹ conducted parameter analysis to optimize the right-angle corners of prismatic LNG storage tanks, meeting the requirements for lightweight and ultimate load-bearing capacity.

Existing studies primarily concentrate on homogeneous materials, while applications involving heterogeneous materials remain largely unexplored. Although corrugated sandwich structures have been extensively studied worldwide in terms of their fabrication, mechanical properties, thermal insulation, and acoustic performance, their application in pressure vessels remains at a nascent stage²⁰. To date, only a limited number of conceptual studies by international experts have been reported, with most investigations remaining theoretical^21,22,23. Moreover, the absence of design methodologies for heterogeneous material pressure vessels, combined with the lack of research on corrugated sandwich rectangular pressure vessels and their structural parameter optimization, remains a significant research gap. Integrating corrugated sandwich structures into pressure vessel designs is regarded as a promising yet complex approach to achieving high-volume, load-bearing, and lightweight performance. Addressing these challenges is considered essential for advancing structural design and optimization in pressure vessels.

In summary, this study aims at achieving both large volume and high load-bearing capacity by innovatively designing a new type of pressure vessel enhanced with a corrugated core structure, thereby achieving a high degree of performance integration. Finite element analysis was utilized to simulate the model, and the results were compared with the design method to validate the correctness of the proposed approach.

Methodological approach

Design of a new type of pressure vessel

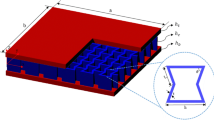
Figure 1 shows this paper introduces an innovative pressure vessel design enhanced with corrugated sandwich structures to improve load-bearing capacity. The proposed pressure vessel is composed of axial and circumferential reinforcement structures and corrugated sandwich structures. These structures are welded together to form an integrated unit, where the corrugated sandwich structure and the axial and circumferential reinforcement structure function as a single entity. Given that large rectangular panels under uniform load can experience large bending stress, the circumferential reinforcement structures are employed to divide the pressure vessel into smaller rectangular sections, thereby reducing the bending stress in the corrugated sandwich structures. Furthermore, the corrugated sandwich structures are utilized in place of traditional homogeneous solid plates, taking its advantage of high bending stiffness and lightweight properties. This design not only enhances volumetric efficiency but also achieves significant weight reduction. Unlike conventional corrugated panels, this design incorporates a discrete corrugated sandwich structure, where adjacent corrugated cores are directly connected to the face panels. When the dimensions of the pressure vessel need to be adjusted, it can be achieved by increasing the number of axial and circumferential reinforcement structures or modifying the spacing between them.

Fig. 1

New pressure vessel structure.

Figure 2 shows a highly symmetric discrete corrugated sandwich structure is employed, allowing for the description of only half of the structure. The discrete corrugated sandwich structure consists of upper panels, bottom panels and corrugated cores, with a unit cell length defined as $l_{c} /2 = l_{c1} /2 + l_{c2} /2 + l_{c3} /2$. Key geometric features of the discrete corrugated sandwich structure include the upper panel thickness ($t_{t}$), bottom panel thickness ($t_{b}$), core height ($h_{c}$), core web thickness ($t_{c}$), and core web length ($l$).

Fig. 2

Schematic diagram of discrete corrugated sandwich structure.

Finite element modelling

To enable the analysis of the novel structural pressure vessel introduced in the previous section, this chapter begins by establishing a baseline model of a pressure vessel with conventional dimensions, following relevant standards²⁴. The pressure vessel model, with overall dimensions of 5790 mm × 2540 mm × 2540 mm and a design pressure load of 1 MPa, as shown in Fig. 1, incorporates both external and internal corrugated sandwich structures, as well as axial and circumferential reinforcement structures. The geometric dimensions for a singleexternal corrugated sandwich structure are specified as follows: $a = 2000\;{\text{mm}}$, $b = 1320\;{\text{mm}}$, $t_{t} = 10\;{\text{mm}}$, $t_{b} = 10\;{\text{mm}}$, $t_{c} = 10\;{\text{mm}}$, $h_{c} = 150\;{\text{mm}}$, $l_{c1} /2 = l_{c3} /2 = 10\;{\text{mm}}$, and $l_{c2} /2 = 100\;{\text{mm}}$. Figure 3 shows the geometric dimensions of the internal corrugated sandwich structure are displayed , featuring a central manhole and a bottom fluid passage hole with radii of 350 mm and 100 mm, respectively. The axial and circumferential reinforcement structures are constructed from square steel tubes with a wall thickness of 10 mm and an internal diameter of 150 mm. All components were made of 07MnCrMoVR steel, whose Young’s modulus and Poisson’s ratio are ${\text{E = 210 }}\;{\text{GPa}}$ and $\mu = 0.3$, respectively. 07MnCrMoVR demonstrates remarkable mechanical properties, making it highly suitable for applications involving high pressure and elevated temperatures²⁵. The material exhibits a minimum yield strength of 345 MPa and a tensile strength ranging from 510 to 650 MPa, providing excellent resistance to substantial stress while maintaining structural integrity. Additionally, with an elongation of no less than 21%, 07MnCrMoVR ensures exceptional ductility, enabling it to withstand complex loading conditions and reducing the likelihood of sudden failure. These attributes collectively establish 07MnCrMoVR as a reliable material for demanding structural applications.

Fig. 3

Geometric dimensions of internal corrugated sandwich structure.

Figure 4 shows the geometric model of the half pressure vessel in the x-direction. Due to the complexity of the model, it was initially constructed using CATIA software to ensure precise geometric representation. The constructed model was then imported into ABAQUS 2022, a widely used finite element analysis (FEA) software, for simulation and analysis. The finite element mesh was generated using C3D8R continuum solid elements, a hexahedral element type with reduced integration and hourglass control. This element type was chosen to ensure computational efficiency while maintaining accuracy in capturing the structural behavior. The inclusion of hourglass control further prevented numerical instabilities, ensuring the stiffness of the elements during the simulation. To balance computational accuracy and cost, a mesh convergence study was performed. Given that the thicknesses of the upper and bottom panels as well as core webs of the corrugated sandwich structure were significantly smaller than the mesh size, two elements were assigned in the thickness direction. Finite element simulations were conducted using mesh sizes of 50 mm, 40 mm, 30 mm, 20 mm, and 10 mm to assess the impact of mesh size on the maximum Mises stress, maximum S22 principal stress, and maximum deformation. After considering the computational resources and time constraints, a mesh size of 20 mm was ultimately selected for the study. The final mesh comprised approximately 1,327,248 elements, providing sufficient resolution for reliable simulation results.

Fig. 4

Geometric model of the half pressure vessel in the x-direction.

Validation of finite element model

At present, there are no experimental and theoretical studies on this novel pressure vessel. Note that the novel pressure vessel is mainly made of corrugated sandwich structures, and it is usually used under internal pressure loads. Therefore, the theoretical result of a corrugated sandwich structure under a uniform load is employed to verify the finite element modelling method used in Section "Finite element modelling". In the finite element model, the material parameters as well as the geometric dimensions of the corrugated sandwich structure are the same as those presented in Section "Finite element modelling".

Based on the theoretical analysis in our previous study²⁶, the theoretical total stress of a corrugated sandwich structure can be calculated by superimposing the local and global bending stresses, where the global bending stress and the local bending stress can be obtained by solving the bending equation of a corrugated sandwich structure with the Galerkin method. According to the theoretical calculation, the total stress of the corrugated sandwich structure under a uniform load of 1 MPa is 306.4 MPa, and the result obtained from the corresponding finite element analysis is 326.7 MPa, yielding an error of 6.21% relative to the theoretical value. Therefore, a good agreement between the result obtained from theoretical and finite element analysis is obtained, validating the finite element modeling method used in this study.

Stiffness evaluation method for axial and circumferential reinforcement structures

In the pressure vessel design, changes in the parameters of the axial and circumferential reinforcement structures alter their structural rigidity, which in turn affects the boundary conditions of the corrugated sandwich structures. Consequently, these changes modify the deformation at the joints between the corrugated sandwich structures and the axial and circumferential reinforcement structures, as well as the maximum stress experienced by the corrugated sandwich structures. The moment of inertia, a geometric parameter, is utilized to describe the cross-section’s resistance to bending. Under constant conditions, an increase in the moment of inertia enhances the structure’s bending resistance. To comprehensively consider the influence of the axial and circumferential reinforcement structures’ parameters on the mechanical response of the corrugated sandwich structures, the coupling relationship between the reinforcement structures and the corrugated sandwich structures is integrated. The ratio of the moment of inertia of the circumferential reinforcement structure ($I_{z\;sq}$) to that of the external corrugated sandwich structure ($I_{z\;sd}$), denoted as $\prod_{1}$, is employed as an indicator, as shown in Eq. (1). Then the relationship between the ratio of bending stiffness of the axial and circumferential reinforcement structures to that of the corrugated sandwich structure and the maximum stress in the corrugated sandwich structure is explored, leading to the determination of the critical ratio where the maximum stress in the corrugated panel remains unchanged with variations in frame thickness.

$$\prod_{{1}} { = }\frac{{I_{z\;sq} }}{{I_{z\;sd} }}$$

(1)

To facilitate a comparative analysis of the bending mechanical properties of the corrugated sandwich structure and the axial and circumferential reinforcement structures under identical conditions. Figure 5 shows the center of the external corrugated sandwich structure is established as the origin, with the horizontal direction designated as the y-axis and the vertical direction as the z-axis. The moment of inertia for both the corrugated sandwich structure and the square steel tube is calculated within this coordinate system, employing the calculation methodology in Eq. (2). This approach ensures a standardized comparison, enhancing the precision of the mechanical performance assessment between the corrugated sandwich structure and circumferential reinforcement structure.

$$I_{z} = \int_{A} {y^{2} dA}$$

(2)

Fig. 5

Coordinate diagram of inertia moment of external corrugated sandwich structure and circumferential reinforcement structure.

In Eq. (2), A is the integration region and is the cross section region.

In this section, the moment of inertia for external corrugated sandwich structure, calculated using Eq. (2), is determined to be $I_{z\;sd} = 6.02 \times 10^{5} \;{\text{mm}}^{4}$. The width $B$ of the circumferential reinforcement structure, a critical parameter of the circumferential reinforcement structure, is the ratio of the width to the overall thickness of the corrugated sandwich structure, is represented by the ratio $\prod_{2}$. The method for calculating this ratio is expressed in Eq. (3). This parameterization facilitates a standardized evaluation of the structural efficiency, enabling an analytical comparison between external corrugated sandwich structure and circumferential reinforcement structure.

$$\prod_{{2}} { = }\frac{B}{{t_{t} + t_{b} + h_{c} }}$$

(3)

In Eq. (3), B is the width of the circumferential reinforcement structure; $t_{t}$ is the thickness of the upper panel, $t_{b}$ is the thickness of the lower panel, and $h_{c}$ is the height of the corrugated core.

Under operational conditions, the novel pressure vessel must withstand static liquid pressure and internal pressure loads resulting from the volatilization of the medium. For the novel pressure vessel, under static loads such as liquid static pressure and internal pressure, the structural design must satisfy the small deformation assumption. Additionally, due to the small contact area of the reinforcement structure and the significantly greater bending resistance of the structure members compared to the corrugated sandwich structure, the following assumptions are made in the mechanical design of the novel pressure vessel:

• 1. The reinforcement structure in the novel pressure vessel is considered rigid under static loads, with no deformation occurring, requiring $\prod_{1} \ge 1.14$ and $\prod_{2} = \, 1.55$.

• 2. The corrugated sandwich structures in the novel pressure vessel are welded to the reinforcement structure, and under static loads, they can be considered as fixed boundary conditions.

To investigate the impact of varying wall thicknesses on the mechanical performance of the novel pressure vessel, square steel tubes with an outer diameter of 58 mm were selected. The value of $\prod_{1}$ was altered by varying the wall thickness, thus examining its influence on the mechanical response of the pressure vessel, with specific parameters summarized in Table 1. On this basis, to explore the effects of different widths of the circumferential reinforcement structure on the pressure vessel’s mechanical performance, two sets of wall thicknesses were configured. Changes in $\prod_{2}$ were achieved by adjusting the circumferential reinforcement structure width, with the respective structural dimensions presented in Table 2. This methodological approach allows for a systematic evaluation of how dimensional changes influence the structural integrity and functionality of the pressure vessel.

Table 1 Moments of inertia of circumferential reinforcement structures with different thicknesses and Π₁.

Table 2 Moments of inertia of circumferential reinforcement structures with different widths, Π₁ and Π₂.

Mechanical properties of pressure vessels

Deformation analysis

The new pressure vessel consists of a multi-section cylinder. For the multi-section cylindrical model, the overall deformation contour is shown in Fig. 6. Due to the geometric symmetry and load symmetry of the model, the deformation field also exhibits a high degree of symmetry. The figure shows that the displacement fields of the two edge sections are highly consistent, as are those of the two central sections. Further analysis indicates that the deformation at the boundaries between adjacent sections is significantly less than that in other regions. This is attributed to the combined effect of the circumferential reinforcement structure and internal corrugated sandwich structure, which provide substantial stiffness at the section connections, thereby reducing deformation. This validates the effectiveness of the circumferential reinforcement structures.

Fig. 6

Deformation contour of the new pressure vessel.

To comprehensively analyze the mechanical response of the pressure vessel, two representative sections from the edge and central regions were selected. Given that the mechanical model of a single section is highly symmetrical and its four corrugated sandwich structures are equivalent, analyzing the corrugated sandwich structures in the two regions will sufficiently reveal the deformation and stress characteristics of the corresponding sections.

Figure 7 shows the deformation contour of the corrugated sandwich structure in the edge section. It can be seen that the maximum deformation of a single section in the edge section occurs near the fixed constraint end on the corrugated core, reaching 3.09 mm. The fixed constraint at the boundary, combined with the support provided by the first corrugated core, results in high bending stiffness of the upper panel, and thus leading to minimal deformation. The corrugated cores, which can be considered as slender rods, undergo “buckling” under uniform load, causing significant deformation, primarily as protrusions in the x-axis direction. The other corrugated cores exhibit deformation that coordinates with the upper panel; although the deformation is more pronounced in the central region, the values are relatively small compared to those in the edge region, generally less than 2.0 mm. The edges of the corrugated cores exhibit almost no deformation, attributable to the axial and circumferential reinforcement structures, which significantly enhance the stiffness at the boundaries, thereby demonstrating the effectiveness of the axial and circumferential reinforcement structures.

Fig. 7

Deformation contour of the corrugated sandwich structure in the edge section.

The maximum deformation of the upper panel is 2.45 mm, occurring near the circumferential reinforcement structure. Although the circumferential reinforcement structure possesses high stiffness, it still undergoes some deformation. The combined effect of the corrugated sandwich structures in the edge and central regions results in significant deformation in this area. Further analysis indicates that the deformation of the upper panel exhibits fluctuations along the width direction of the corrugated sandwich structure. This is due to the support provided by the corrugated cores, which minimizes deformation in the regions where the corrugated cores connect to the upper panel, while local bending occurs between adjacent corrugated cores under uniform load, causing localized deformation. The maximum deformation of the bottom panel is 2.22 mm, also occurring near the circumferential reinforcement structure. Unlike the upper panel, the bottom panel exhibits good continuity in its deformation, with no significant localized deformation observed between adjacent corrugated cores.

Figure 8 shows the deformation contour of the corrugated sandwich structure in the central section. It can be seen that the maximum deformation occurs in the central region of the upper panel, with a deformation magnitude of 3.34 mm, differing from the maximum deformation location of the corrugated sandwich structure in the edge region. The maximum deformation of the upper panel fluctuates along the width direction of the corrugated sandwich structure, consistent with the previously discussed causes of local deformation. For the central region section, the boundary conditions can ideally be considered as fully fixed. However, taking into account the actual deformation of the pressure vessel, the boundary conditions lie between fully fixed and simply supported. The sections at both ends have one end as fully fixed, while the other end’s boundary conditions lie between fully fixed and simply supported. Compared to the corrugated sandwich structure in the edge section, the corrugated sandwich structure in the central section has more pronounced local deformation fluctuations. This is because the central section is directly connected to the circumferential reinforcement structure, which undergoes deformation. Consequently, this deformation amplifies the fluctuation in the upper panel’s deformation. The maximum deformation of the bottom panel is 2.98 mm, with no significant local deformation, demonstrating good continuity.

Fig. 8

Deformation contour of the corrugated sandwich structure in the central section.

To effectively illustrate the overall and localized deformation of the corrugated sandwich structure, a vertical path (Path 1, Fig. 8) through the panel’s center is defined. Displacement data along Path 1 is extracted from the upper panels in both the edge and central regions, and the displacement-distance curves are plotted, as shown in Fig. 9. It can be seen that the corrugated sandwich structure in the edge region exhibits significant deformation near the fixed constraint, which gradually stabilizes with increasing width direction of the corrugated sandwich structure. Conversely, the central region panel, benefiting from symmetric boundary conditions, displays highly symmetric and stable overall and localized deformations. Further analysis reveals that the upper panels in both regions exhibit seven displacement oscillations, with the oscillation periods matching the corrugation pitch, thereby validating the accuracy of the localized deformation observations. When comparing the localized deformations between the two regions, it is also found that the deformations were nearly identical, regardless of whether the panel is in the central or edge region. This indicates that the primary difference between the panels in the two regions lies in the overall deformation, while the localized displacements remain consistent. This consistency further corroborates the accuracy of the previously discussed localized deformation findings.

Fig. 9

Displacement–distance curves on Path 1.

Stress analysis

The multi-section cylindrical model exhibits a high degree of symmetry, and its stress characteristics are similarly consistent. Therefore, analyzing the stress field of a single corrugated sandwich structure in both the central and edge sections is sufficient to determine the stress characteristics of the entire multi-section cylinder. Under uniform load, the maximum stress of a corrugated sandwich structure with fully fixed edges typically occurs at the long edge. Analysis of this stress indicates that the normal stress in the vertical length direction of the single corrugated sandwich structure is the primary component, accounting for the majority of the stress, while the normal stress in the vertical width direction of the single corrugated sandwich structure and the shear stress are relatively minor and can typically be disregarded.

Figure 10 shows the Mises stress contour of corrugated sandwich structure in different sections. It can be seen that the maximum Mises stress in the edge section of the corrugated sandwich structure occurs in the area where the upper panel contacts the first corrugated core near the fixed constraint, with a magnitude of 300.3 MPa. The combined effect of the fixed constraint and the first corrugated core results in significant local stiffness, leading to high local stress under uniform load. On the opposite end, connected to the circumferential reinforcement structures, the reinforcement structure’s deformation reduces the constraint stiffness, causing some deformation and a corresponding reduction in stress. The maximum Mises stress at this end is 238.9 MPa, indicating a significant difference compared to the fixed constraint end.

Fig. 10

Mises stress contour of corrugated sandwich structures in different sections.

For the central region of the section, the boundary conditions at both ends lie between fully fixed and simply supported, and the load and geometric model are symmetrical. Consequently, the stress field in this region is also highly symmetrical. Figure 10 also shows that the stress is higher at the boundaries and lower at the center, displaying a decreasing trend from the boundaries to the center. Further analysis reveals that the maximum Mises stress occurs at the connection between the upper panel and the first corrugated core at both ends, with a value of 282.2 MPa. This is attributed to the significant local stiffness in these areas. Similar to the deformation contour, the stress on the upper panel of the corrugated sandwich structure fluctuates significantly with changes in the width direction of the corrugated sandwich structure. The support from the corrugated core creates high local stiffness at the connections between the core and the upper panel, resulting in higher stress in these regions. The stress in the areas between adjacent cores decreases gradually from the boundaries to the center, resembling the distribution pattern of a corrugated sandwich structure with fully fixed edges under uniform load.

Figure 11 shows the locations of the maximum S22 principal stress on the two corrugated sandwich structures that coincide with those of the maximum Mises stress. The distribution trend of the S22 principal stress is consistent with the Mises stress, both exhibiting fluctuations. The maximum S22 principal stresses in the edge and central section corrugated sandwich structures are 326.5 MPa and 252.0 MPa, respectively, which contribute the majority of the Mises stress. Given the characteristics of the corrugated sandwich structure, the distribution features of the S22 principal stress are more pronounced. Thus, the S22 principal stress effectively illustrates the overall stress characteristics of the structure.

Fig. 11

S22 contour of corrugated sandwich structure in different sections.

As shown in Fig. 12, the maximum S22 principal stress for the two key regions of the corrugated sandwich structures occurs in the edge region. Due to the differences between fixed constraints and semi-fixed constraints, the S22 stress varies significantly on the front half of the corrugated sandwich structure but aligns closely on the rear half. Therefore, it can be concluded that the maximum stress for the entire segment is located in the edge region of the corrugated sandwich structure, specifically where the upper panel contacts the first corrugated core.

Fig. 12

Principal stress S22 versus distance on Path 1.

Characterization of circumferential reinforcement structures

Effect of wall thickness of circumferential reinforcement structures on the displacement of corrugated sandwich structures

Figure 13 shows that as the wall thickness (t) of the circumferential reinforcement structure increases, the average displacement at the junction with the corrugated sandwich structure decreases. However, beyond a specific t, the rate of reduction slows and stabilizes. Under a 0.5 MPa internal pressure load, a t of 4 mm results in an average displacement of 0.78 mm, which decreases to 0.53 mm (32% reduction) at $t = 8\;{\text{mm}}$. Further increasing t to 12 mm decreases the displacement to 0.46 mm (13.2% reduction). Thus, a t of 8 mm provides sufficient stiffness. This critical thickness remains constant under pressure loads of 0.1 MPa and 1 MPa, indicating that the relationship between average displacement and t is pressure-independent. As shown in Table 1, when $t = 8\;{\text{mm}}$, Π₁ reaches 1.14. At this point, the stiffness of the circumferential reinforcement structure is sufficient, and further increases in Π₁ do not significantly decrease the average displacement at the junction with the corrugated sandwich structure.

Fig. 13

Effect of wall thickness and Π₁ of circumferential reinforcement structure on the average displacement of corrugated sandwich structures under different pressure loads.

Figure 14 shows the histogram of displacement decrease with increasing t. Case 1 illustrates the average displacement decrease as t increases from 4 to 6 mm. It can be seen that in the initial stages, the average displacement decreases significantly with increasing t. However, once the t reaches a specific value, further increases result in minimal changes in average displacement. Specifically, when the t increases from 4 to 6 mm, the reductions in displacement under internal pressure loads of 0.1 MPa, 0.5 MPa, and 1 MPa are 0.04 mm, 0.18 mm, and 0.32 mm, respectively, demonstrating a notable decrease. Conversely, when t increases from 7 to 8 mm, the corresponding reductions in displacement are only 0.006 mm, 0.031 mm, and 0.066 mm, indicating a significant slowdown in the rate of decrease, consistent with the previously observed trend.

Fig. 14

Average Displacement decrease with the wall thickness variations.

Effect of wall thickness of circumferential reinforcement structures on maximum stress in corrugated sandwich structures

Given that the mechanical response characteristics of the new pressure vessel remain consistent under different pressure loads, a 0.1 MPa pressure load is sufficient to reflect its mechanical response. Figure 15 shows the stress contour of a single corrugated sandwich structure in the central region of the new pressure vessel under a 0.1 MPa pressure load. It can be observed that the maximum stress of the single corrugated sandwich structure occurs at its edge and does not change with the variations of Π₁, demonstrating good consistency.

Fig. 15

Contour of Stress of a single corrugated sandwich structure under a pressure load of 0.1 MPa.

Under a 0.1 MPa internal pressure load, Fig. 16 shows the maximum stress on the corrugated sandwich structure in the central region generally decreases with increasing t. When $t{ = 4}\;{\text{mm}}$, the maximum stress on the corrugated sandwich structure is 107.6 MPa. When t increases to 8 mm, the stress rapidly decreases to 62.7 MPa, a reduction of 44.9 MPa. However, when t exceeds 8 mm, the influence of increased t on the maximum stress becomes limited. When $t{ = 10}\;{\text{mm}}$, the maximum stress on the corrugated sandwich structure is 59.3 MPa; when $t = 12\;{\text{mm}}$, it is 60.9 MPa, only 1.8 MPa less than that at 8 mm. The large stress on the corrugated sandwich structure at $t{ = 4}\;{\text{mm}}$ is due to the insufficient bending stiffness of the circumferential reinforcement structure, which causes significant displacement at the connections, as shown in Fig. 13. As t increases, the bending stiffness of the circumferential reinforcement structure improves, reducing displacement at the connections and consequently decreasing the maximum stress on the corrugated sandwich structure. When t reaches 8 mm, the stress on the corrugated sandwich structure is significantly reduced, but further increases in t have minimal effect on maximum stress and deformation, as shown in Figs. 13 and 16.

Fig. 16

Effect of wall thickness and Π₁ of circumferential reinforcement structure on the maximum stress of corrugated sandwich structures under different pressure loads.

Under a 0.5 MPa internal pressure load, the maximum stress on the central region corrugated sandwich structure is 543.3 MPa when t = 4 mm and 462.5 MPa when t = 6 mm. When the t increases to 8 mm, the maximum stress decreases significantly to 313.8 MPa. This demonstrates that increasing the t up to 8 mm markedly decreases the maximum stress on the corrugated sandwich structure. However, when the t exceeds 8 mm, the reduction in maximum stress becomes minimal. When t = 12 mm, the maximum stress is 304.5 MPa, only 9.3 MPa less than that at 8 mm, a reduction of just 2.96%. This behavior is consistent with the observations under a 0.1 MPa load. For a 1 MPa internal pressure load, although the load increases tenfold, the maximum stress on the corrugated sandwich structure stabilizes when t reaches 8 mm. Therefore, changes in load do not alter the relationship between circumferential reinforcement structure thickness and load-bearing characteristics.

Figure 16 also shows that the moment of inertia ratio (Π₁) follows a quadratic trend with increasing t. As shown in Table 1, when t = 8 mm, ${\Pi }_{1} = 1.14$, and increasing t to 12 mm raises Π₁ to 1.38. Once Π₁ exceeds 1.14, further increases in Π₁ have little impact on the maximum stress of the corrugated sandwich structure. Thus, for this pressure vessel model, the critical moment of Π₁ is determined to be 1.14.

Regardless of t, Fig. 17 shows the maximum stress on the corrugated sandwich structure exhibits a linear relationship with the applied load. When t is 4 mm or 6 mm, this linear relationship is relatively weak. However, as t increases to 8 mm, the linear relationship between maximum stress and pressure load becomes more pronounced. This is due to that, when $t = 8\;{\text{mm}}$, the circumferential reinforcement structure stiffness is sufficient to ensure that the corrugated sandwich structure and circumferential reinforcement structure respond linearly under uniform load. When t continues to increase to 12 mm, the linear relationship between maximum stress and pressure load persists. Therefore, it can be concluded that when the circumferential reinforcement structure stiffness is adequate, and further increases in circumferential reinforcement structure stiffness do not significantly alter the mechanical response of the novel pressure vessel. Meanwhile, changes in load do not significantly affect the maximum stress behavior of the corrugated sandwich structure.

Fig. 17

Influence of pressure load on the maximum stress of the corrugated sandwich structure in the central section.

Figure 18 shows the histogram of maximum stress decrease with increasing t. Case 1 illustrates the maximum stress decrease as t increases from 4 to 6 mm. It can be seen that upon reaching a specific value, the rate of stress reduction slows and eventually stabilizes. This trend is consistent under internal pressure loads of 0.1 MPa, 0.5 MPa, and 1.0 MPa, indicating a uniform mechanical response for the novel pressure vessel. Specifically, when t increases from 4 to 5 mm, the maximum stress on the corrugated sandwich structure decreases by 25.5 MPa, 80.8 MPa, and 200.6 MPa under internal pressures of 0.1 MPa, 0.5 MPa, and 1.0 MPa, respectively, showing a significant reduction. However, as t increases from 7 to 8 mm, the reduction in maximum stress slows, decreasing by 4.4 MPa, 21.6 MPa, and 44.9 MPa under the same respective pressure loads. This behavior aligns with the previously identified critical point of Π₁ = 1.14, and the extent of stress change is largely independent of the load, demonstrating the generality of this trend.

Fig. 18

Maximum stress decrease with the wall thickness variations.

Effect of the width of circumferential reinforcement structure on the displacement of corrugated sandwich structures

When the width of the circumferential reinforcement structure (B) is less than 90 mm, Figs. 19 and 20 show the displacement decreases minimally with changes in B, indicating that the circumferential reinforcement structure is in a state of small deformation. Case 1 illustrates the average displacement decrease as B increases from 58 to 90 mm. However, once B exceeds 90 mm, the displacement increases sharply. As shown in Table 2, when $t = 8\;{\text{mm}}$, $B = 90\;{\text{mm}}$ is identified as the critical point, corresponding to Π₂ = 1.55. When $t = 12\;{\text{mm}}$, the average displacement is 0.9 mm at $B = 58\;{\text{mm}}$; when $B = 130\;{\text{mm}}$, the displacement reaches 1.15 mm; and further increasing B to 160 mm results in a displacement of 1.50 mm, the displacement increases sharply. Therefore, when $B = 130\;{\text{mm}}$ is considered the critical point for $t = 12\;{\text{mm}}$, corresponding to Π₂ = 2.24.

Fig. 19

Effect of B and Π₂ of circumferential reinforcement structure on the average displacement at the connection between the corrugated sandwich structure and the circumferential reinforcement structure.

Fig. 20

Average displacement amplitude with the width variations.

As shown in Fig. 21, when B is 58 mm and 90 mm, the circumferential reinforcement structure undergoes minimal displacement, maintaining its cross-sectional shape. However, as B increases to 130 mm, significant bending displacement appears around the circumferential reinforcement structure’s periphery. Further increasing B to 200 mm results in severe bending displacement on all four sides, placing the circumferential reinforcement structure in an unstable state. Similarly, in Fig. 22, when B is 58 mm and 90 mm, the circumferential reinforcement structure experiences minimal displacement, preserving its cross-sectional shape. At B of 130 mm, although the top and bottom surfaces of circumferential reinforcement structure remain intact, the sides exhibit some bending displacement. As B increases to 160 mm, the displacement becomes more pronounced, and at 200 mm, all four surfaces of the circumferential reinforcement structure exhibit severe bending displacement.

Fig. 21

Displacement contour of the connection between corrugated sandwich structure and different widths of circumferential reinforcement structure at 8 mm thickness.

Fig. 22

Displacement contour of the connection between corrugated sandwich structure and different widths of circumferential reinforcement structure at 12 mm thickness.

As shown in Table 2, when t of 8 mm and 12 mm, the specific values of Π₂ are identified as 1.55 and 2.24, respectively. When these specific Π₂ values are reached or exceeded, significant displacement is observable on all four surfaces of the circumferential reinforcement structure, causing the cross-sectional shape to become unsustainable and leading to structural instability, thereby markedly increasing displacement. Consequently, for the circumferential reinforcement structures discussed in this text, while ensuring that Π₁ exceeds 1.14, it is imperative to maintain Π₂ below these critical thresholds to prevent instability in the circumferential reinforcement structure.

Effect of width of circumferential reinforcement structure on Maximum Stress in corrugated sandwich structures

Figure 23 shows the relationship between the maximum stress on the corrugated sandwich structure and B and Π₂, while Fig. 24 shows the variation of maximum stress with B. Case 1 illustrates the maximum stress decrease as B increases from 58 to 90 mm. These figures indicate that as B increases, the maximum stress on the corrugated sandwich structure initially decreases and subsequently increases. This pattern occurs because an enhancement in B augments the overall bending stiffness but diminishes the local stiffness, resulting in bending deformation under internal pressure load. When B remains below a specific threshold, the overall bending stiffness of the circumferential reinforcement structure predominates, leading to minimal displacement under internal pressure, and the maximum stress decreases as the overall bending stiffness is enhanced. However, once B surpasses this specific value, the local stiffness becomes the primary influence. In this case, further increments in B will lead to the rapidly increase of local displacement and maximum stress. Consequently, there is a specific Π₂ value at which the stress on the corrugated sandwich structure is minimized, a conclusion supported by earlier displacement analyses.

Fig. 23

Effect of width and Π₂ of circumferential reinforcement structure on the maximum stress at the connection between the corrugated sandwich structure and the circumferential reinforcement structure.

Fig. 24

Maximum stress amplitude with the width variation.

Under the condition of a circumferential reinforcement structure with $t{ = 8}\;{\text{mm}}$, when B is 58 mm, the maximum stress is 625.1 MPa. As B increases to 90 mm, the stress decreases to 606.7 MPa, reflecting the dominance of the overall stiffness of the reinforcement structure, with stress decreasing as B increases. As B further increases to 130 mm, the maximum stress reaches 670.8 MPa, and when B increases to 200 mm, the maximum stress rises to 703.4 MPa. From the previous analysis, it can be concluded that when B is between 58 and 90 mm, the overall stiffness dominates, and the maximum stress decreases as B increases. When B exceeds 90 mm, local stiffness becomes the dominant factor, and the maximum stress increases with B. Therefore, the critical value of Π₂ is 1.55. For a circumferential reinforcement structure with $t{ = }12\;{\text{mm}}$, using the same analysis method, the critical value of Π₂ is also found to be 1.55. Therefore, to minimize stress while ensuring that Π₁ ≥ 1.14, the value of Π₂ should be maintained at 1.55.

Conclusion

This paper proposes a novel pressure vessel reinforced with a corrugated sandwich structure. Finite element analysis is employed to examine its load-bearing characteristics, focusing on the circumferential reinforcement structure’s performance. The accuracy of the finite element analysis method was verified by combining it with theoretical methods, leading to the following key conclusions:

• a. A novel pressure vessel reinforced with a corrugated sandwich structure has been designed to simultaneously achieve large volume, high load-bearing capacity, and lightweight characteristics. Compared to traditional pressure vessel structures, its volume can be increased by 17.2%, demonstrating superior volumetric efficiency.

• b. As Π₁ increases, the maximum stress of the corrugated sandwich structure and the average displacement at the connection between the corrugated sandwich structure and the circumferential reinforcement structure show a decreasing trend. When Π₁ reaches 1.14, neither the maximum stress nor the average displacement decreases further with an increase in Π₁. To isolate the effect of t on the mechanical response of the novel pressure vessel, the impact of B on the average displacement and maximum stress was investigated under the condition of Π₁ ≥ 1.14.

• c. The average displacement increases with the increase of Π₂. When Π₂ is below the specific value, the overall stiffness of the circumferential reinforcement structure dominates, resulting in a smaller displacement gradient. However, when Π₂ exceeds the specific value, the local stiffness of the circumferential reinforcement structure becomes predominant, leading to a steep increase in the displacement gradient. The maximum stress initially increases and then decreases with the increase of Π₂, reaching its minimum value when Π₂ is 1.55.