Introduction

Nonlinear evolution equations are essential across several real-world events, encapsulating the intricacies of dynamic systems. These equations are crucial for comprehending fluid dynamics, as they elucidate wave production and turbulence. In optics, the propagation of light in nonlinear media is modeled, resulting in phenomena such as solitons—stable, solitary wave packets. Nonlinear evolution equations also emerge in biology, elucidating population dynamics and the dissemination of diseases. In finance, they assist in simulating market dynamics and option valuation. Their applications encompass various domains, including geophysics for seismic modeling and engineering for material deformation analysis1,2,3,4,5,6,7,8,9,10. These equations are very important for figuring out how things work in systems where linear approximations don’t work well. They give us a lot of information about the complicated patterns and structures that show up in nature and technology.

Solitons in nonlinear evolution equations (NLEEs) are crucial because of their unique properties and extensive applicability in several scientific fields. These stable and concentrated wave packets result from the complex interplay between nonlinearity and dispersion in nonlinear evolution equations (NLEEs). In contrast to conventional waves, solitons preserve their form and speed over considerable distances and are unaffected by interactions with other solitons. This stability renders them indispensable for modeling and understanding intricate physical processes. Their resilience and stability during interactions render solitons effective instruments for addressing and examining NLEEs, offering insights into the dynamics of intricate, real-world systems. Various techniques are employed to investigate precise soliton solutions across multiple fields, including Exp-function10, (G′/G)-expansion11, unified12, Hirota bilinear13, multiple exp-function14, First integral15, transformed rational function16, unified17,18, modified extended tanh and a novel form of modified Kudryashov19, Modified Sardar sub equation20, Riccati equation mapping21, bilinear22,23,24, modified residual power series25 methods, and so on26,27,28,29,30,31.

Currently, bifurcation analysis is essential for comprehending how minor alterations in system parameters can result in significant changes in the behavior of dynamical systems. This mathematical framework assists in identifying important points at which a system transitions from one state to another, which is vital for predicting and controlling complex behaviors across multiple domains32,33,34,35,36,37,38,39,40. Bifurcation analysis in engineering is employed to anticipate and avert structural problems. By comprehending how systems react to variations in parameters, engineers can create more robust structures and prevent disastrous consequences. Bifurcation analysis in fluid dynamics elucidates the transition from laminar to turbulent flow, offering insights into vortex production and pattern development. This analysis in biology examines population dynamics, disease transmission, and neuronal activity, demonstrating how minor alterations can result in substantial changes in behavior or patterns. Bifurcation analysis in economics aids in modeling market dynamics, forecasting how minor fluctuations in variables such as interest rates can result in economic expansions or contractions. Bifurcation analysis is crucial for comprehending chaotic systems. It assists in identifying pathways to chaos and forecasting chaotic behavior in both natural and manmade systems. Bifurcation analysis serves as a potent instrument for the examination and management of complex systems, yielding essential insights for both scholars and practitioners.

This study aims to apply bifurcation theory to M-fGP-NWE and to create the traveling wave. We obtain the phase portrait and Hamiltonian function under various parametric conditions. We examine the homoclinic and heteroclinic orbits from the phase portrait, together with their associated solitary, bell, and periodic wave solutions. Furthermore, to develop traveling wave solutions, we employed an MSE technique for M-fGP-NWE. The mathematical form of the M-fGP-NWE model41,42,43 is follows:

$$\:{Q}_{\text{x}\text{x}\text{x}\text{y}}+{a}_{1}{D}_{M,t}^{\delta\:,r}{Q}_{\text{y}}+{a}_{2}{\left({Q}^{n}\right)}_{xy}+{a}_{3}{Q}_{\text{x}\text{x}}+{a}_{4}{Q}_{\text{z}\text{z}}=0$$
(1)

Mohan et al.42 proposed an equation and examined its integrability via Painlevé analysis. Employing Cole–Hopf transformations, they formulated a trilinear equation in an auxiliary function that dictates the solutions for higher-order rogue waves and dispersive solitons. This equation characterizes the dynamics of nonlinear wave phenomena, with \(\:Q\left(x,y,z,t\right)\) denoting the wave field. The parameters \(\:{a}_{1}\)controls the influence of the fractional derivative, introducing memory effects and nonlocal interactions, \(\:{a}_{2}\) is the nonlinear coupling coefficient and governs nonlinear interactions, affecting wave steepening and soliton formation, \(\:{a}_{3}\) is the transverse dispersion coefficient and influences transverse wave variations, impacting multidimensional wave behavior. The notation \(\:{Q}_{\text{x}\text{x}\text{x}\text{y}}\)​​ represents the mixed partial derivative with respect to x and y, signifying the spatial fluctuations in two dimensions. The \(\:{a}_{1}{D}_{M,t}^{\delta\:,r}{Q}_{\text{y}}\)​ term represents the temporal evolution of the wave field. The nonlinear interaction is captured by the \(\:{a}_{2}{\left(Q{Q}_{\text{x}}\right)}_{y}\)​ term, highlighting the product of the wave field and its spatial derivative. The term \(\:{a}_{3}{Q}_{\text{x}\text{x}}\)​ incorporates the effect of second-order spatial derivatives into \(\:x\) direction, and the \(\:{a}_{4}{Q}_{\text{z}\text{z}}\) term includes the influence of the second-order spatial derivatives in the \(\:z\)-axis direction This complex interplay of terms characterizes the propagation and interaction of nonlinear waves in various physical systems. The main goal of this study is to utilize bifurcation theory to analyze the critical points and phase portraits of the M-fractional Generalized (3 + 1)-dimensional -type nonlinear wave equation, focusing on system transitions to new behaviors, including stability shifts and the emergence of chaos. To examine the solitary wave solutions and the impact of fractional derivatives, we employ a direct method known as the modified simple equation technique on the M-fGP-NWE. Additionally, we illustrate the complex behaviors of the obtained solutions through three-dimensional, two-dimensional, and density diagrams, and the influence of the fractional parameter is depicted in a two-dimensional diagram.

This study is arranged as follows:

"Methodology" offers the procedure of the MSE technique.

"Bifurcation Analysis" offers the execution of the bifurcation theory for the proposed model and shows the phase portrait, the homoclinic and heteroclinic orbit, and their corresponding traveling wave.

"Traveling wave solution of M-fGP-NWE equation" provides the solution to the proposed model by using the MSE technique analytically.

"Numerical Explanation and Graphical Representation" provides the numerical discussion and graphical analysis of the obtained solutions.

"Comparison and novelty" offers a comparison and the novelty of this work.

"Advantages and limitations of the MSE method" provides the advantages and limitations of the MSE method for solving NLEEs.

"Modulation Instability" provides the Modulation instability of M-fGP-NEW equation.

"Conclusion":provides the overview of this study.

Methodology

In this section, we explain the significance of the fractional derivative and the working rule of the modified simple equation method to solve NLEEs.

M-fractional derivative

Fractional derivatives are essential in studying nonlinear evolution equations (NLEEs) because they model complex phenomena with greater precision than integer-order derivatives. They offer a flexible framework to capture the memory and hereditary properties inherent in many physical, biological, and engineering systems. By incorporating fractional derivatives, NLEEs can describe anomalous diffusion and wave propagation in heterogeneous media, resulting in more accurate predictions and solutions. This enhanced modeling capability is vital in fields such as viscoelasticity, fluid dynamics, and signal processing. Additionally, the use of fractional derivatives in NLEEs promotes the development of new analytical and numerical methods, improving the understanding and resolution of complex nonlinear problems. The increasing interest in fractional calculus highlights its importance in advancing both theoretical and applied research across various scientific disciplines, such as44,45,46,47,48,49,50. There are numerous fractional derivatives, including the Riemann-Liouville, Caputo, Atangana-Baleanu, conformable, and He’s fractal derivative, that have been extensively utilized in diverse contexts to characterize memory effects, hereditary features, and nonlocal behaviors in physical and engineering challenges47,48. In this study, we select the M-fractional derivative for its beneficial characteristics in addressing nonlinear evolution equations. This derivative is especially advantageous for maintaining the essential properties of the original equation while integrating fractional-order effects, rendering it appropriate for the analysis of soliton dynamics and wave propagation in intricate media. The M-fractional derivative provides versatility in mathematical expressions and preserves a balance between local and nonlocal characteristics, which is crucial for accurately representing realistic physical processes49,50. Consequently, the selection of the M-fractional derivative is warranted due to its capacity to yield more precise and physically significant solutions within the specified problem context.

Definition and some features of \(\:\varvec{M}\)-fractional derivative

Definition Given a function \(\:\phi\::[0,\infty\:)\to\:\left(-\infty\:,\:\infty\:\right)\), the \(\:M-\)fractional derivative is well-defined as follows:

$$\:{D}_{M,t}^{{\updelta\:},r}\underset{ϵ\to\:0}{{\varphi\:}_{r}\left(x\right)=\text{lim}}\frac{\phi\:\left(x\:{\varphi\:}_{r}\left(ϵ{x}^{-{\updelta\:}}\right)\right)-\phi\:\left(t\right)}{ϵ}\:,\:t>0,\:r>0.$$

Here, \(\:{\varphi\:}_{r}\left(x\right)\) is a single parameter truncated Mittag-Leffler function clear as51, and taking belongs to \(\:\left(\text{0,1}\right):\)

$$\:{\varphi\:}_{r}\left(x\right)=\sum\:_{n=0}^{k}\frac{{x}^{n}}{{\Gamma\:}(\varphi\:n+1)}$$

Modified simple equation method

In this subdivision, the procedure of the modified simple equation technique52,53 is explained step by step to solve fractional PDEs. Now, we consider the M fractional PDEs in the following form:

$$\:R\left({D}_{M,t}^{\mu\:,N}Q,{Q}_{x},{{D}_{M,t}^{\mu\:,N}Q}_{x},{Q}_{xx},{Q}_{xxx},\right)=0$$
(2)

Step i: We use the following wave transformation to convert Eq. (2) into Ode’s form.

$$\:{\upphi\:}={\beta\:}_{1}\text{x}-{\upomega\:}\frac{{\Gamma\:}\left(N+1\right)}{\mu\:}{t}^{\mu\:};\:\text{Q}\left(x,t\right)=Q\left({\upphi\:}\right)$$
(3)

Step ii: Insert Eq. (3) into Eq. (2).

$$\:R\left(-\omega\:{Q}_{{\upphi\:}},{\beta\:}_{1}{Q}_{{\upphi\:}},{-\omega\:{\beta\:}_{1}Q}_{{\upphi\:}{\upphi\:}},{\beta\:}_{1}^{2}{Q}_{{\upphi\:}{\upphi\:}},{\beta\:}_{1}^{3}{Q}_{{\upphi\:}{\upphi\:}{\upphi\:}},\right)=0$$
(4)

Step iii: The solution of Eq. (4) has the following form.

$$\:Q\left({\upphi\:}\right)=\sum\:_{q=0}^{s}\left({\alpha\:}_{q}{\left(\frac{H{\prime\:}\left({\upphi\:}\right)}{H\left({\upphi\:}\right)}\right)}^{q}\right)$$
(5)

Here \(\:{\alpha\:}_{s}\) is the unfamiliar constant. The balance number \(\:s\) can be derived from the following formula:

$$\:\frac{{d}^{p}Q}{d{{\upphi\:}}^{p}}=s+p\:\:\:and\:\:\:\:{Q}^{q}+{\left(\frac{{d}^{p}Q}{d{{\upphi\:}}^{p}}\right)}^{L}=qs+\text{L}\left(s+p\right)$$

Step iv: The trial solution Eq. (5) and its necessary form are submitted into Eq. (4). After calculation, we have a polynomial as: \(\:P\left(H\left({\upphi\:}\right)\right)={C}_{0}{\left(\frac{1}{H\left({\upphi\:}\right)}\right)}^{0}+{C}_{1}{\left(\frac{1}{H\left({\upphi\:}\right)}\right)}^{1}+{C}_{2}{\left(\frac{1}{H\left({\upphi\:}\right)}\right)}^{2}+{C}_{3}{\left(\frac{1}{H\left({\upphi\:}\right)}\right)}^{3}+,,,\), Now, we set \(\:{C}_{0}={C}_{1}={C}_{2}={C}_{3}=,,,,=0\). Now, using MAPLE 2023, the system of equations is solved for the values of \(\:{\alpha\:}_{q},\:\omega\:,{\beta\:}_{1},\:H\left({\upphi\:}\right)\). If we inject the obtained value of these parameters in Eq. (5), then the required values are obtained.

Bifurcation analysis

The time M-fGP-NWE equation is considered as:

$$\:{Q}_{\text{x}\text{x}\text{x}\text{y}}+{a}_{1}{D}_{M,t}^{\delta\:,r}{Q}_{\text{y}}+{a}_{2}{\left(\frac{{Q}^{n}}{n}\right)}_{xy}+{a}_{3}{Q}_{\text{x}\text{x}}+{a}_{4}{Q}_{\text{z}\text{z}}=0$$
(6)

To convert the Eq. (6) into ODE form, we apply the wave variable as

$$\:\text{Q}\left(x,y,z,t\right)=Q\left({\upphi\:}\right);\:{\upphi\:}={\beta\:}_{1}\text{x}+{\beta\:}_{2}\text{y}+{\beta\:}_{3}\text{z}-{\upomega\:}\frac{{\Gamma\:}\left(N+1\right)}{\delta\:}{t}^{\delta\:}$$
(7)

After inserting Eq. (7) into Eq. (6), the following ODE is obtained

$$\:{\beta\:}_{2}{\beta\:}_{1}^{3}{Q}_{{\upphi\:}{\upphi\:}{\upphi\:}{\upphi\:}}-{\upomega\:}{\beta\:}_{2}{a}_{1}{Q}_{{\upphi\:}{\upphi\:}}+{\beta\:}_{2}{\beta\:}_{1}{a}_{2}{\left(\frac{{Q}^{n}}{n}\right)}_{{\upphi\:}{\upphi\:}}+{\beta\:}_{1}^{2}{a}_{3}{Q}_{{\upphi\:}{\upphi\:}}+{\beta\:}_{3}^{2}{a}_{4}{Q}_{{\upphi\:}{\upphi\:}}=0$$
(8)

.

Integrating Eq. (8) with respect to \(\:{\upphi\:}\) and the following form obtained

$$\:{\beta\:}_{2}{\beta\:}_{1}^{3}{Q}_{{\upphi\:}{\upphi\:}}+{\beta\:}_{2}{\beta\:}_{1}{a}_{2}\frac{{Q}^{n}}{n}+\left({\beta\:}_{1}^{2}{a}_{3}+{\beta\:}_{3}^{2}{a}_{4}-{\upomega\:}{\beta\:}_{2}{a}_{1}\right)Q=0$$
(9)

Equation (9) develops as

$$\:{Q}_{{\upphi\:}{\upphi\:}}=\frac{-{\beta\:}_{2}{\beta\:}_{1}{a}_{2}{Q}^{n}+n\left({\upomega\:}{\beta\:}_{2}{a}_{1}-{\beta\:}_{1}^{2}{a}_{3}-{\beta\:}_{3}^{2}{a}_{4}\right)Q}{n{\beta\:}_{2}{\beta\:}_{1}^{3}}$$
(10)

Equation (10) develop as:

$$\:\left\{\begin{array}{c}\frac{dF}{d{\upxi\:}}=R\\\:\frac{dR}{d{\upphi\:}}=-{\lambda\:}_{1}{Q}^{\text{n}}+{\lambda\:}_{2}Q\end{array}\right.$$
(11)

where, \(\:{\lambda\:}_{1}=\frac{{a}_{2}}{n{\beta\:}_{1}^{2}},\:{\lambda\:}_{2}=\frac{\left({\upomega\:}{\beta\:}_{2}{a}_{1}-{\beta\:}_{1}^{2}{a}_{3}-{\beta\:}_{3}^{2}{a}_{4}\right)}{{\beta\:}_{2}{\beta\:}_{1}^{3}}\)

$$\:\mathcal{H}(Q,R)=\frac{{R}^{2}}{2}+\frac{{\lambda\:}_{1}{Q}^{\text{n}+1}}{\text{n}+1}-\frac{{\lambda\:}_{2}{Q}^{2}}{2}=h$$
(12)

In Eq. (12), the symbol \(\:h\) represents the Hamiltonian constant. From Eq. (11), the following systems are formulated.

$$\:\left\{\begin{array}{l}R=0,\\\:-{\lambda\:}_{1}{Q}^{\text{n}}+{\lambda\:}_{2}Q=0\end{array}\right.$$
(13)

By solving the System in Eq. (13), we get the following equilibrium points

$$\:{P}_{1}=\left(\text{0,0}\right),\:{P}_{2}=\left({\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{n-1}},0\right),\:{P}_{3}=\left(-{\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{n-1}},0\right)$$

From Eq. (13), we get,

$$\:j(Q,R)=\left|\begin{array}{cc}0&\:1\\\:-{\lambda\:}_{1}n{Q}^{\text{n}-1}+{\lambda\:}_{2}&\:0\end{array}\right|=-\left(-{\lambda\:}_{1}n{Q}^{\text{n}-1}+{\lambda\:}_{2}\right)$$
(14)

Based on Eq. (14), we make the following assumptions:

  1. 1.

    If \(\:j\left({P}_{e}\right)<0\), then \(\:{P}_{e}\) becomes a saddle point

  2. 2.

    If \(\:j\left({P}_{e}\right)>0\), then \(\:{P}_{e}\) becomes center point

  3. 3.

    If \(\:j\left({P}_{e}\right)=0\), then \(\:{P}_{e}\) becomes cuspidor point

The results that can be obtained by adjusting the relevant parameter are outlined below:

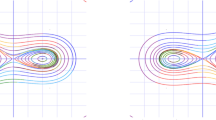
$$\:\mathbf{C}\mathbf{a}\mathbf{s}\mathbf{e}\:1:\:{\lambda\:}_{1}>0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}>0.$$
$$\:\text{W}\text{h}\text{e}\text{n}\:n=2,\:{\lambda\:}_{1}>0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}>0,$$

There are two equilibrium points. At \(\:\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}},0\right)\), the all trajectories are closed, so the point \(\:\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}},0\right)\) is center point. At point \(\:\left(0,0\right)\), the all trajectories are not closed. So, the point \(\:\left(0,0\right)\) is saddle point in Fig. 1(a).

When \(\:n=3\)

There are three equilibrium points. At \(\:\left(-{\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{2}},0\right)\) and \(\:\left({\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{2}},0\right)\), the all trajectories are closed, so the points \(\:\left(-{\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{2}},0\right)\) and \(\:\left({\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{2}},0\right)\) are center point. At point \(\:\left(0,0\right)\), the all trajectories are not closed. So, the point \(\:\left(0,0\right)\) is saddle point in Fig. 1(b).

Fig. 1
figure 1

The two-dimensional phase diagram of the system Eq. (11) for the case \(\:{\lambda\:}_{1}>0\) and \(\:{\lambda\:}_{2}>0\).

Full size image
$$\:\mathbf{C}\mathbf{a}\mathbf{s}\mathbf{e}\:2:\:{\lambda\:}_{1}<0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}>0$$
$$\:\text{W}\text{h}\text{e}\text{n}\:n=2,\:{\lambda\:}_{1}<0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}>0,$$

There are two equilibrium points. At \(\:\left(-\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}},0\right)\), All the trajectories are closed, so the point \(\:\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}},0\right)\) is center point. At point \(\:\left(0,0\right)\). All the trajectories are not closed. So, the point \(\:\left(0,0\right)\) is the saddle point in Fig. 2(a).

$$\:\text{W}\text{h}\text{e}\text{n}\:n=3,\:{\lambda\:}_{1}<0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}>0$$

There are one equilibrium points. At point \(\:\left(0,0\right)\), the all trajectories are not closed. So, the point \(\:\left(0,0\right)\) is saddle point in Fig. 2(b).

Fig. 2
figure 2

The two-dimensional phase diagram of the system Eq. (11) for the case \(\:{\lambda\:}_{1}<0\) and \(\:{\lambda\:}_{2}>0\).

Full size image
$$\:\mathbf{C}\mathbf{a}\mathbf{s}\mathbf{e}\:3:\:{\lambda\:}_{1}>0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}<0.$$
$$\:\text{W}\text{h}\text{e}\text{n}\:n=2,\:{\lambda\:}_{1}>0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}<0.$$

There are two equilibrium points. At \(\:\left(-\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}},0\right)\), All the trajectories are not closed, so the point \(\:\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}},0\right)\) is the saddle point. At point \(\:\left(0,0\right)\), All the trajectories are closed. So, the point \(\:\left(0,0\right)\) is the center point in Fig. 3(a).

$$\:\text{W}\text{h}\text{e}\text{n}\:n=3,\:{\lambda\:}_{1}>0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}<0$$

There is one equilibrium point. At point \(\:\left(0,0\right)\), All the trajectories are closed. So, the point \(\:\left(0,0\right)\) is the center point in Fig. 3(b).

Fig. 3
figure 3

The two-dimensional phase diagram of the system Eq. (11) for the case\(\:\:{\lambda\:}_{1}>0\) and \(\:{\lambda\:}_{2}<0\).

Full size image
$$\:\mathbf{C}\mathbf{a}\mathbf{s}\mathbf{e}\:4:\:{\lambda\:}_{1}<0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}<0.$$
$$\:\text{W}\text{h}\text{e}\text{n}\:n=2,\:{\lambda\:}_{1}<0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}<0.$$

There are two equilibrium points. At \(\:\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}},0\right)\), all the trajectories are not closed, so the point \(\:\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}},0\right)\) is the saddle point. At point \(\:\left(0,0\right)\), all the trajectories are closed. So, the point \(\:\left(0,0\right)\) is the center point in Fig. 4(a)

$$\:\text{W}\text{h}\text{e}\text{n}\:n=3,\:{\lambda\:}_{1}<0\:\text{a}\text{n}\text{d}\:{\lambda\:}_{2}<0.$$

There are three equilibrium points. At \(\:\left(-{\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{2}},0\right)\) and \(\:\left({\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{2}},0\right)\), All the trajectories are not closed, so the points \(\:\left(-{\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{2}},0\right)\) and \(\:\left({\left(\frac{{\lambda\:}_{2}}{{\lambda\:}_{1}}\right)}^{\frac{1}{2}},0\right)\) are saddle points. At point \(\:\left(0,0\right)\), all the trajectories are closed. So, the point \(\:\left(0,0\right)\) is the center point in Fig. 4(b).

Fig. 4
figure 4

The two-dimensional phase diagram of the system Eq. (11) for the case \(\:{\lambda\:}_{1}<0\) and \(\:{\lambda\:}_{2}<0\).

Full size image

Traveling wave solution of M-fGP-NWE equation

In this division, the modified simple equation method is applied to solve the time M-fGP-NWE equation for \(\:n=2\). If we set \(\:n=2\) in Eq. (9), then the following form is obtained:

$$\:{\beta\:}_{2}{\beta\:}_{1}^{3}{Q}_{{\upphi\:}{\upphi\:}}+{\beta\:}_{2}{\beta\:}_{1}{a}_{2}\frac{{Q}^{2}}{2}+\left({\beta\:}_{1}^{2}{a}_{3}+{\beta\:}_{3}^{2}{a}_{4}-{\upomega\:}{\beta\:}_{2}{a}_{1}\right)Q=0$$
(15)

The balance number between \(\:{Q}_{{\upphi\:}{\upphi\:}}\) and \(\:{Q}^{2}\) is \(\:q=2\). So, the trial solution of Eq. (15) is:

$$\:Q={\alpha\:}_{0}+{\alpha\:}_{1}\left(\frac{\psi\:{\prime\:}\left(\phi\:\right)}{\psi\:\left(\phi\:\right)}\right)+{\alpha\:}_{2}{\left(\frac{\psi\:{\prime\:}\left(\phi\:\right)}{\psi\:\left(\phi\:\right)}\right)}^{2}$$
(16)

Equation (16) and the derivative form of this trial solution are inserted into Eq. (15). After simplification, we get the following system of equations:

$$\:\frac{1}{\psi\:(\phi\:{)}^{0}}:\:\left(-\omega\:{a}_{1}{\beta\:}_{1}+{a}_{3}{\beta\:}_{1}^{2}+{a}_{4}{\beta\:}_{3}^{2}\right){\alpha\:}_{0}+\frac{1}{2}{a}_{2}{\beta\:}_{1}{\beta\:}_{2}{\alpha\:}_{0}^{2}=0,$$
$$\begin{gathered} \:\frac{1}{{\psi \:\left( {\phi \:} \right)}}:\:\beta \:_{1}^{3} \beta \:_{2} \alpha \:_{1} \left( {\frac{{d^{3} }}{{d\phi \:^{3} }}\psi \:\left( {\phi \:} \right)} \right) + (\left. { - \omega \:a_{1} \beta \:_{1} + a_{3} \beta \:_{1}^{2} + a_{4} \beta \:_{3}^{2} } \right)\alpha \:_{1} \left( {\frac{d}{{d\phi \:}}\psi \:\left( {\phi \:} \right)} \right) \hfill \\ + a_{2} \beta \:_{1} \beta \:_{2} \alpha \:_{1} \left( {\frac{d}{{d\phi \:}}\psi \:\left( {\phi \:} \right)} \right)\alpha \:_{0} = 0, \hfill \\ \end{gathered}$$
$$\begin{gathered} \frac{1}{{\psi \:(\phi \:)^{2} }}:\:\beta \:_{1}^{3} \beta \:_{2} \left( {2\alpha \:_{2} \left( {\frac{d}{{d\phi \:}}\psi \:\left( {\phi \:} \right)} \right)\left( {\frac{{d^{3} }}{{d\phi \:^{3} }}\psi \:\left( {\phi \:} \right)} \right) + 2\alpha \:_{2} \left( {\frac{{d^{2} }}{{d\phi \:^{2} }}\psi \:\left( {\phi \:} \right)} \right)^{2} } \right.\left. { - 3\alpha \:_{1} \left( {\frac{{d^{2} }}{{d\phi \:^{2} }}\psi \:\left( {\phi \:} \right)} \right)\left( {\frac{d}{{d\phi \:}}\psi \:\left( {\phi \:} \right)} \right)} \right) \hfill \\ + \left( { - \omega \:a_{1} \beta \:_{1} + a_{3} \beta \:_{1}^{2} + a_{4} \beta \:_{3}^{2} } \right)\alpha \:_{2} \left( {\frac{d}{{d\phi \:}}\psi \:\left( {\phi \:} \right)} \right)^{2} + \frac{1}{2}a_{2} \beta \:_{1} \beta \:_{2} \left( {2\alpha \:_{2} \left( {\frac{d}{{d\phi \:}}\psi \:\left( {\phi \:} \right)} \right)^{2} \alpha \:_{0} + \alpha \:_{1}^{2} \left( {\frac{d}{{d\phi \:}}\psi \:\left( {\phi \:} \right)} \right)^{2} } \right) = 0 \hfill \\ \end{gathered}$$
$$\:\frac{1}{\psi\:(\phi\:{)}^{3}}:\:\left({\beta\:}_{1}^{3}{\beta\:}_{2}(\right.-10{\alpha\:}_{2}{\left(\frac{d}{d\phi\:}\psi\:\left(\phi\:\right)\right)}^{2}\left(\frac{{d}^{2}}{d{\phi\:}^{2}}\psi\:\left(\phi\:\right)\right)+2{\alpha\:}_{1}{\left(\frac{d}{d\phi\:}\psi\:\left(\phi\:\right)\right)}^{3}+{a}_{2}{\beta\:}_{1}{\beta\:}_{2}{\alpha\:}_{2}{\left(\frac{\text{d}}{\text{d}\phi\:}\psi\:\left(\phi\:\right)\right)}^{3}{\alpha\:}_{1}=0,$$
$$\:\frac{1}{\psi\:(\phi\:{)}^{3}}:\:6{\beta\:}_{1}^{3}{\beta\:}_{2}{\alpha\:}_{2}{\left(\frac{\text{d}}{\text{d}\phi\:}\psi\:\left(\phi\:\right)\right)}^{4}+\frac{1}{2}{a}_{2}{\beta\:}_{1}{\beta\:}_{2}{\alpha\:}_{2}^{2}{\left(\frac{\text{d}}{\text{d}\phi\:}\psi\:\left(\phi\:\right)\right)}^{4}=0,$$

According to step iv, we solve the above system to find the solution sets:

Set 01: \(\:\omega\:=\frac{{\left(-3{a}_{2}{\alpha\:}_{2}\right)}^{3/2}{\beta\:}_{2}{\alpha\:}_{1}^{2}-18{a}_{2}{a}_{3}{\alpha\:}_{2}^{3}+216{a}_{4}{\alpha\:}_{2}^{2}{\beta\:}_{3}^{2}}{36{a}_{1}{\alpha\:}_{2}^{2}\sqrt{-3{a}_{2}{\alpha\:}_{2}}};{\alpha\:}_{0}=0;{\beta\:}_{1}=\frac{1}{2}\sqrt{-\frac{{a}_{2}{\alpha\:}_{2}}{3}}\)

$$\:Q=-\frac{{\alpha\:}_{1}^{2}{h}_{2}{e}^{\theta\:}}{{\alpha\:}_{2}\left({h}_{1}+{h}_{2}{e}^{\theta\:}\right)}+\frac{{h}_{2}^{2}{\alpha\:}_{1}^{2}{\left({\text{e}}^{\theta\:}\right)}^{2}}{{\alpha\:}_{2}{\left({h}_{1}+{h}_{2}{e}^{\theta\:}\right)}^{2}}$$
(17)

Here \(\:{h}_{1},{h}_{2}\) are arbitrary constants.

For the parametric condition \(\:{a}_{2}{\alpha\:}_{2}<0\), we formulate the following hyperbolic solutions

If \(\:{h}_{1}\ne\:{h}_{2}\), then Eq. (17) becomes,

$$\:Q=-\frac{{\alpha\:}_{1}^{2}}{{\alpha\:}_{2}}\left[\frac{{h}_{1}{h}_{2}}{cosh\theta\:\left({h}_{1}^{2}+{h}_{2}^{2}\right)+2{h}_{1}{h}_{2}+sinh\theta\:\left({h}_{1}^{2}-{h}_{2}^{2}\right)}\right]$$
(18)

If \(\:{h}_{1}={h}_{2}\), then Eq. (17) becomes,

$$\:Q=-\frac{{\alpha\:}_{1}^{2}}{4{\alpha\:}_{2}}\left[{\text{sech}\left(\frac{\theta\:}{2}\right)}^{2}\right]$$
(19)

If \(\:{h}_{1}=\pm\:i{h}_{2}\), then Eq. (17) becomes,

$$\:Q=-\frac{{\alpha\:}_{1}^{2}}{4{\alpha\:}_{2}}\left[\frac{1}{1\mp\:isinh\theta\:}\right]$$
(20)

For the parametric condition \(\:{a}_{2}{\alpha\:}_{2}>0\), we formulate the following trigonometric solutions

If \(\:{h}_{1}\ne\:{h}_{2}\), then Eq. (17) becomes,

$$\:Q=-\frac{{\alpha\:}_{1}^{2}}{{\alpha\:}_{2}}\left[\frac{{h}_{1}{h}_{2}}{cos\theta\:\left({h}_{1}^{2}+{h}_{2}^{2}\right)+2{h}_{1}{h}_{2}+isin\theta\:\left({h}_{1}^{2}-{h}_{2}^{2}\right)}\right]$$
(21)

If \(\:{h}_{1}={h}_{2}\), then Eq. (17) becomes,

$$\:Q=-\frac{{\alpha\:}_{1}^{2}}{4{\alpha\:}_{2}}\left[{\text{sec}\left(\frac{\theta\:}{2}\right)}^{2}\right]$$
(22)

If \(\:{h}_{1}=\pm\:i{h}_{2}\), then Eq. (17) becomes,

$$\:Q=-\frac{{\alpha\:}_{1}^{2}}{{2\alpha\:}_{2}}\left[\frac{1}{2\left(1\pm\:isin\theta\:\right)}\right]$$
(23)
$$\:\text{H}\text{e}\text{r}\text{e}\:\theta\:=-\frac{{\alpha\:}_{1}\phi\:}{{\alpha\:}_{2}},\:\phi\:=\frac{1}{2}\sqrt{-\frac{{a}_{2}{\alpha\:}_{2}}{3}}\text{x}+{\beta\:}_{2}\text{y}+{\beta\:}_{3}\text{z}-\frac{{\left(-3{a}_{2}{\alpha\:}_{2}\right)}^{3/2}{\beta\:}_{2}{\alpha\:}_{1}^{2}-18{a}_{2}{a}_{3}{\alpha\:}_{2}^{3}+216{a}_{4}{\alpha\:}_{2}^{2}{\beta\:}_{3}^{2}}{36{a}_{1}{\alpha\:}_{2}^{2}\sqrt{-3{a}_{2}{\alpha\:}_{2}}}\frac{{\Gamma\:}(r+1)}{{\updelta\:}}{t}^{{\updelta\:}}.$$

Set 02: \(\:{\alpha\:}_{0}=\frac{2\left(\omega\:{a}_{1}{\beta\:}_{1}-{a}_{3}{\beta\:}_{1}^{2}-{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}{\beta\:}_{2}},{\alpha\:}_{2}=-\frac{12{\beta\:}_{1}^{2}}{{a}_{2}},{\alpha\:}_{1}=\frac{12}{{a}_{2}}\sqrt{\left(-\frac{\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{a}_{4}{\beta\:}_{1}{\beta\:}_{3}^{2}}{{\beta\:}_{2}}\right)}\).

$$\:Q=\frac{2\left(\omega\:{a}_{1}{\beta\:}_{1}-{a}_{3}{\beta\:}_{1}^{2}-{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}{\beta\:}_{2}}-\frac{12\left(\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{\beta\:}_{1}{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}^{2}{\beta\:}_{2}}\left[\frac{{e}^{\theta\:}}{\left({h}_{1}+{h}_{2}{e}^{\theta\:}\right)}-\frac{{h}_{2}{\left({e}^{\theta\:}\right)}^{2}}{{\left({h}_{1}+{h}_{2}{e}^{\theta\:}\right)}^{2}}\right]$$
(24)

.

For the parametric condition \(\:\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{a}_{4}{\beta\:}_{1}{\beta\:}_{3}^{2}<0\) and \(\:{\beta\:}_{2}>0\) or \(\:\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{a}_{4}{\beta\:}_{1}{\beta\:}_{3}^{2}>0\) and \(\:{\beta\:}_{2}<0\), we formulate the following hyperbolic solutions

If \(\:{h}_{1}\ne\:{h}_{2}\), then Eq. (24) becomes,

$$\:Q=\frac{2\left(\omega\:{a}_{1}{\beta\:}_{1}-{a}_{3}{\beta\:}_{1}^{2}-{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}{\beta\:}_{2}}-\frac{12\left(\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{\beta\:}_{1}{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}^{2}{\beta\:}_{2}}\left[\frac{{h}_{1}{h}_{2}}{cosh\theta\:\left({h}_{1}^{2}+{h}_{2}^{2}\right)+2{h}_{1}{h}_{2}+sinh\theta\:\left({h}_{1}^{2}-{h}_{2}^{2}\right)}\right]$$
(25)

.

If \(\:{h}_{1}={h}_{2}\), then Eq. (24) becomes,

$$\:Q=\frac{2\left(\omega\:{a}_{1}{\beta\:}_{1}-{a}_{3}{\beta\:}_{1}^{2}-{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}{\beta\:}_{2}}-\frac{6\left(\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{\beta\:}_{1}{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}^{2}{\beta\:}_{2}}\left[\frac{1}{2}sech\left(\frac{\theta\:}{2}\right)\right]$$
(26)

.

If \(\:{h}_{1}=\pm\:i{h}_{2}\), then Eq. (24) becomes,

$$\:Q=\frac{2\left(\omega\:{a}_{1}{\beta\:}_{1}-{a}_{3}{\beta\:}_{1}^{2}-{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}{\beta\:}_{2}}-\frac{6\left(\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{\beta\:}_{1}{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}^{2}{\beta\:}_{2}}\left[\frac{1}{1\mp\:isinh\theta\:}\right]$$
(27)

.

For the parametric condition \(\:\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{a}_{4}{\beta\:}_{1}{\beta\:}_{3}^{2}>0\) and \(\:{\beta\:}_{2}>0\) or \(\:\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{a}_{4}{\beta\:}_{1}{\beta\:}_{3}^{2}>0\) and \(\:{\beta\:}_{2}>0\), we formulate the following trigonometric solutions.

If \(\:{h}_{1}\ne\:{h}_{2}\), then Eq. (24) becomes,

$$\:Q=\frac{2\left(\omega\:{a}_{1}{\beta\:}_{1}-{a}_{3}{\beta\:}_{1}^{2}-{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}{\beta\:}_{2}}-\frac{12\left(\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{\beta\:}_{1}{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}^{2}{\beta\:}_{2}}\left[\frac{{h}_{1}{h}_{2}}{cos\theta\:\left({h}_{1}^{2}+{h}_{2}^{2}\right)+2{h}_{1}{h}_{2}+isin\theta\:\left({h}_{1}^{2}-{h}_{2}^{2}\right)}\right]$$
(28)

If \(\:{h}_{1}={h}_{2}\), then Eq. (24) becomes,

$$\:Q=\frac{2\left(\omega\:{a}_{1}{\beta\:}_{1}-{a}_{3}{\beta\:}_{1}^{2}-{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}{\beta\:}_{2}}-\frac{6\left(\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{\beta\:}_{1}{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}^{2}{\beta\:}_{2}}\left[\frac{1}{2}sec\left(\frac{\theta\:}{2}\right)\right]$$
(29)

If \(\:{h}_{1}=\pm\:i{h}_{2}\), then Eq. (24) becomes,

$$\:Q=\frac{2\left(\omega\:{a}_{1}{\beta\:}_{1}-{a}_{3}{\beta\:}_{1}^{2}-{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}{\beta\:}_{2}}-\frac{6\left(\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{\beta\:}_{1}{a}_{4}{\beta\:}_{3}^{2}\right)}{{a}_{2}{\beta\:}_{1}^{2}{\beta\:}_{2}}\left[\frac{1}{2\left(1\pm\:isin\theta\:\right)}\right]$$
(30)
$$\:\text{H}\text{e}\text{r}\text{e}\:\theta\:=\frac{\sqrt{\left(-\frac{\omega\:{a}_{1}{\beta\:}_{1}^{2}-{a}_{3}{\beta\:}_{1}^{3}-{a}_{4}{\beta\:}_{1}{\beta\:}_{3}^{2}}{{\beta\:}_{2}}\right)}}{{\beta\:}_{1}^{2}},\:\phi\:={\beta\:}_{1}\text{x}+{\beta\:}_{2}\text{y}+{\beta\:}_{3}\text{z}-{\upomega\:}\frac{{\Gamma\:}(r+1)}{{\updelta\:}}{t}^{{\updelta\:}}$$

Set 03: \(\begin{gathered} \:\:\omega \: = - \frac{1}{{36}}\frac{{ - 3a_{2}^{2} \alpha \:_{1}^{2} \beta \:_{2} + 2\left( { - 3a_{2} \alpha \:_{2} } \right)^{{\frac{3}{2}}} a_{3} + 72\sqrt { - 3a_{2} \alpha \:_{2} } a_{4} \beta \:_{3}^{2} }}{{a_{2} \alpha \:_{2} a_{1} }},\alpha \:_{0} = \frac{1}{3}\frac{{6\sqrt { - \frac{{a_{2} \alpha \:_{2} }}{3}} \omega \:a_{1} + a_{2} \alpha \:_{2} a_{3} - 12a_{4} \beta \:_{3}^{2} }}{{a_{2} \beta \:_{2} \sqrt { - \frac{{a_{2} \alpha \:_{2} }}{3}} }}, \hfill \\ \beta \:_{1} = \frac{1}{2}\sqrt { - \frac{{a_{2} \alpha \:_{2} }}{3}} \hfill \\ \end{gathered}\)

$$\:Q=-\frac{{\alpha\:}_{1}^{2}{h}_{2}{e}^{-\frac{{\alpha\:}_{1}\phi\:}{{\alpha\:}_{2}}}}{{\alpha\:}_{2}\left({h}_{1}+{h}_{2}{e}^{-\frac{{\alpha\:}_{1}\phi\:}{{\alpha\:}_{2}}}\right)}+\frac{{h}_{2}^{2}{\alpha\:}_{1}^{2}{\left({\text{e}}^{-\frac{{\alpha\:}_{1}\phi\:}{{\alpha\:}_{2}}}\right)}^{2}}{{\alpha\:}_{2}{\left({h}_{1}+{h}_{2}{e}^{-\frac{{\alpha\:}_{1}\phi\:}{{\alpha\:}_{2}}}\right)}^{2}}$$
(31)

.

For the parametric condition \(\:{a}_{2}{\alpha\:}_{2}<0\), we formulate the following hyperbolic solutions

If \(\:{h}_{1}\ne\:{h}_{2}\), then Eq. (31) becomes,

$$\:Q=\frac{{\alpha\:}_{1}^{2}}{{\alpha\:}_{2}}\left[\frac{{h}_{1}{h}_{2}}{cosh\theta\:\left({h}_{1}^{2}+{h}_{2}^{2}\right)+2{h}_{1}{h}_{2}+sinh\theta\:\left({h}_{1}^{2}-{h}_{2}^{2}\right)}\right]$$
(32)

If \(\:{h}_{1}={h}_{2}\), then Eq. (31) becomes,

$$\:Q=\frac{{\alpha\:}_{1}^{2}}{{2\alpha\:}_{2}}\left[\frac{1}{2}sech\left(\frac{\theta\:}{2}\right)\right]$$
(33)

.

If \(\:{h}_{1}=\pm\:i{h}_{2}\), then Eq. (31) becomes,

$$\:Q=\frac{{\alpha\:}_{1}^{2}}{{2\alpha\:}_{2}}\left[\frac{1}{1\mp\:isinh\theta\:}\right]$$
(34)

For the parametric condition \(\:{a}_{2}{\alpha\:}_{2}>0\), we formulate the following trigonometric solutions

If \(\:{h}_{1}\ne\:{h}_{2}\), then Eq. (31) becomes,

$$\:Q=\frac{{\alpha\:}_{1}^{2}}{{\alpha\:}_{2}}\left[\frac{{h}_{1}{h}_{2}}{cos\theta\:\left({h}_{1}^{2}+{h}_{2}^{2}\right)+2{h}_{1}{h}_{2}+isin\theta\:\left({h}_{1}^{2}-{h}_{2}^{2}\right)}\right]$$
(35)

If \(\:{h}_{1}={h}_{2}\), then Eq. (31) becomes,

$$\:Q=\frac{{\alpha\:}_{1}^{2}}{{2\alpha\:}_{2}}\left[\frac{1}{2}sec\left(\frac{\theta\:}{2}\right)\right]$$
(36)

If \(\:{h}_{1}=\pm\:i{h}_{2}\), then Eq. (31) becomes,

$$\:Q=\frac{{\alpha\:}_{1}^{2}}{2{\alpha\:}_{2}}\left[\frac{1}{2\left(1\pm\:isin\theta\:\right)}\right]$$
(37)
$$\:\text{H}\text{e}\text{r}\text{e}\:\theta\:=-\frac{{\alpha\:}_{1}\phi\:}{{\alpha\:}_{2}},\:\phi\:={\beta\:}_{1}\text{x}+{\beta\:}_{2}\text{y}+{\beta\:}_{3}\text{z}+\frac{1}{36}\frac{-3{a}_{2}^{2}{\alpha\:}_{1}^{2}{\beta\:}_{2}+2{\left(-3{a}_{2}{\alpha\:}_{2}\right)}^{\frac{3}{2}}{a}_{3}+72\sqrt{-3{a}_{2}{\alpha\:}_{2}}{a}_{4}{\beta\:}_{3}^{2}}{{a}_{2}{\alpha\:}_{2}{a}_{1}}\frac{{\Gamma\:}(r+1)}{{\updelta\:}}{t}^{{\updelta\:}}.$$

Numerical explanation and graphical representation

The present study focuses on developing new systems to uncover valuable insights into the theory of solitary waves. In Sect. 3, we present the dynamic observations of the planar dynamical system using bifurcation analysis. We demonstrate how the behavior of this system is influenced by changes in its parameter values, as illustrated in Figs. 1, 2 and 3, and 4. We also presented the homoclinic and heteroclinic orbits. In this section, we visually analyse the solutions to the generalized (3 + 1)-dimensional -type nonlinear wave equation. We select parameters within an appropriate range to enhance our understanding of these solutions. We investigate the real part of the solution to observe its variations along the real axis. Likewise, we analyze the imaginary part to uncover patterns along the imaginary axis. To check the behavior and stability of the phenomena, we use the M-fGP-NWE model. For the special values of the free parameters, we get bright bell and dark bell soliton solutions, as well as cross-periodic and periodic soliton solutions. Bright bell solitons represent localized wave peaks, crucial for studying coherent structures in shallow water waves and internal ocean waves. Dark bell solitons appear as localized depressions in a continuous background, relevant in describing wave interactions in stratified fluids and turbulence. Periodic soliton solutions model repeating wave trains, helping to analyze wave stability, energy transport, and pattern formation in fluid systems. Figure 5 signifies the 3D surface plots and 2D plots with time \(\:t\) and \(\:x\) varies of the bright bell shape from the solutions Eq. (18) for the ideals \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=0.5,{h}_{1}=1,\:{h}_{2}=2,{a}_{1}=2,{a}_{3}=2,{a}_{4}=0.5,\:{a}_{2}=-0.5,\:{\alpha\:}_{1}=1,{\alpha\:}_{2}=0.5,\:r=1.5\). Figure 6 signifies the 3D surface plots and 2D plots with time \(\:t\) and \(\:x\) varies of dark bell shape of the solutions Eq. (18) for the ideals \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=0.5,{h}_{1}=1,\:{h}_{2}=2,{a}_{1}=2,{a}_{3}=2,{a}_{4}=0.5,\:{a}_{2}=-0.5,\:{\alpha\:}_{1}=1,{\alpha\:}_{2}=0.5,\:r=1.5\). Figure 7 signifies the 3D surface plots and 2D plot with time \(\:t\) and \(\:x\) varies the periodic wave of the solutions Eq. (19) for the ideals \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=2,{h}_{1}=1,\:{h}_{2}=1,{a}_{1}=-0.5,{a}_{3}=-2,{a}_{4}=0.5,\:{a}_{2}=0.5,\:{\alpha\:}_{1}=-1,{\alpha\:}_{2}=0.5,\:r=1.5\). Figure 8 signifies the 3D surface plots and 2D plots with time \(\:t\) and \(\:x\) varies of the bright-dark bell wave of the solutions Eq. (20) for the ideals \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=0.5,{a}_{1}=2,{a}_{3}=2,{a}_{4}=0.5,\:{a}_{2}=0.5,\:{\alpha\:}_{1}=1,{\alpha\:}_{2}=-0.5,\:r=1.5\). Figure 9 signifies the 3D surface plots and 2D plots with time \(\:t\) and \(\:x\) varies of the periodic wave of Eq. (35) for the ideals \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=2,{h}_{1}=1,\:{h}_{2}=2,{a}_{1}=1,{a}_{3}=1,{a}_{4}=0.067,\:{a}_{2}=1,\:{\alpha\:}_{1}=0.5,{\alpha\:}_{2}=0.5,\:r=1.5\). Figure 10 signifies the 3D surface plots and 2D plots with time \(\:t\) and \(\:x\) varies of the periodic wave of Eq. (35) for the ideals \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=2,{h}_{1}=1,\:{h}_{2}=2,{a}_{1}=1,{a}_{3}=1,{a}_{4}=0.067,\:{a}_{2}=1,\:{\alpha\:}_{1}=0.5,{\alpha\:}_{2}=0.5,\:r=1.5\).

Fig. 5
figure 5

Profile of bright bell shape of the solutions Eq. (18). \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=0.5,{h}_{1}=1,\:{h}_{2}=2,{a}_{1}=2,{a}_{3}=2,{a}_{4}=0.5,\:{a}_{2}=-0.5,\:{\alpha\:}_{1}=1,{\alpha\:}_{2}=0.5,\:r=1.5\).

Full size image
Fig. 6
figure 6

Profile of bright bell shape of the solutions Eq. (18). \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=0.5,{h}_{1}=1,\:{h}_{2}=2,{a}_{1}=2,{a}_{3}=2,{a}_{4}=0.5,\:{a}_{2}=-0.5,\:{\alpha\:}_{1}=1,{\alpha\:}_{2}=0.5,\:r=1.5\).

Full size image
Fig. 7
figure 7

Diagram of the solutions Eq. (19). \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=2,{h}_{1}=1,\:{h}_{2}=1,{a}_{1}=-0.5,{a}_{3}=-2,{a}_{4}=0.5,\:{a}_{2}=0.5,\:{\alpha\:}_{1}=-1,{\alpha\:}_{2}=0.5,\:r=1.5\).

Full size image
Fig. 8
figure 8

Diagram of the solutions Eq. (20). \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=0.5,{a}_{1}=2,{a}_{3}=2,{a}_{4}=0.5,\:{a}_{2}=0.5,\:{\alpha\:}_{1}=1,{\alpha\:}_{2}=-0.5,\:r=1.5\).

Full size image
Fig. 9
figure 9

Diagram of the solutions Eq. (35). \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=2,{h}_{1}=1,\:{h}_{2}=2,{a}_{1}=1,{a}_{3}=1,{a}_{4}=0.067,\:{a}_{2}=1,\:{\alpha\:}_{1}=0.5,{\alpha\:}_{2}=0.5,\:r=1.5\)

Full size image
Fig. 10
figure 10

Diagram of the solutions Eq. (35). \(\:y=z=1,{\beta\:}_{2}=1,{\beta\:}_{3}=2,{h}_{1}=1,\:{h}_{2}=2,{a}_{1}=1,{a}_{3}=1,{a}_{4}=0.067,\:{a}_{2}=1,\:{\alpha\:}_{1}=0.5,{\alpha\:}_{2}=0.5,\:r=1.5\)

Full size image

Comparison and novelty

In this section, we discuss the comparison of the work in the present study with the work in43, along with the novelty.

Comparison

Here, we compare our obtained results with the results of.

Solution in44

Our solution

\(\begin{array}{*{20}l} {For\:\sigma \: = - \frac{1}{4},\alpha \:_{1} = \frac{1}{3},\alpha \:_{2} = 1,} \hfill \\ {\alpha \:_{3} = - \sqrt 3 ,\alpha \:_{4} = 1,\:k = \sqrt 3 ,\:s = 1,\omega \: = 1} \hfill \\ \end{array}\)

\(\:{u}_{17}={\text{sech}\left(\frac{1}{2}\left(\sqrt{3}x+y+z-\frac{{t}^{\delta\:}}{2\delta\:}\right)\right)}^{2}\)

For, \(\begin{array}{*{20}l} {\beta \:_{2} = \beta \:_{3} = 0.5,a_{1} = 2I,a_{3} = - \frac{1}{{\sqrt 3 }},a_{4} = 3\sqrt { - 3} ,\:a_{2} } \hfill \\ { = - 9,\:\alpha \:_{1} = 2,\alpha \:_{2} = - 1,\:r = - 1} \hfill \\ \end{array}\) the solution Eq. (19) becomes,

\(\:Q={\text{sech}\left(\frac{1}{2}\left(\sqrt{3}x+y+z-\frac{{t}^{\delta\:}}{2\delta\:}\right)\right)}^{2}\)

\(\begin{array}{*{20}l} {For\:\sigma \: = \frac{1}{4},\alpha \:_{1} = \frac{1}{3},\alpha \:_{2} = - 1,\alpha \:_{3} } \hfill \\ { = - \sqrt 3 ,\alpha \:_{4} = 1,\:k = \sqrt 3 ,\:s = 1,\omega \: = 1.} \hfill \\ \end{array}\)

\(\:{u}_{19}={\text{sec}\left(\frac{1}{2}\left(\sqrt{3}x+y+z-\frac{{t}^{\delta\:}}{2\delta\:}\right)\right)}^{2}\)

For, \(\begin{array}{*{20}l} {\beta \:_{2} = \beta \:_{3} = 0.5,a_{1} = 2I,a_{3} = - \frac{1}{{\sqrt 3 }},a_{4} = 3\sqrt { - 3} ,\:a_{2} } \hfill \\ { = - 9,\:\alpha \:_{1} = 2,\alpha \:_{2} = - 1,\:r = - 1} \hfill \\ \end{array}\) the solution Eq. (22) becomes,

\(\:Q={\text{sec}\left(\frac{1}{2}\left(\sqrt{3}x+y+z-\frac{{t}^{\delta\:}}{2\delta\:}\right)\right)}^{2}\).

Novelty

In this work, the modified simple equation method applies to construct soliton solutions. The solutions are expressed as an exponential function, hyperbolic \(\:(cosh,\:sinh,\:sech\)), and trigonometric (\(\:cos,\:sin,\:sec\)) function form. Under some parametric conditions, we get some complex-valued solutions and some real-valued solutions. The numerical forms of the obtained solutions are the bright bell wave, dark bell wave, periodic wave, multi-bell wave including one bright and one dark bell wave, double periodic wave, cross periodic wave, and so on. For the first time, we investigate the double bell solutions, interaction kink, and periodic lump wave. Additionally, we present the bifurcation analysis of the proposed model. By using phase portrait, the stable and unstable solutions are analyzed. Moreover, we also analysis the modulation instability of the proposed model. We also present the effect of the M-fractional derivative on the obtained solutions for different values of the order of fractional derivative at \(\:\mu\:=0.1,\:0.5,\:0.9\)

Advantages and limitations of the MSE method

In this section, we present the advantages and limitations of the modified simple equation method for solving NLEEs.

Advantages of the MSE method

In this subsection, we present the Advantages of the MSE method for solving NLEEs. A key advantage of this approach is that it does not require any auxiliary equations. In contrast, various analytical techniques, such as the (G′/G)-expansion11, unified12, multiple exp-function14, transformed rational function16, modified extended tanh and a novel form of modified Kudryashov19, Modified Sardar sub equation20, Riccati equation mapping21 rely on different auxiliary differential equations, leading to predetermined solutions. However, the MSE method can derive analytical solutions for NLEEs without auxiliary equations, producing solutions that vary depending on the specific NLEE. Moreover, this method is capable of handling equations with a balance number greater than two.

Limitations of the MSE method

The limitations of the MSE Method are:

  • This method may lack efficacy for certain nonlinear evolution equations (NLEEs), especially those characterized by intricate structures or non-integrable attributes.

  • The MSE approach may accommodate equations with a balance number above two, but it may provide processing difficulties for higher-order equations or those including complex nonlinear factors.

  • The method predominantly produces precise analytical solutions; nevertheless, it may not be appropriate for generating a diverse array of solution types, including rogue waves, breather solutions, or chaotic solutions.

Modulation instability

Modulation instability (MI)54,55 refers to the exponential growth of small perturbations in a continuous wave or a uniform background, leading to the formation of localized structures or patterns. This phenomenon arises in nonlinear and dispersive media and plays a crucial role in various physical systems, including optical fibers, fluid dynamics, and plasma physics. The underlying mechanism of MI involves a balance between nonlinearity and dispersion (or diffraction), where a small initial disturbance can draw energy from the continuous background. This process amplifies specific frequencies, causing the system to evolve into localized wave packets or soliton-like structures. In this section, we analyse the modulation instability of M-fractional generalized (3 + 1)-dimensional P-type nonlinear wave Eq. 

$$\:{Q}_{\text{x}\text{x}\text{x}\text{y}}+{b}_{1}{D}_{M,t}^{\delta\:,r}{Q}_{\text{y}}+{b}_{2}{\left({Q}^{2}\right)}_{xy}+{b}_{3}{Q}_{\text{x}\text{x}}+{b}_{4}{Q}_{\text{z}\text{z}}=0$$
(38)

We will perform an MI analysis by looking for perturbed solutions of the following form:

$$\:Q\left(x,y,z,t\right)=g+\epsilon\:H\left(x,y,z,\:t\right)$$
(39)

Inserting Eq. (39) into Eq. (38), we get

$$\:\epsilon\:{H}_{\text{x}\text{x}\text{x}\text{y}}+\epsilon\:{a}_{1}{D}_{M,t}^{\delta\:,r}\left({H}_{\text{y}}\right)+{a}_{2}{\left({\left(g+\epsilon\:H\right)}^{2}\right)}_{xy}+\epsilon\:{a}_{3}{H}_{\text{x}\text{x}}+\epsilon\:{a}_{4}{H}_{\text{z}\text{z}}=0$$
(40)

and linearizing Eq. (40) in \(\:\epsilon\:\)

$$\in H_{{xxxy}} + \in a_{1} D_{{M,t}}^{{\delta \:,r}} \left( {H_{y} } \right) + 2~g \in \:a_{2} H_{{xy}} + \in a_{3} H_{{xx}} + \in \:a_{4} H_{{zz}} = 0$$
(41)

Let us consider the solution of Eq. (41) as:

$$\:P\left(x,t\right)={e}^{\text{i}({\beta\:}_{1}\text{x}+{\beta\:}_{2}\text{y}+{\beta\:}_{3}\text{z}-{\upomega\:}\frac{{\Gamma\:}\left(N+1\right)}{\delta\:}{t}^{\delta\:})}$$
(42)

Inserting Eq. (42) into Eq. (41) and dividing the entire equation by \(\:{e}^{\text{i}({\beta\:}_{1}\text{x}+{\beta\:}_{2}\text{y}+{\beta\:}_{3}\text{z}-{\upomega\:}\frac{{\Gamma\:}\left(N+1\right)}{\delta\:}{t}^{\delta\:})}\), then we get,

$$\in \:\beta \:_{2} \beta \:_{1}^{3} - \in a_{1} \beta \:_{2} \omega \: + 2~g \in a_{2} \beta \:_{1} \beta \:_{2} + \in a_{3} \beta \:_{1}^{2} + \in a_{4} \beta \:_{3}^{2} = 0 $$0$$

The following equation provides the dispersion relation:

$$\in = - \frac{{\beta \:_{2} \beta \:_{1}^{3} + 2~ga_{2} \beta \:_{1} \beta \:_{2} + a_{3} \beta \:_{1}^{2} + a_{4} \beta \:_{3}^{2} }}{{a_{1} \beta \:_{2} }}$$
(43)

It is evident from Eq. (43) that the dispersion is stable and that, for negative values of \(\:\text{ϵ}\), any superposition of the solutions will seem to decay.

Conclusion

In this research, we effectively explored the M-fractional generalized (3 + 1)-dimensional P-type nonlinear wave equation through the use of bifurcation theory and the MSE technique. Bifurcation theory was employed to elucidate the stability of the proposed model. Figures 1, 2 and 3 illustrate the phase portraits of the M-fGP-NWE model, where we identified homoclinic, heteroclinic, and solitary wave solutions. Furthermore, the MSE technique was applied in various domains, including fluid dynamics, and plasma physics. Analytical solutions were derived in trigonometric, hyperbolic, and exponential forms under specific conditions. Both numerical and graphical analyses were conducted to understand wave propagation. The proposed method effectively determined solitary wave solutions in the M-fGP-NWE model, uncovering complex structures including lump, mixed, multi, kink, homoclinic, and periodic wave solutions. The identification of these diverse waveforms highlights the model’s rich nonlinear dynamics and its ability to capture intricate wave interactions. Such solutions provide deeper insights into the underlying physical mechanisms governing wave propagation in complex media. These findings hold significant relevance for applications in fields such as fluid dynamics and plasma physics, where understanding wave behavior is crucial for advancements in theoretical modeling and practical implementations. The integration approaches utilized in this study exhibited efficiency, conciseness, and efficacy. Additionally, we also analyse the modulation Instability of the proposed model. Our findings enhance our understanding of nonlinear phenomena in shallow water waves and suggest the potential for applying our approaches to more intricate nonlinear systems in contemporary engineering and scientific domains. This research facilitates future investigation and underscores the essential importance of interdisciplinary methods in addressing intricate issues in modern research. In future, we will analyse the chaotic nature, Poincare, layponove, and multi-stability of generalized (3 + 1)-dimensional P-type nonlinear wave equation and also present the parametric effect on the solitons.