Introduction

The ability to catch high quality (Q) factors is always desired for optical resonators when enhancing the light-matter interaction during the process of electromagnetic radiation1,2,3. In recent decades, with the development of nanofabrication techniques, high Q optical resonators have triggered anomalous specific physical phenomena and have exceptional applications in lasers4,5, filters6,7, giant nonlinear enhancement8,9 and robustly perfect absorption7. Bound state in the continuum (BIC)10,11 is non-radiating eigenstates within a continuum spectrum with ultra-high Q factors. Ideally, an optical BIC has an infinite Q factor and zero linewidth, thus the BIC is concealed in the radiation continuum and cannot be detected. However, with inevitable material loss, roughness or fabrication imperfections, the BIC can be observed in a way of finite narrow bandwidth and high Q factor with finiteness (i.e., quasi-BIC). A quasi-BIC can also be artificially transformed from an ideal BIC in two ways: the symmetry-protected BIC (breaking the in-plane or the out-of-plane symmetry)12 and the accidental BIC (tuning the parameter of the target system)10. Inspired by this novel and practical physical mechanism, various quasi-BIC metasurfaces have been intensively studied, especially in sensing applications. For example, Romano et al.13 achieved quasi-BICs which can detect liquids with different refractive indices in the visible light region. Li et al.14 designed silicon quasi-BIC metasurface achieving high refractive index sensitivities. Yin et al.15 fabricated quasi-BIC absorber with the structure of metal–insulator–metal (MIM) for sensing in the terahertz (THz) region. Nevertheless, most of quasi-BIC devices based on dielectric or metallic resonators can only work under a certain frequency once after the fabrication, which severely restricts the demand for flexible applications.

Recently, the dynamic tuning of the working frequency of quasi-BICs has attracted strong interests with optically active materials. By using photosensitive chalcogenide glass, Mikheeva et al.16 studied the tunable properties of quasi-BIC in both theory and experiment. Chen et al.17 facbricated a tunable terahertz quasi-BIC metasurface through controlling the temperature of strontium titanate materials. Liu et al.18, He et al.19 and Hou et al.20 tuned the resonance frequency of quasi-BICs based on metasurface which supported by the 3D Dirac semimetals. Danaeifar21 and Roy et al.22 proposed a two-dimensional quasi-BIC metasurface for THz sensing based on graphene dimer resonators. Among the optically active materials, graphene has emerged as remarkable 2D material for tunable devices due to its high electron mobility, wide frequency response range, cost-effective and large area synthesis. More importantly, the electrical conductivity of the graphene can be stably controlled by the voltage or chemical doping23. Although the thickness of the graphene is a single layer of carbon atoms, the light-matter interaction of the graphene can be strongly enhanced by the surface plasmon resonance in the THz region while keeping low ohmic loss24. Thus, to incorporate graphene into the quasi-BICs will not only expand the scope of dynamically tunable BICs, but also will promote the development of high Q feasible 2D planar light-matter interactions. However, so far all the above-mentioned active quasi-BIC studies focus on anisotropic structures. The quasi-BICs obtained by breaking the symmetry can only be excited in a specific polarization direction. Overcoming the polarization limitation in the process of designing dynamically tunable BIC is needed far more in practice.

In this research, to the best of our knowledge, we propose polarization-independent dual quasi-BICs in a graphene-based metasurface for the first time. So far, all the above-mentioned tunable quasi-BICs focus on anisotropic structures, and they are polarization-sensitive. Compared to the polarization-sensitive quasi-BICs, the polarization-insensitive ones are more convenient for practical sensing applications because they can endure changes in polarization states of the incident waves, which eliminates the need for careful and precise alignment with the polarization direction of the laser source. Besides that, the dual band quasi-BICs can solve the time delay problem caused by the single band quasi-BIC when detecting a variety of gas and chemical solvents in sensing applications. After the optimization, dual graphene quasi-BIC resonances can be excited under normal incidence in THz region without breaking the C4v symmetry. Compare with only one operating band, dual bands will reduce time delay introduced by modulation, especially in sensing applications in detecting a variety of gas and chemical solvents. Both the numerical calculations and the coupled mode theory (CMT) shows the Q-factors of dual quasi-BICs follow the inverse square dependence on the asymmetric parameter. The steady-state electric field distribution and surface current distribution further confirm that the metasurface can achieve dual-frequency quasi-BIC modes. Notably, the quasi-BIC spectra can be tuned up to 2.3 THz by varying the graphene’s chemical potential, while keeping the modulation depth of the transmission larger than 50%. Based on the novel properties mentioned above, for the application, we demonstrate biosensors with maximum sensitivity of 6.75 THz/RIU and minimum LOD (the limit of detection) of 0.0214 RIU, which is superior to other types of THz sensors. Moreover, our proposed metasurface can maintain good quasi-BIC characteristics for arbitrarily polarized incident light and various angles of incidences ranging from 0 to 65°, which will greatly enhance the robustness of biosensors. We believe our work provides a valuable reference for actively tunable sensing devices and optical modulators with polarisation-independent, and will promote the development of the class of graphene quasi-BIC metasurfaces.

Structure design and methods

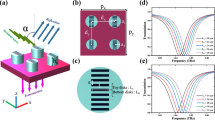
The schematic illustration of the structural super cell for the proposed dual-band polarization-independent graphene quasi-BIC metasurface is shown in Fig. 1a. The metasurface simply consists of a monolayer graphene film on the top of the SiO2 substrate. The graphene film is patterned into a periodic array of coaxial apertures25. Within the period of the unit cell, four coaxial apertures with a finite spacing are placed, as shown in Fig. 1b. The thickness of silicon layer is semi-infinite along the positive direction of the z-axis. After the optimization, the outer and inner diameter of the graphene coaxial apertures D1 and D2 are 1.6 μm and 0.8 μm, respectively. The period Px = Py = P is 4.8 μm. The gap distances between graphene coaxial apertures in a super cell are tx and ty in the x and y directions, respectively. The relative permittivity of the semi-infinite SiO2 substrate is assumed to be 3.926. The surface conductivity of graphene σg is modeled with Kubo’s formula27, which is given by:

Fig. 1
figure 1

(a) Schematic of the super cell for the proposed dual-band polarization-independent graphene quasi-BIC metasurface. (b) Unit cell of the proposed metasurface (vertical view).

Full size image
$${\sigma }_{\text{g}}={\sigma }_{\text{intra}}+{\sigma }_{\text{inter}}.$$
(1)

At far infrared THz frequencies, the interband component of the surface conductivity of graphene becomes negligible, so we have σg ≈ σintra. The dominating intraband one could be approximated by a Drude model:

$$\sigma_{{\text{g}}} = i\frac{{e^{2} E_{{\text{f}}} }}{{\pi \hbar \left( {\hbar \omega + i\tau } \right)}},$$
(2)

where the reduced Planck’s constant ħ = 1.0547 × 10–34 J·s. The electron charge is e = 1.602 × 10–19 C. The chemical potential of the graphene is Ef = 0.8 eV, unless otherwise specified. The relaxation time of graphene is assumed to be 2 ps22, and ω is the angular frequency of the incident plane wave. When doing the full-wave simulation using the open source software ‘East FDTD’ based on finite difference time domain method28,29, the thickness of the graphene layer is set to be tg = 0.34 nm. The bulk complex dielectric constant of graphene can be calculated by the equation εg = 1 + iσg/(ε0ωtg), and ε0 is the permittivity in vacuum. ω = 2πf is the angular operating frequency. In the simulation process, we used transition boundary conditions to simulate graphene layer. Periodic boundary conditions are utilized in the x and y directions of the supercell, and perfectly matched layers are applied to the z direction under and above the supercell. For meshing the substrate, we choose a physics-defined mesh with finer settings. For the graphene boundary layer, a finer settings boundary mesh is defined, and the rest of the other regions with normal triangular elements mesh. For meshing the PML layers, we choose a square-mapped meshing with at least 10 divisions. For the fabrication of our proposed graphene quasi-BIC metasurface, one can follow the standard process30 as below. First, the monolayer graphene film can be grown via chemical vapor deposition method in a high temperature tubular quartz tube with reaction gas mixtures (CH4, H2 and Ar) on a thick Ni or Cu film. Then, the polymer supports such as soft poly(dim-ethylsiloxane) (PDMS) stamps and thermal-release tapes are attached to the graphene films grown on metal layers. The support/graphene/metal layers are soaked with FeCl3 solution to remove metal layers, and then the resulting graphene film on the polymer support is ready to be transferred onto the SiO2 substrates. After removing the polymer supports, focused ion beam milling (FIBM) is employed to pattern the graphene films into a periodic array of coaxial apertures. Finally, Au nano-electrodes array and grounding are patterned on top of graphene to form contacts to modulate the chemical potential of graphene by controlling the changes of carrier concentration.

Results and discussion

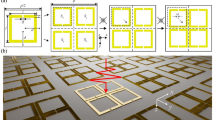
Figure 2a depict the transmission spectra contour of the graphene quasi-BIC metasurface impinged by x-polarized THz wave at normal incidence under perturbation. When the gap distances tx = ty = t0 = 800 nm, we label the metasurface as original state and no perturbation happens. For the perturbation, four graphene coaxial apertures are moved toward the center of the supercell synchronously in both x and y directions, as shown in Fig. 1, and the gap distances tx and ty change simultaneously. Here we define the gap distance offset Δt = t0 − tx (ty). For example, when tx = ty = 700 nm, the gap distance offset Δt = 800 − 700 = 100 nm. From Fig. 2a, it can be seen that we move towards the higher or lower values of the Δt, two transmission dips become prominent, and the resonant dips gradually becomes broad. The frequency of two transmission dips also redshifts. When Δt = 0, two transmission dips have zero bandwidth, which cannot be inspected from the transmission spectrum, indicating the existence of two BIC modes. The two BIC modes in Fig. 2a are labeled as BIC-I and BIC-II in the higher and lower frequency (red dash circles), respectively. To illustrate the evolution of the quasi-BIC transformed from BIC explicitly, a few particular transmission spectra are displayed in Fig. 2b. When Δt = 200 nm, the first quasi-BIC mode named as Q-BIC-I start to appear in the transmission spectra, while the second quasi-BIC mode named as Q-BIC-II creeps in until Δt = 400 nm. In Fig. 2c the Q factors of the dual quasi-BIC modes are plotted with different asymmetric parameter α. α is defined as α = Δt/t0, and the Q factor is defined as31:

Fig. 2
figure 2

(a) Transmission contour of the graphene quasi-BIC metasurface. (b) Evolution of the transmission spectra with various gap distance offset Δt. (c) Q-factors of dual quasi-BIC modes versus asymmetric parameter.

Full size image
$$Q=\frac{{f}_{\text{dip}}}{\gamma },$$
(3)

where fdip is the transmission dip frequency, and γ is the corresponding full-width at half maximum (FWHM). It can be seen that the Q factor of both dual quasi-BIC modes gradually increases as the asymmetric parameter α decreases. At α = 0.875, the Q factors of mode Q-BIC-I and Q-BIC-II are 69 and 70, respectively. When α drops to 0.2, the Q factor of mode Q-BIC-I increases to 176. The dependence of Q-factor on α meet the law of Q ∝ α−2.

The Q factors versus asymmetric parameters plotted in Fig. 2c are obtained by fitting the simulated results with a normalized Fano profile equation32:

$$T={C}_{0}+\frac{{\left[2\left(f-{f}_{\text{dip}}\right)/\gamma +\beta \right]}^{2}}{\left[4{\left(f-{f}_{\text{dip}}\right)}^{2}/{\gamma }^{2}+1\right](1+{\beta }^{2})},$$
(4)

where T represents the transmittance. C0 represents the Fano fitting constant. f represents the frequency of normal incident plane wave. β represents the Fano parameter. The Fano fitting results and numerical calculated transmission are agreed well in Fig. 3b, with C0 = 0.97, β = 0.018, γ = 0.147 THz for mode Q-BIC-I, and γ = 0.129 THz for mode Q-BIC-II. In order to derive and analyze the underlying physical mechanism of the quasi-BIC resonances, the coupled mode theory (CMT)33 is performed and compared with the simulated transmission spectrum in Fig. 3a as following:

Fig. 3
figure 3

(a) CMT and (b) Fano-fitting of the quasi-BIC transmission spectra (red solid line) at Δt = 700 nm. Top view of |E| field distribution (color) and surface current distribution (white arrows) on the x–y plane at (c) 9.04 THz and (d) 10.12 THz.

Full size image
$$\left[\begin{array}{cccc}f-{f}_{1}-i{\gamma }_{1}& {\Omega }_{12}& {\Omega }_{13}& {\Omega }_{14}\\ {\Omega }_{21}& f-{f}_{2}-i{\gamma }_{2}& {\Omega }_{23}& {\Omega }_{24}\\ {\Omega }_{31}& {\Omega }_{32}& f-{f}_{3}-i{\gamma }_{3}& {\Omega }_{34}\\ {\Omega }_{41}& {\Omega }_{42}& {\Omega }_{43}& f-{f}_{4}-i{\gamma }_{4}\end{array}\right]\left[\begin{array}{c}a\\ b\\ c\\ d\end{array}\right]=\left[\begin{array}{c}\sqrt{{\gamma }_{1}}E\\ \sqrt{{\gamma }_{2}}{e}^{i{\phi }_{1}}E\\ \sqrt{{\gamma }_{3}}{e}^{i{\phi }_{2}}E\\ \sqrt{{\gamma }_{4}}{e}^{i{\phi }_{3}}E\end{array}\right],$$
(5)

where the resonance frequency of the for resonators in a super cell is represented by f1 (2, 3, 4), and the corresponding FWHM is represented by γ1 (2, 3, 4). Ωij (i, j = 1, 2, 3, 4) is the coupling coefficient. a, b, c and d are the complex amplitudes of different resonance modes. E is the complex amplitude of the incident THz wave. Ф1 (2, 3) is the phase information. Since only two resonance modes appear in the transmission spectrum, the four resonance frequencies (f1 (2, 3, 4)) degenerate into two resonance frequencies (f1 (2)). The CMT is simplified as:

$$a\left(f-{f}_{1}-i{\gamma }_{1}\right)+b{\Omega }_{12}=\sqrt{{\gamma }_{1}}E$$
$$a{\Omega }_{21}+b\left(f-{f}_{2}-i{\gamma }_{2}\right)=\sqrt{{\gamma }_{2}}{e}^{i\phi }E,$$
(6)

with \(\Omega_{12} = \Omega_{21} = {\text{g}} - {\text{i}}\) \(\sqrt{{γ}_{1}{\text{γ}}_{2}}{e}^{i\phi }\), where g represents the coupling strength and can be obtained as the fitting parameter. The entire transmission spectrum is then given by:

$$T=1-imag\left(\frac{{\gamma }_{2}\left(f-{f}_{1}-\text{i}{\gamma }_{1}\right){e}^{2i\phi }+{\gamma }_{1}\left(f-{f}_{2}-\text{i}{\gamma }_{2}\right)-2g\sqrt{{\gamma }_{1}{\gamma }_{2}}{e}^{i\phi }}{\left(f-{f}_{1}-\text{i}{\gamma }_{1}\right)\left(f-{f}_{2}-\text{i}{\gamma }_{2}\right)-{g}^{2}}\right),$$
(7)

and the match with the numerical spectra is shown in Fig. 3a with g = 0.89 and \(\phi\) = 1.76. The results analyzing by CMT are in good agreements with that by numerical simulation.

To better understand the excitation mechanism of the quasi-BIC and electromagnetic waves transfer energy, the mode profiles of the Q-BIC-I dip and the Q-BIC-II dip are shown in Fig. 3d,c, respectively. The |E| profile in the x–y plane calculated on the graphene layer in Fig. 3c indicates that the electric-field intensity is localized between the edges of coaxial apertures along the illuminated polarization for the plasmonic mode Q-BIC-II. More interestingly, at the resonant frequency of plasmonic mode Q-BIC-I, the electric-field intensity is not only localized between the edges of coaxial apertures inside the super cell, but also with a more concentration of hotspots between the adjacent super cells along the illuminated polarization, as shown in Fig. 3d. To further investigate the origin of the resonance, the surface current distributions are also plotted. Both the surface current distributions in Fig. 3c,d show the trend of accumulation of electrons, which generates strong energy confinement and narrow local hotspots, which is important for the application in the areas of sensing. Both the steady-state electric field distribution and surface current distribution confirm that the metasurface can achieve dual-frequency quasi-BIC modes.

The most attractive feature of graphene is its surface conductivity which can be tuned by thermal stimulation, and electrical or chemical doping34. In Fig. 4a, we discuss the active modulation of the quasi-BIC by tuning the chemical potential. For our structure (α = 0.875), the chemical potential of the graphene can be dynamic reconfigured by applying a gate bias voltage35,36, as shown in Fig. 1. It can be seen that as the chemical potential increases, the overall quasi-BIC transmission dips shift towards higher frequencies. This is because the intraband conductivity of the graphene changes with the increasing of the chemical potential, and make the graphene behaves more like semi-metallic, resulting in a blueshift in the resonant frequency. Besides the frequency shift, we also define an amplitude modulation to quantify the modulation depth of the transmission as following:

Fig. 4
figure 4

(a) Transmission spectra with Ef ranging from 0.70 eV to 0.90 eV while keeping α = 0.875. (b) Transmission contour as a function of polarization angle and incident THz wave frequency.

Full size image
$$\Delta {T}_{max}=\left({T}_{max}-{T}_{min}\right)\times 100\text{\%},$$
(8)

where Tmax and Tmin are the maximum and minimum values of transmittance. Figure 4a shows that ΔTmax gradually increases with the increasing of chemical potential. At Ef = 0.70 eV, the modulation depth ΔTmax = 50%. At Ef = 0.90 eV, the modulation depth increases to ΔTmax = 62%.

Compared to the polarization-dependent quasi-BICs, polarization-independent ones are more desired for practical use because they are immune to the changes of polarization states and angle. However, all dynamic tuning quasi-BICs presented thus far16,17,18,19,20,21,22 are highly sensitive to the polarization angle of incident waves, and can be only supported for a predefined linear polarization state. It is somehow because the symmetry-protected quasi-BICs are easier to be realized by breaking the in-plane symmetry37. The polarization-independent characteristics of our graphene quasi-BIC metasurface are investigated in Fig. 4b. Here we choose Ef = 0.85 eV, while keeping other geometric parameters unchanged (α = 0.875). It can be seen that the quasi-BIC-I transmission dip is constantly maintained at 10.44 THz for all polarization directions on the x–y plane, with ΔTmax larger than 60%. Similar to the quasi-BIC-I, the quasi-BIC-II transmission dip is constantly maintained at 9.31 THz with ΔTmax larger than 50%. This is because when the asymmetric parameter α is introduced, we keep the gap distances tx = ty in the x and y directions, which meet the requirement of C4v symmetry in the square super cell38. Polarization-independent quasi-BIC devices are convenient for practical use, especially in sensing application. It can reduce complex alignment processes, and make the device work under arbitrarily polarized incident light.

The sensing performance of the proposed graphene quasi-BIC metasurface is then studied in Fig. 5. Here the asymmetric parameter is α = 0.875. When increasing the refractive index of the surrounding medium from 1.00 to 1.04, the dual quasi-BIC transmission dips basically do not change, but shift toward lower frequency, as can be seen in Fig. 5a,c, which is promising for liquid and gas sensing. In order to evaluate the quality of a sensor, the sensitivity is defined as S = Δf/Δn, where Δf represents the frequency difference between two adjacent refractive indices, with Δn = 0.01. The calculated sensitivity of mode quasi-BIC-I is shown in Fig. 5b. The frequency shifts corresponding to different refractive indexes exhibit a linear dependence with a slope of 6.75 THz/RIU, ensuring that even a slight change in the refractive index of the surrounding medium can be detected by our proposed metasurface through the measurement of the redshift of the transmission spectra. The calculated sensitivity of mode quasi-BIC-II is 6.02 THz/RIU, and the frequency shifts corresponding to different refractive indexes are shown in Fig. 5d. Besides the sensitivity, the sensing performance can also be quantified by the figure of merit (FOM), which is given by FOM = S/γ. The Q-factor plays a crucial role here, and a large FOM value is desirable for a particular sensor. The LOD = 1/FOM of mode quasi-BIC-I and quasi-BIC-II are calculated to be 0.0218 RIU and 0.0214 RIU, respectively. To further rival the refractive index detection capabilities of our proposed graphene quasi-BIC metasurface, a comparison of THz sensor data information collected from recent literatures is presented in Table 1. We can see most of the THz sensors are lithography-based structures, which are passive, cost-ineffective and lack dynamicity at the operation’s wavelength region. On the contrary, our surface conductivity-based structures are active that maintain the same lithographical configuration. Besides, our proposed polarization-independent graphene quasi-BIC metasurface offers improved performance over the previous works. Although the sensitivity of Ref.39 is higher than that of our work, however, the structures suggested by Ref.40 is polarization-dependent, which can be only supported for a predefined linear polarization state. Other parameters such as the Q-factors, the tunability, and polarization sensitivity are also listed in Table 1 for the comparison.

Fig. 5
figure 5

(a) Transmission spectra with versus different refractive indices for mode quasi-BIC-I. (b) The relationship between frequency offset and refractive index for mode quasi-BIC-I. (c) Transmission spectra with versus different refractive indices for mode quasi-BIC-II. (d) The relationship between frequency offset and refractive index for mode quasi-BIC-II.

Full size image
Table 1 Comparison of sensing performance of the proposed graphene quasi-BIC metasurface.
Full size table

At the end of this paper, we discuss the angle-dependent property of our proposed graphene quasi-BIC metasurface (α = 0.875). Figure 6 shows the transmission contour related to the incident angle (in y–o–z plane). The transmission spectrum maintains good quasi-BIC characteristics for various angles of incidences ranging of 0–65°. The FWHM of mode quasi-BIC-I and quasi-BIC-II overall maintain at 0.147 THz and 0.129 THz, respectively. The modulation depth of the two modes are both larger than 50%. At higher angles > 65°, the transmittance begins decreases with a slight shift in the spectrum. This is because when the period P of our proposed structure is much smaller than the wavelength of incident THz wave, the phase difference of the light field at neighboring graphene coaxial apertures is rather independent of the incident angle, which results in that the resonance frequencies are loosely dependent on the incidence angle.

Fig. 6
figure 6

Transmission contour related to the incident angle (in y–o–z plane).

Full size image

Conclusion

In this study, we propose a novel polarization-independent graphene quasi-BIC metasurface with dual THz working bands. The two quasi-BICs are achieved by perturbation while keeping the requirement of C4v symmetry in the square super cell. The finite value of Q-factor can be up to 176, and follows the asymmetry parameter as, Q ∝ α−2. To better understand the underlying physical mechanism of the dual quasi-BICs, the analytical study has been carried out by Fano-fitting and CMT along with the simulation results. The steady-state electric field distribution and surface current distribution also confirm that the metasurface can achieve dual-frequency quasi-BIC modes. It is significant that the quasi-BIC spectra can be tuned up to 2.3 THz by varying the graphene’s chemical potential, while keeping the modulation depth of the transmission larger than 50%. For the application of our proposed metasurface, we demonstrate biosensors with maximum sensitivity of 6.75 THz/RIU and minimum LOD of 0.0214 RIU, which is superior to other types of THz sensors. Moreover, our proposed metasurface can maintain good quasi-BIC characteristics for arbitrarily polarized incident light and various angles of incidences ranging from 0 to 65°, which will greatly enhance the robustness of biosensors. We believe our work provides a valuable reference for actively tunable sensing devices and optical modulators with polarisation-independent, and will promote the development of the class of graphene quasi-BIC metasurfaces.