Modulation of biofilm growth by shear and fluctuations in turbulent environments

Abstract

This work investigates the role of shear and turbulent fluctuations on multi-species biofilm growth. The study is mostly motivated by understanding biofouling on microplastics (MPs) in oceanic environments. By increasing particle stickiness, biofilms promote MP aggregation and sinking; therefore, a thorough understanding of this multi-scale process is crucial to improve predictions of the MPs fate. We conducted a series of laboratory experiments using an oscillating-grid system to promote biofilm growth on small plastic surfaces under homogeneous isotropic turbulence with grid Reynolds numbers between 305 and 2220. Two configurations were analyzed: one where plastic samples move along with the grid (shear-dominated) and another one where the samples are kept fixed downstream the grid, thus experiencing turbulence but no mean flow (shear-free). Biofilm formed in all cases in a time scale of days, then the biomass formed on the plastic pieces was carefully measured and analyzed as a function of the turbulence level. The shear-free results were further interpreted using a parsimonious physical model, coupling the nutrient uptake rate within the biofilm (Monod kinetics) with the turbulent diffusion of the surrounding bulk liquid. Results show that: (i) under shear-dominated conditions, the biofilm mass initially grows with turbulence intensity before decaying, presumably due to shear-induced erosion; (ii) in the shear-free experiments, the mass increases monotonically following an enhanced availability of nutrients, and then saturates due to uptake-limited kinetics. This latter behavior is well reproduced by the physical model. Furthermore, a subset of plastic pieces were analyzed with a scanning electron microscope, revealing that turbulence also affects the microscopic configuration of biofilm clusters, increasing their compactness as the amplitude of turbulent fluctuations increases. These results contribute not only to our fundamental understanding of biofilms under flow, but can also inform global models of MP transport in marine environments.

Introduction

Biofilms are complex communities of microorganisms, often encased in a matrix of extracellular polymeric substances (EPS)^1,2, which represent a ubiquitous and resilient form of life in nature. During the past four decades, microbiologists have classified bacteria as existing in two primary life forms³: planktonic cells, which are single, independent, free-floating entities; and biofilms, where bacteria aggregate and organize into structured communities. Biofilms in natural and engineered environments predominantly exist as surface-attached communities, adhering to a wide variety of substrates ranging from plastics to natural materials; however, under certain conditions, biofilms can also persist in suspended or planktonic forms, albeit less commonly².

Biofilm formation is relevant in a number of biological processes and engineering applications, including biomedical devices⁴, ship coating^5,6, chemical reactors^7,8,9, and biofouling of (micro)plastics in the ocean^{10,11,12,13,14,15}. The present work is especially motivated by the latter point. Indeed, the behavior of plastic particles in the ocean is dramatically influenced by biofouling, which is conjectured to play a fundamental role in terms of: (i) altering the buoyancy of plastic pieces^16,17; (ii) modifying their surface stickiness^18,19, thereby promoting aggregation (and eventually sinking)^20,21; and (iii) degradation and interaction with fauna²². For all these reasons, understanding the transformation of particles due to biofilm formation is of utmost importance to predict the fate of microplastics^10,13 in aquatic systems – a major environmental challenge and a virtually ubiquitous phenomenon now prevalent in all marine environments worldwide^23,24,25.

In general, biofilms that cover microplastics, as well as other objects in different environments, interact with the surrounding fluid flow, posing a deep and only partially understood scientific challenge due to the intricate interplay between the biota colonies and the underlying hydrodynamic mechanisms, that can profoundly influence their formation, structure, and behavior^{26,27,28,29,30,31}. In fact, fluid flow characteristics, specifically shear stress and turbulence features, may play pivotal roles in shaping the biofilm architecture, determining its mechanical^8,32 and chemical properties^33,34. For instance, shear stress can influence biofilm density^35,36, porosity³⁷, and viscoelasticity³⁸, thereby affecting its resistance to detachment and its ability to adapt to changing environmental conditions³. Despite the beneficial impact of flow turbulence on the advection-diffusion transport of oxygen and nutrients to the cells^39,40,41,42, the increase in shear could lead to erosion processes that are harmful to biofilm colonies^26,35,43. Furthermore, it has been observed that biofilms exhibit distinct structural responses to different flow regimes, with low shear stress favoring the development of thicker, more porous biofilms, while high shear stress is thought to promote denser, more compact structures⁴⁴.

Table 1 Summary of some key studies in the literature that examine the interaction between biofilms and flow mechanisms. The following symbols and acronyms are used: TOC (total organic carbon), CFD (computational fluid dynamics), HSC (high-speed camera), CLSM (confocal laser scanning microscopy), SEM (scanning electron microscopy), $\mu$PTV (micro-particle tracking velocimetry), FRAP (fluorescence recovery after photobleaching), PT (particle tracking), EM (epifluorescence microscopy), HPLC (high-performance liquid chromatography), and HIC (hydrophobic interaction chromatography). Biofilm types are abbreviated as E. for Escherichia, P. for Pseudomonas, S. for Streptococcus or Staphylococcus, and C. for Chlorella. Shear stress ($\tau$) is measured in Pascal (Pa), Re refers to the Reynolds number, and f represents frequency. The final column includes abbreviations for flow types: KHI (Kelvin-Helmholtz Instabilities), LSV (Large Vortex Flow), OF (Oscillating Flow), SVF (Small Vortex Flow), HSF1 (High Shear Flow 1), HSF2 (High Shear Flow 2), SF (Steady Flow), FF (Fluctuating Flow), and LF (Low Frequency).

In this context, as shown in Table 1, recent research has produced numerous hypotheses and findings on biofilm interactions with different hydrodynamic conditions. However, much of the previous work is focused on the effects of mean shear stress under laminar conditions, leaving the need for a clearer and more universal understanding of how turbulent flows, and related nutrient transport mechanisms, affect biofilms⁴⁸. A major challenge lies in differentiating the roles of the shear forces associated with the mean flow from those of nutrient transport enhanced by the turbulent diffusivity, which requires a specific experimental design. Furthermore, studies have largely focused on single-species biofilms, often pre-cultivated, whereas the behavior of diverse, heterogeneous ones, which are relevant across numerous applications^4,5,49, remains under-explored.

In light of the challenges described above, this work reports a combined experimental and theoretical study aimed at exploring the interplay between hydrodynamics and multi-species biofilm structure/growth. Specifically, plastic-attached biofilms were grown using an experimental setup consisting of a cylindrical container filled with marine water and nutrients, wherein different turbulence levels were produced by an oscillating grid. Two different configurations have been considered: (i) a shear-dominated arrangement where the plastic pieces were moving together with the grid; and (ii) a shear-free layout where plastic pieces were kept fixed at a certain distance from the oscillating grid. In the former case, biofilm forms under a superposition of mean shear and turbulent fluctuations, whereas in the latter setup the mean shear is effectively eliminated, allowing to disentangle the phenomena of shear-induced erosion from turbulence-enhanced nutrient uptake. The results are further supported by a theoretical model that couples nutrient transport with metabolic uptake.

Material and methods

Experiments preparation

Laboratory experiments have been conducted at the Institut de Ciències del Mar⁵⁰ and consisted of five different runs that took place between October 2023 and July 2024. The reason for such a time interval is to cover different seasonal changes in marine water in terms of temperature and biogenic presence⁵¹. The biofouling process has been studied on plastics typically found as pollutants in the ocean: polyethylene expanded, polystyrene transparent and polyvinyl chloride^16,23,52. Specifically, the sheets from which the plastic samples were derived have the following characteristics: polyethylene expanded, density of 0.033 $\text {g/cm}^{3}$; polystyrene transparent, thickness 3 mm and density of 0.97 $\text {g/cm}^{3}$; polyvinyl chloride, 1 mm thickness and density of 0.70 g/$\hbox {cm}^{3}$. In terms of size, the samples were cut into squares of size 10 $\times$ 10 mm, the result of a trade-off between the micro-meso plastics size and to allow decent colonization in the time scale of days. Exact surface measurements were obtained from scaled pictures of each piece of plastic. We used Image J software to mark the exact border and calculate the area. This serves to minimize result variability owing to slight differences in the size of the pieces. Moreover, while the polyethylene expanded is a soft material, the other two (particularly the polystyrene) are hard, with a smooth surface. The plastic pieces were pierced to be mounted in the experimental apparatus, then cleaned by immersion in a solution (water + chloride acid at 10%) for 5 h, and finally they were weighted using a laboratory scale system (Mettler Toledo ME204) with a precision of $10^{-4}$ grams. Furthermore, the surface area was carefully measured using Image J software. After such a process, the samples were carefully washed with deionized water and then dried in a laboratory oven at $50^{o}$ C for 24 h. Once the preparation of the plastics was finished, they were immersed in sea water in transparent cylinders of methacrylate. Before each use, the entire material was thoroughly cleaned with a 5% HCl solution or 10% sodium hypochloride solution and rinsed with ultrapure milliQ seawater. The sea water samples were collected from a beach in Barcelona (Platja del Somorrostro, $41^{\circ }$ 23 ’01.3”N $2^{\circ }$ 11’ 47.7”E, NW Mediterranean), close to the ICM. Before conducting the experiment, the marine water was filtered with a 200 $\mu$m Nylon mesh to remove impurities (see Supplementary Material), sand as well as mesozooplankton, which could bias the results. In order to promote plankton growth, seawater was amended with f/2 silicate medium (bottom-right panel in Fig. 1) at a ratio of 1/10. f/2 medium was prepared from stock a solution (nitrate, phosphate, silicate, metals, and vitamins) using autoclaved nutrient-depleted, aged seawater.

Experimental setup: a turbulence generator for biofilm growth

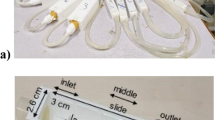
The turbulence generator illustrated in the top panel of Fig. 1 consists of vertically oscillating grids (OGs), powered with a variable speed gear-head motor via an eccentric arm^53,54. The system comprises four motors, each capable of driving two grids, therefore allowing independent adjustment of both the oscillation frequency and amplitude. In particular, the frequency of oscillation f can be adjusted within a range of 0.017 to 0.33 Hz. Together, these parameters allow for a precise control of turbulence levels within a container of volume V. The grids are made of cylindrical stainless steel bars coated with polyamide plastic (a material compatible with biogenic processes), for a final thickness of 3.8 mm and a mesh size of 14 mm. Each grid has a diameter of 125 mm, leaving at least a 4 mm gap between the grid and the container sidewall. The solidity, defined as the percentage of solid surface area perpendicular to the direction of motion, is 37.8%, which is consistent with standard values reported in the literature for oscillating grids^55,56,57. The cylindrical containers used in the experiments are made of methacrylate plastic, with volumes of 2 liters (129 mm inner diameter and 170 mm height) for the first set of experiments and 2.8 liters (133 mm inner diameter and 200 mm height) for the second configuration. This setup was designed and tested to produce acceptable homogeneous isotropic turbulence (HIT) conditions in the cylindrical containers, as reported in previous works^53,58. In particular, to better illustrate the flow state within the cylinder tank, Fig. 2 presents measurements from previous experimental campaigns carried out with exactly the same grids and containers (for a detailed description and analysis, refer to the work by Guadanyol et al.⁵⁸). Specifically, the 3D velocity field was measured using Acoustic Doppler Velocimetry (ADV) from multiple sensors, with a grid oscillation frequency of 0.33 Hz, corresponding to the highest turbulence regime in the present experiment. Data from Sensor 2 (located inside the grid path) and Sensor 5 (located outside the grid path) are shown, as they represent the relevant flow characteristics of the current shear-dominated and shear-free experiments respectively. Several important conclusions can be drawn: (i) the velocity field displays fully developed turbulence both inside and outside the grid path, as demonstrated by the turbulence spectra showing a well-defined inertial range; (ii) the mean velocity field at the probe located outside the grid path is approximately zero, as requested by the shear-free experiments. Of note, here the Sensor 5 is located only 2 cm outside the grid stroke while in the present experiments case is $\sim 3.5$ cm, therefore ensuring even cleaner conditions; (iii) the spectra (panels (a) and (c)) exhibit a slope consistent with the -5/3 Kolmogorov scaling, particularly for Sensor 5, indicating a flow behavior closely resembling local homogeneous and isotropic turbulence. Additional evidence supporting the high turbulence levels associated with increasing grid oscillation frequency, as well as the isotropic characteristics of the flow-especially in regions outside the grid, where turbulence decays similarly to classical HIT-can be found in the Supplementary Material, where the autocorrelation function and the variance of the velocity signals are reported. The apparatus has been extensively used to study bacterial growth under turbulence⁵⁹, nutrients uptake and diatom growth⁶⁰ and particle coagulation under shear flows⁶¹. One of the typical characteristics is the low frequency and large stroke -comparable to the length scale of the container- to produce HIT, which is particularly useful for microcosm experiments as in the case of the present work⁵⁸. As a last point, it should be highlighted that the shear-free experiments (Fig. 1 bottom left panel) were conducted in an environmental chamber maintained at a temperature of 19 ± 1 ^oC, with a 12:12 h light/dark cycle and a light intensity ranging from 180 to 220 $\mu$mol photons $\hbox {m}^{-2}$ $\hbox {s}^{-1}$. The aim of such configuration was to isolate the dynamic of transport of nutrient-oxygen on the biofilm uptake in a controlled light and temperature environment.

Fig. 1

Summary of the experimental apparatus and material prepared. In the top panel, the turbulence generator along with its main features, and a sketch of the oscillating grid with the cylindrical container are shown. The bottom panels depict the two different experimental configurations and the plastic, grid and nutrients composition. The measures and dimensions are expressed in mm.

Fig. 2

Oscillating grid turbulence generator. The top sketch illustrates the cylindrical container along with the positions of the two sensors; the shaded regions indicate the grid excursion. The bottom plots present experimental measurements from Acoustic Doppler Velocimetry, highlighting the turbulence characteristics within the oscillating grid apparatus (data adapted from Guadayol et al.⁵⁸). (a) Velocity spectra for Sensor 2; (b) Instantaneous velocity components measured by Sensor 2; (c) Velocity spectra for Sensor 5; (d) Instantaneous velocity components measured by Sensor 5.

Configuration 1: shear-dominated arrangement

To investigate biofouling in a laboratory setting that emulates marine conditions, an initial experimental setup was designed where plastic pieces were directly attached to the oscillating grid, moving in sync with its motion (see the bottom-right panel of Fig. 1). In this configuration, the plastic samples are subjected to mean shear stresses generated by the oscillating motion, mimicking the conditions found in oceanic environments^62,63. While it is challenging to accurately estimate the profiles of mean shear stress on the plastic surface and the area involved in nutrient uptake, due to the random orientation of the plastic over time, this setup provides a means to investigate the potential role of shear forces in biofilm erosion. Given the novel nature of these experimental campaigns, this configuration was employed to explore several key aspects: (i) the design and replicability of the experiments; (ii) the time required for biofouling colonization; and (iii) the influence of plastic type on the biofouling process. In this case, the average turbulence level sensed by the plastic particles can be measured through the bulk dissipation rate $\varepsilon _{bulk}$ of turbulent kinetic energy (in $\hbox {cm}^{2}$/$\hbox {s}^{3}$) according to the previously developed empirical expression based on the velocity fluctuations (3D) measured using acoustic Doppler velocimetry⁵⁸

$$\begin{aligned} \log _{10}\left( \varepsilon _{bulk}\right) = -3.735 + 1.992 \log _{10} \left( {{S/2}} \right) + 2.003 \log _{10} \left( f \right) - 1.015 \log _{10} \left( V \right) , \end{aligned}$$

(1)

where S, f and V are expressed, respectively, in centimeters, RPM and liters.

Configuration 2: shear-free layout

To disentangle the mechanical effects of mean shear (e.g., attachment and erosion) from the influence of nutrient transport on biogenic growth, it is crucial to employ an experimental setup where the biofilm is exposed solely to turbulent fluctuations. The key objective is to eliminate the influence of mean flow experienced by the biofilms, isolating the effects of turbulence-related nutrient transport dynamics. To achieve this, the experimental design leverages the decaying HIT generated by the oscillating grid, with the plastic samples strategically positioned at a certain distance from the grid. Importantly, the condition of homogeneity downstream of the grid should be understood as local rather than global, due to the self-similar decay occurring in the vertical direction. In other words, in the shear-free experiment, turbulence can be considered locally homogeneous within a small region surrounding the plastic piece (and the biofilm). This setup ensures that the biofilms are subjected to turbulence-driven nutrient transport without the confounding effects of direct shear forces from mean flow, providing a clearer understanding of the interplay between turbulence and biofilm growth. The resulting configuration, denominated as shear-free turbulent boundary layer in previous literature, remains relatively underexplored within the fluid mechanics community. This is primarily due to the experimental challenges involved in generating and maintaining homogeneous isotropic turbulence (HIT) near a solid boundary, a task that is far from straightforward. Consequently, only a limited number of numerical studies have addressed this phenomenon^64,65. The bottom-left panel of Fig. 1 shows the shear-free setup: the plastic samples are kept fixed and attached, through rods, to the bottom of the container. The geometry has been carefully designed to accomplish the following goals: (i) the distance between the top surface of the plastic samples and the lowest point of the grid excursion should be large enough to ensure fully developed and decaying HIT surrounding the plastics. In particular, the distance has been set to 2.5 times the mesh size (of the oscillating grid) as indicated by De Silva et al.^56,57,66. This length ensures that no mean shear (in general, no mean velocity) is experienced by the biofilm developed on the plastics; (ii) the distance between the samples and the sidewall of the container should be relatively large to avoid any influence of the boundary layers and recirculation phenomena from the corners of the cylinder, so that the plastics are located in the center of the bulk volume (see left-bottom of Fig. 1). In this regard, HIT has been observed in the 50% of the internal width of the container^56,67; (iii) the inter-sample distance (i.e., the distance between the plastic pieces) has been designed to avoid reciprocal effect and the so-called Casimir effect, that has been proved to be substantial if the bodies are close⁶⁸; (iv) the height of the four rods is the result of a trade-off between the available length of the container (allowing the stroke length, and distance between the grid and the plastic pieces) and the distance required to ensure a vanishing feedback effect from the bottom wall due to the “reflection” of the velocity fluctuations. In fact, the length of impact of bottom boundaries is a fraction of the turbulence integral scale, which is comparable to a few mesh units⁵⁶. In terms of materials, the base and the rods constitute a unique piece manufactured using a 3D printing process in a polylactic acid, which has been observed to be beneficial for the biofilm growth⁶⁹, and therefore no detrimental material has been employed in the experiential apparatus.

In such experiments, the turbulence level can be parametrized through the local turbulent dissipation, which is the dissipation rate of kinetic energy in the decaying region measured as a function of the virtual origin zand it reads^55,66

$$\begin{aligned} \varepsilon _{z} = c\frac{S^{9/2} M^{3/2} f^{3}}{z^{4}}, \end{aligned}$$

(2)

where M is the mesh size of the oscillating grid. In the same previous experimental campaign mentioned above⁵⁸, the flow field outside the grid path was found to follow this scaling law, and the constant c was estimated to be $\approx 0.02$. The non-dimensional Reynolds number for an oscillating-grid system is defined as $Re_\text {g} = f S^{2}/ \nu$, and it is the main dimensionless parameter to quantify the flow state⁵⁵.

Experimental protocols: biomass measurement and SEM analysis

To obtain a statistically significant dataset, multiple plastic pieces were introduced in the containers, and experiments were run for a sufficiently long time to obtain a robust colonization. At the end of the experiments, the samples were analyzed using two techniques: (i) measurement of biofilm dry mass; and (ii) SEM analysis of a subset of plastic pieces. The dry mass was determined by subtracting the initial weight of the uncolonized plastic from the final weight of the biofouled plastic at the termination of the experiment, after drying the pieces at $50^{o}$ for 24 h. In the shear-dominated experiments, the biofilm mass data were refined using a statistical filtering method, where the lowest and highest 10% percentiles were excluded. In contrast, for the shear-free layout, no specimens were excluded due to the limited number of available samples. Additionally, polyethylene plastic samples were analysed in a $\mu$FTIR (micro Fourier Transform Infrared Spectroscopy) to ensure that no deterioration or chemical alteration of the plastics had occurred during the experiments (see Supplementary Material).

Samples for scanning electron microscopy (SEM) consisted of first fixing the colonized plastic pieces with glutaraldehyde (1% final concentration). Subsequently, dehydration steps followed in increasing alcohol concentrations (30%, 50%, 70% and 100%) for 15 minutes each. Next, the samples were taken to the SEM laboratory and subjected to critical point drying using $\hbox {CO}_{{2}}$ for 2 h, followed by depressurization in a vacuum chamber; such protocol is rather standard in the biofilm literature^70,71,72. In order to be able to observe the organic structures, the process of sputtering (viz. the covering with conductive metal) was then performed in Q150T ES Plus-Turbomolecular pumped coater, where a thin layer of iridium (8 nanometers) was deposited on the samples⁷³. The procedures described above are further illustrated in the Supplementary Material. Finally, the observations were conducted using the Scanning Electron Microscope FE-SEM HITACHI SU8600.

A transport-metabolic-erosion model for the biofilm growth

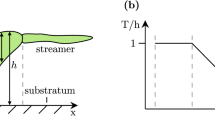
With the aim of providing a framework for interpreting the experimental observations and give more fundamental insight, this section presents a physical model for biofilm growth that focuses specifically on the second experimental configuration (shear-free). Predicting biofilm growth under different hydrodynamic conditions requires modeling the space-time dynamics of the instantaneous concentration $c(\textbf{x},t)$ of a limiting nutrient. As shown in the sketch of Fig. 3, the biofilm is immersed into a turbulent aqueous environment with several primary mechanisms at play: (i) nutrient (and/or oxygen) transport from the fluid phase to the biofilm, due to molecular diffusion (dependent exclusively on the properties of water and nutrients) and turbulent diffusion (contribution of turbulent fluctuations), as well as convection through the mean velocity field U; (ii) the metabolic conversion rate $r(\textbf{x},t)$, defined as the rate at which the biofilm consumes nutrients for growth^41,48,74. (iii) the erosion caused by the mean flow, exerting a shear on the fluid-biofilm interface. Only the two types of diffusion are present in the shear-free experiment, while all the mechanisms mentioned above were present in the shear-dominated experiment.

Fig. 3

Schematic representation of the key mechanisms influencing biofilm development. The biofilm forms on a plastic surface and is subject to various processes: molecular diffusion, turbulent diffusion (present in both experimental configurations), and mass convection along with erosion (occurring only in the shear-dominated experiment where plastic samples are attached to the grid). On the right side of the illustration, the velocity profile within the (oscillatory) boundary layer is shown, with the free-stream velocity described by Eq. (9).

Under these circumstances, the transport equation for the instantaneous concentration of the substrate within both the carrying fluid and the biofilm reads

$$\begin{aligned} \underbrace{\frac{\partial c}{\partial t}}_{\text {time-variation}} = \nabla \cdot \left( \overbrace{\underbrace{D \nabla c}_{Diffusion} - \underbrace{{\textbf {u}} c}_{Advection} }^{Total flux} \right) - \underbrace{r}_{Reaction}, \end{aligned}$$

(3)

where the diffusivity D is equal to the fluid diffusivity $D_f$ in the fluid region ($z<0$) and to the biofilm diffusivity $D_\text {bio}$ within the biofilm ($z>0$), and the term r is only active for $z>0$, where z is the surface-normal coordinate. It is assumed that the biofilm is purely two-dimensional and separated from the surrounding fluid by an infinitely thin interface located at $z = 0$. Each variable appearing in Eq. (3) can be expanded according to the Reynolds decomposition, i.e., as the sum of a mean value plus a fluctuation; e.g., $c = C + c'$, where $C = {\overline{c}}$. It is then convenient to apply a time-averaging operator to Eq. (3), to obtain

$$\begin{aligned} \frac{\partial C}{\partial t} = \nabla \cdot \left( D \nabla C - {{\textbf{U}C}} - \overline{{\textbf {u}}' c'} \right) - R, \end{aligned}$$

(4)

where the mean velocity is zero in the shear-free configuration, which is designed precisely to this purpose, i.e., $\textbf{U} = 0$, while for the shear dominated case the mean flow contributes to the advection of nutrients through the fluid. In addition, due to the homogeneous and isotropic characteristics of the turbulent flow produced by the oscillating grid, the mean concentration C can be assumed to depend exclusively on z. It is important to note that, since the nutrient transport within the biofilm is purely diffusive, the instantaneous reaction rate is equal to its mean counterpart, $r = R$. The mean reaction term R can be modeled through Monod kinetics^38,60,74 as

$$\begin{aligned} R = \frac{V_\text {max} C \rho _\text {bio}}{C + K_{M}}. \end{aligned}$$

(5)

It is clear from Eq. (5) that the nutrient uptake depends directly on (i) its concentration profile within the biofilm, (ii) the maximum specific substrate conversion rate $V_\text {max}$ (defined as the ratio of specific growth rate to the yield of biomass per substrate)⁷⁵, and (iii) the substrate affinity constant $K_{M}$. When the substrate concentration is high ($C \gg K_{M}$), the reaction can be approximated as zero-order. Conversely, at low concentrations ($K_{M} \gg C$), the conversion rate is effectively first-order^60,74,75. Although analytical solutions exist for these two limiting cases, the complete model will be solved numerically here. Importantly, Eq. (4) is unclosed due to the presence of the turbulent flux $-\nabla \cdot \overline{\textbf{u}'c'}$; to close this term, the classical gradient-diffusion modeling strategy is employed, namely

$$\begin{aligned} \nabla \cdot \overline{\textbf{u}'c'} = -D_T \left( \textbf{x} \right) \nabla C, \end{aligned}$$

(6)

where $D_T \left( \textbf{x} \right)$ is a turbulent diffusion coefficient that depends directly on the turbulence length and time scales within the fluid surrounding the biofilm as well as the distance from the virtual origin of the grid $\textbf{x}$ (the details of its calculations are in the Supplementary material).

The ultimate aim of the model is to predict the biomass growth as a function of the turbulence level both in the shear-free layout and in the shear-dominated one. The biofilm mass grown over a period of time T can be estimated by integrating the uptake rate R over time and over the biofilm thickness, yielding

$$\begin{aligned} M = \gamma \int _{L_\text {bio}} \int _T R \, dt \, dz, \quad {{M = \gamma \int _{L_\text {bio}} \int _T R \, dt \, dz - L_{\text {bio}} {\dot{E}} }}, \end{aligned}$$

(7)

where $L_\text {bio}$ is the thickness of the biofilm and $\gamma$ is a metabolic coefficient that accounts for the conversion of nutrient uptake into mass. For the shear-dominated case, biofilm erosion is also accounted for through the erosion rate ${\dot{E}} = \delta \tau ^{\gamma }$, which depends on a semi-empirical detachment coefficient $\delta$ and the wall shear stress $\tau = \partial U_{z} / \partial z|_{z=0}$, where $U_z$ is the vertical component of the mean velocity⁷⁶. The shear stress can be estimated from the velocity gradient within the velocity boundary layer that develops around the biofilm in the shear-dominated regime (see the sketch in Fig. 3). Given that the biofilm is subjected to oscillatory shear, a suitable and straightforward model adopted here relies on Nielsen’s formulation⁷⁷ for oscillatory boundary layers, where the free-stream velocity follows the expression:

$$\begin{aligned} U_{\infty } = U_\text{max} \cos \left( {\omega t} \right) , \quad \omega = 2 \pi f, \quad U_\text{max} = \pi fS, \end{aligned}$$

(8)

where $\omega$ represents the angular velocity of the oscillation, and $U_{Max}$ denotes the maximum velocity during the grid excursion. Using the free-stream velocity, a closed-form expression for the boundary layer profile can be constructed as follows:

$$\begin{aligned} U_{Bl} \left( z, t \right) = \left[ 1 - \psi _{Bl}\left( z\right) \right] U_{\infty }, \quad \psi _{Bl} = \exp \left( -\frac{z}{z_{0}} \right) \cos \left[ - \left( \frac{z}{z_{0}} \right) ^{p} \right] \end{aligned}$$

(9)

where the $z_{0} = 0.50 \sqrt{2 \nu / \omega }$ is a vertical length scale and the exponent $p = 0.326$ is extrapolated from experimental campaigns⁷⁷.

To reduce the dimensionality of the system, the problem is now transformed in dimensionless units. First, the objective function is selected to be the ratio of the mass grown under a certain turbulence level to the mass grown in purely laminar conditions ($M_\text {lam}$), where the only transport mechanism is molecular diffusion. Assuming that $\gamma$ is constant (i.e., it does not depend on the turbulence level), then

$$\begin{aligned} \begin{aligned} {\tilde{m}} = \dfrac{M}{M_\text {lam}}&= f(C, K_M, \rho _\text {bio}, V_\text {max}, L_\text {bio}, T) = \\&= f\left( C(C_\infty , K_M, \rho _\text {bio}, V_\text {max}, L_\text {bio}, D_f, D_\text {bio}, D_T \right) , K_M, \rho _\text {bio}, V_\text {max}, L_\text {bio}, T, U_\text{max}), \end{aligned} \end{aligned}$$

(10)

where $C_{\infty }$ is the nutrient concentration in the bulk fluid, and the second equality emphasizes that C can be in turn determined from Eqs. (4)–(6). According to Buckingham’s theorem, ${\tilde{m}}$ in Eq. (10) can thus be predicted by 7 non-dimensional parameters. Upon choosing the biofilm diffusivity $D_\text {bio}$, the biofilm thickness $L_\text {bio}$, and $C_{\infty }$ as reference parameters, the following 6 non-dimensional quantities can be formed

$$\begin{aligned} \alpha = \frac{D_{f}}{D_\text {bio}}, \quad \beta (z) = \frac{D_{T}(z)}{D_\text {bio}}, \quad Da = \frac{V_\text {max} L^{2}_\text {bio}}{D_\text {bio}}, \quad \tilde{\rho } = \dfrac{\rho _\text {bio}}{C_\infty }, \quad {\tilde{K}}_M = \dfrac{K_M}{C_\infty }, \quad {\tilde{T}} = T\dfrac{D_\text {bio}}{L_\text {bio}}, \quad {{Pe = \frac{U_\text{max}L_\text{bio}}{D_\text{bio}}}}, \end{aligned}$$

(11)

where Da can be regarded as a Damkhöler number quantifying the relative importance between nutrient diffusion over uptake rate, while Pe is the Péclet number which quantifies the relative strength of convection to diffusion. This latter dimensionless group is present only when a mean flow is present therefore in the case of the present work it emerges only in the shear-dominated arrangement. The dimensionless concentration ${\tilde{C}} = C/C_\infty$ is determined from the non-dimensional reaction-diffusion equations expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial {\tilde{C}}}{\partial {\tilde{t}}} = \frac{\partial }{\partial {\tilde{z}}} \left( \alpha + \beta ({\tilde{z}}) \frac{\partial {\tilde{c}}}{\partial z} \right) {{- Pe \frac{\partial }{\partial {\tilde{z}}}\left( \tilde{\textbf{U}}({\tilde{z}}) {\tilde{C}}\right) }}, & \text {fluid region}: {\tilde{z}} < 0, \\ \frac{\partial {\tilde{C}}}{\partial {\tilde{t}}} = \frac{\partial ^{2}{\tilde{C}}}{\partial {\tilde{z}}^{2}} - Da \frac{{\tilde{C}} \tilde{\rho }}{{\tilde{K}}_{M} + {\tilde{C}}}, & \text {biofilm region}: {\tilde{z}} > 0, \end{array}\right. } \end{aligned}$$

(12)

where ${\tilde{z}} = z/L_\text {bio}$. Importantly, the non-dimensional parameter $\beta$ can be expressed as a function of $Re_g$ by quantifying the turbulent diffusivity as a function of the oscillating grid parameters^55,57,58,78 (see Supplementary Material). It is important to highlight that the HIT modeled using a Reynolds-averaged Navier-Stokes (RANS) approach encounters the limitation of not capturing the transition from laminar to turbulent flow. To address this aspect, a specific threshold value for $Re_{g}$ was chosen based on the observed transition regime in the current apparatus⁵⁸, ensuring the activation of turbulent diffusivity aligns with experimental observations. In summary, the non-dimensional mass can be determined as ${\tilde{m}} = F(\alpha , Re_g, Da, \tilde{\rho }, {\tilde{K}}_M, {\tilde{T}}, {{Pe}})$, where the function F can be estimated by integrating Eq. (12) and then using Eq. (7); details about the numerical integration of Eq. (12) are given in the Supplementary Material. As it will be discussed more extensively in the Results section, particular attention will be given to the dependence of ${\tilde{m}}$ on $Re_g$ and Da when comparing the model prediction to the (properly non-dimensionalized) experimental results.

Results and discussion

Summary of experimental runs

The experiments carried out in this work are summarized in Table 2. Three experimental runs were conducted in the shear-dominated configuration, while two were dedicated to the shear-free layout. Each of the five experiments lasted approximately 14 days – a duration carefully chosen to ensure a detectable accumulation of biomass on the plastic pieces while avoiding deterioration of the water quality. The main objective of Exp. 1 was to serve as a pilot study aimed at verifying biofilm growth on the plastic surfaces and determining the timescales at play.

Table 2 Summary of experimental runs. The number of plastic samples refers to those contained in each cylinder, which operates at a specific turbulence level. The types of plastics tested include polyethylene (PE), polystyrene (PS), polyvinyl chloride (PVC). The turbulent dissipation rate $\varepsilon$ should be interpreted as $\varepsilon _\text {bulk}$ for the shear-dominated experiments and as $\varepsilon _z$ for the shear-free ones.

Starting from the second experimental run, Exp. 2, the four set-ups were run to check the response of the biofilm to different turbulence levels, and for different types of plastic surfaces. With the objective of corroborating the results of Exp. 2, Exp. 3 was carried out using exactly the same parameters. Note that for Exp. 2 and 3, a fourth container with still water was included to measure biofouling under quiescent conditions. Experiments 4 and 5 were specifically designed to isolate the contribution of turbulent fluctuations on biofilm growth in the absence of shear and over a wide range of turbulence levels and focusing specifically on polyethylene. This choice was motivated by two key reasons: (i) polyethylene plastics have been demonstrated to maintain their chemical composition throughout the experiments (as evidenced by the $\mu$-FTIR analysis in the Supplementary Material), and (ii) their porous structure facilitates enhanced biofouling, enabling a statistically robust quantification of the average biomass. Biofilm formed across all the experiments conducted within the 14-day duration of the runs. However, the biofilm attachment on the plastic samples exhibited notable variations depending on the flow conditions and plastic type. In the following subsection, the results and observations from the two experimental configurations are presented and discussed.

Biofilm growth in shear-dominated configuration

Figure 4 shows a series of pictures of the biofouled plastic pieces at the end of the shear-dominated experiments (specifically Exp. 2 in Table 2). The pictures qualitatively reveal that biofilm attachment varies according to the type and surface properties of the plastic. The selection of different plastics was guided by their prevalence in marine environments²⁴ and their different surface properties, which could influence the rate of biomass attachment. More importantly, the flow state appears to play a crucial role, with higher turbulence levels leading to more clustered biofilm formations (see Fig. 4g,i), indicating a potential mechanism of mechanosensing as found in other works^30,45,46.

Fig. 4

Image of the biofilm growth for the three different plastic types and Configuration 1 (viz. plastic samples attached to the grid) at the end of experimental run 2. The various columns represent different level of turbulence: panels (a), (e), (i) show the pieces in the still water with no oscillating grid. Panels (b), (f), (j) shows the low level turbulence ($\varepsilon _\text {bulk} \approx 5 \cdot 10^{-3}$ $\hbox {m}^{2}$/$\hbox {s}^{3}$); plots (c), (g), (k) shows the intermediate level turbulence ($\varepsilon _\text {bulk} \approx 2 \cdot 10^{-2}$ $\hbox {m}^{2}$/$\hbox {s}^{3}$); plots (d), (h), (l) show the high level turbulence ($\varepsilon _\text {bulk} \approx 5 \cdot 10^{-2}$ $\hbox {m}^{2}$/$\hbox {s}^{3}$). Top row represent the polystyrene pieces, middle row show the PVC and bottom row show the polyethylene.

This initial observation indicates that turbulence intensity may play a significant role in influencing biofilm growth and attachment. To further investigate this relationship, a more quantitative investigation was conducted by measuring the mass of the biofilm at the end of each experiment. This analysis, presented in Fig. 5, highlights the relationship between turbulence intensity and biofouling. It is important to note that turbulence intensity in this context is quantified using a bulk dissipation rate $\varepsilon _\text {bulk}$. In this configuration, the local dissipation rate sensed by the plastic particles, as well as the local shear stresses, were continuously varying with time and were not quantified. As $\varepsilon _\text {bulk}$ increases, both the turbulence level and the local mean shear stress increase; however, the latter process is thought to dominate over the former. To contextualize the regime of shear with respect to other studies on biofilms (as summarized in Table 2), a rough estimation of the wall shear stress $\tau$ experienced by the plastic samples can be made using classical boundary layer theory. The first step involves defining the local Reynolds number, $Re_{x} = U_{Max} x / \nu$ , where x represents the distance from the leading edge (approximately 1 cm in this case). Considering the improved Prandtl correlation⁷⁹, $c_{f} = 0.0592 / Re^{0.2}_{x}$, and then $\tau = c_{f} \times 2 \rho U^{2}_{Max}$ the wall shear stress is found to range between 5 and 8 mPa. This crude estimation is accompanied by a more in-depth dimensionless analysis presented in Eq. (9), along with the results in Fig. 11, where a model incorporating biofilm erosion due to wall shear stress is thoroughly examined.

The histograms of Fig. 5, accompanied by error bars, reveal an initial enhancement of biofilm growth, a peak at an intermediate turbulence level $\varepsilon _\text {bulk} \approx 0.02$ $\hbox {cm}^2$/$\hbox {s}^3$, and then a decrease in growth. In general, this finding aligns with previous studies that have identified a peak in biofilm mass or growth under moderate flow conditions. In these cases, shear forces are not sufficient to cause significant erosion of the biofilm while still enhancing nutrient transport and surface attachment, thereby promoting growth^26,30,31. Besides, to assess the statistical properties of each sample (i.e., for each flow level), a one-sample t-test was performed using the corresponding SciPy library⁸⁰. The corresponding p-values are under the value of 0.05 indicating statistical significance confirming that each sample follows a normal distribution. In this context, the variation and nature of the flow play a crucial role. Specifically, the type of oscillation significantly influences biofilm development in the following ways: (i) biofilm growth under fluctuating flow conditions progresses through distinct phases, while under steady-flow conditions, it follows four stages: lag, exponential, stationary, and decline. Moreover, low-frequency flow fluctuations promote biofilm growth, whereas high-frequency fluctuations prevent the biofilm from adapting to the external flow environment, leading to increased erosion effects³¹. In the present study, higher oscillation frequencies of the grid result in higher-frequency shear forces acting on the biofilm, ultimately yielding reduced biomass accumulation. To validate the previous statement -specifically, whether the observed trend is driven by shear forces, nutrient transport, or a combination of these factors- the results from the second experimental configuration will be analyzed and discussed below. This setup is designed to decouple and isolate the effects mentioned above, providing a clearer understanding of the mechanisms at play.

Fig. 5

Measurements of the biofilm mass for the shear-dominated experimental runs (Experiments 2 and 3).

Biofilm growth and structure under shear-free conditions

Fig. 6

Biofilm mass measurements for the shear-free configuration (Experiments 4 and 5). The asterisks related to the gray dashed lines connecting the different sample represents the p-value based on pairwise Mann–Whitney U tests.

Figure 6 reports the biofilm mass at the end of Experiments 4 and 5 in dimensional units. Biofilm mass generally increases with turbulence intensity, displaying two distinct phases: (i) initially, for low values of $\varepsilon _z$, the flow is most likely laminar⁵⁸, and the nutrient transport mechanism occurs mostly through molecular diffusion. As a result, the biofilm mass remains nearly constant; (ii) as the value of $\varepsilon _z$ increases, the flow undergoes transition to turbulence and the biofilm mass experiences significant growth, likely driven by enhanced nutrient and oxygen uptake resulting from increased mass transport. Notably, the quantitative consistency across both experimental runs demonstrates the replicability of these results. Furthermore a statistical analysis using a one-sample t-test from SciPy library⁸⁰ was conducted for these observations, confirming that each sample follows a normal distribution and a One-Way ANOVA test (performed using the Statsmodels library⁸¹) resulted in a p-value of 0.0325. Additionally, pairwise Mann-Whitney U tests were conducted to compare the differences between multiple independent groups. The results are illustrated with gray dashed lines, accompanied by asterisks connecting the corresponding histograms. In the next sub-section, a reaction-diffusion model is employed to provide more physical insight into the hydrodynamic mechanisms contributing to biofilm growth. Another interesting observation is that the biofilm mass generated in Experiments 4–5 is significantly larger than that in Experiments 2–3. This discrepancy can likely be attributed to two key factors: (i) the controlled experimental setup, with precise light cycles, used for Exp. 4 and 5 likely enhanced biofilm growth by promoting phototrophic organisms such as diatoms and algae⁸², and (ii) the photosynthetic activity within biofilms may have facilitated localized oxygen production and nutrient cycling, creating a favorable microenvironment for heterotrophic organisms within the biofilm⁸³, and (iii) the effect of mean shear, which may have contributed to biofilm erosion in Exp. 2 and 3. Of note, the results obtained at $\varepsilon _z \approx 2 \times 10^{-3}$ $\hbox {cm}^2$/$\hbox {s}^3$ appear to deviate from the general trend; this is most likely due to the (unintentional) selection of the most biofouled sample for SEM observation.

Fig. 7

Scanning electron images for the samples biofouled in the low turbulence level ($\varepsilon _{z} = 1.3 \cdot 10^{-4}$ $\hbox {cm}^{2}$/$\hbox {s}^{3}$).

In fact, a subset of the plastic samples from Experiment 4 also underwent SEM analysis to observe the micro-scale structure of the biofilms. The analysis of iridium-coated biofilm samples in general reveals a complex multispecies composition, characterized by aggregated microorganisms and fibriform extracellular matrix-like structures (see Figs. 8, 9). These observations highlight the critical influence of turbulent fluctuations on both the morphology of microbial colonies attached to plastics and the composition of the predominant microorganisms. Specifically, at lower turbulence levels (Fig. 7), the biofilm exhibits a more dispersed organization with an abundant extracellular polymeric substances (EPS) matrix. Additionally, a variety of globular microorganisms in the nanoplankton range (2-20 $\mu$m) are observed. In contrast, intermediate and high turbulence levels (Figs. 8, 9) reveal more packed and crowded biofilm colonies, suggesting an increase in biofilm density driven by turbulent fluctuations. Higher turbulence intensities also result in a notable abundance of bacterial species. These findings corroborate the hypothesis of biofilm adaptation to external hydrodynamic cues through complex mechanosensing mechanisms, as previously described^7,30. The flow field, particularly through turbulent fluctuations, exerts mechanical forces on the biogenic communities, prompting them to organize into more compact and dense configurations. Simultaneously, these mechanical forces may act as biological signals, potentially triggering processes such as the activation of cyclic-di-GMP signaling pathways³², which enhance the proliferation of certain biospecies. This phenomenon, known as mechanotransduction, is evident in the variation of species composition and biofilm architecture across different turbulence levels. Under low turbulence conditions (Fig.7), the biofilm is predominantly rich in EPS, visible as a light-colored, irregular matrix-like structure in the SEM images. In contrast, intermediate and high turbulence levels (Figs. 8, 9) display a richer taxonomy. Zoomed panels in these figures reveal the presence of diverse species, including Chaetoceros and other diatoms, which dominate under higher turbulence levels. Such differentiation of species has been possible due to the multispecies nature of the biofilm (contrary to the totality of such type of studies where the investigation is on monoculture biofilms). To conclude, the SEM observations highlight the dual role of turbulence in shaping both the physical structure and biological diversity of the biofilm.

Fig. 8

Scanning electron images for the samples biofouled in the intermediate turbulence level ($\varepsilon _{z} = 8.3 \cdot 10^{-4}$ $\hbox {cm}^{2}$/$\hbox {s}^{3}$).

Fig. 9

Scanning electron micrography for the samples biofouled in a high turbulence fluid environment ($\varepsilon _{z} = 2.0 \cdot 10^{-3}$ $\hbox {cm}^{2}$/$\hbox {s}^{3}$). Main images show the general cluster structures rather packed and dense while the zoomed pictures show the details of structures and species.

Comparison of model predictions with experimental results

To further interpret and characterize the experimental observations presented in the previous section, results from the physical model are now introduced and compared against experimental data. This analysis aims to provide a deeper understanding of the underlying mechanisms and complements the empirical findings by elucidating the behavior of key parameters under varying conditions. In Table 3, the main input parameters of the problem are described, specifically the physical and biological characteristics of the bulk fluid and the biofilm together with the numerical properties of the simulations. The biofilm properties have been chosen in order to simulate realistic conditions according to the problem set-up of the shear-free experiment.

Table 3 Parameters and constants used in numerical simulations. These values are selected in order to be consistent with the range reported in the respective references. The acronyms SD and SF mean shear-dominated and shear-free.

Certain choices regarding the inputs of the model need further explanation. First, the nutrient concentration is based on the limiting nutrient, which, in the selected set-up, is conjectured to be phosphorus⁸⁶. In reaction-diffusion models, the limiting nutrient -the least abundant resource- plays a critical role as it most directly constrains the growth and activity of the biological community⁸⁸ (in accordance with Liebig’s Law of the Minimum). Based on this principle, the parameters used to construct the Monod expression are derived under the assumption of phosphorus limitation, and are carefully chosen to reflect the environmental conditions, such as light and temperature. It is important to highlight that since it was not possible to directly measure the nutrient fluxes in vitro, we cannot discard the hypothesis that oxygen transport is instead the limiting factor in our setup. It should be taken into account, however, that the system is not heterotrophic. Since we did not add any source of organic matter, mostly phytoplankton take advantage of the added inorganic nutrients. In addition, phytoplankton also produce oxygen and, as shown by the SEM images, autotrophs grew on the plastic pieces. On the other hand, in later stages, when there are enough carbon-rich phytoplankton exudates, bacteria could grow and reduce oxygen levels. Therefore, turbulence may increase the availability of oxygen through the same mechanisms discussed in this work. Additionally, the numerical parameters for the in silico experiments, including the time step and mesh size, are calibrated to capture the key mechanisms of the system while maintaining computational efficiency.

The results extracted from the diffusion-reaction model are reported in Fig. 10 for the shear-free configuration, where the dimensionless concentration profile of the limiting nutrient is shown for both the fluid and biofilm regions. In the inset plots (a) and (b), the concentration profile is shown for three different Damkhöler numbers in both laminar conditions (a), where nutrient transport occurs purely through molecular diffusion, and at $Re_g = 10^3$, where mass transport is enhanced by turbulent diffusion (b). As time evolves, a depletion layer forms adjacent to the surface of the biofilm, where the concentration decreases as the nutrient is absorbed by the biofilm. The steady-state solution, namely the concentration of nutrient at the biofilm-fluid interface ($z=0$), is the result of the interplay between the uptake rate (here mostly parametrized by the Damkhöler number Da) and the rate at which the nutrient is replenished by the bulk fluid (here represented by the parameter $\beta$). As shown in the plots (a) and (b) of Fig. 10, larger values of Da lead to a diffusion-limited regime, where the uptake rate is faster than the (turbulent) diffusion by the external fluid. It is important to note that the overwhelming majority of previously developed models have focused on the nutrient diffusion within the biofilm, without taking into account the effect of the external fluid dynamics, which is here parametrized by means of the grid Reynolds number $Re_{g}$. Several additional observations can be made: (i) higher diffusivity causes a reduction of the gradient of concentration at the fluid-biofilm interface, which can be considered a suppression of the depletion boundary layer, i.e., the enhanced diffusion enriches the fluid region of nutrient across the interface; (ii) the higher the turbulence intensity, the faster the concentration profiles achieve a steady-state condition, as it can be observed comparing Fig. 10a where the red curves present a clear time dependence due to the change in the concavity, while in Fig. 10b after just half-diffusion time $\tau _b$ the profiles are already overlapped. Such phenomenon is particularly marked for biofilms with high metabolic rate (i.e., at larger Da). (iii) On equal Damkhöler numbers, the concentration (and consequently the uptake) of nutrients within the biofilm increases with turbulence intensity, but this trend is clearly asymptotic as shown in the panel (c): from $Re_{g} = 10$ to $Re_{g} = 1000$ the difference is very small.

Fig. 10

Results from model and comparison with experiments for the shear-free configuration. Left panels: distribution of nutrients concentration ${\tilde{C}}$ in the bulk fluid and biofilm at different times given by the reaction diffusion model. (a) Pure still case ($Re_{g} = 0$) and (b) High turbulence case ($Re_{g} = 1000$) for different Damkhöler numbers Da (colors) and times $t/\tau _{B}$ = 0.1 (dotted lines), 0.5 (dotted-dashed lines), 1 (dashed lines), 2 (solid lines). (c) Influence of the OG Reynolds number on the nutrients profile. Right panel (d) shows the comparison between the the dimensionless biofilm mass from the experiment and the model (computed in the steady regime viz. $t/\tau _{B}$ = 5) incorporating transition (purple curve) and transition & change in the Monod half-saturation constant.

As a final remark, the comparison between the experimentally measured biomass weight (normalized by the lowest turbulence level, as shown in Fig.6) and the model results provides key insights. The concentration profile, integrated in the biofilm zone as depicted in Eq. (10), once a steady state solution has been achieved ($t/\tau _{B} = 5$) and expressed as a function of $Re_{g}$, demonstrates good agreement between experiments and simulations. In particular, the transition observed at $Re_{g} \approx 650$ corresponding to $\sim 10^{-4}$ $\hbox {cm}^2$/$\hbox {s}^3$ at that distance from the grid bottom position in biofilm mass aligns with the flow transition described in prior studies⁵⁸, underscoring the intricate interplay between flow dynamics and biofilm response. Moreover, while the simpler model addresses the laminar-to-turbulent transition, a more advanced approach involves slightly adjusting the half-saturation constant $K_{M}$ in the Monod equation to calibrate the model and align it with experimental data. Notably, fine-tuning just these two parameters yields an excellent match between experimental and numerical results, demonstrating that the model accurately captures the correct order of magnitude. In general, both experiments and model reveal three distinct regimes: (i) a laminar regime, characterized by a constant biofilm mass; (ii) a transition regime, where biomass grows steeply due to the onset of turbulence; and (iii) a turbulent regime, where biofilm growth saturates. This transition is strongly influenced by Da, underscoring the delicate interplay between flow conditions and biofilm dynamics. Regarding the laminar regime, nutrient transport is governed by slow molecular diffusion, limiting biofilm growth. However, as turbulence emerges, diffusivity increases by two to three orders of magnitude, providing sufficient substrate for biofilm growth. Beyond a certain point, the biofilm’s metabolic capacity becomes the limiting factor, leading to saturation. This asymptotic trend, linking nutrient availability to turbulence levels, is consistent with findings from previous studies^39,41,74,75. However, it is important to note that, unlike the mechanisms presented in this work, those studies involved mean flow, where turbulence manifested primarily through advection and shear effects. Notably, the value of $Re_{g}$ at which the biofilm growth exhibits a transition corresponds to the value of $\varepsilon _{z}$ associated with the laminar-to-turbulent transition previously found in the same oscillating grid system⁵⁸. This remarkable correspondence suggests a strong link between the state of the flow and biofilm development, providing a mechanistic understanding of how turbulence drives biofilm evolution in marine-inspired environments.

The final analysis focuses on comparing the model with experimental results from the shear-dominated setup. As in the previous case, experimental data have been normalized against the smallest $Re_{g}$ case which now is the still water condition. This setup presents additional challenges for the physical model due to several factors: (i) the mass transport equation now includes both diffusion (laminar and turbulent) and convection; (ii) the presence of a significant mean flow introduces shear effects and an oscillatory mechanical boundary layer, making it necessary to account for erosion. Consequently, the 1D computational mesh must be significantly larger to capture the flow region, including the boundary layer, which is more than an order of magnitude thicker than the biofilm. Figure 11 shows the model results, where the purple curve represents the time-integrated solution of the full form of Eq. (7). To achieve a match with experimental data, multiple tuning parameters are available, with the primary adjustable parameter being $\delta$. The dashed green curve, with values shown on the right axis, illustrates the trend of the erosion term, which, as described in the relevant subsection, is directly dependent on the shear stress at the wall. Notably, the experimental trend has been reproduced, as the competing effects of increasing $Re_{g}$-namely, the enhancement of nutrient and oxygen uptake versus the mechanical impact of erosion-result in an optimal growth rate at an intermediate turbulence level.

Fig. 11

Results from the full model, incorporating diffusion, convection, and erosion, compared with experimental data from the shear-dominated setup. The Damkhöler numbers Da and total simulation time remain consistent with those in Fig. 10.

Conclusions

This study investigated the influence of flow state on the growth of multispecies biofilms in a marine-inspired environment, utilizing both experimental and modeling approaches. The experimental runs employed an oscillating grid apparatus, exploring two distinct configurations: (i) a shear-dominated setup, where biofilms grew under oscillatory mean shear stress, and (ii) a shear-free setup, where nutrients transport occurred solely by molecular diffusion and through the fluctuations of homogeneous isotropic turbulence. In the shear-dominated configuration, biofilm biomass exhibited a peak at intermediate turbulence levels (as quantified by bulk dissipation) pointing to a crucial role of the trade-off between flow-enhanced nutrients uptake and shear-induced erosion. Conversely, the shear-free setup revealed an increment of biomass with turbulence intensity, divided into three distinct growth regimes: a laminar regime with negligible biofilm growth due to limited nutrient transport, a transition regime where biofilm mass increased sharply as turbulence enhanced nutrient diffusivity, and a saturation regime at high turbulence levels, where biomass growth plateaued due to metabolic constraints. Notably, this trend mirrors the transition from laminar to turbulent flow in the oscillating grid system. To provide deeper insight into these observations, a parsimonious 1D reaction-diffusion model was developed to incorporate turbulence-driven diffusivity and metabolic uptake, quantified via the Damkhöler number, as well as erosion effects. The results suggest that, in the shear-free configuration, the observed regimes are mostly governed by the interplay between nutrient availability and metabolic demand. Specifically, in the laminar regime, molecular diffusion limits nutrient transport to the biofilm; in the transition regime, turbulence enhances nutrient supply, fostering biomass growth; and in the saturation regime, metabolic limitations prevent further increases in biomass, even when nutrients are readily transported to the biofilm interface. On the other hand, the model showed that, in the shear-dominated arrangement, the emergence of an “optimal” turbulence level for biofilm growth is the result of the competition between enhanced availability of nutrients and increased shear-associated erosion. This combined experimental and modeling approach provides a comprehensive framework for understanding the interplay between hydrodynamics and biofilm growth, with implications for marine biofouling and many other applications.

To the best of the authors knowledge, this study represents the first investigation delving into the effects of pure turbulent fluctuations (shear-free) on biofilm growth, as directly compared with shear-dominated conditions. Achieving this objective required several innovative approaches: first, an oscillating grid apparatus was employed as a turbulence generator, providing a controlled environment to modulate turbulence intensity while strategically positioning plastic samples in the desired locations. This setup enabled precise examination of turbulence effects under both shear-free and shear-dominant scenarios. Second, a multidisciplinary approach combining laboratory experiments with theoretical modeling was adopted, offering a more comprehensive understanding of the observed phenomena. The model used, while simplified and grounded on established literature^38,74, integrates turbulence modeling (via a Reynolds-averaged modeling approach) with biological growth kinetics (via the Monod expression). This novel combination allows for the incorporation of turbulence effects through a simplified eddy-diffusivity parameter, bridging the gap between fluid dynamics and biological processes.

Beyond fundamental insights, the results provided in this work may have practical implications for understanding the role of turbulence-biofilm interaction in marine environments, particularly with relation to microplastics. One key outcome is the recognition that turbulence (and generally flow state) profoundly influences biofilm development, both in terms of biomass quantity & morphology (mechanosensing) and species composition (mechanotransduction). This can directly affect the adhesive properties of biofilms (stickiness), which play a crucial role in the aggregation of microplastic particles. For instance, an intriguing hypothesis from this study involves the production of extracellular polymeric substances (EPS), which appears to be more prominent at lower turbulence levels. This enhanced EPS production can likely increase the adhesive properties of biofouled microparticles at a macroscopic scale. If validated, this phenomenon could result in stickier biofouled particles in marine environments, such as micro- and macroplastics, leading to an elevated tendency for the formation of aggregates under moderate flow conditions. Notably, oscillating or fluctuating flows further emphasize this effect, as biofilm growth is enhanced at lower oscillation frequencies, suggesting that rapid fluctuations (high frequency) may inhibit adhesion and growth due to excessive shear stress. Based on these conjectures and the findings of this study, a key recommendation for future global modeling of microplastics transport is the inclusion of biofilm dynamics as a function of flow conditions. Given the proven utility of existing models in predicting the fate of plastic debris in marine environments^10,23,89, incorporating biofilm-related effects would provide a more comprehensive understanding of aggregation processes, buoyancy changes, and overall microplastic transport in turbulent marine systems.

Limitations & future work

This study has some limitations. The diffusion-reaction model is purely one-dimensional and neglects the displacement of the interface as the biofilm is growing. Furthermore, there are uncertainties associated with several parameters that have not been calibrated, such as biofilm density, Monod coefficients, erosion-related coefficients and biofilm thickness. Furthermore, these parameters may in turn depend on the turbulence intensity. While it was not the objective of this work to carry out a formal model calibration, incorporating the dynamic evolution of the above-mentioned parameters would enhance the model’s realism and should be addressed in future work. The experimental runs also suffered from some limitations: (i) the number of plastic samples was limited, and the selection of random plastic samples for SEM analysis in Experiments 4 introduced a certain bias in the results; (ii) it was not possible to measure the time evolution of biofilm growth, the nutrient flux, nor other biofilm properties except its mass at the end of the experiments. Adopting a more quantitative approach -such as measuring biofilm thickness over time would provide further insights; (iii) while acceptably satisfied, the condition of homogeneous and isotropic turbulence reproduced in the experimental apparatus can only be regarded as an approximation. Furthermore, while biofouling on marine microplastics was the main motivation for this study, caution should be taken in extrapolating the results to real-world conditions, for the following reasons: (i) microplastics are often non-neutrally buoyant, leading to relative velocities with seawater that exceed those in our experiments. However, using non-neutrally buoyant particles in controlled setups is challenging, as they tend to settle or float away quickly. Additionally, biofilm growth alters particle density over time, making their buoyancy dynamic. To avoid gravitational effects, our focus was on isolating biofilm growth under controlled turbulence, emphasizing nutrient transport and shear stress. Despite these limitations, we believe the fundamental mechanisms and overall trends observed remain relevant to natural environments; (ii) the ‘clean’ turbulent conditions that closely resemble homogeneous isotropic turbulence (HIT) established in these experiments only serve as an idealized model for upper-ocean turbulence, where other phenomena, such as shear or Langmuir processes, can influence the flow fields; (iii) biofilm species heterogeneity as well as variability in plastic surface properties (roughness, attachment potential, material composition) were not taken into account and can be part of future work.

Finally, since computational modeling has emerged as a powerful complement for studying biofilm-hydrodynamic interactions, future work could focus on multi-dimensional and multi-physics numerical simulations of biofilm growth under complex flow conditions, for instance using the immersed boundary method to incorporate the spatio-temporal evolution of the biofilm structure. Bridging the gap between experimental observations and theoretical predictions remains a critical challenge in this field.