Introduction

Movement variability is inherent to healthy human movement and corresponds to the normal variations that occur within subsequent repetitions of a motor action1. Briefly, as proposed by Bernstein2, the production of movement patterns consists of a “repetition without repetition” in the sense that patterns are never repeated in the exact same manner. For example, attempting to sustain a submaximal isometric contraction results in fluctuations around an average force value. Recently, is has been shown that these fluctuations possess a deterministic origin3, underscoring the importance of studying how they oscillate over time, as it may provide a deeper insight into force’s motor control process4,5.

The temporal structure of the fluctuations of a given biological signal is termed physiological complexity and reflects the adaptability of the system to environmental challenges4. These fluctuations have been described in the literature in various types of biological time series, e.g., heart rate6, respiratory frequency7, gait8,9, balance10 and torque4,11,12,13. Accordingly, a healthy and adaptable system is characterized by a highly intricate structure with an optimal amount of variability (i.e., high complexity), whereas systems with too much or too little variability are considered less complex and rendered unstable or rigid, respectively1. Fluctuations in torque signals are usually studied through entropy measures, i.e., the loss of information in a time series which allows us to infer about the regularity of the signal12. Accordingly, common indirect measures of complexity in torque signals are approximate entropy13 and sample entropy14. For easiness of comprehension and interpretation, “complexity” terminology will be used throughout this study, but only referring to changes in the regularity of the signal.

Torque complexity provides information about the interactions between components of the neuromuscular system that cooperate to produce complex patterns of force15. Moreover, it has been proposed as an indirect indicator of the functional capacity of the neuromuscular system16. Recent research has demonstrated that neuromuscular fatigue, i.e., a symptom in which physical and cognitive function is limited by interactions between performance fatigability (a decrease in an objective performance measure) and perceived fatigability (the sensations that regulate the integrity of the performer)17,18, leads to a loss of torque complexity and reduces the neuromuscular system’s adaptability to external perturbations in both maximal and submaximal intermittent and sustained isometric contractions19,20. Accordingly, such loss of torque complexity has been suggested to primarily derive from peripheral fatigue mechanisms above the critical torque (CT), i.e., the asymptote of the hyperbolic relationship between torque output and time to task failure21, despite contribution from central mechanisms is likely to be present19. Pethick and colleagues16,19,20,22,23 have been investigating the physiologic mechanisms associated with torque complexity’s changes with fatigue. Importantly, they suggested that the loss of torque complexity and neuromuscular fatigue are processes that are tightly coupled.

Fluctuations in the torque output during sustained muscle contractions are ubiquitous3. To regulate muscle torque and its subsequent fluctuations, common synaptic input to the motoneurons innervating the solicited muscles, and consequent increase in the recruitment of additional motor units and the modulation of active motor units’ firing rates, is required24. This is particularly crucial for compensating for decreases in the torque-generating capacity of the muscle, due to the development of fatigue25. In fact, although fatigue-related increases in common synaptic input have been extensively shown to be associated with increased variability of torque fluctuations during isometric contractions26,27, only recently Fennell and colleagues28 reported increases in common synaptic input with fatigue to be associated with changes in torque complexity, specifically, with increased torque irregularity. The authors further suggest torque complexity likely reflects the neural mechanisms underlying the modulation of torque control28. Accordingly, understanding the relationship between the modulation of force fluctuations with a fatiguing task and the neuromuscular coordination mechanisms may provide valuable insights into the underlying motor control processes, as these mechanisms are dependent on the common synaptic input to the motoneurons.

Based-upon the current knowledge, the aim of the present study was to investigate the association between torque complexity’s changes with neuromuscular fatigue and the individual’s motor unit profile. This relationship could advance our knowledge regarding the underlying modulation of motor control. We also analysed torque complexity before and after a fatiguing task, to study how torque’s motor control is altered with neuromuscular fatigue. Accordingly, we hypothesized torque complexity’s changes would be correlated with motor unit parameters. We further hypothesized torque complexity would be altered with neuromuscular fatigue.

Results

The descriptive statistics for all dependent variables are summarised in Table 1.

Table 1 Descriptive statistics for all the dependent variables. Data are presented as Mean ± SD.
Full size table

Motor unit-related correlations

Average firing rate (aFR)

A strong correlation was found between pairs ΔSampEn and PRE VL aFR (r = − 0.618, p = 0.004, 95% CI [− 1.000, − 0.275]) and ΔSampEn and PRE VM aFR (r = − 0.659, p = 0.002, 95% CI [− 1.000, − 0.337]). Individuals whose SampEn decreased with neuromuscular fatigue presented higher pre-fatigue values of VL and VM aFR, whereas individuals whose SampEn increased with neuromuscular fatigue had lower pre-fatigue values of VL and VM aFR. Figure 1 represents these significant correlations.

Fig. 1
figure 1

Correlation between Vastus Lateralis and Vastus Medialis aFR before (PRE) fatigue and ΔSampEn. Data are presented as individual values. Grey band represents the 95% confidence intervals. “r” represents the Pearson correlation coefficient and “R2” represents the amount of variation of the dependent variable that can be explained by the independent variable. N = 17.

Full size image

Peak motor unit action potential amplitude (MUAPamp)

Strong correlations were found between ΔSampEn and PRE VL MUAPamp (rs = − 0.801, p < 0.001, 95% CI [− 1.000, − 0.712]) and ΔSampEn and PRE VM MUAPamp (rs = − 0.703, p < 0.001, 95% CI [− 1.000, − 0.374]) pairs. Individuals whose SampEn decreased with neuromuscular fatigue presented higher pre-fatigue values of VL and VM MUAPamp, whereas individuals whose SampEn increased with neuromuscular fatigue had lower pre-fatigue values of VL and VM MUAPamp. Figure 2 represents these significant correlations.

Fig. 2
figure 2

Correlation between Vastus Lateralis and Vastus Medialis MUAPamp before (PRE) fatigue and ΔSampEn. Data are presented as individual values. Grey band represents the 95% confidence intervals. “rs” represents the Spearman correlation coefficient and “R2” represents the amount of variation of the dependent variable that can be explained by the independent variable. N = 17.

Full size image

Torque-related parameters

Sample entropy (SampEn)

Knee extension torque sample entropy significantly increased with neuromuscular fatigue (t(20) = − 2.63, p = 0.016, d = − 0.57). Figure 3 represents torque’s sample entropy before and after fatigue.

Fig. 3
figure 3

Torque sample entropy before and after neuromuscular fatigue. Data are presented as individual values. N = 21; * p = 0.016.

Full size image

Peak torque (PT)

Knee extension peak torque significantly decreased with neuromuscular fatigue (t(20) = 9.74, p < 0.001, d = 2.13).

Mean torque (MT) and mean knee joint angle (MKJA)

No effect of neuromuscular fatigue was found for knee extension mean torque (t(20) = 1.11, p = 0.279, d = 0.24) and mean knee joint angle (Z = 109.0, p = 0.838, r = − 0.06).

Coefficient of variation (CV)

No significant effect of neuromuscular fatigue was found for knee extension torque coefficient of variation (t(20) = − 1.29, p = 0.209, d = − 0.28).

Motor unit-related parameters

Average firing rate (aFR)

Average Firing Rate of the Vastus Lateralis (t(16) = − 4.63, p < 0.001, d = − 1.12) and the Vastus Medialis (t(16) =  − 4.02, p < 0.001, d = − 0.97) significantly increased with neuromuscular fatigue.

Peak motor unit action potential amplitude (MUAPamp)

Peak motor unit action potential amplitude of the Vastus Lateralis (t(16) = − 3.70, p = 0.002, d = − 0.89) and the Vastus Medialis (t(16) = − 6.07, p < 0.001, d = − 1.47) significantly increased with neuromuscular fatigue.

Discussion

The present study investigated the association between torque complexity’s changes with neuromuscular fatigue and motor unit parameters. Accordingly, our findings support our hypothesis as we showed torque complexity’s changes pre-to-post neuromuscular fatigue to be negatively correlated with average firing rate and peak motor unit action potential amplitude pre-fatigue. To understand how torque’s motor control is altered with neuromuscular fatigue, we investigated how torque complexity changed with a fatiguing task. As expected, torque complexity was altered with neuromuscular fatigue; however, the direction of change was surprising, as we observed torque output to become more irregular, which diverges from most of the existing literature. Nevertheless, our findings agree with Stergiou and colleagues’1 theoretical model, suggesting increased torque irregularity also renders the system less adaptable and thus, less complex. Moreover, Fennell and colleagues28 also reported an increase in knee extensors torque irregularity following a fatiguing protocol.

Relationship between torque complexity’s changes with neuromuscular fatigue and motor unit parameters

To generate and sustain voluntary muscle contractions, and thus altering torque complexity, several neurophysiological mechanisms interact to produce complex patterns of force29,30. This premise motivated us to investigate the association between torque complexity’s changes with the development of neuromuscular fatigue and motor unit parameters, as the ability of generating and maintaining force output is highly dependent on these parameters31. Here, we showed torque complexity’s changes pre-to-post neuromuscular fatigue to be negatively correlated with average firing rate and peak motor unit action potential amplitude pre-fatigue (Figs. 1 and 2, respectively). Briefly, these findings suggest individuals with higher pre-fatigue values of average firing rate and peak motor unit action potential amplitude exhibited increased torque regularity with neuromuscular fatigue, whereas individuals with lower measures of the same parameters pre-fatigue demonstrated decreased torque regularity with neuromuscular fatigue.

Motor unit recruitment and firing rate behaviour in a normal, non-fatigued state, reflect the fundamental mechanisms of neuromuscular control while providing a reference point to assess divergences, for example, under fatigued or pathological conditions31. To optimize torque-generating capacity while minimizing metabolic cost, the neuromuscular system efficiently regulates these mechanisms32. However, this optimization process can be conditioned by the physical properties of the muscle33. Several studies have proposed that muscle fibre type composition may play a role in regulating motor unit behaviour34,35,36. Colquhoun and colleagues34, for example, demonstrated that subjects with greater Type II fibre areas tended to display lower firing rates for the earliest recruited motor units, but higher firing rates for the latest recruited motor units compared to subjects who had lower Type II fibre areas. Interestingly, we can speculate the relationship between torque complexity’s changes with neuromuscular fatigue and motor unit parameters may also be dependent on the physical properties of the muscle. Individuals with greater type II fibre composition, which exhibit lower firing rates of earlier-recruited motor units and higher firing rates of higher threshold motor units, may benefit from a ubiquitous advantage in the optimization process of torque-generating capacity and the ability to sustain motor unit activity at high levels of excitation34. Likewise, individuals with greater type I fibre composition may have less of an advantage due to the different motor unit behaviour that is dependent on muscle composition, which may potentially elucidate the present study’s findings. Thus, it appears that fibre type composition may provide greater insights on divergent motor unit behaviour between different individuals37 and subsequent motor control strategies.

Torque complexity’s changes with neuromuscular fatigue

Torque complexity has previously been shown to decrease with neuromuscular fatigue12,19,20. Here, we observed an increased irregularity (i.e., higher SampEn) of the torque output after a fatiguing task which led the system towards a self-perceived fatigued state, and we consider to be related with a loss of complexity. A decrease in torque complexity is associated with reduced complex interactions between the multiple control systems, feedback loops, and regulatory processes that operate in the neuromuscular system4, which reflects a decreased adaptability within the system38. Typically, decreases in torque complexity with neuromuscular fatigue have been reported alongside reduced entropy values, implying the torque output becomes more regular and periodic19,20,39. Nonetheless, Stergiou and colleagues’1 “Optimal Movement Variability” theoretical model added a newer perspective, suggesting increases beyond optimal variability (i.e., towards randomness) also constitute a decrease in physiological complexity, rendering the system noisier and unpredictable5,29. Accordingly, the presence of healthy, fractal, temporal variations in the torque output is compromised, with individuals losing the ability to rapidly and accurately adapt muscle force to perturbations associated with neuromuscular fatigue1,29.

It has been suggested that the loss of torque complexity with neuromuscular fatigue occurs exclusively above the critical torque19. Briefly, the neuromuscular adjustments during contractions below the CT are modest, and the progression of fatigue is much slower when compared with contractions performed above CT, where a progressive loss of torque until task failure is observed19,40. Despite the critical torque of the quadriceps having been proposed to range between ~ 25–35% MVIC, the current literature suggests this parameter has high inter-individual variability41. Having that in consideration, we believe the selected submaximal intensity (i.e., 30% MVIC) could have been below the critical torque for some of the participants, as visual inspection of our data highlighted a bi-directional behaviour of entropy as fatigue developed (i.e., some participants had their entropy increased whereas others had their entropy decreased with neuromuscular fatigue; Fig. 3). This hypothesis could provide substantiation for the increased irregularity in the torque output to be related to a loss of torque complexity with neuromuscular fatigue, a phenomenon scarcely reported in the literature28,42. Loss of torque complexity above the critical torque is represented as a smoothing of the torque time series19 which is associated with a more robotic and degrees-of-freedom’ constrained behavior1,43. Contrarily, below the critical torque, we speculate the neuromuscular system could also become less flexible and adaptable to perturbations, but by becoming more irregular and unpredictable, as proposed by Stergiou and colleagues in their model1. Further investigation is necessary to experimentally test this hypothesis; nonetheless, preliminary data analysis of our research group suggests the process of torque regularity adaptation is closely related with critical torque for the same group of muscles (Oliveira et al., in press).

Our findings are consonant with the differently induced neuromuscular changes when tasks are performed below or above the critical torque. Interestingly, the literature suggests that during contractions below the critical torque, the neuromuscular system maintains the torque demand by recruiting additional motor units and by increasing their firing rates44,45. However, above the critical torque, these alterations appear to be associated with an increasing loss of muscle metabolic homeostasis and consequent development of peripheral fatigue leading to a greater reduction of the force-generating capacity40. Both these situations render the system less complex. However, motor control and force-generating processes are employed differently by the neuromuscular system as torque requirement is altered, possibly highlighting an association between motor unit parameters and the bi-directional behaviour of torque’s sample entropy changes with self-perceived fatigue. Nonetheless, caution should be used when interpreting these results as our analysis does not establish a causal relation. While our data strongly suggests torque complexity and neurophysiological parameters are tightly coupled processes, other factors are also acting at the motor control level allowing the neuromuscular system to match the torque demand. Therefore, a necessary next step to advance our knowledge would be to gain insight into torque complexity’s underlying mechanisms establishing a causal relation, possibly through a regression analysis.

Limitations and future directions

An important aspect of this study’s data analysis is the use of entropy in torque signals. We are confident our data analysis was the most appropriate one to study the physiological dynamics of motor control as it uses a sufficient amount of time (i.e., 30 s sampled at 100 Hz) while taking into consideration both the frequency of interest and physiological timescales30,39. Thus, this prevented us from oversampling our data and allowed us to reduce the amount of redundant information in entropy values12. However, the interpretation of our results must be contextualized in some limitations, for which we suggest potential future solutions. Primarily, the criteria for stopping the protocol may have been too subjective, as the final decision was from the participant. Accordingly, factors such as motivation can significantly influence the time to exhaustion and the associated fatiguing effects44. Nonetheless, neuromuscular fatigue was induced as depicted in our peak torque analysis (i.e., a loss of ~ 29%). Moreover, the use of dynamic concentric and eccentric contractions in our fatiguing protocol may represent a more ecological and valid method to induce fatigue instead of using intermittent or sustained isometric contractions, as these dynamic muscle actions are more preponderant in activities of daily living and sporting events45. Additionally, the submaximal trials’ intensity may have been low regarding the critical torque of the quadriceps which has been shown to range from ~ 25–35% MVIC41. As we selected an intensity of 30% MVIC and upon visually inspecting our data, we believe it could have been below the critical torque for most participants, potentially accounting for the increased irregular fluctuations of the torque output. Directly measuring the critical torque would be a necessary next step in a subsequent study. Lastly, when comparing different studies on this matter, the reader should bear in mind entropy values could also be influenced by contraction type. Although most studies reporting entropy metrics employed pushing isometric contractions20, we used holding isometric contractions. Briefly, the neuronal control and physiological aspects of a holding isometric muscle action are closer to a lengthening pattern (i.e., an eccentric action) and the underlying mechanisms of a pushing isometric action are similar to a shortening pattern (i.e., a concentric action)46. Interestingly, a recent study of our research group showed these two isometric tasks to induce different entropy outputs, suggesting divergent motor control strategies are likely used47.

Overall, our findings emphasize the complexity of neuromuscular adaptations to neuromuscular fatigue and underscore the need for further investigating the interplay between torque complexity, motor unit parameters, and contraction characteristics. Future studies should aim towards extending the association between torque complexity’s changes with neuromuscular fatigue and motor unit parameters by further exploring the contributions of a broader range of neuromuscular parameters (e.g., cortical drive, brain activity) to unravel the underlying mechanisms of torque complexity. Furthermore, identifying the critical torque of each individual could contribute towards understanding the bi-directional behaviour of torque’s sample entropy.

Conclusion

In conclusion, our findings supported our hypothesis and added to the current knowledge as we observed torque complexity’s changes with neuromuscular fatigue were associated with motor unit parameters. Specifically, individuals whose average firing rate and peak motor unit action potential amplitude values were higher pre-fatigue, exhibited increased torque regularity with neuromuscular fatigue, whereas individuals with lower measures of the same parameters pre-fatigue demonstrated decreased torque regularity with neuromuscular fatigue. We also demonstrated torque complexity was altered with neuromuscular fatigue, alongside an unexpected increase in torque irregularity. These novel findings suggest a more nuanced understanding of torque complexity dynamics with neuromuscular fatigue, which challenges conventional interpretations.

Methods

Participants

Twenty-one young and healthy male adults aged 18–35 years (age: 24.62 ± 3.51 years; height: 1.77 ± 0.07 m; body mass: 74.57 ± 13.34 kg; BMI: 23.68 ± 3.30 kg/m2) were recruited between 15th February 2022 and 15th July 2022 by word of mouth and took part in the present study. The inclusion criteria included the absence of neurological disorders or lower limb disabilities. Each subject attended one data collection session and signed a written informed consent, approved by the institutional review board of the Faculty of Human Kinetics (approval number #3/2022) and in conformity with the Declaration of Helsinki. The risk of health complications during this experiment was minimal. The participants were supervised and informed of the procedures in real time, with the possibility to pause the experiment at any time in case of self-perceived fatigue.

Experimental design

Participants were instructed to maintain their typical sleep patterns. They were also instructed to abstain from alcohol, caffeine, cacao, tea and other stimulant substances from 8 to 12 h before the day of testing. Furthermore, the participants were also instructed to avoid moderate to vigorous physical activity and resistance training prior to the study.

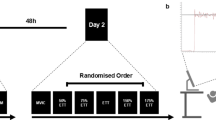
Throughout testing participants were seated in the chair of a Biodex System 3 Pro isokinetic dynamometer (Biodex Medical System 3, Shirley, NY), initialised and calibrated according to the manufacturer’s instructions. Their dominant leg was attached to the lever arm of the dynamometer and the seating position adjusted to ensure that the lateral epicondyle of the femur was aligned with the axis of rotation of the lever arm. The relative hip and knee angles were set at 90° to adjust the position of isokinetic dynamometer. Before testing, participants performed a range of submaximal isometric and isokinetic leg extensions to ensure proper familiarization with the testing task and warm-up. All measures were taken at 70° of knee flexion (full knee extension being 0°), and participants were asked not to alter their posture and focus on the task. The lower leg was attached to the lever arm above the malleoli with a velcro strap. Straps were secured firmly across both shoulders and the waist to prevent extraneous movement and the use of the hip extensors during the contractions. Figure 4 details the experimental design.

Fig. 4
figure 4

Experimental design.

Full size image

Data collection

Participants were asked to perform three knee extension Maximal Voluntary Isometric Contractions (MVIC), each lasting a period of 5 s, with a 60-s interval between trials. They were instructed to produce their maximum force as fast as possible with sturdy oral reinforcement. After a 60-s rest period, the dynamometer mode was set to isotonic, and participants performed two isometric holding contractions at a target torque of 30% of their MVIC for 30 s, based on the recommendations of Bauer and colleagues47. They were given visual feedback through an angular position line of their knee joint angle, which was set at 70° of knee flexion. Throughout submaximal testing, participants were instructed to follow the angular position line of their knee which ensured they remained on the testing angle and also performed 30% of their maximum while their limb was immobile. The submaximal task was performed twice with a 60-s period in between. Shortly after, participants performed the fatiguing protocol, which consisted of a series of concentric and eccentric knee extensions until exhaustion. The isokinetic mode of the dynamometer was used, with the concentric/eccentric option and speed of the dynamometer set at 90°/s. Full extension of the knee was reduced 30° to protect the musculotendinous knee complex. Throughout the fatiguing protocol, participants produced force towards extension and, once full extension was reached, the lever arm moved on its own towards flexion with participants having to produce force towards extension as well. Participants were instructed to produce their maximum effort in every single repetition, until exhaustion. Criteria for exhaustion was defined as the self-perceived inability to resist to the dynamometer’s lever arm during the eccentric phase, which participants had in consideration when deciding to stop testing. Immediately after, participants performed the same tests as prior to the fatiguing protocol.

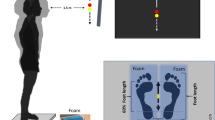
Data was sampled through Biopac MP100 (Biopac Systems Inc.) interfaced with a personal computer. All signals were sampled at 1000 Hz. Torque data was collected in Acknowledge (Version 4.1.1. Biopac Systems, Inc.) and further exported to Matlab® R2023b (The MathWorks, Natick, MA, USA). High-density electromyography (EMGhd) was acquired using a four-channel decomposition EMG Trigno Galileo (Delsys, Natick, MA) placed on vastus lateralis (VL) and vastus medialis (VM), fixed with specially designed detection surfaces. Prior to the electrodes’ placement, the skin was prepared by hair removal and cleaning with alcohol to improve signal conduction. Electrodes were placed according to SENIAM (Surface EMG for Non-Invasive Assessment of Muscles) recommendations and aligned with muscle fibers48. Additionally, tape was used to firmly secure the electrodes to the participants skin to prevent movement artifacts. The electrodes remained positioned on the respective muscles throughout testing, only being removed when testing was complete. Figure 5 demonstrates the experimental setup.

Fig. 5
figure 5

Experimental setup for the submaximal trials from which we extracted entropy metrics. Panel (A) Visual feedback of the knee angle; Panel (B) Participant positioning throughout collection; Panel (C) Electrodes positioning during the entire data collection.

Full size image

Data analysis

All data was analysed using code written in Matlab® R2023b. MVIC torque signals were first low-pass filtered (Butterworth 10 Hz, 4th order). For MVIC trials, Peak Torque (PT) was determined. PT was defined as the highest torque value recorded during the 5-s of the MVIC trials. For statistical purposes, the highest PT values amongst the trials were used for statistical analysis. Regarding submaximal trials, the signals were resampled to 100 Hz after running a power spectral analysis that revealed a maximal frequency across all participants of 13.85 Hz. We, therefore, used the recommendation by Stergiou49 of a sampling frequency 4–6 times greater than the highest frequency in the time series of interest in combination with Raffalt and colleagues’50 recommendations of at least 3000 points to fully capture the dynamics of torque’s motor control. Then, the signals were cropped to remove the ascending and descending components of the isometric contractions. Therefore, the analysed signals only accounted for the time the participant matched the targeted MVIC%. Then, the magnitude of variability and temporal structure of variability were calculated. The Sample Entropy (SampEn)14 was used to determine the temporal structure of the torque output. Sample entropy was solely used in detriment of approximate entropy because the latter was found to suffer from a lack of relative consistency, being highly dependent on data length, and biased toward a more probable outcome as it always includes a self-match for each vector to avoid taking the logarithm of zero12. To offset these issues, sample entropy was developed14. SampEn determines the inverse probability that short sequences of data points are repeated throughout a temporal sequence of points. For a given time series of length \(N, {X}_{N}=[{x}_{1}, {x}_{2}, \dots , {x}_{N}]\), subseries of length \(m\) are constructed and defined as \({X}_{m,i}=\left({x}_{i},{x}_{i+1},\dots , {x}_{i+m-1}\right)\). Then, the probability that any of the vectors will be similar to \({X}_{m}\), is calculated:

$${C}_{i}\left(m,r\right)= \frac{{n}_{i}(m,r)}{N-m+1}$$
(1)

where \({n}_{i}\left(m,r\right)\) represents the number of vectors \({X}_{m,j}\) that are similar to \({X}_{m,i}\) with a constraint

$$d\left({X}_{m,i},{X}_{m,j}\right) \le r$$
(2)

in which \(d\left({X}_{m,i},{X}_{m,j}\right)\) is the maximal difference between vectors \({X}_{m,i}\) and \({X}_{m,j}\) in their respective scalar components. Subsequently, the average probability is computed:

$$\Phi \left(m,r\right)= \frac{1}{N-m+1}{\sum }_{i=1}^{N-m+1}{C}_{i}(m,r)$$
(3)

The same process is repeated for the subseries of length \(m+1\) to calculate \(\Phi \left(m+1,r\right)\). Then, the SampEn is calculated:

$$SampEn\left({X}_{N},m,r\right)= -ln\frac{\Phi \left(m+1,r\right). }{\Phi \left(m,r\right)}$$
(4)

where \(ln\) is the natural logarithm. A time series with repeatable sequences of data points would result in a regular output leading to a lower SampEn value, while the absence of this repeatability of sequences of data points would result in a more irregular output characterized by higher SampEn values. Thus, a perfectly repeatable time series has a SampEn value equal to zero, and a perfectly random time series has a SampEn value converging towards infinity14. In this study, a pattern length (m) of 2, error tolerance (r) of 0.2 and data length (N) of 3000 data points (i.e., 100 Hz × 30 s) were selected and used in the determination of SampEn values51. The reliability of entropy measures was shown to be optimal when these input values are identical for all trials and participants52.

The Coefficient of Variation (CV), a common linear measure that translates the amount of variability within the torque signal was calculated by dividing the standard deviation of the force signal by its mean and converting to percentage (multiplied by 100). Mean Torque (MT) and Mean Knee Joint Angle (MKJA) were also calculated to ensure the target was reached equally and the angle did not differ pre- to post-fatigue, respectively. SampEn, CV, MT and MKJA were extracted from the exact same previously cropped signal. For statistical purposes, the average of the two submaximal isometric trials was used.

EMGhd data was collected in EMG Works (Delsys, Natick, MA) and decomposed using the Neuromap System (Delsys, Natick, MA) to extract the motor units action potential trains of concurrently active motor units53. Data was further exported and analysed in Matlab® R2023b using a custom code. The accuracy of each decomposed MUAP train was then calculated33. We only analysed MUAP trains that were decomposed with an accuracy level > 90%54. Specifically, average firing rate (aFR) and peak motor unit action potential amplitude (MUAPamp), were detected across the four EMG channels54.

Statistical analysis

All statistical analysis was carried out using Jamovi (Version 1.6. Sydney, Australia). Standard descriptive statistics (mean and standard deviation) were used to provide a general overview of the data. All data were tested for normality using Shapiro–Wilk tests. Two-tailed paired samples t-test were used to determine the effects of pre-to-post fatigue in maximal (PT) and submaximal torque parameters (SampEn, CV, MT and MKJA). The Cohen’s d was calculated as a measure of effect size, as d = \(\frac{t}{\sqrt{N}}\), where t stands for the statistical value and N for number of observations. When normality was violated, a non- parametric Wilcoxon signed-ranks test was used. In this case, effect sizes were calculated through r = \(\frac{Z}{\sqrt{N}}\), where Z stands for the statistical value and N for number of observations. Additionally, Pearson and Spearman correlations (when data were and were not normally distributed, respectively) were used to examine the association between pre-to-post fatigue ΔSampEn and VL and VM measures of aFR and MUAPamp pre-fatigue. 95% confidence intervals were analysed to evaluate the strength of the correlation. Regarding motor unit analysis, data quality was only assured for seventeen participants. Statistical significance was set at p < 0.05.