ICRL: independent causality representation learning for domain generalization

Abstract

Domain generalization (DG) addresses the challenge of out-of-distribution (OOD) data; however, the reliance on statistical correlations during model development often introduces shortcut learning problems. Current approaches to mitigating these issues commonly involve the integration of causal inference, formalizing DG problems through a general structural causal model. Nevertheless, ensuring the independence of features when incorporating causal models is often overlooked, leading to spurious causal relationships. In this work, we design three independent feature modules using GAN variants (GAN, WGAN, and WGAN-GP) and select the best-performing WGAN module to integrate into the existing causal model framework, constructing an independent causal relationship learning (ICRL) model. Extensive experiments on widely used datasets demonstrate that our model, with independent causal representations, outperforms the original model in both performance and efficiency, thereby validating the effectiveness of our proposed approach. The code for ICRL can be accessed at: https://github.com/22Shao/ICRL.git.

Introduction

Deep neural networks are rapidly approaching or even surpassing human-level performance in object classification¹, demonstrating outstanding results across various fields such as complex strategy games, medical image analysis, and cross-lingual text translation^2,3,4. However, as real-world tasks become more complex and application scenarios diversify, the limitations of deep neural networks are becoming more apparent. Even minor, imperceptible changes or variations in background, particularly with out-of-distribution (OOD) data, can significantly compromise their predictive accuracy^5,6,7. Consequently, domain generalization (DG) has gained attention, aiming to create models capable of generalizing to unseen target domains by utilizing data from different training domains or environments.

Figure 1

The structural causal model (SCM) for domain generalization (DG) is represented, where solid arrows denote causal relationships from parent to child nodes, while dashed arrows indicate statistical dependencies.

Common strategies to enhance DG performance include invariant feature learning, meta-learning, and adversarial training^8,9,10. However, these methods do not entirely eliminate the shortcut learning problem, which often arises in deep neural network training. When superficial correlations are removed, predictions tend to become random^11,12. To address this, causal representation learning methods with strong assumptions are needed to identify and control confounding factors, reducing spurious correlations and enabling the model to focus on causal features^{13,14,15,16,17}. Causal representation learning frameworks in deep learning typically involve causal variable learning, causal mechanism learning, and causal structure learning. Nonetheless, these models often overlook the control of feature independence, leading to misleading causal relationships^18,19,20,21.

This paper proposes a domain generalization learning model based on independent causal relationships. To better illustrate this model, a structural causal model (SCM) is introduced to represent the intrinsic causal mechanisms between data and labels in domain generalization, enhancing the model’s generalization capability, as shown in Fig. 1. Domain-specific information is treated as causal factors, while domain-invariant factors, such as “animal posture” in the cat-dog classification task, are considered non-causal. In contrast, factors unrelated to the category, such as “image style” in cat-dog classification, are regarded as non-causal and typically domain-dependent. Attention is also given to the independence of causal factors, like “background color and brightness” in cat-dog classification. Each raw data point x is composed of a mixture of causal factors S and non-causal factors U, with only the former influencing the label Y, as depicted in Fig. 1. The goal is to disentangle the independent causal factors S from the input x, reconstructing the invariant causal mechanism, which can be achieved through causal intervention $P(Y \mid do(U), S)$. The do-calculus operator $do(\cdot )$²² represents intervention on the variables. However, since causal relationships cannot be fully formalized and complex dependencies exist among variables in real-world data, designing models that ensure factor independence remains a challenging task.

Figure 2

Explanation of the properties of causal factors.

Inspired by statistical independence, we build upon the findings of studies^23,24,25,26 to establish a hypothesis where causal factors strictly adhere to independence. For the causal factor S to be considered independent, it must satisfy two properties: (1) S follows a normal distribution; (2) the decomposition of S satisfies uncorrelatedness. As shown in Fig. 2a, a dependency exists between the causal factor S and the non-causal factor U. If this dependency is not removed through independence testing, the effect of U on Y may be erroneously attributed to S, leading to confounding bias. Conversely, Fig. 2b illustrates an ideal causal factor S that meets the independence criteria. Based on this, we propose the Independent Causal Relationship Representation for Domain Generalization (ICRL) algorithm, which enforces the learned representation to satisfy the above properties. We further simulate the decomposition of causal factors across each dimension of the representation, resulting in enhanced generalization capabilities.

In summary, for each input, we first design a Generative Adversarial Network (GAN) capable of fitting a standard normal distribution. This model aligns the factors to follow a normal distribution and eliminates the correlation between S and U, before feeding them into an existing causal representation learning model to uncover causal mechanisms, thereby improving generalization. Our contributions are as follows:

• 1. We construct a GAN model to ensure factors follow a normal distribution.

• 2. We develop an ICRL model for domain generalization based on independent causal relationships.

• 3. Extensive experiments and analysis on widely-used datasets demonstrate the effectiveness and superiority of our method.

Related work

Domain generalization

Domain Generalization (DG) refers to a machine learning approach that enables models to perform well across different domains, even when trained only on data from specific domains, demonstrating strong cross-domain generalization capabilities²⁷. Since the introduction of DG, numerous methods have been developed to explore this concept. These include aligning source domain distributions through invariant representation learning^28,29, exposing the model to domain shifts via meta-learning during training^30,31, and augmenting data through domain synthesis³².

Additionally, Multi-Task Learning (MTL)³³ aids in domain generalization by training multiple tasks simultaneously, allowing the model to share feature representations across tasks, which helps maintain performance across different data distributions. In DG, tasks can be treated as proxies for different domains, and MTL enables the model to identify and extract common features across tasks (or domains), thus improving performance in unseen domains.

Data Augmentation³⁴ is another key technique in DG, increasing data diversity to simulate domain variations, thereby helping the model learn more general features. Common techniques include image rotation, flipping, color perturbation, and more complex synthetic data generation methods.

In contrast to the above methods, our approach tackles the DG problem from the perspective of causal feature independence.This approach focuses on reducing confounding factors by making causal features independent, thereby uncovering the underlying causal mechanisms and demonstrating enhanced generalization performance. In contrast to the recent AMCR method³⁵, which relies on sample diversification and data augmentation but is limited when significant discrepancies exist between the target and source domains, our method leverages causal feature independence to learn more accurate causal features, achieving more efficient cross-domain generalization. Furthermore, compared to the bilevel optimization-based meta-learning framework proposed by Chen et al.³⁶, which aligns features between source domains using traditional statistical methods, our approach removes non-causal factors, preventing reliance on domain-specific noise and mitigating the impact of spurious correlations, thereby exhibiting stronger adaptability in large-scale domain shifts.

Causal mechanisms

Since Judea Pearl introduced the theory of causal inference, it has had a profound impact on modern statistics, artificial intelligence, and machine learning³⁷. Unlike statistical correlations, which rely on data trend consistency to determine relationships, causal relationships reflect the intrinsic characteristics and structures within and between variables. In recent years, various methods based on causal relationships have been proposed to discover invariant causal mechanisms^38,39,40 or recover causal features^41,42, thereby improving out-of-distribution (OOD) generalization. However, these methods often depend on restrictive assumptions in causal graphs or structural equations. Recent studies have addressed this issue using counterfactual methods to mitigate data distribution shifts, reduce language bias and enhance class balance^43,44,45. For example, Deng et al.⁴⁶ introduced the counterfactual model CounterAL, which improves performance on under-annotated out-of-distribution (OOD) tasks by better generalizing to unseen data through the use of factual and counterfactual samples. However, these approaches typically focus on sample generation and feature synthesis, often overlooking the in-depth modeling of causal mechanisms and factors. To better explore the relationships between causal factors, Fangrui Lv et al.⁴⁷ introduced an intervention-based Causal Independence Representation Learning (CIRL) method into Domain Generalization (DG). This method explicitly models causal factors using dimensional representations based on theoretical formulations, while relying on more general causal structures without restrictive assumptions.

Our proposed approach is similar to CIRL in its use of intervention-based causal decomposition. However, we reinforce the condition of causal independence during the extraction of causal factors by employing distribution matching techniques to ensure strict independence between factors. In short, our method places greater emphasis on maintaining independence among causal factors.

Statistical independence

Statistical independence describes a lack of any relationship between two events or random variables, meaning that the occurrence or value of one does not affect the occurrence or value of the other⁴⁸. It is commonly expressed as $P(A \cap B) = P(A) \cdot P(B)$, where A and B are two events. Since the assumption of independence contributes to building more robust and generalizable models, testing for feature or factor independence is crucial in domain generalization. Common methods for testing independence include the Chi-Square Test⁴⁹, Spearman and Kendall correlation coefficients⁵⁰, and Mutual Information⁵¹. However, in domain generalization using causal inference, independence testing is often less rigorous. For example, CIRL uses simple correlation tests, which do not fully ensure independence between elements, as statistical uncorrelatedness does not imply independence.

For normally distributed random variables, independence and uncorrelatedness are equivalent. If two random variables X and Y follow a joint normal distribution (i.e., their joint distribution is a bivariate normal distribution), then independence and uncorrelatedness are equivalent. Therefore, our model enhances feature independence by matching the distribution to a normal form after removing correlations, ensuring strict independence between elements.

Methods

In this section, we consider Domain Generalization (DG) from the perspective of independent causal factors, adopting a general structural causal model as shown in Fig. 1. Previous studies have demonstrated^47,52,53 that the intrinsic causal mechanisms (formalized as conditional distributions) are identifiable given the causal factors, and mature frameworks exist for learning causal representations based on the properties of these factors. However, since associations between causal factors may lead to misleading outcomes, we aim for complete independence between the factors when they occur. Therefore, we propose learning causal representations based on the properties of independent causal factors, serving as a mimic while retaining strong generalization capabilities.

Figure 3

ICRL framework. The causal intervention module generates augmented images by intervening on non-causal factors. Both the original and augmented image representations are fed into the decomposition module, which applies a decomposition loss to enforce separation between causal and non-causal factors. The disentangled factors are then processed by the Independence module to ensure they follow a normal distribution. Finally, the Adversarial Masking module performs an adversarial task between the generator and the masker, ensuring that the learned representations possess sufficient causal information for classification.

Causal independence from the perspective of statistical independence

In statistics, proving the independence of two random variables or events typically relies on the relationship between their joint and marginal distributions. The most common method is the direct calculation approach: first, the joint distribution of random variables X and Y, $P(X=x, Y=y)$, is computed, followed by the marginal distributions $P(X=x)$ and $P(Y=y)$. If the product of the marginal distributions equals the joint distribution, i.e., $P(X=x, Y = y) = P(X = x) \cdot P(Y=y)$, then X and Y are proven to be independent.

However, in practical causal inference, it is often challenging to accurately obtain the joint distribution, making it difficult to directly determine independence between X and Y. Therefore, we use correlation coefficients to assess the independence of causal factors. If the correlation coefficient is zero and X and Y follow a normal distribution, then they are independent. We assume that X and Y are jointly normally distributed random variables. According to the definition of a bivariate normal distribution, the joint distribution of X and Y is given by:

$$\begin{aligned} \begin{pmatrix} X \\ Y \end{pmatrix} \sim {\mathscr {N}} \left( \begin{pmatrix} \mu _X \\ \mu _Y \end{pmatrix}, \begin{pmatrix} \sigma _X^2 & \rho \sigma _X \sigma _Y \\ \rho \sigma _X \sigma _Y & \sigma _Y^2 \end{pmatrix} \right) \end{aligned}$$

(1)

For the joint normal distribution of X and Y, the joint probability density function (PDF) is:

$$\begin{aligned} f_{X,Y}(x,y) = \frac{1}{2\pi \sigma _X \sigma _Y \sqrt{1-\rho ^2}} \exp \left( - \frac{1}{2(1-\rho ^2)} \left( \frac{(x-\mu _X)^2}{\sigma _X^2} + \frac{(y-\mu _Y)^2}{\sigma _Y^2} - 2 \rho \frac{(x-\mu _X)(y-\mu _Y)}{\sigma _X \sigma _Y} \right) \right) \end{aligned}$$

(2)

Here, $\rho$ represents the correlation coefficient. When X and Y are uncorrelated, $\text {Cov}(X, Y) = 0$, implying $\rho = 0$. In this case, the joint PDF simplifies to:

$$\begin{aligned} f_{X,Y}(x,y) = \frac{1}{2\pi \sigma _X \sigma _Y} \exp \left( - \frac{(x-\mu _X)^2}{2 \sigma _X^2} \right) \exp \left( - \frac{(y-\mu _Y)^2}{2 \sigma _Y^2} \right) \end{aligned}$$

(3)

This can be viewed as the product of the PDFs of two independent normal distributions:

$$\begin{aligned} f_{X,Y}(x,y) = f_X(x) \cdot f_Y(y) \end{aligned}$$

(4)

where

$$\begin{aligned} f_X(x) = \frac{1}{\sqrt{2\pi \sigma _X^2}} \exp \left( - \frac{(x-\mu _X)^2}{2\sigma _X^2} \right) , \quad f_Y(y) = \frac{1}{\sqrt{2\pi \sigma _Y^2}} \exp \left( - \frac{(y-\mu _Y)^2}{2\sigma _Y^2} \right) \end{aligned}$$

(5)

According to the definition of independence, if the product of the marginal distributions equals the joint distribution, i.e., $P(X=x, Y=y) = P(X=x) \cdot P(Y=y)$, then X and Y are independent.

Causal factor normalization based on the GAN model

Traditional normalization techniques, such as Box-Cox or logarithmic transformations, often perform poorly when applied to high-dimensional data. In contrast, GAN models excel at handling high-dimensional and complex structured data, enabling them to capture intricate distributions in high-dimensional spaces⁵⁴. Thus, we designed a GAN model to ensure that the causal factor X follows a normal distribution. For a set of causal factors X and an outcome variable Y, our goal is for the GAN to generate a normalized causal factor $X'$, such that $X'$ follows a normal distribution while preserving its causal relationship with Y.

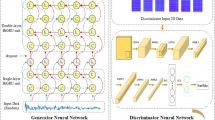
As shown in Fig. 3, the GAN model consists of a generator G that takes a noise vector z as input and produces the causal factor $X' = G(z)$. The discriminator D is trained to distinguish between the real causal factors X and the generated ones $X'$. The discriminator’s objective is to output a decision that separates the generated causal factors from the true ones. The overall optimization objective for the GAN is:

$$\begin{aligned} \min _G \max _D V(D, G) = {\mathbb {E}}_{x \sim p_x}[\log D(X)] + {\mathbb {E}}_{z \sim p_z} \left[ \log \left( 1 - D(G(z)) \right) \right] \end{aligned}$$

(6)

To ensure that the generated causal factors $X'$ follow a normal distribution, we introduce a normalization constraint in the generator’s optimization process. The additional normal distribution loss term is defined as:

$$\begin{aligned} L_{\text {normal}}({\hat{X}}) = \sum _{i=1}^n \left( \frac{({\hat{X}}_i - \mu )^2}{2\sigma ^2} \right) - \log (\sigma ) \end{aligned}$$

(7)

where $\mu$ and $\sigma$ represent the mean and standard deviation of the normal distribution. Accordingly, the generator’s objective function is modified to:

$$\begin{aligned} \min _G \max _D V(D, G) + \lambda L_{\text {normal}}({\hat{X}}) \end{aligned}$$

(8)

Here, $\lambda$ is a regularization coefficient that balances the GAN loss with the normal distribution loss. During optimization, the generator gradually learns to produce causal factors ${\hat{X}} = G(z)$ that approximate the normal distribution ${\mathscr {N}}(\mu , \sigma ^2)$. This means that as the training progresses, the optimization will force the generator to output causal factors that conform to the normal distribution. Additionally, $\sigma$ serves as a lower bound to ensure the data follows the specified distribution (guaranteed through training the discriminator), making this approach an unbiased estimator that can be further applied to causal inference.

Independent causal representation learning

In this section, we present a representation learning algorithm inspired by the concept of independent causal relationships. Briefly, the algorithm first applies Fourier transform to intervene and separate causal factors, followed by normalization. A designed GAN model is then used to transform the intervened factors into a normal distribution while ensuring zero correlation between them. Finally, a masked attention mechanism is employed to extract causal information from sub-dimensions, allowing for a more effective representation. The overall framework is depicted in Fig. 3.

Causal separation module

The first step is to intervene on the causal factors, separating the causal factor S from the non-causal factor U. In most cases, directly extracting causal factors is challenging due to the complexity of data transformations or non-linear mappings in the causal factor extractor $g(\cdot )$. Therefore, we leverage the Fourier transform module proposed by Xu⁵⁵ to capture non-causal factors, as illustrated in Fig. 4.

Figure 4

Fourier transform to separate causal factors.

Based on the characteristics of the Fourier transform: the phase component retains the high-order statistical information of the original signal, while the amplitude component contains classical statistical information^56,57. For the input image $x^0$, its Fourier transform is expressed as:

$$\begin{aligned} {\mathscr {F}}(x^0) = {\mathscr {A}}(x^0) \times e^{-j {\mathscr {P}}(x^0)} \end{aligned}$$

(9)

where ${\mathscr {A}}(x^0)$ and ${\mathscr {P}}(x^0)$ represent the amplitude and phase components, respectively. Using the FFT algorithm, the Fourier transform ${\mathscr {F}}(x^0)$ and its inverse ${\mathscr {F}}^{-1}(x^0)$ can be efficiently computed⁵⁸. We then perform linear interpolation on the amplitude information between the original image $x^0$ and a randomly sampled image from any source domain $\hat{x^0}$:

$$\begin{aligned} \hat{{\mathscr {A}}}(x^0) = (1 - \lambda ) {\mathscr {A}}(x^0) + \lambda {\mathscr {A}}(\hat{x^0}) \end{aligned}$$

(10)

where $\lambda \sim U(0, 1)$ controls the degree of perturbation. The perturbed amplitude is combined with the original phase component, and the enhanced image $\hat{x^0}$ is obtained by applying the inverse Fourier transform:

$$\begin{aligned} {\mathscr {F}}(\hat{x^0}) = \hat{{\mathscr {A}}}(x^0) \times e^{-j {\mathscr {P}}(x^0)}, \quad \hat{x^0} = {\mathscr {F}}^{-1}({\mathscr {F}}(\hat{x^0})) \end{aligned}$$

(11)

The representation generator implemented via a CNN model is denoted as $g(\cdot )$, where $r = g(\cdot ) \in {\mathbb {R}}^{1 \times N}$, with N being the dimensionality. To maintain the invariance of the causal factor S despite the intervention on U, the optimization of g is performed to enforce consistent representation across the intervention:

$$\begin{aligned} \max _g \sum _{i=1}^{B} \text {COR}(r_i^0, {\hat{r}}_i^0), \quad r_i^0 \text { and } {\hat{r}}_i^0 \text { represent the normalized z-scores} \end{aligned}$$

(12)

where ${\hat{r}}^0_i$ and ${\hat{r}}^a_i$ denote the Z-score normalized i-th column of $R^0 = \left[ (r^0_1)^T, \ldots , (r^0_B)^T \right] ^T \in {\mathbb {R}}^{B \times N}$ and $R^a = \left[ (r^a_1)^T, \ldots , (r^a_B)^T \right] ^T$, respectively, $B \in {\mathbb {Z}}_+$ is the batch size, $r^0_i = {\hat{g}}(x^0_i)$ and $r^a_i = {\hat{g}}(x^a_i)$ for $i \in \{1, \ldots , B\}$. And the COR function measures the correlation between representations before and after intervention, achieving the separation of causal and non-causal factors.

Causal independence module

In the process of ensuring independence of causal factors, we strictly adhere to the definition of independence outlined in Sect. 3.1. Therefore, it is necessary to ensure that any two dimensions of the representation are mutually independent:

$$\begin{aligned} \min _g \frac{1}{N(N-1)} \sum _{i \ne j} \text {COR}(r_i^0, r_j^0), \quad i \ne j \end{aligned}$$

(13)

We then employ a GAN model to maintain the normal distribution of the factors. To select the most suitable GAN model, we designed and compared three different types: Vanilla GAN⁵⁹, Wasserstein GAN⁶⁰, and Wasserstein GAN with Gradient Penalty⁶¹. Based on the comparison, the most appropriate GAN model was selected. The loss functions for the three GAN models were defined in Sect. 3.2.

(1) Vanilla GAN

In the context of Vanilla GANs, the loss functions for the generator and discriminator can be expressed as follows:

The objective of a GAN is for the generator to produce a distribution that closely resembles the distribution of real data. The discriminator’s role is to differentiate between real and generated data. The loss function is defined as:

$$\begin{aligned} {\mathscr {L}}_{\text {Vanilla GAN}} = {\mathbb {E}}_{r \sim p_{\text {data}}(r)}[\log D(r)] + {\mathbb {E}}_{z \sim p_z(z)} \left[ \log \left( 1 - D(G(z)) \right) \right] \end{aligned}$$

(14)

where $z$ represents the input noise to the generator, typically sampled from a normal distribution.

(2) Wasserstein GAN

The core idea of Wasserstein GAN (WGAN) is to use the Wasserstein distance to measure the discrepancy between the generated data distribution and the true data distribution. This approach enhances training stability and addresses the gradient vanishing problem commonly encountered in Vanilla GANs. The loss function is defined as follows:

$$\begin{aligned} {\mathscr {L}}_{\text {WGAN}} = {\mathbb {E}}_{r \sim p_{\text {data}}(r)}[D(r)] - {\mathbb {E}}_{z \sim p_z(z)}[D(G(z))] \end{aligned}$$

(15)

In WGAN, the discriminator is referred to as the “critic” because it outputs a score rather than a probability.

(3) Wasserstein GAN with Gradient Penalty

WGAN-GP improves upon WGAN by incorporating a gradient penalty term to ensure a closer approximation of the Wasserstein distance between the generated distribution and the real distribution. The loss function is defined as follows:

$$\begin{aligned} {\mathscr {L}}_{\text {WGAN-GP}} = {\mathbb {E}}_{r \sim p_{\text {data}}(r)}[D(r)] - {\mathbb {E}}_{z \sim p_z(z)}[D(G(z))] + \lambda {\mathbb {E}}_{{\hat{r}} \sim p_{{\hat{r}}}}\left[ \left\| \nabla D({\hat{r}}) \right\| _2^2\right] \end{aligned}$$

(16)

where ${\hat{r}}$ is a sample obtained through interpolation between the real data distribution and the generated data distribution.

To ensure that the loss conforms to a normal distribution, we apply a normal distribution loss directly to the output of the generator. This can be achieved by minimizing the proximity of the generator’s output mean and standard deviation to the desired values, as well as ensuring the difference aligns with a unit variance.

$$\begin{aligned} {\mathscr {L}}_{\text {Normal}} = \frac{1}{2} \left( (\mu _G - \mu _0)^2 + (\sigma _G - 1)^2 \right) \end{aligned}$$

(17)

Ultimately, the loss function can be expressed as a combination of the GAN loss and the normal distribution loss:

$$\begin{aligned} {\mathscr {L}}_{\text {lid}} = {\mathscr {L}}_{\text {GAN}} + \beta {\mathscr {L}}_{\text {Normal}} \end{aligned}$$

(18)

where ${\mathscr {L}}_{\text {GAN}}$ represents the loss function of any of the aforementioned GAN models, and $\beta$ is a hyperparameter used to balance the two components of the loss. This formulation effectively combines the normal distribution loss with the losses from the three types of GAN models.

After achieving complete independence of the features, we conduct a feature analysis. Based on previous literature, we introduce a causal decomposition loss function ${\mathscr {L}}_{\text {Fac}}$, expressed as:

$$\begin{aligned} {\mathscr {L}}_{\text {Fac}} = \frac{1}{2} \left\| \frac{ \langle {\hat{r}}^0_i, {\hat{r}}^a_j \rangle }{ \Vert {\hat{r}}^0_i \Vert \Vert {\hat{r}}^a_j \Vert } - ||\xi _{i,j}||_2 \right\| _2, \quad i, j \in \{1, 2, \ldots , N\} \end{aligned}$$

(19)

For the same dimensions of $R^0$ and $R^a$, the objective is to maximize their correlation; for different dimensions, the goal is to minimize the correlation.

Adversarial encoding module

In multiple source domains, while using monitoring labels y, we cannot guarantee that every dimension of the learned representations corresponds to causal factors for the classification $X \rightarrow Y$. Specifically, there may exist lower-dimensional representations that carry causal information with minimal correlation. Therefore, dimensions with higher correlation require reinforcement to enhance their impact. With the assistance of our independent causal model, the dimensions should also be joint, allowing us to select sub-dimensions that contain diverse new causal information not found in the remaining dimensions, thereby enriching the overall representation. Consequently, we utilize a specially designed adversarial encoding module. By constructing a mask based on a neural network, we represent the learning responsibility of each dimension with $w'$ and define $\epsilon \in (0, 1)$ to indicate which dimensions are optimal while the rest are considered inferior:

$$\begin{aligned} m = \text {Gumbel} - \text {Softmax}({\hat{w}}(r), kN) \in {\mathbb {R}}^N \end{aligned}$$

(20)

Here, we sample from a mask close to a value of 1 for kN, utilizing the commonly used differentiable GumbelSoftmax technique⁶². By multiplying the learned mask with the obtained masks $h_1$ and $1-m$, we can obtain the respective masks for the dimensional values. These masks are then input into two different classifiers, $h_1$ and $h_2$. The loss functions for the optimal and suboptimal representations are defined as follows:

$$\begin{aligned} {\mathscr {L}}^{\sup }_{\text {cls}}= & \ell (h_1(r^0 \odot m^0), y) + \ell (h_1(r^a \circ (1 - m^0)), y), \end{aligned}$$

(21)

$$\begin{aligned} {\mathscr {L}}^{\inf }_{\text {cls}}= & \ell (h_2(r^0 \odot m^1), y) + \ell (h_2(r^a \circ (1 - m^1)), y). \end{aligned}$$

(22)

We optimize the mask by minimizing ${\mathscr {L}}^{\sup }_{\text {cls}}$ and maximizing ${\mathscr {L}}^{\inf }_{\text {cls}}$, while also minimizing the overall loss to generate the models and classifiers $h_1$ and $h_2$.

In summary, our objective is:

$$\begin{aligned} \min _{{\hat{g}}, h_1, h_2} {\mathscr {L}}^{\sup }_{\text {cls}} + {\mathscr {L}}^{\inf }_{\text {cls}} + {\mathscr {L}}_{\text {Fac}} + {\mathscr {L}}_{\text {id}}. \end{aligned}$$

(23)

Experiments

Datasets

In practical applications, numerous challenges arise in the recognition of various digits and objects. To demonstrate that our improved model effectively enhances recognition accuracy of identical items across different environments, we evaluate it on two publicly available datasets: Digits-DG⁶³ and PACS⁶⁴. The Digits-DG dataset includes four subsets-MNIST⁶⁵, MNIST-M⁶⁶, SVHN⁶⁷, and SYN⁶⁵-which feature variations in font styles, backgrounds, and stroke colors. For each domain, we randomly select 300 images per class, splitting the data into 80% for training and 20% for validation. For object recognition, we use the PACS dataset, which encompasses four distinct domains: Art-Painting, Cartoon, Photo, and Sketch. These domains contain seven categories: dog, elephant, giraffe, guitar, house, horse, and person. To ensure a fair comparison with baseline models, we adhere to the original train-validation splits provided by⁵³ when testing the model on this dataset.

Implementation details

Following the commonly used leave-one-domain-out protocol⁶⁴, we designate one domain as the unseen target domain for evaluation while training on the remaining domains. Based on previous experimental findings, for Digits-DG, all images are resized to 32$\times$32, and the network is trained from scratch using mini-batch SGD with a batch size of 128, momentum of 0.9, and weight decay of 5e-4 for 50 epochs. The learning rate is reduced by a factor of 0.1 every 20 epochs. For PACS, all images are resized to 224$\times$224. The network is trained from scratch for 50 epochs using mini-batch SGD with a batch size of 16, momentum of 0.9, and weight decay of 5e-4, with the learning rate decaying by a factor of 0.1 at 80% of the total epochs. The hyperparameters $\kappa$ and $\tau$ are selected based on the results from the source domain validation set, as the target domain is not accessible during training. Specifically, we set $\kappa = 60\%$ for Digits-DG and PACS, and $\kappa = 80\%$ for Office-Home. The $\tau$ value is set to 2 for Digits-DG and 5 for the other datasets. All results are reported as the average accuracy over three independent runs.

Experimental results

The results on the Digits-DG dataset are presented in Table 1, where ICRL outperforms all compared baselines in terms of average accuracy. Notably, ICRL exceeds the performance of domain-invariant representation methods such as CCSA⁶⁸ and MMD-AAE⁶⁹ by 8.5% and 8.4%, respectively, highlighting the importance of uncovering the inherent causal mechanisms between data and labels rather than relying on superficial statistical dependencies. Furthermore, we compare ICRL with CIRL⁴⁷, as both methods utilize similar causal intervention classification and adversarial masking modules. ICRL surpasses CIRL by 0.5%, indicating that enforcing strict mutual independence across the disentangled features of an image further enhances the effectiveness of extracting the intrinsic causal relationships between data and labels. This provides additional validation of the effectiveness of our approach.

Table 1 The results of excluding one domain as the target domain for evaluation on the Digits-DG dataset.

The results on the PACS dataset were obtained using three different GAN models based on ResNet-18 and ResNet-50, as shown in Tables 2 and  3, respectively. It can be observed that the WGAN method outperforms both Vanilla GAN and WGAN-GP, achieving significantly better performance by 4.22% on ResNet-18 and 1.45% on ResNet-50. Additionally, when comparing ICRL with CIRL, which does not strictly enforce causal independence, ICRL shows a slight improvement, outperforming CIRL by 1.06% on ResNet-18 and 0.72% on ResNet-50.

Table 2 The results of evaluating ResNet-18 on the PACS dataset by excluding one domain as the target domain.

Table 3 The results of evaluating ResNet-50 on the PACS dataset by excluding one domain as the target domain.

Vanilla GAN employs the Jensen-Shannon (JS) divergence to measure the difference between the generator’s distribution and the real distribution. However, in practice, the JS divergence tends to a constant when the two distributions have little overlap, leading to vanishing gradients and preventing the generator from updating effectively, thus making the training unstable or prone to collapse. WGAN addresses this issue by replacing the JS divergence with the Wasserstein distance (Earth Mover’s Distance), which offers smoother gradients when the generator’s distribution approaches the real distribution, thereby mitigating the vanishing gradient problem and stabilizing the training process. As a result, WGAN outperforms Vanilla GAN. Moreover, since the data used to train the Vanilla GAN models in this experiment were randomly sampled from a normal distribution within the range of [− 1,1], and WGAN does not require the complexity of gradient penalties on simple data, it performed better than WGAN-GP. Despite using simple random data to train the Vanilla GAN models, our model still performed slightly better than causal representation models without strict independence enforcement. Overall, this demonstrates the advantage of independent causal features.

Experimental analysis

Ablation study

We analyze the impact of the Causal Intervention (CInt.), Causal Independence (CIid.), and Adversarial Masking (AdvM.) modules within CIRL. Table 4 presents the results of different ICRL variants on the PACS dataset using ResNet-18 as the backbone. By comparing variants 1, 2, and 3, we can observe the varying degrees of influence each component has on the model’s performance. This demonstrates that the degree of independence between causal factors significantly affects overall model performance, while the CInt., CIid., and AdvM. modules are interdependent and equally essential for optimal results.

Table 4 Ablation study of ICRL on the PACS dataset using ResNet-18.

Visual explanation

To intuitively validate the claim that ICRL representations can model causal factors, we applied the visualization technique from⁷⁸ to generate attention maps for the last convolutional layer of both the baseline method (DeepAll) and CIRL. The results, shown in Fig. 5, demonstrate that ICRL focuses more on specific regions compared to the baseline, learning representations that are more closely associated with the target class. For instance, in the case of the guitar, the ICRL model places greater emphasis on the guitar body, while CIRL still focuses on the entire guitar (both body and neck), lacking attention to specific parts.

Figure 5

Visualization of the attention maps from the final convolutional layer on the PACS dataset.

Independence of causal representations

To intuitively demonstrate the effectiveness of our causal independence approach, we use $\Vert C \Vert ^2_F = \Vert \text {diag}(C) \Vert ^2$ as a metric, where smaller values indicate greater independence. Here, C represents the correlation matrix. The results, as shown in Fig. 6, clearly illustrate that on both ResNet-18 and ResNet-50, ICRL achieves better independence throughout the entire training process compared to CIRL, validating the effectiveness of the causal independence module we designed. Additionally, the differences in independence among Vanilla GAN, WGAN, and WGAN-GP can be observed in the figure. Consistent with the model performance, WGAN demonstrates a significantly higher degree of causal independence compared to Vanilla GAN and WGAN-GP. This is because WGAN incorporates the Wasserstein distance to measure the difference between the real and generated distributions, unlike Vanilla GAN, which uses the Jensen-Shannon divergence. The Wasserstein distance prevents the vanishing gradient problem during optimization, leading to more stable training. Consequently, WGAN is better able to approximate a normal distribution, ensuring that each causal factor corresponds to a normal distribution, thus achieving independence among the factors. In contrast, WGAN-GP introduces a gradient penalty to enforce the Lipschitz continuity of the discriminator, which requires constraining the critic’s gradients at each training step. This constraint may affect the model’s parameter updates, especially in simpler tasks where the gradient penalty may excessively restrict the generator’s freedom, leading to an overly cautious training process. In this experiment, as we only need to generate and fit a simple standard normal distribution, such excessive regularization can cause overfitting due to the overly conservative training approach. Therefore, WGAN, which fits causal factors to a normal distribution, yields the best independence results in this experiment, thus enhancing the model’s overall domain generalization ability.

Figure 6

Independence of causal representations evaluated on the PACS dataset with Sketch as the unseen target domain, using ResNet-18.

Figure 7

Sensitivity of CIRL to hyperparameters $\tau$ and $\kappa$ evaluated on the PACS dataset with Sketch as the unseen target domain, using ResNet-18.

Table 5 Efficiency comparison between CIRL and ICRL equipped with different GAN models.

Parameter sensitivity

Figure 7 illustrates the sensitivity of CIRL to hyperparameters $\tau$ and $\kappa$, where $\tau \in \{2.0, 4.0, 6.0, 8.0, 10.0\}$ and $\kappa \in \{0.4, 0.5, 0.6, 0.7, 0.8, 0.9\}$. It can be observed that CIRL achieves robust competitive performance with ResNet-18 as the backbone when $4.0 \le \tau \le 10.0$ and $0.7 \le \kappa \le 0.9$, further validating the stability of our approach.

Efficiency comparison

Table 5 presents the average runtime comparison of three models, each incorporating different GAN variants, on ResNet-18 and ResNet-50. The results show that the average runtime across the four domains follows the order: Vanilla GAN < WGAN < WGAN-GP. Additionally, the ICRL models using Vanilla GAN and WGAN demonstrate shorter average runtimes compared to CIRL. In terms of performance, the ICRL model with WGAN outperforms those with Vanilla GAN and WGAN-GP, making WGAN an ideal choice for handling causal independence within the ICRL framework.

Discussion

This paper introduces ICRL model for domain generalization, with a focus on ensuring the independence of causal features in deep learning models. The experimental results demonstrate that ICRL significantly outperforms several baseline models, including domain-invariant representation methods and CIRL approach. These findings underscore the critical role of independent causal feature representations in improving out-of-distribution generalization.

One of the key contributions of this work is the incorporation of strict independence among causal features, a crucial factor often overlooked in prior domain generalization and causal representation learning methods. By enforcing feature independence through a carefully designed GAN-based approach, our model effectively addresses the issue of spurious correlations that often compromise the generalization ability of machine learning models. This advancement is particularly evident in our comparison with CIRL, where ICRL outperformed the latter by a modest but meaningful margin, particularly in tasks involving complex domain shifts. This suggests that enforcing independence not only aids in capturing more accurate causal features but also enhances the model’s robustness when exposed to previously unseen domains.

Additionally, the use of Wasserstein GAN (WGAN) in the ICRL framework proved to be beneficial, offering superior performance compared to other GAN variants like Vanilla GAN and WGAN-GP. The ability of WGAN to provide more stable gradients during training was pivotal in achieving the desired causal independence in the learned representations, further validating the role of WGAN in domain generalization tasks.

Our model’s strong performance across multiple datasets, including Digits-DG and PACS, provides compelling evidence of its utility in real-world domain generalization scenarios. Notably, ICRL’s ability to generalize across diverse domains-such as handwritten digits, artistic styles, and photos-demonstrates its potential to solve a variety of practical machine learning challenges. Furthermore, the results from our ablation study highlight the importance of each component in the ICRL framework, particularly the Causal Intervention and Causal Independence modules, which work synergistically to achieve enhanced performance.

Despite these strengths, there are still limitations to the current work. While the current framework’s dependence on GAN models for distribution matching introduces computational overhead, which could impact scalability when working with very large datasets or real-time applications. This concern becomes even more significant when applying ICRL to high-dimensional data, where the computational costs of ensuring feature independence may become prohibitively large.

Moreover, while ICRL has demonstrated clear advantages in image-related tasks, its applicability in other domains, such as text classification, presents unique challenges. Text data, being sequential and highly context-dependent, requires more nuanced treatment of causal relationships. For instance, in tasks such as sentiment analysis or topic modeling, the structure of sentences, specific keywords, and the broader context play a critical role in determining the label. However, unlike images, where features can be relatively independent, text data inherently involves complex dependencies among words that may complicate the task of ensuring feature independence. In sentiment analysis, for example, individual words might not have a clear causal influence, but only in specific contexts do they form causal relationships. This makes ensuring causal feature independence while preserving contextual meaning more challenging in text classification tasks than in image tasks.

Furthermore, ICRL uses Generative Adversarial Networks (GANs) to transform features into a normal distribution for distribution matching. While this works well in image-based tasks, text representations-particularly when using word embeddings or other forms of vector representations-do not always conform to a normal distribution. The inherent ambiguity and contextual dependencies in language can complicate the process of ensuring both feature independence and contextual relevance. Consequently, adapting ICRL for optimizing text classification tasks remains a significant direction for future research.

Future work could explore ways to ensure causal feature independence while reducing computational costs. Additionally, extending the current method to handle more complex causal structures in multimodal data, such as text, could further enhance the model’s applicability across a variety of machine learning tasks.

Conclusion

This paper highlights the limitations of previous causal representation learning approaches in handling factor independence. We design a WGAN model to enforce a normal distribution on features. Furthermore, we propose the ICRL framework to learn causal representations, emphasizing the independent causal factors with desirable properties. Comprehensive experiments demonstrate the effectiveness and superiority of ICRL.