Introduction

Research background and motivations

With the rapid advancement of technology, Artificial Intelligence (AI) is gradually permeating various aspects of social life, and the field of education is no exception. In sports dance teaching, traditional "one-on-one" or "one-to-many" instructional models, while possessing certain unique advantages, struggle to address challenges such as significant individual differences among students and limited teaching resources1,2,3. In recent years, the rise of AI and the continuous development of deep learning technologies, particularly the graph convolutional network (GCN), as an emerging neural network model, have provided new approaches to tackling complex graph data analysis tasks. GCN is capable of capturing the relationships between nodes and edges in graph structures and effectively extracting features from nodes, making it highly promising in the field of motion capture and recognition. The importance of motion capture technology in sports dance is self-evident. By accurately capturing and analyzing dancers’ movements, both instructors and dancers can better understand their performance, identify issues in a timely manner, and make targeted adjustments and improvements4,5,6. As a specialized neural network model, GCN efficiently handles graph-structured data by transmitting and aggregating features from nodes and edges, enabling feature extraction from nodes7,8,9. Additionally, Siamese neural network (SNN), a deep learning technique, offers new insights and methods for personalized guidance in sports dance teaching.

In recent years, the rapid development of technologies such as object detection and spatiotemporal feature fusion has further driven the application of intelligent analysis. For instance, Dong et al.10 proposed an adaptive feature fusion network combining Convolutional Neural Network (CNN) and Transformers. By employing an innovative local–global feature fusion strategy, this network improved the detection performance of small targets in complex environments. Experimental results show that the model achieved an average accuracy of 91.17% and a detection accuracy of 70.18% for distant small targets. Additionally, it possessed real-time detection capabilities, and demonstrated excellent generalization and efficiency. In another study, Dong et al.11 introduced a bird’s-eye view object detection network based on spatiotemporal feature fusion. By circulating historical information, using a deformable aggregation module, and applying a BEV self-attention mechanism, this network enhanced 3D object detection performance in complex scenarios. These research outcomes provide valuable insights for the intelligent development of motion capture and recognition in sports dance teaching. They also demonstrate that integrating various feature fusion techniques with deep learning models can more effectively address data analysis challenges in complex settings.

Sports dance, as an activity that integrates both athleticism and artistry, demands high levels of physical fitness, technical skill, artistic expression, and psychological resilience from dancers12,13. In traditional teaching models, instructors typically rely on their experience and observations to evaluate students’ dance skills and develop teaching plans accordingly. However, this approach is limited by the instructor’s expertise, teaching experience, and subjective judgment, making it difficult to provide comprehensive, objective, and personalized guidance. Moreover, with increasing numbers of students, it becomes challenging for instructors to offer detailed guidance and feedback to each individual, leading to inconsistent teaching outcomes.

SNN, as a unique neural network architecture, learns by comparing the similarity between two input samples and excels at feature extraction and similarity measurement14,15,16. This characteristic has led to its widespread application in areas such as image recognition, facial recognition, and signature verification. In sports dance teaching, SNN can be applied to the analysis and evaluation of dance movements17. By comparing students’ dance movements with standard movements or exemplary performances, SNN enables an objective assessment of students’ dance proficiency and provides personalized guidance based on the evaluation.

Research objectives

The technical challenges that may arise when applying SNN for personalized guidance in sports dance, such as difficulties in data collection, the complexity of model training, and the need for privacy protection, are thoroughly explored. To address these challenges and issues, the introduction of AI, specifically SNN technology, offers new approaches and methodologies for sports dance teaching. This innovation facilitates the optimized allocation of teaching resources and enhances teaching quality. By incorporating SNN technology within the context of AI into the field of sports dance education, the work holds significant theoretical and practical value. On the theoretical level, it contributes to enriching and refining the application theory of AI technologies in the education sector, promoting innovation and development in educational technology. On the practical level, it offers new insights and methods for sports dance instruction, helping to enhance teaching quality and efficiency, meet the personalized needs of students, and foster the preservation and development of sports dance as an art form.

Literature review

Current research on gesture recognition, motion annotation, and emotion recognition provides valuable reference points for exploring deep learning-assisted dance teaching video generation. These studies have conducted in-depth explorations in areas such as memristor neural networks, motion annotation, and music-dance choreography, and achieved significant results that lay a foundation for the intelligent development of dance education. Research on memristor neural networks has introduced new approaches for intelligent computation and motion feature processing. Wang et al.18 proposed a memristor model with adjustable multistability and developed a memristor-based MFNHNN neural network, revealing its complex dynamic behavior. By implementing an equivalent circuit and designing an image encryption scheme, they validated its superior performance in remote sensing information security. Sun et al.19 introduced a memristor-based LSTM fault diagnosis parallel computation optimization method, and designed four functional modules integrated into a memristor circuit. Experimental results show that the model achieved an accuracy of 98%, significantly enhanced fault diagnosis performance and demonstrated the potential of memristors in optimizing intelligent computing hardware. These studies not only highlight the potential of memristors in intelligent computing but also provide theoretical support for hardware optimization in the field of dance motion recognition.

Significant progress has been made in the field of dance motion annotation and generation. Liu et al.20 developed an automatic dance video annotation method based on foot posture analysis, which identified different dance movements and automatically labeled them, enabling efficient processing and management of dance videos. Feng et al.21 introduced a method called DeepDance for music-dance motion choreography using adversarial learning to generate dance movements. By converting music into dance motion sequences and optimizing them with a Generative Adversarial Network (GAN), the method produced dance choreography synchronized with the rhythm and emotion of the music. Wang et al.22 proposed a model named GraphGAN, a graph convolutional adversarial network for generating realistic dance movements from audio. The model mapped audio features onto a graph structure and used adversarial learning to generate dance motions, enabling the conversion of audio into dance sequences. Additionally, Sun and Wu23 introduced a dance movement design method based on a 3D computer-aided system. This method used computer-aided design technology to precisely design and optimize dance movements, providing a reliable tool for dance creation and performance.

Although the aforementioned research has made significant strides in dance motion recognition and generation, there are still some shortcomings. Most of the existing dance motion annotation and generation methods focus on a single dimension (such as rhythm or foot movements), without fully integrating the spatial layout and temporal similarity features of the motion. Moreover, current dance generation techniques often rely on adversarial learning models. Although capable of generating realistic dance movements, they lack an in-depth analysis of the spatiotemporal dependencies in skeletal motion. In contrast, the proposed GCN-SNN model combines the spatial feature capture capability of GCN and the temporal similarity analysis advantage of SNN, enabling a more comprehensive modeling of the spatiotemporal features of dance movements. This not only improves the accuracy of motion recognition but also provides stronger support for personalized guidance in dance teaching videos, offering a new direction for research in this field.

Research methodology

Action recognition in sports dance teaching

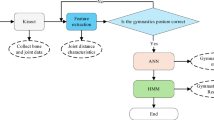
The primary approach for human motion recognition involves detecting human movement information in a computer environment, extracting symbolic action information, and then identifying and understanding the corresponding motion features to classify human behaviors. Human motion recognition can be divided into three main components: motion detection, motion feature extraction, and motion feature interpretation24,25,26. Figure 1 illustrates the typical process of motion feature interpretation. In static images, the human foreground is segmented, while in dynamic videos, motion sequences are segmented. In static images, action detection primarily relies on image segmentation techniques. These techniques divide an image into several sub-regions based on specific criteria and automatically halt once the segmentation is complete. The primary function of image segmentation is to isolate parts of the human actions within the image, simplifying subsequent operations.

Fig. 1
figure 1

Basic process of action recognition.

Full size image

A common approach for action segmentation utilizes direct clustering-based segmentation. This method first extracts features from video frames, such as position, velocity, acceleration, and posture, to describe the kinematic characteristics of dance movements. Then, clustering is performed based on the distance relationships between frame features, grouping video frames with similar characteristics into the same category. This process divides the action sequence into multiple subsequences, each corresponding to an independent dance movement27,28.

The K-means clustering algorithm iteratively partitions the data into K clusters, minimizing the distance between data points within each cluster and maximizing the distance between points in different clusters. In action segmentation, the value of K can be pre-defined, representing the expected number of action categories. Hierarchical clustering, on the other hand, does not require pre-specifying the number of clusters. Instead, it builds a hierarchical clustering tree to gradually merge or split clusters, making it more flexible when dealing with an unknown number of action categories.

Sliding-window-based segmentation is a common indirect segmentation method. First, a neural network classifier is trained using a dataset of video clips containing single actions, enabling it to recognize various dance movements. Then, a sliding window is applied to the action sequence to be segmented, and the video segments within the window are sent to the classifier for recognition. If an action category is identified, the sliding window at that time is considered an initial segmentation result. The window then moves by a certain step size, and the new video segments are similarly identified. If the results remain the same, the current window is merged with the previous one to form a new segmentation result. If the results differ, the boundary of the action is considered to be reached, completing the segmentation process. This method leverages action recognition results to guide segmentation, improving both accuracy and robustness. Moreover, the flexibility of the sliding window allows it to adapt to varying lengths of dance movements.

3D reconstruction model for dance movement data

To extract the movement features of the human body, it is essential to detect keypoints from the video data. Here, the open-source tool OpenPose is used for keypoint detection, which can identify human keypoints and their positions from each frame of the video29,30,31. To eliminate the effects of scale and displacement, keypoint data must be normalized. This involves converting the coordinates of each keypoint into relative coordinates based on the center of the body and normalizing these coordinates to a fixed range. In an action recognition system, the primary task of data preprocessing is to ensure that raw data are prepared for subsequent feature extraction and model training. Figure 2 illustrates the specific steps for data preprocessing.

Fig. 2
figure 2

Data preprocessing steps.

Full size image

OpenPose is a deep learning-based real-time system designed for multi-person detection, which identifies keypoints of the human body, hands, face, and limb connections. It is widely used in fields such as action recognition, pose estimation, and human–computer interaction. After detecting the human position, OpenPose further predicts the location of keypoints (joints) on each detected body. These keypoints typically include positions such as the head, shoulders, elbows, wrists, hips, knees, and ankles. Figure 3 illustrates the keypoint locations of the human body as detected by OpenPose. For each joint, OpenPose provides two coordinate values (typically x and y), which represent the position of the joint in the image, along with a confidence score. The confidence score reflects how reliable the model’s prediction is for that keypoint, with higher scores indicating more accurate predictions.

Fig. 3
figure 3

Illustration of human keypoints detected by OpenPose.

Full size image

Each frame’s keypoint data are constructed into a graph structure where nodes represent the keypoints of the human body and edges represent the relationships between these keypoints. Spatial convolution operations are performed to capture the spatial distribution features of the keypoints. The mathematical representation of spatial feature extraction is as follows:

$$X_{t}^{spatial} = SpatialConv\left( {X_{t} } \right)$$
(1)

In this context, \(X_{t}\) represents the input feature matrix at time step t, \(SpatialConv\) denotes the spatial convolution operation, and \(X_{t}^{spatial}\) is the extracted spatial feature matrix. Temporal convolution operations can identify the temporal patterns and trends in the action sequence. The mathematical representation for temporal feature extraction is:

$$X_{t}^{temporal} = TemporalConv\left( {X_{t} } \right)$$
(2)

Here, \(TemporalConv\) represents the temporal convolution operation, and \(X_{t}^{temporal}\) is the extracted temporal feature matrix.

Visual features are obtained through spatial feature extraction, while sensor data features directly provide information such as acceleration and angular velocity. By performing feature fusion, visual features and sensor features are combined to obtain more comprehensive action information. The mathematical representation for multimodal feature fusion is:

$$X_{fused} = concat\left( {X_{visual} ,X_{sensor} } \right)$$
(3)

Here, \(X_{fused}\) represents the fused feature matrix, \(X_{visual}\) is the visual feature matrix, \(X_{sensor}\) is the sensor feature matrix, and \(concat\) denotes the feature concatenation operation.

The dimensionality reduction technique named Principal Component Analysis (PCA) is used to reduce dimensionality by removing redundant features and retaining the most important features for action recognition. The mathematical representation for feature selection and dimensionality reduction is:

$$X_{reduced} = PCA\left( {X_{fused} } \right)$$
(4)

Here, \(X_{reduced}\) represents the feature matrix after dimensionality reduction.

In a sports dance motion capture system, the working principle of the infrared motion capture system involves placing multiple infrared cameras and sensor devices within the capture area. These infrared cameras and sensors can detect infrared light signals from the surrounding environment. During the capture process, special reflective markers are attached to the target. These markers reflect infrared light signals, which are then captured by the infrared cameras. The system calculates the target’s motion trajectory and posture based on the positions and changes of these markers. Figure 4 illustrates the three-dimensional reconstruction of the infrared motion capture system.

Fig. 4
figure 4

The three-dimensional reconstruction of the infrared motion capture system.

Full size image

When the same marker point is captured simultaneously by multiple cameras, there may be errors in the three-dimensional reconstruction data among them. The true position of the marker point is represented as \(P_{r}\), and the true image points are \(R_{1}\) and \(R_{2}\), with the image points identified as \(I_{1}\) and \(I_{2}\) by the system, and \(\delta u\) and \(\delta v\) representing nonlinear distortions. These can be expressed as:

$$u - \Delta u - \frac{{L_{1} x + L_{2} y + L_{3} z + L_{4} }}{{L_{9} x + L_{10} y + L_{11} z + 1}} = \delta u$$
(5)
$$v - \Delta v - \frac{{L_{5} x + L_{6} y + L_{7} z + L_{8} }}{{L_{9} x + L_{10} y + L_{11} z + 1}} = \delta v$$
(6)
$$\sum\limits_{i = 1}^{c} {\delta U_{i} = 0}$$
(7)
$$\sum\limits_{i = 1}^{c} {\delta V_{i} = 0}$$
(8)

c represents the number of cameras. \(\Delta u\) and \(\Delta v\) denote optical errors, and the parameter \(L_{1}\)–\(L_{11}\) indicates the relationship between the image space and object space coordinate systems. The coordinates \(\left( {x,y,z} \right)\) in object space can be computed based on the coordinates \(\left( {u,v} \right)\) in image space.

The basic principle of optimizing three-dimensional reconstruction is to minimize the uncertainty \(\varepsilon\). The calculation equation for \(\varepsilon\) is given by:

$$\varepsilon = \sqrt {\frac{1}{c}\sum\limits_{i = 1}^{c} {\left( {\delta U_{i}^{2} + \delta V_{i}^{2} } \right)} }$$
(9)

The calculation equations for the uncertainty \(\varepsilon_{a}\) and \(\varepsilon_{b}\) corresponding to single marker points and multiple marker points in multi-frame images are as follows:

$$\varepsilon_{a} = \sqrt {\frac{1}{cf} \cdot \sum\limits_{j = 1}^{f} {\sum\limits_{i = 1}^{c} {\left( {\delta U_{ij}^{2} + \delta V_{ij}^{2} } \right)} } }$$
(10)
$$\varepsilon_{b} = \sqrt {\frac{1}{cfp} \cdot \sum\limits_{k = 1}^{p} {\sum\limits_{j = 1}^{f} {\sum\limits_{i = 1}^{c} {\left( {\delta U_{ijk}^{2} + \delta V_{ijk}^{2} } \right)} } } }$$
(11)

\(f\) represents the number of frames and \(p\) denotes the number of marker points.

Dance motion feature recognition based on GCN-SNN

After constructing the skeleton graph, features are extracted from the nodes and edges of the graph using GCN. GCN generates node representations by aggregating features from the node itself and its neighboring nodes. In skeleton-based action recognition, GCN captures spatial relationships and temporal dynamics between joints, thus generating effective action representations. The neighbor set of a node in GCN is unordered and variable. When dealing with the topology of human skeletons, the Laplacian matrix or adjacency matrix can be used to effectively analyze the inherent properties of the human body32,33,34. The spatial graph convolution operator is defined based on the spatial relationships between the node and its neighbor set. A simple computation method is to average the features of the current node and its neighbor set. The graph is represented as \(G = \left\{ {V,E} \right\}\), where \(V\) is the set of nodes and \(E\) is the set of edges. For spatial partitioning, this work divides the neighbor set into three subsets and uses the centroid of joint coordinates as the partition center. The adjacency matrix is set as \(A\) and the degree matrix is set as \(D\). Then, it can be obtained that:

$$D\left( {i,i} \right) = \sum\limits_{j} {A\left( {i,j} \right) + \alpha }$$
(12)
$$A^{norm} = D^{{ - \frac{1}{2}}} AD^{{ - \frac{1}{2}}}$$
(13)

\(D\left( {i,i} \right)\) denotes the diagonal matrix, and the final graph convolution operation can be represented as:

$$f_{out} \left( {v_{i} } \right) = \sum\limits_{{v_{j} \in B_{i} }} {\frac{1}{{z_{ij} }}f_{in} } \left( {v_{j} } \right) \cdot w\left( {l_{i} \left( {v_{j} } \right)} \right)$$
(14)

\(f\left( * \right)\) represents the feature representation of the node, \(B_{i}\) denotes the set of neighboring nodes, and \(w\left( * \right)\) is the weight computation. By sampling, the neighboring node set is obtained, and a function is used to aggregate the features of the neighboring nodes within the node’s local region.

Subsequently, the features extracted by the GCN are fed into the SNN. The SNN evaluates the similarity between two skeleton sequences by comparing their features. Typically, SNN includes one or more fully connected layers to map the features extracted by the GCN into a lower-dimensional space and assess similarity by calculating the distance (Euclidean distance) or similarity (cosine similarity) between feature vectors30,35,36.

In the SNN architecture (Fig. 5), two samples are input into two identical deep neural networks with shared parameters, known as feature extraction networks. This design enables the network to learn the similarity or dissimilarity between the two input samples without explicitly defining a direct comparison method37,38,39. The feature extraction networks are the core part of the Siamese network, responsible for extracting useful feature representations from the input samples. Since both networks have identical structures and parameters, they process the two input samples in the same manner, ensuring fairness and consistency in feature extraction. When high-dimensional feature vectors are obtained through deep neural networks, these vectors typically reside in a high-dimensional space, where traditional Euclidean distance may no longer be a suitable similarity measure40. This is due to the "curse of dimensionality," which can affect distance metrics in high-dimensional spaces, making them less intuitive. This is because distance metrics in high-dimensional spaces can be affected by the "curse of dimensionality," which causes the metrics to lose their intuitive meaning.

Fig. 5
figure 5

SNN architecture.

Full size image

In dance motion recognition, the GCN-SNN model efficiently extracts the spatial features of dance movements through GCN. The human skeletal topology is a typical graph structure, with key joints as nodes and the connections between joints as edges. GCN can directly operate on this graph structure and capture local spatial relationships by aggregating the features of neighboring nodes while maintaining the coherence of the global structure. To enhance the model’s ability to represent complex spatial features of skeletal movements, a multi-scale feature aggregation mechanism is designed within the GCN. By extracting node features and integrating them within different neighborhood ranges, the model captures the relationships between key points across regions in the motion. This design is particularly suitable for handling complex dance movements such as rotations and jumps. It effectively addresses the issue where traditional 3D CNN models struggle to directly model the intricate spatial relationships between skeletal nodes. Additionally, in temporal feature modeling, the SNN is introduced to dynamically analyze the temporal similarity of skeletal sequences, and it enables accurate modeling of motion temporal dependencies. The SNN uses a dual-network structure with shared parameters to compare the feature representations of two input skeletal sequences, and employs cosine similarity and Euclidean distance as measures of temporal similarity. This design effectively captures the consistency and variation patterns of dance movements along the time dimension. For example, in the fast foot-switching movements of tango, the SNN can precisely identify subtle time differences between motions, and avoid the temporal dependency loss typically caused by gradient vanishing or explosion in traditional Recurrent Neural Network (RNN) models. Moreover, to enhance the model’s robustness, the SNN employs a contrastive loss function. This increases the feature distance between dissimilar samples and reduces the distance between similar ones, further improving sensitivity to changes in motion details.

Furthermore, the GCN-SNN model is optimized in the fusion of spatial and temporal features. In the integration of GCN and SNN, high-dimensional spatial features extracted by GCN are projected into the low-dimensional temporal feature space of the SNN through shared feature representations and a gradual mapping mechanism. This allows for the collaborative modeling of spatiotemporal features. To improve the model’s ability to distinguish motion features, a neighborhood attention mechanism is introduced. By assigning weights to different neighborhood nodes, the model dynamically adjusts the contribution of each node to the final motion representation. This mechanism helps maintain model stability even under multi-view and high-noise conditions. Especially in freestyle dance, it demonstrates remarkable performance, and effectively addresses the robustness issues faced by existing models in complex dance scenarios. Lastly, in the GCN, sparse matrix operations reduce the computational complexity of graph convolutions, while in the SNN, shared network parameters and dimensionality reduction decrease the reliance on high-dimensional feature spaces. These optimizations ensure that the model significantly reduces computational resource consumption while maintaining high accuracy. As a result, the GCN-SNN model is more suitable for real-time motion recognition and dance teaching tasks in practical scenarios, and it offers significant advantages in speed and efficiency compared to dance generation models based on adversarial learning.

In summary, the GCN-SNN model, through multiple innovative designs in spatial feature extraction, temporal similarity modeling, and spatiotemporal feature fusion, overcomes the limitations of existing research in single-dimensional and spatiotemporal modeling. It provides technical support for recognizing complex dance movements and offering personalized guidance in dance teaching videos.

Experimental design and performance evaluation

Experimental materials

The action recognition model proposed is trained and evaluated using the COCO dataset41. This dataset contains over 330,000 annotated images, with 200,000 images labeled and more than 1.5 million individual instances. It features images across 91 different object categories and provides semantic segmentation for 80 of these categories. Data collection for the COCO dataset is conducted using Amazon Mechanical Turk, and the dataset includes three types of annotations: object instances, key points on objects, and image captions, all stored in JSON files.

To promote the development of AI in the field of dance, this work has collected and annotated a dataset specifically designed for dance instruction. The dataset covers various dance styles, including waltz, tango, hip-hop, and others, and includes detailed annotations of movements. The final dataset contains approximately 10,000 video clips, with a total duration of over 50 h. Each clip lasts between 5 and 30 s and includes single, double, and multiplayer dance scenes.

Each video is annotated with specific dance movement types (like forward, backward, and rotation), recording the start and end times of each movement to enable the model to accurately capture temporal dependencies. The same dance is filmed from multiple angles to ensure the model can handle motion recognition from different perspectives.

To ensure data quality, this work conducts a rigorous data cleaning process during the data preprocessing phase. Initially, raw videos are screened to remove those with poor quality or that do not meet the criteria. Furthermore, through a combination of manual annotation and automatic detection, consistency between the movements and their corresponding labels is ensured. Videos with inaccurate or incomplete annotations are either re-labeled or discarded. Given the potential time discrepancies between different recording devices, all videos undergo time synchronization to ensure the accurate alignment of movements with the music beats. To enhance the diversity and robustness of the data, several augmentation techniques, such as rotation, scaling, and cropping, are applied to some videos. Finally, statistical methods are used to detect and remove outliers from the dataset, ensuring that extreme values do not affect the model’s performance.

Experimental environment

The experiments are conducted in a high-performance computing environment equipped with multiple GPUs, such as the NVIDIA RTX 3090. This hardware setup supports efficient training and evaluation of deep learning models. In terms of software, Python is used for programming, along with deep learning frameworks like TensorFlow for model implementation and training. Data preprocessing and feature extraction are carried out using libraries such as OpenCV and SciPy. This experimental environment ensures that the sports dance action recognition system experiments and performance evaluations are conducted under efficient and reliable conditions.

Parameters setting

In the experiments, careful tuning of model hyperparameters and training parameters is essential to ensure that the improved GCN-SNN model can achieve optimal performance. Table 1 presents the key parameter settings used in the experiments. To evaluate the performance of the proposed GCN-SNN model, this work compares it with three other models: Inflated 3D ConvNet (I3D), Spatial–Temporal GCN (ST-GCN), and Video Swin Transformer (VST).

Table 1 Parameter settings.
Full size table

All models are trained using the same dataset of sports dance movements, which contains video clips of various dance actions. This work employs a standard supervised learning approach, using the cross-entropy loss function and the Adam optimizer. During training, the same learning rate scheduling strategy and regularization techniques are applied to all models. All models are trained on the same GPU cluster to ensure consistency in computational resources. Additionally, all models use accuracy and F1 scores as performance metrics. Accuracy evaluates the proportion of correctly classified samples in the test set, reflecting the overall recognition performance of the model. The F1 score measures the classification balance across different categories.

Performance evaluation

To more specifically demonstrate the robustness and generalization ability of the model, key parameters such as learning rate, batch size, and the number of GCN layers are tested. This work sets three different learning rates (0.001, 0.01, and 0.1) for training. The results show that when the learning rate is 0.01, the GCN-SNN model achieves the highest accuracy on the test set, with accuracy decreasing as the learning rate increases or decreases. This indicates that the GCN-SNN model exhibits a certain level of robustness regarding the learning rate.

Next, three different batch sizes (32, 64, and 128) are tested. It is found that the model performs best with a batch size of 64. However, when the batch size increases to 128, there is no significant decline in performance, demonstrating the robustness of the GCN-SNN model regarding batch size. Additionally, this work experiments with GCN models having two, three, and four layers. It is observed that as the number of GCN layers increases, the model’s accuracy improves. However, the performance gain for the four-layer GCN model is not significant, and the training time increases substantially. Therefore, a two-layer GCN is selected as the optimal configuration.

To evaluate the performance of the proposed GCN-SNN model, comparisons are made with three other models: I3D, ST-GCN and VST. Figure 6 shows the accuracy results of each model, while Fig. 7 presents the F1 scores.

Fig. 6
figure 6

Comparison of action recognition accuracy across different models.

Full size image
Fig. 7
figure 7

Comparison of action recognition F1 scores across different models.

Full size image

Figures 6 and 7 show that as the number of iterations increases, both the action recognition accuracy and F1 score of different models on the COCO dataset exhibit an upward trend. Compared to other algorithms, the GCN-SNN model proposed performs best in action recognition, achieving an accuracy of 96.72% and an F1 score of 86.55%. The GCN-SNN model combines the spatial feature extraction capabilities of GCN with the similarity comparison abilities of SNN. This allows the model to effectively analyze similarities in the temporal dimension while extracting complex spatial features, thereby enhancing action recognition accuracy. In contrast to models like I3D, the GCN-SNN model has lower requirements for the format of input data and can better accommodate different formats and qualities of action data. In human action recognition, GCN can directly handle skeletal data or keypoint information without the need to convert these data into image or video formats.

In Table 2, the impact of changing key parameters on the performance of different models is further compared.

Table 2 Impact of changing key parameters on the performance of different models.
Full size table

Table 2 suggests that under noise-free conditions, increasing the input resolution from 360 to 1080p improves the test set accuracy for all models. For example, the accuracy of I3D increases from 87.5 to 90.2%, ST-GCN from 90.2 to 92.1%, and GCN-SNN sees the greatest improvement, rising from 93.4 to 94.7%. This indicates that higher resolution helps the model capture more detailed motion features. Under the 10% AWGN condition, the accuracy of all models decreases, but GCN-SNN shows the strongest robustness with an accuracy of 90.2%, significantly higher than I3D, ST-GCN, and VST. This can be attributed to the GCN module’s ability to effectively model the spatial features of the skeletal graph, while the SNN assesses temporal similarity, enhancing its noise resistance. Overall, the GCN-SNN performs excellently under various resolution and noise conditions. Especially in low-quality input or high-noise scenarios, its robustness and generalization ability outperform other models, confirming its practicality and advantages in complex environments.

To further validate the performance of the proposed GCN-SNN model in dance motion recognition tasks, a confusion matrix analysis is conducted, with results shown in Table 3.

Table 3 Confusion matrix of the GCN-SNN model on the dance dataset.
Full size table

Table 3 suggests that the GCN-SNN model successfully captures the spatiotemporal features of the waltz, particularly in rotational movements, where it accurately identifies changes in the dancer’s body posture. The model demonstrates excellent performance in waltz action recognition, especially when handling rotations and footwork variations. It can accurately capture the temporal dependencies and spatial relationships of the movements, achieving an accuracy of 95.6%. In tango movement recognition, the GCN-SNN model performs exceptionally well, particularly when handling rapid movement transitions. It can accurately capture subtle changes in the dancer’s movements, achieving an accuracy of 94.8%.

In contrast, the GCN-SNN model performs less well in recognizing freestyle dance. Especially when dealing with irregular movements, the model tends to misclassify certain actions from freestyle dance as modern dance or other improvised styles. The accuracy for freestyle dance recognition is 78.2%.

Additionally, to validate the effectiveness of second-order information, the impact of first-order and second-order information on model performance is compared on the dance dataset collected for this work. Table 4 displays the results.

Table 4 Impact of different input features on action recognition performance.
Full size table

Table 4 shows that compared to the baseline model using only first-order information, after incorporating second-order information, the model’s accuracy increases from 91.45 to 96.72%, and the F1 score improves from 81.32 to 86.55%. There is an increase of 5.76% and 6.43%, respectively. This indicates that second-order information plays a significant role in capturing the spatial structural relationships of actions. The model using only second-order information performs slightly lower than the baseline model that uses only first-order information, but still demonstrates some action recognition capability. It suggests that second-order information can serve as an effective feature for capturing action patterns. The combination of first-order and second-order information achieves the highest accuracy and F1 score. This confirms the enhancing effect of second-order information on action recognition tasks, especially in better describing spatial dependencies between key points in complex actions.

To further validate the effectiveness of the proposed GCN and SNN modules and their generalization capability across different models, a series of ablation experiments are designed. By removing or replacing the GCN and SNN modules from the model, the contribution of each module to overall performance is analyzed on the COCO dataset. Specifically, the accuracy and F1 scores of GCN-SNN, GCN, SNN, LSTM-SNN, and GCN-LSTM models are compared. The results are shown in Fig. 8.

Fig. 8
figure 8

Ablation experiment results.

Full size image

Figure 8 shows that the GCN-SNN model achieves a 24.85% and 28.45% increase in accuracy and F1 score, respectively, compared to using only the GCN, and a 29.86% and 32.50% increase compared to using only the SNN. This demonstrates the significant advantages of combining the GCN and SNN modules in spatial feature extraction and temporal similarity assessment. Additionally, after replacing the GCN with an LSTM, the model’s performance declines but remains at a relatively high level, indicating the effectiveness and superiority of the GCN in extracting spatial features from the skeleton graph. Similarly, replacing the SNN with an LSTM also leads to a decrease in performance, further confirming the importance of the SNN module in similarity assessment.

To evaluate the computational complexity and time performance of the proposed GCN-SNN model, a comparison experiment is conducted with other action recognition models such as I3D, ST-GCN, and VST. The parameter scale and runtime are compared. Table 5 displays the results.

Table 5 Comparison of parameter scale and runtime of different models.
Full size table

Table 5 shows that the GCN-SNN model has a parameter scale and complexity superior to the VST, and is close to ST-GCN. Compared to I3D, its parameter scale is reduced by 23.9%, significantly lowering its complexity. The training and inference times of GCN-SNN are between ST-GCN and I3D, outperforming the VST, confirming its good balance between spatiotemporal feature extraction and efficiency. In summary, with a smaller parameter scale and moderate computational overhead, the GCN-SNN model performs excellently in both accuracy and efficiency. This makes it suitable for resource-constrained scenarios and further verifies its innovation and practicality.

In summary, the experiments demonstrate that the GCN-SNN model exhibits powerful spatiotemporal feature capture capabilities for dance action recognition tasks. In recognizing complex spatial movements, the GCN module successfully captures the relationships between different body parts of the dancer by modeling the graph structure of skeletal keypoints. For instance, in the rotational movements of the waltz, the model can accurately track the synchronization of the upper and lower limbs and the posture changes in the spine. By analyzing the trajectory visualization of skeletal keypoints, it is observed that the model can recognize the spatial coordination features hidden in rotational movements, and provide reliable support for the dancer’s movement adjustments. This spatial feature extraction capability is difficult to achieve with traditional 3D CNN-based methods, as 3D CNNs struggle to directly model the topological relationships between points when processing skeletal data. In terms of temporal similarity analysis, the SNN module performs exceptionally well. The frequent footwork switches and rapid transitions in tango pose high demands on temporal dependency modeling. Qualitative analysis shows that the SNN can precisely compare motion features at different time points, such as distinguishing the subtle time differences between the dancer’s forward and backward steps. Additionally, the model captures detailed temporal variation patterns in dance, such as the sudden rhythm switches in tango. These features are often overlooked in traditional RNN-based methods due to gradient vanishing. However, when handling unstructured movements such as freestyle dance, the model reveals some limitations. The irregularity and high diversity of freestyle dance make it prone to misclassifying certain features as other dance types. Visualization analysis of failure cases shows that large movements or rotations in freestyle dance may overlap with certain characteristics of modern dance. This phenomenon indicates that while the GCN-SNN model performs excellently in recognizing structured dance movements, further optimization is needed to enhance its robustness for unstructured movements.

Discussion

In the field of dance action feature recognition, with the rapid development of deep learning technologies, this work proposes a dance action feature recognition method based on GCN-SNN. The aim is to achieve more detailed and accurate analysis and recognition of dance movements by combining the strengths of GCN in spatial feature extraction with the capabilities of SNN in temporal similarity comparison. GCN effectively processes skeletal data or keypoint information, capturing the complex relationships and spatial layout between different body parts of the dancer, thereby providing strong support for spatial feature extraction of dance movements. The introduction of SNN allows for the comparison of movement postures at different time points or between the same action performed by different individuals, thereby extracting temporal similarities and differences. GCN effectively captures spatial relationships in graph structures, making it well-suited for handling complex action sequences. On the other hand, SNN excels at capturing dynamic changes in time-series data, as it simulates the spiking behavior of biological neurons, which is ideal for processing continuous streams of movement. The combination of both can capture spatial and temporal features of actions simultaneously, thereby enhancing the model’s expressive power. Moreover, the spiking mechanism of SNN makes the model more efficient when dealing with sparse inputs, reducing computational resource consumption. This is particularly important for real-time action recognition tasks, as dance movements often have high temporal resolution. GCN, through graph convolution operations, can efficiently propagate features on sparse graph structures, further improving the model’s computational efficiency.

Compared to traditional action recognition methods based on 3D CNN or RNN, the GCN-SNN model shows advantages in handling dance movements, which have distinct graph-structured characteristics. Although 3D CNN can process both temporal and spatial information in video data, it struggles to capture the complex relationships between skeletal joints. SNN, while adept at handling sequential data, often faces issues like vanishing or exploding gradients when dealing with long-distance dependencies. In contrast, the GCN-SNN model leverages the strengths of both approaches. It captures spatial features of dance movements and analyzes their temporal evolution, resulting in a more comprehensive and accurate recognition of dance actions.

Several studies in the dance action recognition field have adopted similar technical frameworks, though each has its own details and implementations. Al-Qaness et al.42 extracted various features from videos (such as gradient direction and optical flow histogram features, audio features) and used feature fusion techniques to combine these features, providing a more comprehensive description of dance movements. This approach enhanced recognition performance by utilizing the complementarity of different features. Dua et al.43 used a 3D-CNN-based skeletal behavior recognition method, stacking 2D human skeleton heatmaps as input for precise recognition of dance actions. Although this method achieved excellent performance on several skeletal behavior datasets, it primarily focused on skeletal data processing with less emphasis on temporal similarity comparison. In contrast, the GCN-SNN model retains the advantages of PoseC3D in skeletal data processing while further enhancing temporal similarity analysis with SNN, providing a deeper understanding of dance actions. Ullah et al.44 combined GCN with LSTM, using LSTM to capture temporal dependencies in action sequences while utilizing GCN to extract spatial features. However, this method may face high computational complexity issues when handling large-scale data. The GCN-SNN model, by optimizing the model structure and algorithm design, reduces computational complexity and improves efficiency, making it more suitable for practical applications.

The GCN-SNN model can capture the dancer’s body posture in real time, and provide personalized posture adjustment recommendations by comparing it with standard movements. For example, the model can detect whether the dancer’s spinal alignment, foot positioning, or arm movements conform to the proper standards and offer specific suggestions for improvement. In addition to focusing on the technical accuracy of the movements, the GCN-SNN model can also assess the dancer’s artistic expression. By analyzing the dancer’s facial expressions, body language, and overall movement fluidity, the model can provide feedback on the artistic quality of the performance, helping dancers enhance their expressive capabilities and improve their overall performance quality.

Conclusion

Research contribution

Action recognition, as a critical research area, exhibits immense application potential across various fields such as video surveillance, human–computer interaction, and sports analysis. Traditional action recognition methods primarily rely on manually designed feature extractors and classifiers, which often yield limited performance in complex scenes and dynamic conditions. This work innovatively proposes the GCN-SNN model and applies it to action recognition tasks, providing new insights for advancing sports dance teaching. Experimental results demonstrate that the GCN-SNN model significantly outperforms traditional models such as 3D CNN, GCN, and ResNet in action recognition tasks. This improvement is largely attributed to the advantages of the GCN-SNN model in feature representation, spatial and temporal feature fusion, and adaptability to complex action data. The model is capable of more accurately capturing the spatial layout and temporal evolution of actions, thereby enhancing recognition accuracy.

Future works and research limitations

With the rise of online education and remote learning, the GCN-SNN model can be applied to cross-platform and remote dance teaching scenarios. By building an online teaching system based on GCN-SNN, students can receive professional dance guidance anytime and anywhere. This breaks the constraints of geography and time, and promotes the popularization and development of dance education. The GCN-SNN model can not only be used for dance instruction but also for the inheritance and innovation of dance art. By recording and analyzing dance movement data, it can help choreographers and artists better understand and grasp the essence of dance art, and enable them to create more creative and expressive dance works.

Although the proposed GCN-SNN model offers new perspectives and possibilities for the field of action recognition, there are still some limitations in practical applications and research. One main issue is that GCN has relatively high computational complexity when handling large-scale graph data, and the introduction of SNN may further increase the computational burden. This limits the model’s deployment in real-time applications or resource-constrained environments. Future research could address these challenges by employing techniques such as graph sparsification and graph pooling to reduce computational load, or by utilizing parallel computing and hardware acceleration technologies to speed up the training and inference processes of the model.