Introduction

The dynamic damping analysis of olive trees subjected to trunk shaking plays a crucial role in optimizing mechanical harvesting systems and reducing potential damage to both trees and fruits. Trunk shakers are widely employed in olive harvesting due to their ability to efficiently detach olives by inducing vibrations. However, the complex mechanical interactions between the tree, its roots, and the surrounding soil make it essential to understand the factors that influence energy transmission and damping during these operations. One of the key parameters influencing energy transmission and damping is the attachment height of the shaker along the trunk, which affects the distribution of actual, elastic, and damping power, as well as the acceleration transmitted through the tree and into the root-soil system. The location of the shaker attachment plays a significant role in determining how energy is dissipated or stored within the tree structure and root-soil system.

Research into the energy requirements for tree shakers has demonstrated a notable difference between theoretical predictions and the actual energy needed during mechanical shaking. Discrepancy arises because the traditional models do not fully account for the role of the root-soil system in the vibrational response of the tree. This system introduces additional complexity to the mechanical behavior of the tree, resulting in greater energy demands than initially predicted1. The energy interactions between the shaker, tree, and surrounding soil lead to dynamic changes that influence the tree’s damping properties, and these interactions are affected by factors such as trunk diameter, attachment height, and the mechanical properties of the soil and tree canopy. Conventional methods of measuring damping, such as drop tests and hammer strikes, have been shown to be insufficient for capturing these complex interactions, especially under high-amplitude vibrations2. As a result, more advanced approaches have been developed to improve the accuracy of energy and damping measurements in olive trees during mechanical shaking. Newer techniques for measuring damping properties focus on directly assessing the vibrational behavior of the tree and soil system. One such method, introduced by Sola-Guirado et al.3, involves using a direct energy measurement technique to evaluate the effective damping coefficients of both the root-soil system and the primary limbs of the tree. Their findings revealed that the soil surrounding the tree contributes significantly to the overall damping effect, as it absorbs a substantial portion of the energy transmitted through the trunk. By analyzing the logarithmic decrement, which reflects the rate of energy loss, they observed that the energy dissipation often aligns with theoretical expectations, providing a more accurate representation of the tree’s damping behavior during mechanical shaking. This research highlights the importance of considering the root-soil system as an integral part of the tree’s vibrational response to mechanical harvesting3. Further investigation into the dynamics of olive trees under mechanical shaking has examined how trunk diameter, canopy structure, and attachment height influence the transmission of vibrational forces. The transmitted acceleration to the root-soil system and tree structure varies with attachment height, as higher attachment points tend to increase the leverage exerted on the tree, resulting in greater acceleration and reduced stiffness. This is particularly evident in the upper parts of the tree, where branches exhibit greater flexibility and experience higher accelerations. The damping characteristics of olive trees are further understood through the analysis of logarithmic decrement, which is a measure of the energy dissipated within the tree structure as vibrations decrease. The value of the logarithmic decrement increases significantly from the trunk to the branches, indicating that branches have a greater capacity for energy dissipation. For example, values of 0.187 near the shaker and 2.623 in the outer branches demonstrate that branches are more effective in dissipating vibrational energy due to their flexibility and lower mass compared to the trunk4. The combination of the tree’s structural characteristics, such as branch flexibility, and the root-soil system’s damping capacity contributes to the overall damping properties observed during mechanical harvesting.

The mathematical modeling of the power requirements for olive tree shakers has provided further insights into the factors influencing damping and energy transmission. Ghonimy et al.5 developed a mathematical equation that predicts the power needed for trunk shaking based on variables such as displacement, fruit detachment force, fruit mass, stem length, damping ratio, and shaking frequency. The derived equation helps to better predict the energy required for effective mechanical harvesting while minimizing the risk of damage to the tree. Additionally, a mathematical formula was developed by Ghonimy6 to forecast the appropriate shaking amplitude of limb tree shakers. The developed equation establishes a correlation between the shaking amplitude, frequency, damping ratio, fruit mass ratio, stem length and the pulling force. The dynamic damping properties of olive trees allow for better optimization of shaking techniques, ensuring that the energy transmitted through the tree and root-soil system is managed effectively to achieve maximum fruit detachment with minimal energy loss7. The integration of direct measurement techniques and sophisticated analytical methods has significantly advanced the field of dynamic damping analysis8. Thus, this research aims to analyze the damping behavior of olive trees under trunk shaking by evaluating transmitted acceleration and logarithmic decrement in the soil and the tree, as well as the actual shaking power, damping power, and elastic power in the tree.

Materials and methods

Theoretical analysis

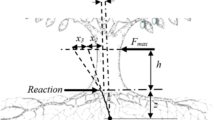
A fruit tree can be modeled as a vibrating system composed of three key parts: the trunk (including primary branches), the vibrating root-soil system, and the vibrating canopy. Each component has its own damping characteristics and understanding these is crucial for calculating losses within the system. The trunk’s elastic displacements and internal losses can generally be ignored as the elastic deformation at a specific trunk height is negligible compared to the total displacement at that point. The maximum work done by inertial force in one cycle, in phase with the velocity, is given by Eq. (1) according to Wu9.

$$\:W=\pi\:m{A}^{2}{\omega\:}^{2}$$
(1)

Where m is the mass of the vibrating system, kg; A is the displacement amplitude, m; and ω is the angular velocity, rad·s− 1.

The relationship between the vibration period (T) and angular velocity determines the formula for maximum power capacity, as given in Eq. (2).

$$\:P=\frac{m}{T}=\frac{m}{2}{A}^{2}{\omega\:}^{3}$$
(2)

Damping in the system is characterized by the work dissipated per cycle, as described by Eq. (3).

$$\:{W}_{d}=\pi\:C{A}^{2}\omega\:$$
(3)

Where C is the damping coefficient, N·s·m− 1.

The logarithmic decrement δ relates the damping coefficient to the system’s mass and angular velocity, as expressed in Eq. (4).

$$\:C=\frac{\delta\:m\omega\:}{\pi\:}$$
(4)

Substituting this into the earlier formulas, the work dissipated due to damping becomes as shown in Eq. (5)

$$\:{W}_{d}=\delta\:m{A}^{2}{\omega\:}^{2}$$
(5)

leading to an expression for damping power (Eq. 6)

$$\:{P}_{d}=\frac{{W}_{d}}{T}=\frac{\delta\:P}{\pi\:}$$
(6)

These calculations are essential to understand how the tree’s various components interact when vibrating and how energy is dissipated through damping.

Elastic power (Pe), which represents the potential energy stored within the system due to deformation, is calculated using Eq. (7)

$$\:{P}_{e}={k}_{e}\frac{{{A}_{e}}^{2}}{2}\omega\:$$
(7)

Where ke is the elastic spring constant and Ae is the elastic displacement at the attachment point. The elastic power increases as the stiffness of the trunk (ke) or the elastic displacement (Ae) grows. Damping power, which is derived from previous equations, represents the energy required to overcome resistive forces like internal friction and air resistance. This damping power plays a critical role in determining how energy is dissipated in the system, ensuring that vibrations gradually subside, and the system stabilizes over time.

The experimental work

The experiment work aimed to evaluate the dynamic damping and logarithmic decrement of an olive tree subjected to trunk shaking. The study focused on the three primary components of the tree system: the trunk (including main limbs), the vibrating root-soil system, and the vibrating tree canopy. The olive tree selected was planted in sandy loam soil, Table 1, in Al-Jouf region, Saudi Arabia (KSA). During the experiments, the moisture content range of the soil varied between 11% at reirrigation and 15% at field capacity. Within this range, the damping ratio remains within a moderate range, as sandy loam does not have a very high damping capacity like clay.

Table 1 Some physical properties of the experimental field soil.
Full size table

To conduct the experiment, a trunk shaker (Fig. 1) was used to apply controlled oscillations to the Picual olive tree trunk. The trunk shaker machine has a length of 1400 mm, a width of 900 mm, and a height of 1100 mm. It can clamp onto trees with a maximum diameter of 300 mm, or up to 500 mm when using the optional large shaker head. Its shaking performance ranges from 150 to 200 trees per hour. The total weight of the machine is 490 kg, and it features an unbalanced mass of 135 kg with an eccentricity of 22 mm. The telescopic function extends by 2 × 1000 mm, with an option for 3 × 1000 mm. The pump’s performance is approximately 40 L per minute. Additional features include a control panel, a PTO shaft drive operating at 540 rpm, and onboard hydraulics.

Fig. 1
figure 1

The olive trunk shaker.

Full size image

Olive trees (Picual variety) that were ten years old were subjected to the olive trunk shaker. At five different heights, 0.4, 0.5, 0.6, 0.7, and 0.8 m above the soil’s surface, the diameters of the olive tree’s trunk were measured. The trunk diameter measurements were 158, 152, 142, 131, and 115 mm. The trunk shaker was thus operated at five different trunk diameters (158, 152, 142, 131, and 115 mm) and five different attachment height levels (0.4, 0.5, 0.6, 0.7, and 0.8 m). The Trunk Shaker was operated for 10 s per tree of operating time10 and at a frequency of 18 Hz11,12.

Measurements and calculations

Dimensional characteristics of olive trees

In Saudi Arabia’s Al-Jouf region, ten-year-old Picual olive trees were studied to assess their dimensional characteristics. The trees were planted with a spacing of 6 m between rows and 6 m within rows, resulting in a density of 278 trees per hectare. The vase-shaped or cup-shaped training system is commonly employed to optimize light exposure and air circulation within the tree canopy. This approach involves selectively pruning the central leader and inner branches to form an open, cup-like structure with a few main scaffold branches extending outward. By creating a more open canopy, this method helps reduce disease risk, enhance fruit quality, and facilitate easier harvesting. Fifteen olive trees were randomly selected for this study, and their dimensional characteristics are measured. The dimensional characteristics of olive trees included the tree height, trunk height, trunk diameter, number of branches, branch length, and canopy diameter. The selected trees were of similar age and managed under uniform agricultural practices, ensuring consistency in the experimental conditions. The selected trees were of similar age (ten years) and were managed under uniform agricultural practices to ensure consistency in the experimental conditions. The agricultural practices included regular irrigation according to the region’s typical water availability, soil management techniques such as periodic fertilization, and pest control measures. All trees were subjected to similar pruning and training methods as per the standard practices for Picual olive cultivation in the region. Furthermore, the experiments were conducted under stable environmental conditions in the Al-Jouf region during November, when temperatures typically range from 20 to 25 °C. The area also experiences moderate humidity, with minimal rainfall, ensuring that soil moisture levels remained consistent during the study period. This combination of consistent agricultural practices and controlled environmental factors helps to reduce the impact of external variables.

The actual shaking (P a), damping (P d), and elastic (P e) powers

To measure the actual shaking power, an oil flow sensor (Flo-tech, FSC-1000, Flotech Solutions Limited, Stockport, UK) and a pressure sensor (Parker, SCP-600, Parker Hannifin Corp., Cleveland, OH, USA) were used to measure the oleo-hydraulic power prior to the hydraulic motor that moves the eccentric mass. The actual shaking power (Pa) required to operate the olive trunk shaker was calculated from Eq. (8).

$$\:{P}_{a}=\frac{Q\times\:h}{600}\:$$
(8)

Where Pa is the actual shaking power (kW), Q is the hydraulic oil flow rate (l·min− 1), and h is the hydraulic oil pressure (bar).

The damping power (Pd) was calculated from Eq. (9):

$$\:{P}_{d}=\frac{\delta\:{.P}_{a}}{\pi\:}$$
(9)

Where Pd is the damping power, W; δ is the logarithmic decrement; and Pa is the actual shaking power, W.

The elastic power (Pe) was calculated using Eq. (10).

$$\:{P}_{e}={P}_{a}-{P}_{d}$$
(10)

Where Pa is the actual shaking power, W; and Pd is the damping power, W.

Acceleration transmitted (a)

Acceleration transmitted to the root-soil system

The acceleration transmitted from the trunk shaker to the root-soil system was measured using a vibration measurement system consisting of four three-axis accelerometers (model 4506, Brüel & Kjær, Nærum, Denmark), each containing three sensors to measure acceleration in the three directions (x, y, and z). The system also included an NI USB-6255 A/D card connected to a notebook computer, and an NI SCXI 1531 signal-conditioning module equipped with a band-pass filter with cut-off frequencies of 0.2 Hz and 500 Hz. The system’s sampling frequency was set to 1000 Hz, and a digital filter was applied to limit the bandwidth to 150 Hz, using a moving-average filter with a 3 dB cut-off frequency.

To measure the acceleration transmitted from the trunk shaker to the root-soil system, four accelerometers were placed at specific distances from the trunk, positioned at 0.5, 1, 2, and 3 m. These sensors were placed at a depth of 10 cm to capture the interaction between the roots and the surrounding soil. Data from these accelerometers allowed precise measurement and analysis of how the vibrations from the trunk were transmitted through the root-soil system. This setup enabled the capture of acceleration at different distances, contributing to an understanding of how the vibrations dissipated across the soil and root structure.

Acceleration transmitted to the olive trees

The acceleration transmitted from the trunk shaker to the trunk and branches was measured by installing five accelerometers on various points of the olive tree, as depicted in Fig. 2. Accelerometer S1 was placed on the trunk at the point where the shaker is attached, at heights of 0.4, 0.5, 0.6, 0.7, and 0.8 m. S2 was positioned at the end of the trunk, where the branching begins, 1 m above the soil surface. S3 was mounted on a branch, 80 cm from the branch’s base, while S4 was located 165 cm from the branch’s base. S5 was positioned 255 cm from the base of the branch, approximately 70 cm from the branch’s tip. Additionally, the diameters of the trunk and limbs were measured at each sensor location. The trunk diameter at S2 was 108 mm, while the branch diameters (Ø) at S3, S4, and S5 were 75, 51, and 44 mm, respectively. The accelerometers were attached to the branch using strong plastic zip ties to securely fasten it without damaging the bark. The accelerometers were installed to ensure that their measurement axes aligned with the primary vibration directions of the tree structure. In all sensor installations, the accelerometer coordinate system was defined such that ax and ay were parallel to the x-y plane of the vibrating object, while az was perpendicular to this plane (Fig. 2). This orientation allows for accurate recording of acceleration components along the primary axes of motion.

Fig. 2
figure 2

Distribution of accelerometers and vibration amplitude sensors on the trunk and branch of the olive tree (Ø branch diameter of the tree in mm).

Full size image

Each measurement was conducted using multiple stimulations to ensure repeatability and minimize variability in the recorded data. Controlled excitations were applied using the trunk shaker, and acceleration signals were captured at each sensor location. The signals were recorded at a sampling rate of 1000 Hz, with a band-pass filter applied to remove noise within a frequency range of 0.2 to 500 Hz. Additionally, a digital moving-average filter was used to limit the bandwidth to 150 Hz, ensuring accurate measurement of vibration characteristics.

Logarithmic decrement (δ)

The logarithmic decrement (damping capacity) is defined as the natural log of the ratio of the amplitudes of any two successive peaks. During the experiment, the trunk shaker was operated to induce vibrations in the tree. The vibration was sustained for ten seconds, ensuring the entire tree system was engaged in oscillation. After stopping the shaker abruptly, the tree was allowed to vibrate freely, and the accelerometers continued to record the oscillations. The recorded signals included the amplitudes of successive oscillations. The data collected was processed. The analysis of data focused on calculating the logarithmic decrement (δ), which quantifies the rate of energy dissipation in the system. The logarithmic decrement of both root-soil system and olive trees were calculated using Eq. (11)13,14.

$$\:\delta\:=\frac{1}{n}ln\frac{{A}_{1}}{{A}_{n+1}}$$
(11)

Where δ is the logarithmic decrement; A1 is the amplitude of the first peak, An+1 is the amplitude of the peak after n periods, n is any integer number of successive, positive peaks.

The measurement system utilizes accelerometers from the KD10 standard series as vibration sensors to capture acceleration and displacement data. These data are then processed by a charge amplifier (model 2692-oS4), which amplifies the signal and converts it into millivolts (mV). Finally, the converted data is collected and analyzed using a National Instruments USB-6210 data acquisition card, allowing for further processing and visualization.

This calculation was performed separately for the data from each accelerometer, allowing for the estimation of dynamic damping for the trunk, root-soil system, and tree canopy.

The experiment was repeated five times to ensure reliability and consistency of the results. Each repetition involved repositioning the accelerometers and repeating the entire shaking and data collection process. The results were then subjected to statistical analysis to determine the significance of the observed differences in damping across the different components of the tree system.

Statistical analysis

CoStat ver. 6.400, a microcomputer program, was used to statistically examine the values of the damping elements. A two-factor model with a randomized complete block design in a factorial experiment was employed to conduct an analysis of variance. The differences in the average values of the damping elements were evaluated.

Results and discussion

Dimensional characteristics of olive trees

The dimensional characteristics of Picual olive trees are illustrated in Table 2. The average tree height of nearly 4 m, along with a trunk height just below 1 m, indicates a robust and mature tree structure. The trunk diameter measurements, which decrease consistently as the height above the soil surface increases, reflect the natural tapering of the tree.

Table 2 Dimensional characteristics of Picual Olive trees.
Full size table

The presence of three main branches, each extending over 3 m in length, combined with a canopy diameter exceeding 3.5 m, suggests a well-developed and expansive canopy. These dimensions highlight the effectiveness of the vase-shaped training system in promoting healthy growth and maximizing the tree’s potential for light exposure and air circulation.

Actual power (P a), elastic power (P e), and damping power (P d)

The average values of actual power (Pa), elastic power (Pe​), and damping power (Pd​) are shown in Fig. 3. The data indicate that the attachment location along the trunk significantly affects the distribution of power. At the base of the tree (0 m attachment location), the Pa power is entirely dissipated as damping power (Pd= 17.9 kW), with no elastic power (Pe= 0.0 kW). As the attachment location moves upwards, there is a progressive increase in elastic power, accompanied by a corresponding decrease in damping power.

At an attachment location of 0.5 m, the elastic power is 6.8 kW, and the damping power is 8.4 kW, indicating that approximately 45% of the total power is being stored elastically within the tree structure. As the attachment location increases, the elastic power reaches a peak of 8.8 kW at the 0.8 m attachment point, while the damping power decreases to 4.8 kW, suggesting a significant shift in energy distribution. Beyond this point, as the attachment location further increases to 1 m, the elastic power slightly decreases to 4.2 kW, and the damping power remains steady at 5.6 kW. This pattern suggests that the tree structure exhibits a more elastic response at higher attachment points, likely due to the reduced stiffness and increased flexibility of the upper trunk and branches. The initial increase in elastic power followed by a slight decrease may indicate a transition point where the tree’s elastic capacity is maximized before the mechanical response is dominated by other factors such as inertia or structural constraints. Statistical analysis was conducted using a one-way ANOVA to determine if the observed differences in elastic power (Pe) across the different attachment locations were statistically significant. The results showed significant differences (p < 0.05), confirming that the attachment location significantly impacts how energy is distributed within the tree.

Thus, the experiment demonstrates that the attachment location along the trunk significantly influences the distribution of actual, elastic, and damping power in olive trees subjected to mechanical shaking. The data suggest that higher attachment points favor an elastic response, which could be optimized in mechanical harvesting practices to minimize energy loss and potential tree damage.

Fig. 3
figure 3

Attachment height vs. actual power (Pa), elastic power (Pe), and damping power (Pd).

Full size image

Acceleration transmitted

Acceleration transmitted to root-soil system

The average values of acceleration transmitted to the root-soil system are presented in Fig. 4. These values were measured at five attachment heights (Ha) and five trunk diameters (Td) across different distances from the tree (0.5, 1.0, 2.0, and 3.0 m). The acceleration values, expressed in m·s⁻², exhibit considerable variation depending on attachment height, trunk diameter, and distance from the tree. The attachment height is associated with a specific trunk diameter, and these relationships directly influence acceleration transmission. As the attachment height increases, the trunk diameter decreases, affecting the amount of acceleration transmitted to the root-soil system.

Fig. 4
figure 4

Transmitted acceleration at a depth of 10 cm in the root-soil system around olive trees.

Full size image

At an attachment height of 0.4 m and a trunk diameter of 158 mm (0.4 Ha + 158 Td), the acceleration measured at 0.5 m from the tree is 20.3 m·s⁻². This represents the lowest acceleration value across all attachment heights, indicating that a larger trunk diameter offers substantial resistance to dynamic forces. As the distance increases, acceleration decreases at 1 m, it drops to 12.2 m·s⁻², at 2 m to 5.2 m·s⁻², and at 3 m to a negligible 0.5 m·s⁻². This pattern suggests that greater trunk diameters and lower attachment heights contribute to stability by dampening transmitted forces. When the attachment height increases to 0.5 m and the trunk diameter decreases to 152 mm (0.5 Ha + 152 Td), the transmitted acceleration values rise. At 0.5 m from the tree, acceleration reaches 22.1 m·s⁻², increasing to 13.6 m·s⁻² at 1 m, 6.9 m·s⁻² at 2 m, and 0.5 m·s⁻² at 3 m. This increase suggests that a higher attachment point, combined with a smaller trunk diameter, enhances the transmission of dynamic forces.

At an attachment height of 0.6 m and a trunk diameter of 142 mm (0.6 Ha + 142 Td), acceleration further increases, reaching 25.2 m·s⁻² at 0.5 m from the tree, 16.1 m·s⁻² at 1 m, 7.9 m·s⁻² at 2 m, and 0.6 m·s⁻² at 3 m. The data indicate that attachment height exerts a stronger influence on force transmission than trunk diameter alone, as higher attachment points result in amplified acceleration.

With an attachment height of 0.7 m and a trunk diameter of 131 mm (0.7 Ha + 131 Td), the transmitted acceleration values continue to rise, particularly at shorter radius. At 0.5 m from the tree, acceleration reaches 29.2 m·s⁻², decreasing to 17.9 m·s⁻² at 1 m, 8.0 m·s⁻² at 2 m, and 0.7 m·s⁻² at 3 m. The increased acceleration at shorter distances is attributed to the leverage generated by a higher attachment point, which intensifies force transmission to the root-soil system. At the highest attachment height of 0.8 m, with a corresponding trunk diameter of 115 mm (0.8 Ha + 115 Td), the highest transmitted acceleration values are recorded. At 0.5 m from the tree, acceleration peaks at 30.7 m·s⁻², followed by 19.9 m·s⁻² at 1 m, 8.1 m·s⁻² at 2 m, and 0.8 m·s⁻² at 3 m. The results confirm that higher attachment points amplify dynamic forces, while smaller trunk diameters offer less resistance, allowing greater acceleration transmission to the root-soil system.

Multiple regression analysis was conducted to predict the acceleration (a) in the root-soil system and its predictors: attachment height (Ha), trunk diameter (Td), and distance from the tree (R). The relationship can be expressed using Eq. (12).

$$\:a=18.022{H}_{a}+0.042{T}_{d}-9.553R+11.139$$
(12)

The coefficient of determination (R2) for this model is 0.932, indicating that 93.2% of the variability in acceleration to the root-soil system can be explained by the predictors included in the model. The adjusted R2 of 0.919 accounts for the number of predictors in the model, providing a reliable measure of the model’s goodness of fit. This statistical model not only quantifies the relationships between attachment height, trunk diameter, distance from the tree, and acceleration but also serves as a predictive tool to estimate acceleration values based on these variables.

Also, analysis of variance was conducted to determine the effect of both attachment heights and trunk diameters on transmitted acceleration. The results indicate a significant effect of attachment height on acceleration (F = 45.72, p < 0.001) and a significant effect of trunk diameter (F = 38.45, p < 0.001). Comparisons using Tukey’s HSD test confirmed that higher attachment heights and smaller trunk diameters result in significantly higher acceleration values. These findings provide strong statistical support for the observed trends and emphasize the critical role of structural parameters in acceleration transmission within the root-soil system.

Acceleration transmitted to Olive trees

The acceleration transmitted to the olive trees is illustrated in Fig. 5. It’s clear that the transmitted acceleration in the x-axis along the olive tree’s structure shows a clear progression from the base of the tree (S1) towards the outer branches (S5). At the base, near the shaker (S1), lower values were recorded, such as 45.37 m·s− 2 for Ha = 0.4 m and Td= 158 mm. However, as we move up to the branches, the acceleration values increase significantly, reaching up to 195 m·s− 2 at S5 for the same conditions. This trend indicates that the branches, particularly the upper parts, are more susceptible to vibration, possibly due to their reduced stiffness compared to the trunk. The acceleration increases further as the height of vibration (Ha) increases, with values peaking at 203 m·s− 2 at S5 when Ha is 0.8 m. This progressive increase in transmitted acceleration suggests that the branches act as resonators, amplifying the vibrational energy transmitted from the trunk. These findings align with studies that show trees with larger trunk diameters can absorb more vibrational energy, leading to higher accelerations in the branches. This behavior likely results from the branches being more flexible and capable of greater displacement under vibrational forces.

On the other hand, the transmitted acceleration in the y-axis (Lateral movement) presents a different behavior. At the base of the tree (S1), we observe the highest values, such as 192 m·s− 2 for Ha = 0.4 m and Td = 158 mm. However, as we move up the trunk and into the branches, the acceleration sharply decreases. For example, at S2, the acceleration drops to 46 m·s− 2, and at S5, it decreases further to 32 m·s− 2. This pattern suggests that lateral vibrations are primarily absorbed by the trunk, which acts as a damping mechanism, significantly reducing the force transmitted to the branches. The stiffer trunk structure is likely responsible for this reduction, as it can resist lateral forces more effectively than the more flexible branches. The reduction in transmitted lateral acceleration as we move up the tree indicates that the branches play a minor role in absorbing lateral vibrations compared to the trunk. Previous studies also support this finding, showing that trees tend to dissipate lateral forces at the base due to the structural rigidity of the trunk.

Fig. 5
figure 5

Acceleration transmitted in olive trees.

Full size image

When analyzing the transmitted acceleration in the z-axis (Vertical movement), we see a more moderate progression compared to the x and y axes. The base of the tree (S1) records lower values, such as 56–64 m·s− 2 depending on Ha and Td. As we move upwards, the transmitted acceleration increases, reaching 210 m·s− 2 at S4 for Ha = 0.8 m. This indicates that vertical forces are efficiently transmitted through the tree’s structure, with the branches experiencing higher levels of acceleration compared to the trunk. Interestingly, at the branch’s end (S5), the acceleration decreases slightly to 188 m·s− 2, which could be attributed to energy dissipation along the branch. The relatively uniform increase in vertical acceleration as we move from the base to the branches suggests that the tree’s structure is well-suited to transmitting vertical forces, particularly in the branches where flexibility allows for greater displacement. These results are consistent with previous studies, which have shown that trees tend to transmit vertical forces more effectively than lateral ones due to the vertical alignment of the tree’s fibers and the natural structure of the branches.

The results of acceleration transmitted, which accounts for the combined effects of x, y, and z accelerations, provide a comprehensive understanding of how vibration is transmitted through the olive tree. At the base (S1), the resulting acceleration values range from 191.9 m·s− 2 to 233.2 m·s− 2, depending on the shaking height and trunk diameter. As we move to S3, near the start of the branches, the values increase significantly, ranging from 233.7 m·s− 2 to 261.6 m·s− 2. The highest transmitted accelerations occur at S4, with values peaking at 309.1 m·s− 2 for Ha= 0.8 m. This peak suggests that the middle sections of the branches are particularly responsive to the vibration, possibly due to a combination of their flexibility and resonance effects. However, the transmitted acceleration decreases slightly at S5, where values range from 215.1 m·s− 2 to 278.5 m·s− 2. This reduction towards the branch’s end indicates that some vibrational energy is dissipated along the length of the branch, which is consistent with the natural behavior of flexible structures.

The results of this study provide insight into the dynamic response of olive trees under vibrational forces. The progressive increase in transmitted acceleration along the x-axis highlights the significant role that the branches play in amplifying vibrations, particularly as the height of the vibration source increases. The sharp reduction in lateral acceleration (y-axis) emphasizes the importance of the trunk in absorbing lateral forces, which is crucial for the tree’s overall stability. The moderate increase in vertical acceleration (z-axis) suggests that vertical forces are more evenly distributed throughout the tree’s structure, with the branches experiencing the highest levels of vibration. These results show that the tree’s structure and material properties, such as diameter and flexibility, play a crucial role in the transmission of vibrational energy. The slight reduction in transmitted acceleration towards the branch tips indicates that energy dissipation occurs along the length of the branch, which is a natural phenomenon in flexible structures. Thus, the trees act as complex mechanical systems, where energy is transferred and dissipated depending on structural characteristics. The higher resulting accelerations in the branches, particularly at S3 and S4, suggest that these parts of the tree are most susceptible to vibrational forces, which may have implications for understanding how external forces, such as wind or mechanical shaking, affect tree stability and fruit detachment.

Thus, the findings from this research contribute valuable insights to the understanding of tree mechanics under vibrational forces, particularly in olive trees, and offer practical implications for agricultural practices involving mechanical tree shaking.

The logarithmic decrement (δ)

Logarithmic decrement for root-soil system

The average values of the logarithmic decrement (δ) for the root-soil system at different distances from the tree are illustrated in Table 3. The logarithmic decrement decreases consistently as the distance from the shaker increases across all attachment height (Ha), showing a clear trend in the soil’s damping behavior. For example, with an attachment height of 0.4 m, the decrement at 0.5 m is approximately 6.283, but it decreases to 0.493 at 3 m. This decrease is observed across all values of Ha, indicating that the soil retains more vibrational energy near the shaker and dissipates it gradually as the distance increases. This pattern highlights the damping characteristic of the soil, as it acts as a natural medium that absorbs vibrational energy. The higher values of δ near the shaker (at 0.5 m) reflect the soil’s capacity to absorb and retain more energy at closer distances. For instance, at an Ha of 0.7 m, δ is 2.945 at 0.5 m, decreasing progressively to 0.429 at 3 m. The consistency of this trend across all values supports the conclusion that soil’s damping capability decreases as the distance from the source increases, aligning with classical wave propagation theory.

Table 3 Logarithmic decrement for soil at different distances from the tree.
Full size table

.

Thus, the results demonstrate that the soil in this study exhibits strong damping characteristics near the shaker, with a consistent decrease in δ as the distance increases. This indicates that the soil effectively absorbs vibrational energy at shorter distances, aligning with previous studies on granular and sandy soils. The findings suggest that soil composition and moisture content play key roles in its damping capacity, with sandy and dry soils contributing to rapid energy dissipation as distance from the source increases.

Logarithmic decrement for olive trees

The average values of the logarithmic decrement (δ) of olive trees under trunk shaking, as shown in Table 4, provide insight into the tree’s damping behavior. The δ values decrease as the distance from the shaker attachment point increases, highlighting the olive tree’s capacity to dampen vibrations, especially within its branches. At an Ha of 0.4 m, the δ value is 2.623 at sensor S1 (located at the shaker attachment point on the trunk). However, δ steadily decreases along the length of the tree to 0.207 at sensor S5, positioned near the branch tip approximately 255 cm from the branch base. This consistent reduction in δ across all attachment heights illustrates the tree’s ability to dissipate vibrational energy as it travels outward, reflecting its intrinsic damping behavior.

Table 4 Logarithmic decrement for olive trees at different attachment heights.
Full size table

It is important to note that is not a constant value; it varies as a function of the distance from the shaker attachment point (denoted as ) and the structural characteristics of the tree. The δ values at different sensor locations were analyzed in relation to both their distance from the shaker and the differing structural properties of the trunk and branches. As expected, the damping characteristic generally decreased with increasing distance from the shaker attachment point, particularly in the branches. The branches, due to their higher flexibility, smaller diameters, and less dense structure compared to the trunk, act as more effective dampers. This suggests that the branches dissipate vibrational energy more effectively than the trunk, which retains more energy due to its greater stiffness and larger diameter. The trend remains consistent across all attachment heights: at an Ha of 0.5 m, δ is 2.547 at S1, reducing to 0.200 at S5, while at an Ha of 0.8 m, δ starts at 2.050 at S1 and falls to 0.154 at S5. This decrease in δ suggests that olive tree branches, with their flexible and narrower structures compared to the trunk, exhibit a higher damping capacity. The branches appear to effectively dissipate the energy generated by trunk shaking, likely due to their ability to bend and absorb internal frictional forces as vibrations propagate. This pattern indicates that the tree’s structural design plays a key role in energy damping, particularly in the branches, which serve as natural dampers.

Overall, these results reinforce the view that the olive tree structure, particularly its branches, serves as an effective damping system under trunk shaking. The decrease in δ from the trunk to the branch tips highlights the tree’s capability to absorb and dissipate vibrational energy, which is central to understanding the damping behavior of olive trees.

Heatmap analysis

Figure 6 presents heatmaps of the transmitted acceleration and the logarithmic decrement (δ) for an olive tree when subjected to shaking. The horizontal axis of the heatmap includes Ha symbols, which represent the attachment height ranging from 0.4 to 0.8 m while the symbol “S” represents the sensor numbers, ranging from 1 to 5. In the heatmap of resultant acceleration, it is observed that as the attachment height increases, the acceleration values generally increase, especially for sensors S3, S4, and S5, which are located farther along the branch. The highest acceleration values are observed at levels of 0.6 m and above, particularly at S4, where values peak, indicating a strong vibrational response at this attachment height. This trend suggests that higher attachment points enhance energy transmission, especially to the more distal parts of the tree. Conversely, the heatmap of the logarithmic decrement shows a reduction in values as Ha increases, with the lowest values observed at sensors S4 and S5 when the attachment height is high. Lower logarithmic decrement values imply less energy dissipation, favoring efficient vibration propagation.

Fig. 6
figure 6

Heatmap of transmitted acceleration and logarithmic decrement in an olive tree.

Full size image

Based on these observations, an of 0.6 m or higher appears to be optimal, as it achieves both increased transmitted acceleration and reduced , which is preferred for maximizing vibrational impact on the tree with minimal energy loss. This damping behavior in olive trees highlights how a higher attachment point promotes efficient vibrational transmission to the branches, making it beneficial in applications like mechanical harvesting, where maximizing fruit detachment with minimal energy loss is desired. The hierarchical clustering dendrograms above and to the left of the heatmap show groupings of similar damping and acceleration characteristics. The vertical clustering on the left groups sensors based on similarity in damping response, while the horizontal clustering at the top groups attachment heights with similar resultant acceleration and damping characteristics. These clusters help identify patterns and differences in the tree’s response to external forces at varying heights and positions along the branch.

Discussion

This research aims to analyze the damping behavior of olive trees under trunk shaking by evaluating transmitted acceleration and logarithmic decrement in the soil and the tree, as well as the actual shaking power, damping power, and elastic power in the tree. The results of this study provide insight into how different attachment heights and trunk diameters influence the energy distribution and the dynamic response of the tree structure under mechanical shaking. The findings reveal distinct patterns in the power distribution and the transmission of accelerations through the tree and its root-soil system, which are critical for understanding the tree’s stability and resilience to external forces like wind or mechanical shaking.

The distribution of actual power (Pa), elastic power (Pe​), and damping power (Pd​) in trees subjected to mechanical shaking is profoundly influenced by the attachment location along the trunk. At the base of the tree, nearly all the shaking power is dissipated as damping power, with no elastic power stored, which clearly indicates that the base plays a crucial role in absorbing dynamic forces. As the attachment location increases along the trunk, there is a progressive shift in energy distribution—elastic power increases while damping power decreases. This shift becomes particularly pronounced at higher attachment points, suggesting that the upper portions of the tree, due to their reduced stiffness and increased flexibility, behave more elastically, whereas the lower portions are more efficient at dissipating energy through damping. This observation is consistent with the findings of Sola-Guirado et al.15, who demonstrated that higher attachment points tend to enhance the elastic response because of the reduced structural stiffness in the upper trunk and branches. Similarly, Tombesi et al.16 observed that tree elasticity increases as the height of the applied force increases, which supports the notion that the structural dynamics of trees are highly dependent on the point of force application, especially in medium-textured soils where root–soil interactions significantly contribute to energy dissipation. In addition, the study by Ghonimy et al.5 on olive mechanical harvesting using trunk shakers further corroborates these findings. Their research reported that the fruit removal efficiency at various attachment heights, specifically ranging from 0.4 to 0.8 m, varied between 88.9% and 91%. This indicates that such a range of attachment heights is highly effective for fruit detachment, thereby confirming the importance of attachment height in optimizing the fruit removal process as well as influencing the energy distribution and dynamic response of the tree structure under mechanical shaking. These findings are reinforced by additional research that has shown similar trends in energy distribution in tree structures under mechanical shaking. However, some studies have provided contrasting results. Hoshyarmanesh et al.17 suggested that the peak elastic response might occur closer to the middle of the trunk rather than at the highest attachment points. They argued that the middle section offers an optimal balance between stiffness and flexibility, making it the ideal location for both energy storage and dissipation. Their findings indicate that, depending on the tree’s structural characteristics and environmental conditions, particularly variables such as species, age, soil type, and moisture content, lower or mid-trunk attachment points might be more effective. These differing viewpoints underscore the complexity of tree dynamics under mechanical shaking. While many studies highlight that higher attachment points tend to favor an increased elastic response and reduced damping, the contrasting perspective offered by Hoshyarmanesh et al.17 suggests that there may be an optimal intermediate location for maximizing both energy storage and dissipation. This complexity implies that the tree’s response to dynamic forces may vary considerably with factors such as species, age, and environmental conditions, including the type of soil and its moisture content. The transmitted accelerations in the root–soil system and across the tree structure provide further insight into the distribution of dynamic forces throughout the tree. Detailed results indicate that both the attachment height and the trunk diameter play critical roles in influencing the transmission of accelerations. Higher attachment points lead to a marked increase in the transmission of dynamic forces—a phenomenon that is especially pronounced under wind forces and when measurements are taken at shorter distances from the tree—while smaller trunk diameters exacerbate this effect. Conversely, larger trunk diameters contribute significantly to the overall stability of the tree by reducing the transmitted acceleration. These observations are robustly supported by the findings of Dahle et al.18, who reported that elevated attachment points amplify dynamic forces through tree structures, and by Stubbs et al.19, who demonstrated that higher attachment points generate greater leverage, thereby leading to enhanced force transmission. Moreover, Stubbs et al.19 further emphasized that although increased attachment height amplifies dynamic forces, the mitigating effect of a larger trunk diameter becomes particularly evident at greater distances from the tree, underscoring the complex interplay between tree dimensions and dynamic force transmission. Together, these studies highlight the importance of considering both attachment height and trunk diameter in understanding and predicting the behavior of tree structures under dynamic loading conditions.

The comprehensive analysis of vibrational energy transmission within tree structures under dynamic loading conditions reveals that both the directional characteristics of the vibrations and the inherent physical properties of the tree play pivotal roles in governing energy distribution. The findings indicate that lateral vibrations, measured along the y-axis, are predominantly absorbed by the stiffer trunk, whereas vertical vibrations, recorded along the z-axis, are more uniformly distributed throughout the tree. This leads to a situation in which the branches, owing to their flexibility, experience higher levels of acceleration. Such observations are strongly supported by the work of Moore et al.20 and Xuan et al.21, who have demonstrated that the rigidity of the trunk is crucial for absorbing lateral forces, while the upper portions of trees exhibit enhanced resonance that facilitates the transmission of vertical vibrations. In addition to these directional effects, the transmission of vibrational energy is significantly influenced by tree dimensions, particularly the trunk diameter. The study by Spatz and Theckes22 has shown that trees with larger trunk diameters tend to absorb a greater portion of vibrational energy at the base, resulting in lower transmitted accelerations toward the branches. This concept is further exemplified in the current investigation involving olive trees, where the branches—characterized by smaller diameters relative to the trunk—experience elevated levels of transmitted acceleration, notably along the x-axis. The observed progressive increase in acceleration from the base to the branches aligns with the findings of Yang et al.23, who reported that trees naturally resonate more intensely in their upper sections due to the flexibility inherent in the branches. This resonance phenomenon likely explains the peak accelerations recorded at specific measurement points, such as S3 and S4, while a subsequent slight decrease at S5 suggests a gradual energy dissipation toward the branch tips. Moreover, detailed analyses conducted by Moore et al.20 have illustrated that the tree’s base, benefiting from both its rigidity and larger diameter, effectively serves as a natural buffer that significantly reduces lateral (y-axis) accelerations as the energy is transmitted upward. Complementarily, the research by Xuan et al.21 indicates that vibrational energy tends to concentrate in the midsections of the branches—particularly in the vertical and longitudinal directions—with a diminishing trend observed closer to the branch tips. These insights collectively provide a coherent explanation for the patterns of energy transmission observed in the current study. On the other hand, contrasting perspectives exist regarding the behavior of trees under vibrational forces. Gardiner24 posited that trees possessing more flexible trunks might display less pronounced variations in transmitted accelerations between the base and the branches because the increased flexibility allows for a more even distribution of vibrational energy throughout the structure. However, the current study’s results, particularly those obtained from olive trees with relatively rigid trunks, indicate that the base absorbs a significant portion of lateral energy. This absorption is evidenced by a marked decline in y-axis accelerations from S1 to S5, suggesting that, for species with rigid trunks, structural rigidity exerts a dominant influence on vibrational energy transmission. This observation stands in contrast to Gardiner’s findings, which were based on species exhibiting higher trunk flexibility. Taken together, the integrated evidence from these studies underscores the critical importance of both the directional properties of vibrational forces and the structural characteristics of trees—such as trunk rigidity and diameter—in determining how dynamic energy is distributed throughout the tree. The interplay between these factors is complex and appears to be highly dependent on species-specific traits and environmental conditions. The analysis of the damping behavior in the root–soil system reveals a multifaceted interplay between vibrational energy, soil type, and distance from the vibration source. The logarithmic decrement (δ) values consistently decrease with increasing distance from the shaker, which aligns with classical wave propagation theory. The high δ values observed near the shaker indicate that the soil effectively absorbs vibrational energy near the source; however, this damping capability diminishes as the distance increases. Lin et al.25 and Taslagyan et al.26 have demonstrated that granular soils, like those used in the current study, exhibit strong damping properties near the vibration source, yet lose this effectiveness over greater distances. This phenomenon is further explained by the theoretical concept that as vibrations propagate through the soil, their amplitude diminishes, and energy dissipation slows down with distance. Lin et al.25 reported a similar decrease in δ with distance in sandy soils under dynamic loading conditions, confirming that granular soils are highly effective at dissipating energy near the source but become less efficient as the distance increases. Likewise, Taslagyan et al.26. found that loose, granular soils show significant energy dissipation near the vibration source, which is consistent with the high δ values observed close to the shaker in this study. In contrast, studies on clay-rich soils, such as those by Sas et al.27. , have found that clayey soils tend to retain vibrational energy over longer distances, exhibiting lower damping properties (lower δ values) compared to granular soils. This contrast in behavior suggests that the soil used in this study is likely sandy or loose in nature, which enhances its ability to absorb and quickly dissipate vibrational energy at close range. Moreover, additional soil characteristics, including particle size, compaction, and particularly moisture content—play a crucial role in influencing damping behavior. Venkateswarlu and Hegde28 noted that higher moisture content increases the soil’s damping ability due to additional mass and cohesive forces, which leads to higher δ values. Therefore, if the soil in the current experiment possesses relatively low moisture content, this could further explain the observed decrease in damping effectiveness at larger distances, as dryer soils tend to dissipate energy less efficiently. In summary, the comprehensive findings from Lin et al.25, Taslagyan et al.26, Sas et al.27, and Venkateswarlu and Hegde28 collectively illustrate that the damping properties of the soil are highly dependent on both its inherent physical characteristics and its proximity to the source of vibration. Granular soils exhibit strong damping near the vibration source that diminishes with distance, whereas clay-rich soils retain energy over longer distances. Additionally, soil moisture content significantly modulates these damping characteristics, highlighting the complex and variable nature of vibrational energy transmission in different soil types. Regarding the logarithmic decrement in olive trees, the observed damping behavior is in strong agreement with previous studies. Grande et al.29 reported that tree branches generally exhibit greater damping than trunks, particularly at locations farther from the vibration source. Their findings suggest that branches, because of their smaller diameters and increased flexibility, are inherently better equipped to dissipate vibrational energy. Similarly, Xuan et al.21 demonstrated that the structural composition of trees, including variations in diameter and branch architecture, contributes significantly to natural damping mechanisms. This structural advantage is evident in the current study, where the trunk retains more vibrational energy while the branches function as effective dampers. Conversely, Moore and Maguire30 emphasized that trunk diameter plays a pivotal role in energy retention, with thicker trunks maintaining higher levels of vibrational energy over longer distances. In this study, the trunk diameter at sensor S2 measures 108 mm, whereas the branch diameter decreases to 44 mm at sensor S5. This clear difference supports the observed damping pattern, wherein branches, owing to their smaller diameters and enhanced flexibility, demonstrate higher damping capabilities. Moreover, other factors such as moisture content and the intrinsic material properties of the tree further influence its damping behavior. Chen et al.31 noted that increased moisture enhances internal friction within the tree structure, thereby boosting its damping capacity. It is plausible that if the branches in this experiment possessed higher moisture content, their ability to absorb vibrational energy would be further improved, which helps explain the observed decrease in δ with distance. Collectively, the evidence from Grande et al.29, Xuan et al.21, Moore and Maguire30, and Chen et al.31 offers a comprehensive perspective on the damping behavior in olive trees. These studies underscore the importance of structural characteristics—such as diameter and branch flexibility—as well as environmental factors like moisture content in determining how vibrational energy is absorbed and dissipated throughout the tree. The results of this study contribute valuable knowledge about the dynamic behavior of olive trees under mechanical shaking. The findings support existing literature and offer insights into the role of tree structure, attachment height, and soil characteristics in determining how energy is distributed and transmitted through the tree and its root-soil system. These results have practical implications for agricultural practices, particularly in improving mechanical shaking methods for fruit detachment and enhancing tree stability in response to dynamic forces.

Conclusion

This study provided detailed insights into the dynamic damping characteristics and logarithmic decrement of an olive tree under trunk shaking, highlighting how different parts of the tree system respond to mechanical stimulation. The attachment location along the tree trunk significantly influences the distribution of actual power (Pa), elastic power (Pe), and damping power (Pd). Lower attachment points result in higher damping power, while higher attachment points increase elastic power, indicating a shift in energy storage from damping to elasticity. Elastic power peaks at an attachment location of 0.8 m, followed by a slight decrease, suggesting that the tree’s structure reaches a maximum elastic capacity before other factors (e.g., inertia) begin to dominate its mechanical response. The transmission of acceleration to the root-soil system is directly influenced by both attachment height and trunk diameter. Lower attachment heights with larger trunk diameters reduce transmitted acceleration, whereas higher attachment points and smaller trunk diameters increase acceleration transmission, particularly at closer distances to the tree. Acceleration in the x-axis increases progressively from the base to the branches, highlighting the greater flexibility and vibrational susceptibility of the branches. In contrast, lateral acceleration (y-axis) is mostly absorbed by the trunk, reducing the force transmitted to the branches. The logarithmic decrement (δ) for both soil and olive trees decrease with distance from the shaker and the attachment point, indicating greater damping at smallest distances. This reflects the soil’s natural damping capacity and the branches’ ability to dissipate vibrational energy more effectively than the trunk.