Optimization of nano-finned enclosure-shaped latent heat thermal energy storage units using CFD, RSM, and enhanced hill climbing algorithm

Abstract

Thermal energy storage plays a critical role in improving energy efficiency and sustainability, particularly in solar energy systems, industrial waste heat recovery, and building temperature regulation. However, traditional latent heat thermal energy storage (LHTES) systems face significant challenges due to the low thermal conductivity of phase change materials (PCMs), leading to prolonged charging/discharging times and reduced efficiency. To address these limitations, this study presents a framework for optimizing nano-finned enclosure-shaped LHTES units that incorporate nano-enhanced phase change materials (NePCMs) and fins. The research employs a novel hybrid approach that integrates computational fluid dynamics (CFD) simulations, response surface methodology (RSM), and an enhanced hill climbing (EHC) optimization technique to explore the complex interplay between fin geometry and nanomaterial characteristics. The influence of key design variables—including three fin geometry parameters (number, length, volume), nanomaterial concentration, and eight nanomaterials (metal, oxide, and carbon-based)—is analyzed to optimize phase change time and total stored energy. Results demonstrate that reduced sixth-degree and reduced quartic polynomial models, developed through RSM, provide high accuracy in predicting total stored energy and melting time, respectively. While the incorporation of nanomaterials generally reduces total stored energy due to their lower latent heat, carbon-based nanomaterials (GNPs, MWCNTs) offer an optimal trade-off, achieving faster melting times with minimal energy storage loss. Among the studied parameters, fin volume fraction plays a more dominant role in determining energy storage capacity compared to nanomaterial volume fraction. The optimal design configuration varies based on the priority assigned to melting time or stored energy. In a melting-time-focused scenario, the optimized unit achieves 63.03 kJ of stored energy with a melting time of 91.76 s. When prioritizing energy storage, the stored energy increases to 66.15 kJ, but the melting time extends to 222.3 s. A balanced optimization scenario yields 64.67 kJ of stored energy and a melting time of 137.4 s. These findings provide valuable insights into the design and optimization of advanced LHTES units for enhanced thermal energy management.

Introduction

The rising global energy demand, coupled with environmental concerns and high infrastructure costs, has driven research into energy storage solutions. While energy storage has faced technical challenges, advancements in the field offer promising alternatives to increasing production capacity. Among these, latent heat thermal energy storage (LHTES) stands out due to its ability to store significant energy efficiently¹. By improving energy utilization and reducing reliance on conventional generation, LHTES plays a crucial role in sustainable energy management, supporting renewable integration and enhancing overall energy efficiency². Phase change materials (PCMs) have emerged as a prominent technology for thermal energy storage in practical engineering applications. Their key advantage lies in their high latent heat of fusion, enabling them to absorb and release significant thermal energy within a defined temperature range during their phase transition³. While pioneering research on PCMs dates back to the work of Telkes and Raymond in the 1940s⁴, it wasn’t until the 1980s that their potential gained widespread recognition. PCMs are currently employed in a vast array of engineering applications, encompassing battery thermal management⁵, electronics cooling⁶, solar power plants⁷, solar systems⁸, photovoltaic systems⁹, energy conservation in buildings¹⁰, waste heat recovery systems¹¹, food applications¹², etc.

Research efforts across various studies have highlighted the advantages of latent heat thermal energy storage units containing PCMs for effective thermal management where a long melting time is preferred and for thermal energy storage where a short melting time is required. Mehdaoui et al.¹³ demonstrated the potential of PCM vertical enclosures in buildings. Their study showed that PCMs can significantly reduce temperature fluctuations within an LHTES unit, enhancing thermal comfort and improving the building envelope’s thermal inertia. Li et al.¹⁴ emphasized the importance of optimizing LHTES unit design for efficient thermal performance. Their research revealed that specific geometric configurations, particularly a tilted top wall, can significantly enhance natural convection and accelerate heat transfer during the PCM melting process. Yadav and Samir¹⁵ reinforced the suitability of PCMs for thermal regulation in buildings. Their study explored the melting behavior of paraffin wax in an LHTES unit (rectangular enclosure), demonstrating its effectiveness for thermal accumulation within an acceptable range of deviation between experimental and numerical results.

Although previous studies have predominantly focused on the use of pure phase change materials within LHTES units, this approach has a critical limitation. Pure PCMs suffer from low thermal conductivity (TC), leading to prolonged charging and discharging times and reduced efficiency¹⁶. This limitation persists despite natural convection, highlighting the need for thermal conductivity enhancements to improve system performance¹⁷. To mitigate these limitations, various strategies have been investigated, including the incorporation of multiple PCMs¹⁸, applying metal foams or porous materials¹⁹, utilizing fins or extended surfaces²⁰, and adding high-conductivity micro/nano-particles^21,22.

Within the spectrum of techniques employed to enhance the thermal conductivity of PCMs, the incorporation of fins and nanomaterials (NMs) has garnered significant interest due to their straightforward implementation. NMs improve thermal conductivity, accelerate heat transfer, and optimize phase transitions by modifying thermophysical properties²³. They also increase specific heat capacity, enhance uniform melting, and reduce supercooling, though maintaining stable dispersion is essential for long-term efficiency. Meanwhile, fins enhance natural convection, increasing heat transfer efficiency by expanding surface area and directing molten PCM flow²⁴. Complex fin geometries, such as branched or radial designs, further improve thermal performance by promoting turbulence and reducing thermal resistance. Together, NMs and fins effectively enhance PCM-based thermal storage systems, ensuring faster energy storage and retrieval.

In this regard, Meizhi et al.²⁵ demonstrated that the incorporation of graphene nanoplatelets (GNPs) can enhance the thermal conductivity of myristic acid PCM by up to 176%. In comparison, MWCNTs and nano-graphite were found to improve TC by 47.3% and 44%, respectively. Kumar et al.²⁶ reported that the addition of CuO nanoparticles resulted in a 150% increase in the TC of pure PCM; however, performance was reduced when the concentration exceeded 0.5 wt%. Similarly, Singh et al.²⁷ observed that the introduction of COOH-functionalized GNPs improved the thermal conductivity of a eutectic salt PCM by 104% at a 5% concentration. Saxena et al.²⁸ showed that the addition of 2 wt% SiO₂ enhanced the TC of paraffin wax-based PCMs by 37%. Gupta et al.²⁹ further reported a 147.5% improvement in the thermal conductivity of PCM with the addition of 0.5 wt% TiO₂. On the other hand, Hasnain et al.³⁰ found that straight and branched fin designs reduced melting times by 45.9%, with the double-branched configuration being the most effective. The addition of Al₂O₃ nanoparticles resulted in an additional 26.8% reduction in melting time. Moreover, Sarani et al.³¹ concluded that discontinuous fins improved energy release time by 89% compared to continuous fins, with further performance enhancements when combined with nanoparticles. In another work, Mudhafar et al.³² demonstrated that the use of tee fins reduced PCM melting time by 33% relative to traditional longitudinal fin configurations.

Recent studies have shown that using innovative fin structures, such as snowflakes and tree-shaped configurations, can significantly enhance the solidification and melting rates of PCMs. For example, snowflake-shaped fins improve the solidification rate and energy storage capacity more effectively than nanoparticle dispersion³³. Similarly, tree-shaped fins have been optimized to improve heat transfer and reduce melting time by 24% in shell-and-tube LHTES units³⁴. The orientation and design of fins, such as Y-shaped and gradient fins, also significantly enhance thermal performance by improving the natural convection and thermal conductivity within the storage units³⁵. Moreover, combining fins with nanoparticles, such as Al₂O₃, has shown substantial improvements in melting and solidification times, with double-branched fins and 1% nanoparticle concentration achieving optimal results³⁶. Gradient fins have also been found to enhance melting performance by up to 180% compared to systems without fins³⁷. Additionally, wire-wound fins combined with GNP significantly reduce charging durations and improve heat fluxes compared to traditional fin designs³⁸. Comprehensive numerical studies confirm that the addition of nanoparticles enhances the thermal conductivity of PCMs, with optimal results achieved with 1% nanoparticle concentration³⁹. A review of nano-enhanced PCMs highlights that Al₂O₃, copper, and carbon-based nanoparticles are particularly effective in improving PCM performance, although fins generally offer superior enhancements⁴⁰. Furthermore, optimizing fin configurations in horizontal shell-and-tube LHTES systems has been shown to significantly reduce melting times, thereby enhancing overall efficiency⁴¹. Overall, the integration of fins and nanomaterials in LHTES units proves to be a highly effective strategy for improving thermal performance, ensuring faster energy storage and retrieval, and enabling more efficient energy storage.

Effective design of thermal energy storage systems requires not only improved materials and techniques, but also powerful modeling and optimization tools. Response surface methodology (RSM) has emerged as a promising tool for modeling and predicting LHTES units with fins or nanoparticles. This technique effectively facilitates the modeling of diverse design goals as functions of independent design variables⁴². In this regard, Lohrasbi et al.⁴³ employed multi-objective RSM optimization for fin-assisted LHTES systems. Their work revealed that fin immersion offered a more pronounced enhancement in solidification rate compared to nanoparticle dispersion, even with a corresponding reduction in PCM mass. Similarly, Huang et al.⁴⁴ utilized RSM to optimize hierarchical fins within horizontal LHTES units. This approach demonstrably improved the charging rate and temperature uniformity when compared to traditional designs. Further research by Alizadeh et al.⁴⁵ employed RSM to optimize both V-shaped fins and single walled carbon nanotubes (SWCNTs) dispersion for triplex-tube LHTES units. Furthermore, studies by Parsazadeh et al.⁴⁶ and Alizadeh et al.⁴⁷ demonstrated that the integration of nanoparticles, particularly when combined with optimized fin configurations, led to enhancements in thermal performance during the initial phase of the PCM melting process. Across the reviewed research, RSM has established itself as a valuable tool for LHTES unit optimization. By enabling the strategic design of fin configurations and the effective use of nanoparticles, RSM has demonstrably facilitated significant advancements in thermal performance.

Despite significant progress in optimizing LHTES units, a critical research gap remains. Prior studies have primarily focused on triplex-tube and shell-and-tube LHTES systems, neglecting enclosure-shaped configurations, which are widely applicable in solar systems, building energy systems, and industrial waste heat recovery. The lack of optimization for enclosure-shaped LHTES units incorporating both fins and nanomaterials limits their practical efficiency. Additionally, while existing research explores either fin geometry optimization or nanomaterial enhancement, a comprehensive multi-objective approach addressing both remains unexplored. This study bridges this gap by presenting the first-ever multi-objective optimization of nano-finned enclosure-shaped LHTES units, integrating nano-enhanced phase change materials and advanced fin designs. Unlike conventional methods, this work employs a novel hybrid computational framework combining computational fluid dynamics (CFD) simulations, response surface methodology, and an enhanced hill climbing (EHC) algorithm. This approach enables a systematic investigation of the interplay between fin parameters (number, length, volume fraction) and nanomaterial properties (type and volume fraction) across metal, metal oxide, and carbon-based nanomaterials. The key objective functions are to minimize phase change time and maximize total stored energy, ensuring faster heat transfer without compromising thermal storage capacity. The research methodology unfolds in three stages: (1) CFD simulations establish a detailed dataset of design variable influences, (2) RSM constructs accurate regression models to predict system behavior, and (3) EHC optimization identifies the most effective LHTES configurations under different performance trade-offs. This methodology provides a robust decision-making framework, allowing practical selection of optimal fin-nanomaterial combinations for enhanced energy storage performance. By systematically optimizing enclosure-shaped LHTES units, this research advances the field of thermal energy storage by offering a scalable, efficient, and application-driven approach for improving renewable energy utilization and industrial heat recovery. Figure 1 depicts the methodological framework employed for optimizing nano-finned enclosure-shaped LHTES units in this investigation.

Fig. 1

The framework employed for optimizing nano-finned enclosure-shaped LHTES units in this research.

Problem description

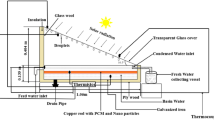
This study employs a simplified, two-dimensional geometric model to represent the nano-finned enclosure-shaped LHTES unit (Fig. 2). The computational domain encompasses aluminum fins embedded within a stainless-steel enclosure (thickness: 1 mm) containing a NePCM, with paraffin wax used as the base PCM. Fin length (L_f) and enclosure internal length (L_e) are designated as key geometric parameters. The initial uniform temperature of the LHTES unit is set at 315 K. To simulate a heat transfer scenario, a constant temperature of 340 K is imposed on the bottom enclosure wall via a virtual hot plate. All other enclosure walls are considered adiabatic. Within the computational domain, no-slip boundary conditions are implemented at all wall interfaces. Paraffin wax was chosen for the nano-finned enclosure-shaped LHTES unit due to its high latent heat, stable thermal cycling, chemical stability, and low cost. Its melting temperature aligns with industrial and residential applications, making it an effective and practical phase change material for thermal energy storage in this study^48,49. Thermophysical properties of the pure PCM are detailed in Table 1⁴⁶. In Table 1, the letter “l” denotes the liquid phase of the PCM, while the letter “s” represents the solid phase of the PCM.

There are a total of 12 design variables. The impact of these design variables, which includes three related to fin geometry, one related to nanomaterial concentration, and eight pertaining to nanomaterial types, is analyzed in nano-finned enclosure-shaped LHTES units. The three design variables related to fin geometry are the number of fins (N_Fin), dimensionless fin length (L_Fin), and fin volume fraction (VF_Fin). The dimensionless fin length is defined as the ratio of actual fin length (L_f) to the enclosure’s internal length (L_e). The fin volume fraction represents the portion of the NePCM enclosure occupied by the fins, calculated as the ratio of fin volume (V_f) to the total enclosure volume (V_t = L_e × L_e × w). Informed by prior research^50,51,52 and preliminary simulations, a lower bound of 0.4 is established for the relative fin length. Values below this threshold yielded unfavorable outcomes. Similarly, to avoid unreasonable reductions in PCM volume and energy storage capacity, the maximum fin volume fraction is capped at 10%. Furthermore, considering the limitations of practical applications and the defined fin volume fraction, the number of fins is restricted to a range of 1 to 5.

Rectangular fins were selected for the nano-finned enclosure-shaped LHTES units in this study due to their prevalent use in industrial applications, where their simple manufacturing process, structural stability, and well-documented performance characteristics are highly valued⁵³. While alternative fin geometries such as snowflake-shaped fins³³, tree-shaped fins³⁴, Y-shaped and gradient fins³⁵, and wire-wound fins³⁸ have been investigated in the literature and may offer enhanced thermal performance under certain conditions, rectangular fins were chosen for this study as they provide a reliable and well-established baseline for comparison. Additionally, rectangular fins align with the shape of the enclosure-shaped LHTES unit and the specific design variables under consideration. This choice facilitates ease of integration into existing systems while ensuring that the study’s findings are broadly applicable and comparable with existing data.

On the other hand, the NePCM formulation incorporates eight widely used and well-established nanomaterials: metals (Ag, Cu), metal oxides (Al₂O₃, CuO, TiO₂), and carbon-based nanomaterials (MWCNT, SWCNT, GNP). These nanomaterials are dispersed within the PCM at pre-defined volume fractions (VF_NM) of either 2.5 vol% or 5.0 vol%. Selection of the nanomaterial volume fraction is critical, as higher concentrations can potentially hinder heat transfer rates, as evidenced in previous studies⁵⁴. The current investigation assumes homogenous dispersion of the nanomaterials throughout the PCM. Furthermore, it is important to acknowledge limitations in existing models for predicting NePCM thermophysical properties at volume fractions exceeding 5%⁴⁶. The thermophysical properties of the nanomaterials, fins, and the LHTES unit frame are presented in Table 2^{55,56,57,58,59}.

The design variable ranges are presented in Table 3. Using these ranges, all possible combinations of input variables are investigated, containing scenarios with and without nanomaterials. This systematic approach results in a total of 680 unique cases to be simulated using computational fluid dynamics. The CFD simulations will subsequently be used to elucidate the influence of each design variable on the chosen objective functions.

Fig. 2

The computational domain of nano-finned enclosure-shaped LHTES unit.

Table 1 Thermophysical properties of the pure PCM (Paraffin wax)⁴⁶.

Table 2 Thermophysical properties of LHTES unit components^{55,56,57,58,59}.

Table 3 Variations range of design variables.

CFD simulation

The methodology of this investigation is centered on the use of CFD simulations to develop robust RSM models for optimizing the performance of nano-finned enclosure-shaped LHTES units. CFD simulations provide comprehensive data on the behavior of the system under various configurations, which are then used to train the RSM models. This model is subsequently employed for multi-objective optimization, balancing the conflicting objectives of minimizing melting time and maximizing total stored energy.

Thermophysical properties of NePCM

The determination of NePCM thermophysical properties with high accuracy traditionally relies on experimental methods, a resource-intensive approach due to inherent costs and time requirements⁶⁰. To overcome this limitation, researchers have explored alternative strategies, such as employing experimental correlations and analytical models, to estimate the influence of nanomaterial inclusion on PCM properties. Fan et al.⁶¹ support this notion by demonstrating good concordance between experimental results and predictions from a combined mixing model and experimental correlation approach, when incorporating low volume fractions of nanomaterials (< 5 vol%) within an LHTES system. Leveraging the findings of Fan et al.⁶¹, this study adopts the simple mixing model equations proposed by Pak and Cho⁶². Their suitability for estimating key NePCM thermophysical properties (specific heat capacity, thermal expansion, latent heat, and density) is particularly advantageous at low nanomaterial volume fractions. Furthermore, the Vajjha et al.⁶³ model has gained recognition for its accurate viscosity prediction in nanomaterial-enhanced PCMs. These models have led to widespread adoption in recent studies⁶⁴ for estimating the thermophysical properties of nano-PCM composites. This investigation utilizes a mixing model approach to determine the specific heat capacity ($\:{C}_{p}$) and density ($\:\rho\:$) of the NePCM. For latent heat ($\:L$) and thermal expansion coefficient ($\:\beta\:$), a reduced form of the mixing model is employed, as detailed in the following equations⁶⁵:

$$\:{\rho\:}_{NePCM}=\left(1-{VF}_{NM}\right){\rho\:}_{PCM}+{VF}_{NM}{\rho\:}_{NM},$$

(1)

$$\:{\left({\rho\:C}_{p}\right)}_{NePCM}=\left(1-{VF}_{NM}\right){\left({\rho\:C}_{p}\right)}_{PCM}+{VF}_{NM}{\left({\rho\:C}_{p}\right)}_{NM},$$

(2)

$$\:{\left(\rho\:L\right)}_{NePCM}=\left(1-{VF}_{NM}\right){\left(\rho\:L\right)}_{PCM},$$

(3)

$$\:{\left(\rho\:\beta\:\right)}_{NePCM}=\left(1-{VF}_{NM}\right){\left(\rho\:\beta\:\right)}_{PCM},$$

(4)

The viscosity ($\:\mu\:$) of the NePCM is estimated using the model proposed by Vajjha et al.⁶³. The specific formulation is presented as follows:

$$\:{\mu\:}_{NePCM}=0.983\:{e}^{\left(12.959{VF}_{NM}\right)}{\mu\:}_{PCM},$$

(5)

The selection of the thermal conductivity model necessitates consideration of the specific nanomaterial structures employed within the NePCM. Consequently, this study incorporates three distinct models to calculate the thermal conductivity of NePCM. For NePCMs containing uniformly sized, spherical nanoparticles (metals and metal oxides), the established Maxwell model⁶⁶ is adopted to estimate thermal conductivity. The specific formulation is provided in Eq. (6). In contrast, predicting the thermal conductivity of suspensions containing carbon nanotubes (CNTs) often relies on empirical approaches. Building upon Maxwell theory, Xue⁶⁷ proposed a model exhibiting good accuracy for such suspensions, as detailed in Eq. (7). Also, for NePCMs containing GNPs, the model developed by Chu et al.⁶⁸ (Eqs. (8) and (9)) is employed. This model incorporates the effects of GNP non-linearity, anisotropy, interfacial thermal resistance, and the aspect ratio ($\:a=100-1000$). In this study, the value of the aspect ratio of GNP nanomaterials is assumed to be 500.

$$\:{k}_{NePCM}={k}_{PCM}\left[\frac{{k}_{NP}+2{k}_{PCM}-2{VF}_{NM}\left({k}_{PCM}-{k}_{NP}\right)}{{k}_{NP}+2{k}_{PCM}+{{VF}_{NM}}_{\:}\left({k}_{PCM}-{k}_{NP}\right)}\right],$$

(6)

$$\:{k}_{NePCM}={k}_{PCM}\left[\frac{1-{VF}_{NM}+2{VF}_{NM}\frac{{k}_{CNT}}{{k}_{CNT}-{k}_{PCM}}\text{ln}\left(\frac{{k}_{CNT}+{k}_{PCM}}{2{k}_{PCM}}\right)}{1-{VF}_{NM}+2{VF}_{NM}\frac{{k}_{PCM}}{{k}_{CNT}-{k}_{PCM}}\text{ln}\left(\frac{{k}_{CNT}+{k}_{PCM}}{2{k}_{PCM}}\right)}\right],$$

(7)

$$\:{k}_{NePCM}={k}_{PCM}\left[\frac{\frac{2}{3}{({VF}_{NM}-\frac{1}{a})}^{\omega\:}}{H\left(a\right)+\frac{1}{{k}_{GNP}/{k}_{PCM}-1}}+1\right],$$

(8)

$$\:H\left(a\right)=\frac{\text{l}\text{n}(a+\sqrt{{a}^{2}-1})a}{\sqrt{{\left({a}^{2}-1\right)}^{3}}}-\frac{1}{{a}^{2}-1},$$

(9)

Building upon the work of Chu et al.⁶⁸, Eq. (9) introduces the GNP geometric coefficient, a function of the aspect ratio ($\:a$). Furthermore, the interaction coefficient, denoted by $\:\omega\:$, accounts for the interaction between the graphene nanoplates within the NePCM. As suggested in prior research⁶⁸, the value of $\:\omega\:$ typically ranges from 1.2 to 2.4. In this study,$\:\:\omega\:$ is considered as the maximum value (2.4) in order to model the highest level of interaction between GNP nanomaterials.

Table 4 presents the thermophysical characteristics of NePCMs as determined by the integration of diverse nanomaterials. These properties were calculated using Eqs. (1)-(9). Also, given the limited VF of nanomaterials used in this study, the melting temperature range remains unaffected by their presence.

Table 4 Thermophysical properties of NePCM influenced by the incorporation of various nanomaterials.

Governing equations

This investigation is founded upon the following key assumptions within the developed numerical model:

• For simplicity, viscous dissipation effects, radiative heat transfer, and volume expansion of the NePCM are disregarded.

• The numerical model neglects close-contact melting phenomena and potential movement or settling of the solid PCM phase.

• The liquid NePCM is assumed to exhibit laminar, incompressible, unsteady state, and Newtonian flow characteristics.

• The stainless-steel frame and aluminum fins are assumed to be homogenous materials throughout their respective domains.

• The nanomaterials are presumed to be uniformly and stably dispersed within the PCM, without agglomeration or sedimentation.

This study employs a two-dimensional LHTES unit model. The rationale behind this simplification lies in the minimal contribution of three-dimensional convection to the melting process⁶⁹. Therefore, building upon the outlined assumptions, the governing equations for this investigation encompass continuity, momentum, and energy conservation and are presented as follows^70,71:

$$\:\nabla\:\cdot\:U=0,$$

(10)

$$\:\rho\:\left(\frac{\partial\:U}{\partial\:t}+\left(\nabla\:\cdot\:U\right)U\right)=-\nabla\:P+\rho\:g+\nabla\:\cdot\:\left(\tau\:\right)+S,$$

(11)

$$\:\rho\:\left(\frac{\partial\:H}{\partial\:t}+\nabla\:\cdot\:\left(UH\right)\right)=\nabla\:\cdot\:\left(k\nabla\:T\right),$$

(12)

Within Eqs. (10)-(12), $\:g$ represents the gravitational acceleration, $\:U$ denotes the velocity vector, $\:\tau\:$ symbolizes the stress tensor, $\:P$ signifies pressure, $\:k$ represents thermal conductivity, $\:H$ denotes enthalpy, $\:S$ shows the momentum source term, and $\:\rho\:$ stands for density.

This investigation employs the enthalpy-porosity method, established by Voller and Prakash⁷² in 1987, to simulate the PCM melting process. A key advantage of this method lies in its ability to circumvent explicit tracking of the liquid-solid interface. Instead, the mushy zone encompassing both liquid and solid phases is treated as a porous material. Consequently, the liquid volume fraction within each computational cell is directly related to its porosity. This liquid fraction is dynamically determined through the enthalpy balance equation during each iteration of the simulation. The influence of the enthalpy-porosity approach manifests as a source term ($\:S$) incorporated into the momentum equation. This term is defined as follows⁵³:

$$\:S=-\frac{{\left(1-\lambda\:\right)}^{2}}{{\lambda\:}^{3}+\epsilon\:}{A}_{mushy}U$$

(13)

,

Where, $\:{A}_{mushy}$, the mushy region constant responsible for modulating the damping effect. Its value typically ranges from 10⁴ to 10⁷ depending on the specific PCM⁷³. In accordance with previous studies^46,54, this investigation adopts a standard value of 10⁵. Additionally, the term $\:\epsilon\:$ serves as a small constant value (typically 0.001) to prevent division by zero during calculations. Finally, $\:\lambda\:$ represents the liquid fraction of the PCM, a critical parameter that dictates its state (solid or liquid). This dimensionless value ranges between 0 and 1 based on the PCM’s temperature and is determined through the following equation⁵³:

$$\:\lambda\:=\left\{\begin{array}{c}0\:\:\:\:\:\:if\:\:\:\:\:\:T\le\:{T}_{s}\\\:\frac{T-{T}_{s}}{{T}_{l}-{T}_{s}}\:\:\:\:\:if{\:\:\:\:\:\:T}_{s}<T<{T}_{l}\\\:1\:\:\:\:\:\:if\:\:\:\:\:\:T\ge\:{T}_{l}\end{array}\right.$$

(14)

Where, $\:{T}_{s}$ corresponds to the solidus temperature, signifying the onset of melting, and $\:{T}_{l}$ represents the liquidus temperature, indicating the completion of melting.

Based on prior research^46,54 as the phase change progresses and liquid PCM accumulates, natural convection becomes the dominant heat transfer mechanism, surpassing conduction. Therefore, to accurately simulate the melting process, it is essential to incorporate the effects of natural convection, particularly the buoyancy forces. This investigation achieves this by applying the Boussinesq approximation⁷⁴. This model treats density as a temperature-dependent property, but maintains it as a constant value within all governing equations except the momentum equation’s buoyancy term:

$$\:\rho\:={\rho\:}_{l}/\left(\beta\:\left(T-{T}_{l}\right)+1\right)$$

(15)

Equation (12) contains the enthalpy term (H), which can be determined using the following relationship:

$$\:H={\Delta\:}H+h$$

(16)

Where, ΔH and h represent the specific contributions of latent and sensible enthalpies, respectively. These terms can be determined through the following relationships:

$$\:h={h}_{ref}+{\int\:}_{{T}_{ref}}^{T}{C}_{p}dT,$$

(17)

$$\:{\Delta\:}H=\lambda\:L$$

(18)

Equation (17) incorporates $\:{h}_{ref}$, which signifies the enthalpy value at a designated reference temperature ($\:{T}_{ref}$).

Numerical procedure

This investigation utilizes a finite volume method (FVM) framework for model development. The model is implemented within the ANSYS-FLUENT commercial CFD software package. For pressure-velocity coupling, the established SIMPLE algorithm is employed. Additionally, the discretization of the governing energy and momentum equations utilizes the second-order upwind method. Furthermore, to enhance the accuracy of the transient simulations, a second-order implicit time integration scheme is adopted. This approach offers improved stability compared to explicit methods, allowing for larger time steps. Additionally, the pressure correction equation utilizes the PRESTO scheme⁷⁵. To ensure convergence and mitigate potential numerical oscillations during the iterative solution process, under-relaxation factors are strategically employed for various governing equations. The energy equation utilizes a factor of 1.0, while the liquid fraction, momentum, and pressure equations are assigned factors of 0.5, 0.5, and 0.15, respectively. These values were chosen to achieve a balance between stability and computational efficiency. To guarantee the achievement of a converged transient solution, stringent convergence criteria are established for the governing equations. These criteria dictate the maximum permissible residuals for the continuity, momentum, and energy equations, set at 10^− 4, 10^− 4, and 10^− 8, respectively. To identify an optimal time step size that balances solution stability and computational efficiency, preliminary simulations were conducted using a trial-and-error approach. This iterative process yielded a time step of 0.05 s, which effectively ensured transient solution stability. To further guarantee convergence within each time step, a fixed number of 100 iterations was chosen.

Grid study

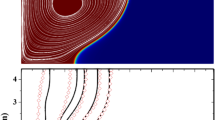
ANSYS ICEM software was utilized to establish the computational domain for this investigation. Considering the geometric features, a structured mesh was generated for efficient grid definition. A refined mesh was implemented within the NePCM region. This enhanced mesh resolution is crucial for capturing the intricate temperature gradients arising during the phase change process. In CFD simulations, achieving grid independence is crucial for guaranteeing the accuracy of numerical results. This study evaluates the influence of grid resolution on the solution by employing five meshes with varying cell counts (3056, 4538, 6019, 7546, and 9070) across different test cases. The objective is to assess whether the numerical solutions exhibit minimal sensitivity to grid size variations. Figure 3 exemplifies this grid independence evaluation by presenting liquid fraction profile over time for each mesh configuration. The test case employs GNP nanomaterials with specific parameters: VF_NM = 2.5%, L_Fin = 0.8, VF_Fin = 5%, and N_Fin=3.

The grid independence analysis focused on the maximum error in the liquid fraction between consecutive grid densities. Notably, the error between the third and fifth grids remained below 1.25%, and the difference between the fourth and fifth grids narrowed to just 0.34%. This iterative refinement process was repeated across various configurations, and consistently, the grid containing 7546 cells exhibited a maximum variation of less than 0.5% in liquid fraction compared to the next finer mesh. Consequently, considering the balance between accuracy and computational efficiency, a grid size of 7546 cells was chosen for all subsequent simulations. Figure 4 presents a meshed computational domain sample for a specific case of a finned enclosure-shaped LHTES.

Fig. 3

Grid independence evaluation for nano-finned enclosure-shaped LHTES unit with GNP nanomaterials, VF_NM = 2.5%, L_Fin = 0.8, VF_Fin = 5%, and N_Fin = 3.

Fig. 4

Meshed computational domain for a sample LHTES unit (L_Fin = 0.6, VF_Fin = 10%, and N_Fin = 2).

Validation

The accuracy of the proposed numerical model for simulating PCM melting is assessed through a comparative analysis with experimental LHTES data reported by Kamkari and Shokouhmand⁷⁶. They explored the melting behavior of lauric acid within a finned enclosure. Their experimental setup mirrored a configuration similar to the present nano-finned enclosure-shaped LHTES units, featuring a constant temperature boundary condition on one wall and adiabatic conditions on the remaining three. Three experimental scenarios with a constant wall temperature of 70 °C are considered for comparison. The enclosure configurations vary, encompassing scenarios with no fins (plane wall), a single fin (1 fin wall), and three fins (3 fin wall).

Figure 5 presents a comparison of the liquid fraction profiles obtained from the numerical model with the experimental data. While a slight discrepancy is observed for the finless LHTES unit scenario, with a maximum relative error of 6.5%, the numerical model exhibits excellent concordance with the experimental data for finned enclosures. This observation suggests that the present numerical scheme demonstrates good reliability in simulating PCM melting, particularly for configurations with fins.

Fig. 5

Comparative analysis of the liquid fraction profiles obtained from the current numerical model and the experimental data reported by Kamkari and Shokouhmand⁷⁶.

Objective functions

TES system design necessitates careful consideration of two critical objectives: energy storage time (charging/discharging durations) and total energy storage capacity. Prior research efforts have primarily focused on one aspect or the other. Some studies have prioritized optimizing charging/discharging times, while others have directed their attention toward maximizing total stored energy. Only a limited body of research has explored the possibility of concurrently optimizing both factors⁵³. This investigation treats total stored energy and phase change time as competing objectives within an LHTES system. The incorporation of fins and dispersed nanomaterials in PCM significantly influences both melting time and stored energy. While these enhancements promote faster melting, they also lead to a decrease in total energy storage capacity. To navigate this inherent conflict, a robust optimization method is employed to identify configurations that achieve an ideal balance between these two crucial performance metrics.

Within this research, melting time (t_m) is defined as the duration required for the NePCM to transition from a solid to a liquid state. This corresponds to a volume-average liquid fraction of $\:{\lambda\:}_{vol-avg}>0.999999$. To quantify the system’s energy storage capacity at each time, the following equation is employed⁷⁷:

$$\:{E}_{t}\left(t\right)={\rho\:}_{NePCM}{V}_{NePCM}{L}_{NePCM}+{\rho\:}_{NePCM}{V}_{NePCM}{{C}_{p}}_{NePCM}\left[{T}_{avg,\:NePCM}\left(t\right)-{T}_{i}\right]+{\rho\:}_{Al}{V}_{Al}{C}_{p,Al}\left[{T}_{avg,Al}\left(t\right)-{T}_{i}\right]$$

(19)

.

The total stored energy (E_t) is obtained at the completion of the melting process (t_m).

The total stored energy, as expressed in Eq. (19), is defined as the sum of the sensible and latent heat stored within the LHTES system upon the completion of the melting process (t_m). This equation comprises three terms: the first term represents the latent heat energy stored in the NePCM, the second term denotes the sensible thermal energy stored in the NePCM, and the third term accounts for the sensible energy stored in the fins. Consequently, according to Eq. (19), the total energy stored in the system depends on the material properties of the NePCM, the mass of NePCM and fins, average temperature ($\:{T}_{avg}$) at t_m and initial temperature ($\:{T}_{i}$), the latent heat of fusion ($\:{L}_{NePCM}$), and the specific heat capacities of both the NePCM and the aluminum fins.

Figures 6 and 7 delve into a comprehensive analysis of the melting time and total stored energy data extracted from the CFD simulations. To facilitate a multifaceted interpretation of the data distribution, three distinct visualization techniques are strategically employed.

Figures 6(a) and 7(a) utilize box plots to provide a concise overview of the distribution patterns for both total energy storage and melting time. These visualizations use quartiles to segment the data. The box itself represents the interquartile range (IQR), capturing the central 50% of the data points. Whiskers extend outward to encompass the lowest and highest data points within 1.5 times the IQR. Any data points considered outliers (red points), falling outside this whisker range, are depicted individually. Based on Fig. 6(a), the median is approximately 61.7 kJ, with the lower and upper quartiles ranging from around 60.9 to 62.8 kJ. Several outliers above 65 kJ are indicated by the red points. Similarly, based on Fig. 7(a), the median appears to be around 230 s, with the lower and upper quartiles ranging approximately from 160 to 300 s.

Figures 6(b) and 7(b) employ frequency distribution histograms to visually depict the prevalence of distinct total energy storage and melting time values within the dataset. These histograms enable the rapid identification of the E_t and t_m ranges that occur most frequently. As shown in Fig. 6(b), a normal distribution curve is overlaid on the histogram, indicating that the energy storage data approximately follows a normal distribution, with a peak around 61–62 kJ. Similarly, Fig. 7(b) features a normal distribution curve overlaid on the histogram, suggesting that the melting time data approximately follows a normal distribution, with a peak frequency occurring around 150–250 s.

On the other hand, Figs. 6(c) and 7(c) utilize violin plots, which offer a combined view of the data’s spread and underlying distribution. This visualization technique merges the strengths of box plots and kernel density estimation. The violin’s form mirrors the data’s density, with wider sections indicating a greater concentration of data points at specific E_t and t_m values. This presentation facilitates the evaluation of the distribution’s symmetry and potential for skewness.

Fig. 6

A detailed description of the E_t CFD data; (a) Box plot, (b) Frequency distribution histogram, and (c) Violin plot.

Fig. 7

A detailed description of the t_m CFD data; (a) Box plot, (b) Frequency distribution histogram, and (c) Violin plot.

RSM predictive modeling

Response surface methodology is a powerful statistical tool widely used for predicting and optimizing thermal energy storage systems efficiently. This methodology systematically analyzes the influence of multiple interacting variables on system performance through a mathematically driven approach⁷⁸. Instead of relying solely on computationally expensive simulations, RSM constructs predictive models that approximate the system’s behavior, allowing for rapid evaluation of different design scenarios. In the context of LHTES design, RSM plays a crucial role in establishing precise relationships between key input variables (fin geometry, nanomaterial type, and concentration) and performance metrics (total stored energy and melting time). One of the greatest advantages of RSM is its ability to identify interactions between factors, recognizing how changes in one parameter affect another and quantifying their combined influence on system performance⁷⁹. By employing polynomial regression models of varying complexity, RSM effectively captures nonlinear dependencies between design parameters, enabling the identification of optimal configurations with minimal computational/experimental effort⁸⁰. This integration of CFD simulations and RSM-based modeling allows for an efficient and systematic optimization process, making it possible to explore a broad range of design variables without excessive computational cost.

RSM analysis hinges on the assumption that the relationship between system responses ($\:{y}_{i}$) and the input vector, $\:x=\left({x}_{1},{x}_{2},\dots\:{x}_{n}\right)$, can be characterized by a linear or non-linear function. This function, denoted as $\:f$, encapsulates the intricate interplay between the input variables and the resulting system outputs^81,82:

$$\:{y}_{i}=f\left({x}_{i1},{x}_{i2},\dots\:{x}_{in}\right)\:\:\:\:\:\:\:\:(i=\text{1,2},\dots\:,M)$$

(20)

.

The core objective of RSM revolves around minimizing the residual, which represents the difference between $\:{y}_{i}$ and the corresponding predictions ($\:{\widehat{y}}_{i}$) generated by the predictive model ($\:\widehat{f}$)^81,82:

$$\:{\widehat{y}}_{i}=\widehat{f}\left({x}_{i1},{x}_{i2},\dots\:{x}_{in}\right)\:\:\:\:\:\:\:\left(i=\text{1,2},\dots\:,M\right),$$

(21)

$$\:\sum\:_{i=1}^{M}{\left[{\widehat{y}}_{i}-{y}_{i}\right]}^{2}\:\:\underrightarrow{\:\:\:\:\:\:\:\:\:}\:\:min$$

(22)

.

For this purpose, various models range from linear representations to higher-order polynomial functions encompassing 2nd-factor interactions (2FI), quadratic terms, cubic terms, and even more complex expressions. To achieve optimal fit, the models’ parameters are adjusted through a least squares technique⁸³.

In this paper, RSM effectively captures the complex interactions between design variables–fin-related variables and nanomaterials type and concentration–in LHTES systems by creating strong regression models that relate these variables to performance metrics containing total stored energy and melting time. To be more precise, RSM constructs a series of polynomial functions based on CFD-simulated data, allowing for the prediction of system behavior across a range of input values. This approach is particularly powerful for exploring non-linear relationships and interactions between variables, such as how different fin-related variables affect phase change behavior and energy storage when combined with specific types and concentrations of nanomaterials.

To ensure models generated through RSM can accurately predict beyond the training data, statistical safeguards against overfitting are implemented. Overfitting describes a model overly tailored to the training data, hindering its ability to generalize. RSM utilizes Predicted R² as a distinct metric, contrasting with traditional R² (coefficient of determination). While R² assesses in-sample fit, Predicted R² uses leave-one-out cross-validation (LOOCV) to evaluate out-of-sample performance. LOOCV iteratively builds the model on all data points except one, predicts the excluded value, and calculates the error. This process provides a more realistic assessment of the model’s ability to handle unseen data, bolstering confidence in its generalizability beyond the training data. Furthermore, to prevent overfitting, RSM uses statistical tests alongside LOOCV. Complex models can capture noise alongside real trends. Analysis of variance (ANOVA) with p-values identifies these terms – a high p-value suggests a term captures noise, not a true effect. Removing such terms via ANOVA simplifies the model and reduces overfitting, leading to more accurate and generalizable predictions⁸³. The RSM analysis is conducted using MATLAB software.

One of the key advantages of RSM is its ability to handle multiple variables simultaneously, making it suitable for systems with complex interactions. Additionally, it reduces the number of simulations needed to achieve reliable results, saving time and resources. However, a limitation of RSM is its reliance on polynomial approximations, which may not fully capture highly non-linear or intricate interactions in high-dimensional parameter spaces. As the number of variables increases, the accuracy of the model may diminish unless more sophisticated techniques or higher-order polynomials are used. Despite this, RSM remains a valuable tool for optimizing LHTES systems, particularly when used in combination with other optimization methods such as EHC for more complex cases.

Total stored energy

Evaluation based on statistical criteria revealed a reduced sixth-degree polynomial model, generated through RSM, as the optimal choice for predicting E_t. Based on the Table 5, this model demonstrated reasonable accuracy and performance. The model captures nearly 98.1% (R² = 0.9809) of the variation in Et. R², ranging from 0 to 1, gauges the model’s ability to explain response variable variance. However, a high R² in complex models can be misleading. Adjusted R² tackles this by penalizing for model complexity, adjusting the R² value based on the number of independent variables. High adjusted R² (0.9791) signifies model robustness and prevents overfitting, indicating strong alignment with observed data. The predicted R² (0.9776) further suggests the model’s capacity for accurate future predictions. In addition, the high Adequacy Precision (AP) of 139.82 signifies a strong signal-to-noise ratio, indicative of a model with good precision. AP, a metric derived by dividing the range of predicted values at the design points by the average prediction error, $\:AP=({\widehat{Y}}_{max}-{\widehat{Y}}_{min})/\sqrt{{p\widehat{\sigma\:}}^{2}/n}$), reflects the model’s ability to distinguish between signal and noise. In the AP formula, $\:\widehat{Y}$ are the predictions, $\:{\widehat{\sigma\:}}^{2}$ is the residual mean square, $\:p$ is the number of terms in the model, and $\:n$ is the number of CFD data. An AP value exceeding 4, as observed here, is desirable and suggests the model’s efficacy in discriminating between signal and noise.

According to Table 5, the low standard deviation (0.2015) signifies a tight clustering of predicted total stored energy values around the actual CFD data points. This suggests a high degree of agreement between the model’s predictions and the observed values. Furthermore, the mean predicted E_t value (61.78) aligns perfectly with the average CFD value, further strengthening the model’s accuracy. Additionally, the coefficient of variation (C.V. %) of 0.3261 indicates minimal relative variability within the model’s predictions. Collectively, these statistical measures demonstrate the model’s robustness and effectiveness in simulating the total stored energy within the nano-finned enclosure-shaped LHTES unit. This high level of reliability makes the model suitable for further analysis, optimization processes, and real-world applications. Details regarding the predictive model’s formulation can be found in supplementary materials.

Table 5 Statistical criteria of the RSM-based E_t predictive model.

Figure 8 offers a visual assessment of the reduced sixth RSM model’s accuracy in predicting total stored energy values. This figure utilizes a regression plot (Fig. 8(a)) to compare the CFD data points with the model’s predictions. The plot reveals a strong correlation, reflected in the high R² value of 0.9809. This value signifies a near-perfect alignment between the predicted and observed data points, suggesting minimal deviations from the Y = X line. In simpler terms, the data points are tightly clustered around the ideal prediction line, indicating the model’s exceptional ability to accurately capture the actual E_t values. Figure 8(b) employs a polar graph to visualize the absolute relative deviation ($\:{ARD}_{i}\left(\%\right)=\frac{\left|{Y}_{i,Pred}-{Y}_{i,CFD}\right|}{{Y}_{i,CFD}}\times\:100$) of the RSM model’s predictions for various combinations of nanomaterials and fins within the nano-finned enclosure-shaped LHTES units. In the ARD formula, $\:{Y}_{i,Pred}$ and $\:{Y}_{i,CFD}$ represent the predicted and actual (CFD) values, respectively. This metric assesses the model’s accuracy across different configurations. The figure indicates that the ARD remains below 1% for all combinations, signifying a high degree of accuracy overall. However, the level of accuracy varies slightly depending on the specific nanomaterial employed. The unit without nanomaterials shows the lowest relative error. Configurations incorporating fins alongside Ag, TiO₂, CuO, and Al₂O₃ nanomaterials exhibit some variability in accuracy. Conversely, units containing carbon-based nanomaterials or Cu nanomaterials exhibit an upper range of ARD values compared to other configurations. Specific details regarding the absolute relative deviation ranges for different unit configurations are as follows:

• Ag/Finned Unit: 0.0021% ≤ ARD ≤ 0.3229%.

• Al₂O₃/Finned Unit: 0.0036% ≤ ARD ≤ 0.3396%.

• Cu/Finned Unit: 0.1209% ≤ ARD ≤ 0.6234%.

• CuO/Finned Unit: 0.0014% ≤ ARD ≤ 0.3476%.

• Finned Unit: 0.0034% ≤ ARD ≤ 0.2691%.

• GNP/Finned Unit: 0.2227% ≤ ARD ≤ 0.7606%.

• MWCNT/Finned Unit: 0.1516% ≤ ARD ≤ 0.6381%.

• SWCNT/Finned Unit: 0.1022% ≤ ARD ≤ 0.6565%.

• TiO₂/Finned Unit: 0.121% ≤ ARD ≤ 0.3972%.

Figure 8(c) employs a margin of deviation (MOD) plot to visualize the relative error ($\:RE\left(\%\right)=\frac{CFD\:value-Predicted\:value}{CFD\:value}\times\:100$) of the RSM model’s E_t predictions. The RE values encompass both positive and negative values, allowing for an assessment of the model’s bias. Positive RE signifies instances where the model underestimates the actual E_t values obtained through CFD analysis. Conversely, negative RE indicates overestimations. The data set exhibits a balanced distribution between these two types of errors, with 340 instances (50%) of both overestimations and underestimations. This suggests that the model does not exhibit a systematic tendency to under or over-predict E_t values. Overestimations reach − 0.754%, while underestimations extend to 0.761%. This variability in prediction errors signifies that the model’s accuracy is not constant and can fluctuate in either direction. Furthermore, Fig. 8(d) utilizes violin diagrams to depict the probability density function (PDF) of the RSM model’s outputs. These diagrams facilitate a visual comparison between the model’s predictions and the CFD data. While the graphical representation suggests a high degree of overlap between the distributions, indicating good agreement, it is essential to acknowledge limitations. The RSM model exhibits some degree of inaccuracy throughout the prediction space. However, it is crucial to note that this inaccuracy is not concentrated in any specific Et value range but rather appears uniformly distributed across the entire predicted range.

Fig. 8

Visual assessment of the reduced sixth RSM model’s accuracy in predicting E_t values; (a) Regression graph, (b) ARD-based polar chart, (c) MOD graph, and (d) Violin plot.

Melting time

Among the evaluated RSM-based melting time prediction models, the reduced quartic polynomial model emerged as the most suitable choice. Table 6 shows the statistical criteria for this model. This model exhibited a high degree of accuracy and effectiveness in capturing the variability within the t_m data. As evident from the R² value of 0.9864, the model explains nearly 98.64% of the observed variance. Furthermore, the adjusted R² of 0.9851 indicates robustness against overfitting and a strong correlation with the CFD data. The predicted R² of 0.9835 further reinforces the model’s potential for accurate future predictions. Additionally, the adequacy precision value of 125.72 signifies a robust signal-to-noise ratio, implying a model with exceptional precision.

Furthermore, the standard deviation of 10.179 indicates a moderate spread of predicted t_m values around the corresponding CFD data points. This suggests a reasonable level of agreement between the model’s outputs and the observed values. Furthermore, the predicted t_m mean (238.42121) aligns closely with the average CFD value, further supporting the model’s accuracy. Additionally, the coefficient of variation (4.269) suggests a moderate degree of relative variability within the model’s predictions. Taken together, these statistical measures demonstrate the model’s robustness and its capability to accurately simulate the t_m within the nano-finned enclosure-shaped LHTES unit. Refer to the supplementary materials for details regarding the model’s formulation.

Table 6 Statistical criteria of the RSM-based t_m predictive model.

Figure 9 provides a visual validation of the reduced quartic RSM model’s effectiveness in predicting melting time values. A regression plot (Fig. 9(a)) is employed to compare the CFD data points with the model’s predictions. The plot reveals a close clustering of data points around the ideal prediction line (Y = X). This signifies a reasonable degree of agreement between the model’s outputs and the observed t_m values, suggesting acceptable accuracy. Furthermore, a separate polar chart explores the ARD of the model’s predictions for various nano-finned enclosure-shaped LHTES configurations involving different nanomaterials and fins (Fig. 9(b)). While the ARD remains below 30% for all configurations, indicating generally good accuracy, some variations exist. The unit without nanomaterials (finned unit) demonstrates the lowest relative errors. Configurations incorporating fins alongside Ag, Cu, and Al₂O₃ nanomaterials exhibit a higher range of ARD values compared to the finned unit. Conversely, units that incorporate CuO, TiO₂, MWCNT, and SWCNT nanomaterials show moderate accuracy. Interestingly, the model in predicting data regarding units containing GNP displays the highest relative errors. Details regarding the specific ARD ranges for each configuration are presented below:

• Ag/Finned Unit: 0.025% ≤ ARD ≤ 7.491%.

• Al₂O₃/Finned Unit: 0.008% ≤ ARD ≤ 7.966%.

• Cu/Finned Unit: 0.057% ≤ ARD ≤ 7.848%.

• CuO/Finned Unit: 0.049% ≤ ARD ≤ 9.252%.

• Finned Unit: 0.004% ≤ ARD ≤ 6.909%.

• GNP/Finned Unit: 0.563% ≤ ARD ≤ 26.890%.

• MWCNT/Finned Unit: 0.036% ≤ ARD ≤ 8.720%.

• SWCNT/Finned Unit: 0.041% ≤ ARD ≤ 9.920%.

• TiO₂/Finned Unit: 0.278% ≤ ARD ≤ 9.905%.

Figure 9(c) employs a MOD plot to visualize the relative error of the model’s t_m predictions. RE values encompass both positive and negative values, providing insight into potential model bias. The data exhibits a balanced distribution, with 49% of predictions overestimating and 51% underestimating actual t_m values obtained from CFD analysis. This suggests that the model does not exhibit a consistent tendency to over or under-predict t_m. However, the observed error magnitudes are noteworthy. Underestimations reach 18.51%, while overestimations extend to -26.89%. Notably, a limited number of data points exhibit overestimations exceeding the typical RE range, suggesting potential outliers. Furthermore, Fig. 9(d) utilizes violin diagrams to depict the PDF of the model’s outputs. While the violin plot suggests a significant overlap between the model’s predictions and the CFD data, indicating good overall agreement, it is crucial to acknowledge some level of inaccuracy persists. Importantly, this inaccuracy is not concentrated in any specific t_m value range, but rather appears uniformly distributed across the entire predicted range.

Fig. 9

Visual assessment of the reduced quartic RSM model’s accuracy in predicting t_m values; (a) Regression graph, (b) ARD-based polar chart, (c) MOD graph, and (d) Violin plot.

Effect of inputs on responses

The RSM-derived models for predicting total stored energy and melting time offer valuable insights into the interplay between input variables and design objectives. This section presents contour plots (Figs. 10, 11, 12, 13, 14 and 15) that illustrate the interactive effects of continuous input variables on the response objectives, with variations across different values of discrete input variables. In Figs. 10, 11 and 12, the performance of the units is organized from highest to lowest based on total stored energy, with the best-performing unit positioned in the upper left and the least-performing in the lower right. Similarly, Figs. 13, 14 and 15 display the units’ performance in terms of melting time, following the same arrangement for clear comparative analysis.

Figure 10 examines the combined effects of fin volume fraction and nanomaterial volume fraction on total stored energy in nano-finned enclosure-shaped LHTES units. These units incorporate different nanomaterials, including metals, metal oxides, and carbon-based variants, each influencing thermal performance differently. A key observation from Fig. 10 is the trade-off between enhanced thermal conductivity and reduced latent heat storage. Increasing VF_NM generally leads to a reduction in total stored energy, as nanomaterials typically possess a lower latent heat capacity than the base PCM. As a result, increasing the nanomaterial concentration diminishes the overall energy storage capacity, despite improving thermal conductivity. Similarly, increasing VF_Fin also reduces total stored energy because a higher fin volume displaces a portion of the PCM, decreasing the amount of material available for latent heat storage. However, the effect of VF_Fin is more pronounced than VF_NM, as indicated by the steeper contour slopes in Fig. 10. This suggests that fin volume plays a dominant role in determining the overall energy storage capacity. Among the nanomaterial types, carbon-based nanomaterials (GNPs and MWCNTs) exhibit the best trade-off between improving heat transfer and minimizing stored energy loss. Their higher thermal conductivity enhances heat dissipation, leading to a more efficient phase change process while maintaining a relatively high energy storage capacity. Units incorporating metallic nanomaterials (Ag and Cu), however, demonstrate the weakest performance, as their relatively high density and moderate thermal conductivity provide less benefit to energy storage efficiency. According to Fig. 10, units containing GNPs and MWCNTs achieve a total stored energy ranging from 61 kJ to over 64 kJ, indicating superior thermal performance. In contrast, units with metallic nanomaterials store only 60 to 63 kJ, confirming that their inclusion results in a lower overall energy storage efficiency.

Figure 11 explores the combined influence of fin volume fraction and dimensionless fin length on total stored energy in nano-finned enclosure-shaped LHTES units. For a clearer comparison, this figure includes a finned unit without nanomaterials, which serves as a reference for evaluating the impact of nanomaterial addition. The results in Fig. 11 reveal that units without nanomaterials achieve the highest stored energy, reinforcing the negative impact of nanomaterial inclusion on latent heat storage. This is due to nanomaterials possessing lower latent heat capacity than the base PCM, reducing the overall energy storage potential despite their thermal conductivity benefits. Interestingly, the interaction between VF_Fin and L_Fin exhibits nonlinear behavior. At low fin volume fractions, increasing L_Fin initially enhances stored energy, likely due to improved heat distribution and enhanced natural convection within the PCM. However, beyond a certain threshold, further increasing L_Fin leads to a decline in stored energy, as elongated fins displace more PCM, reducing latent heat storage capacity. Conversely, at high fin volume fractions, increasing L_Fin consistently reduces stored energy, indicating that excessive fin volume diminishes the available PCM volume to a greater extent than the thermal enhancement benefits provided by the fins. This finding highlights the importance of optimizing both fin volume and length to achieve a balance between heat transfer enhancement and energy storage efficiency. Regarding nanomaterial selection, GNP- and MWCNT-enhanced units again demonstrate the best trade-off between heat transfer improvement and energy storage loss, consistent with Fig. 10. In contrast, units incorporating metallic nanomaterials (Ag, Cu) exhibit the lowest stored energy across all variations of VF_Fin and L_Fin, confirming that their lower latent heat contribution outweighs any conductivity improvements they provide. As shown in Fig. 11, the pure PCM unit achieves the highest total energy storage (ranging from 62 to 64 kJ) across different fin configurations. However, with nanomaterial addition, this range decreases, and for units incorporating metallic nanomaterials, total stored energy is further reduced to 60.5–62.5 kJ. These findings emphasize that while fins play a dominant role in improving heat transfer, excessive fin volume and the inclusion of nanomaterials can negatively impact latent heat storage capacity, making careful design optimization crucial.

Figure 12 examines the influence of fin count on total stored energy in nano-finned enclosure-shaped LHTES units containing GNPs, while also considering the combined effects of nanomaterial volume fraction and fin length. A key observation from Fig. 12 is the nonlinear interaction between fin length and VF_NM in determining energy storage performance. For units with 1 or 2 fins, the highest energy storage occurs at both the shortest and longest fin lengths, suggesting that shorter fins allow for greater PCM volume, while longer fins enhance energy storage potential without significantly reducing the PCM mass. However, this trend shifts in units with 3 to 5 fins. In these cases, increasing L_Fin consistently reduces stored energy, regardless of VF_NM. This decline is due to the cumulative reduction in available PCM volume caused by both the increased fin count and length, limiting the unit’s latent heat storage capacity. The results indicate a tipping point, where adding more fins beyond a certain threshold becomes detrimental, particularly in units with higher nanomaterial concentrations. These findings emphasize the importance of balancing fin count and length to optimize both heat transfer efficiency and energy storage capacity in LHTES unit design.

Fig. 10

The simultaneous effect of the volume fraction of fins and nanomaterials on the total stored energy for different units.

Fig. 11

The simultaneous impacts of the VF_Fin and L_Fin on the total stored energy for various units.

Fig. 12

Combined influence of VF_NM and L_Fin on total stored energy for GNP/finned unit with various number of fins.

Figure 13 explores the combined effects of fin length and volume fraction of nanomaterials on phase change time for nano-finned enclosure-shaped LHTES units containing various nanomaterials. The figure reveals a consistent trend: increasing L_Fin leads to a decrease in phase change time. This effect becomes more pronounced with higher VF_NM, suggesting a synergistic interaction between fin configuration and nanomaterial concentration. Additionally, as expected, increasing VF_NM itself directly reduces phase change time. Interestingly, units containing GNPs demonstrate the most favorable performance in terms of phase change time. Units incorporating CNTs also exhibit good performance, with similar results to GNPs. A noteworthy observation is the relatively good performance of metal nanoparticles in terms of phase change time, despite their lower performance in stored energy. Metal nanoparticles outperform metal oxide nanoparticles in this regard. This difference can be attributed to the thermal conductivity properties of the nanomaterials. Carbon-based nanomaterials possess exceptionally high thermal conductivity, enabling efficient heat transfer throughout the PCM. This expedites both the melting and freezing processes, leading to faster phase change times. While metal and metal oxide nanoparticles offer a balance in conductivity, their values are generally lower compared to carbon nanomaterials. Furthermore, carbon nanomaterials, particularly graphene sheets, have the unique ability to form interconnected networks within the PCM. This network acts as a thermal pathway, significantly enhancing heat transfer throughout the material. Metal and metal oxide nanoparticles tend to be more dispersed within the PCM, limiting their ability to form such effective networks. As illustrated in Fig. 13, for the unit containing GNP, the complete melting of the phase change material takes between 110 and 250 s, depending on the fin length and the volume fraction of nanomaterials. In contrast, this time increases to 160 to 330 s for units with metallic nanomaterials. The longest melting duration is observed in units containing metal oxide nanomaterials, where the complete melting process takes approximately 170 to 350 s.

Figure 14 investigates the combined effects of volume fraction of fins and fin length on melting time for various nano-finned enclosure-shaped LHTES units. Interestingly, the figure reveals that L_Fin exerts a more dominant influence on melting time, particularly for units with lower VF_Fin. Increasing L_Fin leads to a significant reduction in melting time. This can be attributed to the increased surface area for heat transfer provided by longer fins. These fins not only facilitate heat transfer at the PCM’s surface but also act as heat conductors, transferring heat deeper into the material. This deeper penetration promotes a more uniform melting process throughout the PCM volume. Conversely, when L_Fin is short, VF_Fin have a minimal impact on melting time. This suggests that a critical fin length is necessary for VF_Fin to significantly influence the melting process. Consistent with prior observations (refer to Fig. 13), units containing carbon-based nanomaterials exhibit the best performance in terms of melting time. However, a notable finding is that the performance of units incorporating metal nanoparticles and metal oxides is not significantly different from the unit without nanoparticles. This observation can be explained by considering the natural convection ability of the PCM, a key mechanism in its phase change process. It is important to note that the incorporation of nanomaterials can lead to an increase in the dynamic viscosity of the liquid phase of the PCM. This phenomenon can potentially influence heat transfer characteristics within the LHTES unit. Therefore, in units containing nanomaterials with low thermal conductivity (such as metal and metal oxide nanoparticles), the introduction of these materials may impede the natural convection of the liquid phase during melting. This potentially counteracts the benefits of increased thermal conductivity offered by nanomaterials, leading to a similar melting time to the unit without nanoparticles. As shown in Fig. 14, the melting time for units containing carbon nanomaterials, influenced by fin-dependent variables, ranges from 110 to 300 s. However, when the unit contains pure PCM, the melting time increases to 160 to 350 s. Units with metallic nanomaterials exhibit a slight increase in melting time compared to pure PCM. Additionally, replacing metallic nanomaterials with metal oxide nanomaterials results in a 5–10% increase in melting time.

Figure 15 shows the interplay between the number of fins, volume fraction of nanomaterials, and fin length on melting time for finned LHTES units containing GNPs. The figure reveals a clear trend: increasing the number of fins within a fixed volume leads to a decrease in phase change time. This effect intensifies with higher VF_NM and longer L_Fin, suggesting a synergistic interaction between these factors. However, a critical observation is that for unit with only one fin, variations in fin length and VF_NM have minimal impact on melting time. In contrast, for units with multiple fins, changes in these input variables exert a significant influence on melting time. The incorporation of multiple fins, even if they are shorter in length, increases the overall surface area available for heat transfer within the PCM. This principle is analogous to adding lanes to a highway, facilitating a more efficient flow of heat into the PCM and consequently accelerating the melting process.

Fig. 13

Interactive effects of VF_NM and L_Fin on melting time for various units.

Fig. 14

The simultaneous effects of VF_Fin and L_Fin on melting time for various units.

Fig. 15

The mixed effects of VF_NM and L_Fin on melting time for GNP/finned unit with different number of fins.

Multi-objective optimization

Enhanced hill-climbing approach

This section details the optimization process employed for the determining nano-finned enclosure-shaped LHTES unit design variables. A numerical method based on the hill climbing algorithm is utilized. The standard hill climbing method is susceptible to convergence issues, potentially becoming trapped in local optima and generating inaccurate solutions. To address these limitations, an enhanced variant of the hill climbing technique has been developed. This improved method incorporates a mechanism for introducing randomness alongside the evaluation of design points. This allows the algorithm to escape local optima and explore a broader solution space, potentially leading to the identification of a more globally optimal design configuration. The enhanced optimization method can be summarized in four key steps^81,82:

• 1. Let $\:X$ denote a vector representing the design variables ($\:{x}_{i}$, where i ranges from 1 to n) within the optimization domain. The design variables are identical to the input variables, which encompass both fin and nanomaterial variables. This domain is a restricted subset of the broader design space.

• 2. The objective function seeks to optimize a set of $\:m$ response variables denoted by $\:{y}_{j}\left(X\right)$ (where j ranges from 1 to m). In the present problem, two response variables are total stored energy and melting time. In fact, $\:{y}_{j}\left(X\right)$ represents the j-th response variable as a function of the design variables vector $\:X$. These response variables are subjected to a series of constraints. For each response variable $\:{y}_{j}$, a lower bound ($\:{L}_{j}$) and an upper bound ($\:{U}_{j}$) are established, defining the permissible range of values within the optimization process.

• 3. The optimization process aims to achieve an optimal value for the response function, denoted by $\:y\left(X\right)$. To achieve this, an objective function, $\:f\left(X\right)$, is constructed. The specific form of this function depends on the desired optimization direction:

• For maximization problems: $\:f\left(X\right)$, is defined as the negative of the response function, $\:f\left(X\right)=-y\left(X\right)$. This transformation ensures that maximizing $\:f\left(X\right)$ is equivalent to maximizing the original response $\:y\left(X\right)$.

• For minimization problems: $\:f\left(X\right)$ is defined as the response function itself, $\:f\left(X\right)=y\left(X\right)$. In this case, minimizing $\:f\left(X\right)$ directly corresponds to minimizing the original response $\:y\left(X\right)$.

• 4. The optimization process can be further refined by incorporating a set of constraints. These constraints are expressed as a series of non-continuous functions. These functions define the permissible regions within the design space that satisfy the optimization criteria^81,82:

$\:{g}_{j}\left(X\right)={y}_{j}\left(X\right)-{U}_{j}$$\:for\:{y}_{j}>{U}_{j}$,(23)

$\:{g}_{j}\left(X\right)=0$$\:for\:{L}_{j}\le\:{y}_{j}\le\:{U}_{j}$,

$\:{g}_{j}\left(X\right)={L}_{j}-{y}_{j}\left(X\right)$$\:for\:{y}_{j}<{L}_{j}$.

The constraint function $\:{g}_{j}\left(X\right)$ determines whether the response variable $\:{y}_{j}\left(X\right)$ remains within the allowed range $\:[{L}_{j},{U}_{j}]$. The constraints ensure that these values stay within their acceptable ranges, such as specifying a maximum allowable melting time or a minimum required stored energy for the LHTES unit. This equation defines the feasible region in the design space where these conditions are satisfied. The aforementioned approach results in a system with m constraints. These constraints can be addressed by transforming the problem into an unconstrained optimization problem. This is achieved through the penalty function technique. This technique introduces a penalty term into the objective function, which increases in value as the solution violates the defined constraints. By minimizing the modified objective function, the optimization process is effectively guided towards solutions that satisfy all the constraints^81,82:

$$\:Minimize\:\left\{f\left(X\right)+p\sum\:_{j}^{\:}{g}_{j}\left(X\right)\right\},\:\:p>0\:\:for\:\:j=1\dots\:m$$

(24)

,

In Eq. (24), $\:f\left(X\right)$ is the objective function that combines the goals of maximizing stored energy and minimizing melting time, while $\:\:p$ is the penalty parameter that imposes a cost for violating constraints. The constraint function $\:{g}_{j}\left(X\right)$, from Eq. (23), ensures that the design remains within permissible bounds. This equation guides the optimization process by modifying the objective function to include penalties when constraints are violated, such as exceeding the maximum melting time or falling below the minimum stored energy. The penalty parameter ensures that the optimization favors solutions within the feasible region, balancing the trade-offs between stored energy and melting time. For maximizing stored energy, the function $\:{f}_{max}\left(X\right)=-{y}_{1}\left(X\right)$ is used, where $\:{y}_{1}\left(X\right)$ represents stored energy, and the negative sign ensures that maximizing $\:{f}_{max}\left(X\right)$ corresponds to maximizing $\:{y}_{1}\left(X\right)$. For minimizing melting time, $\:{f}_{min}\left(X\right)=-{y}_{2}\left(X\right)$ is applied, where $\:{y}_{2}\left(X\right)$ represents melting time, directly minimizing $\:{y}_{2}\left(X\right)$ to achieve the objective.

Identifying a suitable starting point for the optimization can be challenging. In the context of a simplex downhill multidimensional pattern search, it is recommended to begin with a low penalty value. This allows the initial convergence to occur at a boundary of the design space or a fixed point within the feasible region. Subsequently, the penalty value is gradually increased to refine the search near the initial convergence point. This iterative process continues until convergence is achieved, based on pre-defined criteria. These criteria typically involve a threshold for either the minimal distance moved or the minimal change in the objective function value, often set to a value such as 10^− 6. The EHC technique is implemented using MATLAB software.

For problems involving multiple, potentially conflicting, responses (maximizing energy storage while minimizing melting time), multi-response optimization techniques are necessary. Myers et al.⁸⁴ introduced the desirability function, a popular approach. This method transforms individual responses into a single objective function by assigning desirability values, [0, 1], based on their proximity to desired ranges. A desirability of 1 signifies simultaneous satisfaction of all objectives. The technique employs a geometric mean of these individual desirabilities as the overall objective function, guiding the optimization process towards solutions that balance all response criteria^81,82:

$$\:D={\left({d}_{1}\cdot\:{d}_{2}\cdot\:\dots\:\cdot\:{d}_{n}\right)}^{\frac{1}{n}}={\left(\prod\:_{i=1}^{n}{d}_{i}\right)}^{\frac{1}{n}}$$

(25)

,

where n denotes the quantity of responses and d represents their corresponding desirability. According to the present problem, the stored energy $\:{y}_{1}$​ is associated with a desirability $\:{d}_{1}$​, which is calculated based on how close the stored energy is to the maximum desired value, where a higher energy storage corresponds to a higher desirability. For melting time $\:{y}_{2}$​, the desirability $\:{d}_{2}$ is determined by how close the melting time is to the minimum desired value, with a shorter melting time corresponding to a higher desirability. The overall desirability $\:D$ is the geometric mean of the individual desirability values $\:{d}_{1}$ and $\:{d}_{2}$​, providing a single measure of how well the design satisfies both objectives simultaneously. A higher $\:D$ indicates a better overall balance between energy storage and melting time. If any individual response falls outside their desirable range, the entire evaluation process becomes invalid, thereby hindering the optimization procedure.

Multi-response optimization often involves objectives with varying importance depending on the specific application. The desirability function can be adapted to address this by assigning weighting coefficients to each response within the function itself. This allows the designer to prioritize certain objectives based on their needs. Equation (26) exemplifies this concept, incorporating weighting factors (w_i) into the desirability function to achieve tailored optimization^81,82:

$$\:D={\left({d}_{1}^{{w}_{1}}\cdot\:{d}_{2}^{{w}_{2}}\cdot\:\dots\:\cdot\:{d}_{n}^{{w}_{n}}\right)}^{\frac{1}{\sum\:{w}_{i}}}={\left(\prod\:_{i=1}^{n}{d}_{i}^{{w}_{i}}\right)}^{\frac{1}{\sum\:{w}_{i}}}$$

(26)

In Eq. (26), the weights $\:{w}_{1}={\text{W}}_{E}$ and $\:{w}_{2}={\text{W}}_{T}$​ represent the relative importance of stored energy and melting time, respectively. For instance, if stored energy is more critical, a higher weight $\:{\text{W}}_{E}$ is assigned to the desirability $\:{d}_{1}$​, while if melting time is more critical, a higher weight $\:{\text{W}}_{T}$ is assigned to $\:{d}_{2}$. The weighted desirability $\:D$ is calculated by raising each desirability value to its corresponding weight, multiplying these values, and then normalizing by the sum of the weights. This approach allows for the prioritization of certain objectives over others, making the optimization process more flexible and adaptable to specific needs. Setting a weighting coefficient to zero within the desirability function removes a response from the optimization process. This allows the designer to prioritize specific objectives by essentially reducing the problem to a smaller set of key responses.

Optimization results

A variety of design scenarios can be generated by assigning relative weights to the objectives of the problem, as outlined in Eq. 26. These weights are assigned proportionally to highlight the relative importance of each objective rather than their absolute values. Accordingly, Figs. 16, 17, 18 and 19 display the local optimal values of different variables across various design scenarios. With this approach, when a specific scenario is considered, the designer can obtain local optimal values by weighting the responses and accounting for specific input conditions. The independent variable represented on the x-axis significantly influences the optimized variable, resulting in notable variations in the optimal values on the y-axis. This visualization method was chosen to clearly illustrate the impact of influential variables on the optimal outcomes.

Figure 16 explores the optimal volume fraction of nanomaterials for various nanomaterial types within nano-finned enclosure-shaped LHTES units, considering a scenario where the importance of melting time is weighted five times higher than total stored energy (W_E = 1 & W_T = 5). Based on figure, for all nanomaterials, a VF_NM exceeding 2% appears to be necessary to achieve optimal performance. Furthermore, the figure reveals an interplay between fin volume and optimal VF_NM. Units with smaller fin volumes require a higher VF_NM (above 3.5%) for optimal conditions. Conversely, as fin volume increases, the optimal nanomaterial concentration decreases. This suggests a potential trade-off between fin configuration and nanomaterial utilization. Interestingly, both metallic nanomaterials (Cu and Ag) and metal oxides (Al₂O₃ and TiO₂) exhibit similar trends in their optimal VF_NM. alumina and titanium oxide materials also show the highest optimal concentrations compared to other nanomaterials explored. It is crucial to note that the optimal VF_NM becomes zero when the importance of stored energy is equal to or outweighs that of melting time. In simpler terms, if the unit achieves a desired balance in stored energy, the incorporation of nanoparticles might become counterproductive, potentially hindering performance. This emphasizes the need to carefully consider application-specific priorities when selecting nanomaterials for nano-finned enclosure-shaped LHTES units. It should be noted that, in this particular analysis, the optimized variable (y-axis) and the influential variable (x-axis) are interrelated in a manner that prioritizes a specific scenario: one where the importance of melting time outweighs that of stored energy. In other scenarios, the significance of nanoparticle type and volume fraction diminishes considerably due to the focus on maximizing stored energy, rendering optimization less critical. Consequently, optimization of nanomaterial-related variables becomes relevant primarily when phase change time is a paramount consideration.

Figure 17 shows the optimal number of fins for various dimensionless fin lengths within the LHTES units. Various design scenarios for LHTES units may differ depending on the prioritization of design objectives. In certain applications, phase change time is of greater importance, making configurations that minimize this time critical. Conversely, in other cases, the thermal energy storage capacity may take precedence over melting time. Additionally, in some applications, equal importance may be assigned to both objectives. As a result, in the present paper, three primary design scenarios can be envisioned for LHTES units incorporating nanomaterials and fins, based on the specific requirements of different applications, as outlined below:

• Scenario 1 (W_T=5 & W_E=1): Prioritizes melting time. In this scenario, increasing the dimensionless fin length from 0.4 to 1 leads to a rise in the optimal fin count from 3 to 5. This suggests that a larger number of fins becomes beneficial when melting time is the primary concern and fin length is increased.

• Scenario 2 (W_T=1 & W_E=5): Prioritize stored energy. In this scenario, the optimal fin count exhibits a more complex relationship with fin length. For shorter or longer fins (dimensionless length around 0.4 or 1), a single fin appears optimal. However, for intermediate fin lengths (0.5–0.8), the optimal count increases to 5.

• Scenario 3 (W_T=1 & W_E=1): Equal weight to both objectives. In this scenario, analogous to the preceding scenario, an increase in the dimensionless length of the fins initially leads to a rise in the optimal number of fins from 3 to 5, followed by a reduction to N_Fin=1 at the maximum fin length.

These observations highlight the interdependent nature of fin parameters in determining the optimal fin configuration for nano-finned enclosure-shaped LHTES units. The weighting of performance and the dimensionless fin length can significantly influence the optimal number of fins required within the unit.

Figure 18 shows the optimal length of fins by changing the number of fins based on three defined scenarios:

• Scenario 1 (W_T=5 & W_E=1): In this scenario, melting time is the primary objective, which is reflected in the relatively high dimensionless fin lengths, consistently ranging between 0.9 and 1 for configurations with one to five fins. The focus on minimizing melting time results in an increased fin length to enhance heat transfer efficiency. Longer fins improve the melting rate by increasing the heat transfer surface area, thereby achieving faster thermal response times. This behavior aligns with the prioritization of rapid heat dissipation over stored energy capacity.

• Scenario 2 (W_T=1 & W_E=5): When stored energy becomes the primary objective, the optimal dimensionless fin length is maximized for configurations with fewer fins (one or two), where energy storage may not be limited by the surface area for heat transfer. However, as the number of fins increases from three to five, the optimal dimensionless length significantly decreases, falling between 0.52 and 0.57. This reduction in fin length could be due to diminishing returns on energy storage efficiency with more fins, which introduce additional thermal resistance and reduce the unit’s ability to store energy effectively.

• Scenario 3 (W_T=1 & W_E=1): With both melting time and stored energy given equal priority, the optimal configuration balances these competing objectives. The fin length reaches its maximum values for configurations with one to three fins, allowing an effective compromise between melting time and energy storage. However, with four or five fins, the optimal dimensionless fin length decreases to a range of 0.67 to 0.8, suggesting that beyond a certain number of fins, longer fins may hinder balanced performance, due to increased thermal resistance impacting both objectives.

Figure 19 illustrates the optimal volume fraction of fins across various scenarios and fin counts, analyzed as follows:

• Scenario 1 (W_T=5 & W_E=1): In this scenario, melting time is prioritized, leading to an optimal VF_Fin of 10% for configurations with one to three fins. A higher fin volume fraction in this range enhances the heat transfer rate, which helps reduce melting time by maximizing the surface area for heat dissipation. However, as the number of fins increases to four or five, the optimal volume fraction decreases to between 6% and 8%. This reduction could indicate that beyond a certain number of fins, the increased fin volume becomes less effective for melting time improvement.

• Scenario 2 (W_T=1 & W_E=5): When stored energy is prioritized, the optimal volume fraction of fins is minimized to 5% across all fin configurations. A lower fin volume fraction reflects an attempt to increase PCM volume within the unit, which can enhance its capacity to retain stored energy. Thus, minimizing the fin volume fraction in this scenario aligns with the objective of maximizing stored energy.

• Scenario 3 (W_T=1 & W_E=1): In this balanced scenario, where both melting time and stored energy are given equal priority, the optimal configuration requires a fin volume fraction of 5%, similar to Scenario 2. This suggests that a lower volume fraction strikes an effective balance between enhancing heat transfer for melting and preserving the unit’s energy storage capacity. By maintaining a minimal fin volume fraction, this configuration avoids excessive PCM reduction while ensuring rapid melting, thereby supporting both objectives.

Fig. 16

Optimum VF_NM for various nanomaterials type and different VF_Fin (N = 3 and L_Fin = 0.7).

Fig. 17

Optimum N_Fin for various L_Fin (GNP-Finned unit, VF_Fin = 7.5% and VF_NM = 2.5%).

Fig. 18

Optimum L_Fin for various number of fins (GNP-Finned unit, VF_Fin = 7.5% and VF_NM = 2.5%).

Fig. 19

Optimum VF_Fin for various number of fins (GNP-Finned unit, L_Fin = 1 and VF_NM = 3%).

Figures 16, 17, 18 and 19 illustrate the local optimal designs for various input combinations. To consider all input variables across different scenarios, it’s beneficial to select global optimal designs. To achieve this, Table 7, taking all inputs into account, presents global optimal designs. This table extends the three dual-objective scenarios by incorporating two additional single-objective scenarios (Scenarios 4 and 5). Scenario 1 prioritizes melting time over energy storage, resulting in a moderate energy storage of 63.03 kJ and a relatively short melting time of 91.76 s, with a higher number of long fins and a large fin volume fraction enhancing heat transfer. Scenario 2 reverses this priority, resulting in high energy storage (66.15 kJ) but a moderate melting time (222.3 s) by using only one fin with maximum length and a lower volume fraction of both nanomaterials and fins. Scenario 3 balances the objectives, yielding 64.67 kJ of energy storage and a melting time of 137.4 s, with a moderate fin design. Scenario 4 focuses solely on minimizing melting time, achieving the shortest melting time (66.84 s) at the expense of energy storage (60.21 kJ), with a high-volume fraction of fins and nanomaterials, as well as long fin length and a greater number of fins. Scenario 5, which prioritizes energy storage, results in the highest energy storage (66.36 kJ) but also a long melting time (312.9 s). This scenario uses only pure PCM without nanomaterials and employs the lowest fin volume fraction and the fewest number of fins.

Table 7 Optimal design variables and corresponding objectives for various design scenarios.

In this study, the enhanced hill climbing optimization technique was employed to address the limitations of the traditional hill climbing method, which is prone to becoming trapped in local optima and generating suboptimal solutions. The enhanced version introduces controlled randomness, enabling the exploration of a broader solution space and increasing the likelihood of identifying globally optimal design configurations. Compared to alternative optimization techniques such as genetic algorithms (GA) and particle swarm optimization (PSO), the enhanced hill climbing method offers greater computational efficiency and simplicity, particularly for problems with lower-dimensional design spaces, while still maintaining robust performance in avoiding local optima.

Conclusion

This study presents a groundbreaking investigation into the optimization of nano-finned enclosure-shaped LHTES units incorporating fins and nano-enhanced phase change materials. Through a comprehensive hybrid approach combining CFD simulations, RSM modeling, and EHC optimization, we have identified optimal design configurations that significantly enhance the thermal performance and storage capacity of these units. Our findings reveal that the judicious selection of fin geometry and nanomaterial type can lead to substantial reductions in phase change time and increases in total stored energy. The key findings of this investigation are as follows:

• Reduced sixth-degree and reduced quartic polynomial models constructed through RSM demonstrated high accuracy in predicting total stored energy and melting time, respectively.

• The impact of various design variables on both E_t and t_m was systematically evaluated. The trade-off between maximizing stored energy and minimizing melting time was explored.

• The incorporation of nanomaterials generally led to a decrease in total stored energy due to their lower latent heat compared to the base PCM. However, carbon-based nanomaterials (GNPs, MWCNTs) exhibited the most favorable trade-off, offering faster melting times with minimal reduction in stored energy.

• Fin volume plays a more significant role in determining the overall energy storage capacity compared to the volume fraction of nanomaterials.

• The number of fins, fin volume fraction, and fin length exhibited complex interactions in their influence on both stored energy and melting time. The optimal configuration depends heavily on the weighting assigned to the objectives (melting time vs. stored energy).

• In the optimization process for the scenario that prioritizes melting time, the design results in a moderate energy storage of 63.03 kJ and a relatively short melting time of 91.76 s. When energy storage is highly prioritized, the design achieves a high energy storage capacity of 66.15 kJ, but this comes at the cost of a relatively long melting time of 222.3 s. In a balanced scenario, where equal importance is given to both energy storage and melting time, the design yields 64.67 kJ of energy storage and a moderate melting time of 137.4 s.

The limitations of this study include the potential for inaccuracies in the CFD simulations and the need for further validation through experimental testing. Furthermore, potential scale-up challenges represent another limitation of this research, which should be further investigated. Furthermore, while this study considers the effect of nanomaterials on modifying the thermophysical properties of the PCM, it does not explicitly model the dynamic behavior, migration, or aggregation of nanomaterials during phase transition. This assumption is commonly used in nanofluid PCM modeling to reduce computational complexity while maintaining accuracy in assessing thermal performance improvements. However, in real-world applications, nanoparticles may move, settle, or cluster within the PCM, potentially influencing thermal conductivity and phase change dynamics. Future research could address this limitation by employing multiphase models such as Lagrangian particle tracking or Eulerian two-phase flow models to capture nanoparticle transport behavior during melting and solidification. Additionally, experimental studies could validate the impact of nanoparticle migration and long-term dispersion stability in LHTES units. These considerations will be essential for refining the practical applicability of nano-enhanced PCMs in thermal energy storage systems.