Introduction

Emotion recognition is a core research topic in artificial intelligence focused on analyzing and understanding human emotional states. This technology plays a pivotal role in enhancing human-computer interaction, advancing mental health management, and optimizing user experience design. In recent years, Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTM) networks have been widely applied in emotion recognition and related fields, demonstrating remarkable performance1,2. For instance, Febrian2proposed a Bidirectional LSTM (Bi-LSTM)-CNN model that achieved outstanding results in facial expression recognition. However, occlusions pose a significant challenge to facial expression analysis3. Even with multi-task auxiliary correction (MTAC) methods4, maintaining stability in complex scenarios remains a formidable task. Beyond facial expressions, CNNs and LSTMs have also proven highly effective in physiological signal-based emotion recognition. These models have been successfully applied to classify emotions using signals such as electrocardiogram (ECG)5, electrodermal activity (EDA)6, and electromyography (EMG)7, further validating the potential of physiological signals in this domain. Du8introduced the ATDD-LSTM model, which effectively captures nonlinear relationships between EEG electrodes, significantly improving EEG-based emotion recognition. Additionally, Chakravarthi9developed a CNN-LSTM hybrid framework based on ResNet- 152, achieving highly accurate emotion classification. In another study10, a CNN-LSTM hybrid architecture integrated with a stochastic fractal search optimization algorithm, further improved recognition performance.

Despite significant progress in deep learning-based unimodal emotion recognition, inherent limitations persist across different approaches. For instance, text-based emotion recognition heavily relies on semantic understanding, making it difficult to detect implicit emotions11,12. Similarly, single physiological signal-based emotion recognition faces challenges related to individual differences, signal variability, and environmental noise, which limit its generalization capabilities. To address these issues, integrating multiple physiological signals has emerged as a promising strategy to enhance both generalization and stability. For example, self-supervised multimodal representation learning13, EEG and ECG fusion14, and combining EEG with electrooculography (EOG)15have significantly improved emotion recognition accuracy. Additionally, studies by Li16and Kang17emphasized the effectiveness of extracting features from multiple physiological signals for emotion classification, validating the importance of multimodal data utilization. These studies enhanced emotion recognition performance and broadened its applications, such as in the emotional assessment of gamers18and real-time conversation emotion recognition19. Notably, Wang20and Wang21 developed advanced emotion recognition strategies tailored for noisy environments, combining EEG with other modalities, such as speech and facial expressions.

The high dimensionality and non-linear characteristics of multi-parameter data challenge single algorithms in effectively processing this complexity. Ensemble learning, which combines multiple models for a single prediction task, has proven effective in enhancing model generalization. By integrating different machine learning models, Zhang22significantly improved the performance of emotion recognition algorithms using physiological signals. The two-tier ensemble strategy of deep convolutional neural network models shows the powerful potential of combining deep learning with ensemble learning23. In speech emotion recognition, Aishwarya24significantly improved accuracy by using various feature extraction techniques and ensemble methods, such as CatBoost and Voting classifiers. Furthermore, ensemble learning’s applications extend beyond labs, showing potential in real-world scenarios and maintaining high accuracy in noisy environments, as validated by numerous studies25,26. Zaman27and De28explored ensemble learning in specific applications, such as driver emotion recognition and personalized treatment for Alzheimer’s patients, highlighting its diverse applications and benefits for specific user groups. Finally, Subasi’s29 EEG processing method using ensemble classifiers achieved extremely high accuracy, demonstrating the value of ensemble learning in specialized fields. These findings provide robust evidence for advancements in emotion recognition technology and offer valuable insights for future research directions.

In summary, deep learning algorithms such as CNNs and LSTMs exhibit great potential in emotion recognition. Meanwhile, ensemble learning improves accuracy and robustness by integrating multiple physiological parameters, offering strong support for the development of more stable and efficient recognition systems. Therefore, this study focuses on leveraging ensemble learning methods to recognize emotions from various physiological signals. Specifically, we collected EEG, GSR, ST, and HR signals from subjects watching short videos. These multimodal data were used to construct a multi-parameter emotion recognition dataset. To expand the dataset size, we applied a sliding window technique for data segmentation. A base model was then developed combining CNN and LSTM architectures, and trained using random initialization (RI) and cosine annealing warm restarts (CAWR), with key model weights saved during training. To further optimize performance, a soft voting method was implemented for decision-level fusion. Experimental results showed that the proposed method achieved 96.21% accuracy in multi-task emotion recognition, significantly outperforming single-model performance. These findings validate the effectiveness and robustness of ensemble learning for emotion recognition based on multiple physiological parameters.

The structure of this article is as follows: Sect. Dataset and preprocessing outlines the collection and preprocessing of the multi-physiological parameter dataset for emotion recognition. Section Data collection introduces the proposed emotion recognition framework and model optimization strategies, including the base model architecture integrating CNN and LSTM units, as well as the optimization techniques (RI and CAWR). It also details the soft voting ensemble method, which combines models saved during training to achieve precise identification of seven emotions. Section Results and discussion delves into the analysis and discussion of results obtained from various optimization strategies and ensemble learning experiments. Section Conclusion summarizes the key contributions of this work and outlines its broader implications.

Dataset and preprocessing

Data collection

In this study, we developed the Self-built dataset (SELF dataset), a multi-parameter emotion recognition dataset, by carefully selecting videos specifically designed to elicit basic emotions. A total of 45 participants aged 18–28, all with no history of psychological or mental disorders, were recruited. During the viewing of short videos, physiological data were collected from the participants, including single-channel EEG, GSR, ST, and HR. After a thorough process of data cleaning and validating, the final dataset comprised complete and reliable data from 38 participants.

This study was approved by the Scientific Research Ethics and Science and Technology Safety Committee of South-Central Minzu University, Grant Number: 2022-scuec- 106. Informed consent was signed by all study participants. Eligibility and exclusion criteria for subject recruitment: a convenience sample from healthy adults (18 years or older) who responded to the recruitment flyer. Subjects with a history of major disease were excluded.

Figure 1 illustrates the emotion induction process. The emotion induction materials consisted of six sets of short videos and one long video designed to elicit seven emotions: Calm, Happy, Disgust, Surprise, Anger, Sad, and Fear. Participants watched each set of 10 videos sequentially. Video lengths ranged from 76 to 584 s. After each video, participants completed an emotion questionnaire to report their feelings. After each set of videos, participants watched a neutral video to return to their emotional baseline, preparing for the next set of emotion induction.

Fig. 1
figure 1

Emotion induction process.

Full size image

Data collection equipment included single-channel EEG, GSR, ST, and HR sensors. Sampling frequencies were: EEG at 512 Hz, GSR at 300 Hz, ST at 10 Hz, and HR at 1 Hz. Sensors connected to a computer via serial ports ensured real-time, continuous data reception during video playback. Each data point was timestamped to 1-millisecond precision and saved as a txt file. After data collection, experimenters manually verified timestamps to ensure accurate alignment between physiological data and viewed videos. Emotion questionnaire results labeled physiological data with discrete emotion tags. Finally, data were cleaned, timestamps aligned, and both data and labels saved as.csv files for analysis and research. For a detailed description of the dataset construction process and its usability validation, please refer to30. Detailed dataset information is available at: https://github.com/LiaoEpoch/Dataset-for-Emotion-Recognition-from-Physiological-Signals-Induced-by-Short-Videos.git.

To ensure a fair evaluation of data usability and model performance, this study further validates its findings using the SWELL31and WESAD32 datasets. The SWELL dataset includes physiological signals recording from 25 participants engaged in a three-hour knowledge work task. To control experimental conditions, stressors were introduced by exposing participants to neutral, interruption, and time-pressure scenarios. This study utilizes the raw ECG signals sampled at 2048 Hz and assesses emotional states using the Self-Assessment Manikin (SAM) scale. Based on valence and arousal scores, with a threshold of 4, emotions are classified into High Valence (HV, ≥ 4) and Low Valence (LV, < 4), as well as High Arousal (HA, ≥ 4) and Low Arousal (LA, < 4), resulting in four emotional categories: HVHA, HVLA, LVHA, and LVLA. The WESAD dataset primarily explores wearable-based stress and emotion detection, containing physiological recordings from 15 participants under four emotional states: Neutral, Stress, Amusement, and Meditation. For experimental analysis, this study selects raw ECG, EDA, and temperature (Temp) signals, all sampled at 700 Hz, for experimental analysis. These datasets provide a robust foundation for assessing the generalizability and effectiveness of the proposed emotion recognition framework.

Data preprocessing

This study used a systematic data preprocessing workflow to ensure data quality and analytical accuracy. Figure 2 illustrates the data preprocessing steps of the SELF dataset.

Fig. 2
figure 2

SELF Dataset Preprocessing Workflow.

Full size image

Data denoising and normalization

In the SELF dataset, wavelet denoising is applied to EEG, GSR, and ST signals to eliminate high-frequency noise. Specifically, the raw signals are first decomposed into different scales of components using the wavelet transform. This decomposition separates the signal into approximation coefficients (cA) and detail coefficients (cD). A soft thresholding technique is then applied to the cD to suppress noise. This step involves setting coefficients below a threshold to zero (removing noise) and shrinking larger coefficients (preserving signal characteristics but reducing noise). After thresholding, the signal is reconstructed using the inverse wavelet transform, combining the denoised cD and the original cA components. For EEG signals, a six-level decomposition is performed using the db4 wavelet, with cD1 and cD2 removed and soft thresholding applied to cD3–cD6. GSR signals undergo a nine-level decomposition with the db5 wavelet, where cD1 and cD2 are discarded, and soft thresholding is applied to cD3–cD8. ST signals are processed using a four-level decomposition with the db4 wavelet, removing cD1–cD3 and applying soft thresholding to cD4. The threshold value is empirically set to 0.6745 for all signal types. To ensure uniformity across signals of varying scales, min-max normalization is applied as a preprocessing step. This normalization step scales the data to a consistent range, facilitating subsequent analysis and comparison.

Sliding window segmentation

To address the limited sample size of the SELF dataset, data augmentation is performed using a partially overlapping sliding window approach. Specifically, the preprocessed EEG, GSR, ST, and HR signals are segmented using sliding windows. This method enhances the dataset’s size and diversity by generating multiple overlapping subsequences from the original signals, thereby improving the robustness of subsequent analysis. Each segment is 5 s long, with a window length of \(\:5\times\:{F}_{Signal}\) and a sliding step of \(\:1\times\:{F}_{Signal}\), where \(\:{F}_{Signal}\) denotes the sampling frequency of each signal. Emotion labels are preserved across subsegments to maintain label accuracy.

Linear concatenation of data segments

The EEG, GSR, ST, and HR data from the same participant under the same video condition are concatenated in index order to construct multimodal feature inputs. 

In contrast to the preprocessing approach applied to the SELF dataset, the SWELL and WESAD datasets do not undergo denoising or normalization. Instead, data segmentation is performed using a non-overlapping sliding window strategy. For the SWELL dataset, raw ECG signals are divided into 2-second windows, each containing 2 × 2048 data points, with a step size equal to the window length. Similarly, the WESAD dataset adopts a 5-second window, where each segment consists of 5 × 700 data points, also with a step size matching the window length.

To evaluate the model’s generalization capability to unseen participants, all data from the last participant in each dataset are reserved as an external validation set and processed according to their respective preprocessing pipelines.

After processing, the SELF dataset comprises 45,586 data segments, each containing 4,115 data points and labeled with seven emotional states: Calm, Happy, Disgust, Surprise, Anger, Sad, and Fear. The SWELL dataset generates 91,112 single-channel ECG segments, each with 4,096 data points, categorized into four emotion classes: HVHA, HVLA, LVHA, and LVLA. The WESAD dataset produces 8,973 three-channel physiological signal segments, each consisting of 3,500 data points, annotated with four states: Baseline, Amusement, Meditation, and Stress. Excluding the external validation set, the remaining data are randomly split into training, validation, and test sets in a 6:2:2 ratio for model training, hyperparameter tuning, and final evaluation.

Emotion recognition

This study aims to construct a hybrid model combining CNN and LSTM to evaluate its performance in emotion recognition using multiple physiological parameters. The model is initialized randomly, and systematic training and testing are conducted using the preprocessed dataset to evaluate its performance under five different initialization configurations. A CAWR strategy is introduced to optimize model convergence and prevent it from trapping in local optima. This strategy helps the model in searching for the optimal solution in the global search space, enhancing overall performance. The model state is saved after each training epoch for further analysis and comparison. Additionally, predictions from different models are fused at the decision layer using the soft voting method. By comparing model performance before and after fusion, the impact of ensemble learning strategies on emotion recognition accuracy can be assessed.

Base model

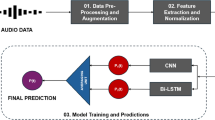
Traditional CNNs struggle to capture complex signal patterns. For long time-series data, they typically require deeper architectures to expand the receptive field and extract global information33, leading to a significant increase in computational cost. In contrast, LSTMs excel in temporal sequence modeling34but face high computational and memory demands when processing ultra-long sequences, along with potential gradient vanishing issues35. To overcome these challenges, we propose a hybrid CNN-LSTM framework for multimodal emotion recognition, as illustrated in Fig. 3. The framework first employs a CNN module to extract signal features and reduce dimensionality, obtaining a compact representation of long time-series data. Then, an LSTM module models and integrates contextual dependencies within these low-dimensional features. Finally, a classification layer generates the emotion recognition results, effectively tackling the complexities of multimodal long-sequence emotion classification.

Fig. 3
figure 3

Base model structure.

Full size image

Due to variations in data formats across different datasets, the model inputs also differ accordingly. Specifically, the SELF dataset input consists of a single-channel signal with a length of 4,115, the SWELL dataset input is a single-channel sequence of length 4,096, and the WESAD dataset input comprises a three-channel signal with a length of 3,500. The CNN layer comprises five one-dimensional convolutional layers, each followed by L2 regularization, ReLU activation, batch normalization, and max-pooling layers. The L2 regularization factor is set to 0.01. The outputs of these convolutional layers are flattened into one-dimensional vectors and fed into three fully connected layers with Dropout. The dropout rate is fixed at 0.4. These vectors then pass through the LSTM layer to capture long-term dependencies. The final output layer contains either 7 or 4 nodes, depending on the classification task, and employs the Softmax activation function to produce class probabilities. During training, the model uses the Adam optimizer with the cross-entropy loss function, evaluating performance based on accuracy.

Random initialization

Model parameters are randomly initialized using five different random seeds (3, 6, 9, 12, 15). All network layers, including convolutional and fully connected layers, use the default initialization method provided by the Keras framework. Five models with different initializations are trained, and each model is saved upon completion of training. The validation set is used to compare the impact of different initialization methods on model performance, aiming to identify the optimal configuration for improving emotion recognition accuracy.

Cosine annealing with warm restarts

In this study, CAWR is employed in addition to RI to optimize the learning rate scheduling process. Within each training cycle, the learning rate decreases gradually following a cosine curve. At the end of each cycle, it resets to a higher initial value before starting the next annealing cycle. This method aims to mitigate the problem of local optima associated with traditional monotonically decreasing learning rate strategies, while ensuring the model retains adequate exploration capability during training36.

Let Epochs denote the current training epoch, starting from 1. T represents the cycle length in epochs. \(\:{\eta\:}_{max}\) is the initial learning rate at the beginning of each cycle, set as the maximum learning rate threshold. \(\:{\eta\:}_{min}\) is the minimum learning rate threshold. Thus, the relative position x of the current training epoch within the cycle can be calculated using Eq. 1.

$$\begin{array}{c}x=\left(\frac{Epochs}{T}\right)\%1\end{array}$$
(1)

The symbol % denotes the modulo operation, ensuring that the relative position x remains within the range [0, 1). Equation 2 calculates the cosine annealing factor α based on the relative position x of the current training epoch within the cycle.

$$\begin{array}{c}\alpha\:=\frac{1}{2}\left(1+\text{cos}\left(\pi\:\times\:x\right)\right)\end{array}$$
(2)

The learning rate \(\:{\eta\:}_{new}\) is updated using the cosine annealing factor α as described in Eq. 3.

$$\begin{array}{c}{\eta\:}_{new}={max}[{\eta\:}_{min},{\eta\:}_{min}+\left({\eta\:}_{max}-{\eta\:}_{min}\right)\times\:\alpha\:]\end{array}$$
(3)

Equation 4 summarizes the formula for updating the learning rate.

$$\begin{array}{c}{\eta\:}_{new}={max}\left\{{\eta\:}_{min},{\eta\:}_{min}+\frac{1}{2}\left({\eta\:}_{max}-{\eta\:}_{min}\right)\left[1+\text{cos}\left(\pi\:\times\:\left(\frac{Epochs}{T}\right)\%1\right)\right]\right\}\end{array}$$
(4)

Formula 4 illustrates the dynamic adjustment of the learning rate based on the current training epoch (Epochs), ensuring it oscillates between the maximum learning rate \(\:{\eta\:}_{max}\) and the minimum learning rate \(\:{\eta\:}_{min}\) in a cosine annealing manner throughout training. The modulo operation ensures the learning rate completes a cosine decay cycle within each cycle T, restarting at the end to begin a new decay process from a higher initial learning rate. In this study, the number of epochs is set to 300, with a cosine annealing schedule of period T = 60. The maximum learning rate is \(\:{\eta\:}_{max}=0.001\), and the minimum learning rate is \(\:{\eta\:}_{min}=0\). Figure 4 illustrates the curve of the learning rate changing throughout the training epochs.

Fig. 4
figure 4

Learning rate change curve.

Full size image

Figure 4 illustrates how the learning rate decreases gradually from \(\:{\eta\:}_{max}\) = 0.001 to \(\:{\eta\:}_{min}\) = 0 within each cycle, following a cosine curve. At the start of each new cycle, the learning rate resets to \(\:{\eta\:}_{max}\), facilitating periodic adjustment and restarting of the learning rate.

This study saved critical model weights during training to thoroughly evaluate the impact of different initialization conditions on model performance. During 300 epochs, each initialized random model saved its state at the end of every cycle. Therefore, with five initializations and five cycles, 25 states were saved for the models. Comparing model states under different initialization conditions and at various training points provides a deeper understanding of how initialization conditions and periodic training strategies influence model learning capacity.

Model ensemble

To enhance predictive performance, reduce overfitting, and improve model robustness, we applied a soft voting method to ensemble models from the 25 saved states. Specifically, the model ensemble was approached from three perspectives: first, integrating models with identical random seeds but varying training epochs to assess how initialization conditions affect predictive performance. Second, integrating models with different random seed initializations but the same number of training epochs to evaluate the effect of training progress variations on model performance. Finally, integrating all models saved during training to achieve comprehensive performance optimization.

Results and discussion

Discussion of random initialization results

This study aimed to investigate the impact of random seed initialization on model performance. The same base model was initialized with five different random seeds (3, 6, 9, 12, 15), and trained for 300 epochs. The batch sizes for the SELF, SWELL, and WESAD datasets are set to 512, 128, and 128, respectively. Models were trained on the training dataset and evaluated continuously on the validation dataset. After training, each model was saved, and their performance on the test dataset was evaluated. Table 1 presents the training and test accuracies of five models initialized with different random seeds across the three datasets.

Table 1 Training and testing results of the base model with RI strategy.
Full size table

The results indicate that random seed initialization significantly impacts model training and generalization. For the SELF dataset, seed 9 achieves the highest accuracy across the training, validation, and test sets, whereas seed 15 may cause the model to fall into a local optimum, resulting in performance degradation. For the SWELL dataset, where overall classification accuracy is relatively high, seed 9 delivers the best test performance, whereas seed 15 impedes model convergence. For the WESAD dataset, although model performance remains stable across different initializations, seed 9 consistently outperforms others. Overall, the choice of random seed is critical for model training and generalization. Seed 9 helps guide the model toward a more stable and generalizable solution, providing a foundation for further optimization strategies and the development of more robust emotion recognition methods.

Discussion of CAWR results

This study introduced the CAWR strategy alongside random seed initialization to adjust the learning rate, aiming to optimize the training effectiveness of the base model. Five different random seeds (3, 6, 9, 12, 15) were used. The dynamic learning rate cycle was T = 60 epochs, with training conducted for 300 epochs. The batch sizes for the SELF, SWELL, and WESAD datasets are set to 512, 128, and 128, respectively. The maximum and minimum learning rates were set at \(\:{\eta\:}_{max}\) = 0.001 and \(\:{\eta\:}_{min}\) = 0, respectively. Throughout the training, the model’s performance was assessed using the validation set, and the model’s state was saved at the end of each learning rate cycle. The accuracy and loss curves during training with random seed 9 for the three datasets are shown in Fig. 5.

Fig. 5
figure 5

Experimental results of the base model with CAWR strategy.

Full size image

Figure 5 clearly illustrates the periodic variation of model accuracy and loss values during the CAWR learning rate process. Throughout the annealing and restart cycle, both training and validation accuracies exhibit steady improvement, while loss values gradually decrease. At the end of each annealing cycle, resetting the learning rate to its initial maximum value enables the model to escape local optima and explore a wider solution space. This strategy significantly enhances model performance, achieving peak validation accuracies of 89.04%, 98.00%, and 98.69% on the SELF, SWELL, and WESAD datasets, respectively. Additionally, the CAWR strategy reduces the number of training epochs required to reach high accuracy. For instance, on the SELF dataset, the model initialized with random seed 9 achieves comparable results to the baseline model trained for 300 epochs in just 100 epochs, when using the CAWR strategy. This improvement not only enhances efficiency but also substantially reduces training time and computational cost.

As the number of training epochs increases, the model shows varying degrees of overfitting. To comprehensively assess the model’s performance, the saved models at the end of training are tested using the testing dataset. Table 2 presents the testing results and performance comparisons before and after introducing the dynamic learning rate.

Table 2 The comparison of testing results with and without CAWR.
Full size table

Table 2 shows that applying the CAWR learning rate adjustment strategy significantly improves the test accuracy of all models, with a notable average increase. For the SELF dataset, the model initialized with random seed 15 achieves an accuracy increase from 48.25 to 86.99%, demonstrating that CAWR effectively mitigates underfitting. Similarly, in the SWELL dataset, the accuracy of the seed 15 model rises from 57.61 to 97.35%, further validating CAWR’s ability to enhance model robustness. Even in the WESAD dataset, where baseline model accuracy is already relatively high, CAWR still delivers consistent performance gains. Additionally, CAWR significantly reduces performance variability caused by random seed initialization. Under the RI training strategy, the accuracy gap between the best and worst models in the SELF dataset is 21.26%, whereas CAWR narrows this discrepancy to just 2.54%, greatly enhancing training stability and reproducibility.

LSTM effectively retains long-term dependencies through its gating mechanism, alleviating the vanishing gradient problem inherent in traditional RNNs, but it remains susceptible to gradient explosion. To address this, CAWR adopts a monotonically decreasing learning rate strategy within each cycle, gradually reducing the learning rate to zero. This approach suppresses instability caused by large gradients and facilitates model convergence. Furthermore, the compatibility between LSTM’s activation functions (Sigmoid for gating and Tanh for state updates) and the cosine annealing strategy further enhances optimization. By periodically adjusting the learning rate, CAWR optimizes weight updates at different training phases, accelerates convergence toward the global optimum, and enhances multi-class classification accuracy. Notably, under constrained training iterations, this strategy maximizes the model’s potential, significantly enhancing overall performance. These results validate the effectiveness of CAWR in multi-physiological signal-based emotion recognition tasks.

Ensemble learning results discussion

The soft voting method was used to combine models from 25 different states, including models with the same random seed but different training epochs, different random seeds but the same training epochs, and all models saved during training. Table 3 presents the test accuracy of different ensemble strategies.

Table 3 Ensemble learning results.
Full size table

The results indicate that all ensemble approaches significantly improve the model’s generalization capability. Whether by varying training epochs with a fixed random seed, using different random seeds with fixed training epochs, or employing a full-model ensemble, ensemble learning effectively addresses both underfitting and overfitting, thereby enhancing prediction stability. The SELF dataset exhibits the most pronounced benefits from these strategies. Ensembling across different training epochs enriches feature representation, while ensembling models trained with different random seeds reduces the impact of initialization variability. The full-model ensemble achieves the highest generalization performance. These findings highlight that a well-designed ensemble strategy not only improves classification accuracy but also enhances model robustness, making it a powerful tool for physiological signal analysis.

After 300 training epochs, the soft voting ensemble strategy, which integrates five models with different random initializations, achieves the highest classification accuracy across all three datasets. Table 4 further evaluates the classification consistency for each emotion category, including precision, recall, and F1-score. These metrics offer a comprehensive evaluation of the model’s performance and its balance across emotion classes.

Table 4 Performance evaluation of the ensemble model.
Full size table

Overall, the model demonstrates high classification performance across all datasets and emotion categories, highlighting its effectiveness in emotion recognition. However, the difficulty of distinguishing between classes varies. In the SELF dataset, all emotion categories achieve F1 scores above 95%. Recognition of Calm, Happy, Anger, Sad, and Fear is well-balanced, whereas Disgust and Surprise exhibit lower recall rates, likely due to high intra-class variability or feature overlap causing misclassification. In the SWELL dataset, all categories achieve F1 scores exceeding 98%, indicating that the model can accurately distinguish between high/low arousal and valence states. However, the recall rate for LVHA is slightly lower, possibly because the boundary between high-arousal/low-valence samples is less distinct. In contrast, HVLA and LVLA show greater stability, likely due to the even distribution of low-arousal state data. For the WESAD dataset, all categories achieve F1 scores above 96%. Recognition of Baseline and Stress is the most accurate, likely because their physiological signal patterns are distinct. However, Amusement shows a lower recall rate, with some samples misclassified as Baseline or Meditation, reflecting lower separability in physiological signals.

To evaluate the model’s generalization capability to unseen subjects or videos, we applied a segment-wise prediction and voting strategy for external validation. Predictions were generated at the segment level on external datasets, with final classifications determined through soft voting. The results showed classification accuracies of 42.86%, 50%, and 50% on the SELF, SWELL, and WESAD datasets, respectively. These findings indicate that the model’s high accuracy on internal data did not generalize effectively to external data. The primary limitation likely arises from individual differences in physiological signals, which significantly impact cross-subject emotion recognition. Future research should prioritize strategies to reduce inter-subject variability, such as domain adaptation or personalized modeling, to enhance the model’s generalizability and enable broader real-world applications.

To validate the effectiveness of our proposed method, we reproduced and compared several representative models from existing studies. Specifically, we strictly followed the original architectures and hyperparameter settings described in the respective papers to replicate DCNN37, CNN38, and Res2 Net39. Additionally, we implemented two widely recognized general-purpose models, DeepConvNet40and EEGNet41, ensuring that their parameter configurations remained consistent with their original implementations. Given the limitations of RNN, GRU, and LSTM in modeling ultra-long time series, we developed hybrid frameworks, CNN + RNN and CNN + GRU, to assess different temporal modeling strategies. Table 5 summarizes the F1 scores of each model across the SELF, SWELL, and WESAD datasets, providing a comprehensive comparison of their classification performance.

Table 5 Comparison with other methods.
Full size table

As demonstrated in Table 5, our approach achieves the best performance across all datasets, outperforming existing models in terms of F1 scores. The SELF dataset has a relatively small sample size and multimodal and complex signal characteristics. While Res2 Net, CNN + RNN, and CNN + GRU outperform traditional CNN and lightweight models, our method further enhances feature learning, achieving superior results. The SWELL dataset consists of large-scale, single-channel ECG signals, which are uniform but extensive in quantity. Models with enhanced feature modeling capabilities, such as Res2 Net, CNN + RNN, and CNN + GRU, achieve high F1 scores, and our method further optimizes performance on this basis. The WESAD dataset contains multi-channel physiological signals, offering rich emotional information. Multi-channel temporal modeling significantly enhances the performance of Res2 Net, CNN + RNN, and CNN + GRU. However, our method surpasses all existing models, demonstrating its strength in integrating and analyzing multimodal physiological signals.

In conclusion, our method demonstrates superior performance in complex emotion classification tasks, proving its competitiveness with state-of-the-art techniques. This study highlights the significant potential of ensemble learning in multimodal emotion recognition. By combining random seed initialization with cosine annealing learning rate adjustment, we effectively enhance model performance. The soft voting strategy not only improves classification accuracy but also ensures stability across diverse emotion categories. Furthermore, extending training epochs and optimizing the learning rate maximize the model’s potential, significantly boosting overall classification performance. These findings underscore the importance of well-designed ensemble strategies and optimized training protocols in addressing complex classification challenges.

Conclusion

This study investigates the application and effectiveness of ensemble learning methods in multimodal emotion recognition using multiple physiological parameters. A high-quality dataset was constructed through systematic preprocessing of EEG, GSR, ST, and HR data collected from 38 subjects watching short videos, including denoising, normalization, sliding window segmentation, and linear concatenation. A hybrid CNN-LSTM framework was developed, integrating random seed initialization, the CAWR strategy, and ensemble methods to optimize training and enhance performance.

The results demonstrate that systematic preprocessing significantly improves data quality, providing a robust foundation for model training. The hybrid CNN-LSTM framework effectively combines the strengths of CNN and LSTM in processing spatial and temporal information. The CAWR strategy accelerates convergence and enhances performance, outperforming traditional training methods. Soft voting across models trained with different random seeds further improves generalization and robustness.

In conclusion, this study demonstrates the effectiveness of ensemble learning and dynamic learning rate adjustment mechanisms in improving emotion recognition performance. By integrating advanced technologies, the proposed method achieves higher accuracy and stability in multimodal emotion recognition tasks, particularly in capturing emotional responses to short videos. These findings highlight the potential of ensemble learning in complex emotion recognition tasks and provide a solid foundation for future research and applications.