Research on collaborative filtering algorithm based on improved K-means algorithm for user attribute rating and co-rating

Abstract

In response to the challenges of information overload in large datasets, as well as issues related to data sparsity and cold starts in traditional recommendation algorithms, this paper proposes a collaborative filtering algorithm based on an enhanced K-means algorithm for user attribute rating and common rating. This proposed algorithm leverages a per-constructed user attribute rating matrix and computes the objective weights of user attribute rating features using variance analysis. Specifically, it is observed that larger sample variances exert greater influence on clustering outcomes. Furthermore, this study integrates the improved K-means clustering algorithm for similarity calculation with user-item common rating similarities to derive a novel similarity computation method. Consequently, a new collaborative filtering model emerges from this approach. To validate the effectiveness of the model, we constructed datasets utilizing samples from Movie-lens 100k and Movie-lens 1 M. Comparative experiments revealed that first, employing both the silhouette coefficient method and cross-validation yielded optimal clustering results at K = 7 and K = 6 respectively. Second, through Mean Absolute Error (MAE) calculations, we verified that the MAE values associated with our proposed improved similarity measure were significantly lower by 65% and 60% compared to those derived from other methods such as Pearson correlation, Jaccard index, and RJ-Pearson similarity calculations. Finally, analyses conducted using two distinct datasets indicated that our enhanced KUR-CF model achieved improvements in Precision values by 60% and Recall values by 35%, relative to other conventional collaborative filtering algorithms. In terms of Recall rate calculations specifically analyzed within this context, our proposed KUR-CF model demonstrated enhancements of 55% and 25% when compared against traditional collaborative filtering approaches. Through the experimental analysis presented above, it can be concluded that the KUR-CF algorithm proposed in this paper significantly enhances recommendation performance. This finding indicates that the proposed method is indeed effective.

Introduction

With the rapid expansion of the Internet in the information age, individuals can effortlessly access a vast array of data on a daily basis. However, this phenomenon also gives rise to challenges such as information overload, exemplified by what is often referred to as an “information maze”^1,2. It has become nearly impossible for individuals to manually sift through the chaotic and extensive volume of data each day in order to locate the specific information that interests them. To tackle the issue of information overload and assist users in swiftly and accurately identifying their desired content, recommendation systems have emerged as a viable solution that can partially alleviate these challenges associated with excessive information.

In contemporary times, search engines^3,4 have proven to be effective tools for assisting individuals in locating desired information within vast datasets. However, their level of sophistication remains relatively low. Users are required to input specific queries each time they seek information, after which the search engine filters and presents a subset of data that aligns with their interests from an extensive pool of information for further consideration. This method inherently lacks user initiative in actively searching for relevant information, as users often find themselves passively adhering to predefined instructions. Conversely, recommendation algorithms possess the capability to proactively suggest content that may pique users’ interest from large datasets. These algorithms offer personalized recommendation services tailored to individual preferences. This approach effectively mitigates issues related to informational pro-activity and overload, thereby enhancing the efficient utilization of available information.

Data sparsity poses a significant challenge in collaborative filtering recommendation algorithms⁵. Limited user ratings for items result in an extremely sparse rating matrix, hindering recommendation systems from effectively capturing user preferences and subsequently impacting the accuracy of recommendation outcomes. To tackle this challenge, this paper introduces an enhanced K-means recommendation algorithm that incorporates user attribute ratings and co-ratings. The K-means clustering algorithm groups similar users or items together, effectively mitigating the sparsity of the rating matrix.

The refined K-means collaborative filtering algorithm enhances classification accuracy by incorporating the center points of users or items. In the conventional K-means algorithm, the initial center points are often randomly selected, potentially leading the algorithm to converge to local optima, thereby compromising the final classification outcomes. To address this issue, the improved algorithm employs a smarter method for selecting center points. Experimental comparisons with traditional recommendation algorithms confirm that our refined algorithm significantly boosts reliability and accuracy, effectively mitigating recommendation biases for initial users in situations of sparse data and cold starts.

Related work

Collaborative filtering algorithm based on user similarity

User-based collaborative filtering algorithm

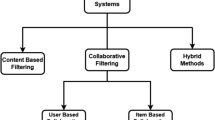
There are primarily two types of traditional collaborative filtering algorithms^3,4,5: one based on users, and the other based on items. The processes for both are essentially similar. Firstly, similarity is calculated based on historical ratings. Secondly, a list of similarity neighbors is generated. Then, predictive ratings are performed, and ultimately, recommendation results are generated based on these predictive ratings. This article primarily focuses on user-based collaborative filtering algorithm for recommendation research, and the specific algorithm flow is illustrated in Fig. 1.

Fig. 1

User-based Collaborative Filtering Algorithm.

Issues in similarity calculation

The traditional methods for calculating similarity mainly include cosine similarity and Jaccard similarity.

(1) Cosine similarity calculation.

The user’s rating for a project is represented as a vector. When a user does not rate a specific project, the default rating value is set to 0. The similarity calculation formula between user u and user v is shown in formula (1).

$$\:sim(u,v)=\frac{\sum\:_{i=1}^{n}\left({r}_{ui}*{r}_{vi}\right)}{\sqrt{\sum\:_{i=1}^{n}{r}_{ui}^{2}}*\sqrt{\sum\:_{i=1}^{n}{r}_{vi}^{2}}}$$

(1)

Here, r_ui and r_vi represent the rating values given by user u and user v, respectively for item i.

(2) Jaccard similarity calculation.

When two users assign similar scores to the same item, it does not necessarily mean that these two users are completely similar. This is because there is another evaluation criterion for similarity calculation, namely the confidence value. Therefore, we can utilize Jaccard similarity as the confidence value. The specific calculation formula is shown in formula (2).

$$\:sim(u,v)=\frac{\left|{\text{I}}_{\text{u}}\cap\:{\text{I}}_{\text{v}}\right|}{\left|{\text{I}}_{\text{u}}\cup\:{\text{I}}_{\text{v}}\right|}$$

(2)

Among them, $\:{\text{I}}_{\text{u}},{\text{I}}_{\text{v}}$ represent the rating values of user u and user v for item i, respectively.

However, the similarity calculation method described above presents the following two issues.

(1) Ignoring the influence of shared ratings on user similarity calculation.

Currently, in movie rating datasets, it’s common for each user to rate only a few movies, leading to a highly sparse user rating matrix. This means there may be very few shared ratings among users. Shared ratings also affect the calculation of user similarity. Let’s assume user u and user v rate five movies, as detailed in Table 1.

Table 1 User rating.

Using Jaccard similarity calculation, the similarity between user u and user v is 1. However, based on user movie rating data, user U prefers Movie1, Movie4, and Movie5, while user V prefers Movie2 and Movie3. The preferences between the two are completely dissimilar. Therefore, simply using traditional Jaccard similarity calculation will deviate from the results of calculating user similarity based on common ratings, leading to a decrease in the accuracy of similarity calculation.

(2) Unable to obtain the distance value between vectors of users.

The traditional cosine similarity measurement method solely considers the angle between vectors, disregarding the specific distance characteristics of the data. If two vectors exhibit significant differences at the same scoring point, their cosine similarity may be low, thus failing to accurately reflect the distance characteristics of the data. Similarly, referring to the case in Table 1 above, the traditional cosine similarity calculation yields a similarity of 0.48 between user u and user v. However, based on the analysis of the data itself, it is evident that user U and user V have completely different preferences. Therefore, the cosine similarity measurement method only considers the direction of the data and disregards its size. Consequently, it is susceptible to the influence of skewed data distribution, leading to bias in similarity calculation and ultimately affecting the accuracy of recommendations.

K-means clustering algorithm

The concept of the k-means clustering algorithm

Clustering algorithms belong to unsupervised learning, which involves dividing data samples from the original data-set into several non-overlapping subsets, with each subset referred to as a cluster. K-means clustering, also known as the k-means clustering algorithm, operates on the basic principle of continuously reassigning samples to clusters based on their proximity, until no further reassignments are possible, resulting in a total of clusters being formed.

Principle of the k-means clustering algorithm

Assuming the original input sample data-set is$\:\:\text{X}\:=\:\left\{\begin{array}{ccc}{\text{x}}_{1},&\:{\text{x}}_{2},&\:\dots\:\end{array},{\text{x}}_{\text{m}}\right\}$, with k clusters initialized, where each cluster’s center point is represented by the centrefold of all objects within that cluster. The basic process of the specific K-means clustering algorithm is as follows.

Input: k: Number of initialized clusters; : A data-set containing m objects.

Output: k cluster sets.

Algorithm steps:

(1) Begin: Choose any k objects from D as the initialization cluster center points;

(2) Repeat.

① Assign each data object to the most similar cluster based on the centrefold points of the objects in the cluster;

② Update the centrefold points of the clusters, that is, recalculate the centrefold values of objects in each cluster.

(3) Until No longer changes.

(4) End Partition and Output k Cluster Sets.

Research on the current situation at home and abroad

Since the 1990s, recommendation algorithms have rapidly developed abroad due to their widespread industrial demand. Researchers and industry engineers have invested a significant amount of effort, leading to remarkable progress in recommendation systems abroad. In 1997, two scholars, Paul Resnick and Hal R. Varian⁶ first explicitly proposed the concept of “recommendation system” in relevant literature. The proposal of this concept marks the beginning of academic attention to recommendation systems as an independent research field. Yehuda Koren¹ fused classic domain models with collaborative filtering based matrix factorization models and achieved excellent results on the Netflix dataset, winning the championship of the Netflix competition. He X, Liao L, Zhang H et al.² proposed an NCF model that combines collaborative filtering and neural networks, and optimized the matrix decomposition to improve the model’s performance on the MovieLens dataset NCDG@10 Reached 0.44. Covington P, Adams J et al.⁷ proposed an efficient recommendation system that utilizes deep learning techniques and performs recommendations in two steps, achieving significant results in YouTube video recommendations. The Google experimental team⁸ proposed the Wide&Deep model, which combines traditional logistic regression models with deep neural network models, retaining both the strong fitting ability of logistic regression and the high generalization ability of deep neural networks. This model does not require separate training and is easy to iterate, providing new ideas for the research of recommendation algorithms in the industry. Shinde et al.⁹ utilized clustering algorithms to tackle the cold start problem in recommendation systems. By employing clustering algorithms, similar groups can be identified based on user or item characteristics, thereby leveraging the behavioral patterns of existing groups to generate more accurate recommendations for new users or items. Ghazanfar et al.¹⁰ employed clustering algorithms to address the “grey sheep” user issue in recommendation systems. “grey sheep” users refer to those who have preferences distinct from the majority and cannot be easily categorized. Through clustering algorithms, these users can be effectively identified and classified into appropriate clusters, thereby enhancing the overall performance of the recommendation system and ensuring that “grey sheep” users also receive accurate recommendations. Deng Ailin et al.¹¹ incorporated the similarity among items into collaborative filtering algorithms, enhancing the traditional similarity measurement methods within the algorithm. Additionally, they presented three conventional similarity measurement methods in recommendation systems: correlation similarity, cosine similarity, and modified cosine similarity, thereby significantly improving the recommendation quality of the system. Yue Xi et al.¹² initially employed a user-based collaborative filtering algorithm to forecast items that had not been evaluated by users. Subsequently, they incorporated the predicted scores into the original user-item rating matrix, thereby mitigating data sparsity. Nawaz¹³ introduced a fully automated approach for early-stage skin melanoma segmentation, leveraging fast region convolutional neural networks (RCNN) and fuzzy k-means clustering (FKM). Anita¹⁴ utilized the RFM model to divide customer groups through dataset segmentation and the K-Means algorithm. Additionally, she employed contour coefficients to validate the efficacy of various data clusters. The findings indicate that analyzing sales transaction data can effectively predict consumer purchasing behavior and related patterns, ultimately enhancing business sales and profits. Aradnia’s¹⁵ proposed method, by incorporating additional Minkowski indices and feature weights in a novel space, enables K-Means to achieve high accuracy in cluster recovery while concurrently reducing memory consumption. Jansson¹⁶ discussed the application of principal component analysis (PCA) and K-means clustering as tools to explore Zn deposits and industrial carbonates in the Sala region of Sweden. Sinaga¹⁷ proposed a new unsupervised k-means (U-k-means) clustering algorithm that does not require initialization and parameter selection, and can automatically find the optimal number of clusters. The article analyzes the computational complexity of the algorithm and demonstrates its superiority through experimental results and comparisons. Ikotun A M¹⁸ pointed out that although the K-means algorithm is widely popular due to its simple implementation and low computational complexity, its performance is limited by issues such as randomness during initialization and sensitivity to initial cluster center selection. Huang¹⁹ introduced a novel robust deep k-means model aimed at performing k-means clustering in a hierarchical manner to explore the hierarchical semantics of data layer by layer. Fard²⁰ proposed a new method that utilizes simple stochastic gradient descent updates to truly jointly optimize representation and k-means clustering loss, thereby improving clustering performance. The experimental results show that this method performs well on multiple datasets and outperforms existing k-Means related deep clustering methods. Yin. H Zhi et al.²¹ proposed a deep learning recommendation algorithm model that integrates spatial data and user behavior. The primary task of this model is to capture the intricate relationship between user behavior patterns and points of interest. By leveraging collaborative filtering algorithms and combining user historical behavior with the behavior patterns of other users, it aims to deliver more personalized POI recommendations. Fan W et al.²²suggested utilizing graph neural networks (GNNs) as an effective tool to capture social relationships and interest similarities among users. Through GNNs, this model integrates users’ social information with their historical behavior information. By utilizing users’ embedded representations in social networks, it enhances the accuracy and relevance of recommendations. Rossi R.A et al.²³ introduced a representation learning method for high-order networks, which involve complex interactions among multiple entities, to capture and analyze the deep structures and patterns within these networks. S. Mandal and A. Maiti et al.²⁴ proposed how to utilize graph neural networks (GNNs) in social recommendation systems to handle heterogeneous trust relationships. This paper aims to enhance the performance of recommendation systems by analyzing trust relationships between users and their impact on recommendation effectiveness. Mandal S et al.²⁵ proposed the GPMF model by combining explicit and implicit feedback, which can more accurately predict users’ ratings of items, improve recommendation accuracy and user satisfaction. This combination not only fully utilizes the various feedback information provided by users, but also explores the deep features hidden behind user behavior, providing new ideas and methods for the development of recommendation systems. Chengkai Liu et al.²⁶proposed an efficient sequence recommendation model based on Behavior-Dependent Linear Recursive Units (RecBLR). This model significantly enhances user behavior modeling and recommendation performance by incorporating gating mechanisms and behavior dependency design. Hwang T.G. et al.²⁷ introduced a movie classification and recommendation algorithm grounded in type correlation. By analyzing the correlations between movie genres, this study refines traditional collaborative filtering methods, thereby significantly boosting the accuracy and diversity of recommendations. Zhenghai Xue et al.²⁸ presented an Adaptive User Retention Optimization (AURO) method rooted in reinforcement learning. This approach aims to tackle the issue of environmental non-stationarity stemming from the constantly evolving user behavior patterns within recommendation systems. The study introduces a state abstraction module and a value-based loss function, allowing recommendation strategies to dynamically adapt to environmental shifts. Additionally, it maintains recommendation quality through a performance-driven rejection sampling strategy. C. Kumar et al.²⁹ authored a comprehensive review paper that summarizes the latest advancements in the field of recommendation systems. The paper places a particular emphasis on the application of deep learning and reinforcement learning within these systems. Furthermore, it delves into the latest research findings in multimodal data fusion, dynamic environmental adaptability, and privacy protection within the realm of recommendation systems.

User attribute rating and collaborative rating based on the improved K-means algorithm

Similarity calculation using the improved K-means algorithm

This paper introduces an improved K-means-based user attribute rating recommendation algorithm to tackle the issue of data sparsity in recommendation algorithms. The traditional K-means algorithm aims to randomly initialize cluster center points, thus only considering local optimal solutions. To circumvent the local optimal solution problem stemming from random initialization, this paper proposes a calculation method based on feature variance weighting. Specifically, it employs the Euclidean distance formula weighted by feature variance. Initially, utilizing the pre-computed user attribute rating matrix, we calculate the objective weights of user attribute rating features using variance. A larger sample variance results in a greater bias on clustering outcomes. This is because a higher variance indicates a more dispersed feature attribute, implying a broader range of values for this type of data within this attribute. This attribute value serves as a significant guide compared to those with minimal or no variation. Additionally, we utilize a variance-weighted distance calculation formula when computing the Euclidean distance, which aids in further optimizing the data. The detailed calculation process is outlined below.

(1) Firstly, let the original user rating matrix be$\:{\:\text{X}}_{\text{m}\text{*}\text{j}}$ and the item attribute matrix be $\:{Y}_{j*n}$. Then, convert them into the user attribute rating matrix $\:{Z}_{m*n}={\text{X}}_{\text{m}\text{*}\text{j}}$*$\:{Y}_{j*n}$, which can be calculated using formula (3), as shown below.

$$\:{Z}_{m*n}=\left[\begin{array}{ccc}{x}_{11}&\:\dots\:&\:{x}_{1j}\\\:\vdots&\:\ddots\:&\:\vdots\\\:{x}_{m1}&\:\dots\:&\:{x}_{mj}\end{array}\right]*\left[\begin{array}{ccc}{y}_{11}&\:\dots\:&\:{y}_{1n}\\\:\vdots&\:\ddots\:&\:\vdots\\\:{y}_{j1}&\:\dots\:&\:{y}_{jn}\end{array}\right]=\left[\begin{array}{ccc}{z}_{11}&\:\dots\:&\:{z}_{1n}\\\:\vdots&\:\ddots\:&\:\vdots\\\:{z}_{m1}&\:\dots\:&\:{z}_{mn}\end{array}\right]$$

(3)

According to formula (3), the feature variance of the j attribute feature value $\:{z}_{i}=\left[\begin{array}{c}{z}_{1i}\\\:\vdots\\\:{z}_{mi}\end{array}\right]$ in the dataset can be obtained, with the specific calculation shown in formula (4).

$$\:\text{S}\left({\text{z}}_{\text{i}}\right)=\frac{\sum\:{({\text{z}}_{\text{i}\text{j}}-\stackrel{-}{\text{z}})}^{2}}{\text{n}}$$

(4)

Among them, $\:\text{S}\left({\text{z}}_{\text{i}}\right)$ denotes the characteristic variance.

Based on the analysis of formula (4), the attribute represented by a feature with a larger variance should be assigned a higher weight. Hence, this paper assigns n feature variance weight values, denoted as $\:{w}_{i}$, for n item attribute values. The specific calculation formula is presented in formula (5).

$$\:{w}_{i}=\frac{S\left({z}_{i}\right)}{\sum\:S\left({z}_{i}\right)}$$

(5)

Among them, $\:{w}_{i}$ denotes the variance weight values of n attribute features.

Finally, based on the given data feature weight values, for each m-dimensional user, the attribute value $\:{\text{z}}_{\text{i}\text{j}}$ corresponds to a feature variance weight value $\:{\text{w}}_{\text{i}}$ for each attribute feature j. The sum of the variance weights of all feature attributes corresponding to each user is equal to 1. Therefore, for each user data point, the improved variance weight Euclidean formula is used to calculate the distance formula from the user to each cluster center point, as shown in formula (6).

$$\:\text{E}({\text{u}}_{\text{i}},{\text{v}}_{\text{j}})=\sqrt{\sum\:_{\text{i}=1}^{\text{n}}\left[{{\text{w}}_{\text{i}}\text{*}({\text{r}}_{{\text{u}}_{\text{i}}}-{\text{r}}_{{\text{v}}_{\text{i}}})}^{2}\right]}$$

(6)

Among them, $\:{\text{u}}_{\text{i}},{\text{v}}_{\text{j}}$represent the attribute ratings of projects evaluated by users$\:{\:\text{u}}_{\text{i}},{\text{v}}_{\text{j}}$ while $\:{\text{r}}_{{\text{u}}_{\text{i}}},{\text{r}}_{{\text{v}}_{\text{j}}}$represent the ratings of projects evaluated by users $\:{\text{u}}_{\text{i}},{\text{v}}_{\text{i}}$; ‘n’ represents the number of project attributes.

(2) Secondly, calculate the average value of the central data points for each category repeatedly, and use the obtained average point as the new clustering center point. If there are no data points that match the central average point, calculate the distance from each data point to the average point using formula (7), and ultimately select the data point closest to the average point as the new clustering center point. The specific formula for calculating the average point is shown in formula (7).

$$\:{dist}_{i}=\frac{1}{{n}_{i}}\sum\:{z}_{i}$$

(7)

Among them, $\:{\text{d}\text{i}\text{s}\text{t}}_{\text{i}}$ represents the average value point for the data of the i-th category, $\:{\text{z}}_{\text{i}}$ denotes the data set pertaining to the i-th category, and $\:{\text{n}}_{\text{i}}$ signifies the number of data points within the data set of the i-th category.

Then, repeat the steps in (1) and (2) above until the specified number of clusters stabilizes. The stabilization of the cluster number is evaluated using the contour coefficient $\:\text{D}\left(\text{S}\right(\text{i}\left)\right)$.

$$\:\text{D}\left(\text{S}\right(\text{i}\left)\right)=\frac{{\text{b}}_{\text{i}}-{\text{a}}_{\text{i}}}{\text{m}\text{a}\text{x}({\text{b}}_{\text{i}},{\text{a}}_{\text{i}})}\:$$

(8)

Among them, $\:{\text{b}}_{\text{i}}$ represents the average value between sample point i and other cluster center points, while $\:{\text{a}}_{\text{i}}$ represents the average value between sample point i and the center point of the same cluster.

• (3) Finally, determine the cluster to which the target user belongs and calculate its similarity value based on the most similar top users within the cluster. Predict the rating for items that have been rated by neighbors with high similarity to the target user but not by the target user itself.

Similarity calculation of joint ratings between users and items

The traditional method for calculating the similarity of joint ratings between users and items may present the following issues:

When the number of common users evaluating two items simultaneously is very small in traditional similarity measurement methods, the similarity of the items obtained according to Eq. (1) is extremely high, and the result is unreasonable, which can lead to problems such as user cold start. At the same time, in the process of calculating user similarity, it will be found that the more common rating values between two users, the higher the similarity value between each other. However, there is a problem: assuming both users $\:{u}_{1}$and $\:{u}_{2}$ have rated three movies, as shown in Table 2 below.

Table 2 User ratings of movies.

However, $\:{u}_{1}$ and $\:{u}_{2}$have different criteria for evaluating their preferences. $\:{u}_{1}$ rates their favorite movies at 4 or above, while user $\:{u}_{2}$ rates theirs at 3 or above. According to traditional similarity calculations, $\:{u}_{1}$ and $\:{u}_{2}$ exhibit a high degree of similarity. Therefore, assuming that new $\:{u}_{3}$ has only commented on Movie1 and Movie2, Movie3 would be recommended to$\:{u}_{3}$ based on traditional similarity calculations. However, this does not align with the preferences of $\:{u}_{1}$ and $\:{u}_{2}$. To address the issue of the limited number of common rating items, the Jaccard similarity measurement method is commonly used, with the specific calculation formula presented in formula (9).

$$\:{Sim}_{\text{J}\text{a}\text{c}\text{c}\text{a}\text{r}\text{d}}(\text{u},\text{v})\:=\:\frac{\left|{\text{I}}_{\text{u}}\cap\:{\text{I}}_{\text{v}}\right|}{\left|{\text{I}}_{\text{u}}\cup\:{\text{I}}_{\text{v}}\right|}$$

(9)

Among them, $\:{\text{I}}_{\text{i}},{\text{I}}_{\text{j}}$ represent the rating sets of users u and v, respectively. $\:{\text{S}\text{i}\text{m}}_{\text{J}\text{a}\text{c}\text{c}\text{a}\text{r}\text{d}}(\text{u},\text{v})$ indicates that the more common rating items two users have, the higher their similarity, which means their preferences align more closely. Conversely, if they have fewer common rating items, their similarity decreases. The Jaccard similarity measurement method effectively reflects the similarity of shared interests and hobbies among users.

Improved similarity calculation

To address the issues of user cold start and similarity calculation bias, this article will enhance the traditional similarity calculation method by utilizing the number of users who have previously rated the item together and the number of users who have not. Specifically, as follows.

This article combines the similarity calculation based on the improved K-means clustering algorithm with the similarity derived from users’ common ratings of items, resulting in a new similarity calculation formula. Specifically, it is presented in Formula 10.

$$\:{R}_{PJ}(u,v)=\alpha\:{Sim}_{pearson\:}(u,v)+(1-\alpha\:){Sim}_{Jaccard}(u,v)$$

(10)

Among them, $\:{\upalpha\:}$represents the weight value, with values ranging from 0 to 1. Different similarity calculation $\:{\upalpha\:}$ values are obtained based on these values.

Algorithm improvement for user attribute rating and co-rating based on k-means

The personalized recommendation algorithm, which incorporates the improved K-Means for user attribute rating and co-rating, is described as follows:

Input: The rating matrix for user-item interactions$\:{\:\text{X}}_{\text{m}\text{*}\text{j}}$ and the attribute matrix for items $\:{Y}_{j*n}$.

Output: Predicted ratings for unrated items by target users.

Specific steps:

(1) Calculate the user attribute rating matrix according to formula (3), and then calculate the feature variance value of each attribute using formula (4).

(2) Calculate the feature variance weight value of each attribute according to formula (5), and then calculate the distance value from each user to each cluster center point through formula (6) to obtain the cluster to which each user belongs.

(3) Calculate the average of the central data points for each category, and use the obtained new average point as the new cluster center point. If there are no data points that are the same as the central average point, use formula (7) to calculate the distance from the data point to the average point.

(4) Repeat the above steps (4) and (5) until the specified number of clusters stabilizes, and use formula (8) to calculate a stable value for the evaluation criteria.

(5) Calculate the cluster to which the target user belongs and calculate their similarity value based on the most similar previous user within the cluster, combined with formula (7) to calculate the similarity value of the user public rating matrix, and finally obtain a new user similarity calculation value. As shown in formula (10).

(6) Finally, predict ratings based on items that have been rated by neighbors with high similarity to the target user but have not been rated by the target user.

Experiments

Experimental dataset

To effectively address issues such as data sparsity and cold start, this article utilizes the Movie-lens 100k and Movie-lens 1 M datasets. The data-set is available at https://grouplens.org/datasets/movielens/. The datasets utilized in this experiment consist of user ratings for movies, user attribute data, and movie attribute data. Data is provided within the supplementary information files. Detailed information about the datasets is presented in Table 3³⁰.

Table 3 Basic information of the Movie-lens 100k Data-set.

The environment utilized for this experiment is Windows 11; the hardware setup includes an AMD Ryzen 7 8845 H processor with Radeon 780 M Graphics, operating at 3.80 GHz, and 32.0 GB of RAM (with 27.8 GB available). The programming language employed is Python version 3.8.

Evaluation metrics

This article employs Mean Absolute Error (MAE), Mean Square Error (RMSE), Precision²⁵, and Recall (ReCall)³¹ as evaluation metrics. MAE and RMSE are commonly used evaluation metrics in recommendation algorithms, both of which indicate that the smaller the value, the more accurate the recommendation effect. Precision and Recall are used to represent the probability of users recommending items that interest them. The specific calculation formulas for the above four evaluation metrics are as follows.

$$\:\text{M}\text{A}\text{E}=\frac{1}{\text{q}}\sum\:_{\text{i}=1}^{\text{q}}\left|{\text{r}}_{\text{i}}-{\text{p}}_{\text{i}}\right|$$

(11)

$$\:\text{R}\text{M}\text{S}\text{E}=\sqrt{\frac{1}{\text{q}}\sum\:_{\text{i}=1}^{\text{q}}{\left({\text{r}}_{\text{i}}-{\text{p}}_{\text{i}}\right)}^{2}}$$

(12)

Among them, q denotes the number of data points in the test set; r_i signifies the user’s actual rating; and p_i stands for the final predicted rating.

$$\:\text{P}\text{r}\text{e}\text{c}\text{i}\text{s}\text{i}\text{o}\text{n}=\frac{\text{C}}{\text{N}}$$

(13)

$$\:\text{R}\text{e}\text{C}\text{a}\text{l}\text{l}=\frac{{\sum\:}_{\text{u}\in\:\text{U}}\left|\text{R}\left(\text{u}\right)\cap\:\text{T}\left(\text{u}\right)\right|}{{\sum\:}_{\text{u}\in\:\text{U}}\left|\text{T}\left(\text{u}\right)\right|}$$

(14)

Among them: _C denotes the number of correct recommendations generated by the system; N denotes the total number of recommendations generated by the recommendation system. R(u) denotes the recommendation list generated based on the user’s u ratings on the training set. T(u) denotes the recommendation list generated based on the user’s u ratings on the test set.

Experimental results and analysis

The experiment primarily consists of four parts:

Experiment 1: To achieve the best clustering effect, this paper employs two datasets and utilizes the silhouette coefficient method and cross-validation as experimental indicators to assess clustering performance.

Experiment 2: To select the optimal value in the improved similarity calculation, this paper utilizes two datasets and employs the MAE value as the evaluation metric for filtering the a value.

Experiment 3: To validate the effectiveness and accuracy of the algorithm proposed in this paper. By comparing our algorithm with existing ones in terms of MAE, RMSE, Precision, and Recall using two datasets under identical parameter settings.

Experiment 4: To calculate the time complexity of the algorithm proposed in this paper. This is achieved by conducting experiments to verify user perception of the recommendation algorithm’s running time.

Silhouette coefficient

To achieve the best clustering effect, we utilize two datasets and employ contour coefficients as the metric for evaluating clustering performance. Different contour coefficient values correspond to varying clustering values k, allowing us to select the optimal k value.

By utilizing the contour coefficient method, we can observe how the contour coefficient values change as k increases, thereby facilitating the identification of the optimal k value. The design philosophy of this approach mirrors that of web search, involving the traversal of parameter k and the selection of contour coefficients to assess clustering effectiveness. For contour coefficient calculations, we set the cluster step size to k = 1. As k increases, the corresponding contour coefficient values change, revealing that in the Movie-lens 100k data-set, the highest contour coefficient value is achieved when k = 7, and in the Movie-lens 1 M data-set, when k = 6. As illustrated in Figs.  2 and 3, we have accordingly selected cluster values k = 7 and k = 6,respectively.

Fig. 2

Line graph depicting k values and their corresponding contour coefficient values.(Movie-lens 100k).

Fig. 3

Line graph depicting k values and their corresponding contour coefficient values.(Movie-lens 1 M).

Cross validation

To further validate the clusters obtained with the best clustering effect, we utilized two datasets, MovieLens100k and MovieLens1M, and employed cross validation as the criterion for evaluating the clustering effect k value. The cross validation values vary with different clustering values k, enabling us to select the optimal k value.

Through cross validation, we observed that as the value of k increases, the corresponding training and testing contour values also change accordingly. This allows us to better identify the optimal value of k. The design concept of this method is similar to the contour coefficient method. By iterating through the parameter k, we measure the clustering effect by selecting the smaller deviation of contour coefficient values between the training and testing sets. When calculating the training and testing contour values, we set the cluster step size to k = 1. We calculated that as k increases, the corresponding contour coefficient deviation values also change accordingly. Ultimately, it was found that in the Movie-lens 100k data-set, when k = 7, the corresponding contour coefficient deviation value was the smallest, as shown in Fig. 4. In the Movie-lens 1 M data-set, when k = 6, the corresponding contour coefficient deviation value was the smallest, as shown in Fig. 5. Therefore, we ultimately selected cluster values k = 7 and k = 6 respectively.

Fig. 4

Line graph depicting k values and their corresponding cross-validation bias values.(Movie-lens 100k).

Fig. 5

Line graph depicting k values and their corresponding cross-validation bias values.(Movie-lens 1 M).

Selection in improved similarity calculation

Utilizing the two datasets, MovieLens100k and MovieLens1M, and based on formula (8), the corresponding values are set to 0.3, 0.4, 0.5, 0.6, and 0.7, respectively. Subsequently, the corresponding MAE, RMSE, Precision, and Recall values are computed. Within the MovieLens-100k and MovieLens1M datasets, it is observed that when the value is set to 0.3, the corresponding MAE, RMSE, Precision, and Recall values attain their optimal levels. Therefore, this value of 0.3 is chosen in formula (8). Refer to Figs. 6 and 7 for detailed illustration.

Fig. 6

Selection in the Improved Similarity Calculation Process(Movie-lens 100k).

Fig. 7

Selection in the Improved Similarity Calculation Process(Movie-lens 1 M).

Effectiveness and accuracy analysis

(1) Comparing Accuracy Across Different Similarity Calculations.

Based on different similarity calculations, the final recommendation accuracy obtained using the MovieLens100k and MovieLens1M datasets varies. Neighbor counts of 5, 10, 20, 30, and 50 were selected, and the MAE values for rating prediction were calculated using each of the four algorithms. The results are shown in Figs. 8 and 9.

Fig. 8

MAE analysis for different similarity calculations(Movie-lens 100k).

Fig. 9

MAE analysis for different similarity calculations(Movie-lens 1 M).

The experimental results demonstrate that the MAE value corresponding to the similarity calculation using formula (8) proposed in this paper is notably smaller than the MAE values corresponding to the other three similarity calculations. In other words, the similarity calculation proposed by KUR-CF significantly reduces the rating prediction error of the recommendation algorithm, thereby enhancing prediction accuracy.

(2) Comparison of Accuracy and Recall of Different Models.

This experiment utilized two datasets, MovieLens100k and MovieLens1M, to evaluate various recommendation models based on accuracy and recall. The detailed results are illustrated in Figs. 10, 11, 12 and 13. The horizontal axis in the diagrams represents the number of recommended top-k items, with the number of recommended items in this experiment ranging from^{4,5,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50}. The KUR-CF proposed in this paper exhibits significant improvements in both accuracy and recall of recommendations, particularly in terms of recommendation accuracy. In the accuracy analysis, it was observed that the KUR-CF model’s accuracy surpassed other traditional collaborative filtering algorithms by 60% and 35% respectively, as determined through experimental analysis of the two datasets. Similarly, the recall rates of the KUR-CF model were found to be 55% and 25% higher compared to other traditional collaborative filtering algorithms, as revealed by the recall analysis based on the two datasets. This underscores the high recommendation performance of the KUR-CF model proposed in this paper, demonstrating notable enhancements in both effectiveness and accuracy of recommendations.

Fig. 10

Analysis of Precision Rates for Different Models(Movie-lens 100k).

Fig. 11

Analysis of Precision Rates for Different Models(Movie-lens 1 M).

Fig. 12

Analysis of Recall Rates for Different Models(Movie-lens 100k).

Fig. 13

Analysis of Recall Rates for Different Models(Movie-lens 1 M).

Time complexity

This experiment compares the collaborative filtering algorithm, which utilizes the improved K-means algorithm for user attribute rating and common rating, with the recommendation algorithm based on singular value decomposition in terms of time efficiency. The results are presented in Figs. 14 and 15, respectively. As evident from Fig. 8, the recommendation algorithm based on singular value decomposition is notably more time-consuming than the KUR-CF algorithm proposed in this paper. In the same dataset, the singular value decomposition method demands considerable time for training matrix data, whereas the KUR-CF algorithm proposed in this paper spends less time in training the dataset. Therefore, it can be deduced that when the recommendation algorithm achieves a certain level of top-k recommendations, the collaborative filtering algorithm based on the improved K-means algorithm for user attribute rating and common rating outperforms the recommendation algorithm based on singular value decomposition in terms of efficiency.

Fig. 14

Comparison of running times between the KUR-CF algorithm and the recommendation algorithm based on singular value decomposition.(Movie-lens 100k).

Fig. 15

Comparison of running times between the KUR-CF algorithm and the recommendation algorithm based on singular value decomposition.(Movie-lens 1 M).

Summary

Based on an in-depth analysis of traditional collaborative filtering algorithms, this article presents a personalized recommendation algorithm that utilizes improved K-means for user attribute scoring and common scoring. This addresses issues such as data sparsity, user cold start, and scalability inherent in traditional collaborative filtering methods. To validate the algorithm’s effectiveness, we determined various thresholds through a series of experiments and compared it with traditional collaborative filtering algorithms. The results indicated that our proposed algorithm enhances recommendation accuracy to some extent and shows improvements in data sparsity, cold start, and scalability. However, there are still shortcomings, such as how to swiftly identify the initialization center point in the k-means algorithm to furnish collaborative filtering algorithms with more precise data, thereby elevating recommendation accuracy. Additionally, considering the evolving user behavior characteristics over time remains a challenge. In the next phase, we plan to integrate user behavior time features into our model, aiming to further bolster the accuracy and overall performance of our recommendation algorithm.