Group decision-making framework using generalized heronian mean operators in quasi rung orthopair fuzzy environment with applications

Abstract

Effective decision-making in complex environments often requires handling fuzzy data with interdependencies. The generalized Heronian mean and geometric Heronian mean operators have proven useful for such analysis. However, existing methods struggle to capture correlations among pq-quasi rung orthopair fuzzy (pqQROF) numbers. This study addresses this gap by extending these operators to the pqQROF setting and developing a novel hybrid decision-making framework. The proposed framework integrates a distance measure, rank sum (RS) method, and aggregation operators to determine both objective and subjective criteria weights. The applicability of the approach is demonstrated through two case studies: project selection and university selection. Finally, a comparative evaluation of the developed operators against existing ones is conducted to assess their effectiveness and highlight the superiority of the proposed decision-making algorithm.

Introduction

Multi-criteria group decision-making (MCGDM) is a process employed to assess and rank alternatives by a team of experts, particularly in situations involving multiple conflicting objectives or uncertainties^1,2,3,4. MCGDM methods offer a systematic approach to scrutinize and compare alternatives based on their respective strengths and weaknesses. The applicability of MCGDM methods extends to various fields such as agriculture⁵, healthcare⁶, marketing and engineering⁷. In the past, decisions often relied on numerical data sets that proved insufficient for addressing real-world operational scenarios, leading to suboptimal outcomes. As systems have grown in complexity over time, traditional methods have become less effective in helping decision experts (DEs) navigate uncertainties in the data.

To address these limitations, researchers have explored fuzzy set (FS) theory⁸, which enables a more flexible representation of uncertainty. Intuitionistic fuzzy sets (IFSs)⁹ extend FSs by incorporating non-membership degrees, while Pythagorean fuzzy sets (PyFSs)^10,11 allow greater freedom in representing imprecise information. Later, Yager¹² introduced q-rung orthopair fuzzy (qROF) sets, further extending the ability to model uncertainty by constraining the sum of the qth power of membership and non-membership grades to be at most one. Numerous researchers have delved into exploring the characteristics of qROF sets. Liu and Liu¹³ put forth a set of qROF Bonferroni mean operators aimed at addressing decision-making (DM) problems. Deveci et al.¹⁴ introduced combined compromised solution (CoCoSo) models utilizing qROF sets to select appropriate sites for floating offshore wind farms in Norway. Additionally, Wang et al.¹⁵ presented similarity measures that consider the membership grade, non-membership grade, and indeterminacy membership grade between qROF sets^16,17,18,19. Akram and Shahzadi²⁰ extended the Yager norm operation to the qROF environment by defining several novel qROF Yager aggregation operators (AOs). Seikh and Mandal²¹ introduced qROF AOs based on Frank t-norm and t-conorm, enhancing the flexibility of DM under uncertainty. In a subsequent study, Seikh and Mandal²² further developed new qROF operational laws grounded in Frank Archimedean t-norm and Archimedean t-conorm, proposing several AOs and demonstrating their applicability in site selection for software operating units. Liu et al.²³ presented an MCGDM approach by integrating the qROF power operator with Maclaurin symmetric mean operators, enabling more effective aggregation of uncertain information. Meanwhile, Tang et al.²⁴ explored a novel approach by combining qROF information with three-way decision theory, formulating an innovative three-way decision model for stock investment evaluation-a significant contribution to decision analysis in financial markets. Depnath et al.²⁵ explored the qROF generalized weighted Bonferroni mean GWBM operator incorporating Aczel-Alsina operations and developed a stepwise weight assessment ratio analysis method for determining criteria weights. In²⁶, Ali tackled the waste management problem by developing a new DM algorithm that overcomes the shortcomings of existing score functions. Aside from this, many other scholars have utilized this concept and presented its several applications in DM^27,28. These advancements significantly improved decision modeling but still had limitations in handling situations where the relationship between membership and non-membership degrees required greater flexibility.

Motivation and need for pq-quasi rung orthopair fuzzy model

Despite the advancements in fuzzy set theory, qROF sets assume a fixed power q for both membership ($\mu$) and non-membership ($\nu$) values. However, in many real-world scenarios, the influence of membership and non-membership grades can vary, necessitating different power parameters. To overcome this limitation, Seikh and Mandal²⁹ introduced the pq-quasi rung orthopair fuzzy (pqQROF) set (pqQROFS) by generalizing the constraint to $0\le \mu ^p+\nu ^q\le 1$. This generalization provides a broader and more flexible representation of uncertainty, making it more suitable for complex DM problems.

The pqQROF model is particularly valuable in MCGDM scenarios where experts provide uncertain or hesitant judgments. Traditional fuzzy models often fail to capture such nuanced uncertainty, leading to imprecise outcomes. By adopting the pqQROF model, decision-makers can better represent and aggregate expert opinions, improving the reliability of the DM process. Several researchers have already explored its applications, such as developing AOs^30,31, MCGDM techniques³², and mathematical frameworks³³.

Challenges in existing studies and research gap

AOs play a fundamental role in MCGDM by systematically combining individual expert opinions into a collective decision. However, existing fuzzy aggregation models often assume that decision criteria are independent of each other, which is rarely the case in real-world DM. In many scenarios, attributes influencing a decision interact in complex ways, meaning that changes in one criterion can influence the importance or perception of another. Ignoring these interdependencies can lead to information loss and, consequently, suboptimal decision outcomes. For instance, in the evaluation of sustainable infrastructure projects, criteria such as cost, environmental impact, and public acceptance are often interrelated. A project with a lower cost may be perceived more favorably, but if it leads to a significant environmental burden, public opposition may rise, altering its overall feasibility. Traditional aggregation methods, such as the arithmetic or geometric mean, treat each criterion independently and fail to capture such interactions. As a result, decision models using these conventional approaches may not reflect the true complexity of the decision problem.

To address this issue, the Heronian Mean (HrM) operator³⁴ provides a mathematically rigorous way to model pairwise interactions between criteria. Unlike standard aggregation functions that assume independence, HrM takes into account the relationships between attributes, ensuring that their mutual influence is reflected in the final decision. Previous studies have explored HrM-based aggregation under different fuzzy environments, such as intuitionistic fuzzy³⁵, interval-valued intuitionistic fuzzy³⁶, and qROF contexts³⁷. Hussain et al.³⁸ integrated the Aczel-Alsina norm with the HrM and proposed a series of operators based on a robust mechanism to enhance the performance of educational institutions. Wang and Feng³⁹ developed intuitionistic fuzzy AOs using Yager’s triangular norms and the HrM operator to address DM challenges. In⁴⁰, Kong introduced a novel complex circular intuitionistic fuzzy HrM approach for monitoring dynamic air quality and assessing public health risks. Naz et al.⁴¹ combined the strengths of power operators with the HrM operator, formulating new AOs that account for the impact of extreme data on decision outcomes. Furthermore, Deng et al.⁴² applied HrM operators in green supplier management, while Hussain et al.⁴³ extended them to t-spherical fuzzy MCGDM problems. However, no existing work has integrated HrM operators into the pqQROF framework, leaving a critical gap in the literature.

Recognizing this gap, this study introduces generalized HrM and geometric HrM (GHrM) operators tailored specifically for pqQROF environments. These new operators provide an advanced approach for aggregating fuzzy data while preserving the essential interdependencies among decision criteria.

Key contributions and their significance

This study aims to bridge the existing research gap by developing and applying novel aggregation techniques based on HrM operators within the pqQROF framework. The main contributions and their significance are as follows:

• 1. Advancing Heronian Mean Operators in the pqQROF Framework

  • This work proposes generalized HrM and GHrM operators for pqQROF settings.

  • These operators overcome the limitations of existing fuzzy aggregation models by effectively capturing correlations among criteria, leading to more accurate and reliable DM.

  • The developed operators satisfy all essential aggregation properties, ensuring their validity and applicability in uncertain decision scenarios.

• 2. Development of an Enhanced DM Framework.

  • A novel MCGDM framework is designed using the proposed HrM-based operators, integrating both subjective and objective weighting mechanisms.

  • This framework offers greater flexibility and adaptability compared to existing methods, making it suitable for handling complex and uncertain information.

  • By incorporating these advanced aggregation strategies, the proposed model ensures higher computational efficiency, interpretability, and accuracy compared to conventional approaches.

• 3. Application to Real-World DM Problems

  • To demonstrate the practical significance of the proposed framework, we apply it to two real-world case studies:

    • Project selection, where different investment alternatives are evaluated.

    • University selection, where multiple institutions are assessed based on various criteria.

  • These applications are expected to highlight the effectiveness and superiority of the proposed approach in solving realistic decision problems under uncertainty.

  • Furthermore, the developed framework is envisioned to be highly adaptable to various domains, including engineering, healthcare, risk assessment, and financial DM.

• 4 Validation of the Proposed Approach

  • A detailed sensitivity analysis is conducted to assess the stability and reliability of the proposed approach under varying parameters. This confirms that the method remains quite consistent and robust across different scenarios.

  • Additionally, a comparative study with existing fuzzy aggregation techniques is be carried out to evaluate the applicability and effectiveness of the proposed framework.

The structure of this paper is as follows: Section Basic concepts introduces the fundamental concepts of pqQROFSs along with the HrM and GHrM operators. Section Some pq-quasi rung orthopair fuzzy heronian mean operators develops the HrM, GHrM, and their weighted variants within the pqQROF framework, while also presenting key properties and theorems. Section Proposed group decision-making methodology proposes a novel MCGDM approach, integrating the newly developed operators with a comprehensive criteria weight determination method. In Section Application, two real-world case studies are conducted, accompanied by an in-depth parameter analysis to assess the stability of the proposed methodology. Section Comparative study presents a comparative evaluation against existing techniques, highlighting the superiority and advantages of the proposed approach. Finally, Section Conclusions concludes the study and outlines potential future research directions.

Basic concepts

Definition 1

²⁹ Let X be a fixed set. A pqQROFS ${\mathscr {T}}$ on X is described as

$$\begin{aligned} {\mathscr {T}}=\left\{ \left( \flat , \mu (\flat ), \nu (\flat ) \right) | \flat \in X \right\} , ~~ {p},{q} \in {{\mathbb {Z}}}^{+}, \end{aligned}$$

(1)

where $\mu (\flat )$, $\nu (\flat ) \in [0,1]$ denote the membership and non-membership grades of $\flat \in X$, respectively, accorded that $0\le \left( \mu (\flat )\right) ^{{p}}+\left( \nu (\flat )\right) ^{{q}} \le 1$. The degree of indeterminacy is $\left( \pi (\flat )\right) ^{\ell }=1- \left( \mu (\flat )\right) ^{{p}}+\left( \nu (\flat )\right) ^{{q}},$ where $\ell$ is the least common multiple (lcm) of p and q. For convince, Seikh and Mandal²⁹ termed ${\mathscr {T}}=\left( \mu , \nu \right)$ a pqQROF number (pqQROFN).

Remark 1

Consider the scenario in which we must determine the minimal value of ${p},{q}\ge 1$ for a given orthopair $\left( \mu , \nu \right)$ such that $\mu ^{{p}}+\nu ^{{q}}\le 1$ is satisfied. Even though there is no closed-form solution, it is always feasible to develop a unique solution to these problems using iterative computing methods. The minimal values of p and q fulfilling $\mu ^{{p}}+\nu ^{{q}}\le 1$ will be referred to as the p, q-niche of $\left( \mu , \nu \right)$. If ${p}^{\prime }$, ${q}^{\prime }$ is the p, q-niche of $\left( \mu , \nu \right)$, then $\left( \mu , \nu \right)$ is valid for all ${p}\ge {p}^{\prime }$ and ${q}\ge {q}^{\prime }$.

Let $X=\left\{ \flat _1,\flat _2,...,\flat _\flat \right\}$ be some supplied data and $\mathscr {F}$ be a fuzzy notion. Assume an expert offers his choice for each $\flat _\iota \in X$ as an orthopair $\left( \mu ({\flat }_\iota ), \nu ({\flat }_\iota )\right)$. Now, the problem is to estimate the proper values of p and q to accurately reflect the data. We may now continue as follows:

• For each p, q-orthopair $\left( \mu ({\flat }_\iota ), \nu ({\flat }_\iota )\right)$ find its p, q-niche, say ${p}_\iota ,{q}_\iota .$

• Set out the ${p}^{*},{q}^{*}$-niche such that ${p}^{*}=\max \limits _{\iota }{{p}_\iota }$ and ${q}^{*}=\max \limits _{\iota }{{q}_\iota }.$

• Then we can represent $\mathscr {F}$ as ${p}^{*}{q}^{*}$QROFS.

Definition 2

²⁹ Let ${\mathscr {T}}$, ${\mathscr {T}}_{1}$ and ${\mathscr {T}}_{2}$ be any three pqQROFNs and $\eta >0$, then the basic rules of operation on them are itemized as

1. ${\mathscr {T}}_{1}\oplus {\mathscr {T}}_{2}=\left( \left( \mu ^{{p}^{*}}_{1} +\mu ^{{p}^{*}}_{2} - \mu ^{{p}^{*}}_{{1}}\mu ^{{p}^{*}}_{{2}}\right) ^{1/{{p}^{*}}}, \nu _{{1}} \nu _{{2}}\right) ;$

2. ${\mathscr {T}}_{1}\otimes {\mathscr {T}}_{2}=\left( \mu _{{1}} \mu _{{2}},\left( \nu ^{{q}^{*}}_{{1}} +\nu ^{{q}^{*}}_{{2}} - \nu ^{{q}^{*}}_{{1}}\nu ^{{q}^{*}}_{{2}}\right) ^{1/{{p}^{*}}}\right) ;$

3. ${\mathscr {T}}^{\eta }=\left( \mu ^{\eta } ,\left( 1-\left( 1-\nu ^{q} \right) ^{\eta }\right) ^{1/{q}}\right) ;$

4. $\eta {\mathscr {T}}=\left( \left( 1-\left( 1-\mu ^{p} \right) ^{\eta }\right) ^{1/{p}},\nu ^{\eta }\right) ;$

5. ${\mathscr {T}}^c=\left( \nu ,\mu \right)$.

Definition 3

²⁹ Let ${\mathscr {T}}$ be a pqQROFN, then the score function is described by:

$$\begin{aligned} S\left( {\mathscr {T}} \right) =\frac{1+\mu ^{{p}}-\nu ^{{q}}}{2}, \end{aligned}$$

(2)

where ${p},{q}\in {{\mathbb {Z}}}^{+}$, $S\left( {\mathscr {T}} \right) \in \left[ 0,1 \right]$. The larger the value of $S\left( {\mathscr {T}} \right)$, the larger the pqQROFN ${\mathscr {T}}$.

Definition 4

²⁹ Let ${\mathscr {T}}$ be a pqQROFN, then the degree of accuracy is described as:

$$\begin{aligned} A\left( {\mathscr {T}} \right) =\left( \mu \right) ^{{p}}+\left( \nu \right) ^{{q}}; ~~ A\left( {\mathscr {T}} \right) \in {{\mathbb {Z}}}^{+}. \end{aligned}$$

(3)

If the calculated score values are analogous, a higher level of accuracy $A\left( {\mathscr {T}} \right)$ corresponds to a larger pqQROFN.

Definition 5

⁴⁴ Consider $\mathscr {N}_{\iota }(\iota =1,2,...,{s})$ be a collection of non-negative numbers. Then the HrM operator is presented as

$$\begin{aligned} HrM\left( \mathscr {N}_{1},\mathscr {N}_{2},...,\mathscr {N}_{{s}} \right) =\left( \frac{2}{{s}({s}+1)}\sum \limits _{\iota =1}^{{s}}\sum \limits _{{j}=\iota }^{{s}}\sqrt{\mathscr {N}_{\iota }\mathscr {N}_{{j}}}\right) . \end{aligned}$$

(4)

Definition 6

⁴⁵ Consider $\mathscr {N}_{\iota }(\iota =1,2,...,{s})$ be a collection of non-negative numbers and $\alpha ,\beta \ge 0$,$\alpha +\beta > 0$. Then the GHrM operator is presented as

$$\begin{aligned} GHrM^{\alpha ,\beta }\left( \mathscr {N}_{1},\mathscr {N}_{2},...,\mathscr {N}_{{s}} \right) =\left( \frac{2}{{s}({s}+1)}\sum \limits _{\iota =1}^{{s}}\sum \limits _{{j}=\iota }^{{s}}\mathscr {N}^{\alpha }_{\iota }\mathscr {N}^{\beta }_{{j}} \right) ^{\frac{1}{\alpha +\beta }}. \end{aligned}$$

(5)

For, $\alpha =\beta =\frac{1}{2}$, Eq. (5) reduces to Eq. (4).

Some pq-quasi rung orthopair fuzzy heronian mean operators

pq-quasi rung orthopair fuzzy generalized heronian mean

Definition 7

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ be a family of pqQROFNs and $\alpha ,\beta \ge 0$, $\alpha +\beta > 0$. Then the pqQROFGHM is the function of dimension s such that

$$\begin{aligned} {p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) =\left( \frac{2}{{s}\left( {s}+1 \right) }\oplus _{\iota =1}^{{s}}\oplus _{{j}=\iota }^{{s}}\left( {\mathscr {T}}^{\alpha }_{\iota }\otimes {\mathscr {T}}^{\beta }_{{j}} \right) \right) ^{\frac{1}{\alpha +\beta }}. \end{aligned}$$

(6)

Theorem 1

The aggregated result of ‘s’ pqQROFNs ${\mathscr {T}}_{\iota }$ utilizing p qQROFGHM operator is also a pqQROFN, and is given by

$$\begin{aligned} {p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) =\left( \frac{2}{{s}\left( {s}+1 \right) }\oplus _{\iota =1}^{{s}}\oplus _{{j}=\iota }^{{s}}\left( {\mathscr {T}}^{\alpha }_{\iota }\otimes {\mathscr {T}}^{\beta }_{{j}} \right) \right) ^{\frac{1}{\alpha +\beta }}\nonumber \\ =\left( \left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu ^{{p}\alpha }_{\iota }\mu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }}, \root q \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}} \right) . \end{aligned}$$

(7)

Proof

According to Definition 2, we have

$$\begin{aligned} & {\mathscr {T}}_{\iota }^{\alpha }=\left( \mu _{\iota }^{\alpha }, \root q \of {1-\left( 1-\nu _{\iota }^{{q}}\right) ^{\alpha }} \right) ,\\ & {\mathscr {T}}_{{j}}^{\beta }=\left( \mu _{{j}}^{\beta }, \root q \of {1-\left( 1-\nu _{{j}}^{{q}}\right) ^{\beta }} \right) . \end{aligned}$$

Therefore, ${\mathscr {T}}^{\alpha }_{\iota }\otimes {\mathscr {T}}^{\beta }_{{j}}=\left( \mu _{\iota }^{\alpha }\mu _{{j}}^{\beta }, \root q \of {1-\left( 1-\nu _{\iota }^{{q}} \right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}} \right) ^{\beta }} \right)$,

Now

$\oplus _{\iota =1}^{{s}}\oplus _{{j}=\iota }^{{s}}\left( {\mathscr {T}}^{\alpha }_{\iota }\otimes {\mathscr {T}}^{\beta }_{{j}} \right) = \left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu _{\iota }^{{p}\alpha }\mu _{{j}}^{{p}\beta } \right) }, \root q \of {\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1-\nu _{\iota }^{{q}} \right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}}\right) ^{\beta } \right) } \right)$.

Then

$\frac{2}{{s}\left( {s}+1 \right) }\oplus _{\iota =1}^{{s}}\oplus _{{j}=\iota }^{{s}}\left( {\mathscr {T}}^{\alpha }_{\iota }\otimes {\mathscr {T}}^{\beta }_{{j}} \right) =\left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu _{\iota }^{{p}\alpha }\mu _{{j}}^{{p}\beta }\right) ^{\frac{2}{{s}\left( {s}+1 \right) }}}, \left( \root q \of {\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1-\nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}}\right) ^{\beta }\right) } \right) ^{\frac{2}{{s}\left( {s}+1 \right) }}\right) .$

Thus

$$\begin{aligned} & {p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) =\left( \frac{2}{{s}\left( {s}+1 \right) }\oplus _{\iota =1}^{{s}}\oplus _{{j}=\iota }^{{s}}\left( {\mathscr {T}}^{\alpha }_{\iota }\otimes {\mathscr {T}}^{\beta }_{{j}} \right) \right) ^{\frac{1}{\alpha +\beta }}\\ & =\left( \left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu ^{{p}\alpha }_{\iota }\mu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }}, \root q \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}} \right) . \end{aligned}$$

Hence, the theorem is verified. $\square$

Theorem 2

If all pqQROFNs ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ are equal, i.e., ${\mathscr {T}}_{\iota }={\mathscr {T}}, \iota =1,2,...,{s},$ then

${p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) ={\mathscr {T}}$.

Proof

As

$$\begin{aligned} & {p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \\ & =\left( \left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu ^{{p}\alpha }_{\iota }\mu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }}, \root q \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}}\right) . \end{aligned}$$

Since ${\mathscr {T}}_{\iota }={\mathscr {T}}$ for all $\iota$. Therefore,

$$\begin{aligned} & {p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \\ & =\left( \left( \root p \of {1-\left( \left( 1-\mu ^{{p}\alpha }\mu ^{{p}\beta } \right) ^{\frac{{s}\left( {s}+1\right) }{2}}\right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }}, \root q \of {1-\left( 1-\left( \left( 1-\left( 1- \nu ^{{q}}\right) ^{\alpha }\left( 1-\nu ^{{q}} \right) ^{\beta } \right) ^{\frac{{s}\left( {s}+1\right) }{2}}\right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}} \right) \\ & =\left( \left( \root p \of {1-\left( 1-\mu ^{{p}\left( \alpha +\beta \right) }\right) } \right) ^{\frac{1}{\alpha +\beta }}, \root q \of {1-\left( 1-\left( 1-\left( 1- \nu ^{{q}}\right) ^{\left( \alpha +\beta \right) } \right) \right) ^{\frac{1}{\alpha +\beta }}} \right) =\left( \mu , \nu \right) . \end{aligned}$$

$\square$

Theorem 3

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ and $\hat{{\mathscr {T}}}_{\iota }(\iota =1,2,...,{s})$ be two families of pqQROFNs. If ${\mathscr {T}}_{\iota }\le \hat{{\mathscr {T}}}_{\iota }$ for all $\iota$, then ${p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {p}{q}QROFGHM^{\alpha ,\beta }\left( \hat{{\mathscr {T}}}_{1},\hat{{\mathscr {T}}}_{2},...,\hat{{\mathscr {T}}}_{{s}} \right)$.

Proof

Since ${\mathscr {T}}_{\iota }\le \hat{{\mathscr {T}}}_{\iota }$ for all $\iota$, then we have $\mu _{\iota }\ge {\hat{\mu }}_{\iota }$ and $\nu _{\iota }\le {\hat{\nu }}_{\iota }$ for all $\iota$. From this, we have

$$\begin{aligned} & \mu ^{{p}\alpha }_{\iota }\mu ^{{p}\beta }_{{j}}\ge {\hat{\mu }}^{{p}\alpha }_{\iota }{\hat{\mu }}^{{p}\beta }_{{j}} \\ & \Longrightarrow \prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu ^{{p}\alpha }_{\iota }\mu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \le \prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-{\hat{\mu }}^{{p}\alpha }_{\iota }{\hat{\mu }}^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}\\ & \Longrightarrow {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu ^{{p}\alpha }_{\iota }\mu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \ge {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-{\hat{\mu }}^{{p}\alpha }_{\iota }{\hat{\mu }}^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}}\\ & \Longrightarrow \left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu ^{{p}\alpha }_{\iota }\mu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }}\ge \left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-{\hat{\mu }}^{{p}\alpha }_{\iota }{\hat{\mu }}^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }}. \end{aligned}$$

Next from $\nu _{\iota }\le {\hat{\nu }}_{\iota }$, we can write

$$\begin{aligned} & \left( 1- \nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}} \right) ^{\beta }\ge \left( 1- {\hat{\nu }}_{\iota }^{{q}}\right) ^{\alpha }\left( 1-{\hat{\nu }}_{{j}}^{{q}} \right) ^{\beta } \Longrightarrow \\ & \prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }}\le \prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- {\hat{\nu }}_{\iota }^{{q}}\right) ^{\alpha }\left( 1-{\hat{\nu }}_{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \Longrightarrow \\ & \left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}\ge \left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- {\hat{\nu }}_{\iota }^{{q}}\right) ^{\alpha }\left( 1-{\hat{\nu }}_{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }} \Longrightarrow \\ & \root q \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}}\le \root q \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- {\hat{\nu }}_{\iota }^{{q}}\right) ^{\alpha }\left( 1-{\hat{\nu }}_{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}}. \end{aligned}$$

Therefore, ${p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {p}{q}QROFGHM^{\alpha ,\beta }\left( \hat{{\mathscr {T}}}_{1},\hat{{\mathscr {T}}}_{2},...,\hat{{\mathscr {T}}}_{{s}} \right)$. $\square$

Theorem 4

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ be a family of pqQROFNs and let ${\mathscr {T}}^{-}=\min \left\{ {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}}\right\}$ and ${\mathscr {T}}^{+}=\max \left\{ {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}}\right\}$. Then ${\mathscr {T}}^{-}\le {p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {\mathscr {T}}^{+}$.

Proof

Based on Theorems 2 and 3, one can easily prove it. $\square$

Arguments often have different ‘weights’ that need to be considered when aggregating them. Therefore, in the following, a weighted version of the pqQROFGHM operator is provided for handling such scenarios.

Definition 8

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ be a family of pqQROFNs and $\alpha ,\beta \ge 0$, $\alpha +\beta > 0$. Then the pqQROFWGHM is the function of dimension s such that

$$\begin{aligned} {p}{q}QROFWGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) =\left( \oplus _{\iota =1}^{{s}}\oplus _{{j}=\iota }^{{s}} \left( \amalg _{\iota }\amalg _{{j}}\left( {\mathscr {T}}^{\alpha }_{\iota }\otimes {\mathscr {T}}^{\beta }_{{j}} \right) \right) \right) ^{\frac{1}{\alpha +\beta }}. \end{aligned}$$

(8)

where $\amalg =\left( \amalg _{1},\amalg _{2},...,\amalg _{{s}} \right) ^{T}$ is the weight vector of ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$, $\amalg _{\iota } >0$ and $\sum \limits _{\iota =1}^{{s}}\amalg _{\iota }=1$.

Theorem 5

The aggregated result of ‘s’ pqQROFNs ${\mathscr {T}}_{\iota }$ utilizing p qQROFWGHM operator is also a pqQROFN, and is given by

$$\begin{aligned} {p}{q}QROFWGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) =\left( \oplus _{\iota =1}^{{s}}\oplus _{{j}=\iota }^{{s}} \left( \amalg _{\iota }\amalg _{{j}}\left( {\mathscr {T}}^{\alpha }_{\iota }\otimes {\mathscr {T}}^{\beta }_{{j}} \right) \right) \right) ^{\frac{1}{\alpha +\beta }}\nonumber \\ =\left( \left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu ^{{p}\alpha }_{\iota }\mu ^{{p}\beta }_{{j}} \right) ^{\amalg _{\iota }\amalg _{{j}}}} \right) ^{\frac{1}{\alpha +\beta }}, \root q \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\amalg _{\iota }\amalg _{{j}}} \right) ^{\frac{1}{\alpha +\beta }}} \right) . \end{aligned}$$

(9)

Proof

The proof is similar to Theorem 1. Therefore, it is omitted. $\square$

Theorem 6

If all pqQROFNs ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ are equal, i.e., ${\mathscr {T}}_{\iota }={\mathscr {T}}, \iota =1,2,...,{s},$ then

${p}{q}QROFWGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) ={\mathscr {T}}$.

Theorem 7

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ and $\hat{{\mathscr {T}}}_{\iota }(\iota =1,2,...,{s})$ be two families of pqQROFNs. If ${\mathscr {T}}_{\iota }\le \hat{{\mathscr {T}}}_{\iota }$ for all $\iota$, then ${p}{q}QROFWGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {p}{q}QROFWGHM^{\alpha ,\beta }\left( \hat{{\mathscr {T}}}_{1},\hat{{\mathscr {T}}}_{2},...,\hat{{\mathscr {T}}}_{{s}} \right)$.

Theorem 8

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ be a family of pqQROFNs and let ${\mathscr {T}}^{-}=\min \left\{ {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}}\right\}$ and ${\mathscr {T}}^{+}=\max \left\{ {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}}\right\}$. Then ${\mathscr {T}}^{-}\le {p}{q}QROFWGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {\mathscr {T}}^{+}$.

pq-quasi rung orthopair fuzzy generalized geometric heronian mean

Definition 9

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ be a family of pqQROFNs and $\alpha ,\beta \ge 0$, $\alpha +\beta > 0$. Then the pqQROFGGHM is the function of dimension s such that

$$\begin{aligned} {p}{q}QROFGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) ={\frac{1}{\alpha +\beta }}\left( \otimes _{\iota =1}^{{s}}\otimes _{{j}=\iota }^{{s}}\left( {\alpha }{\mathscr {T}}_{\iota }\oplus {\beta }{\mathscr {T}}_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1 \right) }} \right) . \end{aligned}$$

(10)

Theorem 9

The aggregated result of ‘s’ pqQROFNs ${\mathscr {T}}_{\iota }$ utilizing p qQROFGGHM operator is also a pqQROFN, and is given by

$$\begin{aligned} {p}{q}QROFGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) ={\frac{1}{\alpha +\beta }}\left( \otimes _{\iota =1}^{{s}}\otimes _{{j}=\iota }^{{s}}\left( {\alpha }{\mathscr {T}}_{\iota }\oplus {\beta }{\mathscr {T}}_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1 \right) }} \right) \nonumber \\ =\left( \root p \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \mu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}}, \left( \root q \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\nu ^{{p}\alpha }_{\iota }\nu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }} \right) . \end{aligned}$$

(11)

Proof

According to Definition 2, we have

$$\begin{aligned} & {\alpha }{\mathscr {T}}_{\iota }=\left( \root q \of {1-\left( 1-\mu _{\iota }^{{q}}\right) ^{\alpha }},\nu _{\iota }^{\alpha } \right) ,\\ & {\beta }{\mathscr {T}}_{{j}}=\left( \root q \of {1-\left( 1-\mu _{{j}}^{{q}}\right) ^{\beta }},\nu _{{j}}^{\beta } \right) . \end{aligned}$$

Therefore, ${\alpha }{\mathscr {T}}_{\iota }\oplus {\beta }{\mathscr {T}}_{{j}}=\left( \root q \of {1-\left( 1-\mu _{\iota }^{{q}} \right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}} \right) ^{\beta }},\nu _{\iota }^{\alpha }\nu _{{j}}^{\beta } \right)$,

Now

$\otimes _{\iota =1}^{{s}}\otimes _{{j}=\iota }^{{s}}\left( {\alpha }{\mathscr {T}}_{\iota }\oplus {\beta }{\mathscr {T}}_{{j}}\right) = \left( \root q \of {\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1-\mu _{\iota }^{{q}} \right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}}\right) ^{\beta } \right) }, \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\nu _{\iota }^{{p}\alpha }\nu _{{j}}^{{p}\beta } \right) } \right)$.

Then

$\otimes _{\iota =1}^{{s}}\otimes _{{j}=\iota }^{{s}}\left( {\alpha }{\mathscr {T}}_{\iota }\oplus {\beta }{\mathscr {T}}_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1 \right) }}=\left( \left( \root q \of {\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1-\nu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\nu _{{j}}^{{q}}\right) ^{\beta }\right) } \right) ^{\frac{2}{{s}\left( {s}+1 \right) }}, \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\mu _{\iota }^{{p}\alpha }\mu _{{j}}^{{p}\beta }\right) ^{\frac{2}{{s}\left( {s}+1 \right) }}}\right) .$

Thus

$$\begin{aligned} & {p}{q}QROFGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) ={\frac{1}{\alpha +\beta }}\left( \otimes _{\iota =1}^{{s}}\otimes _{{j}=\iota }^{{s}}\left( {\alpha }{\mathscr {T}}_{\iota }\oplus {\beta }{\mathscr {T}}_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1 \right) }} \right) \\ & =\left( \root p \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \mu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}}, \left( \root q \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\nu ^{{p}\alpha }_{\iota }\nu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }} \right) . \end{aligned}$$

Hence, the theorem is verified. $\square$

Theorem 10

If all pqQROFNs ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ are equal, i.e., ${\mathscr {T}}_{\iota }={\mathscr {T}}, \iota =1,2,...,{s},$ then

${p}{q}QROFGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) ={\mathscr {T}}$.

Proof

As

$$\begin{aligned} & {p}{q}QROFGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \\ & =\left( \root q \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \mu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}}, \left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\nu ^{{p}\alpha }_{\iota }\nu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }} \right) . \end{aligned}$$

Since ${\mathscr {T}}_{\iota }={\mathscr {T}}$ for all $\iota$. Therefore,

$$\begin{aligned} & {p}{q}QROFGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \\ & =\left( \root q \of {1-\left( 1-\left( \left( 1-\left( 1- \mu ^{{q}}\right) ^{\alpha }\left( 1-\mu ^{{q}} \right) ^{\beta } \right) ^{\frac{{s}\left( {s}+1\right) }{2}}\right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}}, \left( \root p \of {1-\left( \left( 1-\nu ^{{p}\alpha }\nu ^{{p}\beta } \right) ^{\frac{{s}\left( {s}+1\right) }{2}}\right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }} \right) \\ & =\left( \root q \of {1-\left( 1-\left( 1-\left( 1- \mu ^{{q}}\right) ^{\left( \alpha +\beta \right) } \right) \right) ^{\frac{1}{\alpha +\beta }}} \left( \root p \of {1-\left( 1-\nu ^{{p}\left( \alpha +\beta \right) }\right) } \right) ^{\frac{1}{\alpha +\beta }} \right) =\left( \mu , \nu \right) . \end{aligned}$$

$\square$

Theorem 11

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ and $\hat{{\mathscr {T}}}_{\iota }(\iota =1,2,...,{s})$ be two families of pqQROFNs. If ${\mathscr {T}}_{\iota }\le \hat{{\mathscr {T}}}_{\iota }$ for all $\iota$, then ${p}{q}QROFGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {p}{q}QROFGGHM^{\alpha ,\beta }\left( \hat{{\mathscr {T}}}_{1},\hat{{\mathscr {T}}}_{2},...,\hat{{\mathscr {T}}}_{{s}} \right)$.

Proof

Since ${\mathscr {T}}_{\iota }\le \hat{{\mathscr {T}}}_{\iota }$ for all $\iota$, then we have $\mu _{\iota }\ge {\hat{\mu }}_{\iota }$ and $\nu _{\iota }\le {\hat{\nu }}_{\iota }$ for all $\iota$. From this, we have

$$\begin{aligned} & \left( 1- \mu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}} \right) ^{\beta }\le \left( 1- {\hat{\mu }}_{\iota }^{{q}}\right) ^{\alpha }\left( 1-{\hat{\mu }}_{{j}}^{{q}} \right) ^{\beta } \Longrightarrow \\ & \prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \mu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }}\ge \prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- {\hat{\mu }}_{\iota }^{{q}}\right) ^{\alpha }\left( 1-{\hat{\mu }}_{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \Longrightarrow \\ & \left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \mu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}\le \left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- {\hat{\mu }}_{\iota }^{{q}}\right) ^{\alpha }\left( 1-{\hat{\mu }}_{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }} \Longrightarrow \\ & \root q \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \mu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}}\ge \root q \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- {\hat{\mu }}_{\iota }^{{q}}\right) ^{\alpha }\left( 1-{\hat{\mu }}_{{j}}^{{q}} \right) ^{\beta } \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \right) ^{\frac{1}{\alpha +\beta }}}. \end{aligned}$$

Next from $\nu _{\iota }\le {\hat{\nu }}_{\iota }$, we can write $\nu ^{{p}\alpha }_{\iota }\nu ^{{p}\beta }_{{j}}\le {\hat{\nu }}^{{p}\alpha }_{\iota }{\hat{\nu }}^{{p}\beta }_{{j}}$ $\Longrightarrow$ $\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\nu ^{{p}\alpha }_{\iota }\nu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }} \ge \prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-{\hat{\nu }}^{{p}\alpha }_{\iota }{\hat{\nu }}^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}$

$\Longrightarrow$ ${1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\nu ^{{p}\alpha }_{\iota }\nu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \le {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-{\hat{\nu }}^{{p}\alpha }_{\iota }{\hat{\nu }}^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}}$

$\Longrightarrow$ $\left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\nu ^{{p}\alpha }_{\iota }\nu ^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }}\le \left( \root p \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-{\hat{\nu }}^{{p}\alpha }_{\iota }{\hat{\nu }}^{{p}\beta }_{{j}} \right) ^{\frac{2}{{s}\left( {s}+1\right) }}} \right) ^{\frac{1}{\alpha +\beta }}$.

Therefore, ${p}{q}QROFGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {p}{q}QROFGHM^{\alpha ,\beta }\left( \hat{{\mathscr {T}}}_{1},\hat{{\mathscr {T}}}_{2},...,\hat{{\mathscr {T}}}_{{s}} \right)$. $\square$

Theorem 12

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ be a family of pqQROFNs and let ${\mathscr {T}}^{-}=\min \left\{ {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}}\right\}$ and ${\mathscr {T}}^{+}=\max \left\{ {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}}\right\}$. Then ${\mathscr {T}}^{-}\le {p}{q}QROFGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {\mathscr {T}}^{+}$.

Proof

Based on Theorems 10 and 11, one can easily prove it. $\square$

Arguments often have different ‘weights’ that need to be considered when aggregating them. Therefore, in the following, a weighted version of the pqQROFGGHM operator is provided for handling such scenarios.

Definition 10

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ be a family of pqQROFNs and $\alpha ,\beta \ge 0$, $\alpha +\beta > 0$. Then the pqQROFWGGHM is the function of dimension s such that

$$\begin{aligned} {p}{q}QROFWGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) ={\frac{1}{\alpha +\beta }}\left( \otimes _{\iota =1}^{{s}}\otimes _{{j}=\iota }^{{s}}\left( {\alpha }{\mathscr {T}}_{\iota }\oplus {\beta }{\mathscr {T}}_{{j}} \right) ^{\amalg _{\iota }\amalg _{{j}}} \right) . \end{aligned}$$

(12)

where $\amalg =\left( \amalg _{1},\amalg _{2},...,\amalg _{{s}} \right) ^{T}$ is the weight vector of ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$, $\amalg _{\iota } >0$ and $\sum \limits _{\iota =1}^{{s}}\amalg _{\iota }=1$.

Theorem 13

The aggregated result of ‘s’ pqQROFNs ${\mathscr {T}}_{\iota }$ utilizing p qQROFWGGHM operator is also a pqQROFN, and is given by

$$\begin{aligned} {p}{q}QROFWGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) ={\frac{1}{\alpha +\beta }}\left( \otimes _{\iota =1}^{{s}}\otimes _{{j}=\iota }^{{s}}\left( {\alpha }{\mathscr {T}}_{\iota }\oplus {\beta }{\mathscr {T}}_{{j}} \right) ^{\amalg _{\iota }\amalg _{{j}}} \right) \nonumber \\ =\left( \root p \of {1-\left( 1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\left( 1- \mu _{\iota }^{{q}}\right) ^{\alpha }\left( 1-\mu _{{j}}^{{q}} \right) ^{\beta } \right) ^{\amalg _{\iota }\amalg _{{j}}} \right) ^{\frac{1}{\alpha +\beta }}}, \left( \root q \of {1-\prod \limits _{\iota =1,{j}=\iota }^{{s}}\left( 1-\nu ^{{p}\alpha }_{\iota }\nu ^{{p}\beta }_{{j}} \right) ^{\amalg _{\iota }\amalg _{{j}}}} \right) ^{\frac{1}{\alpha +\beta }} \right) . \end{aligned}$$

(13)

Proof

The proof is similar to Theorem 1. Therefore, it is omitted. $\square$

Theorem 14

If all pqQROFNs ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ are equal, i.e., ${\mathscr {T}}_{\iota }={\mathscr {T}}, \iota =1,2,...,{s},$ then

${p}{q}QROFWGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) ={\mathscr {T}}$.

Theorem 15

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ and $\hat{{\mathscr {T}}}_{\iota }(\iota =1,2,...,{s})$ be two families of pqQROFNs. If ${\mathscr {T}}_{\iota }\le \hat{{\mathscr {T}}}_{\iota }$ for all $\iota$, then ${p}{q}QROFWGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {p}{q}QROFWGGHM^{\alpha ,\beta }\left( \hat{{\mathscr {T}}}_{1},\hat{{\mathscr {T}}}_{2},...,\hat{{\mathscr {T}}}_{{s}} \right)$.

Theorem 16

Let ${\mathscr {T}}_{\iota }(\iota =1,2,...,{s})$ be a family of pqQROFNs and let ${\mathscr {T}}^{-}=\min \left\{ {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}}\right\}$ and ${\mathscr {T}}^{+}=\max \left\{ {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}}\right\}$. Then ${\mathscr {T}}^{-}\le {p}{q}QROFWGGHM^{\alpha ,\beta }\left( {\mathscr {T}}_{1},{\mathscr {T}}_{2},...,{\mathscr {T}}_{{s}} \right) \le {\mathscr {T}}^{+}$.

Proposed group decision-making methodology

This section introduces various averaging and geometric AOs, utilizing the proposed operational rules, to efficiently compile pqQROF data.

Consider a finite set of s alternatives denoted by $\aleph _{\iota }\left( \iota =1,2,...,{s} \right)$ and the set of n criteria symbolized by $\nabla _{{j}}\left( {j}=1,2,...,{n}\right)$ with the weight vector $\amalg =\left( \amalg _{{1}},\amalg _{{2}},...,\amalg _{{n}}\right) ^T$ fulfilling $\amalg _{{j}}>0$ and $\sum \limits _{{j}=1}^{{n}}\amalg _{{j}}=1$. Let ${\mathfrak {d}}_{{m}}\left( {m}=1,2,...,\tau \right)$ be a team of DEs with the weight vector ${\Cup }=\left( {\Cup }_{1},{\Cup }_{2},...,{\Cup }_{\tau } \right) ^T$ such that ${\Cup }_{m}>0$ and $\sum \limits _{{m}=1}^{\tau }{\Cup }_{m}=1$. Assume that mth DE provides his/her assessment information about an alternative $\aleph _{\iota }$ with respect to the criteria $\nabla _{{j}}$ as a pqROFN ${\mathscr {T}}^{(m)}_{\iota {j}}= \left( \mu ^{(m)}_{\iota {j}},\nu ^{(m)}_{\iota {j}} \right)$. The preferences of mth DE builds a pqROF decision matrix $M^{({m})}=\left( {\mathscr {T}}^{(m)}_{\iota {j}} \right) _{{s}\times {n}}$.

• Step 1 Normalization MCGDM problems often involve two types of criteria: benefit criteria $\mathscr {B}_{1}$ and cost criteria $\mathscr {B}_{2}$. Consequently, the initial decision matrices need to be normalized using the following formula:

  $$\begin{aligned} {\mathscr {T}}^{(m)}_{\iota {j}}={\left\{ \begin{array}{ll} \left( \mu ^{(m)}_{\iota {j}},\nu ^{(m)}_{\iota {j}} \right) , & \text{ if } {C}_{j}\in \mathscr {B}_{1} \\ \left( \nu ^{(m)}_{\iota {j}},\mu ^{(m)}_{\iota {j}} \right) , & \text{ if } {C}_{j}\in \mathscr {B}_{2}. \end{array}\right. } \end{aligned}$$

  (14)

• Step 2 Weights of the DEs Since several DEs are involved in the MCGDM process within a pqQROF environment. To determine the weight of these DEs, their significance degree is considered in the form of pqQROFNs. For the assessment of the weight of the mth DE, let $\left( \mu _{m},\nu _{m} \right)$ be the pqQROF value for the mth DE. The numerical weight of the DE is then determined by the Eq. (15)

  $$\begin{aligned} {\Cup }_{m}=\frac{\mu _{{m}}^{{p}}+\pi _{{m}}^{{\ell }}\times \left( \frac{\mu _{{m}}^{{p}}}{\mu _{{m}}^{{p}}+\nu _{{m}}^{{q}}} \right) }{\sum \limits _{m=1}^{\tau }\left( \mu _{{m}}^{{p}}+\pi _{{m}}^{{\ell }}\times \left( \frac{\mu _{{m}}^{{p}}}{\mu _{{m}}^{{p}}+\nu _{{m}}^{{q}}} \right) \right) } ~~m=1,2,...,\tau . \end{aligned}$$

  (15)

  Here, ${\Cup }_{m}\ge 0$ and $\sum \limits _{{m}=1}^{\tau }{\Cup }_{m}=1$.

• Step 3 Aggregated decision matrix In this step, we combine the individuals’ opinions into a combined form. For this, we apply the proposed pqQROFWGHM operator to construct the aggregated matrix ${\widetilde{Z}}=\left( \widetilde{{\mathscr {T}}}_{\iota {j}}\right) _{{s}{n}}$, where

  $$\begin{aligned} & \widetilde{{\mathscr {T}}}_{\iota {j}}=\left( {\widetilde{\mu }}_{\iota {j}},{\widetilde{\nu }}_{\iota {j}} \right) = {p}{q}QROFWGHM^{\alpha ,\beta }\left( {\mathscr {T}}^{(1)}_{\iota {j}},{\mathscr {T}}^{(2)}_{\iota {j}},...,{\mathscr {T}}^{(\tau )}_{\iota {j}} \right) = \nonumber \\ & \left( \left( \root p \of {1-\prod \limits _{{m}=1,{m}^{\prime }=m}^{\tau }\left( 1-{\mu _{\iota {j}}^{({m})}}^{{p}\alpha }{\mu _{\iota {j}}^{({m}^{\prime })}}^{{p}\beta } \right) ^{{\Cup }_{{m}}{\Cup }_{{m}^{\prime }}}} \right) ^{\frac{1}{\alpha +\beta }}, \root q \of {1-\left( 1-\prod \limits _{{m}=1,{m}^{\prime }=m}^{\tau }\left( 1-\left( 1- {\nu _{\iota {j}}^{({m})}}^{{q}}\right) ^{\alpha }\left( 1-{\nu _{\iota {j}}^{({m}^{\prime })}}^{{q}} \right) ^{\beta } \right) ^{{\Cup }_{{m}}{\Cup }_{{m}^{\prime }}} \right) ^{\frac{1}{\alpha +\beta }}} \right) . \end{aligned}$$

  (16)

• Step 4 Criteria weights through integrated approach We presume that each criterion has a distinct level of significance. Let $\amalg =\left( \amalg _{{1}},\amalg _{{2}},...,\amalg _{{n}}\right) ^T$ denote the weights for the criteria, where $\sum \nolimits _{{j}}^{{n}} \amalg _{{j}}=1$ and $\amalg _{{j}}\le 1$. In the subsequent analysis, we determine the objective, subjective, and integrated weights using the following procedure:

  Case I: Distance measure-based formula for objective weight In this case, we determine the objective weights, which are obtained from the provided assessment information using the following formulation.

  $$\begin{aligned} \amalg ^{{o}}_{{j}}=\frac{\frac{1}{{s}-1}\sum \limits _{\iota =1}^{{s}}\sum \limits _{k=1, {k}\ne \iota }^{{s}}d\left( {\mathscr {T}}_{\iota {j}},{\mathscr {T}}_{{k}{j}} \right) }{ \sum \limits _{{j}=1}^{{n}}\left( \frac{1}{{s}-1}\sum \limits _{\iota =1}^{{s}}\sum \limits _{k=1, {k}\ne \iota }^{{s}}d\left( {\mathscr {T}}_{\iota {j}},{\mathscr {T}}_{{k}{j}} \right) \right) }~~j=1,2,...,{n}, \end{aligned}$$

  (17)

  where $d\left( {\mathscr {T}}_{\iota {j}},{\mathscr {T}}_{k{j}} \right) =\frac{1}{2}\left( \left| \mu ^{p}_{\iota {j}}-\mu ^{p}_{k{j}} \right| +\left| \nu ^{q}_{\iota {j}}-\nu ^{q}_{k{j}} \right| +\left| \pi ^{\ell }_{\iota {j}}-\pi ^{\ell }_{k{j}} \right| \right)$²⁹.

  Case II: RS method for subjective weight of criteria The pqQROF-RS weighting model procedure aims to aid DEs in identifying the ranking of criteria. By utilizing Eq. (18), the subjective weight of the jth criterion is calculated as

  $$\amalg^{{s}}_{{j}}=\frac{{n}-\varcurlyvee_{{j}} +1}{\sum_{{j}=1}^{{n}}{n}-\varcurlyvee_{{j}} +1};\,\,j=1,2,...,n.$$

  (18)

  Here, $\varcurlyvee_j$ denotes the rank of each criterion $C_{j};j=1,2,...,n.$

  Case III: Integrated weights of criteria Based on the objective and subjective weights established in Case I and Case II, the integrated weight can be obtained via Eq. (19)

  $$\begin{aligned} \amalg _{{j}}=\Xi \amalg ^{{o}}_{{j}}+\left( 1-\Xi \right) \amalg ^{{s}}_{{j}}, \end{aligned}$$

  (19)

  where $0\le \Xi \le 1$ presents a precision parameter of the decision policy.

• Step 5 Aggregated values Employ the proposed pqQROFWGGHM operator Eq. (20) to fuse the criteria values of each alternative into one.

  $$\begin{aligned} & {\mathscr {T}}_{\iota }=\left( \mu _{\iota },\nu _{\iota } \right) = {p}{q}QROFWGGHM^{\alpha ,\beta }\left( \widetilde{{\mathscr {T}}}_{\iota {1}},\widetilde{{\mathscr {T}}}_{\iota {2}},...,\widetilde{{\mathscr {T}}}_{\iota {n}} \right) =\nonumber \\ & \left( \root p \of {1-\left( 1-\prod \limits _{{j}=1,{j}^{\prime }={j}}^{{n}}\left( 1-\left( 1- {\widetilde{\mu }}_{\iota {j}}^{{p}}\right) ^{\alpha }\left( 1-{\widetilde{\mu }}_{\iota {j}^{\prime }}^{{p}} \right) ^{\beta } \right) ^{\amalg _{\iota {j}}\amalg _{\iota {j}^{\prime }}} \right) ^{\frac{1}{\alpha +\beta }}}, \left( \root q \of {1-\prod \limits _{{j}=1,{j}^{\prime }={j}}^{{n}}\left( 1-{\widetilde{\nu }}_{\iota {j}}^{{q}\alpha }{\widetilde{\nu }}_{{\iota }{j}^{\prime }}^{{q}\beta } \right) ^{\amalg _{\iota {j}}\amalg _{{\iota }{j}^{\prime }}}} \right) ^{\frac{1}{\alpha +\beta }} \right) . \end{aligned}$$

  (20)

• Step 6 Score values and ranking Compute the score values of each alternative $\aleph _{\iota }\left( \iota =1,2,...,{s} \right)$ and rank them in descending order with respect to these values.

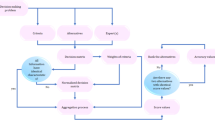
The flowchart illustrating the framed approach is shown in Fig. 1.

Fig. 1

Graphical representation of the proposed approach

Application

In this section, we present two case studies-one focused on project selection and the other on university selection-to illustrate the practical applicability of the proposed framework.

Case study 1

The global tourism industry has faced significant setbacks due to the COVID-19 pandemic, marked by both subjective concerns about health crises during travel and objective limitations imposed by epidemic prevention measures in various regions. As the tourism economy gradually rebounds, consumption patterns are evolving in response to the new external environment. Notably, reports indicate a rising popularity of suburban weekend leisure and ecological health tourism in Pakistan. In light of the ongoing challenges posed by COVID-19, a prominent domestic tourism enterprise is proactively exploring opportunities by venturing into the development of novel rural green ecotourism products.

Recognizing the intricate and uncertain nature of the external landscape, the company has engaged a team of experts to conduct a comprehensive evaluation of potential destination projects. The methodology proposed in this paper is well-suited for such evaluations.

Alternatives (destination projects)

The case study involves evaluating four potential tourism destination projects, denoted as $\aleph _{\iota }\left( \iota =1,2,3,4 \right)$. These represent the four alternative destinations that the company is considering for the development of rural green ecotourism products. The specific characteristics of these destinations would be assessed based on their tourism-related attributes, their ecological appeal, and the economic and societal conditions that could affect the success of ecotourism development in each location.

Criteria for evaluation

The evaluation of the four destination alternatives is based on four key criteria, which are essential for the sustainable development of rural green ecotourism in the post-COVID context:

• Tourism resources $\left( \nabla _{{1}}\right)$: This criterion assesses the availability and quality of resources that can attract tourists, such as natural landscapes, cultural heritage, recreational facilities, and local attractions. Given the rising popularity of suburban weekend leisure and ecological tourism, the presence of diverse tourism resources is critical.

• Ecological environment quality $\left( \nabla _{{2}}\right)$: This evaluates the environmental sustainability of the destination. It includes factors like air and water quality, biodiversity, and the preservation of natural ecosystems. Since ecological health tourism is gaining traction, the destinations with better ecological conditions will be more attractive to tourists seeking environmentally friendly options.

• Economic conditions $\left( \nabla _{{3}}\right)$: This criterion examines the economic viability of the destination. It includes factors such as infrastructure development, ease of access, local economic activity, and tourism-related job creation. The economic conditions will also reflect the potential for long-term profitability and the ability of the local economy to support sustainable tourism.

• Societal conditions $\left( \nabla _{{4}}\right)$: This criterion evaluates the societal environment at the destination, which includes factors such as local community acceptance of tourism, safety, healthcare services, and cultural integration. The pandemic has heightened concerns about health and safety during travel, so societal conditions play a crucial role in ensuring the success of tourism ventures.

These criteria are ranked as $\nabla _{{1}}>\nabla _{{3}}>\nabla _{{2}}>\nabla _{{4}}$. Further, the weight vector representing the significance of the DEs in terms of pqROFNs is ${\Cup }=\left( (0.6,0.4),(0.7,0.4),(0.5,0.5)\right) ^T$. The evaluations provided by the DEs are recorded in the form of pqROFNs and are summarized in Table 1.

Table 1 p q QROF assessment information.

Step 1: Since all the criteria are benefit types, the evaluations provided by three DEs, i.e., Table 1 remain unaltered.

Step 2: Based on Eq. (15), the weight vector of DEs is derived as ${\Cup }=\left( 0.3520,0.4003, 0.2477\right) ^T$.

Step 3: Using Eq. (16) (suppose $\alpha =2,$ $\beta =3$) the aggregated decision matrix is obtained and is shown in Table 2.

Table 2 Aggregated assessment information.

Step 4: According to Eq. (17), the objective weight vector of criteria is computed as $\amalg ^{{o}}=\left( 0.2175,0.2501,0.3253,0.2071\right) ^T$. With the use of Eq. (18), and the given raking of criteria the subjective weight vector is derived as $\amalg ^{{s}}=\left( 0.4000,0.2000,0.3000,0.1000 \right) ^T$. With Eq. (19) (suppose $\Xi =0.5$), we get the integrated weight vector of criteria as follows: $\amalg =\left( 0.3088,0.2250,0.3126,0.1536 \right) ^T$.

Step 5: Following Eq. (20) (suppose $\alpha =2,$ $\beta =3$), the criteria values of each alternative are aggregated as recorded below.

(0.6765, 0.5060), (0.6308, 0.5910), (0.5869, 0.5447) (0.6238, 0.5664).

Step 6: The score values of each alternative $\aleph _{\iota }\left( \iota =1,2,3,4 \right)$ are obtained as $S(\aleph _{1})=0.6008,$ $S(\aleph _{2})=0.5244,$ $S(\aleph _{3})=0.5238,$ $S(\aleph _{4})=0.5342.$ Thus, the ranking of alternatives is $\aleph _{1}>\aleph _{4}>\aleph _{2}>\aleph _{3}$.

Case study 2

In an increasingly interconnected and globalized world, where education is viewed as a cornerstone of personal and professional growth, students are showing a growing interest in pursuing higher studies abroad. This trend reflects aspirations for enhanced academic opportunities, cultural exposure, and personal development. However, the path to enrolling in a foreign university is often fraught with challenges, making the process complex and multifaceted.

Identifying the most suitable university abroad requires students to navigate various obstacles, including financial limitations, stringent academic requirements, and language proficiency barriers. To overcome these challenges and make informed decisions, students frequently seek guidance from a diverse range of experts. These include educational consultants, career counselors, admissions advisors, alumni networks, international student offices, and test preparation centers, among others.

Imagine a student aspiring to secure admission to an appropriate foreign university and evaluating several options, labeled as alternatives $\aleph _{\iota }\left( \iota =1,2,...,5 \right)$. To assist in this DM process, the student engages multiple experts-denoted as ${\mathfrak {d}}_{{1}}$, ${\mathfrak {d}}_{{2}}$ and ${\mathfrak {d}}_{{3}}$-who evaluate the universities based on specific criteria. These criteria include: $\nabla _1$: Academic reputation, $\nabla _2$: Faculty expertise, $\nabla _3$: Research opportunities, $\nabla _4$: Financial aid, $\nabla _5$: Innovation, $\nabla _6$: Cost. The importance of these criteria is ranked in the following order, reflecting their perceived priority: $\nabla _2>\nabla _4>\nabla _1>\nabla _5>\nabla _6>\nabla _3$. Additionally, each expert’s input carries a distinct weight, represented in terms of pqROFNS as, is ${\Cup }=\left( (0.5,0.4),(0.7,0.6),(0.6,0.3)\right) ^T$. The evaluations provided by the DEs are recorded in the form of pqROFNs and are summarized in Table 3 to identify the most suitable foreign university.

Table 3 pQROF assessment information.

Step 1: Since the criteria $\nabla _6$ is of cost type, therefore the data in Table 3 has been normalized accordingly, as shown in Table 4.

Table 4 Normalized pqQROF assessment information.

Step 2: Based on Eq. (15), the weight vector of DEs is derived as ${\Cup }=\left( 0.3070,0.2902,0.4028\right) ^T$.

Step 3: Using Eq. (16) (suppose $\alpha =2,$ $\beta =3$) the aggregated decision matrix is obtained and is shown in Table 5.

Table 5 Aggregated assessment information.

Step 4: According to Eq. (17), the objective weight vector of criteria is computed as $\amalg ^{{o}}=\left( 0.2337,0.1536 ,0.1818,0.1707 ,0.1037,0.1565\right) ^T$. With the use of Eq. (18), and the given raking of criteria the subjective weight vector is derived as $\amalg ^{{s}}=\left( 0.1905,0.2857,0.0476,0.2381,0.1429,0.0952 \right) ^T$. With Eq. (19) (suppose $\Xi =0.5$), we get the integrated weight vector of criteria as follows: $\amalg =\left( 0.2121,0.2197,0.1147,0.2044,0.1233,0.1258 \right) ^T$.

Step 5: Following Eq. (20) (suppose $\alpha =2,$ $\beta =3$), the criteria values of each alternative are aggregated as recorded below.

(0.5921, 0.5004), (0.5301, 0.4353), (0.5578, 0.4953) (0.5825, 0.5081),  (0.5291, 0.4560).

Step 6: The score values of each alternative $\aleph _{\iota }\left( \iota =1,2,3,4 \right)$ are obtained as $S(\aleph _{1})=0.5501,$ $S(\aleph _{2})=0.5458,$ $S(\aleph _{3})=0.5329,$ $S(\aleph _{4})=0.5406$, $S(\aleph _{5})=0.5360.$ Thus, the ranking of alternatives is $\aleph _{1}>\aleph _{2}>\aleph _{4}>\aleph _{5}>\aleph _{3}$.

Sensitive analysis

In what follows, we conduct sensitivity analysis for Case Study 1 to assess how variations in parameters p, q, $\alpha$, $\beta$, and criteria weights impact the ranking of alternatives.

Case I: Sensitivity Analysis with respect to p and q

In this section, we aim to elucidate how adjustments in parameters p and q can impact the outcomes of our DM process. Here, we maintain the Heronian parameters $\alpha =2$ and $\beta =3$ as fixed. Table 6 presents a comprehensive view of score values and resultant ranking orders of alternatives across varying values of p, while q remains fixed at 2. A scrutiny of Table 6 and Fig. 2 reveals a trend: as the value of p increases, the score values of alternatives decrease. Notably, minor fluctuations in ranking occur within the range of p between 2 and 5, stabilizing when p is greater than or equal to 8. Importantly, the optimal alternative remains consistent across these variations. This underscores the significance of adjusting parameter p, affording us the ability to finely regulate and modulate the impact of an alternative’s membership status in the evaluation process. This parameter serves as a crucial tool in fine-tuning how an alternative’s membership status influences the overall evaluation, thus enhancing our ability to tailor DM processes.

Table 6 Obtained results by proposed approach using different values of p.

Fig. 2

Ranking results for different values of p.

Similarly, another table illustrates score values and ranking orders of alternatives for various values of q, while p remains constant at 2, and $\alpha$ and $\beta$ are fixed at 2 and 3, respectively. Examination of this Table 7 and Fig. 3 reveals that score values increase with increasing values of q. For $q=2$ and 3, alternative $\aleph _4$ is preferred over $\aleph _2$, but their positions are swapped for remaining q values, with the ranking being $\aleph _1>\aleph _2>\aleph _4>\aleph _3$ consistently. Remarkably, the optimal alternative in this case remains $\aleph _2$ throughout the variations. This highlights the importance of adjusting parameter q. By doing so, we can control how much level is given to an alternative’s non-membership grade from a particular category, allowing for finer adjustments in the evaluation process.

Table 7 Obtained results by proposed approach using different values of q.

Fig. 3

Ranking results for different values of q.

Optimal selection of p and q

The selection of optimal values for $p$ and $q$ is crucial for achieving stable DM results. To determine reasonable values for these parameters, they should be chosen based on the evaluation values provided by decision-makers. A practical approach is to select the smallest integers $p$ and $q$ that satisfy the inequality $\mu ^p + \nu ^q \le 1$. For example, if a decision-maker provides an evaluation value of $(0.8, 0.7)$, we may set $p = 2$ and $q = 3$, since $0.8^2 + 0.7^2 > 1$, but $0.8^2 + 0.7^3 < 1$, making $p = 2$, $q = 3$ the smallest valid integers. If a DM needs to handle more complex or uncertain data, increasing $p$ and $q$ can expand the information representation space of pqQROFSs accordingly.

Case II: Sensitivity Analysis with respect to Criteria Weights

In this case, we undertake an analysis of the outcomes contingent upon varying values of the parameter $\Xi$, while maintaining $p=q=2$ and the Heronian parameters $\alpha =2$ and $\beta =3$ as constants. The fluctuation in $\Xi$ holds significant import, serving as a pivotal factor in evaluating the method’s sensitivity, as it modulates the weighting preferences between subjective and objective criteria. Table 8 and Fig. 4 present the sensitivity findings elucidating the ramifications of altering $\Xi$ values. According to the findings, for $\Xi =0.0$ and $\Xi =0.1$, the rankings of the alternatives are as follows: $\aleph _1>\aleph _3>\aleph _4>\aleph _2$. Here, $\Xi =0.0$ signifies complete disregard for objective weights, with sole consideration given to subjective weights, while $\Xi =0.1$ denotes minimal emphasis on objective weights relative to subjective ones. Consequently, variations in the ranking outcomes are anticipated.

For $\Xi$ values ranging from 0.2 to 0.4, the rankings shift to $\aleph _1>\aleph _4>\aleph _3>\aleph _2$, and for $\Xi$ values ranging from 0.5 to 1.0, the rankings become $\aleph _1>\aleph _4>\aleph _2>\aleph _3$. This delineation suggests that $\aleph _1$ emerges as the most favorable project, whereas $\aleph _2$ ranks as the least desirable option for $\Xi$ values of 0.1 through 0.4, with R3 assuming the role of the least favorable alternative for $\Xi$ values of 0.5 through 1.0. This analysis underscores the importance of both subjective and objective weightings. Neglecting or disproportionately favoring one over the other engenders variability in the ranking outcomes of the alternatives.

Table 8 Obtained results by proposed approach using different values of $\Xi$.

Fig. 4

Ranking results for different values of $\Xi$

Case III: Sensitivity analysis with respect to $\alpha$ and $\beta$

In this section, we aim to analyze and illustrate how variations in the Heronian parameters $\alpha$ and $\beta$ influence the outcomes of our DM process. For this purpose, we keep the parameters $p=2$ and $q=2$ fixed. Table 9 and Fig. 5 provide a detailed overview of the score values and the resultant ranking order of alternatives under different combinations of $\alpha$ and $\beta$. From Table 9, it can be observed that in the first five cases, the ranking of the alternatives follows the order $\aleph _{1}>\aleph _{4}>\aleph _{3}>\aleph _{2}$. However, in the remaining cases, a positional swap occurs between alternatives $\aleph _{2}$ and $\aleph _{3}$, resulting in an overall ranking of $\aleph _{1}>\aleph _{4}>\aleph _{2}>\aleph _{3}$. Notably, despite these changes, the optimal alternative $(\aleph _{1})$ remains consistent across all scenarios. The variations primarily affect the positions of the least favorable and second least favorable alternatives. These findings demonstrate that the ranking of alternatives is sensitive to the choice of HrM operators. However, the stability of the designed algorithm is evident, as the top-ranking alternative remains unchanged despite parameter variations. This suggests that the algorithm is robust in handling variations in $\alpha$ and $\beta$, ensuring reliable DM outcomes under diverse conditions.

Table 9 Obtained results by proposed approach using different values of $\alpha$ and $\beta$.

Fig. 5

Ranking results for different values of $\alpha$ and $\beta$.

Comparative study

To showcase the advantages of our HrM operators approach, we applied it alongside existing methods^{29,30,31,32,33,46} to the same problem (Section Application, Case Study 1). This analysis yielded optimal scores and ranking orders for all alternatives, presented in Table 10. By comparing these results, we gain valuable insights into the relative performance of each method.

Table 10 Ranking results based on different AOs.

• i). Table 10 demonstrates that the ranking order of alternatives obtained through AAWA³² and WA and WG²⁹ mirrors that derived from our developed approach. Nevertheless, these methods exhibit certain limitations. Ali and Naeem’s approach operates under the prerequisite that criteria and DEs weights must be predetermined, which restricts its applicability. Secondly, Seikh and Mandal’s method employs entropy to derive criteria weights, representing an objective methodology that overlooks subjective considerations. On the other hand, our proposed methodology boasts the capability to derive the DEs weights, and the criteria weights through an integrated approach, accommodating both subjective and objective considerations. Moreover, our operators possess the capability to account for relationships among aggregated arguments, a feature lacking in existing methodologies.

• ii). The AOs utilized in the existing methodologies³¹ and³⁰ offer distinct advantages, such as confidence level consideration and periodicity property, respectively. However, these AOs are based on simple foundational concepts that lack generality and flexibility, thereby limiting their ability to handle interrelationships among criteria. In contrast, the proposed aggregation method incorporates Heronian parameters $\alpha$ and $\beta$. Consequently, the developed operators exhibit enhanced robustness and flexibility in the aggregation process by allowing for the adjustment of these parameters within the aggregation functions. This adaptability renders the aggregation process more refined and seamless, thus better accommodating complex relationships among criteria.

• iii). From Table 10, it is evident that the ranking outcomes obtained from Ahmad et al.’s³³ proposed approach closely resemble those derived through the suggested technique. However, a notable mathematical discrepancy arises in the formulation of the proposed operators, where instead of ($\lambda$-1), (1-$\lambda$) is utilized. This erroneous formulation results in the generation of complex numbers when employing the Hamacher parameter equal to or greater than 3. Consequently, we have rectified this by applying the correct formulation of these formulas. Moreover, as previously discussed, the developed method has the capability to capture pqQROF information, a feature that distinguishes it from existing pqQROF AOs, which lack this capability. This underscores the enhanced versatility and efficacy of the proposed approach in accommodating complex information structures.

• iv). From Table 10, it is evident that the results obtained using the FWA and FWG operators⁴⁶ yield the same ranking order, $\aleph _{1}>\aleph _{4}>\aleph _{2}>\aleph _{3}$, as produced by the proposed approach. This alignment demonstrates the validity and reliability of the proposed operators and methodology. Although the ranking outcomes are consistent, the developed framework offers significant advantages. In addition to the rung parameters, it introduces two additional parameters, $\alpha$ and $\beta$, whereas the methodology by Ali et al.⁴⁶ incorporates only a single Frank parameter alongside the rung parameters. This added flexibility makes our approach more general, providing experts with greater control and more options to fine-tune their inputs, thereby facilitating more tailored and precise ranking outcomes.

• v). From Table 10, we can observe that the integrated approach proposed by Debnath et al.²⁵ also identifies alternative $\aleph _1$ as the optimal choice, consistent with both other existing approaches and the proposed method. However, while the alternatives $\aleph _2$ and $\aleph _4$ are ranked second and third in Debnath et al.’s framework, they are ranked third and second, respectively, in the proposed method. This slight discrepancy may be attributed to the contextual differences in the underlying frameworks-Debnath et al.’s approach is based on the qROF setting, whereas the proposed method operates within the pqQROF context. The existing approach²⁵ is an integrated one, with its primary advantage over the proposed method being the incorporation of the MABAC method alongside Aczel-Alsina operators. In contrast, the developed method relies solely on AOs without incorporating any measure-based methods. Additionally, Debnath et al.’s approach determines criteria weights using a purely subjective technique, specifically the SWARA model. In contrast, the proposed method employs both subjective and objective techniques, enhancing its robustness. More importantly, the proposed framework is based on the pqQROF context, which introduces two rung parameters, thereby increasing its flexibility. While the existing approach utilizes only one rung parameter, it maintains a degree of flexibility due to the presence of Aczel-Alsina parameters and other Bonferroni mean operator parameters.

The presented method offers significant advantages over the existing techniques.

• i). The prevailing techniques^30,31,32,33 often suffer from information loss due to the arbitrary assignment of criteria weights during the aggregation process, which impacts the reliability of preference rankings. By integrating both subjective and objective evaluation approaches, the proposed method ensures a more balanced and accurate determination of criteria weights. This results in realistic and consistent outcomes, making it particularly suitable for addressing MCGDM problems involving pqQROF information.

• ii). In real-world DM problems, interrelationships between criteria often emerge. For example, consider the evaluation of five learning management system packages-Moodle, Sakai, eFront, ATutor, and Dokeos-based on criteria such as course development, activity tracking, assessment, backup and recovery, error reporting, efficiency, troubleshooting, maintenance, and upgrading. In this scenario, activity tracking and assessment are clearly interdependent. Existing pqQROF AOs^{29,30,31,32,33} used for such problems fail to account for these interrelationships among multiple criteria. In contrast, the proposed framework, built on pqQROF weighted HrM AOs, effectively incorporates these interdependencies, offering a more comprehensive and accurate evaluation.

• iii). This study utilizes pqQROF data to assess the significance degrees of DEs, unlike existing approaches that rely on classical data. As a result, the proposed method is better equipped to handle higher levels of uncertainty, making it particularly effective for DM problems involving multiple criteria.

To further highlight the advantages of our presented approach, we present a comparative analysis between the proposed method and existing techniques^{29,30,31,32,33,46}, as outlined in Table 11.

Table 11 Comparative analysis of various approaches.

Conclusions

The HrM represents a class of aggregation techniques capable of effectively capturing relationships among arguments. Building on this foundation, several HrM operators tailored for pqQROFNs have been developed, along with a thorough investigation of their fundamental properties. These operators not only account for the interdependencies among pqQROFNs but also enhance the flexibility and accuracy of information aggregation. Moreover, it is established that the proposed operators satisfy all the required characteristics of AOs, ensuring their validity in DM applications. Utilizing these advanced AOs, a novel MCGDM framework is introduced, where evaluation ratings are expressed using pqQROFNs. The framework incorporates an integrated weighting methodology to determine criterion weights, balancing both subjective and objective considerations. As a result, the proposed approach offers greater adaptability and effectiveness compared to existing methodologies. To demonstrate its practical utility, the developed framework is applied to two real-world case studies-project selection and university selection-highlighting its applicability in diverse DM scenarios. Additionally, sensitivity analysis is conducted, revealing that the developed approach remains stable despite variations in different parameters. Furthermore, a comparative analysis with extant methodologies is conducted in the paper, showcasing the potential and advantages inherent in the framed approach.

As a future work, we recommend extending the proposed framework to encompass other generalized fuzzy contexts, such as interval-valued p,q-rung orthopair FSs³, r,s,t-spherical FSs⁴⁷, and circular PyFSs⁴⁸. Furthermore, while the current formulation for expert weight determination effectively integrates fuzzy logic principles, it does not explicitly account for the level of consensus among different experts. Enhancing the model to incorporate a consensus-driven weighting mechanism would be a valuable improvement, ensuring that decision outcomes reflect both individual expertise and group agreement. Additionally, applying the developed methodology to a broader range of MCGDM problems^49,50,51, including emerging technologies, project implementation, and site selection, is highly encouraged. Such applications could provide valuable insights into the robustness and versatility of the method in diverse contexts.