Application of an improved LSTM model based on FECA and CEEMDAN VMD decomposition in water quality prediction

Abstract

To address the limitations of existing water quality prediction models in handling non-stationary data and capturing multi-scale features, this study proposes a hybrid model integrating Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN), Variational Mode Decomposition (VMD), Long Short-Term Memory Network (LSTM), and Frequency-Enhanced Channel Attention (FECA). The model aims to improve prediction accuracy and robustness for complex water quality dynamics, which is critical for environmental protection and sustainable water resource management. First, CEEMDAN and Sample Entropy (SE) were used to decompose raw water quality data into interpretable components and filter noise. Then, a VMD-enhanced LSTM architecture embedded with FECA was developed to adaptively prioritize frequency-specific features, thereby improving the model’s ability to handle nonlinear patterns. Results show that the model is successful in predicting all six water quality indicators: NH₃-N (ammonia nitrogen), DO (dissolved oxygen), pH, TN (total nitrogen), TP (total phosphorus), and CODMn (chemical oxygen demand, permanganate method). The model achieved Nash-Sutcliffe Efficiency (NSE) values ranging from 0.88 to 0.99. Using dissolved oxygen (DO) as an example, the model reduced the Mean Absolute Percentage Error (MAPE) by 0.12% and increased the coefficient of determination (R2) by 0.20% compared to baseline methods. This work provides a robust framework for real-time water quality monitoring and supports decision making in pollution control and ecosystem management.

Introduction

Water is the foundation of all life on Earth and an indispensable resource for human survival, development, and prosperity. However, with the rapid advancement of industrialization and urbanization, water pollution has become an increasingly critical issue. Moreover, global climate change and the overexploitation of water resources have further exacerbated water stress, heightening the risk of a water crisis¹.

In recent years, machine learning models have gained prominence in water quality evaluation, providing researchers with powerful tools for analysis and prediction^2,3. Haggerty et al.⁴have noted an significant growth in the use of machine learning in Groundwater Quality Monitoring (GWO) modeling. Jongcheol et al.⁵ demonstrated that LSTM networks, as an advanced variant of recurrent neural networks (RNNs), effectively alleviate gradient vanishing, explosion issues and improve prediction accuracy. Comparative studies by Singha et al.⁶revealed that deep learning (DL) models outperform traditional machine learning approaches in groundwater quality prediction. Additionally, Pyo et al.⁷utilized Convolutional Neural Networks (CNN) to predict cyanobacterial concentrations in rivers, demonstrating the feasibility and accuracy of CNNs in water quality monitoring. Sha et al.⁸compared the performance of real-time water quality prediction using various deep learning models and input data preprocessing techniques. This finding suggests that a single model may not fully capture the information embedded in the data, thus limiting predictive performance.

As a result, hybrid models^{9,10,11,12,13,14} have become a promising direction in water quality prediction research. such as CNN-LSTM frameworks¹⁵and EEMD-LSTM models¹⁶, have further enhanced accuracy by integrating signal decomposition with temporal modeling. For instance, Baek et al.¹⁷ combined CNN and LSTM to simulate water quality indices in river basins, achieving significant improvements in simulation accuracy. Similarly, Luo et al.¹⁶integrated ensemble empirical mode decomposition (EEMD) with LSTM, the EEMD-LSTM model outperformed the standalone LSTM model (without EEMD preprocessing) in all evaluation metrics.

Despite these advancements, critical challenges persist¹⁸. Traditional decomposition methods (e.g., EEMD) struggle with non-stationary water quality data, resulting in incomplete feature extraction¹⁹. Recent studies, such as Hussein et al.²⁰ on groundwater quality assessment and Bachir et al.²¹ on Saf-Saf river modeling, further highlight the limitations of conventional techniques in dealing with high-frequency noise and nonlinear dynamics. Moreover, Complex hybrid architectures (e.g., multistage CNN-GRU) require extensive parameter tuning, hindering real-world deployment²².Sensitivity to noise and extremes, models often fail under abrupt environmental changes, such as monsoon-induced turbidity in the Selangor River Basin or noisy sensor data²³, compromising reliability.

To address these gaps, this study proposes an innovative hybrid model integrating CEEMDAN, VMD, LSTM, and FECA. The key innovations include adaptive multi-scale decomposition, where CEEMDAN adaptively decomposes nonlinear and non-stationary data into interpretable components, and VMD refines high-frequency signals to minimize information loss—overcoming limitations of traditional methods²⁴. Additionally, the FECA module dynamically prioritizes critical frequency components, enhancing robustness to noise and extreme conditions, a significant improvement over static attention mechanisms²⁵. Finally, the model achieves computational efficiency without sacrificing accuracy by reducing redundant features and integrating parameter-sharing strategies, addressing bottlenecks in prior hybrid frameworks. These advancements collectively provide a robust and efficient solution for high-frequency water quality prediction.

Materials and methods

Case study

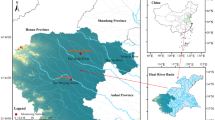
The study area focuses on the Dujiangyan Hydrological Station (103.62°E, 31.01°N) in Sichuan Province, China, a critical monitoring point in the Minjiang River Basin (Fig. 1).

Fig. 1

Location Map of Dujiangyan Hydrological Station(This figure is Generated using ArcGIS Desktop 10.8.URL: https://www.esri.com).

Water quality parameters and data preprocessing

The dataset used in this study is sourced from the National Real-Time Surface Water Quality Inspection and Distribution System (NRWQIS). The input variables for prediction include DO, CODMn, TN, pH, TP, and NH3-N, as shown in Fig. 2. The dataset comprises a total of 1,975 records collected over the period from July 1, 2022, to June 30, 2023, which serve as the basis for the predictive modeling process. In the data preprocessing phase, polynomial interpolation was applied to handle missing values and outliers, which accounted for between 0% and 1.5% of the dataset. To ensure the effectiveness of both model training and validation, the data were split into a training set and a test set. The training set includes 1,875 records spanning from 00:00 on July 1, 2022, to 00:00 on June 14, 2023, used for model training and parameter optimization. The remaining 100 records, covering the period from 04:00 on June 14, 2023, to 16:00 on June 30, 2023, were retained as the test set.

Fig. 2

Historical Distribution Data of Original Water Quality Indicators.

Model architecture and auxiliary approaches

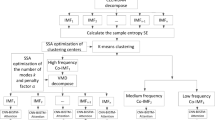
To present more clearly the structure and workflow of the improved LSTM water quality prediction (hereafter abbreviated as CSVLF) model based on FECA and CEEMDAN-VMD decomposition, the design of the CSVLF model architecture is shown in Fig. 3.

Fig. 3

Architecture Diagram of the CSVLF Model.

CEEMDAN decomposition

CEEMDAN¹⁹ is a novel signal processing method that combines the advantages of Empirical Mode Decomposition (EMD) and EEMD²⁶. The specific steps of the CEEMDAN method are as follows:

(1) An initial signal-to-noise ratio α is set and a set of Gaussian white noise sequences $\varepsilon (t)(t=1,2,3,…,n)$satisfying a standard normal distribution is generated. Where$~I$ is the number of noise sequences and n is the length of the time series.

$${\varepsilon _i}(t),\quad t=1,2,3, \ldots ,n,\quad i=1,2,3, \ldots ,I$$

(1)

.

(2)The original time series data were augmented by sequentially adding the generated white noise sequences, resulting in a set of noisy data sequences $f_{t} \left( t \right)\left( {t = 1,\,2,\,3,......,\,\,n;\,\,\,i = 1,\,\,2,\,\,3,........n} \right)$.

$${f_i}(t)=f(t)+\alpha \cdot {\varepsilon _i}(t),\quad t=1,2,3, \ldots ,n,\quad i=1,2,3, \ldots ,I$$

(2)

(3) EMD decomposition is performed on each noisy data sequence to obtain a series of IMFs. The j th IMF is denoted as$E_{j}^{i}(t)$:

$$E_{j}^{i}(t),\quad t=1,2,3, \ldots ,n,\quad j=1,2,3, \ldots ,K$$

(3)

Where K is the number of IMFs and I denotes the I th noisy data sequence.

(4) Perform ensemble averaging on each IMF to obtain the final one.

$$IM{F_j}(t)=\frac{1}{I}\sum\limits_{{i=1}}^{I} {E_{j}^{i}} (t),\quad t=1,2,3, \ldots ,n,\quad j=1,2,3, \ldots ,K$$

(4)

To optimize the decomposition process, the signal-to-noise ratio α can be adjusted based on the specific characteristics of the data. The steps of noise addition, EMD decomposition, and ensemble averaging are repeated iteratively until the desired Intrinsic Mode Functions (IMFs) are obtained.

SE method

Sample Entropy²⁴is a tool for measuring the complexity of time series data, which is based on the concept of information entropy and is used to quantitatively assess the stochasticity and predictability of signals. It is defined as:

$$Sample~Entropy(U)= - li{m_{m \to \infty }}{,_{r \to 0}}\frac{1}{N}\sum\nolimits_{{i=1}}^{N} {logB(m,r)}$$

(5)

Where U is a discrete-time series, N is the length of the sequence, m is the embedding dimension, r is the fraction of the time series standard deviation corresponding to the time series standard deviation as well as$~B\left( {m,r} \right)$is the ratio of the number of matching template vectors with embedding dimension m and r similarity, to the number of total template vectors.

VMD method

VMD²⁷is an advanced signal processing technique that adaptively decomposes a signal into multiple IMFs, with each IMF representing a component of the signal at different frequencies and time scales. VMD aims to minimize the error between the input signal and these IMFs while guaranteeing the diversity and stability of the IMFs. It determines the center frequency of each IMF by minimizing the sum of the estimated bandwidths of the components and using an alternating direction multiplier method.

LSTM model

Fig. 4

LSTM Flowchart.

LSTM is a type of recurrent neural network designed to address the long-term dependency problem in time series data²⁸.It achieves this through a gated mechanism consisting of three main components: the input gate, forget gate, and output gate. These gates regulate the flow of information, allowing the model to retain relevant long-term dependencies while discarding irrelevant information. In this study, we employ a three-layer LSTM architecture with 128, 64, and 32 units in each layer, respectively. This configuration is optimized to capture both short-term fluctuations and long-term trends in water quality data. The structure and operation of the LSTM model are illustrated in Fig. 4, and the specific formulas for the gates and cell states are as follows:

$${f_t} =\sigma ({W_f}{x_t}+{U_f}{h_{t-1}}+{b_f})$$

(6)

$${i_t} =\sigma ({W_i}{x_i}+{U_i}{h_{t-1}}+{b_i})$$

(7)

$${\tilde {c}_t} =tanh({W_c}{x_t}+{U_c}{h_{t-1}}+{b_c}),$$

(8)

$${c_t}={f_t} \odot {c_{t-1}}+{i_t} \odot {\tilde {c}_t}$$

(9)

$${o_t} =\sigma ({W_o}{x_t}+{U_o}{h_{t-1}}+{b_o})$$

(10)

$${h_t} ={o_t} \odot tanh({c_t})$$

(11)

Where ${x_t}$is the water quality input feature vector, ${h_t}$is the LSTM hidden state vector, and ${f_t}$,${i_t}$,${\tilde {c}_t}$,${c_t}$,${o_t}$ denotes the activation vectors of the forgetting gate, input gate, cell input, cell state, and output gate, respectively. W and U are weight matrices for input features and previous hidden states respectively, while $\operatorname{b}$are bias terms added before activation. The symbols $\odot$denote the Hadamard product.

FECA module

Leverage the advantages of the above VMD-LSTM model, and further introduce the frequency-enhanced channel attention module to improve the model’s ability to capture frequency information in time series data. Mathematically, the processing of FECA²⁵ can be expressed as follows: for an input time series.$X \in {R^{C \times T}}$., where C represents the number of channels and T represents the length of the time series, the FECA module first computes the DCT to obtain the frequency spectrum$X\prime \prime$:

$$X\prime =DCT\left( X \right)$$

(12)

.

Subsequently, the channel attention mechanism is applied to obtain the final enhanced frequency spectrum$X\prime \prime$:

$$X\prime \prime =FECA\left( {X\prime } \right)=\sigma \left( {g\left( {X\prime ,W} \right)} \right) \odot X\prime$$

(13)

Where $g( \cdot )$denotes the attention mechanism with parameterW, $\sigma$is the Sigmoid activation function, and $\odot$ denotes the element-by-element multiplication.

Benchmark models and evaluation

Evaluation

In evaluating the model, the model employs a variety of criteria to comprehensively measure the model’s performance. These criteria include NSE, Mean Bias Error (MBE), Theil’s inequality coefficient (TIC), and R², Root Mean Square Error (RMSE), Mean Absolute Square Error (MAE), and MAPE. These criteria measure the model’s goodness-of-fit, prediction accuracy, and relative error of prediction, respectively, and provide a comprehensive assessment of the model.

$$R^{2} = 1 - \frac{{\sum\limits_{{t = 1}}^{n} {(y_{t} - \hat{y}_{t} )^{2} } }}{{\sum\limits_{{t = 1}}^{n} {(y_{t} - \bar{y})^{2} } }},$$

(14)

$$MBE = \frac{1}{n}\sum\limits_{{t = 1}}^{n} {(y_{t} - \hat{y}_{t} )} ,$$

(15)

$$TIC = \sqrt {\frac{{\sum\limits_{{t = 1}}^{n} {\left( {\frac{{y_{t} - \hat{y}_{t} }}{{y_{t} }}} \right)^{2} } }}{{\sum\limits_{{t = 1}}^{n} {\left( {\frac{{y_{t} }}{{y_{t} }}} \right)^{2} } + \sum\limits_{{t = 1}}^{n} {\left( {\frac{{\hat{y}_{t} }}{{y_{t} }}} \right)^{2} } }}} ,$$

(16)

$$RMSE(y,\hat {y})=\sqrt {\frac{1}{n}{{\sum\limits_{{i=1}}^{n} {({y_i} - {{\hat {y}}_i})} }^2}}$$

(20)

,

$$MAE(y,\hat {y})=\frac{1}{n}\sum\limits_{{i=1}}^{n} {|{y_i} - {{\hat {y}}_i}|}$$

(21)

,

$$MAPE(y,\hat {y})=\frac{{100\% }}{n}\sum\limits_{{i=1}}^{n} {\frac{{|{y_i} - {{\hat {y}}_i}|}}{{\hbox{max} (\sigma ,|{y_i}|)}}}$$

(22)

Benchmark models and experimental setup

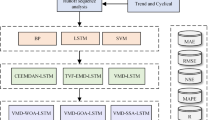
The proposed model was implemented using Python 3.10, PyTorch 2.1.2, and CUDA 11.8 for GPU acceleration. The model was trained and evaluated on a high performance computing system to ensure efficient processing of the water quality time series data. The input configuration included a dateback of 30 (number of previous time steps used for prediction), periods of 50 (number of future time steps to predict), and a timestep of 1 (interval between consecutive time steps). The LSTM network consisted of three hidden layers of 128, 64, and 32 units, respectively, designed to extract complex features hierarchically. The tanh activation function and a dropout rate of 0.2 were used to prevent overfitting. The model was trained for a minimum of 500 epochs with a batch size of 16 using the Adam optimizer (learning rate = 0.001) and early termination (patience = 50). Training data was randomized before each epoch to improve generalization. Also, to compare the effectiveness of the CSVLF model, the study compares the forecasting performance of five models. The five models are:

Model 1: Single-LSTM: To explore the performance comparison between the hybrid model and the single model.

Model 2: CEEMDAN-VMD-GRU: Explore the role of LSTM by replacing it with GRU.

Model 3: CEEMDAN-ISOS-VMD-LSTM: Replacing SE with ISOS and exploring the role as well as the importance of SE, especially the FECA layer.

Model 4: Respective -LSTM: Explore the role of VMD, SE, and FECA in time series modeling by removing these two components.

Model 5: CEEMDAN-CNN-CBAM-LSTM: Replacing the SE, VMD, and FECA modules with CNN, and CBAM to explore the performance comparison.

Results

Data characteristics and preprocessing results

In the data preprocessing stage, this study analyzed the time series data of several water quality indicators for smoothness using the Augmented Dickey-Fuller (ADF) test. The results showed that the ADF test statistic for DO was − 2.59 with a p-value of 0.09, which exceeded the common significance level of 0.05, indicating that the series was non-stationary. Similarly, the ADF test statistic value for NH3-N was − 1.80 with a p-value of 0.38, which also failed to reject the original hypothesis of non-stationarity. P-value of the ADF test for PH, TP, and CODMn were below 0.05, showing that these series were smooth. In particular, TN had an ADF statistic value of -8.73 with a very low p-value (3.21), clearly indicating a strong smoothness.

Table 1 Statistical tests.

In terms of autocorrelation, the results of the Ljung-Box test revealed a p-value of 0.0000 for all series, indicating significant autocorrelation within the data. As presented in the table, the Ljung-Box statistic for DO is 5084.96, and for NH3-N, it is 47466.94. The strong autocorrelation observed in these series necessitates special attention during modeling. To ensure the accuracy of the model, it is often required to mitigate autocorrelation through techniques such as differencing.

Regarding the normality test, the results from the Jarque-Bera test show that all series exhibit a p-value of 0.0000, suggesting that none of the series follow a normal distribution. The non-normality of the distributions may impair the performance of traditional statistical models, which rely on normality assumptions. Consequently, the use of LSTM networks, which are robust to non-normal data distributions, is deemed more suitable for the subsequent analysis²⁹. These results are further detailed in Table 1.

In summary, the time series of the water quality indicators exhibit varied characteristics in terms of smoothness, autocorrelation, and distribution normality, as illustrated in Fig. 5. To address the challenges posed by non-stationary and non-normal distributions, it is recommended to employ the CEEMDAN method, combined with deep learning-based prediction models (such as LSTM), to more effectively capture the complex and dynamic features of the water quality time series.

Fig. 5

ACF and PACF Plots.

Initial modal decomposition

The six raw data parameters were decomposed into several IMF components using the CEEMDAN algorithm, TN was decomposed into 8 components (IMF), pH, DO, and TP into 9 components, and both NH3-N and CODMn were decomposed into 10 variables. As shown in Fig. 6, the decomposition process effectively separates the original time series data into distinct frequency components, highlighting the multiscale characteristics of each parameter. For example, the IMFs for DO (Fig. 6c) reveal both high-frequency noise and low-frequency trends, while the integration results (Fig. 6a) and sample entropy values (Fig. 6b) provide insight into the complexity and predictability of the decomposed components. This decomposition provides a robust basis for subsequent analysis and modeling.

Fig. 6

Diagram of CEEMDAN Decomposition, Sample Entropy, and Integrated Results for DO Parameters.

In Fig. 6(c), illustrates the decomposition process for DO as a representative example.the raw DO data and the nine IMF decomposition results are shown sequentially from top to bottom. The horizontal axis represents the number of time series and the vertical axis represents the water quality values for each component. Since the water quality dataset contains only about 1975 samples, the data volume is small for the deep learning model. Decomposition using the LSTM model directly would lead to poor prediction results because this study uses a Python sampen module to measure the sample entropy of each IMF, which is used to measure the complexity of water quality data. IMFs with similar sample entropy values can be integrated to appropriately reduce the amount of computation, increase the speed of modeling, and avoid overfitting problems. The sample entropy measurements of all IMFs and residuals for the DO variables are presented in Fig. 6(b), where IMF8 corresponds to the residuals. By looking at Fig. b, it can be noticed that the sample entropy values of the first three IMFs (IMF0, IMF1, and IMF2) are all much higher than the other IMFs, showing a complex, variable but unobtrusive pattern. In contrast, the last two IMFs and the residuals (IMF6, IMF7, and IMF8) have lower sample entropy values, obvious water quality trends, and less complexity and volatility. Therefore, it was decomposed into three parts to be studied see Fig. 6(c), high-frequency CoIMF0 (IMF0, 1, 2), CoIMF1 low frequency (IMF3,4,5), and trend CoIMF2 (IMF6,7,8). pH and TP were reconstructed in the same way as DO, and for the other three parameters, NH3-N as well as CODMn, the two parameters with IMF3-5 were reconstructed as low frequencies and IMF6-9 were reconstructed as trend terms. The same IMF0-1 for TN is reconstructed as high frequency, IMF2-4 as low frequency, and IMF5-7 as trend terms.

2.3 Secondary modal decomposition.

The initial decomposition revealed that the high-frequency component (Co-IMF0) exhibited high complexity, making it particularly challenging to predict. Therefore, VMD secondary modal decomposition was performed on this high-frequency component to reduce its complexity (see Fig. 7(a)). The parameter K was set to 5. The sample entropy measurements, illustrates the decomposition process for DO as a representative example. As shown in Fig. 7(b), indicate that the sample entropy of the high-frequency component decreased to below 0.4 after the secondary decomposition. This reduction in complexity provides the potential for improving the final prediction accuracy.

Fig. 7

Sample Entropy Diagram of VMD Decomposition for DO Parameters.

Prediction results

After performing the first two decomposition operations on the parameters, this study then discusses the two underlying frameworks based on those proposed by Feite Zhou³⁰, which are the integrated prediction framework and the independent prediction framework. In the integrated prediction framework, they adopt a global approach to integrate the data of all common empirical modal functions (Co-IMFs) into one LSTM model to improve the prediction performance. After CEEMDAN and sample entropy integration, the input data were converted to matrix form to capture the intrinsic correlation of the time series more comprehensively. We illustrates for DO as a representative example The dissolved oxygen concentration at each time point in the time series was set to correlate with the first 30 time points, and a model structure containing three LSTM layers (128, 64, and 32 cells) was constructed. Although the framework performed well in terms of prediction, there is room for improvement in terms of accuracy in coping with certain inflection points.

On the other hand, the stand-alone prediction framework employs a local prediction strategy that improves the local accuracy of the prediction by modeling each Co-IMF separately and performs more accurately in dealing with the prediction of certain inflection points. Unlike the integrated framework, this framework transforms the input data into vector form for each Co-IMF. The model structure is similar to the integrated framework, which also contains three LSTM layers (128, 64, and 32 cells) and uses the same optimizer and loss function. The final prediction results are obtained by summing the predictions of each Co-IMF to get the integrated prediction of the time series. However, the framework is more complex and takes a longer time for training and prediction.

As a result, the present study has carried out a more in-depth exploration based on the existing research. In the prediction stage of the model study, a composite prediction framework covering the VMD re-decomposition is constructed on the one hand, and on the other hand, the FECA layer is integrated into the LSTM network innovatively. By integrating the FECA layer into the LSTM network, the model can capture and utilize the frequency information in the time series data more efficiently.

In the construction of this prediction framework, the model takes systematic steps to optimize the prediction of water quality indicators. Using the CEEMDAN method, the original time series of the six water quality parameters were decomposed into IMFs and residuals of different frequencies. Through the sample entropy technique, these IMFs and residuals are integrated to form Co-IMFs.For the high-frequency Co-IMF0 which contains more noise, the VMD method is used for further decomposition and combined with the FECA layer for prediction. While the other Co-IMFs apply their respective LSTM prediction methods. Eventually, the prediction results of all Co-IMFs were summarized by the integrated LSTM method to enhance the stability and accuracy of the prediction model.

The model provides an in-depth comparative analysis of prediction models for a variety of water quality indicators including DO, pH, TP, and NH3-N. According to Table 2, the proposed method shows excellent performance in all evaluation indicators, significantly outperforming the existing benchmark models. In predicting DO, the model achieved very low RMSE (0.04) and MAE (0.03), which are much lower than the benchmark models Model1 (RMSE 0.27) and Model2 (RMSE 0.28), showing its high accuracy in DO prediction. Similarly, the RMSE of the model was only 0.01 in predicting pH, reflecting its accuracy in predicting key water quality parameters.

The model also demonstrated significant results in reducing prediction errors. For example, the MAPE was only 0.30% for DO and 0.14% for pH. In terms of bias, the model also had smaller MBE values, especially in the prediction of NH3-N and TP than most of the comparison models.

Despite the advantages of this composite framework in the presentation of experimental results, a slight underperformance on certain metrics (e.g., TIC and MBE) is also found when compared with other models. Specifically, on TIC, the model showed a slight increase relative to Model1 and Model4, and on MBE, the model changed direction relative to Model3 and Model5. The analysis suggests that this may be due to differences in data preprocessing or model parameter settings. With these measures, the model is expected to show a more balanced and comprehensive performance in future releases.

Table 2 Comparison of various model indicators.

To further enhance the credibility of the models, this study further employs two intuitive analytical tools, scatterplot, and boxplot, to provide an in-depth and detailed discussion on the performance of different models in predicting water quality indicators. With the introduction of the VMD re-decomposition technique and the FECA layer, the prediction framework exhibits a significant performance improvement. This enhancement was verified in the results after 500 runs, as evidenced by the best average R² value of up to 0.96 for the six water quality indicators (see General Fig. 8), which not only highlights the effectiveness of the VMD re-decomposition technique and the FECA layer, but also provides a solid foundation for the subsequent analysis.

The scatterplot further validates the accuracy of the model. The left side of the overall Fig. 8 shows the performance comparison of the six water quality indicators, while the right side visualizes the ability of different models to fit the water quality data through scatter plots. By scrutinizing the scatter distributions of predicted and observed values, it can be seen that the correlation between the predicted and observed values of the model is extremely high for several water quality indicators. Especially in the prediction of TN and pH, the distribution of the scatter plot almost exactly matches the trend of the observed values, which fully demonstrates the high accuracy of the model. In contrast, the scatter distributions of other benchmark models such as Model1 and Model2 are more scattered and deviate from the trend of the observed values, which further highlights the significant advantages of the proposed model in this study for water quality prediction.

Fig. 8

Comparison Chart of Results from Different Models.

The boxplot comparison in Fig. 9 shows the prediction errors of different models for six water quality parameters, with our model performing particularly well for key parameters such as DO and NH3-N. For example, for the DO parameter, our model has a more concentrated error distribution, with an interquartile range (IQR) of approximately 0.02–0.04 mg/L, which is significantly narrower than other models, such as Model1’s range of 0.15–0.25 mg/L. This indicates that our model is more accurate in predicting dissolved oxygen levels. For NH3-N, our model also shows a narrower error range, with an IQR of about 0.001–0.003 mg/L, while Model1 and Model2 show wider error ranges of 0.002–0.005 mg/L and 0.003–0.006 mg/L, respectively, further confirming the superiority of our model in handling the dynamics of NH3-N.

Fig. 9

Boxplot Comparison of Errors.

Discussion

The CSVLF model proposed in this study demonstrates a significant improvement in water quality prediction accuracy compared to existing methods. The model establishes a robust framework for high-frequency dynamic water quality prediction for multi-parameter systems by synergistically integrating VMD and FECA into the LSTM architecture. Recent advances in hybrid modeling based on signal decomposition, such as EMD with time series decomposition for water quality prediction³¹, have highlighted the importance of signal separation in dealing with non-stationary water quality data, but traditional methods are often limited by the problems of modal aliasing and noise interference⁷. The present framework effectively solves this limitation through the introduction of VMD, whose noise-resistant decomposition capability provides a purer data base for high-frequency component prediction.

The model performance is consistent with the previous research results, and achieves superior performance in most scenarios. For example, Baek et al.¹⁷ showed that the hybrid model of coupled convolutional neural network (CNN) and LSTM can improve the accuracy of water level and water quality prediction, but its DO prediction accuracy only reaches 0.9283, while the CSVLF model improves the index to 0.9930. Luo et al.¹⁶ demonstrated that the integrated empirical mode decomposition-long and short-term memory network (EEMD-LSTM) model outperforms the single LSTM model in all evaluation indicators, and although its research results are of significant value, the CSVLF model further improves the prediction accuracy of the high-frequency component by introducing the VMD and FECA mechanisms, forming a more advantageous prediction framework. The study on the prediction of chlorophyll a concentration in large lakes using the Kolmogorov-Arnold network (KAN)³²has already emphasized the importance of hierarchical feature extraction and anti-noise decomposition in environmental modeling, while the FECA mechanism innovatively introduced in this model can dynamically optimize the weights of the spectral features, resulting in a significant improvement of the prediction accuracy. This design is in line with the trend of hybrid architecture in environmental science, where the integration of FECA further enhances the adaptability of the model.

This dual-mechanism synergy - the VMD realizes the anti-noise decomposition, and the FECA realizes the frequency-domain feature prioritization - enables the model to perform particularly well in predicting critical water quality parameters. Results show that the RMSE of DO prediction is reduced from 0.269 mg/L to 0.036 mg/L, and the MAPE of TN is improved by a factor of 10 (from 8.10 to 0.83%, compared to model 1). Such performance improvements are consistent with the results of studies that emphasize hybrid architectures that reduce computational complexity while maintaining accuracy³³, but exceed existing benchmarks through targeted optimization of high-frequency components. The dynamic feature selection mechanism of FECA further extends the applicability of the model to complex urban waters, compared to results from river studies where adaptive decomposition techniques have led to improved TN prediction accuracy.

The high accuracy and strong robustness of the CSVLF model in predicting water quality parameters are of great practical significance for ecological environmental monitoring and management. For example, the model’s high-precision real-time prediction capability can support the deployment of a dynamic water quality monitoring system that can realize the immediate detection and rapid response to pollution events; the accurate prediction of dissolved oxygen and TN concentrations provides key data support for maintaining the health of aquatic ecosystems; and the model’s ability to effectively capture the long-term dependence and dynamic changes in water quality can provide a scientific basis for decision-making on ecological restoration and protection. Despite the excellent performance of the CSVLF model in handling routine water quality parameters, its ability to predict extreme values (e.g., sudden ammonia concentration spikes) is still limited. Therefore, future work can integrate spatially explicit covariates (e.g., industrial emission patterns) or adopt an uncertainty quantification framework to improve robustness and further extend the model’s generalization ability in extreme scenarios.

Conclusion

In conclusion, the CSVLF model in this study shows obvious advantages in water quality monitoring. It can effectively extract different frequency components in the water body, which makes the model more adaptable, and the LSTM model can capture the long-term dependence of the water quality time series in modeling, thus predicting the dynamic changes of water quality more accurately. There are some limitations of the model. The model performance may be limited by the data quality and sampling frequency, there is still room for improvement in the handling of certain anomalies, and the construction and tuning of the model may be limited for the adaptability of certain water bodies, which needs to be further verified and optimized in practical applications.