Introduction

The facet joint is a pair of small stabilizing joints located behind the left and right vertebrae, providing stability and enabling various movements such as bending and twisting1,2. Facet joint degeneration (FJD) is primarily attributed to facet joint osteoarthritis, which stems from the deterioration of cartilage on the zygapophyseal joint surfaces. This leads to pain as the cartilage thins, causing bones to rub against each other, impairing joint function, and resulting in increased stiffness and swelling due to inflammation of the facet joint3,4. Asymmetrical degenerative changes in the facet joint can create an uneven load on the spine due to spinal alignment issues, potentially accelerating wear on one side. These degenerative changes in the facet joint are often triggered by spinal injuries, muscle imbalances, and herniated lumbar discs5,6. Unilateral degeneration of the facet joints can contribute to degenerative changes in the contralateral facet joints through an interconnected degenerative process, ultimately leading to bilateral degeneration of the facet joints. Factors driving such compensatory mechanisms include altered spinal alignment and compensatory postures caused by muscle imbalances, which increase stress on the contralateral facet joint due to altered loading patterns. This heightened stress accelerates the degeneration of previously healthy facet joints. To potentially halt this chain reaction of FJD, early intervention targeting unilateral degeneration of the facet joints is essential.

Previous studies on degenerative lumbar spine disease have explored the chain reactions between facet joints and intervertebral discs7,8,9. It is widely recognized that facet joints and intervertebral discs are anatomically distinct. However, Kirkaldy-Willis et al. proposed that external forces and lesions impacting one structure may influence the other as well10. When damage occurs in a specific lumbar segment, adjacent structures are similarly affected. Moreover, degenerative changes in lumbar spine disease can be viewed as a continuous, repetitive process of biological healing following mechanical damage accumulated throughout life. Various spinal structures, including the facet joints, undergo a series of ongoing changes through repeated cycles of damage and healing11,12,13. Therefore, future studies on spinal diseases should investigate the effects of degenerative changes across different spinal structures.

Recently, clinical and finite element analysis (FEA) studies focusing on facet joints have examined the factors contributing to their degeneration in degenerative spinal diseases, as well as the relationship between facet joints and intervertebral discs in spinal disorders14,15,16. Yahara et al. utilized FEA to analyze asymmetric loading and stress distribution in the thoracic facet joints of adolescent idiopathic scoliosis (AIS) patients17. Through numerical analysis, they demonstrated that asymmetric loading could drive degenerative changes in the facet joints, such as subchondral sclerosis and hypertrophy, thereby contributing to scoliosis progression. Their study highlights that, in simulations mimicking spinal behavior, an initial structural imbalance in the spine results in varying loading distributions across the facet joints at each spinal segment. Kim et al. developed a finite element (FE) model to explore the effects of facet joint orientation and tropism on the biomechanics of the lumbar spine18. Their findings suggest that abnormal loading distribution due to facet joint orientation can promote degenerative changes in the facet joints. Facet joint tropism may lead to asymmetry between the left and right facet joints, potentially inducing degenerative spinal disorders. These results indicate that the shape of facet joints influences lumbar spine stability, segmental motion range, and loading distribution. This study investigates the impact of asymmetric degenerative changes in the facet joints on adjacent spinal structures, with a focus on the facet joints, where progressive degenerative changes frequently occur in association with other degenerative spinal disorders.

We drew on previous studies that constructed lumbar FE models to simulate the facet joints of the lumbar spine19,20,21. The L4–L5 functional spinal unit (FSU) was selected as the segment where FJD most commonly occurs, given its relatively higher incidence rate compared to other segments22. The primary factors of FJD include reduced joint space, diminished cartilage, and hypertrophy of the joint processes23. In this study, we quantified FJD by assigning different degeneration grades. The key variables for grading FJD were the gap between the zygapophyseal joints and the coefficient of friction between the joint surfaces. Consequently, this study developed FE models with varying grades of FJD in the L4–L5 FSU.

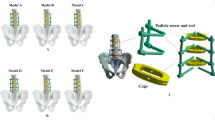
Degeneration grades were classified as follows: Grade 0 (normal condition), Grade 2 (moderate), and Grade 4 (severe). To represent asymmetric degeneration, the left and right facet joints were individually graded: Grade 0 for both joints was denoted as G00, while Grade 4 for the left joint and Grade 0 for the right joint was denoted as G40. We adopted this approach to model asymmetric degeneration by assigning distinct degeneration grades to the left and right facet joints. The resulting lumbar FE models were arranged in order of increasing degeneration severity: G00, G40, G42, and G44. Except for the G00 model, which represented the normal state, all FE models featured Grade 4 degeneration in the left facet joint. The degeneration grades of the right facet joint increased progressively as follows: G0, G2, and G4. This design sought to demonstrate the impact of severe degeneration in one facet joint on the degeneration of the opposing facet joint.

This study sought to analyze biomechanical changes in spinal segments and shifts in stress distribution across adjacent lumbar segments based on the grade of FJD using FEA. In doing so, we aimed to elucidate the effects of the asymmetric progression of FJD on adjacent structures.

Materials and methods

Lumbar FE model

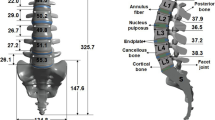
First, a lumbar finite-element model was constructed. The range of the spine was L1-S1, and each segment of the spine was extracted from the Mimics 21.0 (Materialise, Leuven, Belgium) program from the medical imaging data of an adult male. Using the Inventor 2020 (Autodesk, Mill valley, CA, USA) software, we modeled the ground substance, nucleus pulposus, end plates, and seven ligaments (anterior longitudinal ligament (ALL), posterior longitudinal ligament (PLL), ligamentum flavum (LF), intertransverse ligament (ITL), interspinous ligament (ISL), supraspinous ligament (SSL), and facet joint ligament (FJL)), excluding the vertebrae.

As shown in Fig. 1, modeling was performed to distinguish the various components of the vertebral body (cortical bone, cancellous bone, and posterior bone). The material property data for each component of the lumbar spine FE model are listed in Table 119,21,24,25,26,27,28,29,30. The linear isotropic elastic model comprises several components such as the cortical bone, cancellous bone, posterior bone, and end plate of the lumbar spine segment. The Mooney–Rivlin model of non-linear hyperelastic materials was applied to intervertebral discs consisting of a ground substance and a nucleus pulposus. The nonlinear spring element model was applied to seven types of ligaments, and the characteristics of the real ligaments were simulated with a tension-only function.

A normal lumbar L1-S1 finite-element model is shown in Fig. 1. The primary aim of this study was to analyze asymmetric FJD, and the corresponding FE model and scenarios were developed accordingly. The specific region of FJD was defined as the facet joint between the 4th and 5th lumbar vertebrae. According to Weishaupt et al., degeneration grades are classified based on the grade of degeneration observed in the facet, as depicted on medical imaging. This classification serves as a critical criterion for assessing the extent of degenerative changes in the facet joints. According to the literature, the primary variables associated with FJD include the gap between the zygapophyseal joint surfaces, friction coefficient, and the presence of osteophytes23. In this study, the primary factors for each grade of FJD were the gap and friction coefficient between the zygapophyseal joints. Relying on existing literature, the intact facet joint model adopts defined parameters, comprising a 0.5 mm initial gap, a frictionless interface, an exponential approach, and a pressure of 120 MPa under zero-gap conditions19,31. The classification of FJD was classified as Grade 0 (G0, normal), Grade 2 (G2, moderate), or Grade 4 (G4, severe). In Grade0 (G0, normal), the gap between the facet joints is 0.5 mm and the coefficient of friction is 0, indicating that the facet joints are in a normal state. In Grade2 (G2, Moderate), the gap between the facet joints was 0.25 mm and the coefficient of friction was 0.5, indicating moderate degenerative changes. In Grade4 (G4, Severe), the facet joint gap was 0.05 mm, and the coefficient of friction was 0.9, indicating severe degenerative changes. Thus, the facet joint gap and friction coefficient for each grade represented normal, moderate, and severe degenerative changes, respectively. In this study, we adopted moderate (G2) and severe (G4) grades of FJ degeneration, excluding mild. Mild grade was excluded from consideration because the impact of degenerative changes in the facet joint on the adjacent segment was determined to be relatively insignificant32. The degeneration grades of the left and right facet joints are illustrated in Fig. 2 to facilitate the implementation of the FE model in the context of asymmetric degenerative changes in the facet joints. Consequently, in the analysis scenario, four FE models (G00, G40, G42, and G44) were constructed, each representing different degeneration grades of the left and right facet joints between lumbar vertebrae 4 and 5. However, the FE model assuming grade 4 degeneration of the right facet joint was not used in this study.

Fig. 1
figure 1

Positioning of components in the constructed lumbar FE Model, produced using ANSYS Workbench 2023 R2 (https://www.ansys.com/products/ansys-workbench).

Full size image
Fig. 2
figure 2

Positions and degeneration of left and right facet joints at the L4–L5 spinal segment in the sagittal plane, produced using ANSYS Workbench 2023 R2 (https://www.ansys.com/products/ansys-workbench).

Full size image
Table 1 Material properties in the lumbar finite element model192124,25,26,27,28,29,30.
Full size table

The FEA for this study was conducted using ANSYS Workbench 2023 R2 (ANSYS Inc. Canonsburg. PA. USA) software. The computational power utilized for the FEA was provided by an AMD Ryzen Threadripper 3970 × 32-Core Processor operating at 3.70 GHz, with a RAM capacity of 128 GB. Figure 3 illustrates the load and boundary conditions applied in the FEA. The loading condition applied a moment of 7.5 Nm to the upper surface of L1. Through this, we aimed to realize five types of spinal behaviors: extension, left and right lateral bending, and left and right axial rotations. Boundary conditions were fixed at the lower portion of the sacrum33.

Fig. 3
figure 3

Six spinal behaviors such as flexion, extension, left and right lateral bending, and left and right axial rotation, produced using ANSYS Workbench 2023 R2 (https://www.ansys.com/products/ansys-workbench).

Full size image

The constructed FE model was validated based on the results of previous studies. Subsequently, the scenario was analyzed. To enhance the credibility of the outcome data from the analysis scenario conducted in this study, the following were assessed: (1) the range of motion (ROM) during spinal behaviors, including flexion, extension, lateral bending, and axial rotation, (2) the intravertebral pressure between lumbar vertebrae 4 and 5, and (3) the height of the intervertebral disc under follower load. Figure 4 illustrates the results of the structural experiment and FEA by Renner et al., indicating that the findings of the FE model in this study fall within the ROM of L1–S1 and each segment34. Furthermore, Fig. 4 presents the results of the lumbar FE models constructed from previous studies, along with the changes in intravertebral disc pressure observed in vitro21. The resulting data from the FE model in this study, as depicted in the graph, also fell within the range of results from the previous study. Thus, the minimum reliability of the constructed FE model was established, and an analysis scenario was conducted based on the FE model.

Fig. 4
figure 4

Comparison of the ROM of each lumbar segment under spinal behaviors, as compared to the results of Renner et al. flexion + extension (A), right-left lateral bending (B), right-left axial rotation (C), and compression (D). comparison of intervertebral disc pressure between the L4 and L5 segments under compressive loading (E) with results from previous FE models.

Full size image

Results

Range of motion by spinal behavior at the affected segment

To analyze the ROM during spinal behavior resulting from asymmetric degeneration of the facet joints, the degree of bending was compared across the X-, Y-, and Z-axes. As shown in Fig. 3, the bending direction of each axis is as follows: The figure illustrates the anterior and posterior bending movements along the X-axis, rotational movements to the left and right along the Y-axis, and lateral bending movements to the left and right along the Z-axis. As illustrated in Fig. 5, each FE model with varying grades of FJD displayed a ROM across the corresponding three axes during the five spinal behaviors.

First, as FJD of the L4–L5 segment becomes more severe, the angle of posterior bending tends to decrease. Based on the G00 model, the posterior bending angle gradually reduced to 76.3% for the G40 model, 66.8% for the G42 model, and 58.8% for the G44 model, respectively. Some changes were also observed in the movements in other directions, such as anterior bending, lateral bending, and rotational movement. However, the most significant change was a decrease in posterior bending during extension. These results indicate that as spinal degeneration progresses, the posterior bending ability of the L4–L5 segments gradually diminishes. This can be considered as a decrease in the ROM of the affected segment due to degenerative changes in the facet joint.

During lateral bending, changes were evident based on the grade of FJD. In the case of left lateral bending, the left bending angle (− Z-axis) gradually decreased to 81.3% for the G40 model, 81.4% for the G42 model, and 75.2% for the G44 model, respectively. In contrast, movements in other directions were observed with only relatively small changes in the values. In the case of the anterior bending movement of the spine along the (+ X axis), there was a significant increase of approximately 0.156% in the G00 model, which was considered 100%, and approximately 620–629% in the G40 and more advanced degenerative models. In terms of right-lateral bending, the right bending angle (+ Z axis) slightly increased to 104% in the G40 model, 90.6% in the G42 model, and 80.6% in the G44 model, but gradually decreased afterward. In the case of the anterior bending movement (+ X axis), the G40 model showed a significant reduction from 0.127° (considered 100% in the G00 model) to nearly 0%, whereas it sharply increased to 468.3% and 779.9% in the G42 and G44 models, respectively. Owing to asymmetric changes in the degeneration grade of the facet joint, the L4–L5 segment exhibited reduced left bending movement during left lateral bending and a decrease in right bending movement during right lateral bending. In the case of lateral bending, the anterior bending movement increases significantly.

Axial rotation also changes based on the grade of FJD. In the case of left-axial rotation, based on the G00 model, the left bending angle (− Z-axis) tended to decrease to 101% for the G40 model, 71.8% for the G42 model, and 45.9% for the G44 model. The left rotation movement (+ Y-axis) showed a tendency to decrease to 103.2% for the G40 model, 93.1% for the G42 model, and 73.0% for the G44 model, respectively, similar to the left bending movement observed in the G00 model. The bending movements along the Y- and Z-axes remained almost unchanged in the G40 model. A similar decreasing trend was observed in the G42 model. The bending movement along the X-axis shows an anterior bending movement in the G00 and G40 models (+ X-axis), with the G40 model tending to increase by 113.1% compared to the G00 model. At 0.578 ° in the G42 model and 1.04° in the G44 model, a posterior bending movement (− X-axis) was observed. Overall, the indicators showed a tendency for the bending movement of the degenerative segment (L4–L5 FSU) to increase or remain constant up to the G40 model. However, these indicators tended to decrease starting from the G42 model. In particular, it was confirmed that the reduction in left bending and rotational movements increased starting from the G42 model.

Fig. 5
figure 5

Range of motion for bending directions across axes: comparison by facet joint degeneration grades (G00, G40, G42, G44). Extension (A), Left lateral bending (B), Right lateral bending (C), Left axial rotation (D), and Right axial rotation (E).

Full size image

In the case of right-axial rotation, based on the G00 model, the right bending angle tended to decrease to 56.2% for the G40 model, 51.6% for the G42 model, and 46.8% for the G44 model (+ Z-axis). The right rotation movement (− Y-axis) tended to decrease by 77.8% in the G40 model. Similarly, this movement showed decreases of 76.0% and 72.6% in the G42 and G44 models, respectively. This trend was similar to that observed for the right-bending movement. Regarding the bending movement along the X axis, the anterior bending movement was confirmed to be approximately 0.23° (+ X axis) for the G00 model. In contrast, the posterior bending movement (− X-axis) showed a large variation of 1.375° in the G40 model. This movement gradually decreased in models G42 and G44. Overall, as the degeneration grade of the facet joint increased, the bending movement of the degenerative segment tended to decrease. In the bending movement along the X-axis, the G40 model, when compared to the G00 model, exhibited grade 4 degeneration of the right facet joint. This suggests that the G40 model exhibits significant posterior bending movement owing to this instability.

Fig. 6
figure 6

Comparison of the maximum equivalent stress in the L4–L5 intervertebral disc (A) and the maximum equivalent stress on the left and right sides of the L4–L5 intervertebral disc (B) during five spinal behaviors.

Full size image
Fig. 7
figure 7

Distribution of equivalent stress in the L4–L5 intervertebral disc according to the degeneration grades of the facet joints during five spinal behaviors, generated using ANSYS Workbench 2023 R2 (https://www.ansys.com/products/ansys-workbench).

Full size image

Maximum equivalent stress of the intervertebral disc at the affected segment

To analyze the equivalent stress of the intervertebral discs in the L4–L5 segment resulting from the asymmetric degeneration of the facet joint, we compared the maximum equivalent stress for each of the five spinal motions, as well as the left and right equivalent stresses of the intervertebral discs, based on the sagittal plane (Figs. 6 and 7). By comparing the left and right maximum equivalent stresses of the intervertebral discs, we can more closely examine the effects of asymmetric degenerative changes in the facet joint on the L4–L5 segment.

Figure 6A illustrates that the maximum equivalent stress of the intervertebral disc tends to decrease as the FJD of the L4–L5 segment becomes more severe during extension. Based on the G00 model, the G40 model demonstrated a gradual reduction of 87.1%, the G42 model showed a decrease of 59.7%, and the G44 model showed a decrease of 44.0%. In cases of left-lateral bending and right-axial rotation, there was a tendency for a decrease in the maximum equivalent stress of the intervertebral disc as a result of degenerative changes in the facet joint of the L4–L5 segment. Based on the G00 model, the G40 model decreases by 67.1%, the G42 model by 67.3%, and the G44 model by 59.5%, respectively, during left-lateral bending, whereas the G40 model tends to decrease by 81.3%, the G42 model by 73.6%, and the G44 model by 65.5%, respectively. Right-lateral bending and left-axial rotation exhibited a slight increase in the G40 model owing to facet joint degenerative changes in the L4–L5 segment. However, they tended to decrease with higher degeneration grades. Based on the G00 model, the G40 model is 107.9%, the G42 model is 80.6%, and the G44 model is 59.5%, respectively. By contrast, the left axial rotations were 101.6% for the G40 model, 80.3% for the G42 model, and 64.0% for the G44 model, respectively.

In Figs. 6B and 7, the left and right maximum equivalent stresses of the intervertebral discs and the corresponding stress distributions are presented. The differences in the maximum equivalent stresses exerted on the intervertebral discs on the left and right sides (|L − R|) were examined. Notably, in the G00 model, slight differences in stress between left and right sides were observed across lateral bending and axial rotation, ranging from 0.64 to 3.63% of the mean values, indicating minor asymmetry even in the normal state. In terms of the extension, almost no difference was observed between the left and right sides of the G00 model. However, the largest difference between the left and right sides was observed in the G40 model, measuring 88.31 kPa. Subsequently, as the difference in the degeneration grade between the left and right facet joints decreased, particularly in the G42 and G44 models, a difference in the maximum equivalent stress on the left and right intervertebral discs was observed. This difference reduces to 154.82 kPa and 62.64 kPa, respectively. In cases of left lateral bending and left axial rotation, regardless of the grade of FJD, a higher equivalent stress was observed on the left intervertebral disc than on the right side. In the left-lateral bending, the largest difference was observed in the G00 model at 279.79 kPa, whereas the G40 model exhibited a difference of 81.88 kPa. This indicates a significant reduction in the maximum equivalent stress difference between the left and right intervertebral discs. In the left-axial rotation, the largest difference was observed in the G40 model at 210.36 kPa. In the case of right-lateral bending and right-axial rotation, regardless of the grade of FJD, a higher equivalent stress was observed on the right intervertebral disc than on the left. In the G40 model, the right-lateral bending measures 331.40 kPa, whereas the right axial rotation measures 252.65 kPa, indicating the largest difference. In both left and right lateral bending and axial rotation, the difference in the grade of degeneration of the left and right facet joints decreased in the G40 model. This reduction was associated with a tendency to decrease the difference in maximum equivalent stress between the left and right intervertebral discs.

Fig. 8
figure 8

Comparison of the maximum equivalent stress on the left and right sides of the L4 and L5 posterior bone based on the sagittal plane during five spinal behaviors, along with the distribution of equivalent stress in the L4 and L5 posterior bone. extension (A), left lateral bending (B), and right lateral bending (C), generated using ANSYS Workbench 2023 R2 (https://www.ansys.com/products/ansys-workbench).

Full size image

Maximum equivalent stress of the posterior bone of L4 and L5

Figures 8 and 9 illustrate the maximum equivalent stress and stress distribution on the adjacent L4 and L5 posterior bones resulting from the asymmetric degeneration of the left and right facet joints in the L4–L5 segment. Based on the sagittal plane, the left and right maximum equivalent stresses of the posterior bone were analyzed in the same manner as in the previous five spinal motion conditions assessed for the intervertebral discs. The effects of asymmetric degenerative changes in the facet joint on the posterior bone of the L4 and L5 segments during extension were similar (Fig. 8A). The difference in maximum equivalent stress on the left and right posterior bone (|L − R|) in the G40 model is 2.7 MPa and 1.37 MPa, respectively, indicating the largest difference compared to the other grade models.

As shown in Fig. 8B and C, the G40 model exhibits the largest difference in left-right maximum equivalent stress in the posterior bone of the L4 segment, with values of 1.67 MPa for left-lateral bending and 3.46 MPa for right-lateral bending. In the other grade models, the equivalent stress on the posterior bone was predominantly higher in the direction of primary bending for each spinal motion.

Fig. 9
figure 9

Comparison of the maximum equivalent stress on the left and right sides of the L4 and L5 posterior bone based on the sagittal plane during five spinal behaviors, along with the distribution of equivalent stress in the L4 and L5 posterior bone. Extension. left axial rotation (A), right axial rotation (B), generated using ANSYS Workbench 2023 R2 (https://www.ansys.com/products/ansys-workbench).

Full size image

As the degeneration grade of the left facet joint increased from the normal-state G00 model to the G40 model during left and right axial rotation, a significant difference in the equivalent stress between the posterior bone on the left and right sides was observed (Fig. 9A and B). This difference was particularly evident when examining the posterior bone of L4. The left axial rotation exhibited an equivalent stress of 11.47 MPa, whereas the right axial rotation showed an equivalent stress of 19.52 MPa. Next, as the degeneration grade of the right facet joint increased from G40 to G44, the difference between the left and right sides of the posterior bone of L4 gradually decreased. In contrast, the posterior bone of L5 exhibited a slight increase in maximum equivalent stress.

Discussion

In this study, a FE model was utilized to simulate the progressive chain of events from unilateral to bilateral degeneration of the facet joints. Asymmetrically, the left facet joint was assigned the most severe grade (Grade 4), while the right facet joint was modeled at Grades 0, 2, and 4. Based on these conditions, the G40, G42, G44, and G00 models were developed. Changes in the biomechanical properties of the lumbar spine were evaluated across five types of movements—extension, left and right lateral bending, and left and right axial rotation—which replicate spinal motions encountered in daily life. This methodology enabled an analysis of how asymmetric facet joint degeneration affects the ROM of the impacted segment, as well as its influence on the intervertebral discs and posterior bony structures.

The results of FJD during flexion behavior were excluded. Previous studies have employed various methods to implement facet joints in lumbar FE models. However, in this investigation, the facet joints were modeled by applying contact conditions between the zygapophyseal joint surfaces. During flexion, the gap between the lumbar facet joints widens, potentially rendering the contact condition inapplicable. Consequently, extension, left and right lateral bending, and left and right axial rotation were selected as the loading conditions, as these effectively capture the contact characteristics of the facet joints for analysis.

The segment affected by degenerative changes in the facet joints (L4–L5) exhibited behavior that deviated from normal spinal motion. As the degeneration grade of the facet joints increased across the five spinal movements, the ROM of the L4–L5 segment progressively decreased. Compared to the G00 model (representing a normal state), the G44 model showed reductions of 58.8% in extension, 75.2% and 80.6% in left and right lateral bending, and 45.9% and 46.8% in left and right axial rotation, respectively. These findings indicate that facet joint degeneration increases segmental stiffness, consistent with prior studies by Fujiwara et al., who reported reduced lumbar flexibility due to facet joint osteoarthritis, and Chui et al., who linked inflammatory facet joint lesions to decreased spinal mobility and dysfunction35,36. Similarly, Yin et al. suggested that spinal conditions such as aging, spondyloarthritis, and disc herniation contribute to reduced mobility, while Tischer et al. observed cartilage defects in over 80% of L4–L5 facet joint specimens, associating these defects with diminished lower lumbar mobility9,37.

Asymmetric degeneration of the facet joints induced anterior and posterior bending movements during lateral bending and axial rotation. In the G00 model, no anterior bending was observed during left or right lateral bending. However, in cases of FJD, anterior bending emerged during these spinal motions. This effect became more pronounced in right lateral bending as the degeneration grade of the right facet joint increased. Similarly, the G00 model exhibited no posterior bending during left or right axial rotation, yet posterior bending occurred during movements in the opposite direction of the degenerated facet joint. Specifically, posterior bending intensified during left axial rotation as the degeneration grade of the right facet joint progressed. Yin et al. reported that such movements increase with advancing degeneration across the L3-S1 segments, suggesting that asymmetric degeneration contributes to mechanical imbalance in the spine9.

Analysis of the maximum equivalent stress in the intervertebral disc revealed that facet joint degeneration reduced stress on the disc within the affected segment. Asymmetric degeneration resulted in a significant disparity in stress between the left and right sides of the intervertebral disc. However, this difference diminished as the degeneration grades of the left and right facet joints equalized. This pattern reflects the phases of initial dysfunction, instability, and restabilization in FJD. In the G44 group, the reduced stress disparity between the left and right sides indicated a transition toward restabilization, a process during which pain may decrease or resolve, consistent with prior studies1,10. In contrast, analysis of the maximum equivalent stress in the posterior bone showed that the L4 segment was more affected than L5. In the G40 model, where the degeneration grades of the left and right facet joints differed markedly, a pronounced left-right stress disparity was evident between the intervertebral disc and posterior bone of the L4–L5 segment. As facet joint degeneration progressed bilaterally, stress on the intervertebral disc decreased, while stress on the posterior bone increased, highlighting a compensatory mechanism at play.

Elevated equivalent stress in the posterior bone was primarily observed at the zygapophyseal joint surface and the pars interarticularis (PARS) where FJD occurred, as depicted in Figs. 8 and 9. During left axial rotation, as the degeneration grade of the right facet joint increased from the G40 to the G44 model, stress shifted from the right zygapophyseal joint surface to the right PARS. The PARS, a thin and vulnerable region of the lumbar spine, is susceptible to fractures under excessive loading. Connolly et al. reported an association between PARS stress fractures and facet joint degeneration in elite junior tennis players, and the findings of this study corroborate that high stress is exerted on the PARS during various spinal movements, suggesting a potential risk of stress fractures38.

This study has several limitations. First, while the FE model was developed with FJD as an independent variable, it did not incorporate other degenerative changes associated with spinal aging, such as reduced lumbar lordosis or disc height. This approach was chosen to focus specifically on the effects of FJD2,6,39,40. However, the exclusion of these concurrent degenerative factors represents a limitation. Additionally, although the G00 model, designed to represent a normal state, might be thought to maintain left-right symmetry, slight variations in the maximum equivalent stress were observed between left and right movements. These differences ranged from 0.64 to 3.63%, and such unexpected asymmetry likely stems from the complex geometry of the lumbar spine and minor asymmetries introduced during mesh generation and contact condition setup. Similar subtle differences have been observed in prior studies, such as Du et al., and while these variations fall within an acceptable range, they highlight limitations in maintaining symmetry in FE modeling20. Moreover, although the introduction emphasized the importance of cartilage in joint degeneration, cartilage was not modeled as a distinct element in the facet joint implementation. Instead, contact conditions were applied to represent the facet joints, a decision made to avoid convergence issues during the analysis of complex geometries under extension, lateral bending, and axial rotation. This method aligns with approaches used in prior studies, such as Mengoni et al.19, but it precluded a detailed analysis of cartilage role in facet joint degeneration. For model validation, the ROM and IDP were compared with in vivo measurements. However, the absence of in vivo data on FJF prevented direct validation of the FE model biomechanical responses in the facet joints. This limitation is compounded by the significant variability in facet joint model outcomes reported in previous studies.

Second, limitations exist in the settings for gap distance and friction coefficient in the facet joint degeneration model. The gap distance was quantified as a linear percentage relative to a normal state, defined as 100%, based on the study by Weishaupt et al.23, with reference to the Kellgren and Lawrence radiological grading system and clinical data41. However, this approach may not fully capture the variability in degeneration across individual patients, indicating a need for additional clinical data. The friction coefficient was estimated by considering degenerative changes such as cartilage loss and increased surface irregularity; however, due to the current limitations in experimental data, an estimation-based approach was adopted instead of relying on precise numerical values. Nevertheless, this study identified trends in how these settings influence the response patterns of the model based on the degree of degeneration.

Third, while recent FEA studies of the spine have widely adopted techniques to estimate the local modulus of elasticity of bone using the Hounsfield Unit (HU) from CT images42,43, this study did not implement such an approach. Instead, the vertebral bodies were divided into cortical bone, cancellous bone, and posterior bone, with isotropic linear elastic properties assigned to each. This method fails to account for variations in mechanical properties due to bone density distribution, limiting the precision of the analysis despite observed increases in PARS loading44,45. Future research should address these shortcomings by incorporating porous elastic models, additional experimental data, and HU-based techniques.

The findings of this study carry significant clinical implications. The reduction in ROM due to asymmetric facet joint degeneration, along with anterior and posterior bending movements during lateral bending and axial rotation, reflects biomechanical alterations in the lumbar spine. These changes suggest potential functional imbalances and the likelihood of pain induction. Notably, the concentration of stress in the PARS may elevate the risk of stress fractures under sustained loading, a phenomenon consistent with observations in active populations such as elite junior tennis players38. Furthermore, the diminished left-right disparity in intervertebral disc stress and the restabilization process may be associated with pain relief in the later stages of degeneration, offering valuable insights for pain management strategies. These results underscore the importance of prioritizing facet joint condition in the assessment of lumbar disorders. They also provide a foundation for targeted clinical interventions, including early diagnosis of asymmetric degeneration, prevention of PARS injuries, and the development of pain mitigation strategies.

Conclusions

This research utilized FEA to examine how FJD influences lumbar spine dynamics and overall behavior across multiple dimensions. Analysis demonstrated that asymmetric degeneration restricted ROM during five critical movements—extension, lateral bending, and axial rotation—with axial rotation most prominently driving the observed shifts in the L4–L5 segment. Stress levels in the intervertebral disc declined, pointing to a restabilization phase that could potentially mitigate pain over time, whereas elevated stress in PARS highlighted a notable risk of fractures, especially under prolonged loading conditions. These findings emphasize the profound impact of asymmetric degeneration on spinal dysfunction, strongly advocating for early intervention to address such changes. Though challenges arose in modeling cartilage properties and bone density variations, this study offers practical insights into effective strategies for managing spinal conditions and improving patient outcomes.