CMTNet: a hybrid CNN-transformer network for UAV-based hyperspectral crop classification in precision agriculture

Abstract

Hyperspectral imaging acquired from unmanned aerial vehicles (UAVs) offers detailed spectral and spatial data that holds transformative potential for precision agriculture applications, such as crop classification, health monitoring, and yield estimation. However, traditional methods struggle to effectively capture both local and global features, particularly in complex agricultural environments with diverse crop types, varying growth stages, and imbalanced data distributions. To address these challenges, we propose CMTNet, an innovative deep learning framework that integrates convolutional neural networks (CNNs) and Transformers for hyperspectral crop classification. The model combines a spectral-spatial feature extraction module to capture shallow features, a dual-branch architecture that extracts both local and global features simultaneously, and a multi-output constraint module to enhance classification accuracy through cross-constraints among multiple feature levels. Extensive experiments were conducted on three UAV-acquired datasets: WHU-Hi-LongKou, WHU-Hi-HanChuan, and WHU-Hi-HongHu. The experimental results demonstrate that CMTNet achieved overall accuracy (OA) values of 99.58%, 97.29%, and 98.31% on these three datasets, surpassing the current state-of-the-art method (CTMixer) by 0.19% (LongKou), 1.75% (HanChuan), and 2.52% (HongHu) in OA values, respectively. These findings indicate its superior potential for UAV-based agricultural monitoring in complex environments. These results advance the precision and reliability of hyperspectral crop classification, offering a valuable solution for precision agriculture challenges.

Introduction

Accurate identification of crop types is crucial for agricultural monitoring, crop yield estimation, growth analysis, and determining the spatial distribution and area of crops¹. It also provides essential reference information for resource allocation, agricultural structure adjustment, and the formulation of economic development strategies in the agricultural production process. In recent years, with the continuous improvement of spectral imaging technology, hyperspectral imaging (HSI) has become a research hotspot for remote sensing data analysis^2,3. HSI images consist of hundreds or even thousands of spectral channels containing abundant spatial and spectral information. The high spatial resolution of HSI provides new opportunities for detecting subtle spectrial differences between crops, which is beneficial for the fine classification of crops. In addition, HSI is widely used in areas such as plant disease detection⁴, food inspection⁵, reidentification⁶, and geological exploration⁷.

Traditional methods for HSI classification typically include the designed loss⁸ and the designed model⁹. In addition, scholars have also introduced several methods for HSI spectral dimension reduction and information extraction, including principal component analysis, minimum noise fraction transformation, linear discriminant analysis, independent component analysis, and others. However, these methods only consider the spectral information of HSI, ignoring the spatial correlation between pixels in the spatial dimension. This ignores the spatial features contained in the HSI data and ignored rich spatial contextual information, leading to variability in the spectral features of target objects, thus affecting classification performance. To utilize spatial information in the images, scholars have studied various mathematical morphology operators suitable for HSI to extract spatial features from the images, including morphological profile features, extended morphological profile features, extended multi-attribute profile features (EMAP), and extinction profile features^10,11. Although hyperspectral image classification methods based on spatial features can effectively capture the spatial information such as the position, structure, and contours of target objects, they neglect the spectral dimension information of hyperspectral imaging, resulting in less than ideal classification results. The generalization and versatility of traditional HSI classification methods are weak and susceptible to salt and pepper noise, which affects classification accuracy.

In recent years, many deep learning-based methods have been applied to HSI classification^12,13, as illustrated in Fig. 1. Initially, deep belief networks (DBN)¹⁴, recurrent neural networks (RNN)¹⁵, and one-dimensional convolutional neural networks (1D-CNN)¹⁶ was introduced into the HSI classification field. However, these methods only utilize spectral information and ignore the neighborhood information in the spatial dimension, leading to lower classification accuracy¹⁷. To address this issue, researchers proposed an architecture based on two-dimensional convolutional neural networks (2D-CNN)¹⁸. Subsequently, Xu et al.¹⁹ combined 1D-CNN and 2D-CNN, constructing a dual-branch network structure to extract spectral and spatial features. However, this approach extracts spectral and spatial features separately and cannot effectively utilize the 3D spectral-spatial features of HSI. In order to better extract spectral-spatial features, researchers developed the 3D-CNN¹⁸ architecture and applied it to HSI classification. To overcome the limitation of CNN in capturing global information, scholars have proposed two approaches to improve CNN. One approach is to improve the perceptual range directly of the convolutional kernel, including the use of dilated convolutions²⁰ and the construction of a multiscale feature pyramid²¹; the other method is to embed an attention module²² that can capture global contextual information into the CNN structure^23,24, including spectral attention, spatial attention, and spatiotemporal attention. However, these methods still rely on convolutional operations in the backbone network to encode dense features, thus tending to local semantic information interaction²⁵. Capturing long-range dependencies becomes a pivotal breakthrough in overcoming the CNN performance bottleneck.

Fig. 1

HSI classification using deep learning approach.

Recently, a visual transformer (ViT)²⁶ has been applied to various image processing tasks and has been preliminarily applied to the HSI classification field²⁷. ViT originates from the field of natural language processing (NLP) and is a new type of deep neural network composed of a multi-head attention mechanism and feedforward neural network, which can capture long-range dependency relationships in sequences through the multi-head attention mechanism^28,29. Compared to CNN, the self-attention mechanism of the Transformer imitates the saliency detection and selective attention of biological vision, and can establish long-distance dependency relationships, solving the limited receptive field problem of convolutional neural networks³⁰. However, ViT is not good at capturing local features. Given this, some scholars have begun to combine CNN and ViT to jointly capture local information, sequence features, and long-range dependency relationships. Existing HSI classification methods based on CNN-Transformer hybrid architectures²⁵ usually adopt manually specified hybrid strategies, such as using convolution to extract local features in the shallow layers and using a Transformer to extract global features in the deep layers^29,31, or directly adding the features extracted by CNN and Transformer³². Currently, many hyperspectral image classification methods based on hybrid CNN-Transformer architectures employ shallow convolutional layers to extract local features, while introducing Transformers at deeper layers to capture global features. Although this design successfully integrates local and global information, it presents several limitations. First, the direct concatenation or sequential stacking of convolutional layers and Transformers often lacks flexibility in feature fusion, leading to insufficient interaction between local and global information. Second, such methods typically struggle with fine-grained classification in complex scenarios, particularly in agricultural applications where the spectral features of different crops can be highly similar. This similarity makes it challenging to differentiate between crops using global features alone. These limitations highlight the need for a more flexible and integrated approach to feature extraction and fusion. In recent years, hyperspectral imaging has gained attention for crop classification in precision agriculture. However, traditional methods often face limitations due to the use of single-source data. To address this, fusion-based strategies, combining multi-spectral, hyperspectral, and LiDAR data, have been explored to enhance classification accuracy³³. For example, Anandakrishnan et al.³⁴ emphasized the effectiveness of UAV-based hyperspectral imaging in crop monitoring and classification.

In response to these limitations, this study proposes a novel hyperspectral crop classification approach, the Convolutional Meets Transformer Network (CMTNet). CMTNet employs a unique two-branch architecture: a CNN branch extracts local spectral-spatial features, while a Transformer branch captures global spectral-spatial features. This parallel dual-branch design not only mitigates the separation between local and global features seen in traditional methods but also excels in fine-grained classification tasks, particularly in complex agricultural environments. Furthermore, CMTNet enhances the efficiency of feature fusion through a multi-output constraint module, with experimental results demonstrating significant improvements in classification accuracy and generalization capabilities.

The main contributions of this article are given as follows.

• The CMTNet network proposed in this study features a unique dual-branch design that enables parallel extraction and dynamic fusion of local and global features. In contrast to existing hybrid CNN-Transformer methods, which typically stack local and global features sequentially, this design effectively addresses the limitations of traditional feature fusion methods. This innovation not only enhances the model’s performance in fine-grained classification tasks but also improves its adaptability in complex agricultural environments.

• A novel multi-constraint module is introduced to enhance classification accuracy by applying cross-constraints on local, global, and combined features. Unlike traditional decision-level fusion, our approach imposes constraints at multiple stages of feature extraction, improving the utilization of spectral-spatial features and enabling better differentiation of fine-grained classes in complex agricultural scenarios.

• The proposed CMTNet employs a dual-branch structure with CNN and Transformer components to extract both local and global spectral-spatial features. Our approach introduces enhancements, such as a multi-output constraint module and optimized feature extraction, leading to significant improvements in classification accuracy. Experimental results on three datasets demonstrate that our method outperforms several state-of-the-art networks, particularly in complex, low-resolution hyperspectral scenarios in agricultural applications.

The rest of the article is organized as follows: Section 2 reviews related work in hyperspectral image classification and UAV-based precision agriculture. Section 3 describes the architecture and key components of the proposed CMTNet. Section 4 presents the experimental setup and datasets used, followed by the results and discussions. Finally, Sect. 5 concludes the article and outlines potential future directions.

Related work

CNN-based methods

CNN is a powerful tool for analyzing HSI images because they can accurately represent the spectral and spatial contextual information contained in the HSI data cube, extracting highly abstract features from the raw data and achieving excellent classification results³⁵. HSI classification tasks are categorized into three based on the distinct features CNN processes. The initial category involves 1D-CNN, focusing on spectral features. The data input for 1D-CNN is typically a single pixel. Li et al.³⁶ proposed a n feature extraction module and feature interaction in the frequency domain to enhance salient features. Chen et al.³⁷ used a multi-layer convolutional network to extract deep features of HSI, improving the classification results with a few training samples. Yue et al.³⁸ utilized principal component analysis for HSI preprocessing before feature extraction. The second category involves 2D-CNN, focusing on spatial features. Li et al.³⁹ used two 2D-CNN networks to extract high spectral and spatial frequency information simultaneously. Zhao et al.⁴⁰ proposed a 2D-CNN model that initially reduces dimensionality using PCA or another method, followed by data input into the model, where the data undergo initial processing by 2D-CNN to extract spatial information, subsequently combined with spectral information. Haut et al.⁴¹ developed a novel classification model guided by active learning, employing a Bayesian approach. The last category is based on spectral-spatial feature methods. In this case, there are two ways of feature processing. One approach involves the use of 3D-CNN. For instance, Li et al.⁴² introduced a 3D-CNN framework for the efficient extraction of deep spectral-spatial combined features from HSI cube data without preprocessing or post-processing. Another approach involves hybrid CNN, with significant research applying this method^43,44,45. Xu et al.¹⁹ integrated multi-source remote sensing data to enhance classification performance, employing 1D-CNN and 2D-CNN for the extraction of spectral and spatial features, respectively. Diakite et al.⁴⁶ suggested a hybrid network combining 3D-CNN and 2D-CNN. However, the current CNN-based methods overlook important differences between spatial pixels and unequal contributions of spectral bands. Convolutional kernels with limited receptive fields are independent of content, resulting in less accurate recognition of ground objects with local contextual similarity and large-scale variations.

Subsequently, the attention mechanism has been widely integrated with CNN frameworks^43,47,48,49 due to its capability to assign varying weights to input features, enabling the model to concentrate more on crucial task-related information. Haut et al.⁵⁰ introduced a dual data-path attention module as the basic building block, considering both bottom-up and top-down visual factors to enhance the network’s feature extraction capability. Liu et al.⁴³, based on the widely used convolutional block attention module (CBAM) improved accuracy by changing the way the attention module is connected. Tang et al.⁵¹ presented two attention models from spatial and spectral dimensions to emphasize crucial spatial regions and specific spectral bands, offering significant information for the classification task. Additionally, Roy et al.⁵² suggested an attention-based adaptive spectral-spatial kernel to enhance the residual network, capturing discriminative spectral-spatial features through end-to-end training for HSI classification. These attention-based methods are essentially enhanced versions of CNN, yet they are restricted by the inherent constraints of local convolutional kernels. These approaches emphasize local features while neglecting global information, consequently inadequately addressing the remote dependency between spectral sequences and spatial pixels.

Transformer-based methods

The initial design of the Transformer was focused on sequence modeling and transduction tasks. Its remarkable success in natural language processing has prompted researchers to explore its application in the visual domain, where it has demonstrated exceptional performance in tasks such as image classification and joint visual-linguistic modeling. Recent advances in diffusion models^53,54 have significantly enhanced various image synthesis tasks. For instance, Shen et al.⁵⁵ proposed a progressive conditional diffusion model for story generation , while their later work⁵⁶ introduced a customizable virtual dressing model using diffusion-based approaches, further demonstrating the versatility of diffusion models in dynamic and interactive applications. In their work, Hong et al.⁵⁷ were the first to apply the ViT to HSI classification and achieved impressive results on commonly used hyperspectral image datasets. Additionally, He et al.⁵⁸ utilized a well-trained bidirectional encoder transformer structure for hyperspectral image classification. Furthermore, Qing et al.⁵⁹ introduced the self-attention-based transformer network (SAT-Net) for HSI classification, employing multiple Transformer encoders to extract image features. The encoder modules are directly connected using a multi-level residual structure to address the issues of vanishing gradients and overfitting. Tan et al.⁶⁰ introduced the transformer-in-transformer module for end-to-end classification, building a deep network model that fully utilizes global and local information in the input spectral cube. Sun et al.²⁴ proposed the spatial and spectral attention mechanism fusion network (SSAMF) for HSI classification, which incorporates channel self-attention into the Swin Transformer to better encode the rich spectral-spatial information of HSI, contributing to improved classification by the network. Mei et al.⁶¹ proposed the Group-Aware Hierarchical Transformer (GAHT) for HSI classification, applying multi-head self-attention to local spatial-spectral context and hierarchically constructing the network to improve classifying accuracy. Zhong et al.⁶² developed a spectral-spatial transformer network (SSTN) to overcome the constraints of convolutional kernels. Additionally, stable and efficient network architecture optimization is achieved through fast architecture search. It is evident that these previous studies primarily utilize Transformer to learn strong interactions between comprehensive label information through multiple self-attention modules. However, they are troubled by slow processing speed during inference and high memory usage, and these methods have yet to exploit the rich spatial features of HSI fully.

Hybrid methods

Recently, multiple endeavors have sought to integrate CNN and Transformer to build HSI classification networks that leverage the strengths of both architectures. Zhang et al.⁶³ proposed a dual-branch structure, incorporating both CNN and Transformer branches to capture local-global hyperspectral features. In the multi-head self-attention mechanism, convolutional operations were introduced skillfully to unite CNN and Transformer, further enhancing the classification progress. Liang et al.⁶⁴ integrated multi-head self-attention mechanisms in the spatial and spectral domains, applying them to context through uniform sampling and embedding 1D-CNN and 2D-CNN operations. Yang et al.⁶⁵ integrated CNN and Transformer sequentially and in parallel to fully utilize the features of HSI. Qi et al.³¹ developed the global-local spatial convolution transformer (GACT) to exploit local spatial context features and global interaction between different pixels. Additionally, through the weighted multi-scale spectral-spatial feature interaction (WMSFI) module, trainable adaptive fusion of multi-scale global-local spectral-spatial information is achieved. Song et al.⁶⁶ presented a dual-branch HSI classification framework utilizing 3D-CNN and bottleneck spatial-spectral transformer (B2ST), where both branches use a combination of shallow CNN and deep Transformer. Yang et al.⁶⁷ embedded CNN operations into the Transformer structure to capture subtle spectral differences and convey local spatial context information, then encoded spatial-spectral representation along multiple dimensions through a novel convolution displacer. In our earlier work published on arXiv⁶⁸, we proposed a convolutional and transformer hybrid model for hyperspectral image classification, which serves as the foundation for the improvements presented in this manuscript. However, while these methods have been adapted from natural image processing, challenges remain in effectively integrating CNN’s strength in local context exploration with the Transformer’s capability in global spectral-spatial modeling, particularly in achieving adaptive fusion of spectral-spatial features across multiple attributes and scales in low spatial resolution HSI.

Proposed method

The proposed method CMTNet’s framework is illustrated in Fig. 2. CMTNet comprises a spectral-spatial feature extraction module, a local-global feature extraction module, and a multi-scale output constraint module. The spectral-space feature extraction module initially extracts shallow features from hyperspectral images by solely utilizing the spectral-space information present in the images. Subsequently, a parallel local-global feature extraction module, consisting of a Transformer branch and a CNN branch, is employed to deeply extract local and global features from the hyperspectral images. Finally, the classification results are generated using the multi-output constraint module, which calculates multi-output losses and cross-constraints on local, global, and joint features from various feature perspectives.

Fig. 2

CMTNet overall network framework. CMTNet consists of three main modules, spectral-spatial feature extraction module, local-global feature extraction module and multi-output constraint module.

Spectral-spatial feature extraction module

The structure of the spectral-spatial feature extraction module outlined in this study is illustrated in Fig. 2. This module primarily utilizes convolutional neural networks to process the segmented hyperspectral image block. It begins by employing a 3D convolutional layer to extract spectral-spatial features, followed by a 2D convolutional layer to capture shallow spatial features.Let the hyperspectral dataset be denoted as $H \in \mathbb {R}^{h \times w \times d},$ with the spatial dimensions’ height and width represented as h and w, respectively, and the number of spectral bands as d. Each pixel in H comprises d spectral dimensions, with its corresponding class label vector denoted as $V=\left( \textrm{v}_{1}, \textrm{v}_{2}, \ldots , \textrm{v}_{\textrm{n}}\right)$ , where n signifies the number of land cover categories in the hyperspectral scene. To manage the extensive hyperspectral image data, block division is necessary during model training to accommodate the computer’s computational limitations. Following partitioning, each hyperspectral image block is denoted as $X \in \mathbb {R}^{m \times m \times d}$ , with its dimensions specified. Each training image block sample is then inputted into the initial 3D convolutional layer. The convolution kernel within the 3D convolution calculates new convolutional feature maps by summing the dot product between the convolution of the entire spatial dimension and the kernel. The calculation formula is presented in Eq. (1):

$$\begin{aligned} v_{i, j}^{p, q, u}=\sum _{\eta =1}^{\eta } \sum _{h=0}^{h} \sum _{w=0}^{w} \sum _{c=0}^{c} \omega _{i, j, \eta }^{h, w, c} \times v_{i-1, \eta }^{(p+h),(q+w),(u+c)}+b_{i, j} \end{aligned}$$

(1)

Where $\eta$ represents the feature related to the j-th convolutional feature cube of the $i-1$ th layer; $v_{i, j}^{p, q, u}$ represents the convolution output value at position (p, q, u) of the j-th convolutional feature cube of the i-th layer, with the convolution kernel size of (h, w, c); $\omega _{i, j, \eta }^{h, w, c}$ and $b_{i, j}$ represent the weight parameters and bias at position (h, w, c) related to the $\eta$-th convolutional feature cube.

Similar to the 3D convolutional layer, the 2D convolutional layer operates by convolving a two-dimensional kernel to produce new feature maps. The calculation formula for this process is depicted in Eq. (2):

$$\begin{aligned} v_{i, j}^{p, q}=\sum _{\eta =1}^{\eta } \sum _{h=0}^{h} \sum _{w=0}^{w} \omega _{i, j, \eta }^{h, w} \times v_{i-1, \eta }^{(p+h),(q+w)}+b_{i, j} \end{aligned}$$

(2)

$v_{i, j}^{p, q}$ represents the convolution output value at position (p, q) of the j-th convolutional feature cube of the i-th layer, with the convolution kernel size of (h, w) ;(h, w); $\omega _{i, j, \eta }^{h, w}$ and $b_{i, j}$ represent the weight parameters and bias at position (h, w) related to the $\eta$-th convolutional feature cube.

This module consists of two convolutional layers, two batch normalization layers, and two activation layers using the ReLU activation function. The extraction process and calculation formulas of this module are detailed in Eqs. (3) and (4):

$$\begin{aligned} v_{i, j}^{p, q}=\Phi \left( g_{1}\left( v_{i, j}^{p, q \cdot u}\right) \right) \end{aligned}$$

(3)

$$\begin{aligned} y=\Phi \left( g_{2}\left( v_{i, j}^{p, q}\right) \right) \end{aligned}$$

(4)

Where $\Phi (\cdot )$ represents the ReLU activation function, $g_1$ and $g_2$ , respectively, represent three-dimensional batch normalization and two-dimensional batch normalization.

Local-global feature extraction module

• (1) Transformer encoder branch: As shown in Fig. 2, the Transformer encoder branch mainly consists of positional encoding embeddings, multi-head self-attention (MHSA) (Fig. 3a), a multilayer perceptron (MLP), and two normalization layers. Residual connections are designed in front of MHSA and MLP. The output features of the spectral-spatial feature extraction module are flattened and linearly mapped to a sequence vector $T \in \mathbb {R}^{n \times z}$ of length s and channel dimension z. Then, a relative positional information vector $P_s \in \mathbb {R}^{n \times z}$ of length s is embedded into N sequence vectors as the input feature $T_{i n}$ of the Transformer encoder branch.

$$\begin{aligned} T_{i n}=\left[ T^{1}; T^{2}; \ldots T^{N}\right] +P_{s} \end{aligned}$$

(5)

The Transformer encoder’s exceptional performance can be attributed to its MHSA mechanism. MHSA efficiently captures the relationships between feature sequences by utilizing self-attention (SA) (see Fig. 3b). Initially, the Q, K, and V values derived from the convolution mapping are passed to MHSA via SA to extract global features. Within this process, Q and K are used to calculate attention scores, and the softmax function is applied to determine the weights of these attention scores. The formula for SA can be expressed as follows:

$$\begin{aligned} T_{S A}=\operatorname {Attention}(Q, K, V)=\operatorname {soft} \max \left( \frac{Q K^{T}}{\sqrt{d_{K}}}\right) V \end{aligned}$$

(6)

Where $T_{S A}$ represents the output of the SA module, and $d_K$ is the dimension of K. MHSA uses multiple sets of weight matrices to generate Q, K, and V, and through a consistent computation process, multiple attention distributions are obtained. These distributions are then aggregated to obtain a comprehensive attention value. Finally, the features obtained by MHSA are passed to the MLP layer.

Fig. 3

Attention mechanism of the transformer. (a) Multi-head attention mechanism. (b) Self-attention mechanism.

Traditional 3D-CNNs are constrained by fixed receptive fields, which limit their ability to model long-range spectral dependencies-a critical factor in distinguishing crops with subtle spectral differences. In contrast, the self-attention mechanism in CMTNet’s Transformer branch dynamically captures global spectral relationships across all bands and spatial positions.

• (2) CNN branch: As shown in Fig. 2, the CNN branch mainly consists of a 3$\times$3 convolutional layer, two 1$\times$1 convolutional layers, and residual connections, aiming to extract local features of hyperspectral images.

Multi-output constraint module

When calculating the loss, traditional feature constraints are typically restricted to the highest-level network output features, leading to suboptimal utilization of valuable spatial and spectral information. In hyperspectral image classification, high-level spatial and spectral semantic features play a pivotal role, and preserving this valuable information across different scales during multi-scale feature fusion can significantly impact classification performance. To address this limitation, we propose a multi-output constraint module in CMTNet that applies feature constraints at multiple stages (as illustrated in Fig. 4), rather than solely at the final output.

Fig. 4

Multi-output constraint module.

Specifically, the multi-output constraint module independently constrains the local features (CNN branch), global features (Transformer branch), and integration features (fused high-level semantic features). Each feature set $F_L$, $F_G$, $F_I$ is sent to the softmax activation function for classification, resulting in the probability outputs $P_L,$ $P_G,$ $P_I$.The corresponding losses are computed using the categorical cross-entropy loss function:

$$\begin{aligned} {\mathscr {L}}_{L}=-\sum _{i=1}^{N} y_{i} \log \left( P _{L}(i)\right) \end{aligned}$$

(7)

$$\begin{aligned} {\mathscr {L}}_{G}=-\sum _{i=1}^{N} y_{i} \log \left( P _{G}(i)\right) \end{aligned}$$

(8)

$$\begin{aligned} {\mathscr {L}}_{I}=-\sum _{i=1}^{N} y_{i} \log \left( P _{I}(i)\right) \end{aligned}$$

(9)

where ${\mathscr {L}}_L$ is the loss associated with the local features, ${\mathscr {L}}_G$ is the loss associated with the global features, ${\mathscr {L}}_I$ is the loss associated with the integration features, $y_{i}$ represents the true class label, and N is the number of samples. The total loss is then computed as a weighted sum of the individual losses:

$$\begin{aligned} {\mathscr {L}}_{T}=\lambda _{1} {\mathscr {L}}_{L}+\lambda _{2} {\mathscr {L}}_{G}+\lambda _{3} {\mathscr {L}}_{I} \end{aligned}$$

(10)

where ${\mathscr {L}}_T$ is the total loss that combines the contributions from all feature branches, and $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$ are weighting factors that balance the contribution of each feature type. To determine their optimal values, we conducted a random search over the parameter space $\lambda _1, \lambda _2, \lambda _3 \in [0.1, 1.0]$, constrained by $\lambda _1 + \lambda _2 + \lambda _3 = 1$. During backpropagation, these combined losses guide the optimization of network parameters across all branches, ensuring that local, global, and integration features are simultaneously refined. This enhances the interaction and fusion of local and global information, ultimately leading to a more robust feature representation.

This approach contrasts with traditional methods that constrain only the final output, allowing CMTNet to dynamically adjust the importance of each feature type throughout the training process. The multi-output constraint module thus improves gradient flow and convergence during backpropagation, leading to higher classification accuracy and better performance in fine-grained classification tasks, especially in complex agricultural scenarios where differentiating between spectrally similar crops is challenging.

Experiment and analysis

To validate the proposed CMTNet method’s superiority, it is compared with multiple state-of-the-art RF⁶⁹, SVM⁷⁰, 2D-CNN¹⁸, 3D-CNN¹⁸, Resnet⁵², ViT²⁶, SSFTT⁷¹ and CTMixer⁶³ approaches on three large-scale datasets, namely, WHU-Hi-LongKou, WHU-Hi-HanChuan and WHU-Hi-HongHu.

Datasets

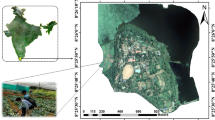
This study used the publicly available HSI datasets. The WHU-Hi dataset^72,73 produced by Wuhan University from a research study located on the Jianghan plain of Hubei Province, China, with flat topography and abundant crop species (Fig. 5).The WHU-Hi LongKou dataset was acquired using the Headwall Nano-Hyperspec unmanned aerial UAV in LongKou town, Hubei Province, China, on July 17, 2018. The image size is $550\times {400}$ pixels, with 270 bands between 400 nm and 1000 nm, and a spatial resolution of approximately 0.463 m. The study area includes 9 land cover types.The image cube and ground-truth image are shown in Fig. 5a. The WHU-Hi HanChuan dataset was acquired using the Headwall Nano-Hyperspec unmanned aerial vehicle hyperspectral imager in Hanchuan City, Hubei Province, China, on June 17, 2016. The image size is $1217\times {303}$ pixels, with 274 bands between 400 and 1000 nm and a spatial resolution of approximately 0.109 m. The study area includes 16 land cover types. The image cube and ground-truth image are shown in Fig. 5b. The WHU-Hi HongHu dataset was acquired using the Headwall Nano-Hyperspec unmanned aerial vehicle hyperspectral imager in Honghu City, Hubei Province, China, on November 20, 2017. The image size is $940\times {475}$ pixels, with 270 bands between 400 and 1000 nm and a spatial resolution of approximately 0.043 m. The study area includes 22 land cover types.The image cube and ground-truth image are shown in Fig. 5c. Table 1 lists the overall crop category names, number of training samples, and number of test samples for these three datasets. Each dataset is divided into training and sample sets, with 0.5 $\%$ randomly selected from the total samples as the training set.

Fig. 5

Wuhan UAV-borne hyperspectral image. A and B denote image cube and ground-truth image respectively. (a) WHU-Hi-LongKou dataset. (b) WHU-Hi-HanChuan dataset. (c) WHU-Hi-HongHu dataset.

Table 1 Training and test sample numbers in the WHU-HiLongKou dataset, theWHU-HiHanChuan dataset, and the WHU-HiHongHu dataset.

Evaluation metrics

This study uses overall classification accuracy (OA), average classification accuracy (AA), kappa coefficient, and accuracy under individual categories as evaluation metrics. It also visually presents classification diagrams as a visualization of the results.

Experimental setup

The experiment utilized the SITONHOLY IW4202 rack server, equipped with an Intel$\circledR$ Xeon$\circledR$ CPU E5-2620 v4 @ 2.10GHz and four NVIDIA TITAN Xp GPUs, each with 12 GB of memory and a total of 128 GB running memory. The software platform included Ubuntu 16.04.6 LTS 64-bit OS, CUDA Toolkit 10.1, CUDNN v7.6.5, Python 3.8, and Pytorch 1.7.0. Each experiment was repeated ten times independently, with the average value taken as the final result to mitigate the impact of random factors. The number of iterations was set to 100, using cross-entropy loss as the loss function and the Adam optimizer for model optimization.

The network, which combines CNN and Transformer, emphasizes global spatial information. To investigate the impact of various input image patch sizes (s) on classification performance, experiments were conducted using image patch sizes ranging from 5 to 15 on three datasets, with adjacent spatial sizes differing by 2. The experimental results are illustrated in Fig. 6. The figure demonstrates that the classification accuracy of the WHU-Hi LongKou dataset increases as the input image s increases. OA initially increases and then stabilizes. The WHU-Hi HanChuan and WHU-Hi HongHu datasets exhibit greater sensitivity to different input image patch sizes, with OA initially increasing and then decreasing with s. When s = 13, the OA of all three datasets approaches the maximum value. Consequently, s = 13 is chosen as the input image block size for the network proposed in this study.

Fig. 6

Impact of different input space sizes on OA.

In order to determine the optimal configuration of the proposed network architecture in terms of learning rate and batch size, a series of targeted experiments were conducted. The experimental results are illustrated in Fig. 7, with Fig. 7a–c representing the WHU-Hi LongKou, WHU-Hi HanChuan, and WHU-Hi HongHu datasets. Different colors in the figures indicate various ranges of OA. It is evident that different learning rates and batch sizes result in different OA values for the same dataset. For the WHU-Hi LongKou dataset (Fig. 7a), the impact of learning rate and batch size on OA is minimal, but there is some interaction between the two. The optimal learning rate and batch size were found to be 1e-3 and 100, respectively. On the other hand, the WHU-Hi HanChuan and WHU-Hi HongHu datasets show significant sensitivity to learning rate due to variations in crop types used for training. Increasing the learning rate initially boosts OA and then decreases, while increasing the batch size also shows a similar trend. For the WHU-Hi HanChuan dataset Fig. 7b), a batch size of 100 resulted in improved classification performance with the selected learning rate. Similarly, for the WHU-Hi HongHu dataset (Fig. 7c), the best classification performance was achieved with a learning rate of 1e-3 and a batch size of 100. Consequently, based on the parameter experiments, the optimal learning rate and batch size for the proposed classification network were determined to be 1e-3 and 100, respectively.

Fig. 7

Effect of different learning rates and batch sizes on performance accuracy OA. (a) Experimental results on WHU-Hi LongKou dataset. (b) Experimental results on WHU-Hi HanChuan dataset. (c) Experimental results on WHU-Hi HongHu dataset.

This study investigates how the number of encoder layers and attention heads can impact the model’s robustness and stability. Experimental results, as shown in Fig. 8, demonstrate the effects on the WHU-Hi LongKou, WHU-Hi HanChuan, and WHU-Hi HongHu datasets. The histograms in Fig. 8a–c reveal that the differences in OA histograms across different layers and heads are minimal, with OAs remaining stable within specific ranges: LongKou: 99.52–99.68, HanChuan: 97.42–97.59, HongHu: 98.51–98.62. To ensure uniformity in the network structure across all datasets, this study opts for the CMTNet with one transformer layer and four attention heads as the final network configuration.

Fig. 8

OA under different numbers of transformer encoder layers and MHSA heads on (a) WHU-Hi LongKou, (b) WHU-Hi HanChuan, and (c) WHU-Hi HongHu, respectively.

Comparison of experimental results with SOTA

The OA, AA, and Kappa values of CMTNet and other comparative methods on the WHU-Hi LongKou, WHU-Hi HanChuan, and WHU-Hi HongHu datasets are presented in Tables 2, 3 and 4, accompanied by visual representations in Figs. 9, 10 and 11. The best values are highlighted in bold in the tables, clearly indicating the superior performance of the proposed CMTNet method. Analysis of Table 2 reveals that CMTNet excels in capturing both global and local spectral features of hyperspectral imaging separately, effectively integrating high-dimensional information to achieve outstanding classification results across different land cover targets. When compared to the CNN and Transformer hybrid networks SSFTT and CTMixer, CMTNet outperforms in final classification results, showing an increase in OA of 0.21 and 0.19, respectively. This improvement can be attributed to the multi-output constraint module of CMTNet, which optimally reallocates feature weights. However, the performance of RF and SVM could be enhanced, particularly in the classification of cotton and soybeans with limited training samples, where individual accuracies fall below 47%. Examination of Fig. 9 demonstrates that CMTNet significantly enhances classification performance, reducing misclassifications and ensuring complete classification edges through the fusion of local-global spectral features.

Table 2 Classification performance obtained by different methods for WHU-Hi LongKou dataset (optimal results are bolded).

Table 3 Classification performance obtained by different methods for WHU-Hi HanChuan dataset (optimal results are bolded).

Table 4 Classification performance obtained by different methods for WHU-Hi HongHu dataset (optimal results are bolded).

Fig. 9

Classification visualization maps of all methods on the WHU-Hi LongKou dataset. (a)–(i) Classification map of RF, SVM, 2-DCNN, 3-D CNN, Resnet, ViT, SSFTT, SSTN, CTMixer, and CMTNet, respectively. (j) Real ground feature map. CMTNet model classification results (OA = 99.58%, Kappa = 99.45).

Fig. 10

Classification visualization maps of all methods on the WHU-Hi HanChuan dataset. (a)–(i) Classification map of RF, SVM, 2-DCNN, 3-D CNN, Resnet, ViT, SSFTT, SSTN, CTMixer, and CMTNet, respectively. (j) Real ground feature map. CMTNet model classification results (OA = 97.29%, Kappa = 96.83).

Fig. 11

Classification visualization maps of all methods on the WHU-Hi HanChuan dataset. (a)–(i) Classification map of RF, SVM, 2-DCNN, 3-D CNN, Resnet, ViT, SSFTT, SSTN, CTMixer, and CMTNet, respectively. (j) Real ground feature map. CMTNet model classification results (OA = 98.31%, Kappa = 97.87).

The WHU-Hi HanChuan dataset captured images in the afternoon with a lower sun angle, resulting in numerous shadow patches. The classification results for the RF and SVM methods show many misclassifications. Both 2D-CNN and 3-DCNN models display significant fragmentation, highlighting the necessity for methods to enhance model generalization. The SSFTT synthesizes the use of 3D convolutional layers and attention mechanism modules to realize the abstraction extraction of joint spectral-spatial features, effectively mitigating classification errors caused by ‘same material different spectrum, different materials same spectrum’. However, owing to its serial extraction of spectral-spatial features without effective selection, there is still a problem of performance plummeting in the classification of small-sample targets, with the OA for categories such as Watermelon and Plastic (NO.6 and 12, respectively) being only 82.42% and 77.92%. ResNet exhibits clear misclassifications of soybeans and gray rooftops. On the other hand, ViT and CTMixer methods achieve high-precision classifications overall, but errors persist in shadow-covered areas. Despite this, CMTNet outperforms in identifying similar spectral features through multi-feature fusion extraction, leading to reduced fragmentation compared to other methods.

In the WHU-Hi HongHu dataset, traditional classification algorithms struggle with misclassifications due to slight spectral differences among crops of the same type. Specifically, Brassica parachinensis, Brassica chinensis, and Small Brassica chinensis exhibit low classification accuracy. Deep learning methods have notably enhanced hyperspectral classification over traditional approaches. However, 2D-CNN and 3D-CNN tend to only capture local features in hyperspectral images, resulting in fragmented classification outcomes. The ViT model, on the other hand, leverages global perceptual spectral features to mitigate this fragmentation. While models like SSFTT and CTMixer combine CNN and Transformer architectures to effectively utilize spectral-spatial information for improved classification, they still struggle with misclassifications in land cover categories with limited samples.CMTNet demonstrates the best effectiveness in categorizing various terrestrial objects due to its capability to capture spatial and spectral characteristics separately, and efficiently filter and integrate high-dimensional information. It delivers exceptionally good results for different categories, with OA for Red roof, Cotton, Rape, Tuber mustard, and Lactuca sativa reaching 98.32%, 99.7%, 98.98%, 98.26%, and 98.08% respectively, and the overall OA and Kappa coefficient being 98.31% and 97.87%. CTMixer focuses on the effective use of global and local multi-scale features, achieving better outcomes in mixed terrestrial feature regions, yet its OA and Kappa coefficients are reduced by 2.52% and 3.19% compared to CMTNet. Visual and quantitative analyses reveal that CMTNet achieves the highest accuracy and excels at classifying land cover categories with limited samples. This suggests that incorporating the multi-output constraint module can enhance the model’s robustness and stability.

Ablation experiments

To thoroughly verify the effectiveness of the proposed method, ablation experiments were conducted on three datasets using different components of the network model. The baseline network was Transformer, with modules from CMTNet sequentially added to assess their contributions. Five combined models were analyzed, and the impact of each component on the OA was measured. The results of all ablation experiments are presented in Table 5. The checkmark symbol “$\checkmark$” indicates module usage, while the cross symbol “$\times$” indicates non-usage. Analysis revealed that using only the Transformer module resulted in relatively low OAs across the datasets, suggesting its limitations in extracting local features for hyperspectral image classification. Addition of the spectral-spatial feature extraction module in Case 2 and Case 3 led to an increase in OA. Case 4 introduced a CNN branch in parallel with the Transformer branch to enhance local feature extraction, resulting in a significant OA improvement. Case 5 further improved the integration of features from each branch by incorporating the multi-output constraint module. Experimental findings demonstrated that Case 5 consistently outperformed Case 4 on all three datasets, highlighting the effectiveness of the Multi-Output Constraint Module (MOCM).

Table 5 Impact of different modules on network OA value (%).

Model efficiency analysis

To evaluate the computational efficiency of the proposed method, we conducted efficiency tests on all approaches, with Table 6 presenting the experimental results. As shown in Table 6, traditional machine learning models (such as RF and SVM) exhibited the fastest running speeds, with RF requiring 36.82, 62.66, and 74.54 s on the three datasets, respectively. In contrast, deep learning models like 3D-CNN, Resnet, and ViT demand significantly more computational resources. For instance, ViT required 857.20, 1458.26, and 1735.34 s on the Longkou, Hanchuan, and Honghu datasets, respectively, reflecting its inherent complexity. Compared with the SSFTT method, the training and testing times for CMTNet are slightly longer, which can be attributed to its dual-branch Transformer architecture that enhances feature representation while introducing additional computational overhead during optimization. In contrast to the CTMixer method, CMTNet requires less running time. Overall, Transformer-based methods demonstrate significantly higher efficiency than CNN-based methods. While CMTNet achieves state-of-the-art classification accuracy, its computational cost is higher than traditional machine learning methods. This trade-off is critical for precision agriculture applications where accuracy is prioritized. Future work will focus on model compression and edge deployment frameworks to further bridge the efficiency gap.

Table 6 Running time of different methods on three datasets (s).

Discussion

While CMTNet achieves state-of-the-art performance on diverse datasets, its accuracy on shadow-affected regions (e.g., WHU-Hi HanChuan) reveals a dependency on consistent illumination conditions. Shadows introduce spectral ambiguities that challenge the current feature extraction modules. To address this, future iterations could integrate shadow-invariant feature learning techniques, such as normalization based on illumination-invariant indices⁷⁴, or leverage multi-temporal data to disentangle shadow effects from intrinsic spectral signatures.

To evaluate the risk of overfitting in classes with limited training samples, we specifically analyze the performance of Cotton (NO.2) and Narrow-leaf soybean (NO.5) in the WHU-Hi LongKou dataset. As shown in Table 2, these classes have only 41 and 20 training samples, respectively. Despite the small sample size, CMTNet achieves OA values of 99.53% for Cotton and 98.61% for Narrow-leaf soybean. However, compared to classes with abundant samples (e.g., Broad-leaf soybean (NO.4) with 316 training samples and 99.67% OA), the accuracy gaps (0.14% and 1.06%) indicate potential overfitting risks. Although MOCM partially alleviates overfitting, the performance of extremely small sample classes (e.g., Narrow-leaf soybean) has not yet reached its optimal level. To address this issue, in future work, we will initialize the feature extractor using a pre-trained model on large-scale hyperspectral datasets (such as WHU-Hi HongHu) and then fine-tune it on the target small-sample classes⁷⁵. Additionally, semi-supervised learning techniques, such as consistency regularization or pseudo-labeling⁷⁶, will be employed to incorporate unlabeled data, which can enhance the model’s generalization without requiring additional labeled samples. These methods can synergistically improve the robustness of CMTNet’s dual-branch architecture in imbalanced agricultural scenarios.

Conclusions

In order to enhance the precision and efficiency of crop classification in areas with imbalanced samples and diverse land cover types, this study introduces a novel method called CMTNet. This method incorporates a dual-branch structure featuring parallel CNN and Transformer components, enabling the extraction of local-global features from hyperspectral images. A convolutional layer combination spectral-spatial feature extraction module is employed to capture low-level spectral-spatial features, while a multi-output constraint module effectively addresses information loss post multi-scale feature fusion. Experimental results demonstrate the method’s effectiveness in enhancing classification performance. Although CMTNet demonstrates excellent performance in complex agricultural scenarios, the current study still exhibits several limitations. Specifically, the model’s robustness against extreme shadows and occlusions requires improvement, and its computational cost restricts deployment on resource-constrained devices. To address these issues, future research will focus on the following directions. First, by integrating multimodal data (e.g., LiDAR elevation information), we aim to enhance classification robustness in complex environments characterized by shadows and occlusions. Second, we plan to optimize real-time performance and explore model compression techniques (such as pruning and quantization) to reduce computational costs. Finally, by incorporating edge computing frameworks, we seek to achieve efficient deployment on drone platforms, thereby advancing real-time monitoring applications in precision agriculture.