Introduction

China, a country endowed with an extensive river network, had constructed 97,036 reservoirs of various types by the end of 2021, alongside maintaining 331,000 km of embankments for Class 5 and above watercourses. Statistical analyses reveal that earth-rock dams constitute the predominant reservoir structure type nationwide. However, significant portions of these hydraulic infrastructures have deteriorated into structurally compromised reservoirs due to historical technological and economic constraints, compounded by recurring natural disasters including seismic events and catastrophic floods. While reservoir dams have played a pivotal role in facilitating socioeconomic development, their potential failure poses catastrophic risks to downstream populations and assets1,2,3,4. Notable historical precedents include the 1963 Vajont Arch Dam collapse in Italy, the 1975 Banqiao Reservoir failure in China, the 1976 Teton Dam in the United States, the 1993 Gouhou Concrete-face Sand-gravel Dam incident in China, and the 2023 Abu Mansur and Al Bilad Dam breaches in Libya. These catastrophic events collectively underscore the devastating consequences of dam failures, resulting in unprecedented loss of life and extensive property damage across affected regions5,6,7.

Given the catastrophic consequences of dam failures, nations worldwide have prioritized dam safety as a critical engineering concern8,9. Since the nineteenth century, researchers have systematically investigated dam-break mechanisms through multidisciplinary approaches encompassing theoretical analyses10,11, physical model testing12,13,14,15, numerical simulations16,17, and studies on dam breach flood computation models18,19. Guan et al.20 advanced the understanding of landslide dam failures by incorporating debris composition and morphometric parameters (dam height and lake volume) into their analytical framework. Their field observations and scaled experiments successfully identified failure modes and enabled peak outflow rate predictions. Chen et al.21 conducted pioneering work on the compound effects of piping and overtopping failure mechanisms through integrated physical modeling and numerical analysis. Their findings revealed that progressive particle loss during piping increases soil void ratios while reducing frictional angles, thereby enhancing dam erodibility. Notably, severe piping prior to overtopping amplifies peak discharge magnitudes and accelerates flood arrival times, though with accelerated flow attenuation along downstream reaches.Zhang et al.22 employed computational fluid dynamics (CFD) simulations to quantify geometric influences on landslide dam breach evolution. Their work yielded empirical equations for predicting three critical parameters at laboratory scale: headcut erosion initiation time, peak discharge timing, and maximum flow rates. Complementing these numerical advances, Takayama et al.23 conducted flume experiments to elucidate how coarse-grained materials modulate breach development during overtopping failures. These findings were operationalized through a novel 2D shallow-water hydrodynamic model capable of forecasting outflow hydrographs for heterogeneous landslide dams containing coarse particles.

Recent years have witnessed significant advancements in governmental initiatives focusing on monitoring and early warning systems development24,25,26,27,28 and analytical methodologies for monitoring data24,29. Dixon et al.26 developed an innovative acoustic emission (AE) measurement sensor, validated through physical modeling experiments to demonstrate its efficacy in detecting accelerated deformation behaviors. Their work established a quantifiable correlation between acoustic emission signals and displacement rates. Building on these technological advancements, Paswan et al.30 engineered a low-cost tilt-based monitoring system for rainfall-induced landslides, utilizing MEMS sensors to track both gradual and abrupt slope displacements. This system not only monitors deformation dynamics but also provides mechanistic insights into landslide triggers. Complementing hardware innovations, Deng et al.31 designed a multi-module AE array monitoring platform integrating field surveillance, data transmission, information management, and early-warning analytics. Deployed across diverse soil landslides in China, this system has demonstrated robust operational reliability in long-term monitoring scenarios. From a predictive modeling perspective, Manconi et al.32 pioneered a statistical framework for failure time estimation by applying inverse velocity theory to near-real-time monitoring data. Their methodology generates confidence intervals for failure predictions, offering critical support for emergency decision-making when displacement or velocity thresholds are exceeded. This approach has direct applications in enhancing the precision of landslide early-warning protocols.

Despite substantial progress in dam-break research, significant gaps persist between academic insights and practical engineering requirements. Proactive forecasting of embankment dam failures remains a critical challenge in dam safety monitoring, as evidenced by numerous failure cases demonstrating that breach development typically follows an extended evolutionary process marked by time-dependent creep behavior – from initiation through progression to ultimate collapse. This study advances the field through controlled physical modeling of dam breaches under both normal operating and rainfall-saturated conditions. Leveraging high-resolution micro-electromechanical system inertial measurement unit (MEMS-IMU) sensors, we developed an integrated dam-break risk monitoring and forecasting framework to:

  1. 1.

    Clarify the evolutionary mechanisms of dam slope breach formation and propagation;

  2. 2.

    Characterize the deformation features during dam slope instability processes;

  3. 3.

    Establish a hierarchical early warning threshold system for different dam breach stages;

  4. 4.

    Achieve prediction of dam breach occurrence timing;

Our findings provide a scientifically grounded methodology for early-warning systems in embankment dam safety management, bridging critical theoretical-practical divides through quantifiable deformation benchmarks and failure progression analytics.

Experimental design

Test equipment

The experiment was conducted in the model test tank at the Feilaixia Test Base of the Guangdong Provincial Institute of Water Resources and Hydropower Research. The main equipment of the model test tank includes a water tank, a tailwater collection pool, a rainfall device, an upstream water tank, and a water supply pump, as shown in Fig. 1. The earth dam model is built in a water tank that is 6 m long, 1 m wide, and 1 m high, placed on a 40 cm high concrete platform. The two sides of the water tank are made of transparent toughened glass, providing great convenience for recording the process of dam failure. The tailwater collection pool is 2 m long, 2 m wide, and 1 m deep, primarily used for collecting the tailwater and sediment of the model test. The rainfall device consists of a booster pump and 20 nozzles, positioned 30 cm above the water tank, with an effective rainfall area of 4 m × 1 m. The simulated rainfall covers the area where the earth-rock dam model is situated, meeting the experimental requirements. The rainfall intensity is adjusted using a dedicated booster pump, with a range of 20 -200 mm/h. Additionally, the main equipment of the experiment includes an upstream water tank with a capacity of 500 L for water supply and a water supply pump with a flow rate of 0.1 m3/s.

Fig. 1
figure 1

Layout of the model experiment.

Full size image

Experimental measurements

The monitoring equipment utilized the low-cost, high-precision dam deformation monitoring device developed by the Guangdong Provincial Institute of Water Resources and Hydropower Research, known as the GDSKY-02 (referred to as MEMU). The MEMU is equipped with an Inertial-Measurement-Unit (IMU) based on Micro-Electro-Mechanical-System (MEMS) technology, providing miniaturization and high integration capabilities that conventional sensors lack. With its core components being gyroscope and accelerometer, the MEMU can precisely measure the three-axis orientation angles and acceleration of objects. The MEMU device has a diameter of 28 mm, a height of 18 mm, a measurement accuracy of 0.005°, and a sampling frequency set at 60 Hz (as shown in Fig. 1, item 5). It includes a built-in power module and Bluetooth transmission module for wireless monitoring data transmission. Moreover, the overflow process of the dam failure flood was recorded and captured using a motion camera (DJI Osmo Action 3).

Experimental design

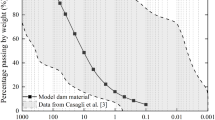
The model dam has a height of 90 cm, a crest width of 20 cm, and a crest length of 100 cm, with a slope ratio of 1:2 for both upstream and downstream dam slopes. The dam construction material is a mixture of sand and clay, with a composition of 80% sand and 20% clay. During the construction of the test dam, a loose soil layer of approximately 0.10 m thick was placed in the water tank each time. Each layer of loose soil was compacted using a rubber hammer. Special attention was paid during compaction to the soil near the sides of the tank to prevent water erosion along the sidewalls. Three MEMU devices were evenly placed along the centerline of the dam crest, at heights of 70 cm and 50 cm on the downstream slope, to monitor deformations on the surface of the dam. Additionally, a motion camera was installed on the upstream, downstream, and side surfaces of the earth dam to record the dam failure process, as shown in Fig. 2.

Fig. 2
figure 2

Layout of model earth dam and monitoring arrangements.

Full size image

Results and analysis

Dam collapse process

The study conducted two sets of control experiments under normal and rainfall conditions, respectively. To better align with real-world scenarios, each model test was divided into two parts. The first part involves the water infiltration process, where the normal water level of the model soil dam needs to be maintained. The occurrence of downstream water seepage indicates the formation of a complete infiltration line within the dam. This also marks the end of the first part, which typically lasts about 2 h. The second part involves operating the soil dam at high water levels until the dam body collapses. This stage aims to simulate the process where, due to the failure of drainage facilities, the infiltration line rises, eventually leading to dam failure. This process is divided into three stages during the experiment.

  1. (1)

    Localized swampification and partial soil slide stage of the downstream dam slope of the earth dam: after operating at a high water level for a period from tA to tB, seepage begins near the toe of the earth dam downstream slope, leading to the appearance of swampification areas on the slope surface. This area exhibits a trend of soil sliding (precursor to soil flow) and triggers multiple tension cracks, as shown in Figs. 3 and 4.

  2. (2)

    Stage of soil flow, partial collapse, and formation of penetrating cracks: At time tC, the exacerbation of soil sliding phenomena leads to the extension of tension cracks, resulting in downstream earth dam slope soil failure, as shown in Fig. 5. With the expansion of the area affected by soil flow, the tension cracks continue to propagate. The earthen dam structure is segmented by these tension cracks, leading to the collapse of the segmented sections. At time tD, due to the intensified erosion of the soil flow, transverse cracks appear on the crest of the dam, as shown in Fig. 6.

  3. (3)

    Stage of dam body collapse, overall sliding failure stage: at time tE, significant collapse occurs on the exposed face, with noticeable sliding movement of the dam body, as depicted in Fig. 7. By time tF, as the sliding intensifies, the dam body undergoes its first occurrence of deep-seated sliding, temporarily stabilizing the dam body, as illustrated in Fig. 8. Subsequently, at time tG, the dam body experiences a second instance of deep-seated sliding, with the sliding mass exhibiting a liquefied consistency. A breach forms in the dam, as shown in Fig. 9. Shortly thereafter, the earthen dam ruptures, leading to a sudden discharge of reservoir water, resulting in a debris flow, as depicted in Fig. 10.

Fig. 3
figure 3

Local flow slip.

Full size image
Fig. 4
figure 4

Tension cracks.

Full size image
Fig. 5
figure 5

Soil flow.

Full size image
Fig. 6
figure 6

Coherent crack.

Full size image
Fig. 7
figure 7

Collapse failure.

Full size image
Fig. 8
figure 8

Deep slip.

Full size image
Fig. 9
figure 9

Breach.

Full size image
Fig. 10
figure 10

Dam burst.

Full size image

It is known from the results of model tests that the breach of an earth-rock dam follows a specific process and goes through different stages, with the dam body showing distinct signs before the breach occurs. Furthermore, rainfall can expedite this process. The initial two stages of the dam breach account for over 85% of the total breach time. During this period, the dam body progresses relatively steadily, with minor occurrences of seepage, flow of soil, and localized collapses. The third stage is the most perilous phase of the breach, characterized by extensive collapses and deep-seated sliding, and the entire process is relatively short in duration. The initial two stages serve as trigger phases for collapses and landslides, while the third stage is the critical phase that ultimately leads to the dam body becoming unstable and breaching. This underscores the importance of initiating emergency response plans promptly in the event of cracking, seepage, marshy conditions on the dam's surface, or flow of soil in order to minimize potential disasters in earth dams.

Analysis of MEMU monitoring data

After conducting initial analysis of the MEMU monitoring data, it was found that the MEMU data located above the dam sliding block is more worthy of attention. Consequently, this study primarily examines the data monitored by MEMU-1, 4, 7 in Experiment 1, and MEMU-3, 6, 9 in Experiment 2. The scope of analysis of the monitoring data extends from the commencement of operation at high water level to the occurrence of significant visible deformation on the downstream dam slope (as depicted in the Fig. 7). In other words, this study establishes that the MEMU devices cease operation when substantial visible deformations emerge on the downstream dam slope.

As shown in Figs. 11, during the process of dam failure development, the angle-time curve of the downstream dam slope exhibits typical creep properties. This creep process can also be categorized into three stages: initial deformation, uniform deformation, and rapid deformation. After a period of operation at high water levels, the dam enters the initial deformation stage of creep. During this phase, the deformation curve of the downstream dam slope maintains a fundamental stability, with subtle alterations in the slope angle. When the high-water operation of the dam persists until time TA, the MEMU detects a gradual increase in the inclination angle of the downstream dam slope, signaling the entrance of the dam failure process into a uniform deformation phase. After time TB, the downstream slope of the dam starts to exhibit a noticeable increase in inclination angle. The slope of the inclined deformation curve is gradually increasing, signaling that the dam is transitioning into a stage of rapid deformation. Subsequently, the inclination angle experiences a sharp increase until the MEMU device ceases operation.

Fig. 11
figure 11

The angle-time curve of the downstream dam slope.

Full size image

Dam break forecast

The improved tangent angle method and the reciprocal of velocity approach have earned the favor of researchers in the field of slope failure, and are widely utilized in predicting the timing of landslide instability33,34,35,36,37. This section introduces these two methods into the prediction of earth dam body failure, validating the applicability and rationality of these approaches.

Improved tangent angle method

Based on existing research findings, it has been demonstrated that the tangent angle of the displacement–time curve can be utilized for landslide forecasting. Furthermore, by using tangent angles of 80° and 85° as dividing criteria, the third stage of creep (rapid deformation stage) can be subdivided into early rapid deformation, mid-rapid deformation, and late rapid deformation, as depicted in Fig. 1238,39. Building upon this foundation, the analysis of the angle-time curve of the downstream slope was conducted using MEMU-4 in model test 1 and MEMU-6 in model test 2 as examples. The relationship curve between the slope angle and time is nonlinear in the initial deformation and rapid deformation stages, but it approximates linearity in the uniform deformation stage. To mitigate the differences in tangent angles of curves resulting from the stretching or compressing of axes, it is necessary to transform the coordinate axes of the angle-time curve obtained by MEMU monitoring according to Eq. (1). Through transformation, the vertical coordinate can be converted to dimensions equivalent to the horizontal coordinate.

$$ T\left( i \right) = \frac{\theta \left( i \right)}{v} $$
(1)

where \(T\left( i \right)\) refers to the ordinate value of the same dimension as time after coordinate transformation; \(\theta \left( i \right)\) refers to cumulative tilting angle; The slope rate of the second creep stage is denoted as v, with a recorded slope of 0.000363°/s by MEMU-4 and a recorded slope of 0.000188°/s by MEMU-9.

Fig. 12
figure 12

Time curve and classification of deformation stages in typical slope failure.

Full size image

Figure 13 depicts the T-t curves of MEMU-4 and MEMU-6 after coordinate transformation. It is not difficult to observe that during the initial deformation stage (corresponding to 0 to tA in Fig. 13), the change in slope angle of the curve is very slight. Beyond tA, the slope of the T-t curve linearly increases, indicating the dam failure has entered the uniform deformation stage. Extracting data from the uniform deformation stage and standardizing the vertical and horizontal coordinates to identical unit values. It can be observed that the tangent angle during this stage is approximately 45°. From tA to tB, the T/t values are approximately equal to 1. After tB, the T/t values begin to increase. Therefore, this time can be regarded as the initiation of rapid deformation of the dam, which closely aligns with the termination time of the uniform deformation stage. In other words, the termination time of the second stage of dam creep is tB; thereafter, the rate of change in the T-t curve increases, the slope exceeds 45°, and the dam enters the third stage of creep: rapid deformation stage.

Fig. 13
figure 13

T-t curve of MEMU.

Full size image

To qualitatively assess the instability information of the downstream dam slope, it is necessary to further calculate the improved tangent angle in the T-t curve. The calculation method is given by formula (2):

$$ a = \arctan \frac{{T\left( i \right) - T\left( {i - 1} \right)}}{{t_{i} - t_{i - 1} }} = \frac{\Delta T}{{\Delta t}} $$
(2)

where: \(a\) is the improved tangent angle; \(t_{i}\) and \(t_{i - 1}\) are the times experienced during the dam failure process;

Figure 14 illustrates the calculated results of the improved tangent angles at the key time points of the uniform deformation stage and the rapid deformation stage. During the initial deformation stage, when the tangent angle of the T-t curve is less than 45 degrees, further investigation may not be warranted. Once the dam failure transitions into the uniform deformation stage, the improved tangent angle of the curve is approximately 45 degrees. After the dam breach enters the rapid deformation stage, the improved tangent angle exceeds 45 degrees. Previous studies have indicated that when the improved tangent angle surpasses 80 degrees, the deformation of the slope notably accelerates. Furthermore, when the improved tangent angle exceeds 85 degrees, signs of imminent sliding emerge on the slope, the deformation rate sharply increases, the slope becomes unstable, and a landslide is imminent. Similarly, the rapid deformation stage of dam failure can be further divided into three stages based on the improved downstream dam slope tangent angle-time curve: the early stage of rapid deformation, the mid-stage of rapid deformation, and the late stage of rapid deformation.

Fig. 14
figure 14

T-t curve with identical axes dimensions.

Full size image

From Figs. 11, 13 and 14, it can be deduced that when the high water level of the earthen dam reaches moment tB, the dam enters the initial stage of rapid deformation. At this point, the cumulative angular changes of MEMU-3 and MEMU-6 are 2.01 degrees and 1.86 degrees respectively. As the high water level progresses to moment tC, at this juncture the improved tangent angle of the curve equals 80 degrees, indicating the dam's transition into the mid-stage of rapid deformation. Subsequently, the cumulative angular changes for MEMU-3 and MEMU-6 are 2.56 degrees and 2.37 degrees. The slope of the tangent angle curve begins to significantly increase. By the time the high water level reaches moment tD, with the improved tangent angle now at 85 degrees, the cumulative angular changes for MEMU-3 and MEMU-6 are 3.49 degrees and 3.15 degrees respectively, marking the dam's entry into the late stage of rapid deformation. Following this, the downstream dam slope enters a precarious state of near-sliding, with the dam at risk of imminent failure.

根Based on the improved tangent angle, we can qualitatively deduce information regarding the instability of the downstream dam slope, providing a scientifically effective new method for determining the basis of warning judgments for the imminent failure of the dam. In Experiment 1, the thresholds for the downstream dam slope angle variations are Y1 = 2.01 degrees, Y2 = 2.56 degrees, and Y3 = 3.49 degrees. In Experiment 2, the thresholds for the downstream dam slope angle variations are Y1 = 1.86 degrees, Y2 = 2.37 degrees, and Y3 = 3.15 degrees. It is evident that, due to the influence of rainfall, the thresholds in Experiment 2 are all lower than those in Experiment 1. In practical engineering applications, emergency reinforcement measures should be implemented when the dam's downstream slope angle variation reaches Y1, and timely warning information should be issued when it reaches Y2.

Reciprocal method of velocity

Through previous analysis, it is evident that when the dam breach enters the rapid deformation stage, the slope rate of the monitoring data curve of MEMU gradually increases. Therefore, the rapid deformation stage is a critical phase for predicting dam failure. By analyzing this stage, new early warning methods can be proposed for dam breaches40.

In order to investigate the failure evolution pattern of the earth dam body, it is necessary to convert the angle-time curve of downstream dam slope deformation into a slope curve. As shown in Fig. 15, the slope can be approximated using Eq. (3) for calculation.

$$ \left| {dv_{i} } \right| = \left( {\frac{{\left| {d\theta } \right|}}{dt}} \right)_{i} = \frac{{d\theta_{i} - d\theta_{i - 1} }}{{t_{i} - t_{i - 1} }}{ , }\left( {i = 1,2, \ldots ,n} \right) $$
(3)

where ti is the time, \(d\theta\) is tilting angle increment from ti-1 to ti, \(dv_{i}\) is tilting rate, that is angle change rate at ti. Then the reciprocal tilting rate can be expressed as:

$$ \left( {\frac{dt}{{\left| {d\theta } \right|}}} \right)_{i} = \frac{{t_{i} - t_{i - 1} }}{{d\theta_{i} - d\theta_{i - 1} }}{ , }\left( {i = 1,2, \ldots ,n} \right) $$
(4)
Fig. 15
figure 15

Method of selecting data for the analysis of the rapid deformation stage of dam breach.

Full size image

Taking into account the fluctuation in monitoring data and the influence of noise, the rapid deformation phase utilizes a data sequence with angular variation intervals of 0.5 degrees (i.e. where \(d\theta\) = 0.5°). Through research, it has been found that there is a certain linear correlation between the negative slope rate and time during the rapid deformation stage. A linear correlation equation has been proposed, which can be formulated as:

$$ \frac{dt}{{\left| {d\theta } \right|}} = B\left( { - t + t_{f} } \right) $$
(5)

where: \(\frac{dt}{{d\theta }}\) represents the inverse number of tilting rates. \(B\) is the coefficient derived from the linear relationship between the reciprocal of the slope rate and time. \(t_{f}\) denotes the time of downstream dam slope failure, assuming a value of 0 for \(\frac{dt}{{d\theta }}\) at that moment. Figure 16 presents the calculated results for MEMU-3 and MEMU-6, using the fitted line to predict the downstream dam slope failure time, which are 11451 s and 9434 s, respectively, closely matching the actual dam slope failure times of 11469 s and 9470 s.

Fig. 16
figure 16

The reciprocal of the rate of change in angle velocity varies with time.

Full size image

Conclusion

In this study, model tests under different conditions were conducted to investigate the tilting characteristics of the downstream slope before dam failure and to summarize the failure process of the dam under various scenarios. The dam exhibited a retrogressive failure mode, and the failure process generally progressed through three stages: tension cracking induced by marshification of the downstream slope, soil flow with localized collapse, and large-scale landslides. Based on the angle-time curve, an improved tangent angle method was proposed to determine dam warning thresholds, and a reciprocal velocity method was introduced to predict the timing of dam failure. The main conclusions are as follows:

  1. (1)

    A low-cost, high-precision dam deformation monitoring device was employed to monitor the dam failure process, yielding an angle-time curve of downstream slope deformation. This revealed the creep characteristics of the downstream slope during dam failure, divided into three stages: initial deformation, uniform deformation, and rapid deformation.

  2. (2)

    Using the improved tangent angle method, the rapid deformation stage of dam failure was further subdivided into three substages: early rapid deformation, middle rapid deformation, and late rapid deformation. This provides a scientifically effective new approach for establishing dam failure warning thresholds. When the improved tangent angle exceeds 45 degrees, dam deformation enters the early rapid deformation stage, requiring immediate reinforcement measures. When the improved tangent angle surpasses 80 degrees, dam deformation progresses to the middle rapid deformation stage, necessitating the issuance of warning information. When the improved tangent angle exceeds 85 degrees, the dam approaches imminent failure.

  3. (3)

    Further analysis of the angle-time curve revealed a linear relationship between the reciprocal of the rate of change in downstream slope angle and time, with an established equation characterizing this relationship. Subsequently, the reciprocal velocity method was proposed to predict dam failure timing. The moment when the reciprocal of the angle change rate reaches zero, as determined by this method, corresponds to the precise instant of dam failure.

Limitations and future work

It should be noted that the current findings are based on controlled laboratory conditions with simplified material compositions and scaled hydrological loads. Future studies should incorporate diverse operational scenarios (e.g. varying rainfall intensities, heterogeneous soil structures) and prototype-scale validations to further verify the universality of the proposed methods under broader geotechnical and hydrological conditions.