Introduction

In recent years, the Acoustic Black Hole (ABH) structure has emerged as a promising concept for structural vibration reduction, exhibiting remarkable performance in vibration control applications. The ABH structure achieves this by manipulating the wavelength and wave speed of bending waves within the structure. This manipulation is achieved by systematically varying the local thickness of the structure according to a power law gradient. This gradient design enables the accumulation and dissipation of energy in a designated “black hole” region. In theoretical frameworks, it is predicted that when the thickness at the sharp edge is reduced to zero, the acoustic black hole is capable of absorbing nearly 100% of the incident wave energy1,2,3,4,5,6,7,8,9.

However, due to limitations in the manufacturing process, the ABH structure exhibits a finite thickness at its edge. Consequently, the structure requires operating above a certain truncation frequency to achieve a satisfactory energy focusing effect6,10,11,12,13,14. Nevertheless, the vibration control of low-frequency bands remains a significant challenge and crucial aspect in practical engineering applications. Addressing this limitation is crucial for the widespread adoption and effectiveness of the ABH structure in vibration reduction.

Currently, there is a paucity of research on the control of low-frequency acoustic waves using ABHs. Some studies have demonstrated that a periodic arrangement of ABHs can significantly enhance the accumulation of low-frequency band energy, leading to improved damping effects when combined with additional damping layers15,16,17,18,19,20. Tang21employed ABHs as fundamental components and integrated them into quasi-periodic structures based on specific layout principles. This periodic design exhibited a band gap effect in the low-frequency domain, offering a novel approach to broaden the application scope of ABHs. Tang and Cheng22 further explored a plate with a periodically arranged double-bladed ABH channel, incorporating a damping layer, and revealed that this configuration can achieve noise reduction even at low frequencies. Gao23,24,25 designed a double-leaf ABH beam with an embedded mass oscillator, demonstrating excellent vibration isolation performance. Moreover, there are related studies exploring the coupling of resonators with ABH structures to achieve low-frequency vibration control. Deng26,27 and Li28 proposed attaching a set of periodic local resonators to the ABH plate, which extends the performance of the ABH plate to lower frequencies. Li29,30introduced a vibration shock system into the ABH beam structure, enabling the rapid transfer of low-frequency vibration energy to higher frequencies for efficient dissipation. However, the impact generated by this approach may produce significant noise, limiting its application scenarios. Yu31and Jia32,33 proposed the integration of ABH structures with Dynamic Vibration Absorber (DVA) to create a composite system capable of compensating for limitations in low-frequency vibration reduction. Both theoretical and finite element analysis has confirmed that ABH + DVA beam structures exhibit ultra-wideband vibration attenuation in the low-frequency domain.

However, despite these theoretical advancements, there remains a lack of experimental verification to support these findings. For one-dimensional ABH beam structures, miniaturized and lightweight DVAs are crucial components. Notably, existing research on DVAs has primarily focused on larger-scale designs, leaving a gap in the knowledge of suitable miniaturized DVAs for integration with ABH beams. Furthermore, the low-frequency multi-mode control effect of ABH + DVA beam structures remains unclear. Therefore, it is imperative to delve deeper into the vibration reduction mechanisms of these composite beam structures and investigate the influence of DVA and ABH design parameters on the overall vibration reduction performance. Such a study would not only validate the theoretical predictions but also provide valuable insights for the design and optimization of ABH + DVA systems for practical applications.

Previous research on the ABH + DVA method has primarily concentrated on theoretical frameworks and simulations, often assuming a point-like or linear coupling between the DVA and ABH. However, in practical scenarios, DVA typically exhibits surface coupling constraints, which introduces complexities that are not fully captured by these simplified assumptions. Furthermore, as the coupling area decreases, the challenges associated with the design and fabrication of the DVA become increasingly significant. Despite this, the precise impact of different coupling types, including point coupling, line coupling, and surface coupling with varying areas, on the vibration suppression characteristics of the ABH + DVA remains elusive. Therefore, this article aims to provide a rigorous and comprehensive comparative analysis and study to address this critical gap in knowledge.

In the rest of the paper is structured as follows. In Sect. Design and manufacturing of the small DVA for ABH beam, a lightweight and minitype DVA is designed and fabricated, based on modal analysis of ABH beam and fix-point theory of DVA. Subsequently, the DVA is subjected to testing to validate its tuning frequency. In Sect. Experiments and numerical simulations, vibration experiments are conducted for three configurations: the standalone ABH beam, the ABH beam coupled with the DVA, and the ABH beam integrated with a damping layer. Correspondingly, numerical models are developed using the Finite Element Method (FEM) to facilitate comparative analysis. Section Results and discussions delves into the vibration attenuation performance of these three models. Experimental results are presented, demonstrating the effectiveness of the ABH + DVA approach. Furthermore, the FEM models of the ABH beam and ABH + DVA configuration are validated against their experimental counterparts. Additionally, this section explores the influence of DVA coupling area on vibration attenuation. To further enhance vibration attenuation capabilities, Sect. Conclusions also introduces a beam design that incorporates four distributed ABHs and four corresponding DVAs. This configuration aims to achieve multimode vibration attenuation within the low-frequency range and comprehensive attenuation across a wide frequency band. Finally, Sect. provides a comprehensive summary of the findings presented throughout the paper, highlighting the key contributions and implications of this research.

Design and manufacturing of the small DVA for ABH beam

Modal analysis of one-dimension ABH beam

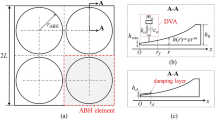
As seen in Fig. 1, a beam embedded with an ABH feature is illustrated. The edge of normal thickness aera with length of Lb, is fully clamped and applied with force Fs. L represents the longitudinal dimension of beam, whereas B denotes its width. Furthermore, LABH signifies the specific length measurement pertaining to the ABH feature. Additionally, h1 corresponds to the maximum thickness achieved by the beam, and h0 represents the truncation thickness, which characterizes a critical aspect of its geometry. The thickness of the ABH feature is precisely tailored in accordance with the power-law relationship, expressed as h(x) = εxm, where ε is constant and m is real constant. The beam is constructed from aluminium alloy, which possesses a Young’s modulus of 70 GPa and a mass density of 2.7 × 103 kg/m3.

Also, Fig. 1 illustrates the integration of an ABH beam with a DVA system, incorporating an attaching length of La. The DVA system comprises three distinct components: a mass block possessing a mass of ma, a spring characterized by a stiffness of ka, and a damping element exhibiting a damping ratio of ca.

The geometric parameters of the beam integrated with an ABH feature discussed in this work, are detailed in Table 1. The clamped area length, denoted as Lb, measures 45 mm, while the excitation force, Fs, is set to 9.8 m/s2. The five modal shapes and their corresponding natural frequencies of the beam with an embedded ABH feature have been accurately computed using the Finite Element (FE) method and are presented in Fig. 2. It is observed that the mode shapes of higher order exhibit increased deformation near the truncation edge of the ABH feature, indicating that the focusing effect of the ABH is more pronounced in higher frequency ranges. Furthermore, the analysis of the four modal shapes reveals that the truncation side’s tip experiences the highest deformation, suggesting that the DVA should be positioned at this location to maximize its effectiveness.

Fig. 1
figure 1

Schematic diagram of a beam embedded with one ABH feature and coupled with one DVA.

Full size image
Table 1 Geometry parameters of the beams embedded with one ABH and 4 ABHs.
Full size table
Fig. 2
figure 2

Five modes and shapes of a beam embedded with one ABH feature.

Full size image

Design and manufacture of the small DVA

Based on the classical fixed-point theory for DVA design, the optimal frequency ratio, denoted as ropt, and the optimal damping ratio, represented by ξopt, can be expressed as follows34:

$${r_{{\text{opt}}}}=\frac{{{\omega _a}}}{{{\omega _1}}}=\frac{1}{{\mu +1}}{\text{ }},{\text{ where }}{\omega _a}=\sqrt {\frac{{{k_a}}}{{{m_a}}}}$$
(1)
$${\xi _{{\text{opt}}}}=\sqrt {\frac{{3\mu }}{{8{{(1+\mu )}^3}}}}$$
(2)

where µ is mass ratio of ma to m1, m1 is mass of main system and ma is mass of DVA. And ωa represents natural frequency of DVA, ω1 represents natural frequency of main system.

The stiffness of the spring in the DVA system can be written as follows:

$${k_a}={m_a}\frac{{{k_1}}}{{{m_1}}}{(\frac{1}{{1+\mu }})^2}$$
(3)

where k1 represents the stiffness of the main system and m1 represents the mass of the main system. The damping coefficient of the damper in the DVA system is written below:

$${c_a}=2{m_a}\sqrt {\frac{{{k_1}}}{{{m_1}}}} \times \sqrt {\frac{{3\mu }}{{8{{(1+\mu )}^3}}}}$$
(4)

Given the minimal size and mass of the beam integrated with an ABH, it is imperative to devise and fabricate a compact and lightweight DVA. The prototype of the DVA we have designed is exhibited in Fig. 3. This DVA system comprises a mass block fabricated through precision 3D printing techniques, four steel expansion springs, and a damper constructed from butyl rubber. The pertinent material properties of these components are outlined in Table 2. The steel spring, 3D-printed base, and 3D-printed mass block are all interconnected through adhesive bonding. Similarly, the damping column is also affixed to both the base and the mass block via adhesive bonding.

Fig. 3
figure 3

(a) Schematics of the small DVA; (b) manufactured of the designed small DVA.

Full size image
Table 2 Material properties and design parameter of DVA system.
Full size table

Firstly, the selection of an appropriate mass ratio (µ ) for the DVA is crucial, as it is determined by the coupling position and size of the DVA. However, due to the unique characteristics of the ABH structure, the equivalent mass at the truncation position is insufficient for optimal DVA design using the equivalent mass design method. Therefore, in this study, the total mass of the ABH cantilever beam is adopted as a reference for designing the DVA. According to the principles of DVA theory, a higher mass ratio generally results in improved vibration reduction effectiveness. However, excessively high values of µ can potentially affect the modal behavior of the original structure.

In our specific case, the mass of the ABH cantilever is 62 g. After comprehensive consideration, a mass ratio of µ = 0.16 is chosen, which corresponds to a DVA mass of 9.9 g. It is noteworthy that due to the low first-order resonance frequency, it is challenging to find a spring with sufficient stiffness to effectively suppress this frequency. Consequently, the target frequency for the DVA designed in this study is set as the second-order resonance frequency of the one-dimensional ABH cantilever beam, which is 607 Hz. Utilizing Eq. (1), the resonant frequency of the DVA can be calculated to be 523 Hz. Furthermore, other parameters of the DVA can be derived using Eq. (1) to (4), as detailed in Table 2.

Tuning frequency test of the DVA

The resonant frequency of the meticulously designed dynamic vibration absorber (DVA) was rigorously tested on a precision vibration test bench. The experimental setup is schematically represented in Fig. 4(a). The base of the DVA was securely affixed to the surface of the vertical vibration test bench to ensure stability. Additionally, a lightweight unidirectional acceleration sensor, weighing less than 0.3 g and accounting for less than 3% of the DVA’s total mass, was positioned above it to meticulously monitor its acceleration along the z-axis, minimizing any potential interference.

A sweep frequency excitation ranging from 200 Hz to 800 Hz was applied to the vibration table in the z-direction. Subsequently, an acquisition device was utilized to meticulously measure and obtain the frequency response function of the DVA. The results of this experimental analysis are presented in Fig. 4(b).

It is evident from the graph that the DVA exhibits a resonant frequency at approximately 534 Hz. When compared to the target frequency of 523 Hz, the error margin falls within acceptable limits of 2%, thus fulfilling all design requirements and validating the effectiveness of our designed DVA.

Fig. 4
figure 4

(a) Experiment setup to measure tuning frequency of the designed small DVA; (b) tuning frequency test result of the designed small DVA.

Full size image

Experiments and numerical simulations

Experiment setup

As depicted in Fig. 1, the beam undergoes an acceleration excitation imparted by the shaking table, specifically applied to the fixture at the fixed end. The magnitude of this excitation measures 9.8 m/s2. Point O, situated at the centroid of the ABH cantilever beam and positioned 60 mm away from the fixed support, functions as the designated monitoring point for assessing the vibration response.

The experimental configuration is presented in Fig. 5. The computer’s integrated acquisition card regulates the software-directed emission of excitation signals. Subsequently, these signals undergo amplification via a power amplifier before being transmitted to the ABH cantilever beam via a shaking table. This arrangement allows for the collection and processing of acceleration signals pertaining to the vibration response.

Finite element model

The three-dimensional FE models of the ABH beam, as well as the ABH beam integrated with the DVA or damping layer, were constructed and discretized using HYPERWORKS. These models were then subjected to computational analysis through MSC.Nastran. For the formation of the beam structure, tetrahedral elements were employed, ensuring accurate representation and simulation of the physical properties and behavior of the system.

Fig. 5
figure 5

Experiment setup for vibration test.

Full size image

The existing literature typically presents the coupling mode between the DVA and the ABH structure as either line contact or point contact for modeling purposes. However, in practical construction scenarios, the coupling area of the DVA cannot be overlooked when compared to the dimensions of the cantilever beam in the ABH system. Consequently, there is a compelling need to develop a simulation model that closely reflects the actual experimental conditions. In this study, we constrain the nodes of the beam within the coupling area to a single point, and this point is then coupled with the CBUSH element, which serves to emulate the spring and damper characteristics of the DVA system. Furthermore, since the mass block in the DVA does not significantly impact its damping effect, it is simplified as a mass point directly connected to the CBUSH element, allowing for a more streamlined and accurate representation of the system’s dynamics. The entire ABH beam is modeled using the PSOLID element, specifically an 8-node hexahedral solid element (CHEXA8). In this study, the element size is uniformly set to 1 mm to ensure a balance between computational accuracy and efficiency, while meeting the mesh quality requirements for vibration characteristic analysis, as seen in Fig. 6.

Fig. 6
figure 6

FE model of the ABH + DVA.

Full size image

The introduction and simulation of the ABH beam coupled with a damping layer serve as a reference model for the investigation of vibration attenuation effects. This damping layer is seamlessly integrated onto the surface of the ABH cantilever beam through the utilization of shared nodes, thereby preserving the identical degree of freedom between the damping layer and the cantilever beam. Additionally, to ensure the precision of the calculations, the grid of the damping layer is meticulously refined into two layers. It is noteworthy that both the quality and thickness of the damping layer are carefully calibrated to match the experimental model, thus ensuring the fidelity of the simulation and its comparability to real-world conditions.

Results and discussions

Experimental investigation of vibration attenuation effect

Vibration experiments have been conducted on three distinct models: an ABH beam, an ABH beam coupled with a single DVA (denoted as ABH + DVA), and an ABH beam coupled with a damping layer (denoted as ABH + Damp). The geometry of the beam and the ABH feature remain identical across all three models. The corresponding geometry and material parameters are outlined in Tables 1 and 2, respectively. The beam material is aluminum alloy, exhibiting a Young’s modulus of 70 GPa and a mass density of 2.7 × 103 kg/m3. Notably, the damping material employed in the ABH + Damp model is identical to that utilized in the fabrication of the DVA in the ABH + DVA model. This damping material is evenly distributed across the surface of the ABH feature. Furthermore, it is worth mentioning that the masses of both the damping layer in the ABH + Damp model and the DVA in the ABH + DVA model are equivalent, ensuring a controlled comparison during the vibration experiments. The damping layer is attached to the whole ABH feature area and its thickness is set to 1 mm, as seen in Fig. 7. The damping layer is made of the same material as the damping in the DVA, and detailed parameters can be found in Table 2.

The acceleration-frequency curves of all three models are presented in Fig. 7. The primary focus of attenuation efforts is directed towards the second resonance of the ABH beam. Notably, a significant attenuation of 21.9 dB is observed when comparing the ABH + DVA configuration to the baseline ABH beam. However, when comparing the ABH + Damp configuration to the ABH beam, the attenuation is slightly lower, amounting to 14.9 dB.

Regarding the third resonance of the ABH beam, both the ABH + DVA and ABH + Damp configurations demonstrate comparable attenuation levels, achieving approximately 26 dB each. Over the entire experimental frequency range of 0–1800 Hz, the ABH + DVA model exhibits the highest vibration attenuation, particularly in the lower frequency band of 0–800 Hz.

Fig. 7
figure 7

Experiment results of ABH beam, ABH beam coupled with one DVA and ABH beam coupled with damping layer.

Full size image

It is worth noting that due to limitations in the experimental setup, frequencies above 1800 Hz were not included in this investigation. Future studies could explore this higher frequency range through finite element (FE) simulations, offering insights into the vibration behavior and potential attenuation mechanisms within this unexplored frequency domain.

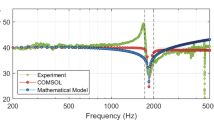
Model validation

A comparative analysis of the simulation and experimental results is presented in Fig. 8; Table 3. For the ABH cantilever beam model, the maximum relative error between the simulation and experimental data occurs at the second formant, reaching 6.75%. Similarly, for the ABH + DVA model, the maximum relative error is observed at the third formant, amounting to 9.0%. In the experimental curves of both the ABH beam and the ABH + DVA beam, a sudden change is observed in the final segment. We hypothesize that this anomaly is likely attributed to the experimental fixture. Consequently, the finite element model, which lacks physical modeling of the fixture, does not exhibit this abrupt change in its computational results. This discrepancy may also be a primary factor contributing to the relatively larger error margins. Regarding the ABH + DVA configuration, the increased error is presumed to stem from the nonlinear stiffness characteristics inherent in the physical DVA’s damping mechanism—a feature not accounted for in the finite element modeling. Despite these considerations, the relative errors remain within a 10% threshold, which we deem acceptable for the purposes of this study. This comprehensive comparison also serves to enhance the reliability and applicability of the simulation model in predicting the dynamic behavior of the cantilever beam configurations under investigation.

An amplitude comparison between experimental and simulated results for the ABH beam reveals minor discrepancies, whereas the ABH + DVA beam exhibits significantly larger amplitude deviations. For the ABH beam, potential sources of amplitude errors may primarily be attributed to two factors: firstly, uncertainties in boundary conditions induced by the fixture in experimental setups, and secondly, the neglect of structural damping in the numerical modeling. In the case of the ABH + DVA system, in addition to these shared factors, two further contributing mechanisms merit emphasis: firstly, simplified DVA modeling, where the simulation employs a reduced-order model comprising CBSUSH spring-damper elements and concentrated mass elements, which may not adequately capture the nonlinear stiffness characteristics of the damping columns in the physical DVA structure; secondly, unmodeled material damping, where the 3D-printed base and mass block in the actual DVA inherently exhibit viscoelastic damping properties, a critical energy dissipation mechanism that is not accounted for within the current linear simulation framework.

Fig. 8
figure 8

Model validation of ABH beam and ABH beam coupled with one DVA.

Full size image
Table 3 Model validation of ABH beam and ABH beam coupled with one DVA through resonance frequency results.
Full size table

Influence of DVA coupling aera on vibration attenuation

In this academic study, we confine our investigation to line coupling and surface coupling for a one-dimensional ABH beam. Precisely, we focus on the first-order resonance frequency of the ABH cantilever, designating it as the tuning frequency. Key parameters are maintained constant throughout our analysis, including a mass ratio of µ = 0.2, stiffness ka = 1.6 N/mm, and damping ratio ξ = 0.21.

To meticulously control the attachment area, we establish a fixed coupling width equivalent to the beam’s width and systematically vary the coupling length La of the DVA. Notably, the DVA’s coupling position is strategically placed at the leading edge of the ABH cantilever’s free end.

Starting from the ABH characteristic tip, we delve into the system’s response by gradually adjusting the coupling length La of the DVA. Specifically, we consider a range of values, including 0 mm (representative of line coupling), 5 mm, 10 mm, 15 mm, and 20 mm. This methodology enables a comprehensive comparison between the practical surface contact model, which accounts for the coupling area, and the theoretical line contact model (ABH + DVA).

Our findings reveal intriguing differences between the two models. While both exhibit comparable vibration responses in the lower frequency ranges, their behaviors diverge significantly in the higher frequencies. As the frequency increases, the discrepancy between the models becomes more pronounced. Furthermore, a notable difference is observed in the magnitude of resonance peaks. Specifically, the line model demonstrates lower peak amplitudes compared to the surface model, albeit sharing a similar trend in amplitude variation. These insights provide valuable understanding into the complex interactions between line and surface coupling in ABH beams and their impact on vibration suppression characteristics.

Figure 9 presents a rigorous comparative analysis of the average acceleration responses exhibited by the ABH + DVA beam, comparing the practical surface contact model with the theoretical linear contact model. Upon close examination of the figure, it becomes evident that the vibration response outcomes of both models align closely in the initial two frequency orders. However, as we delve deeper into the vibration characteristics within the subsequent high-frequency bands, a notable discrepancy emerges, and this inconsistency becomes increasingly pronounced as the frequency continues to rise.

Fig. 9
figure 9

Comparison of average acceleration response between line coupling model and surface coupling model (5 mm × 30 mm).

Full size image

Furthermore, a significant difference is observed in the amplitudes of the corresponding resonance peaks between the two models. Specifically, the amplitude of the resonance peaks in the linear model is observed to be lower than that of the surface model. Despite this notable difference in amplitude, it is noteworthy that both models exhibit a comparable trend in terms of amplitude variation.

This comprehensive comparative analysis provides valuable insights into the distinct vibration behaviors exhibited by the two models. It underscores the importance of considering both theoretical and practical contact models in beam vibration studies, as they offer distinct perspectives on the system’s dynamic response characteristics. Such an approach enables a more comprehensive understanding of the vibration behaviors of beams and can aid in the development of more effective vibration suppression strategies.

Figure 10 presents a rigorous comparative analysis of the average acceleration response of the ABH + DVA beam across varying coupling areas. Upon a meticulous examination of the figure, it becomes evident that the vibration response characteristics remain consistently similar at the target resonance frequency across different coupling areas. Specifically, within the frequency range proximal to 700 Hz, a decrease in the coupling area leads to a more pronounced attenuation of vibration. Notably, the attenuation difference between a coupling length of 5 mm and 20 mm approaches nearly 10 dB, indicating a significant impact of the coupling area on the vibration response. Furthermore, for higher resonance frequencies, the trend of improved vibration efficiency with a decrease in the coupling area persists. This phenomenon can be attributed to the intricate interaction between the DVA and the ABH beam. When the DVA is coupled with the ABH beam, the vibration response at the coupling position necessarily converges, thereby exerting a significant influence on the vibration amplitude at that specific point. A smaller coupling area results in a larger vibration amplitude, which, in turn, enhances the vibration reduction effect generated by the DVA.

Fig. 10
figure 10

Comparison of average acceleration response among various coupling aera of surface coupling models.

Full size image

In practical engineering applications, minimizing the coupling area and designing the DVA as compactly as possible are advisable strategies to ensure optimal vibration reduction performance. This approach offers a promising direction for enhancing the effectiveness of vibration control systems, thereby contributing to the advancement of various engineering fields.

The theoretical linear coupling model exhibits significant deviations from the actual surface coupling model, particularly in terms of resonance frequency and the magnitude of the resonance peak within the mid- to high-frequency ranges. However, it is worth acknowledging that the vibration characteristics at lower frequencies, as well as the overall trend of vibration response changes, remain generally consistent between the two models. Therefore, under certain circumstances, it is permissible to utilize the line-coupled model as an approximation of the surface-coupled model, offering a simplified yet effective approach for vibrational analysis. This approximation allows for a more tractable analysis while preserving key aspects of the vibration behavior.

Multimode vibration attenuation with distributed ABHs and DVAs

Based on the aforementioned research findings, it has become evident that the combined approach of ABH + DVA demonstrates significant effectiveness in vibration reduction across both low-frequency and medium- to high-frequency ranges. Nevertheless, a limitation of the current setup emerges, as the configuration involving a single ABH coupled to a single DVA is insufficient to effectively control the low-order multi-formant vibration reduction scenario. To address this challenge and enhance the vibration control capabilities, we propose a novel structure that incorporates distributed ABHs coupled with distributed DVAs. This advanced configuration is expected to provide a more comprehensive and efficient solution for managing low-order multi-formant vibration reduction problems.

In this academic study, a distributed beam structure featuring four ABHs has been selected, with four DVAs being coupled to each of the four ABH characteristic regions, respectively. The schematic representation of this configuration is depicted in Fig. 12. The geometric parameters of the beam are listed in Table 1 and the material used is 6061 aluminum alloy. The corresponding cut-off frequency of the system is calculated to be 1752 Hz (for the detailed solution process of the cut-off frequency, refer to the referenced source[10], as it will not be repeated in this paper). The boundary condition of the model is set as fixed support at both ends, and the excitation position is situated at the positive center of the beam.

Fig. 11
figure 11

First four modes and shapes of 4 ABHs beam model.

Full size image

The integration of DVA within the ABH structure primarily aims to counteract the challenges associated with suppressing low-frequency vibrations due to the diminished focusing effect exhibited by the ABH structure at the cut-on frequency. Drawing upon the cut-on frequency and modal analysis of the 4 ABH beam, the design parameters of the four DVAs are tailored specifically to target the first three resonant frequencies that coincide with the cut-on frequency of 1752 Hz. Given the symmetric nature of the 4 ABH fixed beam, the overall dynamic response of the beam remains unaffected even when the relative positions of the DVAs are interchanged. Detailed layout schemes and schematics of the DVAs are presented in Table 4.

Fig. 12
figure 12

Schematic of 4 ABHs + 4DVAs beam.

Full size image
Table 4 Various DVA design cases of target resonance for the 4 ABHs + 4DVAs beam.
Full size table

To eliminate the potential impact of variations in quality and damping ratio among the DVAs on the performance of the 4 ABH + 4DVA system, it is crucial to maintain consistency in both the quality and damping ratio of each individual DVA. This ensures that any observed effects can be attributed solely to the intended design parameters and not confounded by extraneous variables. The specific DVA parameters corresponding to different resonant frequencies are detailed in Table 5.

The vibration attenuation values of the twelve cases, relative to the 4 ABH beam, were computed for the first three resonant frequencies and tabulated in Table 6. Additionally, we conducted calculations for the average vibration attenuation across a relatively low-frequency band preceding the cutoff frequency, as well as for the entire frequency range from 0 to 4000 Hz. The results indicate that Case 1 exhibits the most significant vibration attenuation, reaching a maximum of 10.1 dB for the first formant. This case involves positioning the tuning frequencies of the two DVAs near the midpoint, specifically targeting the first formant. Consistent with the mode shape diagram presented in Fig. 13, the two ABH units feature center positions situated near the midpoint, which exhibit the largest amplitudes. Consequently, placing the DVA designed to attenuate the first-order formant at this location ensures maximum effectiveness. Conversely, positioning the DVA targeting the first-order formant at the ABH units located at both ends actually increases the vibration response. Furthermore, based on the mode shapes of the first four orders, the amplitude associated with the first order is relatively the smallest. Even when the DVA is situated at the point of maximum amplitude for the first order, the achieved vibration attenuation remains significantly lower than that observed for vibration reduction schemes targeting the second and third orders.

Table 5 Design parameters of various DVA for different tunning frequencies and resonances.
Full size table
Table 6 The average acceleration Attenuation of 4 ABH + 4DVA relative to 4 ABH in the first three orders and two frequency bands under different layout schemes (Unit: dB).
Full size table
Fig. 13
figure 13

First four modes and shapes of 4 ABHs beam model.

Full size image

For the second-order formant, Case 8 achieved a maximum attenuation of up to 43.2 dB. Similarly, for the third formant, Case 12 demonstrated a maximum vibration attenuation of 37 dB. Analysis of the corresponding mode shape diagrams and the DVA control schemes reveals that optimal vibration reduction efficiency is achieved when two DVAs simultaneously control a specific order of resonance peak and are positioned at the regions of large amplitude within the controlled resonance mode shape. The vibration response-frequency curves for Case 1, Case 8, and Case 12 are plotted in Fig. 14, providing a visual representation of the vibration attenuation achieved in each case.

Fig. 14
figure 14

Average acceleration response curves of 4 ABHs beam, Case1, Case8 and Case12.

Full size image

In academic terms, Case 11 exhibits the most effective damping performance within the first third-order resonance frequency band. This superior performance is attributed to the strategic placement of the DVAs, which are each positioned at the corresponding relative maximum amplitude points to control the three formants individually. On the other hand, Case 12 achieves the highest level of vibration attenuation across the entire frequency range of 0–4000 Hz. Conversely, Case 4 demonstrates the poorest performance in both the relatively low-order frequency band and the overall frequency band within the first third-order formant. This inferior performance can be traced back to the arrangement of each DVA in positions of relatively small amplitude. To further illustrate these observations, the vibration response-frequency curves for Case 4, Case 11, and Case 12 are plotted in Fig. 14.

Conclusions

In this academic study, a lightweight Dynamic Vibration Absorber (DVA), was designed and fabricated to enhance the vibration suppression capabilities of Acoustic Black Hole (ABH) beams. In contrast to prior theoretical and simulation-based research, this investigation validates the practical effectiveness of the ABH beam coupled with one DVA (ABH + DVA) on vibration suppression technique through experimental implementation. Concurrently, the accuracy and reliability of the established finite element model are corroborated by the experimental results. A comprehensive analysis of both experimental and simulation results reveals that the ABH + DVA configuration exhibits superior damping capabilities across both low and high-frequency ranges. Notably, the damping effect is particularly pronounced at frequencies approaching the control frequency of the DVA, indicating optimal performance under these conditions. This configuration effectively addresses the limitations of ABH-based vibration reduction methods, particularly below the cut-on frequency. Furthermore, this study delves into the influence of coupling forms and areas of the DVA on vibration characteristics. Lastly, to underscore the improved vibration reduction efficiency of the ABH + DVA approach at low frequencies, this manuscript also explores the vibration behavior of the beam embedded with 4 distributed ABHs and coupled with 4 distributed DVAs (4 ABHs + 4DVAs). The main conclusions of this study can be summarized as follows:

  1. (1)

    The rigorous analysis of experimental vibration results from three distinct models—ABH beam, ABH + Damp, and ABH + DVA—reveals that the ABH + DVA configuration exhibits the most pronounced vibration reduction effect at the first two order resonance peaks. Within the frequency range up to 1800 Hz, ABH + DVA demonstrates comparable damping performance to ABH + Damp. However, due to the constraints of the experimental setup, data regarding higher frequency bands remains elusive. Additionally, the current DVA design, hampered by limitations in preparation processes and material choice, still possesses a relatively high mass, leaving room for further enhancements in its vibration reduction efficiency.

  2. (2)

    In comparing the surface coupling approach with the linear coupling method of the DVA, it is academically observed that the latter demonstrates a superior vibration reduction effect on the ABH structure outside the tuning frequency range. Conversely, within the proximity of the DVA’s tuning frequency, both coupling methods exhibit comparable vibration reduction capabilities. Furthermore, a meticulous analysis reveals that a reduction in the coupling area results in enhanced vibration attenuation beyond the tuning frequency, while the vibration attenuation characteristics remain largely unchanged in the vicinity of the tuning frequency. However, it is crucial to note that further miniaturization of the DVA design is imperative to minimize the coupling area and thereby enhance the overall wideband damping efficiency.

  3. (3)

    The proposed structure consisting of four ABHs integrated with four DVAs is formulated with the aim of concurrently mitigating the first three formants within the prescribed cut-on frequency. To this end, twelve distinct schemes were devised, encompassing various combinations of tuning frequencies for the four DVAs and their respective targeting of the three formants. Through a rigorous computational analysis of the vibration characteristics associated with these twelve schemes, it becomes evident that optimal vibration suppression is achieved at the targeted formants when each DVA is coupled precisely to the location of maximum vibration amplitude on the original ABH beam, corresponding to the designated tuning frequency. This approach ensures that the overall structure exhibits superior damping performance across the specified frequency range.

  4. (4)

    The integration of distributed ABHs with distributed DVAs offers a highly efficient means of suppressing vibrations associated with low-order multi-mode excitations. This approach not only demonstrates excellent vibration attenuation within the targeted low-frequency range but also exhibits notable suppressive effectiveness in the intermediate and high-frequency bands surpassing the cut-on frequency. Consequently, the combined use of distributed ABHs and DVAs effectively fulfills the objective of achieving ultra-wide frequency vibration attenuation, particularly for low-frequency multi-mode scenarios. This comprehensive approach represents a significant advancement in vibration control technology.