Dynamic characterization and vibration response optimization of EMT system for tracked vehicles

Abstract

Electromechanical composite transmission (EMT) is an important transmission form for heavy-duty tracked vehicles, which has higher requirements for the kinematic performance of the whole vehicle under high-speed driving and cross-country high-mobility working conditions. In this paper, for the drive motor-planet mechanism of the tandem EMT system, the electromagnetic torque, unbalanced magnetic tension, and gear nonlinear meshing excitation are calculated, and the influence law of the excitation source on the vibration response at high rotational speed is revealed. Then, the dynamic model of the drive motor-planet mechanism system is established, and the intrinsic vibration characteristics and forced vibration characteristics are analyzed. Secondly, a tooth profile trimming method of the drive motor-planet mechanism based on the minimization of the out-of-line meshing is proposed. The tooth profile trimming amount in each planetary row is obtained, and the mechanism before and after the trimming is analyzed by dynamic simulation. Finally, a vibration test rig is set up to collect the vibration acceleration data before and after gear trimming and verify the validity of the proposed trimming method. The results show that the vibration characteristics of the system are improved by up to 30% after reshaping, which is in good agreement with the simulation results, and the overall deviation is about 15%.

Introduction

EMT systems are widely used in hybrid vehicles^1,2, electric locomotives³, coal mining machinery⁴, and wind energy generators⁵ due to their advantages of high efficiency, high load capacity, and integration. However, high-speed tracked vehicles have high power density, high component speeds, high load conditions⁶, and long-time service in complex working conditions. The system is prone to vibration impacts and instability, which seriously affects the operation quality and reliability. The motor-planet mechanism coupling will lead to more complex nonlinear excitation, including electromagnetic torque⁷, unbalanced magnetic tension⁸, and time-varying meshing force of gears⁹. Therefore, to reduce the system vibration caused by multiple sources of excitation, it is crucial to carry out research on the analysis and optimization of the dynamics characteristics of the EMT system of tracked vehicles.

In terms of electromagnetic torque, unbalanced magnetic tension, and radial force, Heinrich and Shevchenko¹⁰ investigated the electromagnetic torque pulsations occurring in slotless magneto-electric synchronous motors. Barriere et al.¹¹ proposed an analytical method for calculating the electromagnetic field in the air gap of embedded permanent magnet synchronous motors that are optimized to minimize torque fluctuations. Tatte¹² proposed a direct torque controller for three-phase induction motors to reduce the electromagnetic torque. Xu and Li¹³ considered the effect of tangential motor eccentric force on motor vibration. Li et al.¹⁴ revealed the mechanism of the effect of unbalanced magnetic tension on the dynamic performance of permanent magnet grinding spindles. Werner¹⁵ presented a model of rotor dynamics under electromagnetic excitation in an induction motor considering the eccentricity angle and verified the validity of the model by numerical calculations. Xu et al.¹⁶ proposed a magnetic equivalent circuit (MEC) modeling method to calculate the radial and tangential motor eccentric forces and investigated the nonlinear vibration characteristics.

In terms of modeling and studying vibration characterization of the EMT, Chen et al.¹⁷ established a composite electromechanical hydraulic transmission system with return flow power and analyzed the performance characteristics of the new variable speed system under different operating conditions. Xie et al.¹⁸ established an electromechanical coupled dynamics model under multi-source excitation by using the parametric method of lumped-distributed and experimentally verified the proposed model. Chang et al.¹⁹ modeled the mechatronic dynamics of the generator power system by considering the detailed characteristics of the gear system and the electromagnetic characteristics of the generator. Xuan et al.²⁰ proposed a joint simulation modeling method considering the integration of the electrical subsystem with the complete mechanical subsystem.Mukherjee et al.²¹ presented a novel approach by conducting a complexity-based study of an electromechanical (EM) gearbox system with tooth root cracks, utilizing an analytical model and motor current signals for the first time.This study contributes valuable insights into the behavior of gearbox systems experiencing crack-induced faults.

In terms of nonlinear dynamic modeling and vibration characterization of planetary drives, due to the large mass of the tracked vehicle and the high steering performance requirements, its speed change mechanism and power coupling mechanism mostly use planetary gears. The structure of the planetary mechanism is complex, and its dynamics model has many state quantities. Sharad and Hugh²² established a dynamic model of the bearing cage and rolling element for a wind turbine gearbox under high speed and light load conditions and investigated the bearing vibration characteristics. Xu et al.^23,24 proposed a novel dynamic model of a planetary gear system with positioning errors by considering its effect on the mesh position and separation distance for both external and internal gear pairs.Mo et al.²⁴ introduced gear wear into a dynamics model by combining gear wear with static transmission error to obtain the system in nonlinear dynamic characteristics at different wear levels. Zhang et al.^25,26 presented an original dynamic model of a multistage planetary gearset-bearing-rotor-clutch coupling system with multi-shift and multi-working conditions, which overcomes traditional models that cannot consider the stochastic tooth impacts of detached clutches.Kalay et al.^27,28 proposed a one-dimensional convolutional neural network (1-D CNN) model to diagnose tooth root cracks for standard and asymmetric involute spur gears.A series of vibration experiments were performed on a one-stage spur gearbox to achieve this by using a tri-axial accelerometer under variable working loads. The experimental results show that the use of asymmetric tooth shapes has significant advantages in fault diagnosis.Ma et al.²⁹ developed a dynamic model to simulate crack faults considering the gear foudations.Based on the simulated vibration responses, two novel indicators for distinguishing the crack propagation stages are proposed. The results are important for fault diagnosis and health monitoring of gear systems.

The core components of the EMT studied in this paper include a drive motor and a planetary gear coupling mechanism. The drive motor has a high rotational speed and high vibration. For this type of system, gear tooth profile modification is an important factor in reducing vibration. Bahk et al.³⁰ captured the dynamic excitation of the tooth profile at the planetary gear mesh by building an analytical model to minimize the static transmission error and the dynamic response error. Chen et al.³¹ proposed a general gear mesh stiffness model and argued that tooth profile trimming can effectively reduce transmission error. Xiang³² established three-dimensional models of gear pairs with different drum volumes based on toothwise load distribution and analyzed its influence law on the toothwise load of the gear teeth. Mo et al.³³ investigated the method of mesh stiffness analysis of asymmetric helical gears and used the potential energy principle and the slicing method to study the influence law of the gear’s basic parameters on the mesh characteristics. Lei et al.³⁴ and Du et al.³⁵ used optimization algorithms for the structural optimization of tooth profiles to achieve better vibration performance. Yu and Mechefske³⁶ studied corner contact effects on the mesh stiffness, static transmission error, and the dynamic response of an external gear pair with tooth tip relief.

In the drive motor-planet mechanism, the mechanical transmission is the main source of vibration due to the small excitation of the motor. Therefore, the mechanical transmission optimization can be combined with the gear trimming technique proposed by scholars to achieve system vibration reduction. However, due to the more complex and novel structural form of the planetary row that is the object of study in this paper, the difficulty of theoretical modeling, simulation calculations, and experimental studies related to the work is very high, and there are fewer previous related studies that need to be carried out in-depth research.

In this paper, the multi-source excitation characterization and dynamic modeling method of the drive motor-planet mechanism are first carried out to analyze the intrinsic characteristics and forced vibration responses. Then, a vibration optimization strategy is proposed based on tooth profile trimming, and the tooth profile trimming calculation method to avoid out-of-line meshing is introduced by analyzing the meshing process of the gear pair. Finally, the vibration performance before and after trimming is discussed, and the validity of the gear trimming results is verified experimentally.

Dynamic modeling and vibration characteristics of drive motor-planetary mechanism

Drive motor-planetary mechanism excitation characteristic analysis

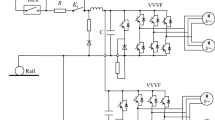
The powertrain system for tracked vehicles studied in this paper is shown in Fig. 1, which can be divided into two parts: the generator set and the EMT system. Among them, the EMT system consists of a “drive motor-planetary mechanism,” which is a left-right symmetric and electromechanical coupling system with double inputs and double outputs. The coupled planetary mechanism includes speed reduction planetary gearsets connected to the two motors, a power coupling planetary gearset, and gearshift planetary gearsets connected to the two driving wheels. Under off-road working conditions, the EMT system is subject to the external excitation of motors and the dynamic meshing forces of the complex coupled planetary mechanism, which results in large vibration impacts and low reliability. Thus, it is important to carry out dynamic modeling, vibration characteristics analysis, and optimization of the EMT system.

Fig. 1

Bilateral motor-coupled drive system structure sketch.

Analysis of motor electromagnetic torque and unbalanced magnetic pulling force

The excitions of the EMT system mainly come from the motor and planetary gearsets, including the motor electromagnetic torque, unbalanced magnetic pull force and the planetary gear meshing forces. The permanent magnet synchronous motor uses an inclined rotor slot structure to avoid the generation of cross currents and additional energy losses during operation caused by straight-arranged rotor slots. A cross-section is intercepted along the vertical direction of the motor shaft, and a two-coordinate system is established, as shown in Fig. 2, with the origin at the intersection of the motor cross-section and the coordinate axis. Along the z-direction of the perpendicular motor cross-section, the air-gap permeability and the three-phase fundamental wave magnetic kinetic potential are constantly changing; the former affects the magnetic field distribution strength, and the latter determines the motor rotating magnetic field direction and speed.

Fig. 2

Model of the motor with an inclined rotor slot structure: (a) static angular eccentricity schematic, (b) motor cross-section schematic, and (c) schematic diagram of tilting rotor microelement model.

The air gap magnetic kinetic potential of the motor is:

$$F\left( {\psi ,t} \right)={F_m}\cos \left( {{\omega _e}t - p\psi } \right)$$

(1)

Let the geometric eccentricities of the motor at every cross section along the axial direction be the same, then,

$$\delta \left( \psi \right) \approx {\delta _0} - r\cos (\psi - \gamma )$$

(2)

where ψ is the air gap direction angle and δ₀ is the average value of air gap length.

The unbalanced magnetic pull in the x-direction and y-direction can be expressed as³⁷:

$$\left\{ {\begin{array}{*{20}{c}} {{F_{ux}}={k_e}\left( {1+\frac{3}{2}\varepsilon _{e}^{2}} \right)x} \\ {{F_{uy}}={k_e}\left( {1+\frac{3}{2}\varepsilon _{e}^{2}} \right)y} \end{array}} \right.$$

(3)

where ${k_{\text{e}}}=\frac{1}{2}\frac{{{\mu _0}{R_p}l\pi F_{\varvec{m}}^{2}}}{{\delta _{0}^{3}}}$ is the electromagnetic stiffness coefficient, µ₀ is the magnetic permeability in vacuum, and ${\varepsilon _e}=r/{\delta _0}$ is the radial relative displacement of the motor rotor.Based on the model of the motor with an inclined rotor slot structure described in Fig. 2, the torque of the entire column microelement is calculated:

$$d{M_m} \approx d \times \sigma {R_r}d\psi dz=(j\cos \psi - i\sin \psi )z\sigma {R_r}\cos \theta d\psi dz$$

(4)

and.

$$d \approx (id\sin {\theta _c}\cos \psi +jd\sin {\theta _c}\sin \psi +kd\cos {\theta _c}),\sigma \approx \sigma (i\cos \psi +j\sin \psi )$$

.

where i, j and k are unit vectors corresponding to the directions of the three coordinate systems.ψ is the angle between vector d and the $ox$ axis, θ_c is the angle between vector d and the $oz$ axis, and d is the magnitude of vector d. The electromagnetic torque of the entire drive motor rotor can be obtained by integrating the cylindrical microelement along the circumferential direction,

$${M_m}=2{R_r}\cos \theta \int_{0}^{{l/2}} {zdz} \int_{0}^{{2\pi }} {\sigma (j\cos \psi - i\sin \psi )d\psi }$$

(5)

In practice, the angle θ of a motor is close to 0, and the cosine function can be approximated as 1. It should be noted that the axial position of the cross section in the middle of the rotor as shown in Fig. 2 is expressed as z = ± l/2. The magnitude of the torque in Eq. (5) is,

$${M_{\text{m}}}=\frac{{2{\mu _0}{R_p}\pi F_{\varvec{m}}^{2}}}{{\theta _{{}}^{2}}}H({\varepsilon _{\text{e}}})$$

(6)

where, $\cos \gamma =\frac{{{\theta _x}}}{\theta }$, $\sin \gamma =\frac{{{\theta _y}}}{\theta }$, $H({\varepsilon _{\text{e}}})=\sum\limits_{{n=1}}^{{11}} {a_{n}^{{}}}$, ${a_1}=\frac{{11}}{3}{\left( {\frac{{\sqrt {1 - \varepsilon _{\varvec{e}}^{2}} }}{{\varepsilon _{\varvec{e}}^{{}}}}} \right)^3}$, ${a_2}= - \arcsin \left( {\varepsilon _{\varvec{e}}^{{}}} \right)$,

$\begin{gathered} {a_3}= - \frac{5}{3}\frac{{{{\left( {1 - \varepsilon _{e}^{2}} \right)}^2}}}{{\varepsilon _{e}^{3}}},{a_4}=\frac{5}{3}\frac{{{{\left( {1 - \varepsilon _{e}^{2}} \right)}^2}}}{{{\varepsilon _e}}},{a_4}=\frac{5}{3}\frac{{{{\left( {1 - \varepsilon _{e}^{2}} \right)}^2}}}{{{\varepsilon _e}}},{a_5}=\frac{5}{3}\left( {1 - \varepsilon _{e}^{2}} \right){\varepsilon _e}, \hfill \\ {a_6}=\frac{{10}}{3}{\varepsilon _e},{a_7}= - \frac{5}{{{\varepsilon _e}}},{a_8}=\frac{3}{2}\ln \left( {\frac{{1+{\varepsilon _e}}}{{1 - {\varepsilon _e}}}} \right),{a_9}=\frac{{19}}{3}\frac{{\sqrt {1 - \varepsilon _{e}^{2}} }}{{{\varepsilon _e}}},{a_{10}}= - \frac{{11}}{{3\varepsilon _{e}^{3}}},{a_{11}}=\frac{5}{3}\frac{{\sqrt {1 - \varepsilon _{e}^{2}} }}{{\varepsilon _{e}^{3}}}. \hfill \\ \end{gathered}$

Analysis of nonlinear meshing excitation of planetary gears

Considering the effects of nonlinear factors such as time-varying meshing stiffness, tooth-side clearance, and manufacturing and installation errors during gear meshing^38,39, the time-varying meshing force and tooth-side clearance functions of the gears are shown in Eqs. (7) and (8):

$$\left\{ \begin{gathered} {F_{{\text{s}}i{\text{p}}ij}}={k_{{\text{s}}i{\text{p}}ij}}f\left( {{L_{{\text{s}}i{\text{p}}ij}},{b_{{\text{s}}i{\text{p}}ij}}} \right)+{c_{{\text{s}}i{\text{p}}ij}}{{\dot {L}}_{{\text{s}}i{\text{p}}ij}} \hfill \\ {F_{{\text{r}}i{\text{p}}ij}}={k_{{\text{r}}i{\text{p}}ij}}f\left( {{L_{{\text{r}}i{\text{p}}ij}},{b_{{\text{r}}i{\text{p}}ij}}} \right)+{c_{{\text{r}}i{\text{p}}ij}}{{\dot {L}}_{{\text{r}}i{\text{p}}ij}} \hfill \\ \end{gathered} \right.$$

(7)

$$f\left( {{L_{sipij}},{b_{sipij}}} \right)=\left\{ \begin{gathered} {L_{sipij}} - {b_{sipij}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {L_{sipij}}>{b_{sipij}} \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {{L_{sipij}}} \right| \leqslant {b_{sipij}} \hfill \\ {L_{sipij}}+{b_{sipij}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {L_{sipij}}<{b_{sipij}} \hfill \\ \end{gathered} \right.$$

(8)

where k_sipij, k_ripij, c_sipij and c_ripij are the mesh stiffness and mesh damping between the sun gear, ring gear, and the jth planet of the ith planetary gear set; L_sipij, b_sipij are the equivalent mesh deformation in the line of action and tooth side clearance between the sun gear, tooth ring, and the jth planet of the ith planetary gear set.

Dynamic modeling of drive motor-planetary mechanism system

The dynamic model of the drive motor-planet mechanism is shown in Fig. 3, where k_m is the mesh stiffness of the gear pair, k_t is the equivalent torsional stiffness of each connecting shaft, and k_b is the equivalent support stiffness of the bearings at each shaft segment; where c_m is the meshing damping of the gear pair, c_t is the equivalent torsional damping of each connecting shaft, and c_b is the equivalent support damping of the bearings at each shaft segment; the subscript m denotes the motor; R and L denote planetary gear set in the left and right, and the subscripts s, r, c, p stand for the sun gear, the ring gear, the carrier and the planet.For example, k_bmL denotes the equivalent support stiffness of the left motor rotor bearing, c_grp2 denotes the meshing damping between the ring gear and the planet, k_tmLs1 denotes the equivalent torsional stiffness of the connecting shaft between the left motor rotor and the sun gear, and c_ts1s2 denotes the equivalent torsional damping of the connecting shaft between the two sun gears.

Fig. 3

Nonlinear dynamics model of drive motor-planetary mechanism.

The torque and transverse forces on the connecting shaft are:

$$\left\{ \begin{gathered} {T_{hlqn}}={k_{{\text{t}}hlqn}}({\theta _{hl}} - {\theta _{qn}})+{c_{{\text{t}}hlqn}}({{\dot {\theta }}_{hl}} - {{\dot {\theta }}_{qn}}) \hfill \\ {F_{{\text{bx}}hlqn}}={k_{{\text{x}}hlqn}}({x_{hl}} - {x_{qn}})+{c_{{\text{x}}hlqn}}({{\dot {x}}_{hl}} - {{\dot {x}}_{qn}}) \hfill \\ {F_{{\text{by}}hlqn}}={k_{{\text{y}}hlqn}}({y_{hl}} - {y_{qn}})+{c_{{\text{y}}hlqn}}({{\dot {y}}_{hl}} - {{\dot {y}}_{qn}}) \hfill \\ \end{gathered} \right.$$

(9)

The differential equations for the vibration of the sun gear can be obtained as:

$$\left\{ \begin{gathered} {m_{{\text{s}}i}}{{\ddot {x}}_{{\text{s}}i}}={m_{{\text{s}}i}}{e_{{\text{Ms}}i}}\omega _{{{\text{s}}i}}^{2}\cos ({\omega _{{\text{s}}i}}t+{\gamma _{{\text{s}}i}}) - \sum\limits_{{j=1}}^{4} {{F_{{\text{sp}}ij}}\sin {\psi _{{\text{s}}ij}}+\sum\limits_{{w=1}}^{W} {{F_{{\text{bx}}hlqn}} - {k_{{\text{xs}}i}}{x_{{\text{s}}i}} - {c_{{\text{xsi}}}}{{\dot {x}}_{{\text{s}}i}}} } \hfill \\ {m_{{\text{s}}i}}{{\ddot {y}}_{{\text{s}}i}}={m_{{\text{s}}i}}{e_{{\text{Ms}}i}}\omega _{{{\text{s}}i}}^{2}\sin ({\omega _{{\text{s}}i}}t+{\gamma _{{\text{s}}i}})+\sum\limits_{{j=1}}^{4} {{F_{{\text{sp}}ij}}\cos {\psi _{{\text{s}}ij}}+\sum\limits_{{w=1}}^{W} {{F_{{\text{by}}hlqn}} - {k_{{\text{ys}}i}}{y_{{\text{s}}i}} - {c_{{\text{ys}}i}}{{\dot {y}}_{{\text{s}}i}}} } \hfill \\ {J_{{\text{s}}i}}{{\ddot {\theta }}_{{\text{s}}i}}= - \sum\limits_{{j=1}}^{4} {{F_{{\text{sp}}ij}}{R_{{\text{s}}i}}+\sum\limits_{{w=1}}^{W} {{T_{hlqn}}} } \hfill \\ \end{gathered} \right.$$

(10)

The differential equations for the vibration of the ring gear are:

$$\left\{ \begin{gathered} {m_{ri}}{{\ddot {x}}_{ri}}={m_{ri}}{e_{Mri}}\omega _{{ri}}^{2}\cos ({\omega _{ri}}t+{\gamma _{ri}})+\sum\limits_{{j=1}}^{4} {{F_{rpij}}\sin {\psi _{rij}}+\sum\limits_{{w=1}}^{W} {{F_{bxhlqn}} - {k_{xri}}{x_{ri}} - {c_{xri}}{{\dot {x}}_{ri}}} } \hfill \\ {m_{ri}}{{\ddot {y}}_{ri}}={m_{ri}}{e_{Mri}}\omega _{{ri}}^{2}\sin ({\omega _{ri}}t+{\gamma _{ri}}) - \sum\limits_{{j=1}}^{4} {{F_{rpij}}\cos {\psi _{rij}}+\sum\limits_{{w=1}}^{W} {{F_{byhlqn}} - {k_{yri}}{y_{ri}} - {c_{yri}}{{\dot {y}}_{ri}}} } \hfill \\ {J_{ri}}{{\ddot {\theta }}_{ri}}=\sum\limits_{{j=1}}^{4} {{F_{rpij}}{R_{ri}}+\sum\limits_{{w=1}}^{W} {{T_{hlqn}}} } \hfill \\ \end{gathered} \right.$$

(11)

The differential equations for the vibration of the carrier are:

$$\left\{ \begin{gathered} {m_{{\text{c}}i}}{{\ddot {x}}_{{\text{c}}i}}={m_{{\text{c}}i}}{e_{{\text{Mc}}i}}\omega _{{{\text{c}}i}}^{2}\cos {\psi _{{\text{c}}i}}+\sum\limits_{{j=1}}^{4} {{F_{{\text{xp}}ij}}\cos {\psi _{{\text{p}}ij}} - \sum\limits_{{j=1}}^{4} {{F_{{\text{yp}}ij}}\sin {\psi _{{\text{p}}ij}}} } \hfill \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}+\sum\limits_{{w=1}}^{W} {{F_{{\text{bx}}hlqn}}} - {k_{{\text{yc}}i}}{x_{{\text{c}}i}} - {c_{{\text{yc}}i}}{{\dot {x}}_{{\text{c}}i}} \hfill \\ {m_{{\text{c}}i}}{{\ddot {y}}_{{\text{c}}i}}={m_{{\text{c}}i}}{e_{{\text{Mc}}i}}\omega _{{{\text{c}}i}}^{2}\sin {\psi _{{\text{c}}i}}+\sum\limits_{{j=1}}^{4} {{F_{{\text{xp}}ij}}\sin {\psi _{{\text{p}}ij}}+\sum\limits_{{j=1}}^{4} {{F_{{\text{yp}}ij}}\cos {\psi _{{\text{p}}ij}}} } \hfill \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}+\sum\limits_{{w=1}}^{W} {{F_{{\text{by}}hlqn}}} - {k_{{\text{c}}i}}{y_{{\text{c}}i}} - {c_{{\text{yc}}i}}{{\dot {y}}_{{\text{c}}i}} \hfill \\ {J_{{\text{c}}i}}{{\ddot {\theta }}_{{\text{c}}i}}= - \sum\limits_{{j=1}}^{4} {{F_{{\text{sp}}ij}}{R_{{\text{s}}i}} - \sum\limits_{{j=1}}^{4} {{F_{{\text{rp}}ij}}{R_{{\text{r}}i}}} +\sum\limits_{{w=1}}^{W} {{T_{hlqn}}} } \hfill \\ \end{gathered} \right.$$

(12)

The differential equations for the vibration of the jth planet are:

$$\left\{ \begin{gathered} {m_{{\text{p}}ij}}{{\ddot {x}}_{{\text{p}}ij}}={m_{{\text{p}}ij}}{e_{{\text{Mp}}ij}}\omega _{{{\text{p}}ij}}^{2}\cos {\psi _{{\text{p}}ij}}+({F_{{\text{sp}}ij}}+{F_{{\text{rp}}ij}})\sin \alpha +{m_{{\text{p}}ij}}\omega _{{{\text{c}}i}}^{2}{x_{{\text{p}}ij}} \hfill \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}+2{m_{{\text{p}}ij}}{\omega _{{\text{c}}i}}{x_{{\text{p}}ij}} - \sum\limits_{{j=1}}^{4} {{F_{{\text{xp}}ij}}\cos {\psi _{{\text{p}}ij}}} \hfill \\ {m_{{\text{p}}ij}}{{\ddot {y}}_{{\text{c}}i}}= - {m_{{\text{p}}ij}}{e_{{\text{Mp}}ij}}\omega _{{{\text{p}}ij}}^{2}\sin {\psi _{{\text{p}}ij}} - ({F_{{\text{sp}}ij}} - {F_{{\text{rp}}ij}})\cos \alpha +{m_{{\text{p}}ij}}\omega _{{{\text{c}}i}}^{2}{y_{{\text{p}}ij}} \hfill \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} - 2{m_{{\text{p}}ij}}{\omega _{{\text{c}}i}}{y_{{\text{p}}ij}} - \sum\limits_{{j=1}}^{4} {{F_{{\text{yp}}ij}}\cos {\psi _{{\text{p}}ij}}} \hfill \\ {J_{{\text{p}}ij}}{{\ddot {\theta }}_{{\text{p}}ij}}={F_{{\text{sp}}ij}}{R_{{\text{sp}}ij}} - {F_{{\text{rp}}ij}}{R_{{\text{rp}}ij}} \hfill \\ \end{gathered} \right.$$

(13)

Dynamic characterization of drive motor-planetary mechanism

Inherent vibration characteristics

Let the internal and external excitations of the system be 0, and neglect the gear tooth side clearance, damping, inertia effect, and time-varying meshing stiffness, the simplified linear free vibration equation of the system is obtained as follows:

$${\mathbf{M\ddot {X}}}+({{\mathbf{\bar {K}}}_{\mathbf{m}}}+{{\mathbf{K}}_{\mathbf{t}}}+{{\mathbf{\bar {K}}}_{\mathbf{b}}}){\mathbf{X}}=0$$

(14)

where ${\mathbf{\ddot {X}}}$, ${\mathbf{\dot {X}}}$ and X are generalized coordinate vectors, M is the generalized mass matrix, ${{\mathbf{\bar {K}}}_{\mathbf{m}}}$ is the average gear meshing stiffness matrix of the system, ${{\mathbf{K}}_{\mathbf{t}}}$ is the connector connection stiffness matrix, and ${{\mathbf{\bar {K}}}_{\mathbf{b}}}$ is the support stiffness matrix.The system eigenvalue equation is as follows:

$$\omega _{n}^{2}{\mathbf{M}}{{\mathbf{\varphi }}_{\mathbf{n}}}=({{\mathbf{\bar {K}}}_{\mathbf{m}}}+{{\mathbf{K}}_{\mathbf{t}}}+{{\mathbf{\bar {K}}}_{\mathbf{b}}}){{\mathbf{\varphi }}_{\mathbf{n}}}$$

(15)

where ω_n is the nth natural frequency, φ_n is the nth mode shape, and the two are collectively referred to as the nth-order intrinsic mode.

According to the system electromechanical coupled dynamics equations, the generalized coordinate vector in Eq. (14) can be expressed as Eq. (16), and the vibration velocity and vibration acceleration vectors can be obtained by yielding their first-order and second-order derivatives, respectively.

$$\begin{gathered} {\mathbf{X}}=[{x_{{\text{s}}1}}{\text{ }}{y_{{\text{s}}1}}{\text{ }}{\theta _{{\text{s}}1}}{\text{ }}{x_{{\text{r}}1}}{\text{ }}{y_{{\text{r}}1}}{\text{ }}{\theta _{{\text{r}}1}}{\text{ }}{x_{{\text{c}}1}}{\text{ }}{y_{{\text{c}}1}}{\text{ }}{\theta _{{\text{c}}1}}{\text{ }}{x_{{\text{p11}}}}{\text{ }}{y_{{\text{p}}11}}{\text{ }}{\theta _{{\text{p}}11}} \ldots {x_{{\text{p14}}}}{\text{ }}{y_{{\text{p}}14}}{\text{ }}{\theta _{{\text{p}}14}} \ldots \hfill \\ {\text{ }}{x_{{\text{pg24}}}}{\text{ }}{y_{{\text{pg24}}}}{\text{ }}{\theta _{{\text{pg24}}}} \ldots {x_{{\text{mA}}}}{\text{ }}{y_{{\text{mA}}}}{\text{ }}{\theta _{{\text{mA}}}}{\text{ }}{x_{{\text{mB}}}}{\text{ }}{y_{{\text{mB}}}}{\text{ }}{\theta _{{\text{mB}}}}{]^{\text{T}}} \hfill \\ \end{gathered}$$

(16)

Equation (15) is solved to obtain each order of the system’s natural frequency and its corresponding mode shape. The system vibration mode vectors are summarized as shown in Fig. 4 for six typical modes. It should be noted that mode #1 is the rigid body mode; mode #2 is the coupled torsional vibration mode of the motor-planetary gear system where the transverse vibrations are nearly zeros; mode #3 is the coupled transverse vibration mode of the motor-planetary gear system where the torsional vibrations are nearly zeros; mode #4 is the torsional vibration mode of the planetary gear system where the transverse vibrations are nearly zeros; mode #5 is the transverse vibration mode of the planetary gear system where the torsional vibrations are nearly zeros; mode #6 is the vibration mode of the planets where the vibrations of all the other rotating members are nearly zeros.

Fig. 4

Typical vibration modes of electromechanical combined drive systems.

Figure 5 represents the relationship between the motor speed and the natural frequencies of the system, which is linearly related to the vehicle speed when skidding is not considered or when the slip rate is low. The motor speed corresponding to each intersection point is shown in Table 1.

Fig. 5

Schematic diagram of resonance speed point.

Table 1 Resonance speed table.

The resonant speeds in Table 1 are grouped, and the corresponding vehicle speeds are calculated as shown in Table 2. It can be noticed that the range of the normal operating speed of the system covers the resonance points. Therefore, prolonged operation in these speed ranges should be avoided as much as possible to shorten the resonance duration during actual driving.

Table 2 Resonance RPM corresponding speed table.

Forced vibration characteristics

The speed range of the motor is 0–12000 r/min, and the output range of the motor torque is 0–920 N·m. In the analysis of the variable speed and load operation conditions, the motor speed is adjusted from 1000 r/min to 12000 r/min with a step of 500 r/min; load torque increase from 10 to 100% of full load.

As shown in Fig. 6, the maximum values of the Root Mean Square (RMS) values of vibration acceleration (m/s2) of each component under the conditions of variable speed and load are 60, 150, 150, 600, 300, and 150, and the RMS values of vibration acceleration show a tendency to increase with the rise of speed and load.

Fig. 6

Surface plot of vibration acceleration of each rotating component.

In summary, it can be seen that the vibration acceleration of the motor is relatively small because the vibration acceleration of the motor is mainly affected by the rotational frequency of the motor, and the rotor inertia of the motor is large. For the reduction and gearshift planetary gearsets, the vibration acceleration of the sun gear is larger than that of the carrier because of the higher rotational speed of the sun gear. For the coupling planetary gearsets, the vibration acceleration of the carrier is relatively large because the two groups of coupling planetary components are connected and the support stiffness is insufficient. The carrier of the coupled gearset is connected to the sun gear of the gearshift gearset. Thus the vibration accelerations of these two components are close. In the planetary gear system, the factor that has the greatest influence on the vibration acceleration of each component is the time-varying gear meshing excitation. Therefore, it is necessary to study gear meshing impact and utilize the method of gear trimming to improve the system vibration characteristics and enhance the dynamic performance of the system.

Optimization of vibration performance of drive motor-planet mechanism based on tooth profile trimming

Tooth profile trimming is mainly carried out to avoid out-of-line meshing by removing the interfering portion of the gear generated during meshing and is usually carried out on the tooth tip. As shown in Fig. 7, there are three elements to be determined for tooth profile trimming: the amount of trimming on the tooth tip, the length of trimming, and the tooth trimming curve. The amount of trimming on the tooth tip is shown by C_a in Fig. 7, which represents the amount of overlap between the addendum circles of the driven gear and the driving gear when the tooth profile of the driving gear just coincides with the theoretical meshing point A. The length of the trimming curve is shown by L_a in the figure. For the linear trimming curve, it represents the distance from the tooth tip of the driven gear to the intersection point between the tooth profile of the driven gear and the tangent line of the driving gear at point A.

Fig. 7

Figure of the gear profile modification to avoid out-of-line meshing.

Amount of trimming on the tooth tip

The state in which the gear teeth are about to enter the mesh zone is shown in Fig. 8. Ideally, the tooth tip of the driven gear should be located at the meshing start point A. Assume that the driving gear rotates about an angle of θ with respect to the initial position, the driven gear rotates about an angle of θʹ, and the interference between the teeth of the driving gear and the teeth of the driven gear is formed as shown in Fig. 8. θ′o2O₂.

Fig. 8

Top of tooth circumferential trimming amount.

The amount of circular interference at the tooth tip of the driven gear is the amount of circumferential modification of the tooth tip of the driven gear, C_a:

$${C_{a2}}={R_{a2}} \cdot \theta ^{\prime}={R_{a2}}\left( {\frac{{{F_g}}}{{{K_g}{R_{b2}}}}+\frac{{{f_{pt1}} \cdot \cos \left( \alpha \right)+{f_{pt2}} \cdot \cos \left( \alpha \right)}}{{{R_{b2}}}}} \right)$$

(17)

where $\alpha$ is the pressure angle, ${R_{a2}}$ is the radius of the addendum circle of the driven gear, and ${R_{b2}}$ is the base radius of the driven gear. F_g is the gear tooth meshing force, and K_g is the single tooth meshing stiffness of the first pair of teeth. ${f_{pt1}}$ and ${f_{pt2}}$ are the individual tooth pitch tolerances for the driving and driven gears, respectively.Similarly, the circumferential tooth profile of the driving gear is trimmed as follows:

$${C_{a1}}={R_{a1}} \cdot \theta ={R_{a1}}\left( {\frac{{{F_g}}}{{{K_g}{R_{b1}}}}+\frac{{{f_{pt1}} \cdot \cos \left( \alpha \right)+{f_{pt2}} \cdot \cos \left( \alpha \right)}}{{{R_{b1}}}}} \right)$$

(18)

where ${R_{a1}}$ is the radius of the addendum circle of the driving gear and ${R_{b1}}$ is the base radius of the driving gear. It should be noted that Eqs. (17), (18) also apply to the internal gear pair.

Trim curve and trim length

Determination of the trim curve and trim length of the external gear pair

A local Cartesian coordinate system ${x_2}A{y_2}$is first established as shown in Fig. 9, and the transformation between it and the global coordinate system $x{o_1}y$ is:

$$\left\{ {\begin{array}{*{20}{c}} {{x_2}=x \cdot \cos \left( {{\alpha _2}} \right) - y \cdot \sin \left( {{\alpha _2}} \right)+{O_1}A \cdot \sin ({\alpha _1}+{\alpha _2})} \\ {{y_2}=y \cdot \cos \left( {{\alpha _2}} \right)+x \cdot \sin \left( {{\alpha _2}} \right)+{O_1}A \cdot \cos ({\alpha _1}+{\alpha _2})} \end{array}} \right.$$

(19)

where ${\alpha _2}={\alpha _{a2}} - \alpha ^{\prime}$, $\alpha ^{\prime}$ is the actual meshing angle of the gear pair, and ${\alpha _{a2}}$ is the pressure angle at the addendum circle of gear 2 (i.e. the driven gear).

The normal to the driving tooth profile at point A is co-linear with the meshing line, and the slope ${k_2}$ of the trim curve in the local coordinate system ${x_2}A{y_2}$ is:

$${k_2}=\frac{{k+\tan \left( {{\alpha _2}} \right)}}{{1 - k \cdot \tan \left( {{\alpha _2}} \right)}}$$

(20)

The equation of this trimmed curve in the local coordinate system ${x_2}A{y_2}$ is:

$${y_2}={k_2}{x_2}$$

(21)

A polar coordinate system is established at point C of the driven gear tooth profile which is the start point of the tooth involute profile to be trimmed and the counterclockwise direction is defined as the positive direction. For any point D on the trimmed curve, the polar coordinate parametric equation of point D is:

$$\left\{ {\begin{array}{*{20}{c}} {{r_{D2}}={R_{b2}}/\cos \left( {{\alpha _{D2}}} \right)} \\ {{\beta _{D2}}=\tan \left( {{\alpha _{D2}}} \right) - {\alpha _{D2}}} \end{array}} \right.$$

(22)

Fig. 9

External gearing trimming.

where ${\alpha _{D2}}$ is the pressure angle corresponding to point D on gear 2.The transformation relationship between the polar coordinate system and the local coordinate system X₂Ay₂ is:

$$\left\{ {\begin{array}{*{20}{c}} {{x_2}= - {r_{D2}} \cdot \sin \left( {\theta ^{\prime}+{\beta _{a2}} - {\beta _{D2}}} \right)} \\ {{y_2}= - {r_{D2}} \cdot \cos \left( {\theta ^{\prime}+{\beta _{a2}} - {\beta _{D2}}} \right)+{R_{a2}}} \end{array}} \right.$$

(23)

where ${\beta _{a2}}$ is the maximum expansion angle of the involute tooth profile of gear 2.

Combining Eqs. (21) and (23) gives ${\beta _{D2}}$, which in turn gives the trimmed length of gear 2:

$${L_{a2}}={R_{a2}} - {r_{D2}} \cdot \cos \left( {{\beta _2} - {\beta _{D2}}} \right)$$

(24)

where${\beta _2}$is the half tooth angle of gear 2 and z₂ is the number of teeth of the driven gear.Similarly, the trim length of gear 1 (i.e. the driving gear) can be derived:

$${L_{a1}}={R_{a1}} - {r_{D1}} \cdot \cos \left( {{\beta _1} - {\beta _{D1}}} \right)$$

(25)

where${\beta _1}$ is the half tooth angle of gear 1 and ${z_1}$ is the number of teeth of the driving gear.

Determination of the trimming curves for the internal gear pair

The trimming curve of the internal gear pair is determined in the same way as that of the external meshing gear. ${r_1},{r_{a1}},{r_{b1}}$ represent the radii of the pitch circle, the addendum circle and the base circle of the driving gear respectively; ${r_2},{r_{a2}},{r_{b2}}$ represent the radii of the pitch circle, the addendum circle and the base circle of the driven gear respectively Then the length of trimming is calculated as,

$${L_{a2}}={r_{{O_2}D}} \cdot \cos \left( {\frac{\pi }{{2{z_2}}}+inv\left( {arccos\left( {\frac{{{r_{{b_2}}}}}{{{r_{{O_2}D}}}}} \right)} \right) - inv\left( {arccos\left( {\frac{{{r_{{b_2}}}}}{{{r_2}}}} \right)} \right)} \right) - {r_{a2}}$$

(26)

Similarly, the trim length of the driving gear can be obtained as:

$${L_{a1}}={r_{a1}} - {r_{{O_1}D}} \cdot \cos \left( {\frac{\pi }{{2{z_1}}} - inv\left( {arccos\left( {\frac{{{r_{{b_1}}}}}{{{r_{{O_1}D}}}}} \right)} \right)+inv\left( {arccos\left( {\frac{{{r_{{b_1}}}}}{{{r_1}}}} \right)} \right)} \right)$$

(27)

Simulation analysis considering tooth profile trimming

In this paper, the gear precision is selected as grade 6. According to the basic parameters of the planetary mechanism, including the reduction gearset, coupling gearset, and gearshift gearset as shown in Fig. 1, the trimming amounts of each component of the planetary gearset are calculated, and simulation analysis of the vibration acceleration of each component before and after trimming are carried out. The gear parameters of the planetary gearsets, individual tooth pitch deviation, and maximum trimming amount are shown in Table 3.

Table 3 Gear parameters, pitch deviations and trimming amounts.

The simulation condition is set to 7500 r/min and 60% of full load, and the time and frequency domain characteristics before and after profile trimming are simulated and compared.

Analysis of the results of the planetary gearsets

The time-domain characteristics of vibration acceleration before and after trimming the profile of each gear of the reduction gearset are shown in Fig. 10. It can be noticed that compared to results before trimming, the amplitudes of the time-history vibration signal of each rotating component reduce and the mesh impacts are alleviated after trimming.

Fig. 10

Time-domain characteristics of vibration acceleration before and after trimming of each gear of the reduction gearset.

The frequency domain characteristics of the vibration acceleration of each gear of the reduction gearset before and after trimming are shown in Fig. 11. It can be noticed that the vibration energy is mainly concentrated on the mesh frequency f_m5 of the reduction gearset and its harmonics, and there are also densely-distributed sidebands around these mesh frequency components. Compared to results before trimming, the amplitudes at these major mesh frequency components reduce after trimming. The spectral pattern of the vibration response of the gear after trimming shows that the position of the main harmonic sub-frequency does not move, but there is a change in the amplitude; the amplitude at the f_m5 decreases, the amplitude at the 2f_m5 increases, and there is a new crest, which is mainly the change in the load of the gear after trimming, resulting in the distribution of the vibration energy being more centralized.

Fig. 11

The frequency domain characteristics of the vibration acceleration of each gear of the reduction gearset before and after trimming.

The time-domain characteristics of the vibration acceleration before and after trimming of each gear of the coupling gearset are shown in Fig. 12. It can be noticed that compared to results before trimming, the amplitudes of the time-history vibration signal of each rotating component reduce and the mesh impacts are alleviated after trimming.

Fig. 12

The time-domain characteristics of the vibration acceleration before and after trimming of each gear of the coupling gearset.

The frequency domain characteristics of the vibration acceleration before and after trimming of each gear of the coupling gearset are shown in Fig. 13. It can be noticed that the vibration energy is mainly concentrated on the mesh frequency f_m1 of the coupling gearset and its harmonics. Compared to results before trimming, the amplitudes at these major mesh frequency components reduce after trimming.

Fig. 13

The frequency domain characteristics of the vibration acceleration before and after trimming of each gear of the coupling gearset.

The time-domain characteristics of the vibration acceleration of each gear of the gearshift gearset before and after trimming are shown in Fig. 14. It can be noticed that compared to results before trimming, the amplitudes of the time-history vibration signal of each rotating component reduce and the mesh impacts are alleviated after trimming.

Fig. 14

The time-domain characteristics of the vibration acceleration of each gear of the gearshift gearset before and after trimming.

The frequency domain characteristics of the vibration acceleration of each gear of the gearshift gearset before and after reshaping are shown in Fig. 15. It can be noticed that the vibration energy is mainly concentrated on the mesh frequency f_m1 of the gearshift gearset and its harmonics, and there are also densely-distributed sidebands around these mesh frequency components. Compared to results before trimming, the amplitudes at these major mesh frequency components reduce after trimming.

Fig. 15

The frequency domain characteristics of the vibration acceleration of each gear of the gearshift gearset before and after trimming.

The changes in the peak values of the time-domain signals before and after trimming of the three planetary gearsets are shown in Table 4. The results show that the vibration acceleration of each component decreases to different degrees.

Table 4 Time-domain peaks before and after reshaping.

As can be seen from Table 4; Figs. 10 and 12, and 14, the amplitudes of the time-domain vibrations for the sun gear, carrier, and ring gear after profile trimming for all gearsets are smaller than those before trimming. The vibrations of the sun gear generally reduce more after trimming compared to those of the carrier and the ring gear. This is possible because the rotating speed of the sun gear is much higher and the profile trimming is more effective to the sun gear due to the higher mesh excitation. As can be seen from Figs. 11 and 13, and 15, the vibration accelerations of the sun gear, carrier, and ring gear of the reduction gearset are mainly concentrated on the mesh frequencies and their harmonics in the frequency domain. This demonstrates that the mesh excitation plays a pivotal role in the vibrations of the planetary gearset. The amplitudes at values at these mesh frequency components reduce obviously when profile trimming is applied. Thus, the proposed profile trimming method is effective in reducing the vibration of the planetary gearset.

Comparative analysis in terms of RMS values

For the time domain values of vibration acceleration from the simulation results, the vibration acceleration data is analyzed using the RMS as shown in Eq. (28):

$$a=\sqrt {\frac{1}{n}\sum {a_{j}^{2}} }$$

(28)

where a_j is the vibration acceleration data at the jth sampling point and n is the number of sampling points.

The RMS values of the vibration acceleration of each member of the three planetary gearsets were calculated, and the comparisons before and after the modification are shown in Fig. 16.

Fig. 16

Comparison of vibration acceleration RMS before and after profile trimming of each component.

From Fig. 16, it can be seen that for the reduction and gearshift gearsets, the decrease ratio of the sun gear is the largest, seconded by the carrier and the ring gear. However, for the coupling gearset, the carrier has the largest decrease ratio, seconded by the sun gear and the ring gear. These phenomena are consistent with the results of Sect “Analysis of the results of the planetary gearsets”.

Bench test for the vibration optimization of drive motor-planet mechanism based on tooth profile trimming

A vibration test rig of the drive motor-planet mechanism is built as shown in Figs. 17 and 18. The power motor is used to simulate the engine characteristics and to drag the generator to generate electricity. The DC power supply is connected to the DC bus to supply power and system voltage stabilization when the engine starts. The left and right dynamometers are used to simulate the road excitations.

Fig. 17

Schematic diagram of the test bench.

Fig. 18

Physical drawing of the test bench.

The test condition is the same as the simulation condition described in Sect “Optimization of vibration performance of drive motor-planet mechanism based on tooth profile trimming”. Triaxial accelerometers are attached to the bearing housing to measure the vibrations of each rotating member of the reduction gearsets in the X (red), Y (green), and Z (blue) directions. For the rotating parts of the driveline studied in this paper, only the X direction can be taken. The time and frequency domain vibration acceleration data of the sun gear, carrier, and ring gear of the reduction gearset obtained from the test before and after tooth profile trimming are shown in Fig. 19.

Fig. 19

Test data of each rotating member of the reduction gearset before and after trimming.

In the time domain analysis, the maximum magnitudes of vibration acceleration before and after trimming of the reduction gearset components are shown in Table 5.

Table 5 Test time-domain data before and after trimming of each part of the reduction gearset.

In the frequency domain analysis, the radial vibration of the sun gear is mainly dominated by the meshing frequency f_m1 and its harmonics nf_m1(n = 1,2…), which is consistent with the simulated results shown in the previous section. As can be seen from Fig. 19 the amplitudes of f_m1, f_m2, f_m3 and f_m5 decrease significantly after the sun gear is trimmed. After the planetary carrier is trimmed, except for the f_m2, f_m3 and f_m4, the amplitudes of other major frequency components are obviously reduced. The amplitudes of f_m2, f_m4 and f_m6 are obviously reduced after the ring gear is trimmed. Comparative analysis of the vibration acceleration test results before and after tooth profile trimming of the above planetary gearset verifies the effectiveness of the modification method proposed in Sect “Optimization of vibration performance of drive motor-planet mechanism based on tooth profile trimming”.

Combined with Sect “Dynamic modeling and vibration characteristics of drive motor-planetary mechanism”, the comparisons between the test results and simulation results before and after trimming the tooth profile of each member of the reduction gearset are shown in Fig. 20. It can be seen that the test values agree well with the simulation values, and the overall deviation is about 15%.

Fig. 20

Comparison between test results and simulation results.

Conclusions

In this paper, the dynamic model of an EMT for the heavy-duty tracked vehicle is established considering the multi-source excitations to study the intrinsic characteristics and forced vibration characteristics. A vibration optimization strategy based on tooth profile trimming is proposed to avoid out-of-line meshing and reduce system components’ vibration. The vibration performance before and after tooth profile trimming is discussed, and a test rig of the drive motor-planet mechanism is built to verify the validity of the proposed tooth profile trimming method. The major conclusions of this study include,

• (1) The vibration acceleration of each component under variable speed and load conditions was analyzed. The results show that the most influential factor on the vibration acceleration of each component of the planetary mechanism is the time-varying meshing excitation of the gears.

• (2) The vibration characteristics of each part of the system before and after trimming are simulated and analyzed. The results show that the peak values of the vibration acceleration of gears with trimming are reduced up to 32.9% in the time domain, the amplitudes at the mesh frequency components are also effectively reduced, and the root mean square value is reduced up to 31%.

• (3) The vibration acceleration test experiments are conducted before and after gear trimming. The results show that the maximum magnitude of vibration acceleration is reduced by 35% after the planetary mechanism is trimmed, and the deviation between the test value and the simulation value is about 15%.