Introduction

Precise clock synchronization signal distribution is of the utmost importance in several applications (financial transactions, classical communications, research activities, etc.)1,2 and the infrastructures for accurate time dissemination are considered as a part of the critical digital infrastructures that our society must protect.3 In the last years, the need to make critical digital infrastructures resilient to cyberattacks has been increased. One of the challenges is to establish network security safe against the development of the quantum computer (QC) that is rapidly scaling up the number of qubits.4 QC could potentially break current cryptographic systems, since their security is related only to computational complexity.5,6

Among quantum communication protocols, Quantum Key Distribution (QKD) is currently the most advanced technology for securely sharing cryptographic keys with security levels independent of computational power.7,8,9,10 However, other promising approaches, such as Quantum Secure Direct Communication (QSDC),11,12,13 are also emerging. As a result, quantum communication infrastructures are being developed worldwide to support these advancements. The consideration of QKD systems and networks from use cases has already started14,15,16,17,18 and QKD metropolitan networks have been demonstrated all over the world;19,20,21 in the UK, metropolitan quantum networks have been built by the Quantum Communications Hub in Cambridge and Bristol, connected by a long connection passing from London.22 Quantum digital signatures were demonstrated in the NICT metro network in Tokyo.23 In China, a \(2000\,\hbox {km}\) backbone connects Beijing and Shanghai, supplemented by ground-satellite QKD that exploits Micius satellite to extend QKD to global distances.24,25

The European Union (EU) is strongly pushing in this direction by signing with all the 27 member states a declaration to work together for the realization of the European Quantum Communication Infrastructure (EuroQCI),26 that aims to realize quantum communication networks in all the EU countries. Within EuroQCI initiative, the italian project QUID (Quantum Italy Deployment)27 proposes to start the deployment of the Italian part of the EU network by spreading QKD systems and networks in different cities, realizing several Quantum Metropolitan Area networks (QMANs). QMANs will be all connected by common fiber backbone, the Italian Quantum Backbone (IQB). This infrastructure was realized by the Italian Metrological Institute INRiM28 and hosts the fiber-based dissemination service of an optical ultra-stable radiation referenced to the national primary frequency standard, which has an accuracy of \(2 \cdot 10^{-16}\),29 and implements the Italian time transfer using the White Rabbit technique,30 an improved version of the Precise Time Protocol (PTP) first defined by IEEE Standard 1588-200829 (see Supplemental Material). PTP technique can achieve accuracy of the order of few hundred nanoseconds. White Rabbit PTP (WR-PTP) was developed at CERN and incorporated in the PTP revision (IEEE 1588 201931): it allows synchronizing distant clocks at nanosecond level or even better in properly designed and calibrated network architectures. A detailed description of the basic WR scheme is provided in the Supplemental Material. For critical applications, the protection of such infrastructures by sharing encrypted WR-PTP signals between two parties might result necessary to avoid attacks tailored on the clock synchronization or time information between parties. However, the WR-PTP is a standard protocol not designed for being easily encrypted. Furthermore, the common electronics devices for WR-PTP transmissions do not easily allow for internal modification of their input or output signals.

Here we show an easy and reliable technique for encrypting WR-PTP transmissions by using QKD, realizing the QKD-protected time dissemination service exploiting the emergent Italian EuroQCI network. The sharing of the same infrastructure for precise time dissemination and QKD services open the way to unique opportunity to simultaneously protect and distribute time information.

To demonstrate the feasibility of our technique, we share encrypted WR-PTP in a real-world scenario between two nodes of the IQB, specifically in the Rome QMAN (see Fig. 1)

Fig. 1
figure 1

Schematic representation of the Italian Quantum Backbone showing the main links. The inset shows the fiber link, inside the city of Rome, on which our technique was experimentally carried out. The maps in this figure were generated using the free OpenStreetMap software, released under the Creative Commons Attribution-ShareAlike 2.0 (CC BY-SA 2.0) license.

Full size image

The work demonstrates the possibility to offer a quantum safe critical service that can be easily implemented and extended to the entire IQB and to all the QMANs in Italy, providing a capillar dissemination of a QKD protected time service.

Results

Encrypted WR-PTP

We consider QKD and WR-PTP transmission in the end-to-end infrastructure that connects IQB nodes in INRiM and Thales Alenia Space Italy (TASI) premises, both in Rome. INRiM is the Alice (A) node, while Bob (B) node is in TASI. A and B host both QKD and WR-PTP equipment and signals are transmitted in the same optical fiber link.

To demonstrate the feasibility of the secure time dissemination, we compare the signals from an high-performance external clock traceable to the Italian time scale UTC(IT), placed in B node, with itself after a round trip, where encryption in A and decryption in B with QKD occur (see Fig. 2).

Fig. 2
figure 2

A schematic representation of the secure time dissemination experiment: a clock reference from Site B is sent to Site A via WR-PTP, encrypted with a QKD-generated key, and returned to Site B as encrypted WR-PTP. At Site B, the signal is decrypted and compared to the original clock reference for verification.

Full size image

The clock reference is an active hydrogen Maser clock (H-Maser) that provides a one pulse per second (1PPS) reference time signal and a frequency signal of \(10\,\hbox {MHz}\). During a standard WR-PTP transmission, A and B share both the time and the frequency reference, coded by the WR-PTP protocol. Sharing the same reference, it is possible to evaluate the real performances of the time encrypted dissemination. The A WR-PTP device, locked to an external frequency reference, converts phase variations of the frequency in temporal delays of the WR-PTP messages exchanged between A and B nodes. If the frequency signal is shifted by a random phase, the time information signal in A and B will suffer of a random temporal delay \(\Delta t\), making impossible for B to estimate the time information present in A, and this is still true for an eventual eavesdropper. We adopt an easy way to encrypt WR-PTP transmission, by using the quantum distributed keys between A and B to generate a secret truly random phase. A and B exchange keys and store them in a local Key Management System (KMS) in A and B. The user in A selects a key, generates the phase shift, applies it to the \(10 \,\hbox {MHz}\) signal and sends the encrypted time signal to B; by using the same key, B is able to locally compensate the phase shift by inserting an opposite phase, obtaining the time signal, synchronized to the clock present in A.

Fig. 3
figure 3

The experimental setup used for the encryption of the time signal with the QKD: at Site B, a maser generates a \(10\,\hbox {MHz}\) clock reference and a 1 PPS signal, which are transmitted to Site A via WR-PTP. At Site A, the WR-PTP signal is encrypted using a function generator with QKD-derived keys provided by the KMS. The encrypted WR-PTP signal is then sent back to Site B via the same classical channel. At Site B, the \(10\,\hbox {MHz}\) signal is decrypted using the “decoder” function generator, while a PPS generator is exploited to realize the 1PPS signal measured with TIC1. Analogously, TIC2 measures encrypted WR-PTP signals. The WR-PTP signals exchange and the classical communication of the QKD devices are multiplexed over the same classical channel, while the QKD quantum channel is used to securely exchange encryption keys, which are managed by the KMS at both sites.

Full size image

We implement the phase shift starting from a white-noise model.32

Since the shared key K is exchanged as an array of random hexadecimal numbers, we organise K in N pairs:

$$\begin{aligned} K = \{(k_1)_\textrm{HEX},\, \ldots ,\,(k_{2N})_\textrm{HEX}\} \end{aligned}$$
(1)

and for each pair we calculate the phase \(\phi _i\):

$$\begin{aligned} \phi _i=\frac{\left( k_{2i}k_{2i+1}\right) _{10}}{C}, \quad i\in [0,N-1] \end{aligned}$$
(2)

where the notation \((x)_{10}\) indicates the hexadecimal number x converted in decimal basis and C is a constant integer number introduced because, without loosing of generality, it is experimentally convenient to limit the White phase noise added to a maximum level, below \(2 \pi\).

Experimental setup

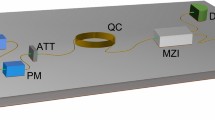
We implement our technique by using the experimental setup depicted in Fig. 3, that shows the architecture for both the quantum key distribution and encrypted time exchange.

The INRiM station hosts the sender part of the QKD system, while the receiver is hosted in TASI location, connected through a fiber link for a total distance of \(13\,\hbox {km}\). The link counts fibers where daily data traffic passes and two standard single-mode optical fibers dedicated to the experiment: one completely dedicated to the photons where the information on the key is encoded (Quantum channel) and one (Classical channel) used to exchange WR-PTP signal, QKD synchronization and classical data for QKD post-processing, by means of multiplexer devices (MUX/DEMUX). The Quantum channel needs a proper characterization to precisely estimate losses and level of background photons present in absence of QKD signal. The QKD modules used to generate and share the keys are the IDQuantique \(\hbox {Clavis}^3\) System, a discrete-variable QKD apparatus designed for research application that exploits two external single-photon detectors to perform key exchange. In our experiment, we used two standard free-running InGaAs/InP Single-Photon Avalanche Diodes (SPADs), operating around \(-50^{\circ }\hbox {C}\) with thermoelectric cooling, with \(20{\%}\) of detection efficiency and and dead time set to \(25\,{\mu }\hbox {s}\). The shared keys are stored and managed by means of local KMSs that can be access by users in A and B in a secure way. In order to test the technique, it is more convenient to use the H-maser present in B as the Master clock of the system. The Master clock of the experiment located in A is thus synchronized with a standard WR-PTP signal to the H-Maser. By doing so it is easier to analyze the timing uncertainty of the encrypted (and decrypted) transmission from A to B. As a matter of fact, the location where we physically install the Master clock is an arbitrary choice for this experiment.

Our WR-PTP network is based on WR-LEN mini switches produced by Seven Solutions. These devices can be configured as Master or Slave30 and allow to exchange WR-PTP traffic, as well as to set the 1PPS and \(10\,\hbox {MHz}\) physical signals as input or output.

To enhance its stability and accuracy, the Master switch internal oscillator can be synchronized to the 1PPS and the \(10\,\hbox {MHz}\) signal from an high-performance external clock. When the Master is connected to another WR-LEN via the network interface, this Slave WR-LEN replicates output signals of 1PPS and \(10\,\hbox {MHz}\) of the external high-performance clock connected to the Master.

In our round trip, the raw 1PPS signal from the Master WR-PTP in B (WR-LEN-GM B), synchronized with the H-Maser, is sent to the WR Slave in A (WR-LEN-SLAVE A).

A signal generator (“Encoder”) varies the phase of the \(10\,\hbox {MHz}\) signal of WR-LEN-SLAVE A with \(\phi\), calculated from the key K exchanged with QKD devices, according to Eq. 2; to account for the limits of our instruments, we set \(C = 4\), leading to a phase shift in the range \({0}^{\circ } \le \phi _i \le {63.75}^{\circ }\), corresponding to a maximum temporal delay \(\Delta t\) of about \(17.71\,\hbox {ns}\).

Without loss of generality, for each interval \(\Delta t\) we set the phase \(-\phi _i\) in A node and \(+\phi _i\) in B node. The signal generator provides an input to the WR Master in A (WR-LEN-GM A). In this way, the WR-PTP signal that the Master in A exchanges with the Slave in B is phase shifted of \(-\phi _i\); the result is that, after a round trip, the WR-LEN-SLAVE B clock (1PPS and \(10\,\hbox {MHz}\) signals) is no more synchronized to UTC(IT), due to the phase shift periodically (every 5 s) and randomly changed.

Then, the \(10\,\hbox {MHz}\) (encrypted) signal obtained from the WR-LEN-SLAVE B is sent to a second signal generator (“Decoder”) that compensates the phase shift, allowing to recover the original time signal exploiting the PPS generator. Both decrypted and encrypted signals are addressed to a Time Interval Counter (TIC): TIC1 and TIC2, respectively, for being compared to the original H-Maser time signal \(t_0\).

Before starting the QKD transmission, we evaluated the presence of background photons in the Quantum fiber; as a matter of fact, Classical and Quantum fibers are part of a bundle of optical fibers, and the presence of unwanted photons due to evanescent coupling from the Classical channel and from data traffic from the other fibers must be evaluated. Thus, we measured for \(24\,\hbox {h}\) the background photons present in the quantum fiber, monitoring any eventual behavior during all the day. We observed a spread distribution of about \((3500\,\div \,6500)\,\hbox {counts/s}\), probably due to the random data traffic. In our case, the intrinsic dark-count rate of the exploited SPAD is \(353\,\hbox {counts/s}\), considerably less than the measured background photons. However, such events are randomly distributed in time, whereas the protocol of our QKD devices works exploiting weak coherent pulses properly synchronized. Considering a transmission with repetition rate of \(1\,\hbox {GHz}\), the background is always less than \(6.5 \cdot 10^{-6}\,\hbox {counts/pulse}\) while the photons of the key are, considering the losses of our Quantum channel (about \(10\,\hbox {dB}\)), about \(0.03\,\hbox {counts/pulse}\). Moreover, since the sum of background and the QKD signal photons always remains below the saturation threshold due to the SPADs deadtime (\(\sim 40\,\hbox {kcount/s}\)), we can conclude that the channel is suitable for QKD transmission. We started the transmission, obtaining an exchange of keys with an average key rate of 1.5 Kbit/s. The QKD devices were able to continuously exchange the keys with a low (about \(2{\%}\)) average Quantum Bit Error Rate (QBER). In Fig. 4 we show both the background photons and the QBER behaviors for similar acquisition time.

Fig. 4
figure 4

(a) Background photons in a 24h acquisition frame. (b) QBER as a function of time during a key exchange process.

Full size image

Measurement results

Starting from the exchanged keys K, we compared both the encrypted and decrypted time signals to the original clock signal from the H-Maser with the two TICs, to directly observe the effect of the encryption (TIC2), and decryption (TIC1) with K.

Figures 5, 6 show the results of the measured decrypted and encrypted delays, respectively.

Fig. 5
figure 5

Decrypted TIC1 measured delay. The blue dots are the result of the measurement after the phase-decryption technique: the red dashed line represents the average value of such a delay. The acquisitions where repeated every \(5\,\hbox {s}\), corresponding to the interval in which the phase remains constant. The system was monitored for more than \(11\,\hbox {h}\).

Full size image
Fig. 6
figure 6

Encrypted TIC2 measured time information signal. The blue dots are the result of the measurement without decrypting the signal: the red dashed line represents the average value of such a delay. Initially, for about \(15\,\hbox {min}\) Alice does not encrypt the WR signal, in order to estimate in the Bob side the real average delay, represented by the dark red line. The acquisitions where repeated every \(5\,\hbox {s}\), corresponding to the interval in which the phase remains constant. The system was monitored for more than \(11\,\hbox {h}\). The green inset highlights the behavior of the delay when Alice turns on the WR-signal encryption.

Full size image

TIC1 measurements show the stability of the delay induced by the phase shift (blue dots) with respect to an average time delay (red dashed line) of \(161.6224(7)\,\hbox {ns}\) during an acquisition time longer than \(11\,\hbox {h}\). On the contrary, TIC2 shows two different behaviors, highlighted into the green inset: a stable and a noisy one. This is due to the fact that we initially did not encrypted the transmission for about \(15\,\hbox {min}\), in order to calibrate the real delay bias (dark red line) of \(129.188(3)\,\hbox {ns}\). Subsequently, we turned on our encoding system, obtaining a spread distribution around a mean (red dashed line) of \(138.00(6)\,\hbox {ns}\). Both the phase shifting of the encrypted signal and the increasing of the dispersion of the time delay are evident, making the transmission not useful for a precise time synchronization.

Furthermore, we characterize the time delay stability of TIC1 and TIC2 measurements. For this analysis, we use the Allan deviation, which is the standard figure of merit in time and frequency metrology for characterizing time delay stability.33 Figures 7 shows the comparison between the Allan deviation of data from TIC1 (blue) and TIC2 (red) as a function of averaging time. In both cases one could recognize the linear behavior (in logarithmic scale) of the Allan deviation typical of white phase noise. However, our technique allowed for a degradation in the encrypted signal of more than two order of magnitude with respect to the decrypted one.

Fig. 7
figure 7

Frequency stability comparison between TIC1 and TIC2 measurements. They are plotted the Allan deviations measured in TIC1 (blue dots) and in TIC2 (red dots) depending on the averaging time with their corresponding uncertainties.

Full size image

Discussion

The results shown in Fig. 6 clearly demonstrate the robustness of our encoding technique, even for long time. Without a deterministic decryption, any measurement does not allow achieving the temporal precision usually granted exploiting the WR-PTP protocol. In addition, in Fig. 7 it is possible to appreciate that our approach allows for gaining almost two order of magnitude in terms of Allan deviation with respect to an eventual eavesdropping. This means that, if a third-part is interested in the estimation of the Alice’s clock frequency stability, our encoding technique would ensure that the information needs more time to be revealed, i.e. diminishing the eavesdropper possibility for extracting information.

In our proof-of-principle experiment, our goal is to demonstrate that the WR signal can be encrypted by introducing any noise model. For this reason, we chose to implement a simple model, specifically white noise. However, although a more elaborated noise model could in principle grant for better results, specially in terms of Allan deviation, there is a physical limit on the allowed range for the introduced phase. Thus, taking into account a reasonable limit for the phase, e.g. \(\phi _i \in ({-360}^{\circ },\,{360}^{\circ })\), the behavior of a more complex noise will converge to a white noise in few steps. Of course, this is mediated by a trade-off between the average step size and the maximum allowed value of the phase. A more detailed analysis of complex noise models, including simulations of different scenarios (even non-Markovian32), is provided in the Supplemental Material. These simulations, conducted within the constrained range \(\phi _i \in ({-360}^{\circ },\,{360}^{\circ })\) while maintaining the same average phase step as in our proof-of-principle experiment, confirm that the transition to a white-noise behavior occurs in fewer than 10 steps. In conclusion, our work demonstrates a robust technique to protect time signal with truly random noise, easily implementable in the quantum communication infrastructures that will host both time dissemination and QKD protocols, even with common electronics usually available in any laboratories. The synchronization information exhibits a stability at 1 s worsened by two orders of magnitude. This proof-of-principle experiment paves the way to a novel technique in quantum-secured synchronization service, ensuring that timing signals remain inaccessible to unauthorized users, similar to the concept of Selected Availability in strategic time distribution systems. Indeed, our approach can be extended to a multi-user network by incorporating a KMS, which enables the secure distribution of QKD-generated keys across multiple nodes.