Introduction

Motivation

DC motors are widely used in modern industries due to their versatility, reliability, controllability and low cost. They are used in a variety of automation applications, such as conveyor systems, assembly lines, and material handling systems. They are employed to power robots and control their movement, speed, and position. DC motors are also good choice to power electric vehicles, such as electric cars, motorcycles, and scooters. They are extensively used in industrial machinery, such as pumps, fans, and compressors, to provide reliable and efficient power. In medical devices, they are used, such as ventilators and dialysis machines, to provide precise and accurate control. These applications demonstrate the versatility and importance of dc motors in modern industries, and they highlight the ongoing development and innovation in this field. Most significantly, recently dc motors are also used in Wind Turbine Emulators (WTEs) for replicating the behavior of real Wind Energy Conversion System (WECS)1,2.

Literature review

Typically, PID (Proportional-Integral-Derivative) or PI controllers are used for speed and torque control of dc motor3. The performance of the PI controllers depends upon proper tuning of PI coefficients, i.e., Kp, Ki and Kd. The Kd term minimizes overshoot slightly but it is avoided because it causes stability problem, as a result PI controller is preferred over PID. The incorrect tuning of PI controllers may cause unsatisfactory control during transient conditions4. The PI controller is a straightforward yet effective algorithm for achieving precise speed regulation of a DC motor5. Its fundamental principle involves continuously adjusting the control input (such as voltage or current) to the motor, ensuring that its speed matches the reference signal6. The PI controller consists of two components: a proportional part that ensures a quick response and reduces steady-state error, and an integral part that eliminates steady-state error and enhances the stability of the closed-loop system7.Tuning the parameters of a PI controller is crucial to ensure the best performance of the dc motor control system8. Many tuning methods have been developed over the years, including trial-and-error, rule-based, and model-based methods. Trial-and-error methods are simple and intuitive, but they can be time-consuming and may not lead to optimal results9. Rule-based methods use heuristics and experience-based rules to adjust the controller parameters, but they may not work well for all dc motor systems10,11. Model-based methods use mathematical models of the dc motor and the control system to tune the PI controller parameters. These methods are more systematic and accurate, but they require more information and computational resources12. An exact mathematical model of the system is required for PI controllers. PI controllers are very sensitive to parameter deviations. PI controllers are preferred because of their robustness against any disturbance13,14. Although, the PI controllers provide robust control in steady-state conditions, but inaccurate coefficients cause a slow response and overshoot. Also, PI controllers have drawbacks of poor stability margin15. In16,17 Fractional Order PID (FOPID) is proposed for improving the speed control response. In18 Particle Swarm Optimization (PSO) is suggested for tuning of the PID. However, it is quite difficult to get optimum values of FOPID coefficients19,20. Different researchers have proposed various methods for tuning of the PI controllers, i.e., Nichols Ziegler (NZ) method; one of the most commonly used methods. However, NZ requires exact mathematical model of the dc motor drive. There are numerous new methods and techniques for tuning of PID controllers21,22. Authors in 23,24 have utilized FLC for motor control. However, if FLC rules are incorrectly defined, the control system’s performance suffers, as FLC depends on user-defined rules. Additionally, reference25 suggests using ANN as a solution.

In recent times, intelligent computational techniques i.e., Ant Bee Colony (ABC), Genetic Algorithm (GA), PSO, Salp Swam Algorithm (SSA) are extensively used for obtaining coefficients of PID controllers26,27. The reference28 also suggested FOPID using ABC algorithm. In29 an intelligent controller for dc motor drive is designed using PSO technique for obtaining the optimal PID controllers’ coefficients. Similarly, reference30,31 presented a PSO technique for finding the optimal parameters of PID controller, for speed control of a linear brushless dc motor. The suggested approach has superior features, including easy implementation, good computational efficiency, and stable convergence characteristic. Furthermore, in reference32,33 GA is used for tuning PID. Reference34 demonstrated PSO and Fuzzy to find the optimum PID coefficients. A literature survey reveals that the majority of researchers35,36,37,38,39,40,41,42,43,44,45 have employed PI controllers for controlling dc motor drive systems, used in WTEs. However, PI controllers are found to be inadequate due to their subpar performance, primarily stemming from a restricted steady gain range. This limited gain results in slow response times, making PI controllers unsuitable for contemporary dc motor drives. Consequently, alternative solutions are necessary. In46examined the impact of feed-forward data in configuring the ANFIS controller by visualizing the DC motor’s speed behavior. Various PID models were implemented and tested under different conditions to generate the training data for the ANFIS controller and assess the performance of the controllers. Using MATLAB Simulink tools, key performance characteristics such as steady-state error, rise time, overshoot, and settling time were observed, all of which play a crucial role in enhancing the DC motor’s performance. In47 low-speed response of the IM drive using the sensor less vector control technique is enhanced through the modified RF-MRAS with various adaptation schemes, including conventional PI and ANFIS controllers, with a comparison of their results. The issues of DC drift and inverter nonlinearity in the RF-MRAS-based technique are mitigated by modifying both the reference and adaptive models. A compensating voltage is introduced into the rotor flux component, while the voltage and current model flux components ensure accurate speed estimation. In addition, Model Predictive Control (MPC) is a powerful control strategy, it can also be used in dc motor control systems due to its ability to handle constraints and optimize performance. However, MPC requires solving an optimization problem at each control step, which can be computationally intensive, especially for real-time applications. Moreover, MPC relies heavily on an accurate mathematical model of the dc motor. Any model inaccuracies due to parameter variations, load changes, or external disturbances can degrade the performance. The ANFIS controller offers improved resistance to variations in machine parameters48,49. In50 ANFIS model, utilizing five triangular membership functions, achieved optimal efficiency with a high prediction rate and an exceptionally low RMSE of 0.0011 after 200 s. The MSE and RMS values for the training, testing, and validation datasets demonstrated the excellent performance and accuracy of the ANFIS controller. In51various experimental tests were conducted under different operating conditions, including sudden load changes and variations in the reference output voltage, which are common in industrial applications. The effectiveness of the proposed control approach was demonstrated through both simulations and experiments. The practical results confirmed the ANFIS controller’s effectiveness in tracking the imposed references and rejecting disturbances affecting the system. Furthermore, the integration of this intelligent controller with a predictive strategy has greatly enhanced the power quality of the power grid. In52 proposes a compound control strategy that combines classical PI control with SMC for vector closed-loop control of stepper motors. The main advantage of this approach lies in leveraging the precision of PI control alongside the robustness of SMC, overcoming the limitations of each method when used independently. A key innovation of this strategy is the introduction of an automatic weight adjustment mechanism, which enables adaptive modulation of the two control strategies based on changing operating conditions, ensuring their coordinated operation.

Research gap

The selection of a particular method among the array of options relies heavily on the unique demands and limitations inherent in the dc motor control system. For instance, in scenarios where the dc motor faces substantial load fluctuations or external disturbances, a model-based tuning methodology might be preferable. Conversely, in situations where the dc motor control system is uncomplicated and does not demand stringent precision, a rule-based tuning approach could adequately meet requirements. An alternative solution must be used to improve the PI controllers because of their imprecise and slow reaction. The existing control system for the dc motor drives, based on PI controllers is not adequate for modern drives, which require accurate and reliable control system.

Research gap and contribution

Despite the use of PI (or PID) controllers for their good stability and zero steady-state error, challenges remain, such as optimal tuning of \(\:{K}_{p}\), \(\:{K}_{i}\), and \(\:{K}_{d}\), along with apparent overshoot and substantial settling time. Tuning PID controller is particularly challenging, and while various PI controller tuning methods can improve performance, they tend to be complex and time-consuming. There are numerous drawbacks of using computational techniques for PI controllers’ parameters tuning. For instance, depending upon the model, the optimization process may be time consuming. Furthermore, these computational techniques are used only to obtain optimal coefficients of PID. Even though, optimal coefficients of PID controllers provide good response. Nevertheless, due to fundamental working mechanism of PID controllers, the overshoot cannot be completely eliminated.

Contribution

The contribution of the research study is highlighted as; an ANFIS based control system is proposed to improve the performance of the controller for dc motor drives. The controller proposed in this study is designed, simulated, implemented and validated empirically with the controller board, i.e., DS1104 R&D from dSPACE. The implementation and validation of the two distinct control methodologies, namely PI controllers and ANFIS controllers, are conducted using the DS1104 R&D Controller Board. This paper presents a performance comparison between these two types of controllers, first detailing the design procedures for the PI controllers, followed by those for the ANFIS controllers.

Proposed DC motor drive system

The proposed dc motor drive system is illustrated in Fig. 1. The experimental implementation of the same is shown in Fig. 2. It consists of a dc motor, DS1104 R&D controller board, 2-quadrant dc-dc converter, current sensor, incremental encoder, MATLAB/Simulink and dSPACE. An IGBT module was used in the design of the power electronic converter. This selection is necessitated by the unidirectional operational requirement of the dc motor utilized in this research. Consequently, the two-quadrant dc-dc converter is deemed suitable. The detailed discussion on the most important components is presented in subsequent sections.

Fig. 1
figure 1

Proposed DC Motor Drive System.

Full size image
Fig. 2
figure 2

Experimental setup.

Full size image

Controller Board(DS1104 R&D)

The controller board DS1104 used in this paper is a powerful and versatile platform designed to meet the demanding requirements of research and development in various industries. It is an advanced hardware tool that provides real-time processing capabilities and reliable performance for control, simulation, and testing applications. The board is based on a high-performance digital signal processor (DSP) with a clock speed of 250 MHz, which enables it to execute complex algorithms and perform real-time processing tasks with precision and accuracy. One of the main functions of the controller board (DS1104 R&D) is to serve as a powerful tool for rapid control prototyping. It provides a flexible and convenient way to develop and test control algorithms and system designs for various applications, including automotive, aerospace, robotics, and industrial automation. With its powerful DSP processor, the board can execute real-time simulations of complex control systems, allowing researchers to fine-tune designs and test them in a virtual environment before implementing them in the actual system. The DS1104 R&D Controller board also provides a powerful tool for testing and validation of complex systems. It is often used to test electronic control units (ECUs), sensors, actuators, and other components of a system in a simulated environment, ensuring that they meet the desired performance and safety standards. The board is also used in hardware-in-the-loop (HIL) testing, where a real-time simulation of a system is performed, and the controller board provides the necessary feedback to ensure that the system behaves as intended. Another important application of the DS1104 R&D Controller board is in the field of research and development. The board’s powerful processor and real-time processing capabilities make it ideal for scientific research, where the accuracy and precision of the data are critical. The board is an essential tool for rapid control prototyping, system testing, and academic research, providing a flexible and convenient way to explore new concepts and test innovative ideas.

This board is equipped with eight 16-bit DAC outputting within a ± 10 V range, 16-bit ADC (four number), and 12bit ADC (also four), with ± 10 V input range. Additionally, it features two incremental encoder (IE) interface channels, utilized in this analysis for measurement of rotational speed. The development software, ControlDesk Next Generation (CDNG) by dSPACE, facilitates seamless ECU implementation, managing all essential tasks and offering an integrated environment throughout the experimental process. A user-interface control panel is created using dSPACE CDNG (*.lay), enabling visualization of output parameters reference torque, torque, torque error, motor reference speed, actual rotational speed and speed error. For interacting with real-time operations on the controller board (DS1104 R&D), ControlDesk next generation concurrently employs several files; executable program (*.ppc), a variable description file (*.sdf) for variable-to-model parameter mapping, and virtual instrument panel layouts (*.lay).

Modeling of DC motor drive system

DC motor modeling

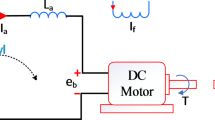
The equivalent circuit of the separately excited dc motor used in this study is shown in Fig. 3. Speed regulation is conducted within the motor’s base speed, which is 1750 rpm. This means that the focus is solely on the torque constant region, and no flux weakening is applied.

Equation 1 below defines the armature voltage of the dc motor, where the back EMF voltage, denoted as eb, is described by Eq. 2. The voltage for the separately excited field (Vf) is specified by Eqs. 3and4 provide the torque generated by the dc motor, and Eq. 5 outlines the motor’s dynamic torque-speed characteristic.

Fig. 3
figure 3

Separately Excited DC Motor.

Full size image
$$\:{V}_{t}=\:{R}_{a}\:{i}_{a}+{L}_{a}\frac{d{i}_{a}}{dt}\:+{e}_{b}$$
(1)
$$\:{e}_{b}={K}_{e}{\upomega\:}$$
(2)
$$\:{V}_{f}=\:{R}_{f}\:{i}_{f}+{L}_{f}\frac{d{i}_{f}}{dt}$$
(3)
$$\:{T}_{m}={K}_{t}\:{i}_{a}$$
(4)
$$\:{T}_{e}=\:{T}_{l}+J\frac{d{\upomega\:}}{dt}$$
(5)

The constants Ke and Kt ​ actually depend on the dc machine’s flux per pole. Nevertheless, the control is restricted to the steady torque region without any flux deteriorating, the flux per pole is considered unchanged.

Figure 4 displays the dc machine’s block diagram following the application of the block diagram transformation procedure. This means that the transfer function between the (\(\:{I}_{a})\) and the \(\:\left({V}_{t}\right)\) includes one zero and two poles, which are figured-out by the machine’s parameters.

Fig. 4
figure 4

Simplified diagram of the DC motor.

Full size image

The rated speed (ω) of the machine is \(\:1750r.p.m\), rated power (P) is \(\:\frac{1}{3}\) h.p i.e., 248.67 W, rated voltage 115 V and rated current Ia is 3.2 A. Other essential parameters, armature inductance (\(\:{L}_{a}\)), armature resistance (\(\:{R}_{a}\)), coefficient of viscous friction (B), moment of inertia (\(\:J\)), torque constant (\(\:{K}_{t})\:\)and back e.m.f constant (\(\:{K}_{e})\) were extracted by performing tests on dc machine. The extracted parameters are depicted in Table 1.

Table 1 The parameters of the DC motor.
Full size table

Control system structure for DC motor drive

The cascaded control structure employs a speed reference signal. To realize this reference speed cascaded control architecture is utilized, as illustrated in Fig. 5. The symbols Ra, La, B, J and K and their respective values are described in Table 1 given above. However, ω, ωref, T, and Tref denote speed, speed reference, torque and torque reference, respectively.

Fig. 5
figure 5

Cascade control of DC motor drive.

Full size image

Design of two quadrant DC-DC converter

The switch mode two-quadrant dc-dc power converter, also known as the half-bridge dc-dc converter is shown in Fig. 6. It comprises two IGBT switches, labeled as T1 and T2, and two diodes D1 and D2. The gates of IGBT are controlled using a PWM signal. These switching signals (PWM) are obtained by comparing the control signal with a triangular wave. The controlled output voltage is connected with the dc motor. When T1 conducts current flows in the positive direction and Vdc equals Va. When D2 conducts Va becomes zero. Similarly, when D1 conducts, Va equals Vdc. Similarly, when T2 conducts Va becomes zero, as depicted in Fig. 7.

Fig. 6
figure 6

Two Quadrant DC-DC power converter.

Full size image
Fig. 7
figure 7

Gating signals for two-quadrant DC-DC power converter.

Full size image

Therefore, in a two-quadrant operation, the output voltage can only be positive. Whereas, the current can be either positive or negative, depending upon the state of the switches. In this research, a 2-Q dc-dc power converter is utilized due to its suitability for the unidirectional operation of the dc motor employed in this study. Consequently, the 2-Q dc-dc converter is an appropriate choice. The controller board (DS1104 R&D) is employed for generating the controlled Pulse Width Modulation (PWM) signals.

Controllers design for DC motor drive

The control structure proposed in this study comprises two loops: an outer speed control loop and an inner torque control loop. It is crucial for the dc motor’s speed to accurately follow the reference speed. This study proposes design, and implements two types of controllers; ANFIS and PI controllers. In contrast, the ANFIS control scheme employs two trained ANFIS controllers.

Use of bode plot design of PI controllers

It is widely used in control system design, especially for dc motor drives, to visualize and analyze the system’s frequency response. The Bode Plot displays the magnitude and phase of the system’s response as a function of frequency. One of the main applications of Bode Plots in control system design for dc motor drives is the determination of the stability of the system. By examining the Bode Plot, the system’s stability margins are determined, and controllers are designed that meet stability requirements. Bode Plots are also useful for characterizing the system’s performance, such as its overshoot, rise time, and settling time. Generally, the phase margin determines the system’s stability, and a large phase margin indicates a more stable system. Bode Plots are a valuable tool for control system design for dc motor drives, providing insight into the system’s stability, performance, and frequency response. Hence, in this study by using Bode Plots, controllers are designed that meet stability requirements, achieve the desired performance, and ensure that the system will respond correctly to different signals.

PI controllers

The speed and torque loops of the studied PI controllers are premeditated using the small signal model (s-s model). This model for the dc machine is derived from Eq. (1) to (5) and is illustrated in the simplified block diagram provided earlier. Given that PWM signals are created by comparing a control signal with triangular wave, it is established that the converter’s s-s model is represented by a simple dc gain, which in this case is 7 (Vdc/2*Vtri) where, Vdc=70 V and tri = 5.The bode plots are used for accurate PI controllers design. To make sure the speed of motor exactly tracks the speed reference, the system’s response must be as quick as possible. This is achieved by maximizing the closed-loop bandwidth. Additionally, to eliminate steady-state error, the dc gain of the open loop transfer function must be very large or infinite. Good stability is also required, which, according to Bode plots, corresponds to a substantial phase margin, typically greater than 650.

Torque PI controller

The design process initiates with the intimate loop, the torque loop, progressing outward to the speed loop. Figure 8 depicts the s-s model of the inner torque loop featuring the PI controller. To ensure that the converter’s switching does not interfere with the torque loop, it is preferred that the converter’s switching frequency be at least a decade lower than the torque’s closed-loop bandwidth, denoted as BWtorque​. Similarly, the speed closed-loop bandwidth is set to be a decade lower than the bandwidth of the torque loop.

Fig. 8
figure 8

Torque Loop-based small signal model.

Full size image

In this study, the converter’s switching frequency (fsw) is set at 5 kHz, resulting in torque and speed bandwidths of approximately 3141.5 rad/sec and 31.415 rad/sec respectively. When integrating loop gain with the PI controller, the selection of \(\:{k}_{p}\) and\(\:{k}_{i}\)values is crucial to meet torque loop control requirements, including rapid response, stability and zero steady-state error. The crossover frequency from the Bode plot, which roughly represents the torque’s closed-loop bandwidth, directs the selection of controller values. Simplifying the PI controller into three terms—integrator, zero location, and dc gain—eases the selection process. Positioning the zero location between the dc motor’s poles allows for convenient adjustment of the dc gain to attain the required crossover frequency without phase interference. These selections are facilitated using the Control System Designer tool in SIMULINK. Ultimately, kp, and ki values of 39 and 3,408, respectively, are chosen for the torque PI controller. These values ensure a crossover frequency of approximately 3141.5 rad/sec and a phase margin exceeding 65°, maintaining the desired control characteristics.

PI speed controller

Due to the substantial disparity in bandwidths between speed and torque, it is reasonable to assume unity for the closed-loop gain of torque when devising the speed controller. Consequently, the proportional gain kp,ω and integral gain ki,ω of the speed proportional-integral (PI) controller are primarily found out by the system’s moment of inertia (J) and viscous friction constant (B). Given that the system features only one pole, the zero location of the PI controller is easily chosen to nullify this pole. Utilizing the control system designer, appropriate values for \(\:{k}_{p,\omega\:}\) and \(\:{k}_{i,\omega\:}\) are selected to ensure that the crossover frequency, denoted as \(\:{\left(BW\right)}_{speed}\), equals 31.415 rad/sec. The finalized values for kp,ω and ki,ω are 0.151 and 0.263, respectively.

ANFIS controllers’ design

In this proposed control scheme, both the speed (outer) controller and torque (inner) controller controllers utilize ANFIS controllers. However, before the ANFIS controllers can be employed, they need to undergo training and optimization. This design process is facilitated through the use of the MATLAB toolbox. It commences with data collection for training purposes, which involves conducting experiments on the control system based on PI controllers. A step-change in the reference speed is applied for gathering this data. The specific points for collecting input-output data are illustrated in Fig. 9. For the speed controller’s training data, the input is derived from the speed error, while the output is taken from the PI speed controller’s output. Similarly, for the torque controller’s training data, the input is obtained from the torque error, and the output corresponds to the torque controller’s output.

Fig. 9
figure 9

Collecting Data for ANFIS Training.

Full size image

Following data collection, the training phase utilizes the Neuro-Fuzzy Designer tool, accessible either through the apps tab or by entering “anfisedit” in the MATLAB command prompt. This tool allows users to specify the quantity and characteristics of Membership Functions (MFs) for both input and output layers of the ANFIS. For each input and output, 20 triangular MFs are assigned, in this study. This choice is made for its simplicity and efficiency in both training and execution. Empirical evidence suggests that beyond 20 MFs, only marginal improvements in results are observed. Subsequently, the training data is loaded into the ANFIS editor. For training configuration, a hybrid optimization approach is employed, combining backpropagation and least-squares algorithms to achieve optimal accuracy. A zero-error tolerance is set, and 100 epochs are selected to achieve the desired training accuracy.

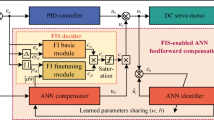
The flowchart for designing the ANFIS controller is shown in Fig. 10. Before the controller can be implemented, it must first be trained and optimized. The ANFIS controller design is carried out using the MATLAB toolbox. The process begins with gathering training data, which, in this study, is obtained by conducting experiments on the PI controller-based control system that has been designed. To collect the data, a step change in the speed reference is applied.

Fig. 10
figure 10

Flowchart of designing ANFIS controller.

Full size image

ANFIS controller structure

ANFIS is composed of five layers (labeled 1–5), with each layer connected by weights, as illustrated in Fig. 11. In the first layer, also known as the input layer, the input data is transformed into membership functions (MFs) to determine the degree of membership for each input. The variables x and y represent the inputs to the ANFIS, with x1 and x2 being the input MFs for x and y1 and y2 the input MFs for y. In the second layer, fuzzy rules are applied to establish the relationship between the inputs and outputs. The third layer normalizes the output and passes it to the fourth layer, where the data is further processed to produce the output MFs. Finally, in the fifth layer, the outputs are aggregated to produce a single output. Although ANFIS is capable of handling multiple inputs, this study focuses on using a single input.

Fig. 11
figure 11

ANFIS structure.

Full size image
Fig. 12
figure 12

Closed loop control structure based on ANFIS.

Full size image

The closed loop control structure employing ANFIS controllers is depicted in Fig. 12. In the proposed controller structure both the controllers are trained ANFIS controllers.

Results and discussion

The outcomes fall into two categories: experimental and simulation. The findings of the experiment are reported after the results of the simulation.

Simulation results based on PI controllers

Figure 13 shows that, despite some initial speed error, the real motor speed was able to keep up with the reference speed. With the least amount of error, the real speed was able to keep up with the rising speed. The percentage overshoot and settling time are calculated to evaluate the performance of the dc motor drive for the proposed and tuned controllers’ parameters.

Fig. 13
figure 13

Simulation results based on PI controller.

Full size image

Simulation results based on ANFIS

In this scheme, both the inner and the outer loops use the ANFIS-based controllers. The responses of the system to a step reference speed are depicted in Fig. 14.

Fig. 14
figure 14

Simulation results based on ANFIS controllers.

Full size image

In terms of the transient response, compared with the PI control scheme, the response obtained from the ANFIS-based controllers produces significant difference. The overshoot in the speed response is completely eliminated; the settling time is just 0.75 s, which is significantly smaller when compared with the PI controller.

Experimental verification of PI controllers

The proposed control structure using the obtained coefficients of the PI controllers is simulated in real-time using the dSPACE DS1104 controller board, whereby the parameters of the dc motor are extracted by performing the experiments on dc motor. A step change in the rotor speed, from 0 to 40 rad/sec, is the input to the DC motor drive. An incremental encoder with \(\:2048p.p.r\) is used to measure the real speed, while a Hall effect sensor is used to detect the armature current, or torque. A digital oscilloscope is used to record and store the signals for the torque, speed, and speed error. MATLAB is then used to plot these signals. Similar to the simulation results, the percentage overshoot and settling time are calculated to assess the enactment of the dc motor drive for the proposed and tuned controllers’ parameters. The corresponding speed and torque characteristic curves are shown in Fig. 15. As anticipated, the speed response for the PI controllers produces an overshoot in the speed, similar to the simulation results. The overshoot was noted as 25.5% and a settling time of 1.8 s. Even though the overshoot and settling time for the experiment and simulation give almost the same values, it is also noted that the speed of response obtained from the experiment is comparatively faster than the one obtained from the simulation.

Fig. 15
figure 15

PI controllers’ response.

Full size image

Experimental results of ANFIS controllers

In this scheme, both the inner and the outer loops employ ANFIS controllers. The responses of the system to a step speed reference are depicted in following Fig. 16. Since the torque controller uses ANFIS, it can be seen from the figure that the overshoot in the torque is suppressed, hence resulted in a slower speed response. In order to avoid the overshoot in the speed, the torque reference during the acceleration is only limited to about 0.5 N.m, i.e., half of the maximum value. The speed response gives 0% overshoot; however, the settling time is 0.18 s.

Fig. 16
figure 16

Speed and torque curves for ANFIS control scheme.

Full size image

Comparative analysis

To check the effectiveness of both the control schemes, the transient responses obtained from the simulation results are compared. As presented in the previous sections, both the control schemes were able to achieve the set rotor speed, however, with a different dynamic response. To perform a fair comparison among the studied controllers, two of the very vital dynamic response evaluation metrics i.e., percentage overshoot and settling time for each case, are tabulated and compared as presented in Table 2.

Table 2 Transient response evaluation of the proposed control schemes.
Full size table

It is evident from the above Table 2 that the proposed ANFIS based control architecture outperforms PI based control scheme in terms of response with lower overshoot and shorter settling time. The ANFIS based control scheme provides a better response than that of the PI control scheme. The response obtained from the ANFIS control shows that there is 0% overshoot and faster response with just 0.75 s settling time. It is crucial to note that in this work, the PI controllers are effectively tuned by using the Control System Designer tool in MATLAB. The PI controllers are tuned based on the closed-loop bandwidth requirements, relative stability, and steady-state error – this has been discussed in earlier sections. The PI controller gives better tracking capability and can produce zero steady state error. However, due to the fundamental working principle of the PI controller, the overshoot cannot be completely removed without decreasing the damping of the system. The speed of response has to be compromised with the relative stability of the system, i.e., overshoot. In other words, to get a faster response, the speed response has to suffer from the increment in the overshoot of the response. The problem of speed overshoot associated with the PI controller is however removed when ANFIS-based controller is used for both the loops. For performing a fair comparison between both studied controllers, two of the very important dynamic response evaluation metrics i.e., percentage overshoot and settling time are calculated for each case and the corresponding outcomes are depicted in Table 3.

Table 3 Transient response evaluation of the proposed control schemes.
Full size table

The capability of an ANFIS-based controller to suppress the overshoot, as seen in the simulation results previously, is again evident in the experiment. The ANFIS control scheme provides better dynamic response than the PI control scheme. It is obvious from the above Table 3 that the ANFIS based control scheme outperforms PI control schemes by achieving the most optimal dynamic response with 0% overshoot and settling time of 0.18 s. The initial values for the Kp and Ki of the PI controllers are designed based on the simulation model using the Control System Designer tool in MATLAB. Similar to the simulation, when using the PI controller, the overshoot and the speed of response has to be compromised. Reducing the overshoot in the speed will cause a slower speed response. However, by employing ANFIS controller for the speed and torque loops, the overshoot in the speed can be removed, without compromising the speed of response. Hence, the robustness of the ANFIS controllers have been assessed by introducing variations in the reference signal. The results demonstrate that the controllers effectively maintain the performance with minimal deviation in transient and steady-state responses, confirming its adaptability to the variations. Comparative simulations and experiments with conventional PI control further validate that ANFIS exhibits superior performance and adaptability under varying reference speed. Though, ANFIS is an effective control technique for DC motor control due to its adaptive learning capability and nonlinear mapping, however, it has some limitations as well. ANFIS involves both fuzzy logic and neural networks, therefore, making it computationally intensive compared to conventional PI controller. Also, the real-time implementation on low-cost microcontrollers or embedded systems is challenging due to high processing and memory requirements. The performance of ANFIS depends heavily on the quality and quantity of training data. If the training dataset is not well-representative of all operating conditions, the controller may fail to generalize effectively.

Conclusion

The PI controllers are extensively used for speed control of dc motor drive system. But they suffer from high overshoot and sluggish response. Therefore, this study proposed replacement of PI controller by ANFIS controllers. Henceforth, two different control schemes are proposed, designed, and implemented. These controllers are implemented both in simulation and experiments. Even though, the PI controllers were able to achieve the set rotor speed with an acceptable dynamic response which shows the effectiveness of the proposed controllers. To perform a fair comparison between both the studied controllers, two of the very fundamental dynamic response evaluation metrics i.e., percentage overshoot and settling time are calculated for both the cases. Despite the tuning of the PI controllers is performed with the help of Control System Designer tool in MATLAB. It is found out that the PI control scheme produces higher overshoot and longer settling time. The results obtained from the tuned PI controllers were used to train the ANFIS controllers for the simulations and experiments. However, even though the PI controllers are properly and systematically tuned, the overshoot could not be completely removed without compromising the settling time and the speed of response. Based on this study, it is observed that the ANFIS-based controller is capable of suppressing the overshoot and contemporaneously satisfactorily maintained the speed of the response. In ANFIS control scheme, for a step reference speed, the overshoot and settling time are found to be 0% and 0.18 s, respectively. Hence, this study proves that ANFIS control scheme outperforms the PI controllers in terms of the dynamic response.

Future work

Future work could explore the applications of PID control integrated with ANFIS. This combination could leverage the strengths of both approaches PID control’s efficiency in real-time adjustments and ANFIS’s ability to model complex nonlinear systems with fuzzy logic. By combining the two, it may be possible to enhance the performance of control systems, especially in situations where the dynamics of the system are uncertain or highly variable. Future studies could investigate the tuning of PID parameters using ANFIS for improved adaptability and precision in various engineering and industrial applications. Furthermore, in this paper only step-signal is tested, which is the standard method of testing the innovative controllers. Nonetheless, validation of controller performance under varying load is a future suggestion, for the extension of this research work. The proposed ANFIS replaces the classical PI controllers. Therefore, as a general thought in every machine (drive), where PI controllers are employed, they can be replaced by ANFIS. However, for specific machine, comprehensive training and testing of ANFIS is necessary depending upon the parameters of the machine and accuracy required. Furthermore, the ANFIS can be used for Induction Motor control, Permanent Magnet Synchronous Machines, and for all types of dc machines, wherever PI controllers are used.