Image dehazing algorithm based on light-value weighted allocation and multi-layer restricted perception

Abstract

In image dehazing, the dehazing performance in bright regions and the model’s robustness to noise are critical evaluation criteria. However, existing dehazing models often suffer from distortions in the bright areas and exhibit weak noise resistance. We propose an image dehazing algorithm based on light-value weighted allocation and multi-layer restricted perception (DWARP) to address these issues. The proposed algorithm first constructs an atmospheric light estimation module based on weighted allocation. It reduces the initial estimation error by zeroing out overexposed pixel values, then identifying key factors affecting atmospheric light estimation and assigning weights accordingly. Finally, a threshold-restricted adjustment is applied to the estimated result, achieving a three-stage refinement in atmospheric light estimation accuracy. Secondly, by computing the universal range of transmittance for both bright and non-bright regions, a multi-layer restricted perception scheme for transmittance is designed. This approach transforms the distortion issue in bright regions into a problem of reducing transmittance estimation errors. Finally, to enhance the visual quality of the dehazed image and improve the model’s noise robustness, a brightness adjustment module and a Gaussian denoising module are embedded into the dehazing model. Experimental results demonstrate that the DWARP algorithm effectively prevents distortion in the dehazing process for bright regions and enhances the model’s noise robustness. The DWARP algorithm achieved an average PSNR of 37.41 dB, an average SSIM of 88.74%, and an average VIF of 0.89 across four datasets, with an average dehazing time of 0.633 s. Compared to the RIDCP algorithm, DWARP improved the PSNR by an average of 6.63 dB, SSIM by 2.18%, and VIF by 0.03 while enhancing dehazing efficiency by an average of 0.055 s. To validate the effectiveness of the DWARP algorithm, we conducted dehazing experiments on four foggy datasets, demonstrating the proposed algorithm’s effectiveness and superiority. The DWARP algorithm not only effectively processes bright regions, such as the sky, in foggy images but also exhibits strong noise resistance, validating the scientific and theoretical correctness of the proposed improvements. This dehazing model provides a novel approach for fog removal in fields such as intelligent transportation, contributing to the advancement and development of these areas.

Introduction

In recent years, haze has significantly hindered progress and development in related fields, such as intelligent transportation, autonomous driving, and waterway transport. It obscures important detail features in images, severely reducing the operational efficiency and accuracy of intelligent systems. At the same time, our daily lives are also severely affected by the haze, which reduces our visibility and diminishes the efficiency and quality of everyday activities. As a result, image dehazing has become a focal point of interest in the field of image processing.

Early dehazing processes often utilized image enhancement techniques, such as the Retinex algorithm¹. However, these methods cannot specifically address haze in images, leading to unsatisfactory dehazing results. In recent years, deep learning-based methods have rapidly developed and achieved significant improvements in dehazing performance². However, most of these approaches are primarily suited for synthetic hazy datasets, and the dehazing results for real hazy images are often unsatisfactory. Additionally, they face challenges in deployment and computation within hardware systems^3,4,5,6,7. Wu et al.⁸ proposed the SwinTieredHazymer (STH) algorithm, a deep learning-based approach aimed at enhancing the generalization performance of dehazing models across different foggy datasets. However, experimental results indicate that the model’s noise resistance still requires improvement. At the same time, some experts and scholars have proposed image restoration-based dehazing methods grounded in the atmospheric scattering model. The Dark Channel Prior (DCP) dehazing algorithm is a typical representative and has been widely applied in the field of dehazing⁹. However, this method still requires enhancements in both the dehazing performance for bright regions and the model’s noise resistance. To address these issues, Xu et al.¹⁰ introduced the concept of deep-color correlation and embedded a multi-scale denoising module. However, this method struggles to balance the relationship between the two performance aspects. Jin et al.¹¹ aimed to enhance dehazing performance and model noise resistance by first employing a Robust Dark Channel Prior (RDCP) method to remove haze, followed by using a Robust Light Channel Prior to eliminate shadows. However, the results indicated that this method also fails to effectively suppress the presence of noise in the images. Li et al.¹² proposed an image dehazing algorithm that combines convolutional neural networks. Experimental results indicate that the complexity of this network is relatively high, and the PSNR performance of the dehazed images is generally below 30 dB. Agrawal et al.¹³ conducted an in-depth analysis of the DCP algorithm and argued that the estimation of the dark channel image introduces certain errors in obtaining the final haze-free image, thereby affecting the dehazing performance. They proposed an alternative method that avoids calculating the dark channel image by estimating transmittance directly. Experimental results indicate that the PSNR performance of the dehazed images remains below 30 dB, and the model’s noise resistance is still not satisfactory. Dwivedi et al.¹⁴ conducted a thorough analysis of the DCP algorithm, pointing out that it only considers a single color channel of the RGB image with the minimum brightness value. This method’s uneven selection eliminates the influence of transmittance across different channels in hazy images, resulting in poor dehazing performance. To address these issues, an extended dark channel prior dehazing algorithm has been proposed, achieving improved dehazing results. In recent years, experts and scholars have begun to use deep network estimation methods to further optimize the parameter values in the atmospheric scattering model^15,16,17 and have introduced methods for directly obtaining haze-free images^4,5,7,18,19. These methods effectively reduce model complexity and, to some extent, improve the computational accuracy of parameters in the atmospheric scattering model, thereby enhancing the visual quality of dehazing. However, these approaches also struggle to guarantee that the model can enhance image quality while maintaining good dehazing visualization, resulting in generally weak PSNR performance for the dehazed images.

To further optimize dehazing performance, a single-image dehazing technique based on edge and texture features was subsequently proposed²⁰. This method uses the core mean vector of window samples to estimate the transmission map, and a second-generation wavelet transform filter is applied to enhance the estimated transmission map. However, the above dehazing model still exhibits slight distortion in the processing of bright regions in the image. In industrial scenes, smoke significantly affects image clarity. A dehazing algorithm based on dark channel prior has been applied to industrial scenarios²¹. This method utilizes a second-generation wavelet filter to further enhance the accuracy of atmospheric light estimation. However, experimental results indicate that the model’s noise resistance still requires improvement. To improve the accuracy of atmospheric light and transmittance estimation and further enhance dehazing performance, some experts and researchers have proposed dehazing methods based on second-generation wavelets and transmission map estimation²². The proposed dehazing method demonstrates the ability to handle images with varying fog densities. However, experimental results show that the average PSNR of images dehazed using this algorithm is generally below 30 dB, indicating that the dehazing performance of the model still has room for improvement. It remains unable to effectively address the issues of distortion in bright regions and weak noise resistance.

In the field of image denoising, numerous methods have emerged. Some experts and researchers have proposed convolutional neural network (CNN) models based on deep learning to effectively remove Gaussian noise from images²³. These CNN models are more effective than traditional image filtering techniques in eliminating Gaussian noise and restoring image details and data information. However, for image dehazing tasks, these models involve significant computational complexity, which increases the model’s complexity and is not conducive to the development of lightweight dehazing models. To improve the quality of CT images, some experts and researchers have proposed a denoising method based on non-subsampled shearlet transform (NSST)²⁴. In the proposed denoising algorithm, Stein’s unbiased risk estimate (SURE) and threshold linear expansion (SURE-LET) are applied to the denoising model, effectively enhancing the quality of CT images. Jiang et al.²⁵ summarized recent efficient deep learning-based denoising models, examining the latest advancements in image denoising from a unique deep learning perspective. To enhance image denoising while preserving edge detail information, a multi-level adaptive denoising method (MLAC) was proposed²⁶. This method effectively combines convolutional neural networks with anisotropic diffusion, significantly advancing the application of image denoising technology in fields such as automatic character recognition. Shen et al.²⁷ proposed an infrared image denoising method to improve the quality of infrared images and obtain more detailed image features. This method utilizes a symmetric encoder-decoder architecture and cleverly captures long-range dependencies through channel self-attention. However, experimental results demonstrate that there is still room for performance improvement in this approach. Considering that medical imaging technologies introduce certain types of noise, some of which are highly corrosive and degrade image quality, interfering with the effectiveness of medical analysis, convolutional neural network-based denoising methods have been applied to the medical field²⁸. Experimental results show that the average PSNR of the denoised images obtained using the proposed method is 25.82 dB, which has not yet reached 30 dB, indicating that there is still room for improvement in denoising performance. Current dehazing models often lack noise handling, resulting in weak noise resistance. Improving dehazing performance in bright regions while effectively enhancing noise robustness has become a critical challenge in the field of image dehazing. To address this issue, we propose an image dehazing algorithm based on light-value weighted allocation and multi-layer restricted perception (DWARP), grounded in the atmospheric scattering model.

The main contribution of this paper is summarized as follows:

• 1. We designed an atmospheric light estimation module based on weighted allocation. This module provides an effective method for reducing atmospheric light estimation errors by considering the original image, the dark channel image, and the final computed atmospheric light value. It overcomes the influence of noise and other factors on the final estimation, achieving a three-stage reduction in atmospheric light estimation errors. In theory, this method enables higher accuracy in atmospheric light estimation, thereby improving the dehazing performance.

• 2. We designed a multi-layer restricted perception module for transmittance. This module transforms the dehazed image into a problem of reducing transmittance estimation errors. Considering that the dark channel prior theory is not applicable in bright regions, we set a universal range for the transmittance values in both bright and non-bright regions to reduce the estimation errors in bright areas. To further minimize transmittance errors and enhance dehazing performance, a secondary restricted perception module for transmittance and a novel haze-free image expression were introduced.

• 3. We designed a brightness adjustment module and a Gaussian denoising module. To enhance the visual quality of the dehazed image, the brightness is appropriately increased, making the dehazed image appear more realistic and natural, closer to a haze-free image. The fundamental reason for the weak noise resistance of the model is that it lacks a denoising mechanism, which means that while the model performs dehazing, it does not effectively remove noise. To address this issue and enhance the model’s noise resistance, a Gaussian denoising module is integrated into the dehazing model.

Related work

To enhance the dehazing performance of images in bright regions, new dehazing methods have continuously emerged in recent years. Dehazing techniques based on data generation^29,30 and prior guidance^31,32 have been proposed in succession. From the experimental results, these methods improve dehazing performance, leading to satisfactory dehazing results in terms of edge detail recovery and visual quality of the dehazed images. To further enhance dehazing performance, some experts and scholars have introduced codebooks for improved dehazing processing^33,34,35. However, experimental results indicate that the PSNR values of the images obtained using these methods generally remain below 30 dB. To improve the dehazing performance in bright regions, some experts and scholars have proposed a domain-adaptive dehazing model²⁹. This model consists of an image translation module and two dehazing modules, with the translation module designed to bridge the gap between the synthetic domain and the real domain. By utilizing the translated images, a dehazing network with consistency constraints was trained. Finally, the proposed dehazing model was compared and analyzed against other mainstream dehazing algorithms on both synthetic and real hazy datasets, validating the effectiveness of the proposed method. However, the experimental results indicate that the performance of the proposed method in terms of PSNR for the images generally remains below 30 dB. To achieve better image dehazing and enhance the model’s generalization performance, the PSD dehazing network was proposel³⁶. The PSD dehazing network allows most existing dehazing models to serve as its backbone. The effectiveness of the proposed model was validated through experiments. Wu et al.³⁷ proposed a real image dehazing network based on high-quality codebook priors (RIDCP). However, this method still fails to ensure good dehazing visualization while simultaneously improving image quality. Currently, data generation methods have been proven to be effective solutions for real-world visual tasks^38,39,40 and have become a hotspot in image dehazing.

From the experimental results, it can be seen that the above dehazing models have enhanced the dehazing visualization to some extent, but distortion issues still commonly occur in bright regions, which severely affect the dehazing performance of the model. Additionally, the noise resistance of current dehazing models is generally weak, leading to residual noise in the dehazed images, which significantly reduces the image quality. Avoiding distortion in bright regions while maintaining good noise resistance in the model remains a major challenge. This study proposes the DWARP dehazing model to address both of the aforementioned dehazing issues. Unlike current dehazing models, our model not only ensures good dehazing performance in non-bright regions of the image but also delivers excellent dehazing results in bright regions. Additionally, unlike existing dehazing models, our model exhibits outstanding noise resistance, effectively filtering out the noise present in dehazed images, thereby improving the overall image quality. Based on the atmospheric scattering model, we have sequentially designed an atmospheric light estimation module based on weighted allocation, a multi-layer restricted perception module for transmittance, a brightness adjustment module, and a Gaussian denoising module. The innovation of the proposed algorithm lies in the fact that we further improve the accuracy of atmospheric light estimation, effectively overcoming the influence of high-intensity pixel values. In terms of transmittance estimation, we have corrected the transmittance in bright regions, significantly enhancing the dehazing performance of the model in bright areas of the image. Finally, we innovatively designed the brightness adjustment and Gaussian denoising modules, which not only make the dehazed image appear more natural and clear but also effectively enhance the model’s noise resistance, improving the quality of the dehazed image. Therefore, the proposed dehazing model effectively addresses both of the aforementioned dehazing issues and provides a new, effective approach for image dehazing.

The structure of the proposed model

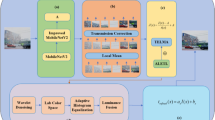
The DWARP network structure we designed is shown in Fig. 1. It first includes the Atmospheric Light Value Solving Module Based on Weight Assignment (ALSWA). This module applies the concept of weighted allocation to solve for the atmospheric light value, reducing the estimation error three times, which helps us obtain a more accurate atmospheric light value. It also includes the Transmittance Primary Restricted Sensing Module (TPRSM) and the Transmittance Secondary Restricted Sensing Module (TSRSM). These two modules provide a novel transmittance estimation method, enabling the dehazing model to effectively handle different regions of the image. Next, the Fog-Free Image Solving Module (FFISM) is included. By incorporating the obtained atmospheric light and transmittance values into this module, we can obtain the initial dehazed image. Finally, the model includes the Image Brightness Adjustment Module (IBAM) and the Gaussian Noise Reduction Module (GNRM). The IBAM module is used to adjust the brightness of the dehazed image, making it appear more realistic and natural with reduced distortion. The GNRM module is used to enhance the model’s noise resistance and reduce the noise content in the dehazed image. In the denoising module, we experimented with three different filter kernel sizes. By evaluating the performance of the dehazed images, we selected the most suitable filter kernel size for optimal results.

Fig. 1

Image dehazing algorithm based on light-value weighted allocation and multi-layer restricted perception.

Design of the atmospheric light value solving module based on weight assignment

This study focuses on the atmospheric scattering model for image restoration, with the first step being calculating atmospheric light values. We have designed an Atmospheric Light Value Solving Module based on weight assignment to improve the accuracy of atmospheric light value estimation. The framework of the proposed method is illustrated in Fig. 2.

Fig. 2

Atmospheric light value solving module based on weight assignment.

Considering that there may be white regions, such as non-sky areas, if the atmospheric light value is estimated from these white regions, it will inevitably lead to an overestimation compared to the true value. This, in turn, negatively affects the final dehazing result. Therefore, eliminating high-intensity pixel values helps the model to identify the optimal atmospheric light value more effectively. Based on the above concept, a scheme for setting high-intensity pixel values to zero was designed to reduce the first estimation error of atmospheric light values. Additionally, considering the presence of noise in the dark channel image, to minimize the impact of noise on the accuracy of atmospheric light value estimation, the brightest pixel values in the dark channel image are also set to zero, further reducing the atmospheric light value estimation error. Finally, the points retained in the dark channel image are mapped to the original image and substituted into the weighted allocation function, as shown in Eq. (1). This allocation function effectively incorporates the semantic correlation before and after the update of the atmospheric light values, it can reduce the solution error of atmospheric light value three times.

The pseudo code for solving the atmospheric light value is as follows:

Algorithm 1

Weighted atmospheric light estimation.

The high-intensity pixels are typically located at the edges or detailed areas of an image. Zeroing out these pixels may reduce the contrast in these regions, leading to blurred edges and loss of details. To address this issue, we first apply bilateral filtering to the original image to preserve edge information, ensuring that the processing of high-intensity pixels does not affect edge sharpness. The purpose of bilateral filtering is to smooth the image while preserving edge details so that the impact of processing high-intensity pixels on edge clarity is minimized.

During the mapping process, if there is no instance where the luminance value corresponding to the mapped pixel of a later point is greater than that of a former point, the luminance value of the formerly mapped pixel is taken as the final atmospheric light value. If the brightness value of the original image pixel corresponding to the mapped intensity of the latter point is greater than that of the former, the brightness value of the latter point is taken as the updated atmospheric light value, while the brightness value of the former point is regarded as the value before the update. At this stage, both the pre-update and post-update atmospheric light values are substituted into the weighted allocation function, and the computed result serves as the atmospheric light value for the next update iteration. This process repeats iteratively. The weighted allocation function designed in this study is as follows:

$${A_2}=A*{A_0}+B*{A_1}+C*0.5*({A_0}+{A_1})$$

(1)

A₂ represents the final atmospheric light value, and A₁ and A₀ represent the atmospheric light values before and after the update, respectively. Parameters A, B, and C represent the weights assigned to the atmospheric light values before and after the update, as well as the average of the two values. The atmospheric light value estimation method above is influenced and determined by three factors, which collectively help to reduce the estimation error. Finally, to avoid significant deviation in the atmospheric light value, a value range for the atmospheric light is set. If the final atmospheric light value is less than 200, A is set to 200; if A is greater than 200, the atmospheric light value remains unchanged. The mathematical expression is shown as Eq. (2):

$${A_2}=\left\{ {\begin{array}{*{20}{c}} {200}&{{A_2} \leqslant 200} \\ {{A_2}}&{{A_2}>200} \end{array}} \right.$$

(2)

Solving the transmittance of bright and non-bright regions

Dehazing methods for image restoration are based on the atmospheric scattering model⁴¹ to recover haze-free images. In this paper, we focus on the atmospheric scattering model for our study, which is expressed as follows.

$$I(x)=t(x)J(x)+A(1 - t(x))$$

(3)

In the equation, I(x) represents the input hazy image, t(x) denotes the transmission value, J(x) refers to the haze-free image to be restored, and A represents the atmospheric light value. According to the definition of the dark channel, we know that:

$${J_{\text{d}\text{a}\text{r}\text{k}}}(x)=\mathop {\hbox{min} }\limits_{{y \in \varOmega (x)}} [\mathop {\hbox{min} }\limits_{{c \in \{ r,g,b\} }} {J^c}(y)]$$

(4)

In the equation, Ω (x) refers to the moving window centered at pixel x, c represents each channel of the image, and${J^c}(y)$denotes any color channel of J. According to the dark channel prior theory, the dark channel value of the haze-free image J (x) in non-sky regions approaches 0, as expressed in Eq. (5).

$${J_{\text{d}\text{a}\text{r}\text{k}}}(x)=\mathop {\hbox{min} }\limits_{{y \in \varOmega (x)}} [\mathop {\hbox{min} }\limits_{{c \in \{ r,g,b\} }} {J^c}(y)] \approx 0$$

(5)

The transformation of Eq. (3) is as follows:

$$\frac{{I(x)}}{A}=t(x)\frac{{J(x)}}{A}+1 - t(x)$$

(6)

Assuming the transmittance t(x) is a constant, denoted as $\tilde {t}(x)$, applying the minimum value operation to both sides of the above equation twice yields:

$$\mathop {\hbox{min} }\limits_{{y \in \Omega (x)}} [\mathop {\hbox{min} }\limits_{c} \frac{{{I^c}(y)}}{{{A^c}}}]=\tilde {t}(x)\mathop {\hbox{min} }\limits_{{y \in \Omega (x)}} [\mathop {\hbox{min} }\limits_{c} \frac{{{J^c}(y)}}{{{A^c}}}]+1 - \tilde {t}(x)$$

(7)

Substituting Eq. (5) into Eq. (7) gives the transmittance value:

$$\tilde {t}(x)=1 - \mathop {\hbox{min} }\limits_{{y \in \Omega (x)}} [\mathop {\hbox{min} }\limits_{c} \frac{{{I^c}(y)}}{{{A^c}}}]$$

(8)

A commonly used factor with a value of 0.95, denoted as w, is introduced to make the dehazing result closer to the haze-free image, as shown in Eq. (9):

$$\tilde {t}(x)=1 - w\mathop {\hbox{min} }\limits_{{y \in \Omega (x)}} [\mathop {\hbox{min} }\limits_{c} \frac{{{I^c}(y)}}{{{A^c}}}]=1 - w\frac{{{I_{dark}}}}{A}$$

(9)

According to the atmospheric scattering model, the expression for the haze-free image J(x) is:

$$J(x)=\frac{{I(x) - A}}{{t(x)}}+A$$

(10)

By substituting the obtained atmospheric light and transmittance values into Eq. (10), the haze-free image can be solved.

The design of the primary restricted perception model for transmittance

Considering that the dark channel prior theory does not hold in the bright regions of the image, the corresponding dark channel values in these regions are close to the atmospheric light value. The expression is as follows:

$${I_{{\text{dark}}}}(x) \approx A$$

(11)

In this case, the expression for solving the transmission rate is as follows:

$$\tilde {t}(x)=1 - w\mathop {\hbox{min} }\limits_{{y \in \Omega (x)}} [\mathop {\hbox{min} }\limits_{c} \frac{{{I^c}(y)}}{{{A^c}}}]=1 - w\frac{{{I_{dark}}}}{A} \approx 0$$

(12)

Equation (12) shows that the dark channel prior theory does not apply to bright areas in foggy images, such as the sky. In this case, the transmission rate is significantly lower than the actual transmission rate. From Eq. (10), it can be concluded that the restored fog-free image will inevitably suffer from distortion, which leads to suboptimal results in bright regions such as the sky when using dehazing algorithms like DCP. To effectively address this issue, we propose the use of a primary restricted perception method for transmission rate estimation, and the mathematical expression is as follows:

$$t=\left\{ {\begin{array}{*{20}{c}} {{t_1}}&{t \leqslant {t_1}}&{{t_1}=\frac{{{t_2}}}{f}} \\ t&{{t_1}<t<{t_2}}&{} \\ {{t_2}}&{{t_2} \leqslant t}&{} \end{array}} \right.$$

(13)

In the equation, t₁ represents the lower bound of the transmission rate t, t₂ represents the upper bound of the transmission rate t, and f is the enhancement factor for the transmission rate. t₁ is set as a constant, while t₂ is the average transmission rate of non-bright regions. The above redefines the value range of the transmission rate, which both reduces the transmission rate error in bright regions and ensures that the transmission rate approaches the average value of non-bright regions. This achieves the goal of transmission rate primarily restricted perception, thereby enhancing the image dehazing effect.

Establishment of the secondary restricted perception model for transmittance and the expression of the dehazed image

To prevent the transmittance values of the image’s bright regions from being fixed and to further improve the accuracy of transmittance values, a secondary restricted perception model for transmittance has been designed. This model is incorporated into the expression of the dehazed image, as shown in Eq. (14).

$$J(x)=\frac{{I(x) - A}}{{\hbox{min} ({t_2},t*\hbox{min} (\frac{{255}}{{I(x)}},f))}}+A$$

(14)

In the equation, t₂ represents the upper limit of the transmittance value, and t represents the transmittance value obtained from the primary restricted perception model. To better distinguish between the bright and non-bright regions of the image, it is defined that pixels with values greater than 225 are considered bright regions, while pixels with values less than 225 are considered non-bright regions. For the bright regions in the image, the ratio of the maximum pixel value (255) to the image pixel value typically falls within the range of [1, 1.13]. In this case, the transmission value will be increased. The transmission value is further expanded based on the initially limited perception of transmission, and then the min function is applied again, comparing it with t₂, ensuring that the final transmission value lies within the range [t× ratio, t₂]. For the non-bright regions of the image, the ratio between the maximum pixel value of 255 and the image pixel value is often greater than 1.13. In this case, the transmission value range is set within the interval [t×f, t₂], which further brings the transmission values of the bright regions closer to those of the non-bright regions, completing the secondary limited perception of transmission. Through the design of the secondary limited perception transmission module, the fog-free image expression not only further improves the precision of transmission value estimation but is also applicable to processing both bright and non-bright regions of hazed images.

Design of a brightness adjustment scheme

The above adjustments to the transmittance values enable them to better adapt to both bright and non-bright regions in the image. Considering that the image brightness directly affects the dehazing visualization results, adjusting the brightness of the image after dehazing has become a significant challenge. To address the above issue, the image after dehazing is converted from the RGB color space to the HSI color space. The intensity (I) component of the transformed image is then individually enhanced, and the adjusted HSI components are converted back to the RGB color space. Meanwhile, to select an appropriate brightness enhancement coefficient, the hazy dataset is used as the experimental subject. By adjusting different brightness enhancement coefficients, dehazing processing is performed on the hazy dataset. The impact of various image brightness levels on the SSIM (Structural Similarity Index) of the images in the dataset is explored. The brightness enhancement coefficient S corresponding to the highest SSIM value is then selected. The image brightness adjustment scheme is shown in Fig. 3.

Fig. 3

Image brightness adjustment scheme.

Design of a denoising module for dehazed images

The absence of a denoising module significantly reduces the noise resistance of the dehazing mode⁴². Removing noise has a direct impact and greatly contributes to improving the quality of the image after dehazing. Considering that images are often contaminated by Gaussian noise, which is the root cause of low PSNR performance, and numerous experiments have shown that Gaussian filtering is suitable for handling Gaussian noise, it can effectively filter out Gaussian noise in the image. Based on the above idea, the Gaussian filtering module is integrated into the dehazing model to improve the quality of the dehazed image. Considering that the Gaussian filtering module has different convolution kernel sizes, which may have varying effects on the denoising performance of the dehazed image. To ensure that the image has a good visualization effect and quality after dehazing, three kinds of convolution kernel sizes of 3 × 3, 5 × 5, and 7 × 7 are added sequentially based on the above brightness adjustment module for dehazing, to explore the effect of adding different sizes of convolution kernel sizes to the model on the final dehazing performance. To comprehensively evaluate the image denoising performance, the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) are selected as the performance evaluation metrics. The block diagram of the image denoising module is shown in Fig. 4.

Fig. 4

Block diagram of the image denoising module.

Transmittance primary restricted perception parameter selection experiment

To accurately calculate the transmission values for bright and non-bright regions, and to initially determine a constrained perceptual range for the transmission value t, experiments are conducted on the RESIDE public foggy dataset. The foggy images containing bright regions are sourced from the RESIDE (OTS) dataset, while the foggy images without bright regions are sourced from the RESIDE (ITS) dataset. To accurately calculate the average transmission values for the bright and non-bright regions of the foggy images, 500 images predominantly featuring white regions, such as the sky, are selected from the RESIDE (OTS) dataset for transmission value calculation. Similarly, 500 images without any white regions are selected from the RESIDE (ITS) dataset for the same calculation. The experimental hardware platform is selected as a Windows 11 system, with a CPU model of the 14th Gen Intel^® Core™ i9-14900HX CPU @ 2.20 GHz, 16.0 GB of memory, and a GPU type of NVIDIA GeForce RTX 4060 Laptop GPU GDDR6 @ 8GB. The software platform is PyCharm, with Python version 3.11.11, and the deep learning framework used is PyTorch. The average transmission values for the two regions are shown in Table 1.

Table 1 Bright area transmittance and non-bright area transmittance.

From the above experimental results, it can be observed that the average transmittance value for the bright region is 0.196. In comparison with the transmittance of the non-bright region, the transmittance value is significantly reduced, leading to distortion in the dehazed image. Based on the method of primarily restricted perception for transmittance and formula (13), this paper sets the transmittance value range for t as [0.85, 0.962], where t₁ is set to 0.85 and t₂ is set to 0.962.

Image dehazing experiment

To validate the effectiveness and generalization performance of the proposed dehazing model, experiments are conducted on four test sets. The proposed dehazing model is based on the atmospheric scattering model and does not require training. The experiment includes four test sets: 500 thin fog images, 500 moderate fog images, 500 dense fog images, and 1000 synthetic foggy images. The thin fog, moderate fog, and dense fog images are sourced from the RESIDE (ITS), RESIDE (OTS), and SOTS datasets, respectively. Based on the fog thickness in the images, the foggy images are classified into three fog levels. The classification criterion used is the Dark Channel Mean (DCM) of the image. Images with DCM values in the range [0.00, 0.20) are classified as thin fog images. These images remain relatively clear, with slightly reduced contrast, and most details are still visible. Images with DCM values in the range [0.20, 0.40) are classified as moderately foggy images. In these images, noticeable blurring appears, the contrast is lower, and some details are lost. Images with DCM values in the range [0.40, 1.00] are classified as dense fog images. These images are severely blurred, appear predominantly white, and the targets are difficult to distinguish. In the atmospheric light value estimation module based on weight allocation, it is considered that the highest pixel value mapped to the original image often corresponds to the final atmospheric light value. Therefore, a weight of 0.5 is assigned to the updated value. Since the pre-update value typically has some deviation from the final atmospheric light value, a weight of 0.2 is assigned to the pre-update value. Additionally, the average value of the pre- and post-update values can provide a comprehensive assessment of the atmospheric light value, so a weight of 0.3 is initially assigned to the average value. In the transmission restricted perception module, the transmission enhancement coefficient f is calculated to be 1.13. The experimental hardware and software platform for the four foggy datasets are the same as those used in the transmittance Primary Restricted Perception Parameter Selection Experiment.

Dehazing comparative experiment in thin fog scenes

To validate the effectiveness of the DWARP algorithm, it is compared with other image enhancement, image restoration, and deep learning-based methods, such as Retinex, Histogram Equalization (HE), C2Pnet³, DCP⁹, DCM², PSD³¹, STH⁸, and RIDCP³⁷. The above dehazing models are tested using open-source public code. The parameters of the DWARP algorithm are normalized, with the minimum filter window size set to 15, and the brightness adjustment and denoising modules are not included in the DWARP algorithm for this test. The visualization and performance evaluation results on the thin fog dataset are shown in Figs. 5 and 6.

Fig. 5

Dehazing visualization results in thin fog scenes.

From the dehazing results above, it can be observed that the dehazing outcomes obtained using the various models exhibit significant differences, primarily in how they handle the bright regions of the foggy images. The results obtained using the Retinex algorithm show some degree of distortion and color shift. The images processed using the HE and DCP algorithms exhibit noticeable distortion in the bright regions, with a considerable difference between the dehazed image and the original image. The dehazing results obtained using the STH algorithm, RIDCP algorithm, and DWARP algorithm exhibit good visual quality, effectively handling bright regions such as the sky. To quantitatively evaluate the dehazing performance of these models, image PSNR, SSIM, VIF, FOM, NIQE, and BRISQUE are selected as the evaluation metrics. The dehazing performance results obtained on the thin fog dataset are averaged, and the statistics are shown in Fig. 6.

Fig. 6

Dehazing performance evaluation results in the thin fog scene.

From the PSNR performance evaluation results of the dehazed images, it can be observed that the PSNR values obtained using the DCM and Retinex algorithms are relatively low, indicating that these dehazing models have poor noise-handling capabilities, leaving a certain level of noise in the dehazed images. The DWARP algorithm achieves the highest PSNR value, reaching 33.07 dB, which demonstrates a clear advantage over other mainstream dehazing models. From the SSIM performance evaluation results, it can be seen that the dehazing results obtained using the PSD algorithm are not ideal, with an average SSIM value of only 68.19%. The dehazing SSIM performance using the STH, RIDCP, and DWARP algorithms all exceeded 90%, with the DWARP algorithm achieving the highest SSIM value of 93.94%. This indicates that the dehazed image obtained using the DWARP algorithm is the most similar to the original image. From the VIF performance evaluation results, the DWARP algorithm still shows a significant advantage over other mainstream dehazing algorithms, indicating that the dehazed image has the best fidelity and the highest structural similarity to the original image. In terms of the FOM performance evaluation results, the DCM algorithm achieves better performance, suggesting that the dehazed image retains the edges well and preserves edge details effectively. The ability to recover edge details is an area that the DWARP algorithm needs to focus on optimizing in the next steps. From the perspective of image NIQE and BRISQUE performance evaluations, the DWARP algorithm demonstrates good dehazing performance. Specifically, the image NIQE performance reaches 3.04, indicating that the dehazed image appears more natural and realistic, with better quality. In summary, the DWARP algorithm shows significant advantages across all evaluation metrics, validating the effectiveness and superiority of the proposed algorithm.

Ablation experiment of the image brightness adjustment module

To explore the impact of brightness enhancement on the dehazing performance of images and select an appropriate image brightness enhancement coefficient S, a study on the brightness adjustment method is conducted based on the models mentioned above. First, the brightness enhancement coefficient S is defined to vary in the range [1.00, 1.1] with a step size of 0.01, and the changes in dehazing performance on the thin fog dataset are calculated. The dehazing visualization results obtained by varying the brightness enhancement coefficient on the thin fog dataset are shown in Fig. 7.

Fig. 7

Dehazing results under different image brightness enhancement factors (s).

As shown in Fig. 7, after adding the brightness adjustment module to the DWARP algorithm, the visual effects of the dehazed image are enhanced. The image features become more pronounced, and some details are revealed. To obtain the optimal brightness adjustment coefficients, this study evaluates the dehazing performance for various brightness enhancement coefficients S, and the results are shown in Table 2.

Table 2 Performance evaluation results under different image brightness enhancement factors (S).

As shown in Table 3, the dehazing performance varies with different brightness enhancement coefficients. In terms of PSNR values, as the image brightness increases, the PSNR value gradually decreases, indicating that enhancing the image brightness can reduce the model’s noise resistance to some extent. Regarding the SSIM performance, the SSIM value first increases and then decreases as the image brightness is enhanced. The peak average SSIM value occurs at S = 1.05. To ensure the dehazed image retains high structural similarity, S = 1.05 is chosen as the optimal brightness enhancement coefficient.

Ablation experiment of the image denoising module

To verify whether the introduction of a filtering module has a beneficial impact on the dehazing performance of images, a Gaussian filtering module is incorporated into the brightness adjustment process. Considering that different kernel sizes in Gaussian filtering may have varying effects on the dehazing result, potentially preventing the achievement of the best dehazing performance, experiments are conducted using three different filter kernel sizes: 3 × 3, 5 × 5, and 7 × 7, which are added to the original model. The dehazing visualization results obtained on the thin fog dataset are shown in Fig. 8.

Fig. 8

Dehazing results with different filter kernel sizes.

To quantify the experimental results, an ablation study is conducted on the thin fog dataset with Gaussian filtering models using different kernel sizes. The experimental results are shown in Fig. 9. When a 3 × 3 image denoising module is introduced, the average PSNR of the image reaches 38.46 dB, but the average SSIM decreases to 91.98%. Similarly, after introducing 5 × 5 and 7 × 7 filter kernels, the results show that while image quality is improved, SSIM performance decreases to some extent. From the VIF performance evaluation results, it can be observed that when the 3 × 3 image denoising module is introduced, the VIF performance reaches its peak, indicating that the introduction of the 3 × 3 denoising module is most beneficial for the model to achieve the best fidelity. Based on the analysis above, we incorporate the 3 × 3 Gaussian denoising module into the dehazing model.

Fig. 9

Changes in dehazing performance after introducing different denoising modules.

Overall, when the denoising module was incorporated into the model, it significantly improved the quality of the dehazed images, but at the same time, it reduced the similarity between the dehazed images and the GT ones. Considering the overall performance, when the brightness enhancement module and the 3 × 3 Gaussian denoising module were added, the proposed dehazing model exhibited good dehazing performance. Therefore, the final model integrates both the brightness enhancement and the 3 × 3 Gaussian denoising module based on the original model. It is also important to note whether other dehazing algorithms could similarly benefit from the integration of image brightness adjustment and denoising modules to achieve superior dehazing performance. To explore this hypothesis, ablation experiments were conducted. First, image brightness enhancement (+ S) was applied to all the dehazing algorithms to investigate the effect of brightness adjustment on dehazing performance. Then, on this basis, a Gaussian filtering denoising module (+ S + G) was incorporated to explore the impact of integrating both modules on the dehazing performance of the algorithms. The dehazing performance evaluation results after incorporating the brightness adjustment and Gaussian denoising modules into the dehazing algorithm are shown in Table 3.

Table 3 Dehazing performance of other models with the addition of the two modules above.

Based on the above experimental results, after incorporating the brightness adjustment and Gaussian denoising modules into the dehazing algorithms, the DWARP algorithm still demonstrates a relatively higher advantage. The average PSNR value of the image is 38.46 dB, and the average SSIM value is 91.98%, outperforming the dehazing performance of other mainstream algorithms. When the brightness adjustment module is added to the above dehazing models, the trend of the dehazing performance changes is generally consistent. The PSNR values of the images all decrease to some extent, while the SSIM values show a certain level of improvement. This further indicates that enhancing the image brightness reduces the model’s noise resistance but also enhances the visual quality of the image. Building on this, when a 3 × 3 Gaussian denoising module is further integrated, it can be observed that the PSNR values of the dehazed images increase. This indicates that the introduction of the Gaussian filter module effectively reduces the noise content in the images and enhances the model’s noise resistance. However, the inclusion of Gaussian filtering also leads to a reduction in the visual quality of the dehazed images.

In summary, whether after brightness adjustment or the integration of the denoising module, the DWARP algorithm consistently demonstrates strong performance. When brightness adjustment and Gaussian denoising modules are incorporated into other dehazing algorithms, they improve the model’s noise resistance but also reduce the visual quality. When a denoising module is introduced individually into other dehazing models, it improves the model’s noise resistance but also increases the image’s blurriness. In the case of the algorithm proposed in this paper, it is suitable to integrate both modules. Although the brightness adjustment module reduces the model’s noise resistance, it enhances the visual quality of the dehazed image to a certain extent. When both modules are integrated into the model, they not only improve the model’s noise resistance but also reduce the blurring effect introduced by the denoising module to some extent. Based on the above analysis, other dehazing models are not suitable for image brightness adjustment and denoising processing.

Parameter selection cross-validation experiment

We have selected the most suitable brightness adjustment parameter and the optimal size for the Gaussian denoising module for our model. To verify whether these parameter choices maintain consistent performance across different datasets, we conducted a parameter selection cross-validation experiment on a moderate haze dataset. Similarly, we defined the brightness enhancement coefficient S and varied its value within the range [1.00,1.10] with a step size of 0.01, then evaluated the dehazing performance on the moderate haze dataset. The results are presented in Table 4.

Table 4 Performance evaluation of cross-validation under different enhancement coefficients S.

As shown in Table 4, the experimental results on the moderate haze dataset are consistent with previous findings. As image brightness increases, noise amplification becomes more pronounced, leading to a gradual decline in the model’s noise robustness. Meanwhile, the Structural Similarity Index (SSIM) and Visual Information Fidelity (VIF) metrics exhibit an increasing trend followed by a slight decline. Notably, at an enhancement coefficient of S = 1.05, both SSIM and VIF reach their peak values. However, it is worth noting that at S=1.06, the VIF performance remains the same as at S = 1.05, while the SSIM performance is slightly lower. Therefore, we select S = 1.05 as the optimal brightness enhancement coefficient. Based on this, we further integrate Gaussian denoising modules of different sizes, and the resulting dehazing performance is presented in Table 5.

Table 5 Performance evaluation of cross-validation under different filter kernel sizes.

From the experimental results, it can be observed that incorporating denoising modules of different sizes into the model significantly enhances its noise robustness. However, this comes at the cost of a gradual decline in SSIM and VIF performance. Notably, when integrating a 3 × 3 Gaussian denoising module, the model achieves the optimal SSIM and VIF values. Considering the impact of different denoising modules on dehazing performance, we select the 3 × 3 Gaussian denoising module for integration into the dehazing model. These experimental results also validate the consistency of our parameter selection for brightness adjustment and the Gaussian denoising module.

Dehazing comparison experiment in moderate haze scenario

To further validate the generalization and effectiveness of the proposed algorithm, the above models are re-tested on the moderate fog dataset. The brightness enhancement module with a brightness enhancement coefficient S = 1.05 and the Gaussian denoising module with a 3 × 3 filter size and a standard deviation of 1 are added to the DWARP algorithm, while these two modules are not included in the other dehazing models. The dehazing visualization results for the above models are shown in Fig. 10.

Fig. 10

Dehazing results of the proposed method and mainstream algorithms in moderate haze scenes.

From the above dehazing visualization results, it can be observed that when processing moderately foggy images, the dehazing results obtained using the HE and DCP algorithms still exhibit significant distortion. In the case of the DCP algorithm, the dark channel prior theory is not suitable for handling the bright regions of foggy images. The computed transmission values are lower than the actual values, leading to distortion. Similarly, the dehazing effect obtained using the PSD algorithm in the bright regions is also not ideal. The dehazing results obtained using other algorithms exhibit a certain degree of color shift, such as with the PSD algorithm, leading to a significant loss of detail information in the dehazed image compared to the original clear image. The dehazing results obtained using the RIDCP and DWARP algorithms are relatively better, with lower distortion and the dehazed images being closer to the original images. To quantitatively assess the dehazing performance of each algorithm, performance evaluations of the dehazed results from the above models are conducted, and the results are shown in Fig. 11.

Fig. 11

Dehazing performance evaluation results in the moderate fog scene.

From Fig. 11, it can be seen that the dehazing results obtained using the above models vary. In terms of the PSNR performance of the dehazed images, the dehazing performance of all the algorithms is generally below 30 dB. However, the DWARP algorithm achieves an average PSNR value of 39.99 dB, showing a clear advantage over other mainstream dehazing algorithms. From the SSIM performance evaluation results, the STH algorithm achieves the best dehazing results, with the DWARP algorithm coming second, achieving 88.41% dehazing performance. However, in terms of PSNR performance, DWARP performs significantly better than STH. According to the VIF performance evaluation results, the DWARP model achieves the optimal dehazing performance with a value of 0.89, indicating that the dehazed image has the highest similarity to the original image and the best fidelity. From the FOM performance evaluation results, the DCM and DWARP algorithms achieve relatively good dehazing performance, indicating that these two dehazing models have certain advantages in preserving edges. According to the NIQE and BRISQUE performance evaluation results, both the DCM and DWARP algorithms also show good dehazing performance, suggesting that the dehazed results obtained from these two models are more natural and realistic, with better image quality. From the BRISQUE performance evaluation results, it can be seen that the dehazing performance of the above models is generally higher than 20, indicating that there is still room for improvement in the image quality after processing. Overall, the DWARP algorithm maintains good dehazing performance on the moderate fog dataset, further validating the effectiveness of the proposed algorithm.

Dense fog scene dehazing comparison experiment

Dense fog is an effective scenario for testing the model’s effectiveness and generalization performance. The above models are re-tested on the dense fog dataset. The DWARP algorithm includes a brightness enhancement module with a brightness enhancement coefficient S = 1.05 and a Gaussian denoising module with a 3 × 3 filter size and a standard deviation of 1. The dehazing results and performance evaluation results are shown in Figs. 12 and 13, respectively.

Fig. 12

Dehazing results of the proposed method and mainstream algorithms on the dense fog dataset.

Fig. 13

Dehazing performance evaluation results in dense fog scenarios.

From Figs. 12 and 13, it can be observed that the proposed algorithm still demonstrates good performance on the dense fog dataset. The image PSNR achieved by the proposed algorithm is 38.29 dB, and the SSIM performance is 83.81%, indicating that the proposed dehazing algorithm also has certain advantages in dense fog scenes compared to other mainstream dehazing algorithms. The DWARP algorithm achieves noise resistance performance above 30 dB across all three fog datasets, showing that the dehazing model not only performs well in dehazing but also maintains good denoising capabilities, thereby improving the quality of the dehazed images. From the image VIF performance evaluation results, the DWARP algorithm demonstrates good image fidelity. Regarding the image FOM performance evaluation, the C2Pnet algorithm achieves the best dehazing performance, indicating that the C2Pnet algorithm has strong edge recovery capability on the dense fog dataset. From the image NIQE performance evaluation results, both the RIDCP and DWARP algorithms achieved good dehazing performance, further validating that these two dehazing models produce more natural and realistic post-dehazed images. According to the image BRISQUE performance evaluation results, the DCM, RIDCP, and DWARP algorithms achieved good dehazing performance, indicating that these models yield better dehazing results. These experimental results once again confirm that the proposed dehazing model demonstrates strong overall performance.

Comparative experiment of defogging under synthetic foggy

To further verify the generalization and effectiveness of the proposed model, experiments were conducted on a self-constructed synthetic foggy dataset. The synthetic foggy dataset contains 1,000 pairs of foggy and clear images. The clear images are sourced from the RESIDE (OTS) dataset and real-world images collected from actual scenes, while the corresponding foggy images are generated by applying an atmospheric scattering model to simulate fog. Foggy images with varying levels of fog density were generated by controlling the fog density parameter β. Four different β values (β = 0.05, 0.1, 0.15, and 0.2) were used to add fog to the clear images, with 250 foggy images generated for each β value. The DWARP algorithm was enhanced by incorporating a brightness enhancement module with a coefficient S = 1.05, along with a 3 × 3 Gaussian denoising filter with a standard deviation of 1. The dehazing results obtained using the above model on the synthetic foggy dataset are shown in Fig. 14.

Fig. 14

The dehazing visualization results of the above dehazing model on the synthetic hazy dataset.

The experimental results above show that the dehazing models yield significantly different results on the synthetic foggy dataset. To better observe the dehazing effects in the bright areas of the images and the recovery of detailed information by the different models, a set of experimental results has been selected for a more detailed analysis, as shown in Fig. 15.

Fig. 15

Comparison of dehazing effects in the bright areas of the images by the above dehazing models.

The experimental results show that the dehazing effects of the HE, DCP, and PSD algorithms in the bright areas of the synthetic hazy images exhibit significant distortion. The dark channel prior theory is not suitable for processing bright areas, such as the sky, which distorts these regions when using the DCP algorithm. The dehazing results obtained by the C2Pnet and DCM algorithms also lead to the loss of a substantial amount of image detail, resulting in a certain degree of color shift compared to the original image. The dehazing results obtained using the RIDCP and DWARP algorithms exhibit good visual effects with relatively low image distortion. Among them, the dehazing results obtained by the DWARP algorithm are closest to the original image in terms of color and detail recovery, and the dehazed images appear more realistic and natural. Through the above experiments, it can be observed that image enhancement-based dehazing algorithms often perform poorly in processing bright regions, failing to effectively handle the bright areas of the image. Similarly, deep learning-based dehazing methods show varying dehazing results on the synthetic hazy dataset. To further validate the performance and complexity of the above models, we evaluate the dehazing performance of these models, and the results are shown in Fig. 16.

Fig. 16

Dehazing performance evaluation results of various dehazing models on the synthetic hazy dataset.

From the image PSNR performance evaluation results, it can be observed that the dehazing models exhibit weak noise reduction performance, with the PSNR values of the dehazed images generally below 30 dB, indicating that there is still some noise in the dehazed images, which severely affects their quality. In contrast, the dehazed images obtained using the proposed dehazing model achieved a PSNR value of 38.28 dB on average, indicating that the proposed model exhibits good noise reduction performance. From the SSIM performance evaluation of the dehazed images, the proposed dehazing model also shows a clear advantage, with an average SSIM value of 88.81%. According to the VIF performance evaluation results, both the C2Pnet and DCM algorithms achieved comparable dehazing performance, while the DWARP algorithm achieved the best dehazing performance, indicating that the dehazed images have the best fidelity and the highest similarity to the original images. From the FOM performance evaluation results, the DCM algorithm achieved the best dehazing performance, with the DWARP algorithm coming second, also showing good dehazing performance. This indicates that both of these dehazing models achieved better edge restoration effects. According to the NIQE and BRISQUE performance evaluation results, the DCM, RIDCP, and DWAEP algorithms achieved relatively good dehazing performance. The DWAEP algorithm achieved a performance of 5.04 in NIQE and 32.55 in BRISQUE, which demonstrates a clear advantage. Overall, the proposed dehazing algorithm demonstrates good generalization performance, achieving significant advantages on the self-made synthetic hazy dataset as well, thereby validating the effectiveness of the proposed model. To verify the dehazing efficiency of the proposed algorithm, the average dehazing time for the models discussed above and the proposed model across four datasets was statistically analyzed. The experimental environment and parameters were consistent with those mentioned earlier, and the results are shown in Fig. 17.

Fig. 17

Dehazing efficiency of the above dehazing models on four datasets.

As shown in Fig. 17, the dehazing efficiency of the above models varies. Overall, image enhancement-based dehazing algorithms achieved better dehazing efficiency. However, the dehazing results from these algorithms are not ideal as they exhibit distortions, particularly in bright areas. The DCP algorithm does not perform well in bright areas of the image and has relatively poor noise resistance. Although it achieves good dehazing efficiency in the above datasets, its dehazing results still need improvement. In comparison, deep learning-based dehazing methods, such as DCM, tend to have lower dehazing efficiency, but they can deliver better dehazing performance. The STH algorithm generally achieves better dehazing results, but its dehazing efficiency is relatively low. The DCM, RIDCP, and DWARP algorithms, overall, deliver good dehazing performance and also excel in dehazing efficiency. Among them, the DWARP algorithm has significant advantages in both dehazing visualization effects and efficiency, achieving real-time performance. Overall, the DWARP algorithm not only effectively handles bright areas in images, such as the sky, but also demonstrates good dehazing efficiency and excellent noise resistance, validating the effectiveness and superiority of the proposed algorithm. The DWARP algorithm can be applied in related fields, such as intelligent transportation, driver assistance, and maritime safety, providing clearer and higher-quality images. This contributes to advancements in these areas, improving the efficiency and accuracy of intelligent systems in daily operations, and has a positive impact on our work and daily lives.

Conclusions

In the field of image dehazing, the dehazing performance in bright areas and the model’s noise resistance are important performance evaluation metrics. Currently, dehazing algorithms do not handle these two issues effectively. To address these problems, we propose a dehazing algorithm based on light value weight allocation and constrained perception (DWARP). We sequentially designed the following modules: the atmospheric light value estimation module, the transmittance-constrained perception module, the haze-free image estimation module, and the brightness adjustment and image denoising module. First, the effectiveness of the DWARP algorithm was validated on the light fog dataset through experiments. Then, brightness adjustment was applied to enhance the visualization effects, and a denoising module was added based on brightness adjustment. This module selects the most suitable Gaussian filter kernel size for the model, effectively improving the quality of the dehazed image. Finally, to validate the effectiveness of the proposed algorithm, we conducted dehazing comparison experiments with mainstream dehazing algorithms in moderate fog, dense fog, and synthetic fog scenarios. The experimental results show that the DWARP model also yields good dehazing results on the aforementioned datasets. To validate the dehazing efficiency of the proposed algorithm, a comparison was made with mainstream dehazing algorithms. The results indicate that the proposed dehazing model demonstrates good dehazing efficiency. This research effectively prevents distortions in the dehazing results of bright areas in images and enhances the model’s noise resistance. It provides a new method and approach for image dehazing in fields such as intelligent transportation, contributing to the progress and development of these related areas.