Introduction

Understanding the risk of flood hazards is important to reduce damages and support infrastructure design and operations. Flood patterns can be affected by changes in streamflow, the accumulated winter snowpack, and the timing of snowmelt. Although the risk of flooding varies across the United States (US), most areas, including dry and mountainous regions, are susceptible to floods1,2. Human-induced climate change may cause river floods to become larger or more frequent than usual in some places, yet smaller and less frequent in others3. Studies have shown that global warming will cause more intense and frequent precipitation events4, which, in turn, will affect river flooding5. In the Western United States (WUS) region, river flows are regulated by the mountainous snowpack that serves as a natural reservoir, storing water during the wet season and gradually releasing it through melting during the warmer months. In recent years, however, the WUS has experienced extreme snowpack variability, coupled with a significant decline over the past few decades6, and an anomalously high snowpack accumulation during the 2022–2023 winter7. Warmer winters also lead to more precipitation falling as rain6,8 and earlier snowmelt, which can overwhelm reservoirs in spring and contribute to drier conditions during the summer9. All these phenomena have made it increasingly challenging to predict changes in streamflow.

The scientific literature offers several studies of flood changes over different parts of the globe10 including southeast Asia11,12, central Europe13,14 and over the contiguous United States (CONUS)16,17,18,19,20. For example, a recent study20, using a conventional statistical approach to estimate changes in the projected flood magnitude, revealed a robust spatial pattern across models, indicating a general increase in flooding throughout CONUS, particularly in the Northeast and Southeast regions, and decrease in Southwest regions. An earlier study19 highlighted the impact of climate change on flood magnitude in the Pacific Northwest, noting a shift from snowmelt-driven floods to those driven more by precipitation. Another study18 examined changes in floods over the past 60 years in the WUS and found a decrease in the frequency and magnitude of rain-on-snow floods. Additionally, recent research10 suggested that global warming, with temperature increases of 1.5 to 3.0 °C, will lead to more frequent and severe floods in many parts of the world. However, these studies lack a detailed basin-level flood frequency analysis, and the underlying causes of flood patterns are still underexplored in the existing literature. In the present work, we aim to build upon previous research by analyzing projected flood patterns over CONUS at a basin level and provide insights about the possible drivers of such patterns.

Streamflow is a hydrological variable essential for monitoring and forecasting floods and droughts. It provides timely information on water availability at the basin outlet by integrating all the losses from precipitation and incorporating the time delay after snow accumulation. Given its importance, the U.S. Geological Survey (USGS) maintains thousands of stream gauge networks across the United States21 to collect measurements. This observational USGS dataset is a critical resource for analyzing weather and climate-driven flood frequency for the historical period. A well-calibrated model for discharge estimation is thus essential to assess the impacts of climate change on future flooding.

In recent years, Deep Learning has been widely used to tackle complex calibration issues in traditional hydrological models. In particular, Long Short-Term Memory (LSTM) network has become an increasingly popular solution due to its ability to process sequential data22. LSTM is a type of recurrent neural network that includes dedicated memory cells to store long-term information. Specifically, its “gates” configuration can control the flow of the information within the LSTM model22. These memory cells are thus comparable to the state vectors used in traditional dynamic models, making LSTM a strong candidate for modelling hydrological processes such as watershed dynamics and discharge. Several hydrological studies have been conducted based on the LSTM model. For example, an LSTM model has also been used to analyze flood susceptibility in China to capture local spatial information on flood23. Another LSTM-based study14 was used to demonstrate that the recent changes in river flood in Europe were primarily driven by the changes in precipitation, antecedent precipitation (i.e., excessive soil moisture), and snowmelt. For the US area, several studies21,22,23 have showcased the ability of the LSTM model to estimate the long-term timeseries of streamflow comparable to the values observed at existing gauges and to provide reasonable estimates at ungauged sites. These promising LSTM applications suggest that this modeling framework has the potential to be extended by incorporating climate projection inputs to simulate future river discharges, thereby facilitating flood frequency analysis.

In this study, we expand on previous efforts25,26 and leverage the LSTM capabilities to estimate discharge at diverse basin scales (from 100 km2 to 39,000 km2). Our results are derived by training the LSTM model using downscaled and bias-corrected climate input datasets at 638 river gauge locations. Our goal is to analyze future changes in flood frequency and intensity in response to future climate change over CONUS, while maintaining the ability to analyze results at a basin level. The scientific questions we aim to explore are: (i) In which areas of CONUS will floods become more/less frequent in the future? and (ii) What are the underlying causes governing the regional changes in future flood trends?

Methodology

LSTM model framework and input datasets

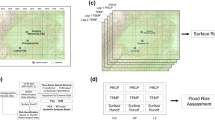
Figure 1 presents the study framework outlined in this research. Our first step (Fig. 1, block 1) is to train the LSTM model to estimate long-term (~ 50 years) daily discharge across multiple basins within CONUS22. More specifically, the LSTM model is here employed26 in a sequence-to-value mode, which takes time-series inputs for each individual gauge location, to predict the discharge at the next time step, following the method established in ref26. We trained the model at 638-gauge locations where target discharge data are available over the 1981–2020 period. The training period uses data spanning from 1981 to 2000, while the validation period uses data from 2001 to 2020. We tested the model in basins different from the ones the model was trained on. Hence, a traditional “out-of-sample test” was done with k-fold cross validation by randomly splitting the basins into k groups of approximately equal size25 (in our case k = 12). The model was then trained with basins in k-1 groups and tested with the hold-out group. By repeating the procedure k times, the out-of-sample predictions were made available for each basin. The training loss function of the LSTM model is the Nash-Sutcliffe Efficiency (NSE29, Methods), averaged over the basins within the training batch. This metric is preferable to the traditional Mean Squared Error (MSE) to avoid overweighting the mean large streamflow values30. As described in Table 1, the input variables to the LSTM model include three types of information: (1) basin-averaged time-series of 5 different meteorological variables (i.e., daily precipitation, maximum and minimum temperature, solar radiation, and specific humidity) from the reference Gridded Surface Meteorological (gridMET) dataset31 at 4 km resolution; (2) static (climatological) climate indices; and (3) static basin attributes (such as the catchment elevation, slope, size, land cover, and soil properties, from HydroAtlas32). Fig. S1 illustrates the input data time-series driving the LSTM model and their corresponding target, i.e., the estimated streamflow time-series, at one of the gauged sites. Observed long-term streamflow time-series (target data) are derived from USGS dataset at the 638 river sites.

Fig. 1
figure 1

Schematic of the study workflow and objectives: (1) training of the LSTM model; (2) utilizing the trained LSTM model to simulate projected streamflow; (3) performing flood frequency analysis with the simulated streamflow using the best fitted distribution among Generalized Extreme Value (GEV), General Pareto (GP), and Log-Pearson3 (LP3).

Full size image

The model input sequence length is optimized to be 270, where 269 days of inputs are used to predict the discharge of the 270th day26. We trained the model for 30 epochs with batch size of 1028, randomly selected from multiple basins. Other hyperparameters are learning rate and dropout that are kept 0.3, and 0.45 respectively. The model has one layer that includes 256 hidden state cells.

Simulation of projected streamflow

Our second step (Fig. 1, block 2) is to use the trained LSTM model to simulate the historical, and the projected streamflow under the Representative Concentration Pathways (RCP) 8.5 emission scenario. To predict historical and future flood changes, we incorporate climate information simulated by 16 Global Climate Models (GCMs) of CMIP533 (Table 2) that have been downscaled and bias-corrected by the Multivariate Adaptive Constructed Analogs (MACA)34 project. The multi-step MACA bias correction method uses a constructed analog approach for developing fine-scale gridded meteorological data using a library of observed (gridMET) patterns for the CONUS region34. The climate variables are downscaled to 4 km spatial resolution at a daily scale using gridMET31 as the reference meteorological dataset. Note that, for consistency, the gridMet observational dataset used in MACA is also the dataset that we choose to employ on our LSTM model training to improve the predictability of our projected discharge.

Flood frequency analysis (FFA)

Our third and final step (Fig. 1, block 3) is to estimate flood return periods and intensities under both current and future climate scenarios. To calculate the flood threshold for specific return periods, we evaluated the goodness-of-fit (GoF) of different distributions—Generalized Extreme Value (GEV), General Pareto (GP), and Log Pearson Type 3 (LP3)—against the observed annual maxima using the skill score (SS). The SS was calculated for each of the 638 sites. A perfect value for SS is 1. For each distribution we then derive the boxplot of the SS values from all the sites (see results in Fig. 3b). The key finding of this test was that LP3 best fits the observed maxima in most CONUS sites as the boxplot shows that the median of LP3 is closer to 1 than the other distributions. We then used LP3 to conduct flood frequency analysis to understand the climate impacts on the future floods. By comparing the simulated discharge-driven flood frequency curve for the future early-century (2006–2054), and late-century (2050–2098) with respect to the historical baseline period (1951–1999) using the LP3 distribution, we determined the relative changes of future 10-year and 100-year flood magnitudes.

Results

LSTM model performance and feature importance analyses

We first evaluated the LSTM model performance in accurately predicting river discharges at the untrained gauged sites using the NSE29 metric (Fig. 2a). The results indicate that LSTM can achieve an overall satisfactory performance, with median NSE values greater than 0.65. In the Eastern CONUS, the model achieved NSE values exceeding 0.8, while there are a few sites in the midwestern region where the NSE values remain between 0.2 and 0.3. Overall, the median NSE values give us confidence that the LSTM model should be able to predict discharge at the ungauged sites with reliable accuracy. To assess the accuracy of the peak streamflow estimation, we also calculate the NSE of the 99th percentile flow. Fig. S2 shows an NSE value above 0.6 for predicting the 99th percentile of streamflow at most sites (median), indicating a high level of accuracy in the peak discharge prediction. Note that we also conducted an analysis comparing the performance of our LSTM model to various traditional physical hydrological models, obtaining competitive skill of the LSTM in predicting daily discharge (see Fig. S3, and the discussion in the Supplementary Materials).

Fig. 2
figure 2

(a) LSTM performance over CONUS river sites based on the Nash-Sutcliffe Efficiency (NSE) metric, and (b) Feature importance test of the LSTM model. The x-axis reports the selected predictors, and the y-axis indicates the corresponding decrease in NSE triggered by varying the predictor for the validation period of the daily discharge. The boxplot distributions summarize the NSE change results for the selected 638 basins. It indicates the median (horizontal bar), the 25th and 75th percentile interval (box) and the maximum and minimum values (whiskers).

Full size image

We then tested the relative feature importance of the input variables35 within the LSTM model to estimate the relative contribution of each predictor to the streamflow estimation. To do so, we performed a permutation importance test35 (see Methods for details) by randomly shuffling one of the predictors. Figure 2b shows the relative decrease in model performance (measured in terms of NSE changes) resulting from permuting each predictor individually in the LSTM model in all 638 basins. This test reveals that the time-varying precipitation and the basin static attributes are the most important predictors. These results are consistent with our scientific understanding of hydrological modeling, where basin hydrographic properties, soil features, and precipitation are considered the most important drivers of river runoff or streamflow simulations36. In contrast, the NSE median values for temperatures and solar radiation variables lie above zero (dashed line in Fig. 2b), but with a large range of variability: this suggests that these variables, while important predictors for some specific sites, such as in the western CONUS (Fig. S4), are less relevant in other regions. In contrast, specific humidity seems to be a less important feature, when compared to other used predictors.

Selection of the LP3 as the best fitting distribution for flood frequency analysis

Once we estimate the streamflow timeseries with the trained LSTM model, we perform an FFA based on an extreme value (EV) distribution to derive the return period curves. In this section, we show the analyses and results that led us to select the Log-Person III (LP3) as the distribution best fitting the observed annual maximum discharges across years. Figure 3 illustrates the results of the conducted GoF analysis for one site, the Klamath River in California (panel a) and for the aggregated 638 CONUS sites (panel b) summarized as boxplots of Skill Score (SS) values. For the Klamath River site, the reported SS score of 0.87 indicates that LP3 is the best fitted distribution to observations. Similarly, the overall GoF results over CONUS (Fig. 3b) indicate that the SS values for the LP3 distribution are, on average, higher than for other distributions, and closer to the “one” upper bound. The LP3 scores also show a narrower variability range across sites, as compared to the other distributions. Based on this GoF analysis, we chose the LP3 statistical distribution as the best fitting model to estimate the parameters we need for future flood frequency analysis.

Fig. 3
figure 3

(a) Flood Frequency Analysis at the Klamath River in CA using three different fitted extreme value distributions: the Generalized Extreme Value (GEV), the Log-Pearson III (LP3) and the Generalized Pareto (GP). Blue circles represent the annual maximum discharge for each year over the 1971–2020 period (b) Boxplot for skill score of the employed Extreme Value Distributions over the 638 available sites over CONUS.

Full size image

CMIP-based model predictions of flood changes

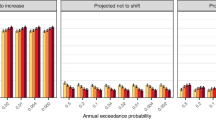
By using parameter estimates of the LP3 distribution, we can now derive the 10-year and 100-year return period curves. As an example, Fig. 4 shows the change in the 10-year flood return period for the late-century period, as estimated from the LSTM simulated flows, based on inputs from each of the 16 individual MACA-derived GCMs. More 10- and 100-year return period results can be found in Figs. S5, S6, and S7. In Fig. 4, the size of the scatter points indicates the historical flood magnitude in m3/s, whereas its color indicates the changes in flood magnitude relative to the historical flood (with blue scale for a decrease, and red scale for an increase). For both return periods, the majority of GCMs show a consistent geographical pattern of future trends. This pattern indicates an increasing trend in flood magnitude ranging from + 10% to + 40% in the East and West coast region, whereas a decreasing trend from − 10% to − 30% in the Southwest part of CONUS for both 10- and 100-year flood events. This emerging geographical pattern is remarkably robust across the 16 different GCMs (Fig. 4) albeit some model discrepancies exist in terms of model sensitivity and variability features. For example, the GCM, MIROC537 predicts between − 10 to + 10% changes in 10-year flood intensity by the late century for the sites in Missouri, where all the other climate models indicate a + 30% to + 40% change. Similarly, IPSL-CM5A-LR and MIROC5 predict decreasing trends of about − 10–0% for the Southern Texas sites (colors from blue to white), while all the other GCMs predict an increase in flood intensity (mostly red scatters). Overall, the results indicate that the climate models tend to agree on the trend of the future floods. To illustrate this, we added In the Supplementary Material a figure (Figure S8) showing the percentage of agreement across models.

Fig. 4
figure 4

Changes in 10-year floods at the mid of the 21st century (2006–2054) with respect to the historical period, as projected by 16 GCMs. Each subplot for the different climate models shows a similar pattern, indicating strong agreement among the models regarding the projected patterns of future floods.

Full size image

Changes in future floods at individual basins

From the flood frequency analysis (FFA), we first check if the LSTM model with inputs from GCMs can reproduce the observed discharges in the historical periods. At each selected site in Fig. 5, we note that the available observed historical annual maxima (scatter points) fall within the variability range of simulated historical FFA-derived values (grey-shaded area) with the observed values sitting closely to the mean historical maxima (solid black line). This indicates that the river discharge predicted via LSTM model using inputs from the historical climate simulations realistically represents the observed discharge values during the overlapping historical period.

Fig. 5
figure 5

Projected flood changes at selected sites. Subfigures a-f show the FFA results for individual sites, with historically observed annual maxima depicted as scatter plots, overlaid by the mean FFA results from the GCM ensemble (solid lines), and shaded areas represent the spread from the mean ± standard deviation of the FFA curve across GCMs for each specified period. The two center panels summarize the late-century changes in 10-year and 100-year floods, averaged across 16 GCMs.

Full size image

We also find that, for the sites where flood risk is projected to increase, the FFA mean curve and shaded regions (yellow for the early-century and orange for the late-century) lie above the historical shaded region (grey). For example, in Fig. 5b, showing the FFA results for the Feather River at Oroville in California, a 100-year flood event during the historical period can reach a discharge value of 11,575 m3/s; at the end of the century, however, such a flood event may become an 8-year returning flood event, with more floods beyond that threshold expected. Again, FFA results in Fig. 5a, d-h show that the 100-year flood event may become almost a 9-year to a 50-year flood event depending on the location, indicating that severe floods will occur more often in the late century at those sites. Overall, in most of the sites of the States depicted in red, floods are going to be more frequent in the future, compared to the historical baseline period, with an increase in flood intensity between the early and the late century for both 10-year and 100-year floods. In contrast, for States shown in blue flood magnitudes and occurrences are projected to decrease. For example, in Fig. 5c, the FFA results at Bear River, Utah, shows a decreasing trend of flood intensity and frequency. At this river site, a 10-year flood (of 120 m3/s discharge) during the historical period, may become a 40-year flood event in the early century, and a 100-year flood in the late-century, indicating that the event is expected to be less frequent than during the historical period. Similarly in Cedar Creek, North Dakota (Fig. 5i), a 10-year flood event is expected to become less frequent, transitioning to a 25-year flood by the late century. To facilitate the visualization of results at a basin level, we developed an interactive map of CONUS where the FFA results (as displayed in Fig. 5a-h of selected 9 sites) can be visualized for each of the 638 analyzed sites. The interactive map can be accessed in this link here: https://software.llnl.gov/flood_changes/.

Analysis of underlying mechanisms driving contrasting flood trend

What are the underlying causes governing the pattern in flood trends? To investigate this question, we performed a seasonal climatological cycle analysis of monthly average streamflow from the 16 GCMs. We clustered the 638 basin sites into two groups based on the projected flood trend direction. Group 1 includes 521 sites with increasing trends, whereas Group 2 includes 117 sites with decreasing trends. The goal is to identify, for each group, the potential shifts in the timing, magnitude, and overall pattern of peak streamflow occurrences for the historical and future periods.

The monthly flow climatology for the sites of Group 1 in Fig. 6a indicates a significant projected change in the climatological annual cycle of streamflow. The peak flow is expected to rise from 23 m3/s in March of the historical period, to 25 m2/s in March by mid-century, and 28.5 m2/s in February at the end of the century. These future peak flows are anticipated to occur earlier in the year compared to the historical period, with a decrease in amplitude from April to October. In contrast, Fig. 6b showing the results for Group 2, indicates a significant reduction in peak streamflow from March to August. In May, the peak flow is projected to decrease from 10.5 m2/s for the historical period to 8.5 m2/s by mid-century and 7.5 m2/s at the end of the century. The secondary peak observed in June during the historical period is also expected to become less prominent in the future.

Fig. 6
figure 6

Climatology of the seasonal discharge at the sites that show (a) increasing (b) decreasing trend across CONUS in the future RCP 8.5 scenario; changes in winter Rx5-day precipitation in (c) early century and (e) late century; relative difference of climatological snow fraction between the historical and future (d) early century and (f) late century in the snow dominant catchments.

Full size image

Further analyses of the peak flood months at each site for all three periods; the historical, early, and late 21st century (Fig. S9) show that the peak flood months are shifting 1–2 months earlier, specifically in the mountainous Nevada, Colorado, Wyoming, and North Dakota sites, (belonging to Group 2) where snowpack plays an important role to the streamflow amount.

The increasing flood trend in Group 1 gauged sites can be attributed to the increase in future precipitation. To understand this impact of precipitation on the flood trend, we analyzed the changes in Rx5-day, an annual index capturing the maximum amount of precipitation that falls over a 5-day period. The results indicate a 6–12% increase in precipitation (Fig. 6c and e) across CONUS during the peak flood seasons which vary depending on the site locations (see all seasons in Figs. S10 and S11).

To understand why flood peaks in Group 2 are projected to decrease despite the projected increase in Rx5-day, we examine if there is any significant shift in precipitation from snow to rainfall at these sites. To do this, we first identified the snow-dominated catchments (Methods, Fig. S12) based on the average snow fraction across GCMs (see Methods for more details). As shown in Fig. 6d and f, the snow fraction in the snow-dominant catchments is projected to decrease significantly in the future, from 30 to 15% in the early century, and by more than 50% in the late century, thus leading to a decrease in the streamflow and flood peaks in these domains.

Discussion

Accurate estimations of the peak flow or discharge is necessary to perform river flood frequency analysis and estimate projected streamflow at any location. In this study, we used a deep learning-based LSTM model for estimating long-term daily streamflow values for any ungauged site. The LSTM model, trained using both dynamic meteorological forcing variables as well as static inputs, shows that the model has satisfactory predictive skill (i.e., NSE above 0.6) for both small and large basins. The minimal difference between the simulated historical and observed annual maxima discharges at selected sites (Fig. 5) indicates that the LSTM model trained with gridMET dataset is reliable, giving us confidence that it can be used to estimate future discharge values at both gauged and ungauged sites, driven by the climate model inputs.

Despite discrepancies in the magnitude of relative changes in future floods, most GCMs agree on the overall pattern of changes. Overall, the gauged sites in Southwestern states (Nevada, Colorado, Wyoming, Utah, Arizona, New Mexico) and North Dakota show a decreasing trend (central panel in Fig. 5) of approximately − 10 to − 30%. In contrast, the remaining part of the CONUS shows an increasing trend, particularly in the eastern and western coastal gauged sites (+ 10 to + 40%). This distinct projected regional pattern corroborates with the future flood pattern described in a recent study20, while our research includes FFA results at the basin level, along with analysis of the underlying mechanisms driving these trends.

We conducted further investigations into the changes in seasonal flow and precipitation patterns to understand the underlying causes for the observed regional patterns with contrasting flood trends. In most sites (Group 1, with increasing flood trends) the seasonal cycle shows an increase in winter discharge and a decrease in spring/summer discharge with a clear earlier peak flow in the future. This shift likely results in earlier and intensified winter floods risks in the future. In contrast, The sites in Southwestern CONUS (Group 2) show a decrease in discharge from April to October, possibly due to earlier snowmelt, causing flood peaks to be intensified in winter and consequently reduced in spring and summer9. Various mechanisms have been proposed in the literature to explain these results. For example, mechanism identified for higher streamflow are (i) heavier precipitation events driven by the enhanced moisture-holding capacity of the atmosphere as a result of global warming, lead to increased streamflow5, and (ii) Early snow melt intensifies the peak flood discharge38. Again, prior studies have identified three different mechanisms for a decrease in streamflow: (a) a precipitation shift from snow towards rain that leads to a decrease in streamflow and floods39,40,41; (b) a decrease in snow fraction, with less energy needed to melt snow, allowing for more energy to be available for evaporation, which in turn leads to a decrease in streamflow42; (c) earlier and slower snowmelt accompanied by less snowfall that can be the primary reason for streamflow declines43,44. Our findings identify mechanisms reported in the literature. For instance, increased streamflow is attributed to higher total seasonal rainfall and intensified winter peak due to earlier snow melt (mechanism i and ii), and a decline in streamflow is driven by shifts in precipitation pattern, including less snow and early snow melting (mechanism a, and c).

In our study, it is assumed that basin static variables (one of the leading predictors of the LSTM model) will be unchanged in the future. This is a caveat of our analysis, as basin characteristics, such as land use and land cover, could be altered in the future, and potentially impact future discharge estimates and flood risk. In addition, we also assumed stationary statistical distributions of streamflow for future FFA by considering that the statistical properties (mean and variance) of the LP3 distributions will remain unchanged throughout each of the entire 50-year periods (historical baseline, and, future early, and late century). In future work, we are planning to account for non-stationarity in the fitted statistical distributions.

Conclusions

The results of this study indicate that changes in flood intensity and frequency, in response to climate change, are significant and consistent among different climate models (in terms of the direction of the changes). Regionalization of the changes at a State level helps to interpret more conclusive results on the flood frequency analysis. Overall, our results suggest that the Eastern and Western parts of the CONUS may experience increased precipitation in the future, accompanied with earlier (in the season) and intensified flood events. We offer possible interpretations of the results: an increase in peak discharge and precipitation for the increasing flood trend regions; a decrease in snowpack for decreasing trend regions. Our performance results show reliable skill of the LSTM model to estimate discharge at different basin scales and for both gauged and ungauged sites. Moreover, the developed interactive map allows to drill down the analysis at a basin level for all the 638 analyzed basins. Despite the limitations of the study, the application of the modeling framework can be expanded to any part of the globe for future flood trend analysis, thus enhancing the planning and managing of water resources, and supporting the infrastructure design and maintenance.

Methods

LSTM model input and target data

Inputs: Three types of input data are needed to develop the LSTM river model as described in Table 1. First, the LSTM model was trained using reference basin averaged gridMET31 daily meteorological forcing inputs over the 1981–2020 period. The data are supplemented with both static catchment attributes and static climate attributes incorporated at each time step to represent the basin’s static properties. The static basin attributes are provided from the HydroAtlas32 datasets (basin averaged) and described in the Caravan dataset45, while the static climate indices are calculated as climatology from meteorological gridMET forcing inputs26.

For future climate impact analysis, the static attributes are kept unchanged in the LSTM model. However, the employed meteorological forcing inputs are derived from RCP8.5 climate projections from a total of 16 CMIP5 climate models (Table 2). We retrieved this future projection of the meteorological forcing inputs (Table 1) from the Multivariate Adaptive Constructed Analogs (MACA34) datasets.

Target: The LSTM model predict daily discharge data as outputs (Table 1). To train and validate the LSTM model, we have used the reference discharge data from the United States Geological Survey (USGS; https://waterdata.usgs.gov/nwis/uv/?referred_module=sw) as target data.

Analyzed sites: We selected gauged sites that (1) have a long record of observed data; (2) are not downstream of any dams or reservoirs; and (3) where streamflow is characterized as natural and not controlled by human activities. We gathered a total of 638 sites with catchment areas ranging from 100 km2 to 39,000 km2.

Table 1 LSTM model inputs and target data. All inputs values are averaged over each of the 638 basins of consideration from the 4-km resolution datasets (gridMET, MACA). Target data are USGS station observations of streamflow.
Full size table
Table 2 Details of the 16 GCMs from CMIP5 downscaled and bias-corrected by the MACA project.
Full size table

Evaluation metric for the LSTM model performance

We have used Nash-Sutcliffe Efficiency (NSE29) to evaluate the LSTM model discharge performances. NSE is calculated as:

$$NSE = 1 - \frac{{\mathop \sum \nolimits_{{i = 1}}^{n} \left( {S_{i} - O_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{{i = 1}}^{n} \left( {O_{i} - \bar{O}} \right)^{2} }}$$
(1)

where \(\:{O}_{i}\) is the observed data, \(\:{S}_{i}\) is the simulated data, \({\bar{O}}\)is the mean observed data and n is the total number of time steps. The optimum NSE is 1. The NSE value can become infinitely negative, but below 0, the simulation is not better than the average of the observations46. A NSE value greater than 0.75 is considered “good,” while NSE values between 0.75 and 0.36 are considered “satisfactory”30. The NSE metric is widely used in hydrology because its emphasis on squared errors helps improve estimates of high flows or peak annual flow.

Feature importance test

To identify the relative importance of each predictor, we performed a permutation test35. Specifically, we considered the effect of randomly permuting the values of a specific predictor while holding the values of other predictors unchanged. We then computed the NSE of the model predictions for that shuffled predictor configuration to quantify the NSE change of the predictions compared to the model with unchanged predictors:

$$\:Decrease\:in\:NSE=\:NS{E}_{all\:correct\:feature}-\:NS{E}_{shuffled\:feature}$$
(2)

The higher the decrease in NSE the more important the feature is. For each shuffled predictor, we calculate the decrease in NSE using Eq. 2. Results are reported in Fig. 2b.

Evaluation metric for goodness of fit (GoF)

The LP3 selection was based on the Skill Score (SS) as a goodness of fit metric47,48 illustrated in Eq. (3):

$$\:SS=\:{\rho\:}_{{Q}_{1{Q}_{2}}}^{2}-{\left[{\rho\:}_{{Q}_{1}{Q}_{2}}-\left(\frac{{\sigma\:}_{{Q}_{1}}}{{\sigma\:}_{{Q}_{2}}}\right)\right]}^{2}-{\left[\frac{{(\mu\:}_{{Q}_{1}}-{\mu\:}_{{Q}_{1}})}{{\sigma\:}_{{Q}_{2}}}\right]}^{2}$$
(3)

where \(\:{Q}_{1},\:{Q}_{2}\) are the quantile estimates based on the simulated flow and the observation, respectively, and \(\:{\rho\:}_{{Q}_{1}{Q}_{2}}\) is the correlation coefficient between \(\:{Q}_{1}\) and \(\:{Q}_{2}\). \(\:\sigma\:\) and \(\:\mu\:\) are the standard deviation and mean of \(\:{Q}_{1},\:{Q}_{2}\). A perfect value for SS is 1.

Estimation of snow fraction

Snow fraction is defined as the fraction of precipitation that fall as snow. When the daily mean temperature is below 1 °C, precipitation is considered as snow40. Following this temperature threshold, we identified the days of snow from the precipitation field and calculate the daily total annual snow (S), the daily total annual precipitation (P), and therefore the annual snow fraction (S/P). For snow fraction greater than 0.15, the basin is considered as a “snow- dominant,” basin39. For each snow-dominant catchment, the changes in the snow fraction (results shown in Fig. 6d and f) are estimated as the relative difference of climatological snow fraction between the historical and future periods.