Introduction

Launched on 5 August 2022, the Korea Pathfinder Lunar Orbiter (KPLO) called ‘Danuri’ after the portmanteau of the Korean da for the moon and nuri for enjoy. This mission is a significant milestone for South Korea’s growing space exploration effort1. Danuri, which was developed by the Korea Aerospace Research Institute (KARI), demonstrates South Korea’s deep space exploration capabilities for gathering critical lunar scientific data. The payload includes the space-hardened KPLO Magnetometer (KMAG) that provides high resolution images of the lunar magnetic field1.

KMAG is a vector magnetometer recording the lunar magnetic field at the nominal altitude of 100 km that will decay during the mission’s final phase to about 30 km. The magnetic field from the lunar crust is relatively weakly expressed in the satellite magnetometer measurements, although strong remanent magnetizations characterize the rock samples collected by the Apollo missions2.

In contrast to the Earth’s magnetic field, the lunar magnetic field is no longer dynamo driven. Thus, the KMAG measurements yield important insights on the Moon’s remnant crustal magnetic effects at the impact basins and their antipodes3,4,5,6,7, and more generally on the origin and processes of lunar magnetism (e.g.,8,9,10). They also help constrain our understanding of the interactions of the Moon’s magnetic field with solar wind plasma11,12,13, and the utility in exploring the lunar crust for resources14,15. KMAG’s magnetic field measurements also facilitate mapping subsurface magnetic structures for further insights on lunar magnetism and its evolution.

The resolution of KMAG’s measurements is comparable to that of Japan’s SELENE (a.k.a., Kaguya) lunar mission16. However, the KMAG’s fluxgate magnetometers are operated from the end of a 1.2 m boom, in contrast to the 3.6 m and 12.0 m booms used for NASA’s Lunar Prospector17, and Japan’s SELENE (a.k.a., Kaguya)18 satellite missions, respectively. Due to the KMAG’s shorter boom length, relatively higher levels of instrumental magnetic noise contaminate the lunar magnetic field measurements that are suppressed in the final data processing stage19.

The KMAG’s data processing for crustal magnetic anomalies follows the NASA Planetary Data System’s PDS4 standard. The raw data (RAW) processing stage, for example, extracts the telemetry data recorded on the sensor. Next, the partially processed (PP) stage considers the instrumental calibration with the vector components corrected for orthogonality. The PP-level data are useful for the lunar studies involving magnetic anomalies that substantially exceed the spacecraft/instrument noise and ambient thermal effects, which are mitigated in the final calibration (CAL) level of the data processing19.

The Korea Aerospace Research Institute (KARI)’s planetary data system (KPDS20) at http://kari.re.kr/kpds currently archives all available RAW-to-CAL level KPLO data. However, as of Sept. 13, 2024, when the data for this study were downloaded, the public may only access the RAW- and PP-level KMAG data for the six-month period (Jan. 1 to Jun. 30, 2023). Each data file contains lunar magnetic vector components at the 1 Hz interval in both selenographic (SEL) and selenocentric solar ecliptic (SSE) coordinates19.

This study obtains the first KPLO lunar crustal magnetic anomaly estimates at about 100 km altitude from the PP-level data for the areas of the Gerasimovich crater, Serenitatis Basin’s antipode, Hayford crater, Crisium basin, and Abel crater. Located close to the Crisium basin’s antipode, the Gerasimovich crater may host Crisium basin ejecta with post-deposition remanent magnetic components to further help constrain the magnetic evolution of the lunar crust3,4,5,6,7. The next section outlines the methodology for processing the PP-level data for the latitudinal Bθ, longitudinal Bϕ, and radial Br crustal magnetic anomaly components. The section thereafter demonstrates the capacity of the KPLO anomalies to reproduce earlier crustal anomaly estimates from the LP and Kaguya21 satellite magnetometer observations shown in Fig. 1 for further insights on the lunar crust.

Fig. 1
figure 1

The moon’s topography from Lunar Orbiter’s Laser Altimetry22 with superposed TSH21 magnetic total field anomaly estimates at 100 km altitude. The solid yellow lines delineate the study areas for the (A) Gerasimovich crater (i.e., antipode of Crisium basin), (B) Serenitatis basin, (C) Hayford crater, (D) Crisium basin, and (E) Abel crater study areas, whereas the dashed contours annotated by lower-case letters delineate the applicable antipodes.

Full size image

Methods

The KPLO-measured vector components over each study area or patch were processed for crustal magnetic anomalies according to the Fig. S1 flowchart in the supplementary information file. The KPLO orbits cover polar orbital planes in local time, where the dawn-dusk plane moves every six months to the noon-midnight plane. However, data measured only in the nighttime lunar wake region were selected for the crustal analysis because they tend to be minimally contaminated by external magnetic field effects from the interacting solar wind19. Table 1 summarizes the data processing attributes for the study areas.

Table 1 KPLO data track processing information for the study areas in Figs. 3 and 4, and 5.
Full size table

These data were next separated into subparallel sets of the descending and ascending polar orbital passes to facilitate pass-to-pass wavenumber correlation filtering to help suppress non-crustal anomaly effects23,24,25,26. The ascending and descending passes were further grouped into temporal periods with an approximate repeat interval of nearly 13.7 Earth days to limit altitude variations between neighboring passes in the correlation filtered data. In the case of Gerasimovich crater area, for example, the altitude differences do not exceed 0.5 km for geographically adjacent passes separated in longitude by about 1°.

Over the six-month data collection period, typically 6-to-7 subsets for each set of ascending and descending passes were obtained for each study area. However, before pass-to-pass wavenumber correlation filtering the orbital passes, each of them was least squares fitted with a low-order polynomial that was removed to enhance the higher frequency lunar crustal magnetic components16,27. The passes were also visually screened to exclude some 26 passes that were prominently inconsistent in high frequency and amplitude measurements28. The residual anomalies were next compared with the spherical harmonic TSH21 and/or RSH27 vector anomaly predictions. The subset that differed with the lowest standard deviation and/or highest correlation coefficient was then selected for further processing.

The TSH and RSH anomaly predictions must be used with care here because they are not unique, subject to data measurement and processing errors, and unconstrained by magnetic measurements at the high KPLO altitudes. The TSH21 model, for example, is based on Kaguya and Lunar Prospector magnetic observations at 10–45 km altitudes, whereas the RSH27 model incorporates data only from the Lunar Prospector’s extended mission at 12–48 km altitudes. Thus, the consistencies of the KPLO anomaly predictions with the spherical harmonic anomaly estimates provide insights on the veracity of the KPLO measurements for mapping crustal magnetic anomalies. On the other hand, they also help affirm the utility of the spherical harmonic anomaly estimates at the KPLO altitudes for studies of the lunar crust.

For the selected KPLO subsets, the subparallel passes at the equator are sequentially spaced by an interval of almost 1° in longitude. WCF was then applied pass-by-pass to help suppress the non-crustal noise effects23,24,25,26. Figure S2 in the supplemental information file graphically shows an example for the Gerasimovich crater of how the filtered signals were derived from the raw KPLO vector magnetometer measurements. The supplemental information file provides further details on the WCF in this study.

Figure 2 shows a processing example for estimating the vector magnetic anomalies for the Gerasimovich crater (Fig. 2E) by combing the two subsets in Table 1. Here, the residuals were obtained by subtracting the low-order polynomial fitted curves (Fig. 2A and B), which then were wavenumber correlation filtered to enhance the magnetic crust’s static signals (Fig. 2C and D). Figure S2 of the supplemental information file further illustrates how the filtered signals for the Gerasimovich crater were extracted from the raw KPLO vector magnetometer measurements.

Fig. 2
figure 2

Track-to-track processing of the KPLO vector magnetometer data over Gerasimovich crater. The columns from left to right correspond to Bθ, Bϕ, and Br vector magnetic components. (A) The descending-track residuals where the 2nd order polynomial was subtracted from each descending pass in the selected subset. (B) The ascending-track residuals where the 2nd order polynomial was subtracted from each ascending pass in the selected subset. (C) The wavenumber correlation filtered anomalies extracted from the residuals in (A). (D) The wavenumber correlation filtered anomalies extracted from the residuals in (B). (E) gives the combined wavenumber filtered anomalies from the orbital tracks in the (C) and (D). The black dotted circle delineates the antipodal boundary of the Crisium basin. Table 1 gives further information on the data subsets.

Full size image

The next section compares the gridded KPLO magnetic anomaly features with the prominent higher altitude Lunar Prospector and Kaguya lunar magnetic anomaly estimates over the Gerasimovich crater (Fig. 3), the Serenitatis basin’s antipode (Fig. 4), and the Hayford crater, Crisium basin, and Abel crater (Fig. 5). Figures S3–S7 in the supplemental information file provide additional details on processing the above areas’ KPLO magnetometer data for the crustal magnetic anomalies.

Fig. 3
figure 3

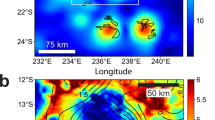
Gerasimovich crater vector magnetic anomaly maps in nT. The columns from left to right give the Bθ, Bϕ, and Br vector magnetic components and total field anomalies. (A) KPLO color-filled vector magnetic anomaly estimates from the residual anomalies in Fig. 2E. The bold black dashed circle approximates the Crisium basin’s boundary about its antipode. Superposed are the contoured TSH anomaly predictions up to degree 100 at the average altitude of 97 km, where the thin black solid and dashed contours mark the positive and negative values, respectively. The correlation coefficients (CC) between the color-shaded and contoured anomalies are posted in the top right corners of the maps. (B) Color-filled anomaly predictions from the vertical cylinder model at the 100 km altitude with the KPLO magnetic anomaly contours superposed. The white dashed circle represents the vertical cylinder model. (C) Color-filled TSH magnetic anomaly predictions at 30 km altitude and degree 450 with the superposed magnetic anomaly contours from the vertical cylinder described in the text.

Full size image
Fig. 4
figure 4

KPLO vector magnetic anomalies in nT over the Serenitatis basin’s antipode with the columns from left to right showing the Bθ, Bϕ, and Br vector magnetic components and the total field anomalies. (A) Color-filled KPLO vector magnetic anomaly estimates at 100 km altitude from the residual anomalies in Fig. S3B. The thick dashed black semicircle approximately delineates the Serenitatis basin’s boundary centered on its antipode. The thin solid and dashed black contours mark positive and negative TSH21 anomaly predictions up to degree 100 at the average mission altitude of 97 km. The correlation coefficients (CC) between the color-filled and contoured anomalies are posted in the top-right corners of the maps. (B) Color-filled, anomaly predictions from the vertical cylinder described in the text at the 100 km altitude with the superposed KPLO anomaly contours. The white dashed circle represents the vertical cylinder model. (C) Color-filled TSH predictions up to degree 450 at 30 km altitude with superposed anomaly contours of the magnetic vertical cylinder.

Full size image
Fig. 5
figure 5

Color-filled KPLO magnetic anomaly estimates over (A) the Hayford crater area with the superposed contours of the RSH27 anomaly predictions up to degree 100. The black thin solid and dashed contours respectively mark positive, and negative anomalies at the mean 98 km altitude of the KPLO data. The thick black dashed circle delineates the poorly known crater boundary (centered at 12.9°N 170.5°W) directly east of the Hayford crater which is present with a small black thick dashed circle centered at 12.7°N, 178.4°W. (B) the Crisium basin with superposed TSH model anomaly predictions up to degree 100 at the KPLO’s mean altitude of 104 km. The thick black dashed line delineates the inner Crisium basin; and (C) the Abel crater with TSH anomaly predictions up to degree 100 at the mean KPLO altitude of 102 km. The thick dashed black circle delineates the Abel crater. All maps are in nT. The columns from left to right show maps of the Bθ, Bϕ, and Br magnetic vector components, and the total field anomalies. The correlation coefficients (CC) between the color-filled and contoured anomaly grids are in Table 1.

Full size image

Discussion

To help test the veracity of the KPLO anomaly predictions, their similarities with the prominent magnetic anomalies mapped by previous satellite magnetometer missions were investigated for the impact crater, antipode, and basins listed in Table 1. The Gerasimovich crater anomaly (Figs. 1 and 2), for example, is well defined at 100 km altitude16 near the Crisium basin’s antipode6. Hence, the anomaly’s source may involve highly magnetized ejecta from the Crisium basin’s impact5,7,29, although iron-rich ejecta from the South Pole Aitken basin’s impact may also have contributed5. Furthermore, the prominent anomaly has been investigated for its effects on the solar wind particles11,30.

Figure 3A shows the KPLO crustal magnetic vector component anomaly estimates for the Gerasimovich area overlaid on the TSH vector anomaly predictions up to degree n = 100 at the data’s average altitude of 97 km. As noted by the correlation coefficients (CC), the KPLO anomalies generally align well with the TSH and RSH models’ predictions. However, the horizontal components show lower similarity than does the radial component due likely to the smaller external field influences on the radial component measurements30.

To first order, the lunar anomaly predictions in Fig. 3A are consistent with the remanently magnetized effects in Fig. 3B from a regional 40 km thick vertical crustal cylinder centered on Crisium’s antipode at (123.5°W, 16.6°S) that may be linked to possible mantle uplift due to crustal disturbances31,32,33. The cylinder model parameters include the radius of 50 km with the depth-to-top of 25 km below the lunar surface, and the magnetization of intensity 0.2 A/m, inclination 20°, and declination 10°.

The black contours in Fig. 3B give the KPLO anomalies superposed on the commensurate color-filled TSH anomalies. The predominantly positive correlation coefficients (CC) between the black-contoured and color-filled grid maps are posted in the upper right corners of the maps. However, at 30 km altitude (Fig. 3C), the anomalies exhibit lower coefficients and high frequency effects, which the lower altitude stage of the KPLO mission can test for further insights on the Gerasimovich crust.

As a further test of the KPLO anomaly estimates, consider the prominent magnetic anomaly maximum over the Serenitatis basin’s antipode on the Moon’s far side in Fig. 4. The anomaly maximum overlies terrain with grooves, mounds, and other landform modifications that are consistent with the effects of Imbrium impact-forming events5,6. Figure 4A shows that the KPLO anomaly estimates generally align well with the TSH anomaly predictions both graphically and quantitatively.

Figure 4B gives the magnetic effects from the Gerasimovich-sized vertical cylinder centered on (165.3°W, 21.5°S) that broadly accommodate the 100 km altitude KPLO anomaly estimates. Here, the vertical cylinder is 50 km in radius, 40 km in thickness, 30 km in depth-to-top, but with magnetization inclination and declination of about − 5° and 0°, respectively. Like for the Gerasimovich crater, the TSH anomaly predictions at 30 km (Fig. 4C) show more higher frequency content. Furthermore, the cylindrical source’s apparent offset from the Serenitatis basin’s antipode may reflect mantle uplift possibly from the effects of the Moon’s largest impact that produced the South Pole-Aitken basin34. Additional constraints on the antipode’s magnetic crust may result as the KPLO mission descends to test the 30 km altitude TSH anomaly predictions in Fig. 4C.

As a further example, Fig. 5A considers the KPLO magnetic anomaly estimates for the area centered on (172.0°W, 14.5°N) that is about 170 km east of Hayford crater. The KPLO anomaly estimates align more closely with the RSH than with the TSH spherical harmonic anomaly predictions as shown in Table 1. Both spherical harmonic models used magnetic anomaly estimates from measurements taken at altitudes below 50 km. However, the TSH model included both the LP and Kaguya data, whereas the RSH model involved only the LP along-track data gradients. The models also differed in how their coefficients were determined. For example, the TSH modeling adopted surface vector mapping (SVM) to transition from regional mapping to global spherical harmonic modeling, whereas the RSH model employed magnetic monopole modeling of the along-track field differences to enhance spatial resolution of the magnetic anomaly predictions.

At 100 km altitude, the CC’s in Table 1 indicate that the two spherical harmonic models at degree 100 yield only marginally coherent anomaly predictions over the Hayford crater area. At 30 km altitude, the correlation coefficients (CCs) between these model predictions at degree 450 are also notably low (0.85 for Bθ, 0.24 for Bϕ, and 0.49 for Br components) relative to the anomaly coherencies of the other study areas.

Paleopole analysis35 of this anomaly area using the LP vector observations at approximately 22 km altitude revealed low inclinations (~ 10°) that align with RSH anomaly predictions. The low-altitude measurements from the KPLO mission’s final phase will provide further constraints on the Hayford anomaly’s characteristics.

On the Moon’s near side, previously mapped magnetic anomalies also validate the KPLO magnetic anomaly estimates for the Crisium basin in Fig. 5B, which likely are linked to partial melting of the mantle from the basin-forming event36. These estimates reveal two distinct dipole features near the basin’s northern and southern rims that are marginally more aligned with the TSH model’s predictions in Table 1. Magnetic point dipole modeling37,38 suggests that the Crisium basin’s magnetic anomalies may involve sources extending from 30 km to as much as 85 km below the lunar surface. The point dipole depth estimates are not unique, so that by the magnetic potential’s equivalent source principle39, the anomalies may also be modeled by sources at shallower depths. The lower altitude KPLO magnetometer measurements clearly may further constrain the crustal sources of the basin’s magnetic anomalies.

A further prominent near-side magnetic anomaly overlies the Abel crater as shown in Fig. 5C, with characteristics similar to the isolated strong anomalies overlying the Reiner-Gamma, Descartes and Sylvester craters16,28,40. The Abel crater’s KPLO magnetic anomaly estimates align well with the higher altitude predictions of both spherical harmonic models in Table 1.

This region also is associated with a lunar crustal swirl41,42 and its strong magnetic effects40, which may involve narrow magnetization variations up to a few kilometers wide buried within a few kilometers of the lunar surface43. The high-through-low altitude KPLO magnetic anomaly estimates will provide comprehensive constraints for enhanced crustal analyses of the Abel crater’s magnetic attributes.

In general, the higher altitude magnetic observations from the KPLO mission may be effectively processed to reduce time varying external magnetic field noise to better resolve the Moon’s static crustal magnetic anomalies. Thus, the magnetometer data from the complete KPLO mission will help test and augment previously mapped anomalies to further enhance studies of the lunar crust.

Conclusions

  1. 1.

    Vector magnetometer observations from the first six months of the KPLO mission confirm several strong lunar magnetic anomalies in the TSH and RSH spherical harmonic models at altitudes of roughly 100 km. Both spherical harmonic models excluded the high-altitude data in their production21,27, to enhance the resolution of their predictions. However, at the higher altitudes, the crustal magnetic anomaly estimates from the spherical harmonic models and KPLO’s measurements are largely consistent and well aligned.

  2. 2.

    To date, lunar crustal analyses have generally ignored the higher altitude magnetic anomalies because of the external magnetic field noise in their marginal amplitudes. However, the KPLO anomaly estimates obtained by this study suggest that the external field noise in the higher altitude observations may be broadly suppressed to the more attenuated noise levels in the lower altitude measurements. Thus, the higher altitude magnetic anomalies have utility in augmenting lower altitude crustal anomalies to further conceptualize and quantify the lunar crust’s magnetic attributes.

  3. 3.

    KPLO’s magnetometer observations are also being processed to suppress spacecraft/instrument noise and ambient thermal effects. This enhancement together with the Danuri’s high-through-low altitude coverage will significantly amplify the utility of the KPLO’s magnetometer observations for lunar crustal studies.