Introduction

By the end of 2019, Wuhan, China, was the source of the corona virus 2019 (COVID-19), which is caused by SARS-COV-2 (severe acute respiratory syndrome corona virus 2). Subsequently, the epidemic\pandemic swiftly spread reached over 210 nations1,2 and continues to pose serious health and socioeconomic difficulties in several regions of the globe. Scientists continue to develop safe COVID-19 vaccines and advance innovative diagnostics. As of now, there isn’t a safe and efficient vaccination or antiviral to combat the pandemic. International and local communities are focused on identify key parameters that influence the virus transmission to control its spread. Various government estimates suggest various preventive strategies to stop the spread of COVID-19, such as wearing a mask, maintain a physical distance, routinely weekly wash your fingers, and escaping sickening persons3,4.

The infectious disease COVID-19 can be transmitted by direct human contact as well as droplet aerosols5,6,7. This illness has ruined many people with few resources across various countries, making it a serious problem for human society. Since COVID-19 is more contagious and more likely to cause a pandemic than SARS, it has spread quickly over the world. This World health Organization (WHO) declared the COVID-19 flare-up to be a global pandemic on March 11 due to the significant increase in the spread of the infection. Fever, cough, malignancy, exhaustion, sputum production, headache, diarrhoea, dyspnoea, and lymphopenia are the signs and symptoms of COVID-198. COVID-19 can result in pneumonia and possibly mortality in more severe situations1. COVID-19 can take up to 14 days to incubate, with a median of about 5.2 days9. A useful tool to concentrate on the mechanism via that a viral illness can spread over a population is mathematical modelling.

Evaluating the safety and quality of vaccinations is the primary goal of the World Health Organization (WHO). In order to ensure vaccine efficacy, WHO works together with researchers throughout the globe to create and implement international standards and norms. While some scientists have researched models of dynamic delaying differential for the COVID-19 outbreak10,11, many others have been drawn to develop alternative models12,13,14,15,16 that deal with vaccination strategies to limit the spread of epidemic diseases. Recently, a number of articles17,18,19,20,21,22 on the effectiveness of newly approved vaccinations have been released. To the best of our knowledge, a few research studies17,23 have been released in an effort to shed light on the relationship between vaccine choice and the (COVID-19) epidemic’s expansion. No one has ever fully analysed the Corona pandemic mathematically using a vaccination model.

The differential equations utilised in the models that were given had some restrictions on their order, but they were still based on classical derivatives. Butt et al. provide a description of the mathematical model of Corona illness in24. Using the integer order SEIQR epidemic model, the author examined the corona virus disease. This study determines the fundamental reproduction number in addition to containing the discrete model, finding the fundamental reproduction number in order to assess stability.

The current paper is organized in a friendly manner. In “Derivation of corona model” section, the mathematical model is introduced and its parameters are thoroughly examined also describle the flow chart of Fig. 1. The fundamental reproduction numbers are defined and analyzed in “Flow diagram” section. The global stability of the disease-free conditions under the NSFD scheme is assessed using the properties of the Lyapunov function in “Feasible region of corona model” section, which also discusses the local stability of the disease-free equilibrium point using the Schur-Cohn criterion. We agree that the numerical solution of the system of ODEs contributes to the methods’ comparatively large complexity. The results are given in the closing segment to represent the entire manuscript.

Fig. 1
figure 1

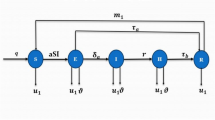
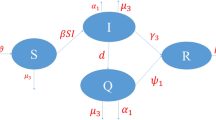
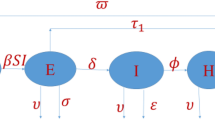
A graphic depiction of the illness energetic in a compartmental model (1).

Full size image

Derivation of corona model

Depending on how the corona virus disease spreads, a number of alternative mathematical models with varying assumptions have been proposed in the literature to far25,26. These models offer numerous benefits to public health planners and policy makers. By adding a class of vaccinated humans, we have created a new SEIQR COVID-19 pandemic model for the actual world in this part.

The following variables were used to model the dynamics of the coronavirus’s transmission among individuals: The human population at time t is divided into five divisions by the model in the susceptible \({\mathbb{S}}(t)\), exposed \({\mathbb{E}}(t)\), infected \({\mathbb{I}}(t)\), quarantine \({\mathbb{Q}}(t)\) and recovered \({\mathbb{R}}(t)\). are the entities in question.

The following set of ordinary differential equations, which are taken from Fig. 1, describe the SEIQR mathematical framework for the corona virus circulation in an organization:

Flow diagram

$$\begin{aligned}\frac{d{\mathbb{S}}}{dt} & =\rho -{\tau }_{1}{\mathbb{S}}{\mathbb{I}}-{\tau }_{2}{\mathbb{S}}{\mathbb{E}}-\omega {\mathbb{S}} \\ \frac{d{\mathbb{E}}}{dt} & ={\tau }_{1}{\mathbb{S}}{\mathbb{I}}+{\tau }_{2}{\mathbb{S}}{\mathbb{E}}-({\upsilon }_{1}+\omega +\Lambda +{\varphi }){\mathbb{E}} \\ \frac{\text{d}{\mathbb{I}}}{\text{dt}} &=\Lambda {\mathbb{E}}-(\omega +{\theta }_{1}+c){\mathbb{I}} \\ \frac{d{\mathbb{Q}}}{dt} &={v}_{1}{\mathbb{E}}-(\delta +\omega +{\theta }_{2}){\mathbb{Q}}\\ \frac{d{\mathbb{R}}}{dt} & ={\varphi }{\mathbb{E}}+c{\mathbb{I}}+\delta {\mathbb{Q}}-\omega {\mathbb{R}}.\end{aligned}$$
(1)

With \({\mathbb{S}}\left(0\right)>0,{\mathbb{E}}\left(0\right)>0,{\mathbb{I}}\left(0\right)>0,{\mathbb{Q}}\left(0\right)>0 and {\mathbb{R}}\left(0\right)>0\).

The state variable and related limits of the recently proposed paradigm, known as COVID-19 are explained in depth in model (1).

Feasible region of corona model

Adding above five equations of the system (1), we have

$$N(t)={\mathbb{S}}+{\mathbb{E}}+{\mathbb{I}}+{\mathbb{Q}}+{\mathbb{R}}$$
$$\frac{dN}{dt}=\rho -\omega {\mathbb{S}}-{v}_{1}{\mathbb{E}}-\omega {\mathbb{E}}-\omega {\mathbb{I}}-{\theta }_{1}{\mathbb{I}}+{p}_{1}{\mathbb{E}}-\omega {\mathbb{Q}}-{\theta }_{2}{\mathbb{Q}}-\omega {\mathbb{R}}$$

From above eq. we can write

$$\frac{dN}{dt}\le \rho -\omega {\mathbb{S}}$$

And

$$\underset{n\to \infty }{\text{lim}}SUP N\le \frac{\rho }{\omega }.$$

where \(N(t)\) is the original inhabitants scope. In specific, \(N\left(t\right)\ge \frac{\rho }{\omega }.\) Thus N and entirely extra variable of the ideal (1) are circumscribed in a section. Thus

$$\Pi =\left\{({\mathbb{S}},{\mathbb{E}},{\mathbb{I}},{\mathbb{Q}},{\mathbb{R}}\varepsilon {\mathbb{R}}_{+}^{5};0\le N(t)\le \frac{\rho }{\omega } :{\mathbb{S}},{\mathbb{E}},{\mathbb{I}},{\mathbb{Q}},{\mathbb{R}}\ge 0 \right\}.$$
(2)

Equilibrium point

A unique non- negative Corona free equilibrium for the model (1) Exist at the point.

  1. a.

    Disease Free Equilibrium \((DFE)=(\frac{\rho }{\omega }, \text{0,0},\text{0,0})\)

  2. b.

    Disease Endemic Equilibrium \(\left(DEE\right)=\left({\mathbb{S}}_{a}^{*},{\mathbb{E}}_{a}^{*},{\mathbb{I}}_{a}^{*},{\mathbb{Q}}_{a}^{*},{\mathbb{R}}_{a}^{*}\right)\)

    $${\mathbb{S}}_{a}^{*}=\frac{\left({v}_{1}+\varphi +\Lambda +\omega \right)\left(c+\omega +{\theta }_{1}\right)}{{\tau }_{1}\Lambda +{\tau }_{2}\left(c+\omega +{\theta }_{1}\right)}>0,$$
    $${\mathbb{E}}_{a}^{*}=\frac{\left(\rho -\omega {\mathbb{S}}_{a}^{*}\right)\left(c+\omega +{\theta }_{1}\right)}{{\tau }_{1}\Lambda +{\tau }_{2}\left(c+\omega +{\theta }_{1}\right){\mathbb{S}}_{a}^{*}}>0,$$
    $${\mathbb{I}}_{a}^{*}=\frac{\Lambda {\mathbb{E}}_{a}^{*}}{\left(c+\omega +{\theta }_{1}\right)}>0,$$
    $${\mathbb{Q}}_{a}^{*}=\frac{{v}_{1}{\mathbb{E}}_{a}^{*}}{\left(\rho +\omega +{\theta }_{2}\right)}>0,$$
    $${\mathbb{R}}_{a}^{*}=\frac{1}{\omega }\left[\varphi {\mathbb{E}}_{a}^{*}+c{\mathbb{I}}_{a}^{*}+\delta {\mathbb{Q}}_{a}^{*}\right]>0.$$

Threshold quantity \(\left({\mathcal{R}}_{0}\right)\)

An estimate derived from epidemiological foundations, the basic reproduction ratio shows the total number of related diseases that result from a only diseased soul in a society that is entirely exposed to the illness throughout that time. The matrices developed for the original disease and the prerequisite for the illness evolution are F(x) and M(x). We used the same methodology as defined in27.

Suppose

$$\mathcal{F}\left(\text{x}\right)=\left(\begin{array}{c}{\uptau }_{1}{\mathbb{S}}{\mathbb{I}}-{\uptau }_{2}{\mathbb{S}}{\mathbb{E}}\\ 0\\ 0\\ 0\\ 0\end{array}\right).$$

And

$$\mathcal{M}\left(x\right)=\left(\begin{array}{c}({\upsilon }_{1}+\omega +\Lambda +{\varphi }){\mathbb{E}}\\ \left(\omega +{\theta }_{1}+c\right){\mathbb{I}}-\Lambda {\mathbb{E}}\\ \left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}-{v}_{1}{\mathbb{E}}\\ \omega {\mathbb{S}}-\rho \\ \omega {\mathbb{R}}-{\varphi }{\mathbb{E}}-c{\mathbb{I}}-\delta {\mathbb{Q}}\end{array}\right).$$

The amount of transmission into and available of the exposed, infected, and quarantine classes, as well as the rate of original contagion positions entering, are represented by functions F and M, accordingly, as fellows

$$F=\left(\begin{array}{c}{\uptau }_{1}{\mathbb{S}}{\mathbb{I}}-{\uptau }_{2}{\mathbb{S}}{\mathbb{E}}\\ 0\\ 0\end{array}\right),$$

where the transition rate of a present or moved case is represented by matrix M, which is calculated as

$$M=\left(\begin{array}{c}({\upsilon }_{1}+\omega +\Lambda +{\varphi }){\mathbb{E}}\\ \left(\omega +{\theta }_{1}+c\right){\mathbb{I}}-\Lambda {\mathbb{E}}\\ \left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}-{v}_{1}{\mathbb{E}}\end{array}\right).$$

The number of \({\mathcal{R}}_{0}\) for the model (1) is the largest absolute eigenvalue of the matrix gives the basic reproduction number,\({\mathcal{R}}_{0}.\) In terms of terminology,

$${\mathcal{R}}_{0}=\frac{\rho [{\tau }_{1}\Lambda +{\tau }_{2}(c+\omega +{\theta }_{1})}{(c+\omega +{\theta }_{1})({v}_{1}+\varphi +\Lambda +\omega )}.$$

Non-standard finite difference scheme (NSFD)

We propose an NSFD approach for model (1). The plan is based on the non-standard finite difference numerical modelling known as Mickens Theory28,29,30,31. Specify the kinds of problem solved using NSFD scheme or rephrase for precision29,32. In these cases, it is essentially necessary that the mathematical answer achieved preserves each property of a dynamic model. It is demonstrated that, for large step sizes, the NSFD structure yields more accurate results than the alternative method. As fellowships, we design the NSFD numerical scheme for the suggested model (1).

Structure of NSFD scheme

On behalf of system (1), we indicate \({\mathbb{S}}_{m},{\mathbb{E}}_{m},{\mathbb{I}}_{m},{\mathbb{Q}}_{m}\) and \({\mathbb{R}}_{m}\) as the numerical estimation of \({\mathbb{S}}\left(t\right),{\mathbb{E}}\left(t\right),{\mathbb{I}}\left(t\right),{\mathbb{Q}}(t)\) and \({\mathbb{R}}(t)\) at \(=m\) \(\Psi\). Anywhere \(m=\text{0,1},\text{2,3}\dots .\) and the discretization time step is denoted by \(\Psi .\)

$$\frac{{\mathbb{S}}_{m+1}-{\mathbb{S}}_{m}}{\Psi }=\rho -{\tau }_{1}{\mathbb{S}}_{m+1}{\mathbb{I}}_{m}-{\tau }_{2}{\mathbb{S}}_{m+1}{\mathbb{E}}_{m}-\omega {\mathbb{S}}_{m+1}$$
$$\frac{{\mathbb{E}}_{m+1}-{\mathbb{E}}_{m}}{\Psi }={\tau }_{1}{\mathbb{S}}_{m}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{S}}_{m}{\mathbb{E}}_{m+1}-({\upsilon }_{1}+\omega +\Lambda +{\varphi }){\mathbb{E}}_{m+1}$$
$$\frac{{\mathbb{I}}_{m+1}-{\mathbb{I}}_{m}}{\Psi }=\Lambda {\mathbb{E}}_{m}-{\theta }_{1}{\mathbb{I}}_{m+1}-c{\mathbb{I}}_{m+1}$$
(3)
$$\frac{{\mathbb{Q}}_{m+1}-{\mathbb{Q}}_{m}}{\Psi }=\varphi {\mathbb{E}}_{m+1}-(\delta +\omega +{\theta }_{2}){\mathbb{Q}}_{m+1}$$
$$\frac{{\mathbb{R}}_{m+1}-{\mathbb{R}}_{m}}{\Psi }=\varphi {\mathbb{E}}_{m}+ \text{c}{\mathbb{I}}_{m}+\delta {\mathbb{Q}}_{m}-\omega {\mathbb{R}}_{m+1}.$$

We make the assumption that \({\mathbb{S}}_{0}\ge 0,{\mathbb{E}}_{0},{\mathbb{I}}_{0},{\mathbb{Q}}_{0},\) and \({\mathbb{R}}_{0}\ge 0\). are the beginning values of the discontinuous NSFD SEIQR model (3), which are also non-negative. The discrete NSFD scheme (3) can be derived in its formal version as

$${\mathbb{S}}_{m+1}=\frac{{\mathbb{S}}_{m}+\Psi \rho }{1+\Psi ({\tau }_{1}{\mathbb{S}}_{m+1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{S}}_{m+1}{\mathbb{E}}_{m}-\omega )}$$
$${\mathbb{E}}_{m+1}=\frac{{\mathbb{E}}_{m}+\Psi {\tau }_{1}{\mathbb{S}}_{m}{\mathbb{I}}_{m}}{(1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+{v}_{1}+\Lambda +\varphi )}$$
$${\mathbb{I}}_{m+1}=\frac{{\mathbb{I}}_{m}+\Psi (\Lambda {\mathbb{E}}_{m})}{(1+\Psi ({\theta }_{1}+c))}$$
(4)
$${\mathbb{Q}}_{m+1}=\frac{{\mathbb{Q}}_{m}+\Psi (\varphi {\mathbb{E}}_{m+1})}{(1+\delta +\omega +{\theta }_{2})}$$
$${\mathbb{R}}_{m+1}=\frac{{\mathbb{R}}_{m}+\Psi [\varphi {\mathbb{E}}_{m}+c{\mathbb{I}}+\delta {\mathbb{Q}}]}{(1+\Psi \omega )}.$$

Positivity and boundedness of NSFD scheme

For the distinct structure (4), we can define a feasible region similarly to the continuously model (1). NSFD Schemes can preserve the non-negativity of solutions, ensuring that the numerical solution remain bounded such as

$${N}_{m}={\mathbb{S}}_{m}+{\mathbb{E}}_{m}+{\mathbb{I}}_{m}+{\mathbb{Q}}_{m}+{\mathbb{R}}_{m}.$$

Then equations that results from adding each of the five of the equations in (3)

$$\frac{{N}_{m+1}-{N}_{m}}{\Psi }=\rho -\omega {N}_{m+1}\iff \left(1+\Psi \omega \right){N}_{m+1}=\Psi \rho +{N}_{m}$$

And

$${N}_{m+1}\le \frac{\Psi \rho }{1+\Psi \omega }+\frac{{N}_{m}}{1+\Psi \omega }\iff\Psi \omega \sum_{k+1}^{m}{\left(\frac{1}{1+\Psi \omega }\right)}^{k}+{N}_{0}{\left(\frac{1}{1+\Psi \omega }\right)}^{m}$$

Using the discrete form of Grӧnwall inequality that is discrete33,34,35, if \(0<N(0)<\frac{\rho }{\omega }\), then

$${N}_{m}\le \frac{\rho }{\omega }\left(1-\frac{1}{{\left(1+\Psi \omega \right)}^{m}}\right)+N\left(0\right){\left(\frac{1}{1+\Psi \omega }\right)}^{m}=\frac{\rho }{\omega }+\left(N\left(0\right)-\frac{\rho }{\omega }\right){\left(\frac{1}{1+\Psi \omega }\right)}^{m}$$

Since \(\frac{1}{1+\Psi \omega }<1,\) so we get \({N}_{m}\to \frac{\rho }{\omega }\) as \(m\to \infty .\)

Therefore the feasible region for NSFD scheme (4) become

$$\mathcal{K}=\left\{({\mathbb{S}},{\mathbb{E}},{\mathbb{I}},{\mathbb{Q}},{\mathbb{R}}\varepsilon {\mathbb{R}}_{+}^{5}:0\le {\mathbb{S}}_{m}+{\mathbb{E}}_{m}+{\mathbb{I}}_{m}+{\mathbb{Q}}_{m}+{\mathbb{R}}_{m}\le \frac{\rho }{\omega }\right\}.$$
(5)

We now determine the conditions under which the DFE points are stable. We first analyze the local stability of the equilibrium points.

Local stability of disease free for NSFD scheme

To clarify the locally asymptotically stability (LAS) of DFE points, we take into

$${\mathbb{S}}_{m+1}=\frac{{\mathbb{S}}_{m}+\Psi \rho }{1+\Psi ({\tau }_{1}{\mathbb{S}}_{m+1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{S}}_{m+1}{\mathbb{E}}_{m}-\omega )}={G}_{1}$$
$${\mathbb{E}}_{m+1}=\frac{{\mathbb{E}}_{m}+\Psi {\tau }_{1}{\mathbb{S}}_{m}{\mathbb{I}}_{m}}{(1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+{v}_{1}+\Lambda +\varphi )}={G}_{2}$$
$${\mathbb{I}}_{m+1}=\frac{{\mathbb{I}}_{m}+\Psi (\Lambda {\mathbb{E}}_{m})}{(1+\Psi ({\theta }_{1}+c))}={G}_{3}$$
$${\mathbb{Q}}_{m+1}=\frac{{\mathbb{Q}}_{m}+\Psi (\varphi {\mathbb{E}}_{m+1})}{(1+\delta +\omega +{\theta }_{2})}={G}_{4}$$
$${\mathbb{R}}_{m+1}=\frac{{\mathbb{R}}_{m}+\Psi [\varphi {\mathbb{E}}_{m}+c{\mathbb{I}}+\delta {\mathbb{Q}}]}{(1+\Psi \omega )}={G}_{5}.$$

As mentioned in Lemma 1, we drive apply the resulting Schur-Cohn criterion36,37 to determine that DFE points are locally asymptotically stable.

Lemma 1

The solutions of equation \({\Gamma }^{2}-{\Gamma \Delta }+\mathcal{W}=0\) satisfy \(\left|{\Delta }_{k}\right|<1, k=\text{1,2}\) , if and only if the following conditions are fulfilled.

  1. 1.

    \(\mathcal{W}<1\),

  2. 2.

    \(1+\Gamma +\mathcal{W}>0\),

  3. 3.

    \(1-\Gamma +\mathcal{W}>0\),

where \(\mathcal{W}\) and \(\Gamma\) respectively denote the determinant and trace of Jacobian matrix.

Theorem 1

If \({R}_{0}<1\), then the DFE point \({E}_{0}\) of the discrete NSFD model (3) is locally asymptotically stable for all \(\Psi >0.\)

Proof

By replacing \({G}_{1},{G}_{2}, {G}_{3},\) \({G}_{4}\) and \({G}_{5}\) in Jacobian matrix and then putting DFE point \({E}_{0}\), we consider the Jacobian matrix

$$\text{J}\left({\mathbb{S}},{\mathbb{E}},{\mathbb{I}},{\mathbb{Q}},{\mathbb{R}}\right)=\left|\begin{array}{ccccc}\frac{\partial {G}_{1}}{\partial {\mathbb{S}}}& \frac{\partial {G}_{1}}{\partial {\mathbb{E}}}& \frac{\partial {G}_{1}}{\partial {\mathbb{I}}}& \frac{\partial {G}_{1}}{\partial {\mathbb{Q}}}& \frac{\partial {G}_{1}}{\partial {\mathbb{R}}}\\ \frac{\partial {G}_{2}}{\partial {\mathbb{S}}}& \frac{\partial {G}_{2}}{\partial {\mathbb{E}}}& \frac{\partial {G}_{2}}{\partial {\mathbb{I}}}& \frac{\partial {G}_{2}}{\partial {\mathbb{Q}}}& \frac{\partial {G}_{2}}{\partial {\mathbb{R}}}\\ \frac{\partial {G}_{3}}{\partial {\mathbb{S}}}& \frac{\partial {G}_{3}}{\partial {\mathbb{E}}}& \frac{\partial {G}_{3}}{\partial {\mathbb{I}}}& \frac{\partial {G}_{3}}{\partial {\mathbb{Q}}}& \frac{\partial {G}_{3}}{\partial {\mathbb{R}}}\\ \frac{\partial {G}_{4}}{\partial {\mathbb{S}}}& \frac{\partial {G}_{4}}{\partial {\mathbb{E}}}& \frac{\partial {G}_{4}}{\partial {\mathbb{I}}}& \frac{\partial {G}_{4}}{\partial {\mathbb{Q}}}& \frac{\partial {G}_{4}}{\partial {\mathbb{R}}}\\ \frac{\partial {G}_{5}}{\partial {\mathbb{S}}}& \frac{\partial {G}_{5}}{\partial {\mathbb{E}}}& \frac{\partial {G}_{5}}{\partial {\mathbb{I}}}& \frac{\partial {G}_{5}}{\partial {\mathbb{Q}}}& \frac{\partial {G}_{5}}{\partial {\mathbb{R}}}\end{array}\right|.$$
(6)

We first locate all of the derivatives utilised in (6) in the following.

$$\begin{aligned}\frac{\partial {G}_{1}}{\partial {\mathbb{S}}}&=\frac{1}{1+\Psi ({\tau }_{1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{E}}_{m}+\omega )}\frac{\partial {G}_{1}}{\partial {\mathbb{E}}}=\frac{-\omega {\tau }_{2}({\mathbb{S}}_{m}+\omega \rho )}{{(1+\Psi ({\tau }_{1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{E}}_{m}+\omega )}^{2}}\frac{\partial {G}_{1}}{\partial {\mathbb{I}}} \\ & =\frac{-\omega {\tau }_{1} ({\mathbb{S}}_{m}+\omega \rho )}{{(1+\Psi ({\tau }_{1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{E}}_{m}+\omega )}^{2}}\frac{\partial {G}_{1}}{\partial {\mathbb{Q}}}=0,\frac{\partial {G}_{1}}{\partial {\mathbb{R}}}=0. \\ \frac{\partial {G}_{2}}{\partial {\mathbb{S}}} & =\frac{\Psi {\tau }_{1}{\mathbb{I}}_{m}-\Psi {\tau }_{2}({\mathbb{E}}_{m}+\Psi {\tau }_{1}{\mathbb{S}}_{m}{\mathbb{I}}_{m})}{1-\Psi ({\tau }_{1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{E}}_{m}+\omega )} \\ \frac{\partial {G}_{2}}{\partial {\mathbb{E}}} & =\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))} \\ \frac{\partial {G}_{2}}{\partial {\mathbb{I}}} & =\frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}\frac{\partial {G}_{2}}{\partial {\mathbb{Q}}}=0, \frac{\partial {G}_{2}}{\partial {\mathbb{R}}}=0\frac{\partial {G}_{3}}{\partial {\mathbb{S}}}=0, \\ \frac{\partial {G}_{3}}{\partial {\mathbb{E}}} & =\frac{\psi\Lambda }{1+\psi ({\theta }_{1}+c)},\frac{\partial {G}_{3}}{\partial {\mathbb{I}}}=\frac{1}{1+\psi ({\theta }_{1}+c)},\frac{\partial {G}_{3}}{\partial {\mathbb{Q}}}=0, \\ \frac{\partial {G}_{3}}{\partial {\mathbb{R}}} &=0\frac{\partial {g}_{4}}{\partial {\mathbb{S}}}=0,\frac{\partial {G}_{4}}{\partial {\mathbb{E}}}=\frac{\psi \varphi }{1+\delta +\omega +{\theta }_{2}},\frac{\partial {G}_{4}}{\partial {\mathbb{I}}}=0,\frac{\partial {G}_{4}}{\partial {\mathbb{Q}}}=\frac{1}{1+\delta +\omega +{\theta }_{2}},\frac{\partial {G}_{4}}{\partial {\mathbb{R}}}=0 \frac{\partial {G}_{5}}{\partial {\mathbb{S}}}=0, \\ \frac{\partial {G}_{5}}{\partial {\mathbb{E}}} &=\frac{\psi \varphi }{1+\psi \omega },\frac{\partial {G}_{5}}{\partial {\mathbb{I}}}=\frac{\psi c}{1+\psi \omega },\frac{\partial {G}_{5}}{\partial {\mathbb{Q}}}=\frac{\psi \delta }{1+\psi \omega },\frac{\partial {G}_{5}}{\partial {\mathbb{R}}}=\frac{1}{1+\psi \omega }\end{aligned}$$
$$J=\left|\begin{array}{ccccc}\frac{1}{1+\Psi ({\tau }_{1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{E}}_{m}+\omega )}& \frac{-\omega {\tau }_{2}({\mathbb{S}}_{m}+\omega \rho )}{{(1+\Psi ({\tau }_{1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{E}}_{m}+\omega )}^{2}}& \frac{-\omega {\tau }_{1} ({\mathbb{S}}_{m}+\omega \rho )}{{(1+\Psi ({\tau }_{1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{E}}_{m}+\omega )}^{2}}& 0& 0\\ \frac{\Psi {\tau }_{1}{\mathbb{I}}_{m}-\Psi {\tau }_{2}({\mathbb{E}}_{m}+\Psi {\tau }_{1}{\mathbb{S}}_{m}{\mathbb{I}}_{m})}{1-\Psi ({\tau }_{1}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{E}}_{m}+\omega )}.& \frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}& \frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}& 0& 0\\ 0& \frac{\psi\Lambda }{1+\psi ({\theta }_{1}+c)}& \frac{1}{1+\psi ({\theta }_{1}+c)}& 0& 0\\ 0& \frac{\psi \varphi }{1+\delta +\omega +{\theta }_{2}}& 0& \frac{1}{1+\delta +\omega +{\theta }_{2}}& 0\\ 0& \frac{\psi \varphi }{1+\psi \omega }& \frac{\psi c}{1+\psi \omega }& \frac{\psi \delta }{1+\psi \omega }& \frac{1}{1+\psi \omega }\end{array}\right|$$
(7)

Putting the values of all the derivative in (7) we obtain, and also put the DFE point \({E}_{0}=\left(\frac{\beta }{\theta },\text{0,0},\text{0,0}\right)\) From above, we get

$$J({E}^{0}-\Delta =\left|\begin{array}{ccccc}\frac{1}{1+\Psi +\omega )}-\Delta & \frac{-\omega {\tau }_{2}({\mathbb{S}}_{m}+\omega \rho )}{{(1+\Psi +\omega )}^{2}}& \frac{-\omega {\tau }_{1} ({\mathbb{S}}_{m}+\omega \rho )}{{(1+\Psi +\omega )}^{2}}& 0& 0\\ 0& \frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\Delta & \frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}& 0& 0\\ 0& \frac{\psi\Lambda }{1+\psi ({\theta }_{1}+c)}& \frac{1}{1+\psi ({\theta }_{1}+c)}-\Delta & 0& 0\\ 0& \frac{\psi \varphi }{1+\delta +\omega +{\theta }_{2}}& 0& \frac{1}{1+\delta +\omega +{\theta }_{2}}-\Delta & 0\\ 0& \frac{\psi \varphi }{1+\psi \omega }& \frac{\psi c}{1+\psi \omega }& \frac{\psi \delta }{1+\psi \omega }& \frac{1}{1+\psi \omega }-\Delta \end{array}\right|$$

Expending \({C}_{1}\)

$$\frac{1}{1+\Psi \omega }-\Delta \left|\begin{array}{cccc}\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\Delta & \frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}& 0& 0\\ \frac{\psi\Lambda }{1+\psi ({\theta }_{1}+c)}& \frac{1}{1+\psi ({\theta }_{1}+c)}-\Delta & 0& 0\\ \frac{\psi \varphi }{1+\delta +\omega +{\theta }_{2}}& 0& \frac{1}{1+\delta +\omega +{\theta }_{2}}-\Delta & 0\\ \frac{\psi \varphi }{1+\psi \omega }& \frac{\psi c}{1+\psi \omega }& \frac{\psi \delta }{1+\psi \omega }& \frac{1}{1+\psi \omega }-\Delta \end{array}\right|=0.$$

The above matrix has the following eigenvalues

$$\Delta =\frac{1}{1+\Psi \omega }$$

Expending \({C}_{4}\)

$$\frac{1}{1+\psi \omega }-\Delta \left|\begin{array}{ccc}\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\Delta & \frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}& 0\\ \frac{\psi\Lambda }{1+\psi ({\theta }_{1}+c)}& \frac{1}{1+\psi ({\theta }_{1}+c)}-\Delta & 0\\ \frac{\psi \varphi }{1+\delta +\omega +{\theta }_{2}}& 0& \frac{1}{1+\delta +\omega +{\theta }_{2}}-\Delta \end{array}\right|=0.$$

The above matrix has the following eigenvalues

$$\Delta =\frac{1}{1+\psi \omega }$$

Expending \({C}_{3}\)

$$\frac{1}{1+\delta +\omega +{\theta }_{2}}-\Delta \left|\begin{array}{cc}\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\Delta & \frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}\\ \frac{\psi\Lambda }{1+\psi ({\theta }_{1}+c)}& \frac{1}{1+\psi ({\theta }_{1}+c)}-\Delta \end{array}\right|=0$$

The above matrix has the following eigenvalues

$$\Delta =\frac{1}{1+\delta +\omega +{\theta }_{2}}$$

To determine the two eigenvalues that are left. From the previous equation, the quadratic equation below is simply derived.

$$\left|\begin{array}{cc}\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\Delta & \frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}\\ \frac{\psi\Lambda }{1+\psi ({\theta }_{1}+c)}& \frac{1}{1+\psi ({\theta }_{1}+c)}-\Delta \end{array}\right|=0.$$

The below quadratic equation can easily be obtained from above equation

$$\begin{aligned} & {\Delta }^{2}-\Delta \left(\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}+\frac{1}{1+\psi \left({\theta }_{1}+c\right)}\right) \\ & \quad +\frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}=0\end{aligned}$$
(8)

Comparing Eq. (8) with \({\Delta }^{2}-\Delta T+D=0\), we get \(T=\left(\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}+\frac{1}{1+\psi \left({\theta }_{1}+c\right)}\right)\) and \(D=\frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}\) If \({R}_{0}<1,\) then all the three condition of lemma 1 remain fulfilled.

  1. 1.

    \(D=\frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}<1.\)

  2. 2.

    \(1+T+D=1+\frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}+\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}+\frac{1}{1+\psi \left({\theta }_{1}+c\right)}>0.\)

  3. 3.

    \(1-T+D=1-\frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}+\frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}+\frac{1}{1+\psi \left({\theta }_{1}+c\right)}>0.\)

Therefore, whenever \({R}_{0}<1\), entirely of the desires for the Schur-Cohn criteria [] covered in Lemma 1 remain fulfilled. Consequently, given that \({R}_{0}<1\), the discrete NSFD scheme (1)'s DFE point \({E}_{0}\) is LAS.

The Fig. 2 illustrates the dynamic behavior of the system, showcasing the intricate relationship between the variable. This physical interpretation of the Fig. 2 offers valuable insights into the system behavior allowing for a deeper understanding of the underlying mechanisms and their implications.

Fig. 2
figure 2

Numerical simulation of SEIQR model (1) by using NSFD scheme with \(\left(\text{a}\right)\Psi = 0.1, \left(\text{b}\right)\Psi = 0.5,\left(c\right)\Psi =1,\left(d\right)\Psi =2.5\) other parameters remain fixed as Table 1.

Full size image
Table 1 The values and description of the related parameters24.
Full size table

The mathematical imitations displayed in Fig. 2a–c additionally display that the discrete NSFD scheme is unconditionally convergent for model (1) if \({R}_{0}\le 1\); conversely, if \({R}_{0}\ge 1\) then the answers of NSFD structure (3) diverges to the DEE point for any step size; further demonstrating the unqualified divergence of the discrete NSFD scheme in Fig. 2d.

Theorem 2

The EE point \({E}^{*}\) of NSFD system (4.6) is LAS, if \({R}_{0}>1.\)

Proof

Let us we take the Jacobian matrix from the above theorem.

In order to determine the eigenvalues of the given matrix, we take the derivative of the matrix and insert additional points.

$$\left|{J}_{{E}^{*}}-\Delta \right|=\left|\begin{array}{ccccc}\frac{1}{1+\Psi \left({\tau }_{1}{\mathbb{I}}_{m}^{*}+{\tau }_{2}{\mathbb{E}}_{m}^{*}+\omega \right)}-\Delta & \frac{-\omega {\tau }_{2}({\mathbb{S}}_{m}^{*}+\omega \rho )}{{(1+\Psi ({\tau }_{1}{\mathbb{I}}_{m}^{*}+{\tau }_{2}{\mathbb{E}}_{m}^{*}+\omega )}^{2}}& \frac{-\omega {\tau }_{1} ({\mathbb{S}}_{m}^{*}+\omega \rho )}{{(1+\Psi ({\tau }_{1}{\mathbb{I}}_{m}^{*}+{\tau }_{2}{\mathbb{E}}_{m}^{*}+\omega )}^{2}}& 0& 0\\ \frac{\Psi {\tau }_{1}{\mathbb{I}}_{m}-\Psi {\tau }_{2}({\mathbb{E}}_{m}^{*}+\Psi {\tau }_{1}{\mathbb{I}}_{m}^{*}{\mathbb{S}}_{m}^{*})}{1-\Psi ({\tau }_{1}{\mathbb{I}}_{m}^{*}+{\tau }_{2}{\mathbb{E}}_{m}^{*}+\omega )}.& \frac{1}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}-\Delta & \frac{\Psi {\tau }_{1}{\mathbb{S}}_{m}}{1-\Psi ({\tau }_{2}{\mathbb{S}}_{m}+({V}_{1}+\omega +\Lambda +{\varphi }))}& 0& 0\\ 0& \frac{\psi\Lambda }{1+\psi ({\theta }_{1}+c)}& \frac{1}{1+\psi \left({\theta }_{1}+c\right)}-\Delta & 0& 0\\ 0& \frac{\psi \varphi }{1+\delta +\omega +{\theta }_{2}}& 0& \frac{1}{1+\delta +\omega +{\theta }_{2}}-\Delta & 0\\ 0& \frac{\psi \varphi }{1+\psi \omega }& \frac{\psi c}{1+\psi \omega }& \frac{\psi \delta }{1+\psi \omega }& \frac{1}{1+\psi \omega }-\Delta \end{array}\right|.$$

Let us we consider the values

$$\left|{J}_{{E}^{*}}-\Delta \right|=\left|\begin{array}{ccccc}{k}^{1}-\Delta & {k}^{2}& {k}^{3}& 0& 0\\ {k}^{4}& {k}^{5}-\Delta & {k}^{6}& 0& 0\\ 0& {k}^{7}& {k}^{8}-\Delta & 0& 0\\ 0& {k}^{9}& 0& {k}^{10}-\Delta & 0\\ 0& {k}^{11}& {k}^{12}& {k}^{13}& {k}^{14}-\Delta \end{array}\right|.$$
(9)

Here,

\({k}^{14}=\frac{1}{1+\psi \omega }\),\({k}^{10}=\frac{1}{1+\delta +\omega +{\theta }_{2}}\),

\({\Delta =k}^{14}\),\(\Delta {=k}^{10}\) and remaining are given by solving the matrix (9)

$$\left({k}^{1}-\Delta \right)\left|\begin{array}{cc}{k}^{5}-\Delta & {k}^{6}\\ {k}^{7}& {k}^{8}-\Delta \end{array}\right|-{k}^{4}\left|\begin{array}{cc}{k}^{2}& {k}^{3}\\ {k}^{7}& {k}^{8}-\Delta \end{array}\right|=0.$$
(10)

To solving the above matrix to get the characteristic eq

$$\left[{\Delta }^{3}+{U}_{3}{\Delta }^{2}+{U}_{2}\Delta +{U}_{1}\right]=0.$$

This revenue;

$${U}_{3}=\left({k}^{1}+{k}^{5}+{k}^{8}\right)>0.$$
$${U}_{2}={k}^{2}{k}^{4}+{k}^{1}{k}^{5}+{k}^{1}{k}^{8}+{k}^{5}{k}^{8}+{k}^{6}{k}^{7}>0.$$
$${U}_{1}={k}^{1}{k}^{5}{k}^{8}+{k}^{1}{k}^{6}{k}^{7}+{k}^{2}{k}^{4}{k}^{8}-{k}^{3}{k}^{4}{k}^{7}>0.$$
$${U}_{1}{U}_{2}-{U}_{3}=\left({k}^{1}{k}^{5}{k}^{8}+{k}^{1}{k}^{6}{k}^{7}+{k}^{2}{k}^{4}{k}^{8}-{k}^{3}{k}^{4}{k}^{7}\right)\left({k}^{2}{k}^{4}+{k}^{1}{k}^{5}+{k}^{1}{k}^{8}+{k}^{5}{k}^{8}+{k}^{6}{k}^{7}\right)-\left({k}^{1}+{k}^{5}+{k}^{8}\right)>0.$$

Altogether the principles are confident, this is arithmetically verified, we dismiss thus states that \({U}_{1},{U}_{2},{U}_{3}>0.\)

Thus the Routh- Hurwitz Criterion38 is fulfilled. So DEE point \({E}^{*}\) of NSFD structure (4.6) is LAS, if \({R}_{0}>1.\)

Since all of the numbers are positive and can be demonstrated mathematically, we may state that \({U}_{1},{U}_{2},{U}_{3}>0.\) Consequently, the Routh-Hurwitz Criterion38 is met. Therefore, if \({R}_{0}>1.\) DEE point \({E}^{*}\) of the NSFD system (4.6) is LAS.

Global stability of equilibria

To find the global stability of DFE and DEE points for NSFD scheme (4), we describe the function \(\text{N}(y)\ge 0\) such that \(\text{K}\left(y\right)=\text{T}-lnT\) and so \(lnT\le T-1.\)

The function ε(y) ≥ 0, such that \(\text{K}\left(y\right)=\text{T}-lnT\) and hence \(lnT\le T-1\), is described in order to determine the global stability of DFE and DEE points for NSFD scheme (4).

Theorem 3

For all \(\Psi >0,\) the DFE point is globally asymptotically stable (GAS) for NSFD model (4) whenever \({\mathcal{R}}_{0}<1.\)

Proof

Create a discrete Lyapunov Function.

$${Y}_{m}\left({\mathbb{S}}_{m},{\mathbb{E}}_{m},{\mathbb{I}}_{m},{\mathbb{Q}}_{m},{\mathbb{R}}_{m}\right)={\mathbb{S}}^{0}N\left(\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}^{0}}\right)+{\varphi }_{1}{\mathbb{E}}_{m}+{\varphi }_{2}{\mathbb{I}}_{m}+{\varphi }_{3}{\mathbb{Q}}_{m}+{\varphi }_{4}{\mathbb{R}}_{m}.$$

where \({\varphi }_{k}>0\) meant for entirely \(k=\text{1,2},\text{3,4},5.\) Therefore, \({Y}_{m}>0\) meant for entirely \({\mathbb{S}}\left(0\right)>0,{\mathbb{E}}\left(0\right)>0,{\mathbb{I}}\left(0\right)>0,{\mathbb{Q}}\left(0\right)>0 and {\mathbb{R}}\left(0\right)>0\).In adding, \({Y}_{m}=0,\) if and only if \({\mathbb{S}}_{m}={\mathbb{S}}^{0}\), \({\mathbb{E}}_{m}={\mathbb{E}}^{0}\),\({\mathbb{I}}_{m}={\mathbb{I}}^{0}\) \({\mathbb{Q}}_{m}={\mathbb{Q}}^{0}\) and \({\mathbb{R}}_{m}={\mathbb{R}}^{0}.\) We take

$$\Delta {Y}_{m}={Y}_{m+1}-{Y}_{m}$$
$$\Delta {Y}_{m}={\mathbb{S}}^{0}F\left(\frac{{\mathbb{S}}_{m+1}}{{\mathbb{S}}^{0}}\right)+{\varphi }_{1}{\mathbb{E}}_{m+1}+{\varphi }_{2}{\mathbb{I}}_{m+1}+{\varphi }_{3}{\mathbb{Q}}_{m+1}+{\varphi }_{4}{\mathbb{R}}_{m+1}-({\mathbb{S}}^{0}N\left(\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}^{0}}\right)+{\varphi }_{1}{\mathbb{E}}_{m}+{\varphi }_{2}{\mathbb{I}}_{m}+{\varphi }_{3}{\mathbb{Q}}_{m}+{\varphi }_{4}{\mathbb{R}}_{m}).$$
$$={\mathbb{S}}^{0}\left(\frac{{\mathbb{S}}_{m+1}}{{\mathbb{S}}^{0}}-\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}^{0}}+ln\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}_{m+1}}\right)+{\varphi }_{1}\left({\mathbb{E}}_{m+1}-{\mathbb{E}}_{m}\right)+{\varphi }_{2}\left({\mathbb{I}}_{m+1}-{\mathbb{I}}_{m}\right)+{\varphi }_{3}\left({\mathbb{Q}}_{m+1}-{\mathbb{Q}}_{m}\right)+{\varphi }_{4}\left({\mathbb{R}}_{m+1}-{\mathbb{R}}_{m}\right).$$

Expending the inequity \(lnT\le T-1\) above equation become

$$\begin{aligned}\Delta {Y}_{m} & \le {\mathbb{S}}_{m+1}-{\mathbb{S}}_{m}+{\mathbb{S}}^{0}\left(-1+\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}_{m+1}}\right) \\ & \quad +\left(-1+\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}_{m+1}}\right){\varphi }_{1}\left({\mathbb{E}}_{m+1}-{\mathbb{E}}_{m}\right)+\left(-1+\frac{{\mathbb{I}}_{m}}{{\mathbb{I}}_{m+1}}\right){\varphi }_{2}\left({\mathbb{I}}_{m+1}-{\mathbb{I}}_{m}\right) \\ & \quad +\left(-1+\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}_{m+1}}\right){\varphi }_{3}\left({\mathbb{Q}}_{m+1}-{\mathbb{Q}}_{m}\right)+\left(-1+\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}_{m+1}}\right){\varphi }_{4}\left({\mathbb{R}}_{m+1}-{\mathbb{R}}_{m}\right).\end{aligned}$$
$$\begin{aligned} &=-\left(1-\frac{{\mathbb{S}}^{0}}{{\mathbb{S}}_{m+1}}\right)\left({\mathbb{S}}_{m+1}-{\mathbb{S}}_{n}\right) \\ & \quad -\left(1-\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}_{m+1}}\right){\varphi }_{1}\left({\mathbb{E}}_{m+1}-{\mathbb{E}}_{m}\right)-\left(1-\frac{{\mathbb{I}}_{m}}{{\mathbb{I}}_{m+1}}\right){\varphi }_{2}\left({\mathbb{I}}_{m+1}-{\mathbb{I}}_{m}\right) \\ & \quad -\left(1-\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}_{m+1}}\right){\varphi }_{3}\left({\mathbb{Q}}_{m+1}-{\mathbb{Q}}_{m}\right)-\left(1-\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}_{m+1}}\right){\varphi }_{4}\left({\mathbb{R}}_{m+1}-{\mathbb{R}}_{m}\right).\end{aligned}$$

Using system (3), above eq. can be expressed as

$$\begin{aligned}\Delta {Y}_{m} & \le -\left(1-\frac{{\mathbb{S}}^{0}}{{\mathbb{S}}_{m+1}}\right)\left(\rho -{\tau }_{1}{\mathbb{S}}_{m+1}{\mathbb{I}}_{m}-{\tau }_{2}{\mathbb{S}}_{m+1}{\mathbb{E}}_{m}-\omega {\mathbb{S}}_{m+1}\right) \\ & \quad +\left(1-\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}_{m+1}}\right){(\varphi }_{1}{\tau }_{1}{\mathbb{S}}_{m}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{S}}_{m}{\mathbb{E}}_{m+1}-({\upsilon }_{1}+\omega +\Lambda +{\varphi })){\mathbb{E}}_{m+1}+\left(1-\frac{{\mathbb{I}}_{m}}{{\mathbb{I}}_{m+1}}\right){\varphi }_{2}(\Lambda {\mathbb{E}}_{m}-{\theta }_{1}{\mathbb{I}}_{m+1}-c{\mathbb{I}}_{m+1} \\ & \quad +\left(1-\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}_{m+1}}\right){\varphi }_{3}\left(\varphi {\mathbb{E}}_{m+1}-\left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}_{m+1})+\left(1-\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}_{m+1}}\right){\varphi }_{4}(\varphi {\mathbb{E}}_{m}+ \text{c}{\mathbb{I}}_{m}+\delta {\mathbb{Q}}_{m}-\omega {\mathbb{R}}_{m+1})\right).\end{aligned}$$

Let \({\varphi }_{k}>0\) for all \(k=\text{1,2},\text{3,4}\) be nominated so that.

$$\left(\rho -{\tau }_{1}{\mathbb{S}}_{m+1}{\mathbb{I}}_{m}-{\tau }_{2}{\mathbb{S}}_{m+1}{\mathbb{E}}_{m}-\omega {\mathbb{S}}_{m+1}\right)={(\varphi }_{1}{\tau }_{1}{\mathbb{S}}_{m}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{S}}_{m}{\mathbb{E}}_{m+1}-({\upsilon }_{1}+\omega +\Lambda +{\varphi })){\mathbb{E}}_{m+1}$$
$${\varphi }_{2}(\Lambda {\mathbb{E}}_{m}-{\theta }_{1}{\mathbb{I}}_{m+1}-c{\mathbb{I}}_{m+1}={\varphi }_{3}\left(\varphi {\mathbb{E}}_{m+1}-\left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}_{m+1}\right)$$
$$\left(\varphi {\mathbb{E}}_{m+1}-\left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}_{m+1}\right)={\varphi }_{4}\left(\varphi {\mathbb{E}}_{m}+ \text{c}{\mathbb{I}}_{m}+\delta {\mathbb{Q}}_{m}-\omega {\mathbb{R}}_{m+1}\right).$$

Putting the above values, from above eq. we get

$$\begin{aligned}\Delta {Y}_{m} & \le -\left(\left(1-\frac{{\mathbb{S}}^{0}}{{\mathbb{S}}_{m+1}}\right)\left(\rho -{\tau }_{1}{\mathbb{S}}_{m+1}{\mathbb{I}}_{m}-{\tau }_{2}{\mathbb{S}}_{m+1}{\mathbb{E}}_{m}-\omega {\mathbb{S}}_{m+1}\right) \right. \\ & \quad \left. +\left(1-\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}_{m+1}}\right){(\varphi }_{1}{\tau }_{1}{\mathbb{S}}_{m}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{S}}_{m}{\mathbb{E}}_{m+1}-({\upsilon }_{1}+\omega +\Lambda +{\varphi })){\mathbb{E}}_{m+1} \right. \\ & \quad \left. +\left(1-\frac{{\mathbb{I}}_{m}}{{\mathbb{I}}_{m+1}}\right){\varphi }_{2}(\Lambda {\mathbb{E}}_{m}-{\theta }_{1}{\mathbb{I}}_{m+1}-c{\mathbb{I}}_{m+1}+\left(1-\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}_{m+1}}\right){\varphi }_{3}\left(\varphi {\mathbb{E}}_{m+1}-\left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}_{m+1}\right) \right. \\ & \quad \left. +\left(1-\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}_{m+1}}\right){\varphi }_{4}(\varphi {\mathbb{E}}_{m}+ \text{c}{\mathbb{I}}_{m}+\delta {\mathbb{Q}}_{m}-\omega {\mathbb{R}}_{m+1})\right).\end{aligned}$$

Simple calculation yields

$$\begin{aligned}\Delta {Y}_{m} & \le -\left(\left(1-\frac{{\mathbb{S}}^{0}}{{\mathbb{S}}_{m+1}}\right)\left(\rho -\left(1-\frac{{\mathbb{I}}^{0}}{{\mathbb{I}}_{m+1}}\right){\varphi }_{1}\left({\upsilon }_{1}+\omega +\Lambda +{\varphi }\right)\right){\mathbb{E}}_{m+1} \right. \\ & \quad \left. +\left(1-\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}_{m+1}}\right){\varphi }_{2}{\tau }_{2}{\mathbb{S}}_{m}{\mathbb{E}}_{m+1}-\left(1-\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}_{m+1}}\right){\varphi }_{3}\left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}_{m+1}+\left(1-\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}_{m+1}}\right){\varphi }_{4}\delta {\mathbb{Q}}_{m}\right).\end{aligned}$$

As \({\mathbb{S}}^{0}=\frac{\rho }{\omega }\) which implies that \({\mathbb{S}}^{0}\omega =\rho .\) By Substituting \(\rho\) in above, we get

$$\begin{aligned} \Delta {Y}_{m} & \le -\left(1-\frac{{\mathbb{S}}^{0}}{{\mathbb{S}}_{m+1}}\right)\left({\mathbb{S}}^{0}\omega -\omega {\mathbb{S}}_{m+1}-\left(1-\frac{{\mathbb{I}}^{0}}{{\mathbb{I}}_{m+1}}\right){\varphi }_{1}\left({\upsilon }_{1}+\omega +\Lambda +{\varphi }\right){\mathbb{E}}_{m+1} \right. \\ & \quad \left. +\left(1-\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}_{m+1}}\right){\varphi }_{2}\rho {\mathbb{S}}_{m}-\left(1-\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}_{m+1}}\right){\varphi }_{3}\left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}_{m+1}+\left(1-\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}_{m+1}}\right){\varphi }_{4}\delta {\mathbb{Q}}_{m}\right)\end{aligned}$$
$$\begin{aligned}&=\frac{-\omega }{{\mathbb{S}}_{m+1}}{\left({\mathbb{S}}_{m+1}-{\mathbb{S}}^{0}\right)}^{2}-\left(1-\frac{{\mathbb{I}}^{0}}{{\mathbb{I}}_{m+1}}\right){\varphi }_{1}\left({\upsilon }_{1}+\omega +\Lambda +{\varphi }\right){\mathbb{E}}_{m} \\ & \quad +{\varphi }_{2}\frac{\rho [{\tau }_{1}\Lambda +{\tau }_{2}(c+\omega +{\theta }_{1})}{\left(c+\omega +{\theta }_{1}\right)\left({v}_{1}+\varphi +\Lambda +\omega \right)}-{\varphi }_{3}\left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}_{m+1}+{\varphi }_{4}\delta {\mathbb{Q}}_{m}.\end{aligned}$$

Let \({\text{ H}}_{1}=\frac{\rho [{\tau }_{1}\Lambda +{\tau }_{2}(c+\omega +{\theta }_{1})}{\left(c+\omega +{\theta }_{1}\right)\left({v}_{1}+\varphi +\Lambda +\omega \right)}\)

$$\begin{aligned} & =\frac{-\omega }{{\mathbb{S}}_{m+1}}{\left({\mathbb{S}}_{m+1}-{\mathbb{S}}^{0}\right)}^{2}-\left(1-\frac{{\mathbb{I}}^{0}}{{\mathbb{I}}_{m+1}}\right){\varphi }_{1}\left({\upsilon }_{1}+\omega +\Lambda +{\varphi }\right){\mathbb{E}}_{m} \\ & \quad +{\varphi }_{2 } {\text{ H}}_{1}{R}_{0}-{\varphi }_{3}\left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}_{m+1}+{\varphi }_{4}\delta {\mathbb{Q}}_{m}.\end{aligned}$$

The Fig. 3 illustrate the dynamic behavior of the system, showcasing the intricate relationship between the variable. This physical interpretation of the Fig. 3 offers valuable insights into the system behavior allowing for a deeper understanding of the underlying mechanisms and their implications.

Fig. 3
figure 3

Numerical simulation for model (1) by using NSFD scheme with \(\left(\text{a}\right)\Psi = 0.1, \left(\text{b}\right)\Psi = 1,\left(c\right)\Psi =10,\left(d\right)\Psi =30 .\)(a–c) Stable DFE point with \({\tau }_{1}=0.005\) (d) Unstable DFE point \({\tau }_{2}=1.05\) Other parameters stay stable as Table 1.

Full size image

Hence, if \({R}_{0}\le 1\) then from (above), we can write \(\Delta {Y}_{m}\le O\) on behalf of entirely \(m\ge 0\). Subsequently, \({Y}_{m}\) is a non-increasing arrangement. Consequently, around occurs a persistent \(Y\) such that \({\text{lim}}_{n\to \infty }{Y}_{m}=Y\) which implies that \({\text{lim}}_{n\to \infty }\left({Y}_{m+1}-{Y}_{n}\right)=0\). Since structure (3) and \({\text{lim}}_{n\to \infty }\Delta {Y}_{m}=0\) we have \({\text{lim}}_{n\to \infty }{\mathbb{S}}_{m+1}={\mathbb{S}}^{0}\) and \({\text{lim}}_{n\to \infty }({R}_{0}-1){R}_{n}=0.\) For the case \({R}_{0}<1,\) we have \({\text{lim}}_{n\to \infty }{\mathbb{S}}_{m+1}={\mathbb{S}}^{0}\) and \({\text{lim}}_{n\to \infty }{\mathbb{E}}_{m}=0,{\text{lim}}_{n\to \infty }{\mathbb{I}}_{m}=0.\) From system (3), we obtain \({\text{lim}}_{n\to \infty }{\mathbb{E}}_{m}=0,,{\text{lim}}_{n\to \infty }{\mathbb{I}}_{m}=0\) and \({\text{lim}}_{n\to \infty }{\mathbb{Q}}_{m}=0.\) On behalf of the situation \({R}_{0}\le 1,\) we must \({\text{lim}}_{n\to \infty }{\mathbb{S}}_{m+1}={\mathbb{S}}^{0}.\) Consequently, since structure (3), we gain \({\text{lim}}_{n\to \infty }{\mathbb{R}}_{m}=0,{\text{lim}}_{n\to \infty }{\mathbb{Q}}_{m}=0,{\text{lim}}_{n\to \infty }{\mathbb{E}}_{m}=0,\) and \({{\text{lim}}_{n\to \infty }I}_{n}=0\). Therefore, \({E}_{0}\) is (GAS) globally asymptotically stable.

Theorem 4

For all \(\Psi >0,\) the DEE point is globally asymptotically stable (GAS) for NSFD model (4) whenever \({\mathcal{R}}_{0}>1.\)

Proof

Let us define

$${Y}_{m}\left({\mathbb{S}}_{m},{\mathbb{E}}_{m},{\mathbb{I}}_{m},{\mathbb{Q}}_{m}{\mathbb{R}}_{m}\right)={\mathbb{S}}^{*}N\left(\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}^{*}}\right)+{\varnothing }_{1}{\mathbb{E}}^{*}N\left(\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}^{*}}\right)+{\varnothing }_{2}{\mathbb{I}}^{*}N\left(\frac{{\mathbb{I}}_{m}}{{\mathbb{I}}^{*}}\right)+{\varnothing }_{3}{\mathbb{Q}}^{*}N\left(\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}^{*}}\right)+{\varnothing }_{4}{\mathbb{R}}^{*}N \left(\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}^{*}}\right)$$

where \({\varnothing }_{i}>0,i=\text{1,2},\text{3,4},5.\) Which we use later . it is clear that \({Y}_{m}\left({\mathbb{S}}_{m},{\mathbb{E}}_{m},{\mathbb{I}}_{m},{\mathbb{Q}}_{m}{\mathbb{R}}_{m}\right)>0\) for all \({\mathbb{S}}_{m}>0, {\mathbb{E}}_{m}>0\),\({\mathbb{I}}_{m}>0{\mathbb{Q}}_{m}>0{\mathbb{R}}_{m}>0.\) and \({Y}_{m}\)(\({\mathbb{S}}^{*}\),\({\mathbb{E}}^{*}, {\mathbb{I}}^{*}, {\mathbb{Q}}^{*}, {\mathbb{R}}^{*})=0.\)

$$\Delta {Y}_{m}={Y}_{m+1}-{Y}_{m}.$$

So,

$$\begin{aligned}\Delta {Y}_{m} & =\left({\mathbb{S}}^{*}N\left(\frac{{\mathbb{S}}_{m+1}}{{\mathbb{S}}^{*}}\right)+{\varnothing }_{1}{\mathbb{E}}^{*}N\left(\frac{{\mathbb{E}}_{m+1}}{{\mathbb{E}}^{*}}\right) \right. \\ & \quad \left. +{\varnothing }_{2}{\mathbb{I}}^{*}N\left(\frac{{\mathbb{I}}_{m+1}}{{\mathbb{I}}^{*}}\right)+{\varnothing }_{3}{\mathbb{Q}}^{*}N\left(\frac{{\mathbb{Q}}_{m+1}}{{\mathbb{Q}}^{*}}\right)+{\varnothing }_{4}{\mathbb{R}}^{*}N \left(\frac{{\mathbb{R}}_{m+1}}{{\mathbb{R}}^{*}}\right)\right) \\ & \quad -\left({\mathbb{S}}^{*}N\left(\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}^{*}}\right)+{\varnothing }_{1}{\mathbb{E}}^{*}N\left(\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}^{*}}\right)+{\varnothing }_{2}{\mathbb{I}}^{*}N\left(\frac{{\mathbb{I}}_{m}}{{\mathbb{I}}^{*}}\right)+{\varnothing }_{3}{\mathbb{Q}}^{*}N\left(\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}^{*}}\right)+{\varnothing }_{4}{\mathbb{R}}^{*}N \left(\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}^{*}}\right)\right)\end{aligned}$$
$$\begin{aligned} & {\mathbb{S}}^{*}\left(\frac{{\mathbb{S}}_{m+1}}{{\mathbb{S}}^{*}}-\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}^{*}}+ln\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}_{m+1}}\right)+{\varnothing }_{1}{\mathbb{E}}^{*}\left(\frac{{\mathbb{E}}_{m+1}}{{\mathbb{E}}^{*}}-\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}^{*}}+ln\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}_{m+1}}\right) \\ & \quad +{\varnothing }_{2}{\mathbb{I}}^{*}\left(\frac{{\mathbb{I}}_{m+1}}{{\mathbb{I}}^{*}}-\frac{{\mathbb{I}}_{m}}{{\mathbb{I}}^{*}}+ln\frac{{\mathbb{I}}_{m}}{{\mathbb{I}}_{m+1}}\right)+{\mathbb{Q}}^{*}\left(\frac{{\mathbb{Q}}_{m+1}}{{\mathbb{Q}}^{*}}-\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}^{*}}+ln\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}_{m+1}}\right) \\ & \quad +{\varnothing }_{4}{\mathbb{R}}^{*}\left(\frac{{\mathbb{R}}_{m+1}}{{\mathbb{R}}^{*}}-\frac{{\mathbb{R}}_{m}}{{\mathbb{S}}^{*}}+ln\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}_{m+1}}\right).\end{aligned}$$
(11)

By using the inequality \(lnA\le A-1\) Now 12 Equation become

$$\begin{aligned}\Delta {Y}_{m} & \le {\mathbb{S}}^{*}\left(\frac{{\mathbb{S}}_{m+1}-{\mathbb{S}}_{m}}{{\mathbb{S}}^{*}}+\frac{{\mathbb{S}}_{m}}{{\mathbb{S}}_{m+1}}-1\right)+{\varnothing }_{1}{\mathbb{E}}^{*}\left(\frac{{\mathbb{E}}_{m+1}-{\mathbb{E}}_{m}}{{\mathbb{E}}^{*}}+\frac{{\mathbb{E}}_{m}}{{\mathbb{E}}_{m+1}}-1\right) \\ & \quad +{\varnothing }_{2}{\mathbb{I}}^{*}\left(\frac{{\mathbb{I}}_{m+1}-{\mathbb{I}}_{m}}{{\mathbb{I}}^{*}}+\frac{{\mathbb{I}}_{m}}{{\mathbb{I}}_{m+1}}-1\right)+{\varnothing }_{3}{\mathbb{Q}}^{*}\left(\frac{{\mathbb{Q}}_{m+1}-{\mathbb{Q}}_{m}}{{\mathbb{Q}}^{*}}+\frac{{\mathbb{Q}}_{m}}{{\mathbb{Q}}_{m+1}}-1\right)+{\varnothing }_{4}{\mathbb{R}}^{*}\left(\frac{{\mathbb{R}}_{m+1}-{\mathbb{R}}_{m}}{{\mathbb{R}}^{*}}+\frac{{\mathbb{R}}_{m}}{{\mathbb{R}}_{m+1}}-1\right)\end{aligned}$$
$$\begin{aligned} & =\left(1-\frac{{\mathbb{S}}^{*}}{{\mathbb{S}}_{m+1}}\right)\left({\mathbb{S}}_{m+1}-{\mathbb{S}}_{m}\right)+{\varnothing }_{1}{\mathbb{E}}^{*}\left(1-\frac{{\mathbb{E}}^{*}}{{\mathbb{E}}_{m+1}}\right)\left({\mathbb{E}}_{m+1}-{\mathbb{E}}_{m}\right) \\ & \quad +{\varnothing }_{2}{\mathbb{I}}^{*}\left(1-\frac{{\mathbb{I}}^{*}}{{\mathbb{I}}_{m+1}}\right)\left({\mathbb{I}}_{m+1}-{\mathbb{I}}_{m}\right)+{\varnothing }_{3}{\mathbb{Q}}^{*}\left(1-\frac{{\mathbb{Q}}^{*}}{{\mathbb{Q}}_{m+1}}\right)\left({\mathbb{Q}}_{m+1}-{\mathbb{Q}}_{m}\right) \\ & \quad +{\varnothing }_{4}{\mathbb{R}}^{*}\left(1-\frac{{\mathbb{R}}^{*}}{{\mathbb{R}}_{m+1}}\right){({\mathbb{R}}}_{m+1}-{\mathbb{R}}_{m}).\end{aligned}$$
(12)

By applying system (3), 12 become

$$\begin{aligned}\Delta {Y}_{m} & \le \left(1-\frac{{\mathbb{S}}^{*}}{{\mathbb{S}}_{m+1}}\right)\left(\rho -{\tau }_{1}{\mathbb{S}}_{m+1}{\mathbb{I}}_{m}-{\tau }_{2}{\mathbb{S}}_{m+1}{\mathbb{E}}_{m}-\omega {\mathbb{S}}_{m+1}\right) \\ & \quad +{{\varnothing }}_{1}\left(1-\frac{{\mathbb{E}}^{*}}{{\mathbb{E}}_{m+1}}\right)\left({\tau }_{1}{\mathbb{S}}_{m}{\mathbb{I}}_{m}+{\tau }_{2}{\mathbb{S}}_{m}{\mathbb{E}}_{m+1}-\left({\upsilon }_{1}+\omega +\Lambda +{\varphi }\right){\mathbb{E}}_{m+1}\right) \\ & \quad {+{\varnothing }}_{2}\left(1-\frac{{\mathbb{I}}^{*}}{{\mathbb{I}}_{m+1}}\right)(\Lambda {\mathbb{E}}_{m}-{\theta }_{1}{\mathbb{I}}_{m+1}-c{\mathbb{I}}_{m+1})+{{\varnothing }}_{3}\left(1-\frac{{\mathbb{Q}}^{*}}{{\mathbb{Q}}_{m+1}}\right)(\varphi {\mathbb{E}}_{m+1}-\left(\delta +\omega +{\theta }_{2}\right){\mathbb{Q}}_{m+1} \\ & \quad +{{\varnothing }}_{4}\left(1-\frac{{\mathbb{R}}^{*}}{{\mathbb{R}}_{m+1}}\right)\left(\varphi {\mathbb{E}}_{m}+\text{ c}{\mathbb{I}}_{m}+\delta {\mathbb{Q}}_{m}-\omega {\mathbb{R}}_{m+1}\right).\end{aligned}$$

After simplification we get,

$$\begin{aligned}\Delta {Y}_{m} & \le \frac{-{\tau }_{1}}{{\mathbb{S}}_{m+1}}{\left({\mathbb{S}}_{m+1}-{\mathbb{S}}^{*}\right)}^{2}-{\varnothing }_{1}{\mathbb{E}}^{*}(N\left(\frac{{\mathbb{S}}^{*}}{{\mathbb{S}}_{m+1}}\right) \\ & \quad +N\left(\frac{{\mathbb{S}}_{m+1}{\mathbb{R}}_{m}{\mathbb{E}}^{*}}{{\mathbb{S}}^{*}{\mathbb{R}}^{*}{\mathbb{E}}_{m+1}}\right)+N\left(\frac{{\mathbb{I}}^{*}{\mathbb{E}}_{m+1}}{{\mathbb{E}}^{*}{\mathbb{I}}_{m+1}}\right)+{\mathbb{E}}^{*}\left(\frac{{\mathbb{R}}^{*}{\mathbb{I}}_{m+1}}{{\mathbb{R}}_{m+1}{\mathbb{I}}^{*}}\right) \\ & \quad -{\varnothing }_{2}{\upsilon }_{1}{\mathbb{E}}^{*}(N\left(\frac{{\mathbb{S}}^{*}}{{\mathbb{S}}_{m+1}}\right)+N\left(\frac{{\mathbb{S}}_{m+1}{\mathbb{R}}_{m}{\mathbb{R}}^{*}}{{\mathbb{S}}^{*}{\mathbb{I}}^{*}{\mathbb{R}}_{m+1}}\right)+{\mathbb{E}}^{*}\left(\frac{{\mathbb{R}}^{*}{\mathbb{R}}_{m+1}}{{\mathbb{E}}_{m+1}{\mathbb{I}}^{*}}\right) \\ & \quad -{\varnothing\Lambda }_{3}{\mathbb{E}}^{*}(N\left(\frac{{\mathbb{S}}^{*}}{{\mathbb{S}}_{m+1}}\right)+N\left(\frac{{\mathbb{S}}_{m+1}{\mathbb{R}}_{m}{\mathbb{E}}^{*}}{{\mathbb{S}}^{*}{\mathbb{R}}^{*}{\mathbb{E}}_{m+1}}\right)+N\left(\frac{{\mathbb{R}}^{*}{\mathbb{E}}_{m+1}}{{\mathbb{R}}^{*}{\mathbb{R}}_{m+1}}\right).\end{aligned}$$

Hence, \({Y}_{m}\) is an increasing sequence and there exist \({\text{lim}}_{n\to \infty }{Y}_{m}=Y.\) Therefore, \({E}^{*}\) is (GAS) globally asymptotically stable.

Conclusions

This work discusses and analyses a mathematical model that sheds light on the COVID-19 spread mechanism. It estimates the fundamental reproduction number, a key factor in analyzing the local and global stability of DFE and DEE points. The reproduction rate indicates that COVID-19 is moreover below regulator or getting inferior done period. The NSFD systems are established to evaluate some of the simulation’s properties, such as local and global stability of DFE and DEE points, as well as the positivity and boundedness of the solutions. It has been discovered that other schemes, such as Euler and Rk-4, are convergent for small step sizes and divergent for large step sizes. Nonetheless, the NSFD method is created, which yields results on behalf of the uninterrupted ideal that are exact, mathematically and biologically plausible, and unconditionally convergent. The NSFD scheme’s local and global stability of DFE and DEE points is established through the application of various criteria and conditions. With the associated continuous model, it is confirmed that the suggested NSFD scheme is very dependable for all time step sizes. Our study is advanced in that it develops and tools a novel Non-Standard Finite Difference (NSFD) scheme to analyse the convergence and stability properties of the integer-order COVID-19 model, which has never been done before. Numerical imitations need remained used to confirm the validity of theoretical results. Future work will, include bifurcation analysis and the development of optimal control strategies to better manage the virus’s propagation. And also applying this model to real-world datasets or extending the model to include vaccination strategies.