Abstract
In the context of telecommunications, AI enhances network efficiency by predicting and managing traffic. In many decision-making scenarios, decision-makers choose the more flexible structure that can handle all kinds of information. Bipolarity is the only case in which we can discuss the positive and negative aspects of certain scenarios. On one side, AI enhances network efficiency, proactive maintenance, and personalized customer experience but on the other hand, it has also some negative aspects (1) implementing AI infrastructure can be costly (2) Uses of AI in telecommunication may raise data security concerns and user privacy (3) AI can lead to potential issues if system fail or misused. To cover these issues, the idea of an interval-valued bipolar fuzzy soft set (IVBFSS) has been developed that can deal with both positive and negative aspects of AI. Some basic operational laws for IVBPFS numbers are developed. Several fundamental aggregation operators have been introduced like arithmetic average and geometric average aggregation operators, indicating our main contribution. An algorithm is developed to discuss the application perspective of the initiated approaches. We have utilized these developed notions to classify AI-driven techniques in the telecommunications sector to discuss the applicability of the initiated notions. A comparative analysis of the developed approaches shows the advantages and superiority of the introduced work.
Similar content being viewed by others
Introduction
Importance of AI in telecommunication
Through better network management, enhanced customer satisfaction, and more operational efficiency, artificial intelligence has changed the telecoms sector. AI can proactively detect and fix network problems before they affect users, which lowers downtime and improves service dependability. Chatbots and virtual assistants driven by AI are revolutionizing customer service by managing common questions and providing individual assistance. Furthermore, by dynamically assigning resources in response to demand patterns, AI algorithms provide intelligent traffic management while guaranteeing effective data flow. AI improves threat identification in network security by instantly spotting irregularities and possible online dangers. AI is also simplifying the deployment and administration of 5G, guaranteeing a smooth interaction with current infrastructure. AI’s predictive analytics are also helping with network planning and design by assisting in the determination of the best locations for equipment and network topologies. Telecom companies can better comprehend user preferences and customize their solutions to match particular demands by leveraging machine learning. Natural language processing (NLP) improves communication services by enabling effective text and speech recognition. In the end, AI is helping telecom firms become more customer-focused and nimble, which will put them in a position to quickly adjust to new technological developments.
AI-powered methods are having a significant effect:
Network optimization and management
Telecom businesses may better manage bandwidth and prevent congestion, particularly during peak hours, by using AI algorithms that can predict network traffic patterns. By automatically modifying parameters, AI improves network performance by lowering latency and increasing connection dependability without the need for human involvement.
Improving customer services
Chatbots and virtual assistants powered by AI offer immediate assistance, resolving common problems and referring clients to human agents when needed. This enhances client happiness and cuts down on wait times. Telecom firms may proactively address unfavorable emotions and enhance user experience by using AI-powered sentiment analysis to evaluate consumer feedback from various channels.
Fraud detection and security
AI systems track transaction patterns to spot odd or possibly fraudulent activities, sending out real-time notifications to stop data breaches and financial loss. AI can identify abnormalities that point to security vulnerabilities by examining trends in large datasets, enabling telecom companies to react quickly to threats.
Data-driven decision making
AI helps with decision-making processes ranging from network construction to market strategy by analyzing enormous volumes of data to find patterns and produce useful insights. Particularly helpful in unstable or fiercely competitive markets, predictive analytics assists telecom businesses in anticipating client requests and modifying services accordingly.
Researchers focused on studying the importance of AI in the telecommunication sector and many new developments have been made in this regard. Yrjola et al.1 discussed the exploratory analysis of 6G’s potential for organizational ability by showing the importance of AI in the telecommunication sector. Alsaroah and Al-Turjman2 discussed cloud computing with AI and its impact on the telecom sector. Balmer et al.3 have discussed the application of AI in telecommunication and other network industries. Dimcheva4 studied the opportunities for the application of AI in telecommunication. Moreover, Chen et al.5 explored the success factor that impacts AI adoption in the telecom industry in China5.
Literature review
Zadeh6 developed the fuzzy set (FS) theory to address the intended situation, promoting growth in many scientific and technological domains. Many researchers have used the notion of FS structures to show the usefulness of the FS in AI. Steimann7 debated the use and usefulness of FS in medical AI. Garibaldi8 focused on the need for fuzzy AI. Furthermore, Yager9 debated Fuzzy logic and AI. Also, Marisa et al.10 use the fuzzy AHP method for intelligence gamification mechanics. By extending the idea of FS, Atanassov11 proposed an intuitionistic fuzzy set (IFS) that took membership grade (MG) and non-membership grades (NMG) into account. According to IFS, the sum of MG and NMG must belong to [0, 1]. This property makes IFS dominant in FS theory. The foundation of a wide range of human decisions is double-sided which includes both positive and negative aspects. Examples of two sides in decision and coordination include collaboration and competition, effects and side effects, likelihood and unlikelihood, etc. are often the two-sided aspects. So, based on these observations the idea of the bipolar fuzzy set (BPFS) has been established by Zhang12. Many developments have been made based on the notion of BFS, for example, Akram and Al-Kenani13 produced the BPF PROMETHEE process and used these notions to MCGDM problems for the selection of green suppliers. Also, Hashim et al.14 introduced the notion of neutrosophic BPFSs and applied these notions to the medical field. The MADM ELECTRE II method under the environment of BPFS has been proposed by Akram and Al-Kenani15. Alsolami and Alshehri16 proposed the extension of the VIKOR method for MCDM by using the notion of BPFS. BPF TOPSIS and BPF ELECTRE-I methods have been given by Akram and Arshad17. Experts in a variety of sectors recognize and apply the aforementioned theories and their accompanying DM methods. These methods, however, are unable to address parameterization issues. As a result, Molodtsov18 covered this issue and proposed the conception of a soft set (SS). Maji et al.19 defined some fundamental operations to address DM problems. Moreover, Shabir and Naz20 use the concept of soft topology and introduce the notion of soft topological space. Many new theories have been developed based on the notion of SSs. Selvachandran and Peng21 developed the notion of a modified TOPSIS method on parameterized vague SSs and proposed its applications to supplier selection problems. Moreover, a novel approach to bipolar SSs has been given by Mahmood22. Wen et al.23 integrated the 2-tuple linguistic representation and SSs to solve supplier selection problems. Many hybrid notions based on SS theory and FS theory have been developed like the idea of a fuzzy soft set (FSS)24, intuitionistic fuzzy SS (IFSS)25, Pythagorean fuzzy SS (PyFSS)26, and q-rung orthopair fuzzy SS (q-ROFSS)27. Fuzzy set extensions mentioned are powerful concepts, and numerous research studies have been conducted on them by various scholars since their appearance. Nonetheless, there exist significant deficiencies in the dominant concepts of uncertain extensions, due to which their concepts fail to deal with the situations. For instance, all these parameterized structures discussed above can only discuss one side of the picture however, a lot of human decision-making is based on dual-sided, positive and negative thinking. So, to cover this issue, the idea of bipolar FSS (BPFSS) has been developed28. The subject quickly attracted the attention of many researchers29,30.
Aggregation operators (AOs) are fundamental tools for reducing the total amount of data to a single value, so new AO developments have been presented and applied by scholars. For example, Xu and Yager31 initiated some geometric AOs under the notion of IFS. Also, Mahmood et al.32 proposed several hybrid AOs for triangular IFS and their application to MCDM problems. Ye33 established prioritized AOs of trapezoidal IFS and used these notions to MCDM problems. Imran et al.34 discussed an MCGDM approach for robot selection under the notion of interval-valued IFS.
Furthermore, IF geometric Heronian mean AOs have been given by Yu35. Liu et al.36 initiated two flexible degree-driven consensus models in group DM with IF preference relation. Generalized IF geometric aggregation operators have been introduced by Tan37 and PyF power Aos have been delivered by Wei and Lui38. Arora and Garg39 introduced robust AOs based on IFSS. Zulqarnain et al.40 initiated the conception of AOs based on PyFSS and established their application to green supplier chain management.
Jana et al.41 used BPFSS in MCDM problems and established some BPFS average and geometric aggregation operators. Based on T-BSS, some algebraic structures are defined in42. Moreover, Khan et al.43, Wang and Li44, Kumar and Chen45, and Asif et al.46 illustrated fundamental aggregation operators and applied them to decision-making problems in Pythagorean fuzzy environment, Hadi et al.47, Shit and Ghorai48, and Mateen et al.49 in Fermatean fuzzy environment, Ashraf and Abdullah50, Khan et al.51, Mahnaz et al.52, Debnath and Roy53, Hussain and Ullah54 with spherical fuzzy information, Garg55, Jana et al.56, Senapati57, and Ullah et al.58 under picture fuzzy environment, Khan et al.59, Garg and Chen60, and Gayen et al.61 with q-ROF information, among others. Additionally, interval-valued aggregation operators were suggested in the relevant literature. But they have been introduced relatively less than single-valued ones. For instance, Peng and Yang62 introduced interval-valued aggregation operators under Pythagorean fuzzy environment, Seikh and Mandal63 proposed interval-valued Dombi aggregation operators with Fermatean fuzzy information, Mandal and Seikh64 presented interval-valued Dombi aggregation operators with spherical fuzzy content, and Jabeen et al.65 demonstrated interval-valued Aczel–Alsina aggregation operators under picture fuzzy context. Dong et al.66 introduced interval-valued some essential aggregation operators in q-ROF environment. Under a bipolar fuzzy soft set environment, only a few uncertain concepts are studied67.Saeed et al.68 investigated distance measures in water resource treatment in the notion of interval-valued neutrosophic fuzzy soft set have been developed. Moreover, Kannan et al.69 discussed the linear Diophantine fuzzy CODAS method for logistic specialist selection. For dual information consisting of positive and negative aspects, the notion of bipolar complex fuzzy soft Dombi aggregation operators was proposed in70 and the WASPAS approach was delivered to utilize these notions in decision-making approaches. Rehman71 proposed the selection of a database management system by using the MADM approach. Ozer72 invented the notion of complex picture fuzzy Hamacher aggregation operators and utilized these notions in decision-making approaches. Moreover, Javed et al.73 proposed the notion of spherical fuzzy neutrality aggregation operators and discussed its applications for olive tree plantation site selection. Khan et al.74 proposed confidence level measurement of mobile phone selection under the idea of the T-spherical fuzzy MADM approach.
However, to better model uncertainty, none of the fuzzy bipolar sets-based papers considered interval values.
Motivation of the proposed work
If we discuss the limitations of the existing theories, we can observe that.
-
1.
The notion of IFS proposed by Atanassov11 can only discuss MG and NMG and this structure lacks the property to discuss the parameterization tool. Moreover, we can see that IFS cannot discuss the negative aspects of certain decision-making situations. So IFS has limited structure in this regard.
-
2.
Also if we discuss the structure of IFSS25, PyFSS26, and q-ROFSS27, we can see that although all of these notions can consider the parameterization tool but all the above existing notions cannot discuss the negative aspect of a certain decision-making situation. This shows the limitation of the existing notions. It means that all these limitations in previous notions took our attention to the new theory that can handle all such kinds of limitations.
-
3.
Notice that although the notion of BPFSS28 can discuss the positive and negative aspects and can handle the parameterization tool. Whenever a decision-maker wants to take the information of positive membership function and negative membership function in the form of intervals then this structure can never discuss such kind of information. So the limitation of BPFSS is obvious in this situation.
-
4.
The consideration of positive and negative aspects in one structure is very necessary because there are many real-life situations in which positive and negative are discussed. For example, in the field of medical, medicine has positive and negative aspects. To deal with such kind of information there is a need to define such structure to cover real-life problems. Similarly, the utilization of AI in the telecommunication sector has some positive as well as negative aspects. To discuss this situation, we have to discuss and develop such structure that can deal with such kind of data. Hence, to cover these gaps, the developed theory IVBFSS can discuss the positive and negative aspects in one structure in the form of positive and negative grades.
Contribution and advantages of proposed work
From the above comprehensive literature survey and our knowledge, there has been no work on the aggregation operators of interval-valued bipolar fuzzy soft sets. In this work, therefore, we develop the basic notion of interval-valued bipolar fuzzy soft set (IVBPFSS) as well as introduce fundamental rules for this developed notion. Additionally, we suggest the notion of interval-valued bipolar fuzzy soft weighted arithmetic average (IVBPFWSAA) and interval-valued bipolar fuzzy soft weighted geometric average (IVBPFSWGA) aggregating operators. The basic properties of these notions are developed as well. Moreover, we develop an algorithm and establish a descriptive example for the classification of the most exciting artificial intelligence (AI)-powered innovations. A comparative assessment of the initiated work is performed to show the advantages of the introduced work. Consequently, the article has enough room for new research for the defining of future motives.
Hence main advantages of the proposed theory are.
-
1.
To develop a new path for researchers that can handle both situations like positive membership function, negative membership function, and parameterization tool.
-
2.
The main advantage of the established theory is that it provides more space to decision-makers in the form of an interval-valued bipolar fuzzy soft structure. Moreover, the characteristic analysis of the proposed theory with some other existing notions is given in Table 1.
Arrangement of the article
This work has been arranged as follows. The next section reviews the relevant literature. In Sect."Interval-valued bipolar fuzzy soft set (IVBPFSS)", we have reviewed the notions of FS, SS, FSS, and BPFSS. The idea of an IVBPFSS is given in Sect."Interval-valued bipolar fuzzy soft weighted arithmetic average (IVBPFSWAA) operator". Moreover, we have investigated the basic operational laws for IVBPFSS in Sect."Interval-valued bipolar fuzzy soft weighted arithmetic average (IVBPFSWAA) operator". We have initiated the notion of IVBPFSWAA and IVBPFSWGA operators in Sect."Interval-valued bipolar fuzzy soft weighted arithmetic average (IVBPFSWAA) operator". In Sect."Model for MCGDM method by using IVBPFS information", we have developed an algorithm for MCDM problems. Moreover, Sect."Numerical Example"deals with a descriptive example of the introduced notion for the applicability of the introduced notion. Section"Comparative Analysis"elaborates on the comparative study of the developed work and the last section discusses the concluding remarks.
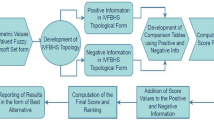
Moreover, the graphical representation of the proposed theory is given in Fig. 1.
Preliminaries
Here in this section, we will discuss the basic notions of FS, SS, FSS, and BPFSS. Moreover, we will discuss some basic operational laws for these notions.
The idea of FS is the generalization of crisp set theory. Crisp set theory is based on the characteristic function that provides information about the belonging and non-belonging of an element of a set. If an element belongs to a set, then its membership value is regarded as 1 and if it does not belong to a set, then its membership value is regarded as 0. To generalize this theory, the idea of FS was introduced by Zadeh6.
Definition 16 :
Suppose \(\:\mathfrak{U}\) is the general, then FS is given by
where \(\:\mathbb{G}\left(\mathbbm{z}\right)\) denote the membership grade (MG).
Traditional mathematical tools like FS and probability theory have limitations in dealing with problems where parametrization tools are necessary. To cover these issues in FS, the idea of SS has been developed to handle vague and imprecise information.
Definition 218 :
Let \(\:\mathfrak{U}\) be the general set and \(\:\mathcal{E}\) denote the parameters set. For any \(\:\text{{\rm\:H}}\subseteq\:\mathcal{E}\) such that \(\:\:\text{{\rm\:H}}\ne\:\varnothing\:\) a function \(\:{f}_{1}:\text{{\rm\:H}}\to\:P\left(\mathcal{E}\right)\:\) over \(\:\mathcal{E}\) is called a SS.
To handle vague and imprecise information more flexibly, there was a need to define such a flexible and useful framework that can handle the fuzzy information and parameterization tool as well. So, knowing these characteristics in one structure, the idea of FSS has been developed.
Definition 325 :
Suppose \(\:\mathfrak{U}\mathfrak{\:}\)and \(\:\mathcal{E}\) denote the general set and set of parameters respectively. Let \(\:P\left(F\right)\) is a power set of FS. Let \(\:\:P\subseteq\:\mathcal{E}.\mathcal{\:}\) A pair \(\:\left(I,\:P\right)\:\) is called FSS over \(\:\:\mathfrak{U}\), where \(\:I\) is the map \(\:I:P\to\:P\left(F\right).\)
The ideas of FS and SS are effective in dealing with imprecise information in decision-making problems. To handle the situation where both positive and negative aspects exist, the notion of BFSS has been delivered.
Definition 428 :
Let \(\:\mathfrak{U}\) be the general set, \(\:\mathcal{E}\) denotes the set of parameters, and \(\:\text{{\rm\:H}}\subseteq\:\mathcal{E}\) such that\(\:\:\text{{\rm\:H}}\ne\:\varnothing\:.\) Define a mapping \(\:{f}_{1}:\text{{\rm\:H}}\to\:P\left(BF\right),\:\)where \(\:P\left(BPF\right)\) denote the power set of bipolar fuzzy subset over\(\:\:\mathfrak{U}\). Then the pair \(\:\left({f}_{1},\:\text{{\rm\:H}}\right)\) is called BPFSS over \(\:\mathfrak{U}\) and it is defined by\(\:\mathfrak{A}\left({\mathfrak{e}}_{\check{\rm r}}\right)=\left\{{\mathbbm{z}}_{\check{\rm r}},\:{\mathbb{G}}^{+}\left({\mathbbm{z}}_{\check{\rm r}}\right),\:{\mathbb{G}}^{-}\left({\mathbbm{z}}_{\check{\rm r}}\right)|{\mathbbm{z}}_{\check{\rm r}}\in\:\mathfrak{U}\mathfrak{\:}and\:{\mathfrak{e}}_{\check{\rm r}}\in\:\mathcal{\:}\mathcal{E}\right\}.\)
Operational laws like sum, product, scalar multiplication, and scalar power play a vital role in managing the theory of aggregation operator. Based on the idea of BFSS, these basic operational laws are defined as follows:
Definition 528 :
Let\(\:\:{\mathfrak{A}}_{{\mathfrak{e}}_{11}}=\left\{\left({\mathbb{G}}_{11}^{+}\right),\:\left({\mathbb{G}}_{11}^{-}\right)\right\}\) and \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{12}}=\left\{\left({\mathbb{G}}_{12}^{+}\right),\:\left({\mathbb{G}}_{12}^{-}\right)\right\}\) be two BPFSNs then fundamental rules can be defined by
Interval-valued bipolar fuzzy soft set (IVBPFSS)
The importance of positive and negative aspects cannot be denoted in any real-life situation. If we discuss the case study in this article, we can see that on one side AI-driven techniques standardized the telecommunication section, but there may be the possibility of negative aspects like (1) implementing AI infrastructure can be costly (2) Uses of AI in telecommunication may raise data security concern and user privacy (3) AI can lead to potential issues if system fail or misused. Hence in this case there is a need to define such a structure that can handle the positive and negative aspects of certain problems. All existing notions in6,22, and23 are free to discuss both of these aspects in one structure. Hence our main motive is to define the basic notion of IVBPFSS. The overall discussion is given by.
Definition 6
Suppose \(\mathfrak{U}\) is the universal set and \(\:\mathcal{E}\) is the parameters set. Let \(\:\mathfrak{A}\subset\:\mathcal{E}\). Then a mapping \(\:\mathfrak{H}:\mathfrak{A}\to\:P\left(IVBPFS\right)\) where \(\:P\left(IVBPFS\right)\) is the family of IVBPFS. Then the pair \(\:\left(\mathfrak{H},\mathfrak{\:}\mathfrak{A}\right)\) is called IVBPFSS and it is defined by a set
where \(\:{\mathbb{G}}^{+}\left({\mathbbm{z}}_{\check{\rm r}}\right)=\left[{\left({\mathbb{G}}^{+}\left({\mathbbm{z}}_{\check{\rm r}}\right)\right)}^{L},\:{\left({\mathbb{G}}^{+}\left({\mathbbm{z}}_{\check{\rm r}}\right)\right)}^{U}\right]\subset\:\left[0,\:1\right]\) represents positive membership function and \(\:{\mathbb{G}}^{-}\left({\mathbbm{z}}_{\check{\rm r}}\right)=\left[{\left({\mathbb{G}}^{-}\left({\mathbbm{z}}_{\check{\rm r}}\right)\right)}^{L},\:{\left({\mathbb{G}}^{-}\left({\mathbbm{z}}_{\check{\rm r}}\right)\right)}^{U}\right]\subset\:\left[-1,\:0\right]\) represents negative membership function with condition that \(\:-1\le\:{\left({\mathbb{G}}^{+}\left({\mathbbm{z}}_{\check{\rm r}}\right)\right)}^{L}+{\left({\mathbb{G}}^{-}\left({\mathbbm{z}}_{\check{\rm r}}\right)\right)}^{L}\le\:1\) and \(\:-1\le\:{\left({\mathbb{G}}^{+}\left({\mathbbm{z}}_{\check{\rm r}}\right)\right)}^{U}+{\left({\mathbb{G}}^{-}\left({\mathbbm{z}}_{\check{\rm r}}\right)\right)}^{U}\le\:1.\)
Example 1
Suppose \(\:\mathfrak{U}=\left\{{\mathcalligra{l\:}}_{1},\:{\mathcalligra{l\:}}_{2},\:{\mathcalligra{l\:}}_{3},\:{\mathcalligra{l\:}}_{4}\right\}\) be the set of four laptops and \(\:\mathcal{E}=\left\{{\mathfrak{e}}_{1}=Display,\:{\mathfrak{e}}_{2}=RAM\:and\:ROM,\:{\mathfrak{e}}_{3}=Battery,\:{\mathfrak{e}}_{4}=High\:resolution\:screen\right\}\) denote parameters set. Then for \(\:\mathfrak{A}=\left\{{\mathfrak{e}}_{1},\:{\mathfrak{e}}_{2},\:{\mathfrak{e}}_{3}\right\}\subset\:\mathcal{E}\), we can define IVBPFSS as
For simplicity, we denote \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}}}\left({\mathbbm{z}}_{\mathbbm{s}}\right)=\left\{{\mathbbm{z}}_{\mathbbm{s}},\:\left[{\left({\mathbb{G}}_{\check{\rm r}}^{+}\left({\mathbbm{z}}_{\mathbbm{s}}\right)\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}}^{+}\left({\mathbbm{z}}_{\mathbbm{s}}\right)\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}}^{-}\left({\mathbbm{z}}_{\mathbbm{s}}\right)\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}}^{-}\left({\mathbbm{z}}_{\mathbbm{s}}\right)\right)}^{U}\right]\right\}\) by \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left\{\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\right\}\) and this notation is named interval-valued bipolar fuzzy soft number (IVBPFSN).
For the application of the introduced notion, it is necessary to define the score function for the ranking purpose of two or more IVBPFSNs.
Definition 7
Let \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{11}}=\left\{\left[{\left({\mathbb{G}}_{11}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{11}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{11}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{11}^{-}\right)}^{U}\right]\right\}\) be an IVBPFSN then SF and AF for “\(\:{\mathfrak{A}}_{{\mathfrak{e}}_{11}}\)” can be defined by
where \(\:Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}}\right)\in\:[0,\:1]\) and
where \(\:Ac\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}}\right)\in\:\left[0,\:1\right].\)
Example 2
\(\:{\mathfrak{A}}_{{\mathfrak{e}}_{11}}=\left\{\left(\left[0.3,\:0.5\right],\:\left[-0.6,\:-0.3\right]\right)\right\}\) be IVBPFSN, then SF and AF can be calculated as
and
Now, we define the order relation between two IVBPFSNs.
Definition 8
Let
and
be two IVBPFSNs then
-
1.
If \(\:Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}}\right) < Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{12}}\right)\) then \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{11}}<{\mathfrak{A}}_{{\mathfrak{e}}_{12}}\)
-
2.
If \(\:Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}}\right)>Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{12}}\right)\) then \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{11}}>{\mathfrak{A}}_{{\mathfrak{e}}_{12}}\)
-
3.
If \(\:\text{I}\text{f}\:Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}}\right)=Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{12}}\right)\) then
-
1)
If \(\:Ac\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}}\right) < Ac\left({\mathfrak{A}}_{{\mathfrak{e}}_{12}}\right)\) then \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{11}}<{\mathfrak{A}}_{{\mathfrak{e}}_{12}}\)
-
2)
If \(\:Ac\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}}\right)>Ac\left({\mathfrak{A}}_{{\mathfrak{e}}_{12}}\right)\) then \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{11}}>{\mathfrak{A}}_{{\mathfrak{e}}_{12}}\)
-
3)
If \(\:Ac\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}}\right)=Ac\left({\mathfrak{A}}_{{\mathfrak{e}}_{12}}\right)\:\) then \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{11}}={\mathfrak{A}}_{{\mathfrak{e}}_{12}}.\)
Interval-valued bipolar fuzzy soft weighted arithmetic average (IVBPFSWAA) operator
This section introduces new aggregation operators called IVBPFSWAA aggregation operators. Moreover, we elaborate on some basic characteristics of these AOs.
Operational Laws for interval-valued bipolar fuzzy soft numbers
Definition 9
Let
and
be two IVBPFSNs then fundamental rules can be defined as follows
Interval-valued bipolar fuzzy soft weighted arithmetic average (IVBPFSWAA) aggregation operators
Definition 10
Let \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left\{\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\right\}\) be the family of IVBPFSNs where \(\:\check{\rm r}=\text{1,2},\dots\:,\:m\) and \(\:\mathbbm{s}=1,\:2,\:\dots\:,\:n.\) Also, assume that \(\:{{\varphi}_{\mathbbm{s}},\:{\Phi}}_{\check{\rm r}}\) are weight vectors (WVs) for parameters \(\:{\mathfrak{e}}_{\mathbbm{s}}\) and experts \(\:{\in}_{\check{\rm r}}\) with condition that \(\:{{\varphi}_{\mathbbm{s}}>0,\:{\Phi}}_{\check{\rm r}}>0\) and \(\:\sum_{\mathbbm{s}=1}^{n}{\varphi}_{\mathbbm{s}}=1,\:\sum_{\check{\rm r}=1}^{m}{{\Phi}}_{\check{\rm r}}=1,\:\)then the IVBPFSWA operator is a mapping \(\:IVBPFSWAA:\:{\sigma}^{\mathfrak{n}}\to\:\sigma\:\) given as
Theorem 1
Let \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left\{\hspace*{-6pt}\begin{array}{c}\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\\\:\:\:\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\end{array}\hspace*{-6pt}\right\}\) be the family of IVBPFSNs where \(\:\check{\rm r}=\text{1,2},\dots\:,\:m\) and \(\:\mathbbm{s}=1,\:2,\:\dots\:,\:n\), the aggregated result for \(\:IVBPFSWAA\) aggregation operator is again a\(\:IVBPFSN\)
Proof
For \(\:\:m=1,\) we get \(\:{{\Phi}}_{1}=1.\) By definition (9), we get
Now for \(\:n=1,\) we get \(\:{\varphi}_{1}=1.\) Now, we have\(\:IVBPFSWAA\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}},\:{\mathfrak{A}}_{{\mathfrak{e}}_{12}},\:\dots\:,\:{\mathfrak{A}}_{{\mathfrak{e}}_{mn}}\right)={\oplus\:}_{\check{\rm r}=1}^{m}{{\Phi}}_{\check{\rm r}1}{\mathfrak{A}}_{{\mathfrak{e}}_{1\mathbbm{s}}}\)
Thus, the results are true for \(\:m=1\) and \(\:n=1.\) Assume that the result is true for \(\:n={\text{d}}_{1}+1,\:m={\text{d}}_{2}\) and \(\:n={\text{d}}_{1},\:m={\text{d}}_{2}+1\), therefore
and
Now for \(\:n={\text{d}}_{1}+1,\:m={\text{d}}_{2}+1,\:\)we get
We can observe that the aggregated value is also \(\:IVBPFSN.\:\)Hence, it is true for \(\:n={\text{d}}_{1}+1\) and \(\:m={\text{d}}_{2}+1,\) and so by induction, the results hold for all \(\:m,\:n\ge\:1.\)
Remark 1
If only one parameter \(\:{\mathfrak{e}}_{1}\) is used i.e., \(\:n=1,\) then IVBPFSWAA operators reduce to IVBPFWA aggregation operators defined by
Thus it is clear that the IVBPFWA aggregation operator is taken as a special case of the proposed IVBPFSWAA operator.
Example 3
Suppose \(\:{\in}=\left\{{\in}_{1},\:{\in}_{2},\:{\in}_{3},\:{\in}_{4}\right\}\) be the set of experts who are going to assess the performance of an ultrasound machine under parameters\(\:\mathfrak{\:}\mathfrak{e}=\left\{{\mathfrak{e}}_{1}=Dimension\:and\:weitage,\:{\mathfrak{e}}_{2}=Image\:quality,\:{\mathfrak{e}}_{3}=Availabilty\:of\:battry\:backup\right\}\). Assume that the experts provide their data as IVBPFSNs \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left\{\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\right\}\) for each parameter given in Table 2.
Assume that \(\:\varphi=\left\{0.32,\:0.48,\:0.20\right\}\) and \(\:{\Phi}=\left\{0.22,\:0.26,\:0.34,\:0.18\right\}\) be the WVs for parameters and experts respectively, then
Now, we prove the fundamental properties of IVBPFSWAA aggregation operators.
Theorem 2
Let \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left\{\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\right\}\) be the family of IVBPFSNs where \(\:\check{\rm r}=\text{1,2},\dots\:,\:m\) and \(\:\mathbbm{s}=1,\:2,\:\dots\:,\:n.\) Also, assume that \(\:{{\varphi}_{\mathbbm{s}},\:{\Phi}}_{\check{\rm r}}\) are WVs for parameters \(\:{\mathfrak{e}}_{\mathbbm{s}}\) and experts \(\:{\in}_{\check{\rm r}}\) with condition that \(\:{{\varphi}_{\mathbbm{s}}>0,\:{\Phi}}_{\check{\rm r}}>0\) and \(\:\sum_{\mathbbm{s}=1}^{n}{\varphi}_{\mathbbm{s}}=1,\:\sum_{\check{\rm r}=1}^{m}{{\Phi}}_{\check{\rm r}}=1,\:\)then the following characteristics hold for IVBPFSWAA.
1. (Idempotency): If \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}={\mathfrak{A}}_{\mathfrak{e}}=\left\{\left[{\left({\mathbb{G}}^{+}\right)}^{L},\:{\left({\mathbb{G}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}^{-}\right)}^{L},\:{\left({\mathbb{G}}^{-}\right)}^{U}\right]\right\}\) for all \(\:\check{\rm r},\:\mathbbm{s},\) then we get\(\:IVBPFSWAA\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}},\:{\mathfrak{A}}_{{\mathfrak{e}}_{12}},\:\dots\:,\:{\mathfrak{A}}_{{\mathfrak{e}}_{mn}}\right)={\mathfrak{A}}_{\mathfrak{e}}.\)
Proof
As all \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}={\mathfrak{A}}_{\mathfrak{e}}=\left\{\left[{\left({\mathbb{G}}^{+}\right)}^{L},\:{\left({\mathbb{G}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}^{-}\right)}^{L},\:{\left({\mathbb{G}}^{-}\right)}^{U}\right]\right\},\:\)then
Hence proof is complete.
2. (Boundedness): Let \(\begin{aligned} {{\mathfrak{A}}^{-}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\:=\left(\hspace*{-6pt}\begin{array}{c}\left[\underset{\mathbbm{s}}{{m\check{\rm r}n}}\:\underset{\check{\rm r}}{{m\check{\rm r}n}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L}\:,\:\underset{\mathbbm{s}}{{m\check{\rm r}n}}\:\underset{\check{\rm r}}{{m\check{\rm r}n}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\:\right],\\ \noalign{\vskip6pt}\:\:\left[\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L}\:,\:\:\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\:\right]\end{array}\hspace*{-6pt}\right)\end{aligned}\) and \(\:{{\mathfrak{A}}^{+}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left(\hspace*{-6pt}\begin{array}{c}\left[\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L}\:,\:\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\:\right],\\ \noalign{\vskip6pt} \:\:\left[\underset{\mathbbm{s}}{{m\check{\rm r}n}}\:\underset{\check{\rm r}}{{m\check{\rm r}n}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L}\:,\:\underset{\mathbbm{s}}{{m\check{\rm r}n}}\:\underset{\check{\rm r}}{{m\check{\rm r}n}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\:\right]\end{array}\hspace*{-6pt}\right),\) then
Proof
Since
is an \(\:IVBPFSN,\) then\(\:\underset{\mathbbm{s}}{{min}}\:\underset{\check{\rm r}}{{min}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L}\le\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L}\le\:\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L}\)
That is,
Hence,
Similarly, we can prove that
Also,
\(\:\iff\:{\left(\underset{\mathbbm{s}}{{min}}\underset{\check{\rm r}}{{min}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L}\right)}^{\sum_{\mathbbm{s}=1}^{n}{\varphi}_{\mathbbm{s}}}\le\:{\prod}_{\mathbbm{s}=1}^{n}{\left(\prod_{\check{\rm r}=1}^{m}{\left({\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L}\right)}^{{{\Phi}}_{\check{\rm r}}}\right)}^{{\varphi}_{\mathbbm{s}}}\le\:{\left(\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L}\right)}^{\sum_{\mathbbm{s}=1}^{n}{\varphi}_{\mathbbm{s}}},\) and hence we get
Similarly, we can prove that
Now let \(\:{\Theta\:}=\left\{\left[{\left({\mathbb{G}}_{{\Theta\:}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{{\Theta\:}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{{\Theta\:}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{{\Theta\:}}^{-}\right)}^{U}\right]\right\},\) then from Eqs. (5), (6), (7), and (8), we get
Similarly, we can get that
Now from the definition of the score function, we get
Now the following cases arise.
Case 1
If \(\:Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right)<Sc\left({{\mathfrak{A}}^{+}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right)\) and \(\:Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right)>Sc\left({{\mathfrak{A}}^{-}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right),\) then using the comparison results for two \(\:IVBPFSNs,\) we have
Case 2
If \(\:Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right)=Sc\left({{\mathfrak{A}}^{+}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right)\) that is
then using the above inequalities, we have
\(\:{\left({\mathbb{G}}_{{\Theta\:}}^{+}\right)}^{L}=\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{{\Theta\:}}^{-}\right)}^{L}=\underset{\mathbbm{s}}{{min}}\underset{\check{\rm r}}{{min}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L}\) and
Thus,
Now by using the comparison results for two \(\:IVBPFSNs,\) we get
Case 3
If \(\:Sc\left({\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right)=Sc\left({{\mathfrak{A}}^{-}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right)\) that is
then using the above inequalities, we have
and
Thus,
By using the comparison results for two \(\:IVBPFSNs,\) we get
Hence, the property was proved.
3. (Shift-invariance): If \(\:{\mathfrak{A}}_{\mathfrak{e}}=\left\{\left[{\left({\mathbb{G}}^{+}\right)}^{L},\:{\left({\mathbb{G}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}^{-}\right)}^{L},\:{\left({\mathbb{G}}^{-}\right)}^{U}\right]\right\}\) is another \(\:PF{S}_{ft}N,\:\)then
Proof
Since \(\:{\mathfrak{A}}_{\mathfrak{e}}\) and \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\:\)are \(\:IVBPFSNs,\:\) so
Hence
4. (Homogeneity): For any real number \(\:\mathfrak{y}>0,\:\) we have
Proof
For any real number \(\:\mathfrak{y}>0,\:\)we get
Hence
Hence, the property holds.
Interval-valued bipolar fuzzy soft weighted geometric average (IVBPFSWGA) aggregation operators
Definition 11
Let \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left\{\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\right\}\) be the family of IVBPFSNs where \(\:\check{\rm r}=\text{1,2},\dots\:,\:m\) and \(\:\mathbbm{s}=1,\:2,\:\dots\:,\:n.\) Also, assume that \(\:{{\varphi}_{\mathbbm{s}},\:{\Phi}}_{\check{\rm r}}\) are WVs for parameters \(\:{\mathfrak{e}}_{\mathbbm{s}}\) and experts \(\:{\in}_{\check{\rm r}}\) with condition that \(\:{{\varphi}_{\mathbbm{s}}>0,\:{\Phi}}_{\check{\rm r}}>0\) and \(\:\sum_{\mathbbm{s}=1}^{n}{\varphi}_{\mathbbm{s}}=1,\:\sum_{\check{\rm r}=1}^{m}{{\Phi}}_{\check{\rm r}}=1,\:\)then the IVBPFSWGA operator is a mapping \(\:IVBPFSWGA:\:{\sigma\:}^{\mathfrak{n}}\to\:\sigma\:\) given as
Theorem 3
Let \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left\{\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\right\}\) be the family of IVBPFSNs where \(\:\check{\rm r}=\text{1,2},\dots\:,\:m\) and \(\:\mathbbm{s}=1,\:2,\:\dots\:,\:n\), the aggregated result for \(\:IVBPFSWGA\) aggregation operator is again a \(\:IVBPFSN\)
Proof
For\(\:\:m=1,\) we get \(\:{{\Phi}}_{1}=1.\) By using definition (9), we get
For \(\:n=1,\) we get \(\:{\varphi}_{1}=1.\) Now, we have
So, the results are true for \(\:m=1\) and \(\:n=1.\) Assume that result is true for \(\:n={\text{d}}_{1}+1,\:m={\text{d}}_{2}\) and \(\:n={\text{d}}_{1},\:m={\text{d}}_{2}+1\), therefore
and
Now for \(\:n={\text{d}}_{1}+1,\:m={\text{d}}_{2}+1,\:\) we get
We can observe that the aggregated value is also \(\:IVBPFSN.\:\)Hence, it is true for \(\:n={\text{d}}_{1}+1\) and \(\:m={\text{d}}_{2}+1,\) and so by induction, the results hold for all \(\:m,\:n\ge\:1.\)
Example 4
Considering the data of example 1 and using IVBPFSWGA AOs, we get
Thus, we proved the fundamental properties of IVBPFSWGA aggregation operators.
Theorem 4
Let \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left\{\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\right\}\) be the family of IVBPFSNs where \(\:\check{\rm r}=\text{1,2},\dots\:,\:m\) and \(\:\mathbbm{s}=1,\:2,\:\dots\:,\:n.\) Also, assume that \(\:{{\varphi}_{\mathbbm{s}},\:{\Phi}}_{\check{\rm r}}\) are weight vectors WVs for parameters \(\:{\mathfrak{e}}_{\mathbbm{s}}\) and experts \(\:{\in}_{\check{\rm r}}\) with condition that \(\:{{\varphi}_{\mathbbm{s}}>0,\:{\Phi}}_{\check{\rm r}}>0\) and \(\:\sum_{\mathbbm{s}=1}^{n}{\varphi}_{\mathbbm{s}}=1,\:\sum_{\check{\rm r}=1}^{m}{{\Phi}}_{\check{\rm r}}=1,\:\)then the following properties hold for IVBPFSWGA operators.
-
1.
(Idempotency): If \(\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}={\mathfrak{A}}_{\mathfrak{e}}=\left\{\left[{\left({\mathbb{G}}^{+}\right)}^{L},\:{\left({\mathbb{G}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}^{-}\right)}^{L},\:{\left({\mathbb{G}}^{-}\right)}^{U}\right]\right\}\) for all \(\:\check{\rm r},\:\mathbbm{s},\) then we get\(\:IVBPFSWGA\left({\mathfrak{A}}_{{\mathfrak{e}}_{11}},\:{\mathfrak{A}}_{{\mathfrak{e}}_{12}},\:\dots\:,\:{\mathfrak{A}}_{{\mathfrak{e}}_{mn}}\right)={\mathfrak{A}}_{\mathfrak{e}}.\)
-
2.
(Boundedness): Let \(\:{{\mathfrak{A}}^{-}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left(\left[\begin{array}{c}\underset{\mathbbm{s}}{{min}}\underset{\check{\rm r}}{{m\check{\rm r}n}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L}\:,\\\:\:\underset{\mathbbm{s}}{{min}}\underset{\check{\rm r}}{{m\check{\rm r}n}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\:\end{array}\right],\:\left[\begin{array}{c}\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L}\:,\\\:\:\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\:\end{array}\right]\right)\) and \(\:{{\mathfrak{A}}^{+}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left(\begin{array}{c}\left[\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L}\:,\:\underset{\mathbbm{s}}{{max}}\:\underset{\check{\rm r}}{{max}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\:\right],\\\:\:\left[\underset{\mathbbm{s}}{{min}}\underset{\check{\rm r}}{{min}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L}\:,\:\underset{\mathbbm{s}}{{min}}\underset{\check{\rm r}}{{min}}{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\:\right]\end{array}\right),\) then
3. (Shift-invariance): If \(\:{\mathfrak{A}}_{\mathfrak{e}}=\left\{\left[{\left({\mathbb{G}}^{+}\right)}^{L},\:{\left({\mathbb{G}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}^{-}\right)}^{L},\:{\left({\mathbb{G}}^{-}\right)}^{U}\right]\right\}\) is another \(\:PF{S}_{ft}N,\:\)then
4. (Homogeneity): For any real number \(\:\mathfrak{y}>0,\:\)we have
Model for MCGDM method by using IVBPFS information
A crucial component of many MCGDM processes is uncertainty. Due to objective complexity and ambiguity in human subjective assessment, handling uncertainty demands a strong and adaptable instrument. The theory of IVBPFSS is one of the most recent methods for handling uncertainty. So, based on the notion of IVBPFSWAA and IVBPFSWGA aggregation operators, in this part of the article, we will establish the MCGDM approach in the environment of IVBPFSNs.
Let \(\:{\rm\:Y}=\left\{{{\rm\:Y}}_{1},\:{{\rm\:Y}}_{2},\:\dots\:,\:{{\rm\:Y}}_{z}\right\}\) be the collection of “\(\:z\:\)” alternatives that are evaluated by \(\:m\) experts\(\:\:\left\{{\in}_{1},\:{\in}_{2},\:{\in}_{3},\:\dots\:,\:{\in}_{m}\right\}\) under the constraint of “\(\:n\)"parameters\(\:\:E=\left\{{\mathfrak{e}}_{1},\:{\mathfrak{e}}_{2},\:\dots\:,\:{\mathfrak{e}}_{n}\right\}\). Let\(\:\:\varphi={\left\{{\varphi}_{1},\:{\varphi}_{1},\:\dots\:,\:{\varphi}_{n}\right\}}^{T}and\:{\Phi}={\left\{{{\Phi}}_{1},\:{{\Phi}}_{2},\:\dots\:,\:{{\Phi}}_{m}\right\}}^{T}\:\)be the WVs for parameters \(\:{\mathfrak{e}}_{\mathbbm{s}}{\prime\:}s\) and experts \(\:{\in}_{\iota\:}\) respectively having a condition that \(\:{{\varphi}_{\mathbbm{s}}>0,\:{\Phi}}_{\check{\rm r}}>0\) and \(\:\sum_{\mathbbm{s}=1}^{n}{\varphi}_{\mathbbm{s}}=1\) and \(\:\sum_{\check{\rm r}=1}^{n}{{\Phi}}_{\check{\rm r}}=1.\) These experts provide their preference information as \(\:IVBPFSNs.\) Hence the collective decision matrix is obtained in the form of \(\:M={\left({\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right)}_{m\times\:n}.\:\)Using the information of experts, the aggregated “\(\:IVBPFSN{\:{\rm\:B}}_{l}\)” for alternatives \(\:{{\rm\:Y}}_{l}\left(l=1,\:2,\:3,\:\dots\:,\:z\right)\:\)is\(\:\:{{\rm\:B}}_{l}=\left\{\left[{\left({\mathbb{G}}_{l}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{l}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{l}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{l}^{-}\right)}^{U}\right]\right\}\) by using the IVBPFSWAA and IVBPFSWGA operators. Finally, the formula of the score function is used for \(\:IVBPFSNs\) to rank the alternatives.
The step-wise discussion is given below.
Step 1
Gather the information about each alternative under the various criteria and arrange it in the form of an IVBPFS matrix\(\:\:M={\left\{\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\right\}}_{m\times\:n}\)given by
Step 2
Normalize the collective data decision matrix by using the formula given by.
where\(\:{\left({\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}\right)}^{c}=\left\{\left[{1-\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:1-{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{|\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L}\left|-1,\:{|\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right|-1\right]\right\}\) is the complement of \(\:\:{\mathfrak{A}}_{{\mathfrak{e}}_{\check{\rm r}\mathbbm{s}}}=\left\{\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{\check{\rm r}\mathbbm{s}}^{-}\right)}^{U}\right]\right\}.\)
Step 3
Use \(\:\:IVBPFSWAA\)and \(\:IVBPFSWGA\) operators to aggregate\(\:\:IVBPFSNs\) for each alternative \(\:{{\rm\:Y}}_{l}\left(l=1,\:2,\:3,\:\dots\:,\:z\right)\:\)into a collective decision matrix\(\:{{\rm\:B}}_{l}=\left\{\left[{\left({\mathbb{G}}_{l}^{+}\right)}^{L},\:{\left({\mathbb{G}}_{l}^{+}\right)}^{U}\right],\:\left[{\left({\mathbb{G}}_{l}^{-}\right)}^{L},\:{\left({\mathbb{G}}_{l}^{-}\right)}^{U}\right]\right\}.\)
Step 4
By using the definition of the score function, find the score value of \(\:{{\rm\:B}}_{l}\) for each alternative\(\:{{\rm\:Y}}_{l}\left(l=1,\:2,\:3,\:\dots\:,\:z\right).\)
Step 5
Rank the alternatives and choose the best result.
The advantages of the delivered MCGDM approach are given by.
-
a)
If the decision-makers provide their assessment in the form of IVBPFSS, then this approach can be utilized for decision-making situations.
-
b)
This delivered approach can provide more space for researchers to discuss the notion of IVBPFSS.
-
c)
If we discuss the decision-making algorithm provided by (Abdullah et al.28 ), then we can see that the delivered approach lacks the property to discuss the interval-valued information while the proposed MCGDM algorithm can discuss this property. So, the proposed approach has many advantages.
For easy understanding and utilization of the proposed algorithm, we have provided the flow chart of the algorithm in Fig. 2.
Numerical example
AI is transforming the telecom industry by altering how customers interact with networks and enabling service providers to offer unprecedented levels of assistance. Telcos are now able to process client data fast, precisely, and affordably thanks to AI-driven automation. AI algorithms can be taught to identify patterns in client experiences, allowing them to promote services and deals that are specific to each person’s interests. The telecom industry’s approach to network management is also changing as a result of AI. AI-driven analytics can identify possible risks, find anomalies in network traffic, and enhance network efficiency.
The adoption of AI in the telecoms sector is giving telcos new chances to boost income. Tools backed by AI in marketing can assist telcos in locating high-value clients. The telecoms sector is being revolutionized by AI, which is driving cost savings, enhancing customer service, and generating new revenue streams. The way organizations interact is changing thanks to the application of AI in telecom solutions. Communications companies can give their clients quicker and more dependable services thanks to AI-based solutions.
Here are some benefits that AI can provide to telecommunications providers.
-
1.
AI-based systems can automate procedures like network setup and maintenance, customer support inquiries, and other administrative work. Costs are brought down, and productivity is increased.
-
2.
By maximizing network resources, AI-based solutions can aid in boosting network capacity. Customers will have access to the services they require when they need them.
-
3.
By offering customers better customer service, quicker response times, and more personalized services, AI-based solutions can enhance the customer experience.
Nowadays literature is reached about the application of AI in different fields. Singh et al.60 proposed a review of AI technologies for tackling Covid-19. Similarly, Xie and Wang61 established an AI-based news feature mining system based on multi-sensor fusions. Al-Adhaileh62 uses the AI framework for modeling and predicting crop yield to enhance food security in Saudi Arabia. Here are some of the most appealing AI-driven developments that are transforming the telecommunications sector.
Automated chatbots
Automated chatbots are software applications that resemble human conversation and react instantly to user requests. These chatbots use AI and natural language processing to comprehend and respond in a human-like manner. AI-powered chatbots and rule-based chatbots are two different forms of automated chatbots. Rule-based chatbots respond to user input based on predetermined rules and specified keywords or patterns. They are unable to comprehend complex queries well and frequently need upgrades to improve. Conversely, AI-powered chatbots use NLP models and machine learning algorithms to comprehend and provide responses. Through user interactions, these chatbots can learn and get better over time. They can respond with greater accuracy and context-relevant information because they are more adaptable in how they handle different types of requests. Telecommunications firms utilize chatbots that are AI-powered to offer automated services to their customers. When consumers have more complicated problems, these chatbots can even point them in the direction of the appropriate department.
Predictive maintenance
To predict when machinery or equipment is likely to break down or need maintenance, predictive maintenance is a proactive maintenance method that makes use of data analysis and machine learning techniques. It seeks to minimize unplanned downtime, increase asset uptime, and lower maintenance costs. In the past, maintenance tasks were either scheduled proactively based on preset intervals or reactively after a problem had already happened. These methods, however, may be ineffective and result in unneeded upkeep or unforeseen breakdowns. On the other hand, predictive maintenance makes use of data and analytics to anticipate the performance and health of equipment. Predictive maintenance tools powered by AI are being used to spot and fix issues with telecommunications networks before they result in outages. AI-driven systems can forecast when maintenance is required and take preventative action to keep services operating smoothly by continuously monitoring networks.
Fraud detection
The process of locating and stopping fraudulent activity or transactions within a system or organization is known as fraud detection. To find trends, abnormalities, or suspicious activity that could point to fraudulent operations, requires applying a variety of methodologies, technologies, and data analytic methods. In many industries, including finance, e-commerce, insurance, healthcare, and more, fraud detection is used. Keeping up with evolving fraud strategies is a continual process that necessitates constant monitoring, analysis, and modification. Organizations may efficiently identify and stop fraudulent actions by combining a variety of strategies and utilizing cutting-edge technologies, shielding themselves and their clients from monetary losses and reputational harm. To identify fraud in telecommunications networks, AI-driven technologies are being employed. AI solutions can identify fraudulent activity and take action to safeguard clients by analyzing customer data.
Network Security
Network security refers to the policies and procedures put in place to guard against unauthorized access.
Network security has seen a sharp rise in the use of AI in recent years. AI technologies can completely change how businesses identify and respond to cyber threats as they advance in sophistication. Security solutions driven by AI are meant to detect threats more quickly and precisely than conventional techniques. AI may be used to automate security procedures like patch management and vulnerability assessments in addition to its capacity to detect threats. This enables businesses to use less physical labor, work more efficiently, and lower the possibility of human error. In addition to being able to recognize trends in user behavior, AI-driven security solutions may also identify criminal activities more precisely. For detecting advanced persistent attacks, which might overcome conventional security measures, this skill is very helpful. To guarantee the privacy, integrity, and accessibility of network resources, a combination of hardware, software, and policy is used. The following are some important features and elements of network security, (1) Firewalls (2) Virtual Private Networks (3) Encryption (4) Network monitoring and logging, etc. Solutions for network security that are AI-powered are being used to safeguard customers against online dangers. AI technologies can identify suspicious activity and take action to stop harmful traffic by continuously monitoring networks.
Assume that the experts have to analyze these four alternatives \(\:{{\rm\:Y}}_{1},\:{{\rm\:Y}}_{2},\:{{\rm\:Y}}_{3},\:{{\rm\:Y}}_{4}\:\)based on the following five parameters
with WVs\(\:\:\left(0.29,\:0.19,\:0.27,\:0.11,\:0.14\right).\:\)The panel of five experts \(\:{\in}_{1},\:{\in}_{2},\:{\in}_{3},\:{\in}_{4},\:{\in}_{5}\) with WVs \(\:\left(0.31,\:0.32,\:0.11,\:0.1,\:0.16\right)\) must assess the four alternatives \(\:{{\rm\:Y}}_{\check{\rm r}}\:\left(\check{\rm r}=1,\:\text{2,3},\:4\right).\)
Utilization of Step-wise algorithm by using IVBPFSWAA AOs
Now we utilize the step-wise algorithm to discuss the utilization of the prosed theory.
Step 1
The experts provide their assessment of each alternative in the form of IVBPFSNs and overall data can be seen in Tables 3, 4, 5 and 6.
Step 2
As all parameters are of the same type so no need to normalize the above-given data.
Step 3
The expert’s opinion against each alternative has been aggregated by using Eq. (4) and the overall results are given by.
Step 4
By using the definition of the SF we calculate the score values as given by.
Step 5
Rank the alternatives and choose the best one. Hence the ranking result is given by.
So, we can see that \(\:{{\rm\:Y}}_{1}\) is the best alternative.
Utilization of Step-wise algorithm by using IVBPFSWGA AOs
Step 1
Same as above.
Step 2
Same as above.
Step 3
The expert’s opinion against each alternative has been aggregated by using Eq. (9) and the overall results are given by.
Step 4
By using the definition of SF we calculate the score values as given by.
Step 5
Rank the alternatives and choose the best one. Hence the ranking result is given by.
So, we can see that \(\:{\varvec{{\rm\:Y}}}_{1}\) is the best alternative.
Utilization of the developed approach in the classification of AI tools in network optimization
Network Optimization
Through the analysis and modification of a network’s design, protocols, and routing techniques, network optimization aims to increase a network’s performance, efficiency, and dependability. To provide efficient and economical data transfer, it seeks to optimize network throughput, lower latency, enhance capacity utilization, and minimize packet loss. Numerous network types, such as computer networks, telecommunications networks, and even supply chain or transportation networks, might benefit from network optimization.
Assume that four AI tools are used in network optimization and experts have to analyze these four alternatives \(\:{{\rm\:Y}}_{1},\:{{\rm\:Y}}_{2},\:{{\rm\:Y}}_{3},\:{{\rm\:Y}}_{4}\:\)based on the following fiveparameters
With WVs\(\:\:\left(0.21,\:0.23,\:0.19,\:0.25,\:0.12\right).\:\)The panel of five experts \(\:{\in}_{1},\:{\in}_{2},\:{\in}_{3},\:{\in}_{4},\:{\in}_{5}\) with WVs \(\:\left(0.11,\:0.20,\:0.18,\:0.29,\:0.22\right)\) must assess the four alternatives \(\:{{\rm\:Y}}_{\check{\rm r}}\:\left(\check{\rm r}=1,\:\text{2,3},\:4\right).\)
In this case, we assume that the experts provide their assessment in the form of IVBPFSNs and data is given in Tables 3, 4, 5 and 6. The overall results are given in Table 7.
Hence by utilization of the proposed, we can see that the developed approach can be easily utilized in other sectors where AI is playing its role. Moreover, we can observe that this developed approach can only be used in those areas or those problems or those situations where problems contain positive and negative aspects of certain situations. Because the whole theory is based on IVBPFSNs it is the specialty of this structure to discuss the positive and negative aspects of certain situations and where other theories like IFS, PyFS and q-ROFS fail to handle such data. The developed nations can generalize these ideas and provide the space for decision-makers to take their data in the form of positive and negative membership grades to make their decision.
Comparative analysis
In this section of the article, we will establish a comparative assessment of the introduced work. We will compare our work with Xu and Yager’s31 method, Mahmood et al.32 approach, Ye33 approach, Tan’s37 method, Wei and Lu’s38 method, Arora and Garg’s39 method, Zulqarnain et al.40 method and Jana et al.41 method. The main discussion is given below.
Example 6
The technique of protecting networks, computers, servers, mobile devices, electronic systems, and data from attack is known as cyber security (CS). It is often referred to as electronic information security or information technology security. CS is essential because it protects all forms of data from loss and theft. Assume that there are four CS tools that CS analyst uses to secure their data as an alternative.
-
\(\:{{\rm\:Y}}_{1}=\) Encryptoion tool
-
\(\:{{\rm\:Y}}_{2}=\) Antivirus software tool
-
\(\:{{\rm\:Y}}_{3}=\) Network security monitoring tool
-
\(\:{{\rm\:Y}}_{4}=\) Network intrusion detection system
We aim to choose the best alternative from these four choices. Assume that experts \(\:{\in}_{1},\:{\in}_{2},\:{\in}_{3},\:{\in}_{4},\:{\in}_{5}\) provide their assessment corresponding to five parameters.
e1 = Protection from threats, e2 = Quick response, e3 = Data loss protection, e4 = Application and devise control, e5 = Rapid detection.
Suppose the WVs for experts are \(\:\left(0.32,\:0.17,\:0.13,\:0.15,\:0.23\right)\) and WVs for parameters are \(\:\left(0.31,\:0.19,\:0.14,\:0.16,\:0.20\right).\) Assume that experts provide their assessment in the form of IVBPFSNs as given in Tables 8, 9, 10 and 11. The results are given in Table 12.
From the analysis of Table 12, we can observe that
-
1.
The notion introduced by Xu and Yager31 is based on IFS and we can see that IFS cannot discuss the both positive and negative aspects in one structure. While in the application section, we have utilized the data in which positive and negative aspects are discussed. The AI-driven techniques have some positive and negative aspects and keeping in mind this situation, whenever the decision-makers establish the data in the form of IVBPFSNs then the existing notion fails to handle this situation. While the introduced approach can handle such kind of situation.
-
2.
The idea of Mahmood et al.32 is based on hybrid aggregation operators but these aggregation operators are based on triangular IFS. The data discussed in this example is based on IVBFSNs and this information can never be handled by Mahmood et al.32 approach. We can notice from Table 12 that no result exists in the case of Mahmood et al.32 approach.
-
3.
If we compare our work with the Ye33 approach, we can notice that Ye33 approach is limited because it is based on trapezoidal IFS and some prioritized aggregation operators are delivered by Ye33.However, the information covered in this example is based on IVBFSNs and this data can never be discussed by Ye33 approach. The proposed data cover the positive and negative aspects of certain situations while the existing approach is limited and can never discuss both aspects in one structure. Hence, we can say that the developed approach is more flexible and superior to the existing notion.
-
4.
Also, Tan37 developed generalized IF geometric AOs and their application to MCGDM. But when observing the proposed theory in37, we can see that it is again based on IFS which is free bipolarity and cannot discuss the positive and negative aspects. Moreover, we can say that this existing approach is free to discuss the parameterization tool. It means that when data is given in the form of packets then it fails to handle this situation. While the established approach can handle this situation.
-
5.
Although the AO theory established by Wei and Lu38 is based on a more generalized form of PyFS as compared to IFS still it has a limited structure because it cannot discuss the positive and negative aspects and free form parameterization tool. When we see the data in row 1 and column of the Table 8, that is
$$\begin{aligned}\:\left(\hspace*{-6pt}\begin{array}{c}\left[0.11,\:0.12\right],\\\:\:\left[-0.13,\:-0.11\right]\end{array}\hspace*{-6pt}\right)\end{aligned}$$We can observe that this data considers the negative values and so cannot be managed by the PyF structure. While the developed approach can deal with such kind of data. Hence the developed approach provides the feasibility to decision makers to take the data in the form of IVBPFSNs in such situations where they want to discuss the positive and negative aspects of certain situations. This characteristic makes IVBPFSS more advanced and stronger than existing notions.
-
6.
Arora and Garg’s methods39 and Zulqarnain et al.40 method only consider the intuitionistic fuzzy soft and Pythagorean fuzzy soft data while the data given in Tables 8, 9, 10 and 11 consist of IVBPFSs, the data given in Tables 8, 9, 10 and 11 cannot be handled by both of these methods. Moreover, we can see that the proposed aggregation operators can tackle this data effectively and the results are given in Table 12. Be aware that ranking some eligibility and non-eligibility criteria requires the use of two-dimensional viewpoints. So, the existing theories cannot consider the two-dimensional perspective while the proposed work can consider this viewpoint. Hence, established work is more reliable.
-
7.
Also, note that although Jana et al.41 methods consist of bipolar fuzzy soft data but the proposed notion is more advanced consisting of interval-valued bipolar fuzzy soft information. This means that the Jana et al.41 method cannot consider the interval-valued information due to a lack of structure. On the other hand, the proposed work can handle such kind of hurdle. So proposed work is more general.
-
8.
We can see that interval-valued bipolar fuzzy soft data provide more space to decision makers and they can utilize this type of information in a more general situation. All the above-given theories are unable to use interval-valued information while introduced notions can handle that hurdle efficiently. So, initiated notions are stronger and more reliable. Moreover, the results of Table 12 are given in Fig. 3.
Geometrical presentation of data given in Table 12.
Conclusion
IVBPFSSs are used to handle the uncertainties associated with contrasting the options, standards, and judgments of decision-makers to resolve this problem. So, based on these observations, here in this article we have established the notion of IVBFSS. Moreover, based on this notion we have developed some basic operational laws for IVBPFSNs. Moreover, we have constructed several fundamental AOs such as arithmetic average and geometric average AOs based on introduced ideas. Furthermore, we have elaborated on the basic properties of these introduced notions. We have developed an algorithm for multi-criteria decision-making problems under the environment of IVBPFSS and used these notions for classifications of AI-driven techniques in the telecommunication sector. Also, we have given a descriptive example to show the working of initiated notions. Moreover, to prove the effectiveness and superiority of established work, we have proposed a comparative assessment of established work.
The developed nations are limited due to the limitations of their structures. When decision maker provides their assessment in the form of rough ideas then the introduced ideas can never discuss the rough data. Similarly, complex data can never be discussed by the developed approaches. For example, if the decision-makers provide theory assessment in the form of complex bipolar fuzzy data, then the introduced notions can never discuss such kind of information. Moreover, the complex bipolar fuzzy rough data can never be discussed by the introduced notion.
In the future, we can extend this work to spherical fuzzy soft rough sets given by Zheng et al.75.Moreover, some new developments can be made based on the introduced notion as given by Wang et al.76.We can define the technique like the DEMATEL method as proposed in77 based on the proposed theory to strengthen the developed approach.
Data availability
The data generated or analyzed for this article is entirely contained in the article and anyone can use it by just citing the article.
References
Yrjölä, S. et al. Artificial Intelligence in the Telecommunication Sector: Exploratory Analysis of 6G’s Potential for Organizational Agility. In Entrepreneurial Connectivity. (ed. Ratten, V.) (Springer, Singapore, 2021). https://doi.org/10.1007/978-981-16-5572-2_5.
Alsaroah, A. H. & Al-Turjman, F. Combining cloud computing with artificial intelligence and its impact on Telecom sector. NEU J. Artif. Intell. IoT, 2(3), (2023).
Balmer, R. E., Levin, S. L. & Schmidt, S. Artificial intelligence applications in telecommunications and other network industries. Telecomm Policy. 44(6), 101977 (2020).
Dimcheva, G. Opportunities for application of artificial intelligence in telecommunication projects. Eng. Proceed. 70(1), 18 (2024).
Chen, H., Li, L. & Chen, Y. Explore success factors that impact artificial intelligence adoption on Telecom industry in China. J. Manag Analytics. 8(1), 36–68 (2021).
Zadeh, L. A. Fuzzy sets. Inf. Control. 8(3), 338–353 (1965).
Steimann, F. On the use and usefulness of fuzzy sets in medical AI. Artif. Intell. Med. 21(1–3), 131–137 (2001).
Garibaldi, J. M. The need for fuzzy AI. IEEE/CAA J. Auto Sinica. 6(3), 610–622 (2019).
Yager, R. R. Fuzzy logics and artificial intelligence’. Fuzzy Sets Syst. 90(2), 193–198 (1997).
Marisa, F. et al. Intelligent gamification mechanics using fuzzy-AHP and k-means to provide matched partner reference. Discrete Dyn. Nat. Soc. https://doi.org/10.1155/2022/8292991 (2022).
Atanassov, K. T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20(1), 87–96 (1986).
Zhang, W. R. Bipolar fuzzy sets and relations: a computational framework for cognitive modeling and multiagent decision analysis’ In NAFIPS/IFIS/NASA’94. Proceedings of the First International Joint Conference of The North American Fuzzy Information Processing Society Biannual Conference The Industrial Fuzzy Control and Intelligence (pp. 305–309). IEEE, December. (1994).
Akram, M. & Al-Kenani, A. N. Multi-criteria group decision-making for selection of green suppliers under bipolar fuzzy PROMETHEE process’. Symmetry 12(1), 77 (2020).
Hashim, R. M., Gulistan, M., Rehman, I., Hassan, N. & Nasruddin, A. M. Neutrosophic bipolar fuzzy set and its application in medicines preparations. Neutrosophic Sets Syst. 31, 86–100 (2020).
Akram, M. & Al-Kenani, A. N. Multiple-attribute decision making ELECTRE II method under bipolar fuzzy model. Algorithms 12(11), 226 (2019).
Alsolame, B. & Alshehri, N. O. Extension of VIKOR method for MCDM under bipolar fuzzy set’. Int. J. Anal. Appl. 18(6), 989–997 (2020).
Akram, M. & Arshad, M. Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput. Appl. Math. 39(1), 1–21 (2020).
Molodtsov, D. Soft set theory—first results. Comput. Math. Appl. 37(4–5), 19–31 (1999).
Maji, P. K., Biswas, R. & Roy, A. R. Soft set theory. Comput. Math. Appl. 45(4–5), 555–562 (2003).
Shabir, M. & Naz, M. On soft topological spaces. Comput. Math. Appl. 61(7), 1786–1799 (2011).
Selvachandran, G. & Peng, X. A modified TOPSIS method based on vague parameterized vague soft sets and its application to supplier selection problems. Neural Comput. Appl. 31(10), 5901–5916 (2019).
Mahmood, T. A novel approach towards bipolar soft sets and their applications. J. Math. 2020, 4690808 (2020).
Wen, T. C., Chang, K. H. & Lai, H. H. Integrating the 2-tuple linguistic representation and soft set to solve supplier selection problems with incomplete information. Eng. Appl. Artif. Intell. 87, 103248 (2020).
Maji, P. K., Roy, A. R. & Biswas, R. Fuzzy soft sets. J. Fuzzy Math. 9, 589–602 (2001).
Maji, P. K., Roy, A. R. & Biswas, R. On intuitionistic fuzzy soft sets. J. Fuzzy Math. 12(3), 669–684 (2004).
Peng, X. D., Yang, Y., Song, J. P. & Jiang, Y. Pythagorean Fuzzy Soft Set its Application Comput. Eng., 41(7), 224–229, (2015).
Hussain, A., Ali, M. I., Mahmood, T. & Munir, M. q-Rung orthopair fuzzy soft average aggregation operators and their application in multicriteria decision‐making. Int. J. Intell. Syst. 35(4), 571–599 (2020).
Abdullah, S., Aslam, M. & Ullah, K. Bipolar fuzzy soft sets and its applications in decision making problem. J. Intell. Fuzzy Syst. 27(2), 729–742 (2014).
Delgado, M., Marín, N., Pérez, Y. & Vila, M. A. Bipolar queries on fuzzy univalued and multivalued attributes in object databases. Fuzzy Sets Syst. 292, 175–192 (2016).
Ma, Z. & Yan, L. Data modeling and querying with fuzzy sets: A systematic survey. Fuzzy Sets Syst. 445, 147–183 (2022).
Xu, Z. & Yager, R. R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 35(4), 417–433 (2006).
Mahmood, T., Liu, P., Ye, J. & Khan, Q. Several hybrid aggregation operators for triangular intuitionistic fuzzy set and their application in multi-criteria decision making. Gran Comput. 3(2), 153–168 (2018).
Ye, J. Prioritized aggregation operators of trapezoidal intuitionistic fuzzy sets and their application to multicriteria decision-making. Neural Comput. Appl. 25(6), 1447–1454 (2014).
Imran, R., Ullah, K., Ali, Z., Akram, M., Multi-Criteria, A. & Group Decision-Making approach for robot selection using Interval-Valued intuitionistic fuzzy information and Aczel-Alsina bonferroni means. Spec. Decis. Mak. Appl. 1(1), 1–32. https://doi.org/10.31181/sdmap1120241 (2024).
Yu, D. Intuitionistic fuzzy geometric Heronian mean aggregation operators. Appl. Soft Comput. 13(2), 1235–1246 (2013).
Liu, F., You, Q., Hu, Y. & Pedrycz, W. Two flexibility degrees-driven consensus model in group decision making with intuitionistic fuzzy preference relations. Inf. Fusion. 88, 86–99 (2022).
Tan, C. Generalized intuitionistic fuzzy geometric aggregation operator and its application to multi-criteria group decision making. Soft Comput. 15, 867–876 (2011).
Wei, G. & Lu, M. Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 33(1), 169–186 (2018).
Arora, R. & Garg, H. A robust aggregation operators for multi-criteria decision-making with intuitionistic fuzzy soft set environment. Sci. Iran. 25(2), 931–942 (2018).
Zulqarnain, R. M., Xin, X. L., Garg, H. & Khan, W. A. Aggregation operators of pythagorean fuzzy soft sets with their application for green supplier chain management. J. Intell. Fuzzy Syst. 40(3), 5545–5563 (2021).
Jana, C., Pal, M. & Wang, J. A robust aggregation operator for multi-criteria decision-making method with bipolar fuzzy soft environment. Iran. J. Fuzzy Syst. 16(6), 1–16 (2019).
Mahmood, T., Asif, M., ur Rehman, U. & Ahmmad, J. T-Bipolar soft semigroups and related results. Spec. Mech. Eng. Oper. Res. 1(1), 258–271 (2024).
Khan, A. A. et al. Pythagorean fuzzy Dombi aggregation operators and their application in decision support system. Symmetry 11(3), 383 (2019).
Wang, L. & Li, N. Pythagorean fuzzy interaction power bonferroni mean aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 35(1), 150–183 (2020).
Kumar, K. & Chen, S. M. Group decision making based on entropy measure of pythagorean fuzzy sets and pythagorean fuzzy weighted arithmetic mean aggregation operator of pythagorean fuzzy numbers. Inf. Sci. 624, 361–377 (2023).
Asif, M., Ishtiaq, U. & Argyros, I. K. Hamacher aggregation operators for pythagorean fuzzy set and its application in multi-attribute decision-making problem. Spec. Oper. Res. 2(1), 27–40 (2025).
Hadi, A., Khan, W. & Khan, A. A novel approach to MADM problems using fermatean fuzzy Hamacher aggregation operators. Int. J. Intell. Syst. 36(7), 3464–3499 (2021).
Shit, C. & Ghorai, G. Multiple attribute decision-making based on different types of Dombi aggregation operators under fermatean fuzzy information. Soft Comput. 25(22), 13869–13880 (2021).
Mateen, M. H., Al-Dayel, I. & Alsuraiheed, T. Fermatean fuzzy fairly aggregation operators with Multi-Criteria Decision-Making. Axioms 12(9), 865 (2023).
Ashraf, S. & Abdullah, S. Spherical aggregation operators and their application in multi-attribute group decision-making. Int. J. Intell. Syst. 34(3), 493–523 (2019).
Khan, Q., Mahmood, T. & Ullah, K. Applications of improved spherical fuzzy Dombi aggregation operators in decision support system. Soft Comput. 25(14), 9097–9119 (2021).
Mahnaz, S., Ali, J., Malik, M. A. & Bashir, Z. T-spherical fuzzy Frank aggregation operators and their application to decision making with unknown weight information. IEEE Access. 10, 7408–7438 (2021).
Debnath, K. & Roy, S. K. Power partitioned neutral aggregation operators for T-spherical fuzzy sets: an application to H2 refueling site selection. Expert Syst. Appl. 216, 119470 (2023).
Hussain, A. & Ullah, K. An intelligent decision support system for spherical fuzzy Sugeno-weber aggregation operators and real-life applications. Spec. Mech. Eng. Oper. Res. 1(1), 177–188 (2024).
Garg, H. Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab. J. Sci. Eng. 42(12), 5275–5290 (2017).
Jana, C., Senapati, T., Pal, M. & Yager, R. R. Picture fuzzy Dombi aggregation operators: application to MADM process. Appl. Soft Comput. 74, 99–109 (2019).
Senapati, T. Approaches to multi-attribute decision-making based on picture fuzzy Aczel–Alsina average aggregation operators. Comput. Appl. Math. 41(1), 40 (2022).
Ullah, K., Naeem, M., Hussain, A., Waqas, M. & Haleemzai, I. Evaluation of Electric Motor Cars Based Frank Power Aggregation Operators under Picture Fuzzy Information and a Multi-Attribute Group Decision-Making Process, IEEE Access, 11, 67201–67219, (2023).
Khan, M. R., Wang, H., Ullah, K. & Karamti, H. Construction material selection by using Multi-Attribute decision making based on q-Rung orthopair fuzzy Aczel–Alsina aggregation operators. Appl. Sci. 12(17), 8537 (2022).
Garg, H. & Chen, S. M. Mult attribute group decision making based on neutrality aggregation operators of q-rung orthopair fuzzy sets. Inf. Sci. 517, 427–447 (2020).
Gayen, S., Sarkar, A. & Biswas, A. Schweizer-Sklar operations-based hybrid aggregation operator to dual hesitant q‐rung orthopair fuzzy set and its application on MCGDM. Expert Syst. 40(1), e13257 (2023).
Peng, X. & Yang, Y. Fundamental properties of interval-valued pythagorean fuzzy aggregation operators. Int. J. Intell. Syst. 31(5), 444–487 (2016).
Seikh, M. R. & Mandal, U. Interval-valued fermatean fuzzy Dombi aggregation operators and SWARA based PROMETHEE II method to bio-medical waste management. Expert Syst. Appl. 226, 120082 (2023).
Mandal, U. & Seikh, M. R. Interval-valued spherical fuzzy MABAC method based on Dombi aggregation operators with unknown attribute weights to select plastic waste management process. Appl. Soft Comput., 145, 110516 (2023).
Jabeen, K., Ullah, K., Akram, M. & Haleemzai, I. Interval Valued Picture Fuzzy Aczel–Alsina Aggregation Operators and Their Application by Using the Multi attribute Decision Making Problem, J. Math., 2023. (2023).
Dong, X., Ali, Z., Mahmood, T. & Liu, P. Yager aggregation operators based on complex interval-valued q-rung orthopair fuzzy information and their application in decision making. Complex. Intell. Syst. 9(3), 3185–3210 (2023).
Wang, J. Y., Wang, Y. P. & Liu, L. Hesitant bipolar-valued fuzzy soft sets and their application in decision making, Complexity, 1–12, 2020. (2020).
Saeed, M., Kareem, K., Razzaq, F. & Saqlain, M. Unveiling efficiency: investigating distance measures in wastewater treatment using Interval-Valued neutrosophic fuzzy soft set. Neutrosophic Syst. Appl. 15, 1–15 (2024).
Kannan, J., Jayakumar, V. & Pethaperumal, M. Advanced fuzzy-based decision-making: the linear Diophantine fuzzy CODAS method for logistic specialist selection. Spec. Oper. Res. 2(1), 41–60 (2025).
Jaleel, A. WASPAS technique utilized for agricultural robotics system based on Dombi aggregation operators under bipolar complex fuzzy soft information. J. Innov. Res. Math. Comput. Sci. 1(2), 67–95 (2022).
ur Rehman, U. Selection of database management system by using multi-attribute decision-making approach based on probability complex fuzzy aggregation operators. J. Innov. Res. Math. Comput. Sci. 2(1), 1–16 (2023).
Ozer, O. Hamacher prioritized aggregation operators based on complex picture fuzzy sets and their applications in decision-making problems. J. Innov. Res. Math. Comput. Sci. 1(1), 33–54 (2022).
Javed, M., Javeed, S., Ullah, K. & Haleemzai, I. An approach to multi-attribute decision-making for Olive trees plantation site selection using spherical fuzzy neutrality aggregation operators. IEEE Access. 11, 117403–117422 (2023).
Khan, M. R., Ullah, K., Khan, Q. & Haleemzai, I. Confidence levels measurement of mobile phone selection using a Multi-attribute Decision-Making approach with unknown attribute weight information based on T‐Spherical fuzzy aggregation operators. Discret Dyn. Nat. Soc. 2024(1), 6572374 (2024).
Zheng, L., Mahmood, T., Ahmmad, J., Rehman, U. U. & Zeng, S. Spherical fuzzy soft rough average aggregation operators and their applications to Multi-Criteria decision making. IEEE Access. 10, 27832–27852 (2022).
Wang, P., Liu, P. & Chiclana, F. Multi-stage consistency optimization algorithm for decision making with incomplete probabilistic linguistic preference relation. Inf. Sci. 556, 361–388 (2021).
Gazi, K. H., Raisa, N., Biswas, A., Azizzadeh, F. & Mondal, S. P. Finding the most important criteria in women’s empowerment for sports sector by pentagonal fuzzy DEMATEL methodology. Spec. Decis. Mak. Appl. 2(1), 28–52 (2025).
Acknowledgements
All the authors are thankful to the referees for their valuable suggestions in the improvement of the manuscript.Also, the authors extend their appreciation to Deanship of Scientific Research at Imam Mohammad Ibn SaudIslamic University (IMSIU) for funding this research work through grant number IMSIU-DDRSP2502.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn SaudIslamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Author information
Authors and Affiliations
Contributions
Jabbar Ahmmad and Tahir Mahmood prepared the main manuscript while Meraj Ali Khan and Ibrahim Aldayel validate the results, proofread the manuscript and made corrections wherever needed.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
The authors state that this is their original work and it is neither submitted nor under consideration in any other journal simultaneously.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ahmmad, J., Khan, M.A., Aldayel, I. et al. Significance and classification of AI-driven techniques in telecommunication sectors based on interval-valued bipolar fuzzy soft aggregation operators. Sci Rep 15, 14126 (2025). https://doi.org/10.1038/s41598-025-97866-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-97866-8