Management of power in single rotor wind turbine systems using fuzzy controller based on fractional order error approaches

Abstract

Fuzzy Logic (FL) is a well-established artificial intelligence technique, particularly valuable in control applications where system modeling is either highly complex or impractical. However, its dependence on heuristic knowledge and rule-based decision-making can limit its precision and adaptability in dynamic environments. To address these challenges, this study introduces an enhanced FL-based control strategy that incorporates fractional-order error (FOE) to improve control performance in a single-rotor wind turbine system. The proposed FOE-based FL approach is applied to overcome the problems of the direct power control (DPC) of doubly-fed induction generators (DFIGs), leveraging fractional calculus to enhance system response, robustness, and efficiency. Extensive MATLAB-based simulations validate the effectiveness of the DPC-FOE-FL method with pulse width modulation compared to conventional DPC-FL control. The comparative analysis reveals that the proposed method significantly reduces energy fluctuations and harmonic distortion in the stator current, achieving a 40.85% reduction in the first test and a 34.21% reduction in the second test relative to traditional DPC-FL control. Additionally, the DPC-FOE-FL approach effectively suppresses reactive power overshoot, demonstrating reductions of 96.28%, 96.27%, and 54.56% across multiple test scenarios. Active power ripples are also minimized by 64.37%, 62.59%, and 62.96%, highlighting the method’s superior dynamic performance. These findings confirm that integrating FOE into FL-based controllers significantly enhances power control stability and efficiency in wind energy systems. The DPC-FOE-FL technique offers a promising solution for optimizing renewable energy applications, particularly in fluctuating wind conditions, by ensuring greater precision, adaptability, and robustness in power regulation.

Introduction

Research background

Currently, there is a major shift towards using wind energy (WE) as the primary source of electrical power (EP) generation gradually due to the issues of non-renewable energy sources and increasingly serious environmental pollution¹. However, the power systems relying on WE have several problems such as insufficient frequency modulation and the ability to resist disturbance in the power system (PS). These defects lead to prevalent power outages. Also, WE are a volatile energy which causes fluctuation in EP generation². Power quality (PQ) and current are among the most significant factors in knowing the efficiency of the PS, as the low quality of power sent to the network causes several unwanted defects³. Significant current ripples can disrupt the performance of devices and the PS itself. Consequently, a PS with high efficiency and strong resilience to both external and internal disturbances needs to be developed⁴. Wind turbines (WTs) are commonly employed to harness WE and are categorized into horizontal-axis and vertical-axis types⁵. Their primary purpose is to transform WE into mechanical power. The latter is mainly converted using a double-fed induction generator (DFIG) into EP^3,4. Recently, innovative WTs known as multi-rotor WTs (MRWTs) have emerged to maximize the utilization of WE⁶. The maximum power point tracking (MPPT) approach is used to determine the maximum value of energy from wind, as the energy produced by the generator becomes related to the change in wind speed (WS)⁷. The current experimental study mainly focuses on the PQ and current output from DFIG to ensure high PQ in the grid. The latter feeds the DFIG, where both the grid-side inverter (GSC) and the machine-side inverter (MSC) are used for this purpose⁸. Moreover, to control the DFIG and get good operation both the MSC and GSC must be controlled independently. GSC is often used with diodes to simplify control and the PS itself. Controlling the MSC well contributes greatly to raising the fineness of the power sent to the network and increasing the robustness of the PS, as there has recently been great interest in this inverter by specialists and academics⁹.

Related works

Recently, DFIG-based PSs have gained widespread interest among researchers and policymakers, with researchers paying close attention to the control approaches of both MSC and GSC, especially RSC. Many control approaches were used to control these inverters, such as vector control (VC)¹⁰, direct power control (DPC)¹¹, sliding mode control (SMC)¹², field-oriented control (FOC)¹³, backstopping control (BC)¹⁴, synergetic control¹⁵, direct torque control (DTC)¹⁶, etc. A control system was proposed for both MSC and GSC to obtain high PQ and fewer fluctuations in the generated torque. The results of the simulation analysis showed that controlling the two inverters together contributes significantly to increasing the robustness of the PS. However, implementing separate controls for both the MSC and the GSC introduces several drawbacks, including increased system complexity, higher system costs, challenges in implementation, and a substantial reduction in PQ during system malfunctions¹⁷. Hence, it is crucial to develop a control strategy that offers significant advantages, such as simplicity, high robustness, fewer control parameters, lower cost, ease of implementation, improved system efficiency, enhanced PS characteristics, and fast dynamic response (DR)^11,14. The proposed approach should also be independent of the machine’s mathematical model (MM), enabling reliable performance even in the event of generator malfunctions. A modified SMC approach was suggested in¹⁸ as a suitable solution for the MSC control of a DFIG. This approach is described by its simplicity, low gain, fast DR, ease of realization, and high efficiency, as demonstrated through simulation results compared to the DPC method and other studies. However, a drawback of this control method is its dependence on energy estimation, making it susceptible to variations in PS parameters, as highlighted in robustness tests. An alternative simple method proposed in¹⁹ is a simplified super-twisting control (STC) approach for managing the MSC of DFIG-based MRWT systems. In this approach, the GSC operates with an uncontrolled inverter to simplify the PS while improving PQ. The results indicate the efficacy of this method in enhancing PS characteristics compared to DPC. Nonetheless, robustness tests reveal a significant augment in fluctuation values for current, torque, and energy, which is a drawback. Additionally, an increase in the total harmonic distortion (THD) of the current is observed, further reducing the current quality. In⁸, an efficient and adaptive nonlinear control model for a WE conversion system based on DFIG is presented. A model combining the VC technique and the nonlinear BC method is developed to control the rotating currents and mechanical speed of the DFIG to extract maximum generated power. This proposed approach is characterized by high performance and great robustness compared to the traditional approach. The performance of the proposed approach was tested using a 10 kW generator, comparing results with the PI controller in terms of reference tracking and robustness against DFIG parameter variations. The MATLAB/Simulink program was used to implement and verify the proposed approach, where a variable WS was used. The results highlight the superiority of the designed technique in terms of energy ripples and reference tracking. However, this designed technique has drawbacks that lie in complexity and the presence of a significant number of gains, which makes it difficult to use smart strategies to set the optimal values of gains. A new strategy proposed in²⁰ is based on using a modified DPC method to adaptively change the reference values based on the severity of the voltage drop (VD). In the proposed modified DPC (MDPC) method, the parameters of PI controllers are tuned using the imperial competitive algorithm (ICA). Also, low voltage capacity through LVRT was used to enable the DFIG-wind farm (WF) to remain online to support the electrical grid during a fault condition. To improve the capability of LVRT, a voltage dip index (VDI) is proposed that is updated within a moving time window including samples measured by phase measurement unit (PMU). To evaluate the path mean square (RMS) value of the voltage from the values measured by the PMU, the DFT technique is used. The proposed approach has high fault performance, as the DFIG will be able to smooth out the DC link voltage fluctuations and significantly reduce the oscillations of the stator and rotor currents. This studied PS was implemented in a MATLAB environment, where the simulation results show the effectiveness of the proposed control strategy to improve the LVRT capacity of DFIG. In²¹, the author conducted a comparative study between two different techniques: BC and PI control. These two strategies were applied to control the power of DFIG. Also, the BC strategy was applied to improve the characteristics of the MPPT method. Using the MPPT-BC strategy allows for improving the energy gained from wind. These strategies were applied to the machine inverter only without the grid inverter. MATLAB was used to implement these designed techniques, and two different tests were used to study the efficiency and effectiveness of each strategy. Test results highlight the superiority of the BC strategy over the PI strategy in terms of DR, ripples, and overshoot value of DFIG power. These results make the BC strategy of interest in the future.

When PS parameters change, the control approach used to control the inverters has some ability to decrease the impact of these parameter changes on the system. However, some approaches cannot overcome this change, such as VC and FOC approaches. The high robustness of the designed PS control approach is among the priorities that should receive great attention in the WE system. By using robust and high-performance controls, the PQ, performance, robustness, DR, and stability of the PS can be improved²². Merging controls is one of the solutions that have recently appeared as an alternative to usual controls, where two different or similar controls are combined to augment the competence and robustness of the systems. This proposed method provided satisfactory results and is demonstrated by the increasing work in this regard, where new solutions have been proposed based on the integration of existing traditional controls. In²³, the author used a combination of SMC and synergetic control (SC) to control the MSC, and the resulting approach was used to determine the voltage reference values (VRVs) and thus control the powers. The advantages of this proposed method are simplicity, a small number of gains, high robustness, it does not use an MM of the machine, and it can be implemented practically easily, which makes it most suitable for controlling generators in the future. The use of this designed combination led to a significant enhancement in the quality of the current and thus the PQ and this is demonstrated by the results of the tests presented. STC and SC techniques have been combined in²⁴ to control the RSC of DFIG-MRWT systems. This designed controller does not require information on the MM of the PS, but rather it is applied directly and its dominant advantage is high competence and great robustness against changing generator parameters. Also, there is little gain which makes it easy to adjust which is a huge plus in helping to control the dynamic power response. Two controls from this proposed controller were used to control powers and produce VRVs, as VRVs are used to generate control pulses in the MSC. All completed tests show the competence, efficiency, and ability of the suggested regulator to enhance the features of the PS, and this is demonstrated by the high rates of fluctuation minimization compared to usual controls and some existing works. But the negative of this control lies in its reliance on energy estimation, which makes it slightly affected if the PS parameters change and this is what the completed robustness test shows, as it was observed that there is a noticeable effect, which is negative. In²⁵, the author combined neural networks (NNs) and a DPC approach to control the MSC of 1500 kW DFIG. The advantages of the designed control are simplicity, ease of realization, does not depend on the MM of the DFIG, and a small number of gains, which makes it easy to adjust and control. In this integration, NNs were used to compensate for the state table in the DPC to produce the necessary pulses. In this technique, problems can be overcome and the PQ can be significantly improved, which is what the completed simulation results provide. The negative of this proposed control lies in the lack of a mathematical rule that facilitates the process of determining the number of layers needed and the number of neurons that can provide excellent results. Also, its reliance on power estimation contributes greatly to raising the current/torque ripples in the event of a malfunction in the PS, which is a negative matter. Another combination of two different approaches was done in²⁶, where both VC and third-order SMC (TOSMC) approaches were combined. In this work, the author used TOSMC as a solution to increase the robustness of the VC approach and enhance the competence of the DFIG-MRWT, where the usual regulators were dispensed with and replaced with the TOSMC controller. Therefore, using the TOSMC technique led to a slight augment in the degree of complexity, but the results show the high competence of the suggested approach, especially in the robustness test compared to the usual control, which is a positive thing. The negative of this designed technique lies in its use of PS parameters, which is an undesirable negative, while its reliance on power estimation increases the degree of vulnerability to changing machine parameters. In addition to the control approach, there are approaches for generating control pulses in the inverter that are no less important than the controls mentioned above, as pulse width modulation (PWM) is often used with controls to control DFIG inverters. Using this approach contributes greatly to increasing the current ripples and thus minimizing the fineness of the current, which is negative. In²⁷, the neural PWM technique was used to produce the pulses needed to run the RSC. Using this smart approach led to a significant enhancement in the current quality, and this is shown by the listed THD values, which is a positive thing. Another alternative approach to the PWM technique was proposed in²⁸, where the fuzzy logic (FL) approach was used as a solution to increase the competence of the PWM technique in improving the features of the inverter. As is known, the FL technique is among the smart approaches that rely on experience and do not require information about the MM of the PS, which allows it not to be affected by the external and internal factors of the PS. The FL-PWM approach was verified by simulation and its behavior was compared with neural-based space vector modulation (SVM), as it provided a better value for the resulting THD of a current than DFIG, which is positive. As is known, the SVM approach is considered one of the most famous approaches proposed to control inverters, but it has the drawback of complexity and difficulty of realization, especially in multi-level inverters (MLIs), which allowed researchers to try to search for another approach with high competence, but less complex and more Ease of application in case of MLIs. Therefore, the author in²⁹, proposed a new SVM approach to control the MSC. This approach is called the simplified SVM technique, as it is described by high competence and this is demonstrated by the results obtained. This designed technique was experimentally confirmed in the work³⁰ using the dSPACE 1104 card, where the empirical results showed high competence of this approach compared to several other approaches. The neural simplified SVM technique was also experimentally verified using the dSPACE 1104 card in³¹, where a 2-level inverter was used. The use of NNs led to an enhancement in the SVM approach and thus in the inverter characteristics compared to both the PWM technique and SVM strategy. Therefore, choosing an inverter control approach is necessary, which greatly contributes to simplifying the PS from its complexity, increasing performance and robustness, and improving the quality of the PS. The author used the five-level fuzzy SVM (FSVM) to augment the competence and features of DFIG³². Using this approach led to a significant minimization in the THD of the current and thus improved the quality of the current, as it is noted that the shape of the current is perfectly sinusoidal compared to the traditional approach. The disadvantage of using the five-level FSVM technique lies in the increase in complexity and in the use of the FL technique itself, as there is no mathematical rule that determines the number of rules needed to obtain a good response. In addition, using several FL rules contributes to the slowdown of the PS, which is a negative thing. One of the most widely used control strategies is the DPC strategy, which has been used in many PSs. There are various DPC strategies, and two of them are discussed in³³. The first is the rotor flux estimation-based DPC technique and the other is the stator flux estimation-based DPC strategy. Both strategies use a switching table to control the generator’s inverter. The results showed that the stator flux estimation based on the DPC reduces the ripples by 50% and 83.33% for both active and reactive power (Ps and Qs), respectively, compared to the rotor flux estimation based on DPC. The flux estimation based on the DPC approach also reduces the THD of current by 69.14% compared to the rotor flux estimation based on the DPC technique. Another DPC strategy was proposed in³⁴ for controlling DFIG. This strategy is the voltage-modulated DPC (VM-DPC) strategy using extended power theory. Its high robustness is a major advantage compared to the conventional DPC strategy, and the results demonstrated its superiority in improving the properties of the studied system. However, despite this performance, its complexity is a significant drawback compared to the conventional DPC technique. In³⁵, the DPC strategy with an optimum switching table is proposed to replace the traditional DPC technique of DFIG. This strategy does not use traditional controllers to control the power. This proposed strategy is characterized by complexity and complicated calculations compared to the traditional DPC approach, which is a disadvantage.

Research gaps and challenges

The DFIG has gained a strong reputation among researchers and students in the field of renewable energy, particularly in variable WS applications. However, its use faces numerous challenges. The most significant of these challenges is the lack of a reliable control strategy that combines simplicity, high robustness, ease of implementation, high efficiency, and low cost for power control. By scanning the literature, it is observed that complexity, the presence of a significant number of gains, and the vulnerability to DFIG parameter changes are among the most prominent drawbacks and challenges that hinder the spread of several strategies such as FOC and DPC. As is well known, the DPC strategy is characterized by simplicity, ease of implementation, and rapid DR. However, this strategy is affected by changes in machine parameters due to the presence of traditional controllers used to control power. Power fluctuations are also a major challenge hindering the spread and use of this strategy in DFIG-based PSs. Power fluctuations significantly impact the grid, causing numerous shortcomings and reducing the lifespan of the PS itself. DFIG-based PSs are one of the most important and indispensable solutions, having proven their high capacity, high efficiency, and effectiveness in overcoming the problem of global warming and the increasing energy demand. Therefore, these systems must be developed with effective and appropriate solutions, especially for the problem of low power/current quality and durability. Choosing a control strategy for power control is a complex issue in DFIG-based PSs because several factors must be considered, creating numerous challenges for improving power/current quality and enhancing durability. The use of a DFIG generator relies on the use of two different inverters, each with its control. Furthermore, control strategies such as SVM or PWM are used to control an inverter. Using the SVM strategy offers superior performance compared to using the PWM strategy. However, using the SVM strategy in a DFIG-based PS presents several challenges, including increased complexity, costs, and increased implementation difficulty. Complexity is one of the most significant challenges that must be addressed in DFIG-based PSs. As is well known, complexity plays a significant role in reducing the cost of implementing PSs, thus reducing electricity generation and consumption bills. Complexity also plays a significant role in DR, with lower complexity resulting in faster DR. Several solutions have been proposed to overcome the problems and challenges of DFIG-based PSs. In³⁶, the author used the three-level neural SVM technique with the DPC approach to control the DFIG, eliminating the need for traditional controllers and state tables. In this way, the cons of the DPC technique can be defeated and the current quality can be improved, as a proportional-integral (PI) control is used to determine the reference values of the voltage. Therefore, simplicity and robustness are among the most important features of this approach, as the simulated results show the high competence of this approach compared to traditional control in terms of improving the quality of current and power. The negative of this control lies in its use to estimate powers and the effect of the PI regulator on changing PS parameters. This appears in the robustness test, where it is observed that there is a noticeable augment in the value of THD of current and energy fluctuations. Experimental validation is essential for confirming the effectiveness of proposed control strategies for DFIG systems. For instance, in³⁷, the author experimentally demonstrated the performance of feedback PI regulators applied to the DPC technique of DFIG-MRWT systems. Alongside feedback PI controllers, the PWM technique was employed to generate the pulses required for operating the MSC of the DFIG-MRWT. To simplify the experimental setup, the GSC was paired with an uncontrolled inverter. The experimental results closely aligned with simulation outcomes, confirming their accuracy. While feedback PI controllers significantly enhanced PQ, the presence of ripples was identified as a drawback. In³⁸, a novel DPC approach to DFIG is proposed and experimentally implemented using a dSPACE 1104 card using variable WS. In this work, NNs were used to replace both traditional controls and state tables, where simplicity and robustness are among the most prominent features of this new approach. The features of this new approach were validated through both experimental testing and simulations, utilizing a 1.5 kW DFIG for comparison with the DPC technique. The new DPC method delivered satisfactory experimental performance, as evidenced by reduced fluctuations in energy, torque, and current. However, a notable drawback of this approach is its reliance on energy estimation, which introduces ripples, particularly during robustness tests where these ripples increase. In this study, the author tested three different approaches using a dSPACE 1104 card, all of which were applied to the MSC of the 1.5 kW DFIG. These controls are the DPC technique, BC approach, and neural DPC technique. These controls were used to control the MSC of 1.5 kW DFIG, where two different WS profiles were used to experimentally study the behavior of these approaches. Empirical results show that the PQ is better when using the NN-DPC approaches compared to both DPC and BC techniques. In addition, the empirical results are almost the same as the simulated results, but it is observed that ripples remain present in all the proposed approaches. This searches for another approach that has high competence in terms of minimizing current fluctuations and increasing PQ in the event of a defect in the circuit of the PS. In³⁹, two different controllers are proposed to overcome the drawbacks of the DPC strategy of DFIG. The first controller is a vector proportional-integral (VPI) controller and the second is a proportional-integral-resonant (PIR) controller. The Bode curve is used to study the stability of the two approaches, and MATLAB is used to implement both approaches under different operating conditions. The results show that the proposed DPC using VPI has superior performance in steady state and transient conditions with simple implementation. DPC based on fractional-order PI controllers is a suitable solution proposed in⁴⁰ to overcome the problems of the DPC strategy of DFIG. In this proposed strategy, both the arithmetic optimization technique (AOA) and the cuckoo search algorithm are used to calculate the gains values of the fractional-order PI controller. MATLAB is used to verify the effectiveness and efficacy of the proposed strategy in improving the PQ, overshoot, and SSE of DFIG energy. The results demonstrate the effectiveness of the proposed configuration and regulator in improving the performance of DFIG integration in a WE control system under wind fluctuations and short-circuit faults. Moreover, the AOA method is better than the angular search method in accurately tuning the FOPI controller settings.

In⁴¹, the authors proposed two artificial intelligence-based control strategies, neural hysteresis DPC (NH-DPC) and fuzzy hysteresis DPC (FH-DPC) for improving the performance of DFIG-based WE systems. These approaches enhance the conventional DPC (C-DPC) by reducing power ripples, minimizing current distortion, and optimizing local Qs and Ps control. The artificial intelligent-driven techniques achieve superior PQ by eliminating switching frequency variations and enhancing PS robustness under dynamic wind conditions. A key advantage of the proposed strategies is their ability to maintain high efficiency across all DFIG operating modes, including overspeed, synchronous, sub-synchronous, and super-synchronous modes. Furthermore, extensive validation under realistic WS profiles demonstrates a significant reduction in THD by an average of 77% compared to C-DPC. However, the study is primarily simulation-based, lacking real-world validation under extreme grid conditions. Practical implementation may face challenges such as sensor inaccuracies, computational delays, and scalability to large-scale WFs. Future work should focus on experimental validation and addressing these real-world constraints. In⁴², the FL-based 12-sector DPC (F12-DPC) approach to enhance WTs using DFIGs is proposed. It addresses the limitations of conventional DPC by incorporating the FL technique to mitigate power fluctuations and reduce THD. The proposed method significantly improves PQ, reducing Ps and Qs ripples by 72.7% and 79.2%, respectively, while achieving a substantial decrease in THD across various operational modes. One of the key advantages of F12-DPC is its adaptability to different WS conditions, ensuring stability and efficiency. The use of the FL technique eliminates the reliance on precise PS parameters, enhancing robustness and simplifying implementation.

In reference⁴³, the authors propose a model predictive DTC (MP-DTC) strategy for DFIG-based WE systems. The suggested control method integrates a robust predictive control (RPC) approach with the SVM technique to improve the dynamic performance of the WE conversion system. By incorporating a novel cost function, the controller effectively enhances reference tracking, disturbance rejection, and robustness to parameter variations. The MP-DTC-SVM approach ensures a fixed switching frequency, reducing torque and flux ripples while improving power capture efficiency. The advantage of this method is its superior adaptability to fluctuating wind conditions, maintaining high-performance torque and speed regulation. The predictive approach also minimizes steady-state errors (SSEs) and enhances grid compatibility. Simulation results validate the effectiveness of the controller, demonstrating optimized energy extraction and improved system stability. The author in⁴⁴ gives a control strategy that is different from the works in^41,42 in terms of performance, structure, robustness, and effectiveness in improving power/current quality. In this work, the author combines the FL technique and fractional calculus strategy to control the power of a DFIG-based MRWT system. The fractional-order FL technique is a new strategy that has high performance, great robustness, and superior performance compared to both the PI and FL techniques. The results demonstrated the effectiveness of the fractional-order FL technique in improving the PS properties compared to the conventional approach. This effectiveness is demonstrated by improving the Ps ripples by 69.23% and 96% in the variable WS and durability tests, respectively. The approach also improved the THD of current by 52.54% and 57.67% in all tests compared to the conventional approach. The fractional-order FL technique improves the SSE value of the Ps by 86.73% and 63.01% compared to the conventional approach. This effectiveness of the fractional-order FL technique was verified in⁴⁵ by applying it to an induction motor, where it gave satisfactory results and great effectiveness in improving the quality of current and torque.

Another strategy based on the FL strategy was proposed in⁴⁶ to replace traditional strategies such as DPC. This strategy is fuzzy cascaded control. High robustness, excellent performance, and the absence of an MM of the DFIG are the main features of this strategy. This strategy has been used to control the power of DFIG-based MRWT systems. Compared with the conventional approach, this proposed strategy improves the DR of the Ps by 83.76%, 65.02%, and 91.42% in all tests. Furthermore, this proposed strategy improves the Ps ripple value by 37.50%, 32.20%, and 38.46% compared to the conventional approach. Despite this performance, the proposed approach has drawbacks, including complexity and a large number of gains due to the use of four controls. Furthermore, its reliance on power estimation makes the approach susceptible to changes in machine parameters. This is demonstrated by robustness testing, which observes an increase in the ripple value and the THD of the current. This necessitates an ongoing search for a strategy that is not affected by machine parameter changes and offers robustness and outstanding performance. In⁴⁷, a combination of fractional-order technique and type 2 FL controller was proposed to achieve a high-performance and robust controller. This proposed controller was used to overcome the DPC strategy problems. Also, a genetic algorithm was used to calculate the gain values ​​of the proposed approach. The results showed that the proposed approach reduced the THD of current compared to the traditional technique by percentages estimated at 80%, 33.87%, and 32.50% in all tests. Furthermore, this approach reduces the SSE, undershoot, fluctuations, and overshoot of direct current link voltage compared to the type 2 FL controller based on genetic algorithms by percentages estimated at 1.54%, 33.04%, 25%, and 33.04%, respectively. This proposed strategy has drawbacks that lie in its complexity and reliance on estimating powers, which makes it expensive.

In order to obtain a distinctive and effective performance of DFIG, it was proposed in⁴⁸ to use the three-level fuzzy SVM method to control the machine inverter. This strategy was used in addition to the indirect VC technique to control the power. The use of this proposed strategy depends largely on experience, as the FL technique with 49 rules was used to obtain a fast DR. This proposed strategy relies heavily on power estimation to calculate the power error. Using the indirect VC technique makes the control system related to the DFIG parameters, which is a negative thing that makes the system affected by changing the DFIG parameters, which is highlighted by the simulation results. The simulation results show that the use of the three-level fuzzy SVM method gave satisfactory results in terms of PQ and reduced THD of current compared to the traditional approach. However, in the robustness test, it is noted that there is a noticeable effect on the designed technique, and this appears through the increase in the value of the energy ripples and the value of the THD of current, which searches for the best control strategy continuously. The second-order SMC (SOSMC) strategy is combined with the FL strategy in⁴⁹ to obtain a reliable controller to overcome the problems of the DPC strategy of DFIG. The proposed controller has several advantages, including ease of implementation, no knowledge of the machine model, and high robustness. Using this approach with an SVM strategy significantly reduces power and current ripples compared to the DPC approach. The downside of this approach is that it uses estimation of capabilities and no rule facilitates the application of the FL strategy, as it relies heavily on experience.

Motivation

The literature and research work cited above have shown that the most prominent proposed control strategies, particularly power control for DFIGs, have several problems and drawbacks. The most notable of these drawbacks include poor PQ, high THD of current, slow DR, high complexity, a large number of gains, and the use of an MM for the machine. In addition, the low durability, high SSE, and overshoot of DFIG power are factors that create a strong incentive to develop more effective solutions to improve the reliability of WT-based PSs. Furthermore, the rise in global warming is increasing the desire to propose more efficient energy solutions to reduce the use of conventional sources. On the other hand, providing electrical power without fluctuations and without resorting to the use of auxiliary systems provides a kind of incentive for the discovery, development, and research of highly efficient PSs capable of supplying the grid with high-quality electrical power without resorting to the use of filters or any other technology. In most scientific work, especially in the field of WE, less efficient control strategies are used, relying on traditional controllers such as PIs. The use of traditional controllers in WE systems hurts quality/current power, SSE, response time (RT), and overshoot of DFIG power, especially when the machine parameters change. Examining the above-mentioned literature, particularly the use of FL controls and fractional calculus strategies, is an effective and efficient solution. These two strategies can be relied upon to provide different motivational dimensions and another conceptual framework for overcoming the most significant drawbacks that limit the deployment of DFIG-based PSs.

The use of the FL technique and fractional calculus strategies individually has shown satisfactory results in improving energy/current quality and DR. However, the application of these two strategies in DFIG-based PSs remains unexplored. Combining these strategies is a promising, efficient, and reliable solution that allows for the creation of new strategies with exceptional and high performance. Therefore, combining control strategies encourages the creation of solutions with significant potential to improve current/power quality. However, validation of the proposed solution’s effectiveness, efficiency, and reliability through experimental work is essential. Furthermore, emphasis on simplicity and ease of implementation is a key consideration in DFIG-based PSs. This proposed work relies on the use of the DPC strategy for power control and development, as it is a simple and easy-to-implement strategy. To improve the properties of DFIG-based PSs, the proposed approach should be focused on. This work combines FL technique and fractional calculus in a way different from the literature to obtain a control approach that combines several different features such as high efficiency, strong performance, simplicity, high robustness, ease of implementation, and high efficiency to increase the reliability of DFIG-based PSs.

Major contributions/novelties

In this simulation study, the fractional-order error (FOE) strategy is proposed as a suitable and effective solution to overcome the problems and drawbacks of control. The FOE strategy is the first major contribution of this paper. The strategy is characterized by its simplicity and ease of control. For the first time, the use of the FOE strategy in the field of renewable energy is addressed, making this solution of great importance and promise. This proposed strategy is applied to the FL controller to improve its performance and effectiveness in overcoming the low PQ problems caused by PSs. Therefore, the FOE-based FL (FOE-FL) approach is the second major contribution of this paper. The FOE-FL controller is a new approach that has not been previously discussed and is different from the aforementioned controllers. The FOE-FL controller features excellent performance, high robustness, ease of tuning, fast DR, and no knowledge of the MM of the PS under study is required. The FOE-FL controller can be easily applied to complex PSs, making it a reliable solution in the future.

In this paper, the effectiveness and efficacy of the FOE-FL controller is verified by using it to overcome the shortcomings of the DPC approach used for DFIG power control. Therefore, the DPC-FOE-FL strategy is the third major contribution of this paper. The proposed DPC-FOE-FL strategy in this paper is different from the DPC, FOC, and VC strategies. The DPC-FOE-FL strategy is simple, easy to implement, inexpensive, and does not use an MM of the machine, unlike the BC, SMC, and VC strategies. In this proposed method, the FOE-FL controller is used to control the DFIG’s power. In addition to the FOE-FL controller, the PWM strategy is used to control the operation of the machine’s inverter.

The proposed DPC-FOE-FL strategy aims to overcome the problems of the DPC strategy of DFIG and improve power/current quality without resorting to inverter control, making this work of great importance in the energy field. The work proposed in this paper provides a promising solution for researchers and decision-makers in the energy field.

MATLAB was used to implement and validate the effectiveness and efficacy of the DPC-FOE-FL approach and compare its performance with the DPC-FL approach. To demonstrate the robustness and performance of the approach in improving the characteristics of the studied PS, three different tests were used. The performance of the proposed approach was compared with the DPC-FL approach in terms of reference tracking and reductions in fluctuations, response time (RT), overshoot, and SSE of DFIG power. Also, the comparison was made in terms of reduction in THD of current. Furthermore, the work was compared with other related works. The results of the tests demonstrated the effectiveness, robustness, and efficiency of the designed approach compared to the DPC-FL approach, as demonstrated by the numerical results obtained.

These obtained results make the DPC-FOE-FL technique of great importance in other industrial applications such as photovoltaic systems, electric vehicles, and electronic applications.

The objectives achieved from the work completed are determined as follows:

• Overcoming the drawback of the DPC-FL approach.

• Increasing the current/power quality.

• Minimizing the undershoot value of DFIG energy.

• Improving the robustness of the DFIG-based WT system.

• Reducing the SSE value of the DFIG power.

• Significantly improve the THD of the current.

Organization of the paper

The remainder of this paper is organized as follows:

Sect. “Proposed WE system” presents the proposed energy system, providing mathematical modeling of both the turbine and the DFIG. Section “Proposed DPC-FOE-FL technique” describes the DPC-FOE-FL technique used to control the inverter, highlighting the key features of this strategy. Sect. “Simulation results” discusses the simulation results and comparative analysis. Finally, Sect. “Conclusion” summarizes the conclusions drawn from this work and proposes future research directions.

Proposed WE system

The PS proposed in this paper relies on the use of WE as the primary source of electricity generation. Therefore, this proposed PS is of great importance in the energy field, as its use can mitigate the effects of global warming. Furthermore, this PS can be easily deployed in isolated areas, allowing for the deployment and use of electricity in areas suffering from energy problems. The use of this PS helps overcome the problem of high energy demand, making it of great importance, especially for non-oil governments. The use of this PS allows for overcoming the problem of high energy demand, making it of great importance, especially for non-oil governments.

The most prominent components of this PS under study include the turbine, inverter, and generator. A single-rotor WT was proposed for this PS. This WT was chosen for its low cost compared to MRWTs. It also requires less maintenance. Furthermore, a DFIG generator was used to convert WE into electricity. This generator was chosen for its numerous advantages over other generators, such as synchronous generators.

The DFIG is connected directly to the grid via the stator and connected using two inverters on the rotor, allowing for precise control of the output power. This feature makes this generator highly efficient even when WSs vary.

To implement this studied PS, mathematical modeling of its main components is required. The next subsection will address the mathematical modeling of the WT.

Turbine model

Wind turbines are among the most prominent solutions proposed as an effective way to convert WE into mechanical energy. These turbines can be classified into two types: horizontal-axis WTs and vertical-axis WTs. The difference between these two types lies in cost, performance, efficiency, and energy yield. According to the work done in⁵⁰, the energy gained from the wind is related to the dimensions of the WT and the WS. Therefore, to obtain greater power, a WT with large dimensions must be used. Another thing that enters into the value of the energy gained from the wind is the WS, as the greater the WS, the greater the energy produced. The energy gained from wind is expressed by Eq. (1)⁵¹.

$$P_{t} = \frac{1}{2}C_{P} \left( {\lambda ,\beta } \right)R^{2} \rho \, v^{3}$$

(1)

where, Cp is the coefficient of power, v is the speed of wind, R is the blade length, and ρ is the density of air.

Equation (2) expresses the mathematical relationship by which the value of Cp can be calculated. The latter has a value related to both tip speed ratio (λ) and bit angle (β)⁵².

$${\text{C}}_{{\text{P}}} = - 0.0018 \, ({\uplambda } - 3)({\upbeta } - 2) + (0.5 - 0.167)({\upbeta } - 2)\sin \left[ {\frac{{\pi ({\uplambda } + 0.1)}}{{18.5 - 0.3({\upbeta } - 2)}}} \right]$$

(2)

The value of λ is related to the WS, as the greater the WS, the lower the value of λ and therefore the greater the torque value. But if the WS is lower, the value of λ is greater, and therefore the torque is less. λ can be mathematically expressed by Eq. (3)⁵³.

$${\uplambda } = \frac{{\Omega_{{\text{t}}} {\text{R}}}}{{\text{v}}}$$

(3)

The energy generated by the turbine is used by the generator to convert it into electrical current. The generator is the heart of the PS under study. Therefore, it is necessary to provide an MM for it. This model is presented in the next subsection.

DFIG model

Traditionally, DFIG is one of the most common and widely used types of induction machines. According to the work done in⁵⁴, the DFIG type generator is one of the most widely used types in renewable energy applications, due to its many advantages. Low cost, minimal maintenance, ease of control, and high durability are some of the key features of this generator. It can also operate at high speeds⁸. This generator employs two inverters in its supply PS, enabling effective power control, particularly under variable WS conditions—a capability not commonly found in other machines. The machine’s MM has been extensively studied in various scientific papers^55,56, often utilizing the Park transform for analysis. The power generated by the DFIG can be calculated by measuring voltage and current, with Eq. (4) providing the means to determine these power values⁵⁷.

$$\left\{ \begin{gathered} Q_{s} = \frac{3}{2}( - V_{ds} I_{qs} + V_{qs} I_{ds} ) \hfill \\ P_{s} = \frac{3}{2}(V_{qs} I_{qs} + V_{ds} I_{ds} ) \hfill \\ \end{gathered} \right.$$

(4)

The rotor voltage and flux of DFIG can be expressed mathematically by Eq. (5), where the rotor flux and voltage value are related to the rotor current^16,17.

$$\left\{ \begin{gathered} \psi_{dr} = MI_{dr} + L_{r} I_{dr} \hfill \\ \psi_{qr} = MI_{qr} + L_{r} I_{qr} \hfill \\ V_{dr} = R_{r} I_{dr} + \frac{d}{dt}\psi_{dr} - \omega_{r} \psi_{qr} \hfill \\ V_{qr} = R_{r} I_{qr} + \frac{d}{dt}\psi_{qr} + \omega_{r} \psi_{dr} \hfill \\ \end{gathered} \right.$$

(5)

Equation (6) expresses the torque and speed of the DFIG. The torque value relates to both flux and current, so to change the torque value it is sufficient to change the current. Also, using Eq. (6) it is possible to control the development of the speed value, as according to the value of the difference between the two torques (T_e-T_r) the operation of the generator can be regulated²².

$$\left\{ {\begin{array}{*{20}c} {T_{e} - T_{r} = J \cdot \frac{d\Omega }{{dt}} + f \cdot \Omega } \\ {T_{e} = \frac{3}{2}p\frac{M}{{L_{r} }}(I_{dr} .\psi_{qs} - I_{qr} .\psi_{ds} )} \\ \end{array} } \right.$$

(6)

The stator voltage and flux of the machine are represented in Eq. (7). The values of the flux and voltage for this section are used to estimate the power^55,57.

$$\left\{ \begin{gathered} V_{ds} = \frac{d}{dt}\psi_{ds} + R_{s} I_{ds} - \omega_{s} \psi_{qs} \hfill \\ V_{qs} = \frac{d}{dt}\psi_{qs} + \omega_{s} \psi_{ds} + R_{s} I_{qs} \hfill \\ \psi_{ds} = MI_{dr} + L_{s} I_{ds} \hfill \\ \psi_{qs} = MI_{qr} + L_{s} I_{qs} \hfill \\ \end{gathered} \right.$$

(7)

In the field of control, several strategies have been proposed for controlling DFIGs. The most prominent of these strategies are direct torque control, DPC, and VC techniques. These strategies often use traditional controllers, which can lead to unsatisfactory results, especially when the machine parameters change. To overcome this problem, the next section addresses a new control approach based on the improved DPC strategy.

Proposed DPC-FOE-FL technique

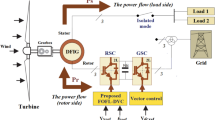
In this section of the paper, a new control strategy for DFIG power control is presented. This new strategy, DPC-FOE-FL, is an evolution of the traditional approach. The DPC-FOE-FL approach is considered a hybrid approach based on a combination of both the DPC technique and FOE-FL controller, where simplicity and high robustness are the most important features of this approach. Also, this approach is described by ease of realization and high competence due to the use of the FOE-FL technique. The DPC-FOE-FL approach is a change and modification of the DPC technique, where the PWM strategy is used in place of a switching table to control the operation of the DFIG inverter. Also, FOE-FL controllers are used to control powers. This proposed strategy uses two FOE-FL controllers to control the powers. The inputs of these controls are power error values, and the outputs are voltage reference values. These voltage reference values play an important role in the operation of the machine’s inverter, as they generate the necessary pulses.

Figure 1 represents the DPC-FOE-FL technique for DFIG. From this figure, it is evident that the proposed approach has a similar structure to the conventional DPC approach while maintaining the simplicity of the conventional approach. This proposed strategy was applied to the DFIG inverter only to demonstrate its ability to improve PQ and reduce the THD of current without requiring control of the DFIG inverter. Therefore, the proposed power system is simple, easy to implement, inexpensive, and has the potential to significantly improve durability and performance.

Fig. 1

DPC-FOFL approach of DFIG-WT.

In this proposed approach, power estimation is used. Power estimation is necessary to calculate the power error, and the same estimation equations are used in the conventional DPC technique. Furthermore, the reference value of Ps in this approach is calculated using the MPPT approach. Using the MPPT approach has several advantages. It allows the turbine to be protected from strong winds and to capture more energy from the wind. Also, using the MPPT approach makes the values of current, Ps, and torque related to the changing WS.

Power estimation

Power estimation is an essential component of the proposed approach, and is indispensable. Power estimation relies on measuring both voltage and current. The power estimation in the DPC-FOE-FL approach is the same as the power estimation used in the DPC technique of DFIG, where the same equations are used. To estimate the power, the flux must first be estimated.

In this work, the flux of the rotor section of the machine is estimated which requires measuring the rotor voltage and current. In estimating powers, the stator flux estimate of the machine can be used. According to the work⁷, the flux in the stator of the DFIG is estimated using Eq. (8).

$$\left\{ {\begin{array}{*{20}c} {\mathop \psi \nolimits_{s\alpha } = \int\limits_{0}^{t} {(\mathop v\nolimits_{s\alpha } } - \mathop R\nolimits_{s} \mathop i\nolimits_{s\alpha } )dt} \\ {\mathop \psi \nolimits_{s\beta } = \int\limits_{0}^{t} ( - \mathop R\nolimits_{s} \mathop i\nolimits_{s\beta } + \mathop v\nolimits_{s\beta } )dt} \\ \end{array} } \right.$$

(8)

The rotor flux of the DPC-FOE-FL technique is estimated using Eq. (9). This flux has an important role in estimating powers, as this flux is used to estimate powers.

$$\left\{ {\begin{array}{*{20}c} {\mathop \psi \nolimits_{r\alpha } = \int\limits_{0}^{t} ( - \mathop R\nolimits_{r} \mathop i\nolimits_{r\alpha } + \mathop V\nolimits_{r\alpha } )dt} \\ {\mathop \psi \nolimits_{r\beta } = \int\limits_{0}^{t} ( - \mathop R\nolimits_{r} \mathop i\nolimits_{r\beta } + \mathop V\nolimits_{r\beta } )dt} \\ \end{array} } \right.$$

(9)

With:

$$\left\{ \begin{gathered} \mathop \psi \nolimits_{s} = \sqrt {\mathop \psi \nolimits_{s\alpha }^{2} + \mathop \psi \nolimits_{s\beta }^{2} } \hfill \\ \mathop \psi \nolimits_{r} = \sqrt {\mathop \psi \nolimits_{r\alpha }^{2} + \mathop \psi \nolimits_{r\beta }^{2} } \hfill \\ \end{gathered} \right.$$

(10)

Rotor flux angle is represented by the Eq. (11).

$$\mathop \theta \nolimits_{r} = arctg(\frac{{\mathop \psi \nolimits_{r\beta } }}{{\mathop \psi \nolimits_{r\alpha } }})$$

(11)

Employing the last equations, the powers are estimated according to the Eqs. (12) and (13).

$$P_{s} = - \frac{3}{2}\frac{{(Vs.\psi_{r\beta } )}}{\sigma \times Ls \times Lr}Lm$$

(12)

$$Q_{s} = - \frac{3}{2}( - \frac{Vs}{{\sigma .Ls.Lr}} \cdot \psi_{r\alpha } .Lm + \frac{Vs}{{\sigma .Ls}} \cdot \psi_{r\beta } )$$

(13)

With:

$$\sigma = - \frac{{\mathop M\nolimits^{2} }}{{\mathop L\nolimits_{r} \mathop L\nolimits_{s} }} + 1$$

(14)

Power estimation is used to calculate power errors. This error is used as an input to the controller used to control the power. Several different controllers have been used, the most prominent of which is the PI controller. Using a PI controller yields good results in terms of DR and does not complicate the PS. However, the use of a PI controller does not provide satisfactory results in terms of robustness and power/current quality. Therefore, an effective and suitable solution is proposed in the next subsection for power control.

FOE-FL controller

In this subsection, a different controller from the literature is discussed for controlling the powers. The controller proposed in this paper is the FOE-FL controller, which differs from the FL controller in terms of structure, principle, performance, effectiveness, and efficiency in mitigating power fluctuations and THD of current.

The FOE-FL controller is a development and modification of the FL approach. This proposed approach is based primarily on the FL approach, combined with a fractional calculus strategy. As is well known, the FL technique offers superior performance and robustness compared to traditional controllers such as PI. Also, using the FL does not require data from the MM of the PS⁵⁸, which makes it easy to apply and use. According to the work done in⁵⁹, the FL technique relies heavily on experience. Its use allows for significant improvement in the characteristics of systems. In the work⁶⁰, the use of the FL technique significantly improved the characteristics of the MPPT strategy compared to the traditional strategy. These results make the FL approach of interest in this paper.

The FOE-FL approach is based on integrating the properties of both fractional calculus and the FL approach. In this proposed controller, the fractional-order error is used as an input to the FL controller. The output of the proposed approach is an output of the FL technique. FOE-FL approach relies heavily on experience in determining the number of rules needed. The FOE-FL approach relies on using the FOE technique instead of using linear error. This strategy makes the controller described by high competence and great robustness. Prominent features of the FOE-FL approach include its simplicity, ease of implementation, low cost, and ease of configuration. Furthermore, this controller does not require knowledge of the machine’s mathematical model, making it a suitable solution for complex systems.

A control was used to control the powers. The inputs of these approaches are the power error values and the outputs are the VRV.

Figure 2 represents the proposed FOE-FL controller used to control the generator’s powers, where each regulator has one output and one input. Also, three gains were used to adjust and change the DR, which helped get better results. These gains can be calculated using intelligent approaches such as genetic algorithms or using experimentation and simulation methods.

Fig. 2

FOE-FL power controller.

Eq. (15) represents the MM of the designer’s approach. This equation highlights the simplicity and ease of implementation of the proposed controller.

$$y(t) = fuzzy(\mathop X\nolimits^{\alpha } )$$

(15)

where, y(t) is the output of the FOE-FL and α represents fractional calculus.

As shown in Fig 2, gains K1, K2, and K3 are used to adjust and modify the DR of the power. Gain α is also used to adjust this response, making this approach more flexible and efficient.

In this proposed controller, the value of α is used to control the operation of the controller. Depending on the value of α, the proposed controller can play two different control roles. If α takes the value of 1, the designed FOE-FL approach becomes FL control. A condition of the designed FOE-FL approach is that the value of α does not take the value 0.

If α does not take the value 0 and the value 1, the designed approach is the FOE-FL technique.

Since the FOE-FL controller uses the FL technique, it relies heavily on experience to determine the appropriate number of rules to achieve high performance and fast DR. To accomplish the FOE-FL controller, 49 rules (7×7) were used, and these rules are represented in Table 1. As is known, the number of rules contributes significantly to improving the DR and characteristics of the systems, as the larger the number of rules, the better the results. However, the increase in the number of rules causes a significant slowdown in the PS, as its response becomes much heavier, which is a negative thing. Choosing the appropriate number of rules for the FL approach depends mainly on experience. In this work, an FL controller containing an acceptable number of rules was used to simplify the complexity of the FL controller. In this work, it was suggested to use 49 rules because it is not a large number, which allows obtaining a fast DR and good results at the same time.

Table 1 FOE-FL technique rules.

In Fig. 3, the FOE-FL functions used to form the FOE-FL power regulator are shown, where 7 triangular-type functions were used for the inputs and outputs. Choosing the number of rules required to implement the proposed controller can be considered a drawback of this controller, as there is no mathematical rule that facilitates choosing the optimal number to achieve satisfactory results. Using a larger number results in excellent results, but the system becomes slower. Using a smaller number of rules results in faster system response, but results are unsatisfactory.

Fig. 3

FOE-FL functions of inputs.

In Table 2, the features of the FOE-FL approach used to control the powers are shown.

Table 2 Parameters of the FOE-FL technique.

Table 3 represents a comparison between the proposed control approach and the traditional DPC strategy. Also, this table compares the proposed approach with the work done in⁴¹. In this table, the similarities and differences between the works done, the traditional strategy, and the proposed approach in⁴¹ are given. As presented in Section “Proposed DPC-FOE-FL technique”, the proposed DPC-FOE-FL approach with the PWM method differs from the traditional DPC technique and the work done in⁴¹ in terms of the structure and controls used to control the powers. The proposed approach is similar to the proposed approach and the work done in⁴¹, where the similarity lies in the use of the same estimation equations for the powers.

Table 3 Comparison between the work done and both the traditional approach and the work proposed in⁴¹.

In⁴¹, two different DPC strategies were used, the first being DPC based on fuzzy hysteresis comparators and the second being DPC based on neural hysteresis comparators. These proposed strategies use a switching table to control the inverter of the 7.5 kW DFIG. The DPC-FOE-FL-PWM strategy differs from the strategies proposed in⁴¹, as this strategy does not use a switching table to control the DFIG power.

As is well known, the use of a switching table allows for introducing unwanted frequencies into the inverter output, which creates several undesirable problems at the network level. However, the DPC-FOE-FL-PWM approach does not use a switching table, which results in providing high-quality current at the inverter output of the machine. Therefore, the lack of a switching table in the DPC-FOE-FL-PWM approach is considered one of the major advantages compared to the work⁴¹. Another advantage of the DPC-FOE-FL-PWM approach compared to the work⁴¹ is the reduced THD of current. From the results obtained in Sect. “Simulation results” of this paper, the THD value in the first test was estimated to be 0.42% while in the work⁴¹ it was 8.80%, 2.27%, and 2.31% for the conventional DPC strategy, DPC based on neural hysteresis comparators, and DPC based on fuzzy hysteresis comparators, respectively. From Table 3and the results obtained from this work and the results in⁴¹, the DPC-FOE-FL-PWM approach has an advantage over the traditional DPC technique and the strategies proposed in⁴¹ due to the use of the FOE-FL controller and not using a switching table.

To study the stability of the proposed approach, the Bode curve or Lyapunov’s theory can be used. Using Lyapunov’s theorem requires complex calculations, as the derivation is calculated, which makes it somewhat complicated. However, the Bode curve is an easy way to prove the stability of control strategies. The Bode curve is a graphical method based on calculating both Magnitude (dB) and phase (deg). According to the values of phase margin and gain margin, the stability of control strategies can be proven. In this paper, the Bode curve was used to prove the stability of the proposed approach. Figure 4 represents the Bode curve for two controls. In Fig. 4, a curve is given for Magnitude (dB) and Phase (deg) for two controls.

Fig. 4

Bode curves.

Figure 4a represents the Bode curve for the DPC-FL approach. Through this figure, the value of Magnitude (dB) and phase (deg) change with changing frequency, as the value of Magnitude (dB) changes from 10 dB to −30 dB. The value of phase (deg) for the DPC-FL approach changes from 0 to −90 degrees. In the case of Magnitude (dB) it is equal to 0 dB, then the value of phase (deg) is approximately equal to the value of −65 degrees. Therefore, the value of the phase margin is equal to 115 deg. With the value of phase margin positive the DPC-FL approach is stable.

Figure 4b represents the Bode curve for the proposed approach. From this figure, it is noted that the value of both phase (deg) and Magnitude (dB) take negative values. Also, the value of Magnitude (dB) and Phase (deg) changes depending on the change in frequency. The Magnitude (dB) value changes from 10 dB to −30 dB, and the phase value changes from 0 to −90 degrees, which are the same changes as in the DPC-FL strategy. If the Magnitude (dB) is equal to the value 0 dB, then the phase is approximately equal to the value −60 deg. Therefore, the phase margin value is positive. As long as the phase margin value is positive, the proposed DPC-FOE-FL approach is stable.

Simulation results

In this section, MATLAB is used to realize the proposed DPC-FOE-FL approach and compare it with the DPC-FL approach, where a variable WS is used for this purpose. The machine parameters are listed in Table 4. The effectiveness and efficiency of the proposed approach were tested using the MPPT strategy and not using it, comparing the results in terms of ripple reduction, RT, overshoot, and SSE of DFIG power.

Table 4 System parameters.

First test: with MPPT technique

In this test, the effectiveness and efficiency of the proposed DPC-FOE-FL-PWM method were studied using the MPPT strategy, while comparing the results with the DPC-FL strategy. In this test, a variable WS was used. The WS used in this test is shown in Fig. 5a, where its variability is employed to evaluate the efficiency of the DPC-FOE-FL approach. Graphical results are presented in Fig. 5b to Fig. 5g, while numerical results are summarized in Table 5. The Ps and current vary in response to changes in WS (Figs. 5b and 5 d), with the energies closely tracking their reference values and exhibiting rapid DR for both control methods. However, the Qs remain unaffected by WS changes (Fig. 5c), maintaining a constant value of 0 VAR throughout the simulation. The current waveform retains a sinusoidal shape in both approaches, but the DPC-FOE-FL approach demonstrates superior smoothness compared to the DPC-FL approach.

Fig. 5

First test results.

Table 5 Value/Ratios of undershoot, RT, SSE, and energy fluctuations of DPC-FL and DPC-FOE-FL.

Figure 5e illustrates the power factor for both methods, which remains stable at a value of 1 regardless of WS fluctuations. The fluctuations are more pronounced with the DPC-FL approach compared to the proposed DPC-FOE-FL approach. Figure 5f and Fig. 5g depict the THD of the current, with values of 0.71% and 0.42% for the DPC-FL and DPC-FOE-FL approaches, respectively. This indicates that the DPC-FOE-FL approach significantly outperforms the DPC-FL approach by reducing THD by approximately 40.85%. This improvement highlights the high effectiveness of the DPC-FOE-FL approach in enhancing current quality compared to the DPC-FL approach. On the other hand, it is noted that the amplitude value of the fundamental signal (50 Hz) was 2.79 A and 2.785 A for both the DPC-FL approach and the proposed approach, respectively. Through these values, it is observed that the amplitudes are almost equal for the two controls, with an advantage for the DPC-FL approach over the proposed approach. Therefore, the amplitude can be considered a negative of the proposed approach in this test. This negativity can be attributed to the gains values of the proposed approach, as it can be overcome in the future by using the grey wolf optimization strategy.

Figure 6 provides a detailed view of the first test results. It is observed that the proposed DPC-FOE-FL approach effectively minimizes ripples in power, current, and power factor compared to the DPC-FL approach. This demonstrates the superiority of the DPC-FOE-FL method.

Fig. 6

Zoom (Test 1).

The numerical results listed in Table 5 show the advantage of the DPC-FOE-FL approach over the DPC-FL approach in terms of fluctuations, overshoot, and SSE of DFIG energy. Accordingly, the reduction of these values was estimated at rates of 64.37%, 71.86%, 0.19%, and 37.41% for each of the fluctuations, overshoot, RT, and SSE of Ps. In the case of Qs, these ratios were estimated at 23.66%, 96.28%, and 76.67% for each of the fluctuations, overshoot, and SSE of Qs. These ratios indicate the high competence of the DPC-FOE-FL approach, making it a promising solution for the future. However, in terms of the Qs of RT, the DPC-FOE-FL approach provided unsatisfactory results compared to the DPC-FL approach, as this negativity can be attributed to the values of the DPC-FOE-FL approach gains. Therefore, the RT is negative for the DPC-FOE-FL approach in this test, which can be defeated by using other approaches such as grey wolf optimization to calculate the DPC-FOE-FL approach parameters.

Second test: robustness test with MPPT technique

The robustness of the proposed DPC-FOE-FL-PWM method was evaluated under variations in DFIG parameters. In this test, the resistance values were multiplied by 2 and the inductance values were multiplied by 0.5. The control was tested using variable WS as shown in Fig. 5a. The results are illustrated in Figs. 7a to 7f, with numerical data provided in Table 6.

Fig. 7

Second test results.

Table 6 Ratios of overshoot, RT, SSE, and power fluctuations of DPC-FL and DPC-FOE-FL (Test 2).

From the graphical results, it is observed that Ps and current vary in response to changes in WS (Figs. 7a and 7c). However, Qs and the power factor remain unaffected by WS changes (Fig. 7b), with Qs maintaining a constant value of 0 VAR and the power factor consistently equal to 1 (Fig. 7d), consistent with the observations from the first test. Additionally, the energies closely track their reference values, though with some fluctuations.

Figures 7e and 7f indicate that the THD of the current was 0.76% for the conventional approach and 0.50% for the proposed DPC-FOE-FL technique. This demonstrates that the DPC-FOE-FL approach significantly reduced THD by approximately 34.21% compared to the DPC-FL approach. This improvement underscores the designed approach’s high efficiency and its ability to produce a significantly smoother current waveform. From Figs. 7e and 7f, it is noted that the amplitude value of the fundamental signal (50 Hz) in this test was 2.794 A and 2.789 A for both the DPC-FL approach and the DPC-FOE-FL-PWM method, respectively. These values show that the amplitude value is very close for the two controls, with an advantage for the DPC-FL approach over the designed technique. Therefore, the amplitude value can be considered negative according to the DPC-FOE-FL-PWM method in this test. This negativity can be overcome in the future by using other strategies, such as the genetic algorithm or the particle swarm algorithm.

Figure 8 represents the zoom in results of the test 2. It is observed that the DPC-FOE-FL strategy reduced the ripples of power, current, and power factor well compared to the DPC-FL strategy.

Fig. 8

Zoom (Test 2).

The numerical results of this test are summarized in Table 6. The proposed DPC-FOE-FL approach demonstrated outstanding performance in reducing fluctuations, overshoot, and SSE in DFIG power. The calculated reduction percentages were 62.59%, 65.52%, 0.19%, and 71.36% for fluctuations, SSE, and overshoot of Ps, respectively. For Qs, these reductions were 23.59% for fluctuations, 58.15% for SSE, and 96.27% for overshoot. However, the proposed DPC-FOE-FL technique showed a longer RT for Qs compared to the DPC-FL, technique which is a drawback likely attributable to the designed gain values of the DPC-FOE-FL technique. This limitation can be addressed and improved in future iterations.

Table 7 represents a study of the effect of the value of THD and fundamental signal (50 Hz) between the second test and the first test. From this study, it is noted that the THD value increased in the second test compared to the first test for the two controls. This increase is due to the change in DFIG parameters in the second test. Therefore, changing the parameters affects the THD value negatively. The difference in THD value between the two tests was estimated at 0.07% and 0.08% for both the DPC-FL approach and the proposed DPC-FOE-FL approach, respectively. Therefore, the DPC-FOE-FL-PWM method provided the greatest difference for THD compared to the DPC-FL approach. This difference in THD value was estimated at 16% for the proposed DPC-FOE-FL approach and 8.97% for the DPC-FL approach. So the DPC-FOE-FL-PWM method provided a greater percentage of change in THD than the DPC-FL approach.

Table 7 Effect study change of fundamental signal (50 Hz) amplitude and THD current in the third test compared to the first test.

The amplitude of the fundamental signal (50 Hz) in the second test increased significantly compared to the first test for the two controls. This amplitude increased as a result of changing the values of the DFIG parameters in the second test. Therefore, it can be said that the amplitude value is negatively affected by changing the values of the DFIG parameters. This increase in amplitude value was estimated at 0.14% for two controls. It is noted that the two controls have almost the same effect on changing the amplitude value.

Test 3: Without MPPT technique

This third test is different from the previous tests. In this test, the efficiency and effectiveness of the proposed approach are verified without using the MPPT strategy, while comparing the results with the DPC-FL approach. The graphical results are represented in Fig. 9 and Fig. 10. The numerical results for the third test are listed in Table 8.

Fig. 9

Third test results.

Fig. 10

Zoom (Test 2).

Table 8 Ratios of overshoot, RT, SSE, and energy fluctuations of DPC-FL and DPC-FOE-FL (Test 3).

Figure 9a represents the change in Ps as a function of time for the two controls. Despite not using the MPPT strategy, the Ps still follow the reference well, with a fast dynamic response to two controls. Also, the Ps takes a negative value, indicating that the DFIG generates power. It is also observed that there are ripples at the level of this energy if the two controls are used.

Figure 9b represents the change in Qs as a function of time for the two controls. From this figure, it is noted that the Qs follow the reference well despite not using the MPPT strategy. The Qs remain 0 VAR throughout the simulation period. Also, it is observed that the Qs have a rapid DR to two controls with the presence of ripples.

Figure 9c represents the change of current as a function of time for the two controls. From this figure, it can be seen that the current for the two controls changes according to the change in the Ps. The value of the current for the two controls increases and decreases with increasing and decreasing Ps, which is the same as the results of the previous tests. Also, the current for the two controllers remains sinusoidal despite not using the MPPT strategy. Figure 9d represents the change in the value of the power factor as a function of time for the two controls. It is noted that despite not using the MPPT strategy, this power factor remains equal to 1 for the two controllers with ripples. The power factor remains at 1 throughout the simulation period, indicating that the Qs is 0 VAR.

Figure 9e and Fig. 9f represent the THD of current and amplitude of a fundamental signal (50 Hz) for the two controls. With these two figures, the THD value was 0.62% and 0.38% for DPC-FL and DPC-FOE-FL, respectively. These values indicate that the THD value is low if the DPC-FOE-FL-PWM method is used compared to the DPC-FL approach. Therefore, despite not using the MPPT strategy, the DPC-FOE-FL-PWM method reduces the value of THD by an estimated percentage of 38.71% compared to the DPC-FL approach. In terms of the amplitude value, the two approaches provide almost the same amplitude. The value of this amplitude was 3.419 A and 3.409 A for both the DPC-FL approach and the DPC-FOE-FL-PWM method, respectively. Through these values, the DPC-FL approach is preferred over the DPC-FOE-FL approach in terms of the largest advance amplitude. This negativity can be attributed to the gain values of the DPC-FOE-FL-PWM method, as other smart strategies can be relied upon in the future to calculate the gain values and thus improve the amplitude value of the fundamental signal (50 Hz).

Figure 10 represents Zoom in the results of the third test for the two controls. Through this form, the DPC-FOE-FL-PWM method works to significantly reduce the ripples of power, current, and power factor compared to the DPC-FL approach. In the case of the power factor, the ripple value was 0.008 and 0.002 for both the DPC-FL approach and the DPC-FOE-FL-PWM method, respectively. So the DPC-FOE-FL-PWM method reduces the power factor ripples by an estimated rate of 75%. This percentage indicates the high performance of the DPC-FOE-FL-PWM method compared to the DPC-FL approach, which makes it a subject of future interest in other fields.

Table 8 represents the reduction ratios and values of ripple, response time, SSE, and overshoot of DFIG power for the two controllers. From this table, it is noted that the DPC-FOE-FL-PWM method provided satisfactory results for ripples, overshoot, and SSE of DFIG power compared to the DPC-FL approach. In the case of Ps, the DPC-FOE-FL-PWM method gives better values for ripple, RT, SSE, and overshoot compared to the DPC-FL approach. The DPC-FOE-FL-PWM method reduces the values of ripple, RT, SSE, and overshoot by percentages estimated at 62.96%, 8.33%, 29.75%, and 30.11%, respectively, compared to the DPC-FL approach. In the case of Qs, the DPC-FOE-FL-PWM method gave better values for ripples, SSE, and overshoot compared to the DPC-FL approach. The DPC-FOE-FL-PWM method reduced the values of ripple, SSE, and overshoot by percentages estimated at 36.20%, 67.86%, and 54.56%, respectively, compared to the DPC-FL approach. Despite this high performance with the designed control strategy, this approach gave an unsatisfactory time for the Qs compared to the DPC-FL approach. The DPC-FL approach improves the RT of Qs by an estimated 24% compared to the DPC-FOE-FL-PWM method. Therefore, the RT of the Qs can be considered the negative of the DPC-FOE-FL-PWM method in this test. This negativity can be attributed to the gains values of the designed technique. This negative can be overcome in the future by using other strategies such as grey wolf optimization.

Table 9 represents a study of the change in the values of both amplitude and THD of current for two controls between the third test and the first test. According to this table, the THD value was affected in the third test compared to the first test for the two controls. The THD value decreased in the third test compared to the first test for the two controls. The difference in THD value was 0.09% and 0.04% for both the DPC-FL approach and the designed technique, respectively. Therefore, the DPC-FOE-FL-PWM method provided the least difference in the THD value compared to the DPC-FL approach. The percentages of change in the THD value were 12.68% and 9.52% for both the DPC-FL approach and the DPC-FOE-FL-PWM method, respectively. The designed control strategy gave a lower percentage of change than the DPC-FL approach.

Table 9 Effect study change of fundamental signal (50 Hz) amplitude and THD current in the third test compared to the first test.

According to Table 9, the amplitude value was affected in the third test compared to the first test. The value of this amplitude increased in the third test compared to the first test for the two approaches. This difference in amplitude was estimated at 18.40% and 18.30% for both the DPC-FL approach and the designed strategy, respectively. Therefore, the DPC-FOE-FL-PWM method provided a lower percentage of change in amplitude compared to the DPC-FL approach. This table shows the strength and efficiency of the DPC-FOE-FL-PWM method in giving satisfactory results for the amplitude and value of THD of current.

Table 10 represents a comparison with related works in terms of the THD value of the current. This table highlights the extent to which the DPC-FOE-FL-PWM method outperforms several related works in terms of reducing the value of THD of current. The DPC-FOE-FL-PWM method gave a better value for THD than several strategies such as DTC-PI (12%) in⁶¹. Also, the DPC-FOE-FL-PWM method gave a better value for THD than the integral SMC approach (9.7%) in the work⁶². This comparison made in Table 10 makes the proposed approach the best solution in terms of improving the THD value, which can be said that the DPC-FOE-FL-PWM method significantly improves the quality of the current compared to several other existing strategies. This comparison makes the DPC-FOE-FL-PWM method of future interest in other industrial applications.

Table 10 Comparison with related works in terms of THD of the current.

Table 11 represents a comparison with related works in terms of RT to powers. From this table, it is noted that the DPC-FOE-FL-PWM method gave an RT to the Ps much better than several scientific works. For example, the proposed approach gave a time to the Psbetter than the work done in⁷⁶, in which the RT to the Ps was estimated at 17 ms. This comparison, presented in Table 11, makes the DPC-FOE-FL-PWM method have a very fast DR compared to several existing strategies. Therefore, the DPC-FOE-FL-PWM method outperforms several strategies in terms of DR to power, which makes it of interest in other applications such as photovoltaic systems.

Table 11 A comparison between the DPC-FOE-FL-PWM method and related papers in terms of response time of DFIG power.

Table 12 represents a comparison with related works in terms of the percentage of reduction of Ps ripples. From this table, it is noted that the DPC-FOE-FL-PWM method gave a percentage of reducing power ripples greater than several research papers. In the first test, the DPC-FOE-FL-PWM method gave a ripple reduction ratio for Psestimated at 64.37%. This reduction percentage is greater than the percentage presented in both⁸⁷ and⁸⁸, which makes the DPC-FOE-FL-PWM method of interest in the future. This comparison highlights the superiority of the DPC-FOE-FL-PWM method over several works such as⁸⁹ in terms of improving PQ (10% and 5.88%). This comparison highlights the effectiveness, strength, and efficiency of the proposed approach compared to several other related works.

Table 12 Comparison with related works in terms of active power ripple reduction ratio.

Table 13 represents a comparison with related works in terms of the overshoot percentage of DFIG power. Through the comparison made in this table, the proposed approach gave a much higher reduction percentage than several different works. For example, work⁸⁸ provided reduction rates estimated at 25.04% and 6.44% for both Ps and Qs, respectively. In work⁹⁴, reduction rates were estimated at 7.23% and 16.59% for both Ps and Qs, respectively. Also, in work⁹³ the ratios were estimated at 20.10% and 49.32% for both Ps and Qs, respectively. All of these percentages presented are less than the ratios of the proposed approach in the first test, where the DPC-FOE-FL-PWM method gave reduction percentages estimated at 71.86% and 96.28% for both Ps and Qs, respectively. This completed comparison highlights the superiority of the DPC-FOE-FL-PWM method and its power in improving the characteristics of the studied control system, which makes it of interest in other industrial applications in the future.

Table 13 Comparing the DPC-FOE-FL technique with some papers in terms of the reduction rates obtained for overshoot of DFIG power.

Conclusions

The simulation study focused on the DPC approach utilizing a FOE-FL controller for the DFIG-WT system. To simplify the PS, the DPC-FOE-FL approach was applied solely to the MSC inverter, with the PWM technique employed for MSC control. The designed approach is characterized by simplicity, ease of implementation, robustness, and exceptional capability in enhancing system performance. Following the development of mathematical models for the WT and DFIG, the principles and equations governing the DPC-FOE-FL technique were presented. MATLAB was used for implementation, involving two distinct tests.

The simulation results highlighted the effectiveness of the DPC-FOE-FL technique in reducing fluctuations, SSE, and overshoot compared to the conventional DPC-FL technique. Furthermore, the DPC-FOE-FL technique achieved reductions in current THD of approximately 34.21% and 40.85% in the respective tests, demonstrating its significant ability to enhance current quality. It also improved overshoot and SSE values for DFIG-WT power.

However, the study had some limitations. The DPC-FOE-FL technique was evaluated using only two WS profiles. Future work will address this by conducting additional tests, including robustness analysis and scenarios with network faults. The approach will also be extended experimentally, leveraging real equipment. Comparisons will be made with other nonlinear methods, such as the SMC technique, to further validate the performance of the DPC-FOE-FL technique.