Algorithm for investigating risk analysis and factors affecting suicidal attempts under uncertainty

Abstract

Many people die from suicide, and it is a significant challenge in most societies, which calls for improved assessment procedures. This work presents a risk assessment model and outlines the risk factors for suicidal attempts under conditions of risk uncertainty. This algorithm assesses risk factors entirely using an interval-valued q-rung orthopair fuzzy (ivq-ROF) set information based Sugeno–Weber aggregation operators and EDAS method. Second, it applies Positive Distance from the Average (PDA) and Negative Distance from the Average (NDA) to balance an assessment, normalize various criteria, and rank them into higher order. We proposed ivq-ROF Sugeno–Weber weighted averaging (ivq-ROFSWWA), ivq-ROFS weighted geometric (ivq-ROFSWG) operators and EDAS method for improving the process of aggregation of fuzzy information. In the final type of stage, add up the PDA and NDA scores to determine the critical risk factors. This approach also increases the accuracy of predicting suicide risk, which is a vital asset for mental health researchers and practitioners to build effective intervention and prevention initiatives. Also, the nature of the algorithm renders decisions on compound data interfaces beneficial to numerous public health situations. Its application may include understanding factors that should inform policies that touch on mental health services and enhance the utilization of scarce resources in meeting the growing demand for such services. In conclusion, this study aspires to avoid future suicides due to a solid analytical framework for the research problem.

Introduction

Evaluating the risk analysis concerning suicidal attempts, along with the identification of risks under conditions of uncertainty, is significant for planning effective prevention measures. That is the goal of assessment of risk factors: knowing the psychological processes, social relationships, financial state, or environmental conditions that have been discovered to relate to violent behavior or factors that may be known to relate to causes of violence. These factors, therefore, require risk analysis, particularly under conditions of uncertainty, including crisis and mental health difficulties. Understanding these risks allows the development of specific interventions by healthcare professionals as well as governmental and non-government organizations, a decrease in preventable mortality and enhancement of mental health stability in unstable environments. Suicide risk assessment model based on fuzzy mathematics discussed by Xu et al.¹. Fuzzy logic detection of medically serious suicide attempt records in major psychiatric disorders utilized by Modai et al.². The development of a fuzzy logic model-based suicide risk assessment tools used by Ayhan et al.³. Explainable AI for suicide risk assessment using eye activities and head gestures discovered by Liu et al.⁴.

The crisp set theory concerns the set frontiers, which are specified. Crisp’s theory is clear that an element is either entirely in a set or not at all. There is no other option. Every member of a universal set belongs to a subset or is not part of it, for the elements of a subgroup are exhaustive. Crisp set has a clear definition; hence, the issue of ambiguity on the part of an element to be in or out of the set is eliminated.

Significance of fuzzy sets

A fuzzy set (FS) defines the generalization of the crisp set concept. This element can belong to a specific set to a certain degree, as proposed by Lotfi A. Zadeh⁵ in 1965. FS theory can be applied well when there is confusion, fuzziness, lack of clarity, or indefiniteness, such as uncertainty. In Zadeh’s concept, the fuzzy set addresses the aspect referred to as the degree of membership, which ranges between 0 and 1. FS theory, there is the function that maps the nonempty set to the closed interval of the real numbers $[0, 1]$, where the number in the interval represents the degree of membership of an element to a set. It is helpful for decision-making, detecting patterns, diagnosing, etc., that is why it is abbreviated as FS.

Another generalization of FS is that put forward. A Zadeh is called an interval-valued fuzzy set (ivFS). The membership degree (MD) inside ivFS is described by an interval, which is a subinterval of $[0, 1]$. It is the same as FS, whereby IvFS is helpful in disciplines such as decision-making and pattern recognition.

Atanassov⁶, an extension of FS, initiated the concept of IFS. In IFS, there are two functions: the MD and the NMD; they must be in the closed interval 0,1. Several authors have employed IFS to build applications for decision-making, pattern recognition, etc. Interval-valued intuitionistic fuzzy sets have been introduced by Atanassov and Gargov⁷. In movies, the degrees of membership MD and NMD are defined as intervals of form a, $b \subseteq [0, 1]$ and the condition holds that $\sum max {b}_{i}\in \left[0, 1\right]$.

Now interval-valued q-rung orthopair fuzzy set (ivq-ROFS)⁸ is a mathematical framework which is extended from the q-rung orthopair fuzzy set to deal with uncertainty and vagueness in the decision-making processes. The idea of interval values extended the notions of q-rung orthopair fuzzy sets. Therefore, it becomes more flexible and adaptable for applications with ill-defined and precise numerical values. By adopting interval-based MD and NMD, the resulting approach offers an effective means for the representation and processing of complex data, wherein the concept of such degrees better accommodates the inherent uncertainty in real-world scenarios. ivq-ROFS has applications in the fields of multi-criteria decision-making, resource allocation, and intelligent systems for dealing with challenges in uncertain environments. Interval-valued q-rung orthopair fuzzy sets (ivq-ROFS) are efficiently applied to suicide risk assessment by considering the uncertainties and complexities associated with assessing multiple risk factors. ivq-ROFS models can represent imprecision and incomplete knowledge by using interval values for representing MD and NMD. It is flexible enough to include and integrate diverse criteria of psychological, social, and biological types and allow for overlapping or conflicting factors. Such an approach enables systematic and reliable decision-making. It provides a robust framework for labeling, which is thought to be an intervention for handling the multifaceted problems of suicide risk assessment.

The thought of aggregation operators (AOs) is a fundamental concept in fuzzy set theory for assessing uncertain and fuzzy information. Many mathematicians worked hard to diagnose many AOs, as discussed in references such as Aczel–Alsina Power Aggregation Operators proposed by Khan et al.⁹, Archimedean aggregation operator by Khan et al.¹⁰, Aczel–Alsina power aggregation operators by Khan et al.¹¹, Frank Choquet Bonferroni Mean Operators of Bipolar by Wang et al.¹².

Intuitionistic fuzzy sets (IFS) by Atanassov⁶ have been developed from the basic fuzzy sets where the sum of the membership and non-membership values is between 0 and 1. In contrast, Pythagorean fuzzy sets (PyFS)¹³ are developed again from IFS but with the sum of the squares of the membership and non-membership values between 0 and 1. In research work by Zhang et al.¹², interval-valued Pythagorean fuzzy sets referred to as ivPyFS have been presented. ivPyFS is derived from PyFS, a splendid tool to address the uncertainty or ambiguity inherent to the MCDM problems. Foundations of this set have been investigated in the previous literature. q-rung orthopair fuzzy set (q-ROFS) is one of the other advanced generalizations of fuzzy set theory that can represent uncertainty and imprecision much more flexibly. In q-ROFS, the sum of MD raised to the power q and non-membership degree raised to the power q cannot exceed 1, thereby offering the flexibility of expressing the uncertain situation by ranking in more applications and fields. On this foundation, the interval-valued q-rung orthopair fuzzy set (ivq-ROFS) further develops q-ROFS through interval representation of both MD and NMD. This interval representation covers the broader range of uncertainty, automatically making the ivq-ROFS tool more suitable for solving complex decision-making issues and tasks with higher ambiguity and fuzziness.

Das et al.¹⁴ use the idea of a hesitant fuzzy soft set and hesitant bipolar-valued fuzzy soft set used by Das et al.¹⁵, weighted hesitant bipolar-valued fuzzy soft set in decision-making by Das et al.¹⁶, An innovative fuzzy multi-criteria decision-making by Das et al.¹⁷, fuzzy soft group decision-making using weighted average ratings Das et al.¹⁸ and in Das et al.¹⁹ decision making. Gitinavard et al.²⁰, employed the model to evaluate the risk factor in their studies, An extended multi-attribute group decision approach by Gitinavard et al.²¹, intuitionistic fuzzy group decision analysis for sustainability risk assessment by Gitinavard et al.²², An extended multi-attribute group decision approach by Gitinavard et al.²³ also use the dynamic intuitionistic fuzzy group decision making for the assessment of risk by Gitinavard et al.²⁴. Yin et al.²⁵ used Entropy Weight for Financial Risk Measurement and Analysis to Enhance Energy.

Role of TNM and TCNM

Data aggregation can be carried out more flexibly and realistically relying on the concepts of t-norm and t-conorm. Many mathematicians have proposed many TNM and TCNM operations for diverse fuzzy structures in this regard. For example, Menger first proposed probabilistic metric spaces²⁶. Another topic he discussed concerned the importance of TNM and TCN in FS theory. Furthermore, the way of Einstein TNM and TCNM was discovered by Wang and Liu²⁷; Archimedean TNM and TCNM by Xia et al.²⁸. Liu et al.²⁹ discussed the idea of Hamacher’s fuzzy TCNM and TNM concepts. Deschrijver et al.³⁰ discussed Lukasiewicz TNM and TCNM and proposed the notions of AA sum and AA product, the TNM and TCNM operations, respectively. Frank³¹, and so forth, discovered the Frank TNM and TCNM.

To handle ambiguous data successfully in the analysis of suicidal risk, the Sugeno–Weber aggregation operators model the non-linear relationships. They can be effectively applied to the modeling of uncertain data. They are based on triangular norms TNM and TCNM, which provide a flexible structure to aggregate criteria in a fuzzy environment. The Sugeno–Weber operators are more flexible, more theoretically consistent, and more efficient than the Dombi, Aczel–Alsina, Frank, Einstein, Archimedean, and other TNMs and TCNMs operational laws. Strategically, it allows for interactions between psychological, social, and environmental risk factors and captures them correctly. Using these operators, our algorithm yields actionable insights to clinicians and policymakers and hence is preferable to real-world risk analysis under uncertainty.

Sugeno³² has introduced a family of nilpotent TNMs, including the asymptotic members, drastic sum, and probabilistic sum. On the other hand, Weber³³ defined a family of nilpotent TNM one of which is a variant of product and drastic product that are asymptotic members. Sugeno–Weber TNM and TCNM of Sugeno and Weber are prestigious for their flexibility and accuracy in aggregating under uncertainty. In this regards many scholars proposed multiple MCDM approaches using the Sugeno–Weber operations for examples Yager³⁴ proposed them, and Klement et al.³⁵ provided a comprehensive theoretical foundation for TNM and TCNM. The use of Sugeno–Weber operations combined with Heronian mean operators to Picture FS was carried out by Zhang et al.³⁶. Recently, Hussain and Ullah³⁷ discussed the application of Sugeno–Weber operators in modern decision-making problems to present their flexibility and robustness in depicting the reality of different fuzzy environments and real-world challenges.

Role of the EDAS method for fuzzy information

It is a robust multi-criteria decision making (MCDM) technique that evaluates the alternatives based on distance from the average solution; this is the EDAS (evaluation based on distance from average solution). Being the risk analysis tool, its significance lies in its capability to deal with complex, uncertain, and scenic cases with multiple criteria. With its focus on relative distances instead of absolute ones, EDAS is excellent at dealing with incomplete or noisy data and performing balanced and unbiased evaluations. This offers precise, interpretable results to the stakeholders so that decisions can be made based on that. EDAS offers highly scalable and flexible integration with various advanced techniques, including probabilistic modeling, making it a system choice for systematic decision-making in uncertain environments. In deciding the multicriteria decision-making, an essential component of any decision-making process, the EDAS method Zhang et al.³⁸ plays a vital role because the evaluations systematically balance all the options under the conflicting criterion. The main idea of the EDAS approach is to rank an alternative according to its similarity to an average solution obtained for a particular criterion. This distance is measured in two ways: positive distance from the average (PDA) to express how much an alternative is better than the average and negative distance from the average (NDA) to express how much the average is better than the concerned alternative.

Although positive and negative distances are incorporated into the essential appraisal, EDAS guarantees all other alternatives are examined holistically, and their drawbacks weighed against their merits. Further, to introduce uniformity in the criteria in different units and scales, EDAS incorporates a normalization process. In the stakeholder context, it becomes easy to make decisions when the criteria adopted are organized in various levels of hierarchical importance. The last step in ranking alternatives is weighing each criterion’s total PDA and NDA scores and arriving at the most preferred alternative.

The primary goal of EDAS is to solve problems through decision-making rather than just managing them. It is perfect in trade-off considerations within a given choice. It has a well-defined and standard method of comparing choices without the added dimension of strategy-to-alternative mapping. As a result, EDAS is shown to have the ability to have a relatively simple, diverse, yet effective solution for MCDM by weighing the advantages and disadvantages.

Research gap

While substantial progress has been made in the investigation of suicide in terms of its multicausality, the lack of effective stochastic models of suicidal behavior warrants renewed efforts. Most conventional risk assessment frameworks cannot adequately manage the fuzziness inherent in actual data while simultaneously providing robust predictive modeling results. However, the application of MCDM approaches has been relatively scarce within this line of research.

The risk analysis for suicidal attempts is a complex decision-making process that inevitably requires balancing various psychological, social, and environmental factors. Usually, methods for assessing the risk of suicidality are subjective and susceptible to biases and inconsistencies. In addition, available frameworks are complex to utilize to foretell human behavior and risk variables. In order to overcome these limitations, this paper proposes a novel, objective approach that integrates diffusion-based behavior modeling and an advanced MCDM framework. By alleviating subjectivity in suicide risk assessment under uncertainty, the proposed method is helpful for clinical applications and addressing robust policy questions by providing actionable insights.

In particular, the literature lacks studies using interval-valued q-rung orthopair fuzzy sets (ivq-ROFS) to improve the richness and accuracy of risk evaluations. Moreover, although the EDAS method has been widely used in different decision-making fields, its future in analyzing suicidal risk has not been explored much. Some significant contributions are listed as follows:

• Propose a new algorithm that integrates ivq-ROFS and EDAS.

• Develop the Sugeno–Weber AOs for a holistic, fair, and precise evaluation of suicidal risk factors.

• To investigate the applicability of the proposed theory, we investigate some fundamental axioms of AOs, such as boundedness, monotonicity, and idempotency

• The detailed MCDM algorithm is provided based on the proposed AOs and EDAS approach.

• The case study on assessment of risk in a suicidal attempt

• Present a real-life numerical example of investigating risk analysis and factors affecting suicidal attempts based on the proposed theory.

• Make a deep comparison with some existing MCDM models.

• Also, a sensitive analysis to check the variation of the parameter.

• Filling these gaps, the research will enhance the range of preventive measures and interventions with the ultimate goal of decreasing suicidal attempt rates.

Risk assessment and ivq-ROFS

We quantify risk factors using ivq-ROS to encapsulate the lack of data in Granovetter’s model and the uncertainty and imprecision they embody. Such a process involved the Specialists allotted weigion of ivq-ROFSs to categorise the risk levels into low, medium, and high systematically. Subsequently, ivq-ROF information inference systems were leveraged based on expert knowledge and based on the identified risk factors to elucidate their interrelationships. The meticulous selection of parameters included ivq-ROFS and AOs for handling vagueness and supporting versatility in decision-making. These parameters were chosen because they represented the values in the model with significance to a particular risk domain with sufficient arithmetic efficiency to prevent computational waste.

This is the proposed study’s breakthrough, which combines the EDAS method with Sugeno–Weber t-norm and t-conorm to make the risk assessment more precise. It uses a hybrid approach that results in a more robust evaluation of restaurants by combining distance-based decision-making with advanced fuzzy aggregation techniques. This model will significantly help industries like finance, healthcare, and engineering in uncertainty handling and decision accuracy. Similarly, this approach would improve investment strategies and reduce financial losses. Optimizing risk assessment in manufacturing’s production process could mean savings in operational costs. The study offers economic benefits and better decision-making in risk-sensitive sectors; these advancements have industrial relevance.

Organization of the proposed study

The organization of the proposed work is given as follows: “Preliminaries” section discusses some preliminaries, and “Operations of Sugeno–Weber triangular norm based on ivq-ROFS” section presents the ivq-ROFS based t-norm and t-conorm operational rules. The ivq-ROFS information-based AOs established in “Interval-value Q-rofvs based Sugeno–Weber aggregation operators” and “EDAS method” sections discussed the EDAS method for ivq-ROFS based information and the MCDM algorithm for proposed AOs. The case study is offered in “Case study”” section and the numerical example is solved in “Numerical example” section. The comparison with other present AOs is provided in “Comparative study” section, and the conclusions are discussed in “Conclusion” section. Figure 1 presents the graphical overview of the proposed study.

Fig. 1

Flow chart for a case study.

Preliminaries

To substantiate the presumptions of this paper, there is some basic concept of Sugeno–weber triangular norms, $IvqROFS,$ and some fundamental axioms for this paper have been found. Table 1 shows the details of the mathematical symbol.

Table 1 Explanation of the mathematical symbol.

Definition 1

³⁹ The Sugeno–Weber t-norm and t-conorm are defined as follows:

$$\acute{\Upsilon} = \left\{ {\begin{array}{*{20}l} {\Upsilon_{R} \left( {{\ddot{\mathfrak{K}}}, {\ddot{\mathfrak{A}}}} \right),} \hfill & {if\;\upsilon = - 1} \hfill \\ {\max \left( {0,\frac{{{\mathfrak{K}} + {\mathfrak{A}} - 1 + \upsilon {\ddot{\mathfrak{K}}\ddot{\mathfrak{A}}}}}{1 + \upsilon }} \right),} \hfill & {if\; - 1 < \upsilon < + \infty } \hfill \\ {\Upsilon_{S} \left( {{\ddot{\mathfrak{K}}}, {\ddot{\mathfrak{A}}}} \right),} \hfill & {\upsilon = - \infty } \hfill \\ \end{array} } \right.$$

and

$$\acute{Z} = \left\{ {\begin{array}{*{20}l} {{\rm Z}_{R} \left( {{\ddot{\mathfrak{K}}}, {\ddot{\mathfrak{A}}}} \right), } \hfill & {if\;\upsilon = - 1} \hfill \\ {\min \left( {1,{\mathfrak{K}} + {\mathfrak{A}} - \frac{\upsilon }{1 + \upsilon }{\ddot{\mathfrak{K}}\ddot{\mathfrak{A}}}} \right),} \hfill & {if - 1 < \upsilon < + \infty } \hfill \\ {{\rm Z}_{S} \left( {{\ddot{\mathfrak{K}}}, {\ddot{\mathfrak{A}}}} \right),} \hfill & {\upsilon = + \infty } \hfill \\ \end{array} } \right.$$

where $\Upsilon_{R} \left( {{\ddot{\mathfrak{K}}}, {\ddot{\mathfrak{A}}}} \right)$ and ${\rm Z}_{R} \left( {{\ddot{\mathfrak{K}}}, {\ddot{\mathfrak{A}}}} \right)$ are expressions of drastic t-norm and t-conorm, respectively. In addition, $\Upsilon_{S} \left( {{\ddot{\mathfrak{K}}}, {\ddot{\mathfrak{A}}}} \right)$ and ${\rm Z}_{S} \left( {{\ddot{\mathfrak{K}}}, {\ddot{\mathfrak{A}}}} \right)$ is the probabilistic addition of t-norm and t-conorm.

Definition 2

⁴⁰ An q-ROFS ${\breve{G} }$ is stated:

$$\breve{G} =\left\{\varpi ,\left[\left(\mu \left(\varpi \right), \varepsilon \left(\varpi \right)\right)\right]|\varpi \in \breve{G} \right\},$$

where $\mu \left(\varpi \right)$ indicates the MD, $\varepsilon \varpi$ indicates the NMD. with some realistic restrictions:

$$0 \le {\left(\mu \left(\varpi \right)\right)}^{q}+{\left(\varepsilon \left(\varpi \right)\right)}^{q}\le 1, \varpi \in \breve{G} , q\ge 2$$

$r\left(\varpi \right)=\sqrt[q]{1- sum\left({\left(\mu \left(\varpi \right)\right)}^{q},{\left(\varepsilon \left(\varpi \right)\right)}^{q}\right)}$, denotes the hesitancy degree of q-ROFS.

Definition 3

⁸ Consider $\breve{G}$ to be the set of the universe of discourse, the ivq-ROFS stated as:

$$\breve{G} =\left\{\varpi , \left(\begin{array}{c}\left[{\mu }^{l}\left(\varpi \right), {\mu }^{u}\left(\varpi \right)\right],\\ \left[ {\varepsilon }^{l}\left(\varpi \right), {\varepsilon }^{u}\left(\varpi \right)\right]\end{array}\right)|\varpi \in \breve{G} \right\},$$

where ${\mu }^{l}\left(\varpi \right)$ indicates the lower MD, ${\mu }^{u}\left(\varpi \right)$ indicates the upper MD, ${\varepsilon }^{l}\left(\varpi \right)$ indicates the lower NMD and ${\varepsilon }^{u}\left(\varpi \right)$ indicates the upper NMD.

$r\left(\varpi \right)=\left[\sqrt[q]{1- sum\left(\begin{array}{c}\left[{\left({\mu }^{l}\left(\varpi \right)\right)}^{q},{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q}\right], \\ \left[{\left({\mu }^{u}\left(\varpi \right)\right)}^{q},{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\right]\end{array}\right)}\right]$, represents the hesitancy degree.

Definition 4

⁴¹ Let ${\alpha }_{1}$ and ${\alpha }_{2}$ be the two ivq-ROFS, then.

• $1.\quad \alpha ^{c} = \left\{ {\begin{array}{*{20}c} { < \varpi ,~\left[ {\left( {\mu ^{l} \left( \varpi \right)} \right)^{q} ,~\left( {\mu ^{u} \left( \varpi \right)} \right)^{q} } \right],} \\ {~\left[ {\left( {\varepsilon ^{l} \left( \varpi \right)} \right)^{q} ,~\left( {\varepsilon ^{u} \left( \varpi \right)} \right)^{q} } \right] > |\varpi \in } \\ \end{array} } \right\}$

• $2. \quad {\alpha }_{1}\oplus {\alpha }_{2}=\left\{\begin{array}{c}<\varpi , \left[\begin{array}{c}\sqrt[q]{\begin{array}{c}{\left({\mu }^{l}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q}\\ -{\left({\mu }^{l}\left(\varpi \right)\right)}^{q}{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q}\end{array}}, \\ \sqrt[q]{\begin{array}{c}{\left({\mu }^{u}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\\ -{\left({\mu }^{u}\left(\varpi \right)\right)}^{q}{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\end{array}}\end{array}\right],\\ \left[\begin{array}{c}{\left({\mu }^{l}\left(\varpi \right)\right)}^{q}{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q},\\ {\left({\mu }^{u}\left(\varpi \right)\right)}^{q}{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\end{array}\right]\\ >\varpi \in \breve{G} , q\ge 2\end{array}\right\}$

• $3.\quad {\alpha }_{1}\otimes {\alpha }_{2}=\left\{\begin{array}{c}\begin{array}{c}<\varpi ,\left[{\left({\mu }^{l}\left(\varpi \right)\right)}^{q}{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q}, {\left({\mu }^{u}\left(\varpi \right)\right)}^{q}{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\right]\\ \left[\begin{array}{c}\sqrt[q]{\begin{array}{c}{\left({\mu }^{l}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q}\\ -{\left({\mu }^{l}\left(\varpi \right)\right)}^{q}{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q}\end{array}}, \\ \sqrt[q]{\begin{array}{c}{\left({\mu }^{u}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\\ -{\left({\mu }^{u}\left(\varpi \right)\right)}^{q}{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\end{array}}\end{array}\right]>\varpi \in \breve{G} \end{array}\\ q\ge 2\end{array}\right\}$

Definition 5

Consider an ivq-ROFS $\varphi = \left( {\left[ {\mu^{l} , \mu^{u} } \right], \left[ {\varepsilon^{l} , \varepsilon^{u} } \right]} \right)$ the score function and accuracy function are, respectively, represented as:

$$\mathcal{S}\left(.\varphi \right)=\left(\begin{array}{c}\left[{\left({\mu }^{l}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q}\right]\\ -\left[{\left({\mu }^{u}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\right]\end{array}\right), \mathcal{S}\left(\varphi \right)\in \left[-1, 1\right]$$

$$\mathfrak{A}\left(\varphi \right)=\left(\begin{array}{c}\left[{\left({\mu }^{l}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q}\right]\\ +\left[{\left({\mu }^{u}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\right]\end{array}\right), \mathfrak{A}\left(\varphi \right)\in \left[{0,1}\right], q\ge 2$$

If two ivq-ROFVs ${\varphi }_{1}=\left(\left[{\mu }_{1}^{l}, {\mu }_{1}^{u}\right], \left[{\varepsilon }_{1}^{l}, {\varepsilon }_{1}^{u}\right]\right)$ and ${\varphi }_{2}=\left(\left[{\mu }_{2}^{l}, {\mu }_{2}^{u}\right], \left[{\varepsilon }_{2}^{l}, {\varepsilon }_{2}^{u}\right]\right)$, then we have $\mathcal{S}\left({\varphi }_{1}\right)<\mathcal{S}\left({\varphi }_{2}\right)$ if ${\varphi }_{1}<{\varphi }_{2}$ and $\mathcal{S}\left({\varphi }_{1}\right)>\mathcal{S}\left({\varphi }_{2}\right)$ if ${\varphi }_{1}>{\varphi }_{2}$. When $\mathcal{S}\left({\varphi }_{1}\right)=\mathcal{S}\left({\varphi }_{2}\right)$ then $\mathfrak{A}\left({\varphi }_{1}\right)=\mathfrak{A}\left({\varphi }_{2}\right)$ if ${\varphi }_{1}\approx {\varphi }_{2}$.

Operations of Sugeno–Weber triangular norm based on ivq-ROFS

Based on ivq-ROFS-based information, some necessary operations of Sugeno–weber triangular norms are defined. These aggregation expressions are used very uniquely in the proposed work.

Definition 6

For three ivq-ROFVs,$\alpha = \left( {\left[ {\mu^{l} , \mu^{u} } \right], \left[ {\varepsilon^{l} , \varepsilon^{u} } \right]} \right)$, $\alpha_{1} = \left( {\left[ {\mu_{1}^{l} , \mu_{1}^{u} } \right], \left[ {\varepsilon_{1}^{l} , \varepsilon_{1}^{u} } \right]} \right)$, and $\alpha_{2} = \left( {\left[ {\mu_{2}^{l} , \mu_{2}^{u} } \right], \left[ {\varepsilon_{2}^{l} , \varepsilon_{2}^{u} } \right]} \right)$.Basic operations of the Sugeno–Weber Triangular norm are given as:

• $(a)\quad \left({\alpha }_{1}\oplus {\alpha }_{2}\right)=\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[q]{{\mu }_{1}^{l}+{\mu }_{2}^{l}-\frac{\upsilon }{1+\upsilon }{\mu }_{1}^{l}{\mu }_{2}^{l}},\\ \sqrt[q]{{\mu }_{1}^{u}+{\mu }_{2}^{u}-\frac{\upsilon }{1+\upsilon }{\mu }_{1}^{u}{\mu }_{2}^{u}}\end{array}\right),\\ \left(\begin{array}{c}\sqrt[q]{\frac{{\varepsilon }_{1}^{l}+{\varepsilon }_{2}^{l}-1+\upsilon {\varepsilon }_{1}^{l}{\varepsilon }_{2}^{l}}{1+\upsilon }}\\ \sqrt[q]{\frac{{\varepsilon }_{1}^{u}+{\varepsilon }_{2}^{u}-1+\upsilon {\varepsilon }_{1}^{u}{\varepsilon }_{2}^{u}}{1+\upsilon }}\end{array}\right)\end{array}\right]$

• $(b)\quad \left({\alpha }_{1}\otimes {\alpha }_{2}\right)=\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[q]{\frac{{\varepsilon }_{1}^{l}+{\varepsilon }_{2}^{l}-1+\upsilon {\varepsilon }_{1}^{l}{\varepsilon }_{2}^{l}}{1+\upsilon }}\\ \sqrt[q]{\frac{{\varepsilon }_{1}^{u}+{\varepsilon }_{2}^{u}-1+\upsilon {\varepsilon }_{1}^{u}{\varepsilon }_{2}^{u}}{1+\upsilon }}\end{array}\right),\\ \left(\begin{array}{c}\sqrt[q]{{\mu }_{1}^{l}+{\mu }_{2}^{l}-\frac{\upsilon }{1+\upsilon }{\mu }_{1}^{l}{\mu }_{2}^{l}},\\ \sqrt[q]{{\mu }_{1}^{u}+{\mu }_{2}^{u}-\frac{\upsilon }{1+\upsilon }{\mu }_{1}^{u}{\mu }_{2}^{u}}\end{array}\right)\end{array}\right]$

• $(c)\quad {\alpha }^{\varpi }=\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[q]{\frac{\upsilon }{1+\upsilon }\left(1-{\left(1-{\varepsilon }_{l}^{q}\left(\frac{\upsilon }{1+\upsilon }\right)\right)}^{\varpi }\right)},\\ \sqrt[q]{\frac{\upsilon }{1+\upsilon }\left(1-{\left(1-{\varepsilon }_{u}^{q}\left(\frac{\upsilon }{1+\upsilon }\right)\right)}^{\varpi }\right)}\end{array}\right),\\ \left(\begin{array}{c}\sqrt[q]{\left(\left(1+\upsilon \right){\left(\frac{{\mu }_{l}^{q}+1}{1+\upsilon }\right)}^{\varpi }-1\right)\frac{1}{\varpi } },\\ \sqrt[q]{\left(\left(1+\upsilon \right){\left(\frac{{\mu }_{u}^{q}+1}{1+\upsilon }\right)}^{\varpi }-1\right)\frac{1}{\varpi }}\end{array}\right)\end{array}\right]$

• $(d)\quad \varpi \alpha =\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[q]{\left(\left(1+\upsilon \right){\left(\frac{{\varepsilon }_{l}^{q}+1}{1+\upsilon }\right)}^{\varpi }-1\right)\frac{1}{\varpi } },\\ \sqrt[q]{\left(\left(1+\upsilon \right){\left(\frac{{\varepsilon }_{u}^{q}+1}{1+\upsilon }\right)}^{\varpi }-1\right)\frac{1}{\varpi } }\end{array}\right),\\ \left(\begin{array}{c}\sqrt[q]{\frac{\upsilon }{1+\upsilon }\left(1-{\left(1-{\mu }_{l}^{q}\left(\frac{\upsilon }{1+\upsilon }\right)\right)}^{\varpi }\right)}, \\ \sqrt[q]{\frac{\upsilon }{1+\upsilon }\left(1-{\left(1-{\mu }_{u}^{q}\left(\frac{\upsilon }{1+\upsilon }\right)\right)}^{\varpi }\right)}\end{array}\right)\end{array}\right]$

Example 1

Consider $\alpha =\left\{\left({0.77,0.49}\right), \left(0.58, 0.72\right)\right\}$, ${{\alpha }}_{1}=\left\{\left({0.69,0.72}\right), \left(0.51, 0.63\right)\right\}$ and ${{\alpha }}_{2}=\left\{\left({0.83,0.56}\right), \left(0.60, 0.73\right)\right\}$ be the three ivq-ROFVs and $q=3$ $\upsilon =2$, then

$$\left({\alpha }_{1}\oplus {\alpha }_{2}\right)=\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[3]{0.69+0.83-\frac{2}{1+2}0.69\times 0.83},\\ \sqrt[3]{0.51+0.60-\frac{2}{1+2}0.51\times 0.60}\end{array}\right),\\ \left(\begin{array}{c}\sqrt[3]{\frac{0.72+0.56-1+2\left(0.72\times 0.56\right)}{1+2}}\\ \sqrt[3]{\frac{0.63+0.73-1+2\left(0.63\times 0.73\right)}{1+2}}\end{array}\right)\end{array}\right]=\left\{\left(0.9821, 0.7127\right), \left(0.9298, 0.7527\right)\right\}$$

$$\left({\alpha }_{1}\otimes {\alpha }_{2}\right)=\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[3]{\frac{0.83+0.69-1+2\left(0.83\times 0.69\right)}{1+2}}\\ \sqrt[3]{\frac{0.72+0.56-1+2\left(0.72\times 0.56\right)}{1+2}}\end{array}\right),\\ \left(\begin{array}{c}\sqrt[3]{0.51+0.6-\frac{2}{1+2}\left(0.51\times 0.6\right)},\\ \sqrt[3]{0.63+0.73-\frac{2}{1+2}\left(0.73\times 0.63\right)}\end{array}\right)\end{array}\right]=\left\{\left(0.8218, -0.4848\right),\left(0.7127, -0.7827\right)\right\}$$

$${\alpha }^{3}=\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[3]{\frac{2}{1+2}\left(1-{\left(1-{0.77}^{3}\left(\frac{2}{1+2}\right)\right)}^{3}\right)},\\ \sqrt[3]{\frac{2}{1+2}\left(1-{\left(1-{0.49}^{3}\left(\frac{2}{1+2}\right)\right)}^{3}\right)}\end{array}\right),\\ \left(\begin{array}{c}\sqrt[3]{\left(\left(1+2\right){\left(\frac{{0.72}^{3}+1}{1+2}\right)}^{3}-1\right)\frac{1}{3} },\\ \sqrt[3]{\left(\left(1+2\right){\left(\frac{{0.58}^{3}+1}{1+2}\right)}^{3}-1\right)\frac{1}{3}}\end{array}\right)\end{array}\right]=\left\{\left(0.7618, 0.5252\right), \left(-0.8930, 0.9323\right)\right\}$$

$$3\alpha =\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[3]{\left(\left(1+2\right){\left(\frac{{0.77}^{3}+1}{1+2}\right)}^{3}-1\right)\frac{1}{3} },\\ \sqrt[q]{\left(\left(1+2\right){\left(\frac{{0.49}^{3}+1}{1+2}\right)}^{3}-1\right)\frac{1}{3} }\end{array}\right),\\ \left(\begin{array}{c}\sqrt[3]{\frac{2}{1+2}\left(1-{\left(1-{0.72}^{3}\left(\frac{2}{1+2}\right)\right)}^{3}\right)}, \\ \sqrt[3]{\frac{2}{1+2}\left(1-{\left(1-{0.58}^{3}\left(\frac{\upsilon }{1+2}\right)\right)}^{3}\right)}\end{array}\right)\end{array}\right]=\left\{\left(-0.6026, -0.6554\right), \left(0.4294, 0.3377\right)\right\}$$

Interval-value Q-rofvs based Sugeno–Weber aggregation operators

Sugeno–weber T-norms are based on operational laws, and this paper expresses the new mathematical approach of ivq-ROFV based information: ivq-ROFSWWA and ivq-ROFSWWG operators.

Definition 7

Let a class of ivq-ROFVs $\alpha_{\chi } = \left( {\left[ {\mu_{\chi }^{l} , \mu_{\chi }^{u} } \right], \left[ {\varepsilon_{\chi }^{l} , \varepsilon_{\chi }^{u} } \right]} \right), \chi = 1, 2,3, . . . , \kappa$. The iv-ROFSWWA operator is categorized as follows:

$${{ivq}} - {{ROFSWWA}} \left( {\alpha_{1} , \alpha_{2} , \alpha_{3} \ldots , \alpha_{\kappa } } \right) = \oplus_{\chi = 1}^{\kappa } {\mathcal{R}}_{\chi } \alpha_{\chi }$$

Theorem 1

For classes ${\alpha }_{\chi }=\left(\left[{\mu }_{\chi }^{l}, {\mu }_{\chi }^{u}\right], \left[{\varepsilon }_{\chi }^{l}, {\varepsilon }_{\chi }^{u}\right]\right), \chi =1, {2,3}, . . . , \kappa$, the accumulated value of the ivq-ROFSWWA operator is still an ivq-ROFV, then find the following.

$$ivq-ROFSWWA\left({\alpha }_{1}, {\alpha }_{2}, {\alpha }_{3}\dots , {\alpha }_{\kappa }\right)=\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[q]{\frac{1+\upsilon }{\upsilon }\left(1-\prod_{\chi =1}^{\kappa }{\left(1-{\mu }_{\chi }^{l}\left(\frac{\upsilon }{1+\upsilon }\right)\right)}^{\varpi }\right)}, \\ \sqrt[q]{\frac{1+\upsilon }{\upsilon }\left(1-\prod_{\chi =1}^{\kappa }{\left(1-{\mu }_{\chi }^{u}\left(\frac{\upsilon }{1+\upsilon }\right)\right)}^{\varpi }\right)}\end{array}\right),\\ \left(\begin{array}{c}\sqrt[q]{\frac{1}{\varpi }\left(\left(1+\upsilon \right)\prod_{\chi =1}^{\kappa }{\left(\left(\frac{{\varepsilon }_{\chi }^{l}+1}{1+\upsilon }\right)\right)}^{\varpi }-1\right)},\\ \sqrt[q]{\frac{1}{\varpi }\left(\left(1+\upsilon \right)\prod_{\chi =1}^{\kappa }{\left(\left(\frac{{\varepsilon }_{\chi }^{u}+1}{1+\upsilon }\right)\right)}^{\varpi }-1\right)}\end{array}\right)\end{array}\right]$$

Proof

See appendix.

Theorem 2

Assume that the classes ivq-ROFVs ${\alpha }_{\chi }=\left(\left[{\mu }_{\chi }^{l}, {\mu }_{\chi }^{u}\right], \left[{\varepsilon }_{\chi }^{l}, {\varepsilon }_{\chi }^{u}\right]\right), \chi =1, {2,3}, . . . , \kappa$, which implies that ${\alpha }_{\chi }=\alpha$. Then.

$$ivq-ROFSWWA\left({\alpha }_{1}, {\alpha }_{2},\dots , {\alpha }_{\kappa }\right)=\alpha$$

Proof

See appendix.

Theorem 3

For any two sets of ivq-ROFVs ${\alpha }_{\chi }=\left(\left[{\mu }_{\chi }^{l}, {\mu }_{\chi }^{u}\right], \left[{\varepsilon }_{\chi }^{l}, {\varepsilon }_{\chi }^{u}\right]\right),$ and ${\alpha }_{\chi }{\prime}=\left(\left[{{\mu }{\prime}}_{\chi }^{l}, {{\mu }{\prime}}_{\chi }^{u}\right], \left[{{\varepsilon }{\prime}}_{\chi }^{l}, {{\varepsilon }{\prime}}_{\chi }^{u}\right]\right), \chi =1, {2,3}, . . . , \kappa$ which implies that ${\alpha }_{\chi }={\alpha }_{\chi }{\prime}$. Then.

Proof

See in appendix.

Theorem 4

For a set of ivq-ROFVs ${\alpha }_{\chi }=\left(\begin{array}{c}\left[{\mu }_{\chi }^{l}, {\mu }_{\chi }^{u}\right], \\ \left[{\varepsilon }_{\chi }^{l}, {\varepsilon }_{\chi }^{u}\right]\end{array}\right), \chi =1, {2,3}, . . . , \kappa .$ If ${\alpha }^{-}=\left({min}\left\{{\mu }_{\chi }\right\},{max}\left\{{\varepsilon }_{\chi }\right\}\right)$ and ${\alpha }^{+}=\left({max}\left\{{\mu }_{\chi }\right\},{min}\left\{{\varepsilon }_{\chi }\right\}\right)$, then.

Proof

See in appendix.

Definition 8

Consider the class of ivq-ROFVs ${\alpha }_{\chi }=\left(\left[{\mu }_{\chi }^{l}, {\mu }_{\chi }^{u}\right], \left[{\varepsilon }_{\chi }^{l}, {\varepsilon }_{\chi }^{u}\right]\right), \chi =1, {2,3}, . . . , \kappa$, the ivq-ROFSWWG operator is expressed as:

$$ivq-ROFSWWG\left({\alpha }_{1}, {\alpha }_{2},\dots , {\alpha }_{\kappa }\right)={\otimes }_{\chi =1}^{\kappa }{\mathcal{R}}_{\chi }{\alpha }_{\chi }$$

Theorem 5

Consider the class of ivq-ROFVs $\alpha_{\chi } = \left( {\left[ {\mu_{\chi }^{l} , \mu_{\chi }^{u} } \right], \left[ {\varepsilon_{\chi }^{l} , \varepsilon_{\chi }^{u} } \right]} \right), \chi = 1, 2,3, . . . , \kappa$, the ivq-ROFSWWG operator is expressed as:

$${{ivq}} - {{ROFSWWG}}\left( {\alpha_{1} , \alpha_{2} , \ldots , \alpha_{\kappa } } \right) =$$

$$\left[\begin{array}{c}\left(\begin{array}{c}\sqrt[q]{\frac{1}{\varpi }\left(\left(1+\upsilon \right)\prod_{\chi =1}^{\kappa }{\left(\left(\frac{{\varepsilon }_{\chi }^{l}+1}{1+\upsilon }\right)\right)}^{\varpi }-1\right)},\\ \sqrt[q]{\frac{1}{\varpi }\left(\left(1+\upsilon \right)\prod_{\chi =1}^{\kappa }{\left(\left(\frac{{\varepsilon }_{\chi }^{u}+1}{1+\upsilon }\right)\right)}^{\varpi }-1\right)} \end{array}\right),\\ \left(\begin{array}{c}\sqrt[q]{\frac{1+\upsilon }{\upsilon }\left(1-\prod_{\chi =1}^{\kappa }{\left(1-{\mu }_{\chi }^{l}\left(\frac{\upsilon }{1+\upsilon }\right)\right)}^{\varpi }\right)},\\ \sqrt[q]{\frac{1+\upsilon }{\upsilon }\left(1-\prod_{\chi =1}^{\kappa }{\left(1-{\mu }_{\chi }^{u}\left(\frac{\upsilon }{1+\upsilon }\right)\right)}^{\varpi }\right)}\end{array}\right)\end{array}\right]$$

Proof

See in appendix.

Theorem 6

Consider the class of ivq-ROFVs ${{\alpha }}_{\upchi }=\left(\left[{\upmu }_{\upchi }^{{l}}, {\upmu }_{\upchi }^{{u}}\right], \left[{\upvarepsilon }_{\upchi }^{{l}}, {\upvarepsilon }_{\upchi }^{{u}}\right]\right),\upchi =1,{ 2,3}, . . . ,\upkappa$, which implies that ${{\alpha }}_{\upchi }={\alpha }$. Then.

$$ivq-ROFSWWG\left({\alpha }_{1}, {\alpha }_{2},\dots , {\alpha }_{\kappa }\right)=\alpha$$

Proof

See in appendix.

Theorem 7

Consider the set of ivq-ROFVs ${{\alpha }}_{\upchi }=\left(\left[{\upmu }_{\upchi }^{\text{l}}, {\upmu }_{\upchi }^{\text{u}}\right], \left[{\upvarepsilon }_{\upchi }^{\text{l}}, {\upvarepsilon }_{\upchi }^{\text{u}}\right]\right)$ and $\upalpha _{\chi }^{\prime } = \left( {\left[ {\upmu _{\chi }^{{\prime l}} ,~\upmu _{\chi }^{{\prime u}} } \right],~\left[ {\varepsilon _{\chi }^{{\prime l}} ,\varepsilon _{\chi }^{{\prime u}} } \right]} \right),~\chi = 1,~2,3, \ldots ,~\kappa$. If $\upalpha _{\chi } \le \upalpha _{\chi }^{\prime}$, then.

$$ivq-ROFSWWG\left({\alpha }_{1}, {\alpha }_{2},\dots , {\alpha }_{\kappa }\right)\le ivq-ROFSWWG\left({\alpha }_{1}{\prime}, {\alpha }_{2}{\prime},\dots , {\alpha }_{\kappa }{\prime}\right)$$

Proof

See in appendix.

The proposed ivq-ROFSWWG operators also satisfy the essential conditions of AOs, such as boundedness, idempotency, and monotonicity. The proof is simple and can be stated below as Theorems 2, 3, and 4.

EDAS method

In this discussion, it is said that EDAS is very useful for solving daily life problems, and the EDAS method is subdivided into the following steps.

Step 1 Initially, Experts elect the attribute for the selection of the top alternative.

Step 2 Decision experts take a fuzzy decision matrix that contains the alternatives and criteria.

$${\varvec{\Upsilon}}={\left[{\boldsymbol{\Upsilon}}_{{\varvec{i}}{\varvec{j}}}\right]}_{{\varvec{m}}\times {\varvec{n}}}=\left[\begin{array}{cccc}{\boldsymbol{\Upsilon}}_{11}& {\boldsymbol{\Upsilon}}_{12}& \cdots & {\boldsymbol{\Upsilon}}_{1{\varvec{n}}}\\ {\boldsymbol{\Upsilon}}_{21}& {\boldsymbol{\Upsilon}}_{22}& \cdots & {\boldsymbol{\Upsilon}}_{2{\varvec{n}}}\\ \vdots & \vdots & \vdots & \vdots \\ {\boldsymbol{\Upsilon}}_{{\varvec{m}}1}& {\boldsymbol{\Upsilon}}_{{\varvec{m}}2}& \cdots & {\boldsymbol{\Upsilon}}_{{\varvec{m}}{\varvec{n}}}\end{array}\right]$$

where $\mathbf{i}$ and $\mathbf{j}$ denote the alternative and attribute, respectively.

Step 3 The average solution for all alternatives is evaluated by the formula mentioned below.

$$\mathbf{\rm Z}\left({\varvec{j}}\right)=\frac{\sum_{{\varvec{i}}=1}^{{\varvec{n}}}\boldsymbol{\Upsilon}}{{\varvec{n}}}$$

Step 4 Evaluation of PDA and NDA.

For the evaluation of PDA, use the formula.

$${{\varvec{\Omega}}}_{{\varvec{i}}{\varvec{j}}}=\frac{{\varvec{max}}\left(0,\boldsymbol{ }\left({\boldsymbol{\Upsilon}}_{{\varvec{i}}{\varvec{j}}}-\boldsymbol{\rm Z}\left({\varvec{j}}\right)\right)\right)}{\boldsymbol{\rm Z}\left({\varvec{j}}\right)}$$

For the Evaluation of NDA

$${{\varvec{\lambda}}}_{{\varvec{i}}{\varvec{j}}}=\frac{{\varvec{max}}\left(0,\boldsymbol{ }\left(\boldsymbol{\rm Z}\left({\varvec{j}}\right)-{\boldsymbol{\Upsilon}}_{{\varvec{i}}{\varvec{j}}}\right)\right)}{\boldsymbol{\rm Z}\left({\varvec{j}}\right)}$$

Step 5 Evaluate weight for PDA and NDA, as listed.

$${\varvec{\acute{Z}}}_{{\varvec{i}}}=\sum_{{\varvec{i}}=1}^{{\varvec{\tau}}}{{\varvec{\Upsilon}}}_{{\varvec{i}}}{\boldsymbol{\Omega }}_{{\varvec{i}}{\varvec{j}}}$$

$${\varvec{\acute{Z}}}_{{\varvec{i}}}=\sum_{{\varvec{i}}=1}^{{\varvec{\tau}}}{{\varvec{\Upsilon}}}_{{\varvec{i}}}{{\varvec{\lambda}}}_{{\varvec{i}}{\varvec{j}}}$$

where ${\boldsymbol{\Upsilon}}_{{\varvec{i}}}$ is a weight of the criteria.

Step 6 Normalization of PDA and NDA. The normalization of values is calculated by the formula given below.

$${{\mathbb{N}}\boldsymbol{\Omega }}_{{\varvec{i}}{\varvec{j}}}=\frac{{\boldsymbol{\Omega }}_{{\varvec{i}}{\varvec{j}}}}{{\varvec{max}}\left({\boldsymbol{\Omega }}_{{\varvec{i}}{\varvec{j}}}\right)}$$

Step 7 Score function.

Score values are calculated by the formula given below.

$$\boldsymbol{\Upsilon}\left(\mathcal{o}\right)=\frac{1}{2}\left({{\mathbb{N}}\boldsymbol{\Omega }}_{{\varvec{i}}{\varvec{j}}}+{\mathbb{N}}{{\varvec{\lambda}}}_{{\varvec{i}}{\varvec{j}}}\right)$$

Step 8 Ranking of Alternatives.

Sorting the alternatives on the base of the highest values of the score function results in the best alternatives.

EDAS method, based on the given algorithm, applied the operators to real-life problems to find the best one. Specialists allotted weight to every attribute.

Proof

Step 1 Initially, to select the best alternative, choose attributes.

• ${\text{X}}_{1}=\text{Logistic Regression}$

• ${\text{X}}_{2}=\text{Random Forest}$

• ${\text{X}}_{3}=\text{Neural Networks}$

• ${\text{X}}_{4}=\text{Bayesian Networks}$

• ${\text{X}}_{5}=\text{Gradient Boosting Algorithms}$

Step 2. Decision matrix having ivq-ROFS based values. Shown in Table 2.

Table 2 Positive distance value.

Step 3. Average solution for all aggregated values.

Step 4. Evaluation of PDA and NDA as listed in Tables 2 and 3.

Table 3 Negative distance value.

Step 5. Next, the weight of PDA and NDA is calculated, as shown in Tables 4 and 5.

Table 4 Weight for positive distance from averaging.

Table 5 Weight for positive distance from averaging.

Step 6 Normalization of ${\Omega }_{ij}$ and ${\lambda }_{ij}$ as shown in Table 6.

Table 6 Normalize the value for positive and negative distance from averaging.

Step 7. The score function formula calculates the score values, as shown in Table 7.

Table 7 Show the score value of the aggregated outcome.

Step 8 Arrange all the values of the score function in increasing order. To find the ranking of alternatives.

Table 8 shows the data noticed out of all the possibilities using the EDAS method ${\text{\rm X}}_{1}$ be the best solution for investigating risk analysis and factors affecting suicidal attempts.

Table 8 Show the ranking of the score value function.

Algorithm based on proposed AOs

The following section aims to determine the best solution using the MCDM method. Also, let the group of attribute $\upupsilon =\left({\upupsilon }_{1}, {\upupsilon }_{2}, {\upupsilon }_{3}\dots ,{\upupsilon }_{n}\right)$ and the alternative set ${\rm X}=\left({\rm X}_{1}, {\rm X}_{2}, {\rm X}_{3},\dots , {\rm X}_{n}\right)$ where the weight vector WV ${\text{\rm E}}_{i}=\left({\rm E}_{1}, {\rm E}_{2},{\rm E}_{3}, . . . , {\rm E}_{n}\right), \sum_{i=1}^{n}{\rm E}_{i}=1$. Data should be taken from specialists in ivq-ROFVs ${\alpha }_{\chi }=\left({\mu }_{\chi }, {\varepsilon }_{\chi }\right)$, must satisfy the term $0 \le \left(\left[{\left({\mu }^{l}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{l}\left(\varpi \right)\right)}^{q}\right]+\left[{\left({\mu }^{u}\left(\varpi \right)\right)}^{q}+{\left({\varepsilon }^{u}\left(\varpi \right)\right)}^{q}\right]\right)\le 1$. The decision matrix completed by the ivq-ROFV is shown below. The evaluation method of ivq-ROF data can be described according to the following MCDM algorithm that was defined:

Step 1 The decision matrix filled by the specialist’s data has ivq-ROF.

Step 2 The whole data is usually categorized into positive and negative data types. Then, normalize all the data with the same type with the help of the following formula.

$$\alpha =\left\{\begin{array}{c}\mu \left(\varpi \right) if\;positive\;type\\ \varepsilon \left(\varpi \right) if\;negative\;type\end{array}\right.$$

Step 3 The data can be aggregated by applying the proposed operators ivq-ROFSWWA and ivq-ROFSWWG.

Step 4 Using the score function, the best option is determined.

Step 5 Ranking of alternatives on the base of highest values.

Step 6 Final result.

Figure 2 presents the graphical representation of the proposed work.

Fig. 2

Graphical representation of the proposed study.

Case study

Globally, suicide is considered to be a public health issue and is associated with multiple and varied determinants. Solving this problem is possible only with the use of tools that allow identifying and assessing suicidal behavior, including situations that are far from clear and when data is incomplete and rapidly changing. The paper considers five algorithmic options and assesses them, considering the four primary features to determine the finest approach for searching for the factors connected with suicides. The details of alternatives are given as follows:

• (1) Logistic regression: Logistic Regression is an essential basic statistical model for binary classification, which makes it very suitable to evaluate suicidal risk. This model works by establishing a link between different input values and the probability of a suicide attempt with a logistic function. This model is also highly interpretable as coefficients show how much each risk factor contributes, which allows for identifying the most essential components. Besides, Logistic Regression is computationally efficient and has good performance on a small scale. Therefore, Logistic Regression is well-equipped to serve as an initial analysis. However, the prerequisite in the above is that the input variables are assumed to be linearly combined with the natural log of the odds of the outcome and neglect more complex, nonlinear interactions between risk factors. In addition, it suffers from extreme dimensions and does not inherently require uncertainty in features in assessing risk for suicide, among other problems in the analysis of high-dimensional data.

• (2) Random forest: Random Forest is an ensemble-based learning method, which, during training, generates several decision trees and ensembles them to boost accuracies and robustness. In particular, it is very well suited to handle the nonlinear relationship and vast dimensions of data, thus making it an excellent instrument to assess the complex risk factors related to suicidal behavior. Another unique feature is they can calculate these feature importance scores, helping to pinpoint which essential risk factors include a history of past attempts at suicide or high use of substances. Random Forest is also robust to overfitting and handles missing data well when you have it in a real-world example of the dataset. Nevertheless, although superior to simpler models such as Logistic Regression in terms of performance, it lacks interpretive power as it is an ensemble. Moreover, Random Forest has no intrinsic probabilistic modeling of probabilistic outcomes, which is key in suicidal risk analysis when data is typically incomplete or ambiguous.

• (3) Neural networks: Deep learning models mimic the structure as well as the function of the human brain, and those models are called Neural Networks. These are deeply interconnected layers of many nodes, which are highly effective for tasks requiring processing large datasets with many features because they learn very complex, non-linear representations of the patterns in data. In terms of disrupting complex interactions between psychological, social, and environmental factors related to suicidal risk, Neural Networks can help better describe these than simpler models might. They are at ease, can learn from the data, and do not need explicit feature engineering. Nevertheless, Neural Networks are resource- and highly data-intensive, which may be a limitation in smaller or less complete datasets. The big drawback, however, is their lack of interpretability, which is often referred to as “a black box,” as it is difficult to understand what was added to this output. In clinical settings, this can be a significant barrier to understanding the reasoning behind risk predictions before making a decision.

• (4) Bayesian networks: Probabilistic graphical models of variables representing the variables and dependency relationships using directed acyclic graphs defined using the Bayesian Networks. Because they are particularly good at handling uncertainty and probabilistic reasoning, they are especially suited for analyzing suicidal risk, for example, when the data is incomplete or ambiguous. Explicit in Bayesian Networks is how risk factors, depression severity, and the social support they do and do not provide are entwined, and they provide a clear graphical representation of these dependencies. This increases the interpretability as well as gives clinicians insight into how various factors contribute to suicide risk. Bayesian Networks also allow prior knowledge or expert opinions to be included, giving them flexibility in the context. Nevertheless, knowledge or assumption of the network’s structure is required when constructing an accurate Bayesian network, which can be challenging in complex domains such as suicidal behavior. Additionally, they can become computationally expensive for large networks, thereby preventing some applications’ scalability.

• (5) Gradient Boosting Algorithms: Gradient Boosting Algorithms, being a robust machine learning technique, is a technique of building models sequentially using decision trees by combining many weak learners. Overall, it’s about enhancing accuracy, as the previous models were rejected due to errors. Gradient Boosting is a potent technique in suicidal risk analysis as it can capture highly complex and non-linear relationships between risk factors (for example, depression severity, social isolation, and availability of resources for people with mental health problems) and the probability of suicide attempt. This can efficiently work with both categorical and numerical data and yields the feature importance scores of the key risk factors. However, the tuning has to be made carefully enough to avoid overfitting, which can be computationally expensive. While it might be less interpretable than simpler models, SHAP can improve its explanatory power and, thus, make it worthwhile for algorithms that should study suicidal risk in uncertainty.

The details of attributes are given as follows:

• (1) Accuracy of risk assessment: The term accuracy of risk assessment means that the algorithm can be able to detect people who are at high risk of suicidal attempts. This attribute is vital within the context of your research because of the enormous consequences of even minor prediction errors. This guarantees high accuracy so that it can be reasonably sure not only to identify those at higher risk of suicide but also to do so with certainty around differences in depression severity, social isolation, and access to mental health resources. Real-world scenarios involve noisy, incomplete, and uncertain data, and the algorithm must handle this very well to reach this. By integrating probabilistic reasoning and systematic evaluation of risk factors, diffusion-based behavior modeling and advanced Multi-Criteria Decision Making (MCDM) can improve accuracy. To allow for actionable insights to clinicians and policymakers, providing them the ability to know about future risks and to intervene promptly and effectively, it is critical for our understanding of risk to exist in all practical accuracy.

• (2) Practical applicability: The practical applicability involves the ability of the algorithm to be used in practical implementation matters in the real-world context, for instance, in clinical practices, community mental health intervention, or even in emergency services. This characteristic emphasizes your research and the need for the algorithm to be user-friendly, scalable, and adaptable for different populations and settings. Moreover, the algorithm’s applicability is practical in that it requires computational efficiency, ease of integration, and the capacity to process real-time data. The algorithm can also be formulated such that it can meet end users’ requirements (i.e., mental health professionals) with high performance and reliability by integrating interpretable models (e.g., Logistic Regression, fed in feature importance from Gradient Boosting) and a robust framework to address uncertainty.

• (3) Adaptability to uncertainty: The algorithm is adaptable to uncertainty since there is no certitude when it comes to analyzing suicidal risk. Data are incomplete, subject to self-report and risk factors change. Your algorithm is told to effectively model and quantify this uncertainty in order to get reliable risk assessments. Probabilistic data can be handled with techniques such as Bayesian Networks and Monte Carlo simulations, which can run a number of different scenarios. Moreover, diffusion models help the algorithm simulate variability in behavioral patterns over time. This algorithm can help make more robust and realistic predictions about risk, and this information can be used when making decisions in an environment that is not certain.

• (4) Interpretability: Interpretability refers to the capability of the algorithm to provide clear and understandable insights into the prediction outcomes and related decision-making processes. In the domain of suicidal risk assessment, interpretability is critical as clinicians and policymakers need to understand.

  • i. Why did the algorithm label some individuals as being at high risk?

  • ii. What are the predominant contributors to such risk? Interpretability is inherent in Logistic Regression and Random Forest models; the coefficient in Logistic Regression models and their feature importance scores in Random Forest models. On the other hand, for more complex models, Neural Networks, or Gradient Boosting, to name a few, SHAP (Shapley Additive explanations) or similar techniques are needed to understand the predictions made. As such, a high level of interpretability guarantees that the algorithm’s outputs are trustworthy outputs that can be acted upon, improving communications and making decisions with stakeholders based on facts.

Numerical example

Let us consider the set of alternatives and attributes in the shape of the decision matrix presented in Table 9. Where the considered alternatives ${\text{\rm X}}_{i} \left(i=1, 2, 3, 4, 5\right)$ and ${\upsilon }_{1} \left(1, 2, 3, 4\right)$ is known as a set of attributes presented column-wise. The procedure for evaluating the best alternative is given as follows:

Table 9 Interval-valued q-rung orthopair fuzzy decision matrix ${\left[{\Upsilon}_{ij}\right]}_{m\times n}$.

Step 1 The decision matrix filled by the specialist’s data has ivq-ROFS based information.

Step 2 Given data is in positive type, normalization of the matrix is not required.

Step 3 By applying our proposed Aggregation operators to the information in Table 9 and results in Table 10, which is given as.

Table 10 Aggregated value to applying ivq-ROFSWWA and ivq-ROFSWWG.

Step 4 Applying the score function for the optimal solution, shown in Table 11:

Table 11 Score value for every alternative.

According to ivq-ROFSWWA and ivq-ROFSWWG operators, the outcome represents the light blue for the operator outcome and the light red shown in Fig. 3.

Fig. 3

Graphical view of score function.

Step 5 Ranking.

Table 12 shows that applying both ivq-ROFSWWA ${\rm X}_{1}$ is the best option, and the ivq-ROFSWWG operator ${\text{\rm X}}_{4}$ be the best for investigating risk analysis and factors affecting suicidal attempts.

Table 12 Show the score value ranking.

Sensitive analysis

The developed model consists of a parameter also; thus, the developed approach becomes flexible. In the following, we have observed the ranking of the alternatives based on different values. The ranking obtained is shown in Tables 13 and 14.

Table 13 Ranking at various values of the involved parameter for ivq-ROFSWWA.

Table 14 Ranking at various values of the involved parameter for ivq-ROFSWWG.

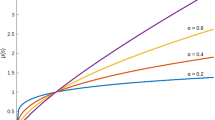
The results remain consistent across different parameter values. We manipulated the parameter values within the range of 3 to 15. We also consistently obtained an identical ranking of the alternatives. Thus, we can infer that the parameter value may be picked solely by those who decide based on their liking. The graphical representation of the ranking of the alternatives as obtained at several parameter values is shown in Fig. 4 as well as Fig. 5, respectively.

Fig. 4

Variation of parameter for ivq-ROFSWWA.

Fig. 5

Variation of parameter for ivq-ROFSWWG.

The graphical representation of ivq-ROFSWWA is given in Fig. 4. When we change the value of the parameter in ivq-ROFSWWA, values slightly change, but the ranking of alternatives remains unchanged.

The graphical representation of ivq-ROFSWWG is given in Fig. 5. When we change the value of the parameter in ivq-ROFSWWG from 3 to 15, values slightly change, but the ranking of alternatives remains unchanged.

Comparative study

In this section, we evaluate the introduced aggregation operator’s efficiency and accuracy in utilizing real-life cases of suicidal risk factors. The derived aggregation operators based on interval-valued q-rung orthopair fuzzy sets give experts more confidence in decision-making. To ensure the credibility of our proposed aggregation operators, the results have been compared to other methods developed by different authors. In particular, we employed the properties of interval-valued q-rung orthopair fuzzy weighted averaging (ivq-ROFWA) and interval-valued q-rung orthopair fuzzy weighted geometric (iv-ROFWG) described by Joshi et al.⁸ and interval-valued q-rung orthopair fuzzy exponential weighted averaging (ivq-ROFEWA) and interval-valued q-rung orthopair fuzzy exponential weighted geometric (ivq-ROFEWG) discussed by Garg⁴². However, in the case of interval-valued intuitionistic fuzzy Einstein weighted averaging (iv-IFEWA) and interval-valued intuitionistic fuzzy weighted Einstein geometric (iv-IFEWG) AOs for multicriteria decision-making methods stated in Wang and Liu⁴³ also compare with the existing operators which are defined by Gitinavard et al.⁴⁴ the values were more significant and could not be aggregated. The proposed operator was better than others, drastically escalating extraneous data’s effects, as shown in Table 15. This method can ensure that the experienced staff pick the most appropriate one that will bring the best results for them.

Table 15 Comparative study of the proposed approach with other previously developed articles.

Table 15 shows the comparative study of the proposed approach with the other existing operators. As a result of ranking, ${\text{\rm X}}_{1}$ is the best alternative while using the ivq-ROFSWWA, and Χ4 is the best alternative by using the ivq-ROFSWWG. In a comparative study, many existing operators fail to provide the results. The reason behind this scenario is the limitations of that operator. Likewise, the operator used by Gitinavard et al.⁴⁴, Fan et al.⁴⁵, and Wang and Liu⁴⁶ failed to provide the results. Still, the proposed study is based on the interval-valued q-rung orthopair fuzzy, in which we deal with the lower MD, NMD, and also upper MD, NMD. The existing AOs are unable to evaluate the data like the proposed AOs. Figure 6 presents the graphical overview of the comparative study.

Fig. 6

Graphical view of comparative analysis.

Managerial implications

The contribution of the proposed model is to provide critical actionable areas for improvement in suicide risk assessment and prevention strategies, specifically among managers. A data-driven approach to handling uncertainty in risk evaluation can be achieved through the EDAS method, which integrates the Sugeno–Weber t-norm and t-conorm. This allows mental health professionals to get mental health checkups to higher risk people more precisely, therefore allowing timely interventions and ideal resource organization. These insights are helpful to policymakers to develop more effective, evidence-based suicide prevention programs that will improve public health strategies. This approach refines risk classification, decreasing operational inefficiencies and properly targeting and achieving cost-effectiveness of preventive measures, thus enhancing suicide prevention initiative impact.

Some other Managerial implications are discussed as follows: For the construction of a hospital in a pandemic situation. Decision makers collect the data in the form of ivq-ROF; after collecting the data, apply the EDAS method with the Sugeno–Weber t-norm and t-conorm to aggregate the data for the selection of the best alternative based on the highest score values. In the end, the ranking of alternatives.

The same new entrepreneur wishes to invest a big cap in the stock market. At the outset, they have a lot of competing firms, and they are in a complex and perplexing environment in which they have to make decisions. In order to identify the safest and most promising investment option, the suggested MAGM methodology is applied. An interval-valued q-rung orthopair fuzzy value (ivq-ROFV) is the best way to collect pertinent information under the condition of uncertainty and ambiguity by the decision maker. Following this, a finite selection of companies is made as alternatives, where the key attributes in selecting the options are those of safety protocol, public interest, political stability, and financial performance. The ivq-ROFSWWA and ivq-ROFSWWG operators then synthesized the data and ranked it in the end. A well-structured method that helps the decision maker to decide the best of the company for a protected and profitable investment, making a well-informed and dependable choice.

Conclusion

In this study, the work has established an interval-valued q-rung orthopair fuzzy sets (ivq-ROFS) model to analyze and identify the factors influencing suicidal attempts and risks under uncertain conditions. With the help of the ivq-ROFS mechanism, suggested on this basis, we defined a means for more appropriate modeling of uncertainty and vagueness between the suicidal factors or risks. The interval-valued approach enabled more accurate consideration of the grades of belief and credibility because the evaluation base was a fuzzy number.

Including ivq-ROFS in our algorithm helped develop a multidimensional risk approach to determine and prioritize risk factors for interventional action in mental health. The findings suggest that ivq-ROFS could improve the consistency and validity of risk assessments to provide a valuable resource for professionals to identify those at most significant risk and implement prevention strategies wisely. More research studies should be conducted to improve the algorithm or to further extend its use in the overall realm of mental health. However, real-time data and increased utilization of other enhanced techniques in the system could sharpen the prophecy feature of the model, leading to improvements in the lives of persons at risk of undertaking a suicidal attempt.

In the future, we will extend our proposed theory for multiple fuzzy frameworks, such as the complex fuzzy framework proposed by Garg and ur Rehman⁴⁷, and Khan et al.⁴⁸ presented the rough fuzzy set-based AOs, and Ahmad et al.⁴⁹ present the entropy measure for q-rung orthopair fuzzy soft set, and Hussain et al.⁵⁰ presents T-Spherical Fuzzy Information and Schweizer-Sklar Operations Based Maclaurin Symmetric Mean Operator Nazeer et al.⁵¹ present interval-valued t-spherical fuzzy using AA AOs. Some Pythagorean fuzzy set-based AOs for decision-making problems were discussed by Hussain and Pamucar⁵².