HarSoNet: a two-stage point cloud registration method integrating soft and hard matching

Abstract

The purpose of point cloud registration is to determine the transformation parameters among multiple partially overlapping point clouds, and it plays an important role in various scenarios such as simultaneous localization and mapping (SLAM), scene reconstruction, industrial manufacturing and so on. However, due to the unordered and irregular nature of point clouds, accurately establishing correspondences poses a significant challenge. Coarse-to-fine methods, consisting of coarse and fine matching stages, have become popular in point cloud registration due to their effectiveness in handling repeatable keypoints. However, these methods are highly sensitive to the correspondences generated during the coarse-matching stage, where low-quality correspondences can lead to complete registration failure. Furthermore, the hard matching approach employed in coarse and fine matching stages often introduces a large number of outliers into the established correspondences. To overcome these challenges, this study introduces HarSoNet, a two-stage Hard-to-Soft Network designed for end-to-end point cloud registration. In the hard matching stage, the model incorporates a hybrid similarity fusion module, which combines similarity scores obtained from different algorithms to establish superpoint correspondences. These superpoint correspondences, along with their neighboring points, are then grouped into fuzzy patch correspondences. In the soft matching stage, patch correspondences are refined into point correspondences by calculating and adjusting the similarity matrix for each fuzzy patch. Finally, all local point correspondences are aggregated into global correspondences, and the transformation parameters are computed using the weighted singular value decomposition (SVD) algorithm. Experimental results demonstrate that HarSoNet achieves Error(R) = 1.376 and Error(t) = 0.015 on noisy, partially overlapping point clouds, demonstrating high registration accuracy and strong generalization performance.

Introduction

Point cloud registration enables the alignment of point clouds from different data sources or acquisition perspectives, providing critical data support for decision-making, design, and research in fields such as industrial manufacturing, autonomous driving, and robotic navigation^1,2. In particular, laser manufacturing systems require multiple scans of large and complex components from various directions, followed by precise alignment of these point clouds to construct a 3D surface model of the components^3,4. Nevertheless, point cloud registration presents a multitude of challenges and difficulties. On one hand, the sparsity and noise interference in point cloud data make it challenging to accurately identify corresponding points. On the other hand, existing methods often exhibit low efficiency and struggle to ensure accuracy when processing complex scenes and large-scale point cloud data.

Traditional point cloud registration methods, such as ICP⁵, NDT⁶, and FGR⁷, perform registration by iteratively optimizing an error metric. These methods are simple to implement and widely applicable but may suffer from slow convergence and a tendency to fall into local minima under poor initial registration or partial overlap. In recent years, numerous learning-based point cloud registration methods^{8,9,10,11,12,13,14,15,16} have utilized rotation-invariant features to establish correspondences between two point clouds, eliminate outlier matches, and apply robust estimator to compute the optimal transformation parameters, thus achieving accurate point cloud registration. It is noteworthy that establishing accurate correspondences constitutes the critical determinant of registration success, whose quality fundamentally governs both the stability of subsequent transformation estimation and the ultimate registration precision.

Soft matching correspondence-based approaches permit each point to establish multiple potential correspondences, each associated with a probability or weighting factor. DCP¹⁰determines soft correspondences by calculating similarity scores between point-wise features of two point clouds. Since not every point is repeatable, RPM-NET¹²assigns weights to each soft matching correspondence to select the final match. ROP-NET¹³refines the similarity matrix iteratively to achieve high-quality soft matching correspondences. However, these methods perform poorly in large-scale real-world tests and fail to resolve the low-overlap registration problem. Hard matching methods require a unique match for each point in the source point cloud. D3 Feat¹¹employs a density-invariant keypoint selection strategy to identify repeatable keypoints between two point clouds for registration. Predator¹⁴ achieves robust registration results for low-overlap problems by predicting the overlap region of two point clouds and selecting correspondences with high matching scores within that region. However, these approaches face challenges in identifying accurate correspondences when encountering substantial deformations or notable local geometric variations.

Inspired by the coarse-to-fine strategy in image matching^17,18,19, CoFiNet¹⁵establishes correspondences between two point clouds using a two-stage matching process. In the coarse matching stage, the input point cloud is downsampled to generate superpoints by introducing sparsity. The similarity matrix, constructed from the superpoint features, is iteratively refined using Sinkhorn to determine hard matching correspondences. In the fine matching stage, superpoint correspondences are combined with neighboring points to form fuzzy patch correspondences. Finally, meaningless entries in the similarity matrix, constructed from block correspondences, are masked by the density-adaptive matching module to obtain final point correspondences. This coarse-to-fine matching mechanism mitigates the risk of losing correspondences due to downsampling, enhancing the efficiency and robustness of the identified correspondences. However, this approach relies heavily on the accuracy of the superpoint correspondences obtained during the coarse-matching stage. GeoTrans¹⁶ employs a Transformer model to learn rotation-invariant geometric features for superpoint matching, improving the quality of superpoint correspondences. However, as both matching stages are based on hard matching, other potential relationships between points are overlooked, leading to final correspondences that are still not sufficiently accurate or robust.

Fig. 1

Patch correspondences in the soft matching stage.

This paper addresses the shortcomings of existing two-stage matching methods, such as the presence of numerous outliers, by proposing a network model that combines soft and hard matching. In the hard matching stage, a hybrid similarity fusion module is employed to assess feature similarity by combining scaled dot product and pairwise distance similarity results, thereby obtaining superpoint correspondences. In the soft matching stage, each point in the two slices of the point cloud is assigned to the nearest superpoint in geometric space to form fuzzy patch correspondences. As shown in Fig. 1, points of the same color in the two point clouds form the patch correspondences. By restricting the estimated soft assignments between the two point clouds to the range of patch correspondences, the probability of false matches is effectively reduced. The final point correspondences are then obtained by calculating and adjusting the similarity matrix for each patch. Finally, all local point correspondences are combined into global point correspondences, and the final transformation parameters are computed using weighted SVD.

The main contributions of this paper are as follows:

• 1) A combined soft and hard matching approach is proposed, where high-quality superpoint correspondences from the hard matching stage provide a clear search direction for soft matching, which assigns multiple potential matching probabilities to each point along that direction. The robust point correspondences established by the combination of two-stage soft and hard matching lead to fast and reliable matching.

• 2) A hybrid similarity fusion module is designed, where distance-based similarity captures the spatial distribution and local similarity of features, while matrix multiplication-based similarity captures the global structure of the point cloud and feature interactions. The combination of both methods allows for a more comprehensive evaluation of feature similarity.

Related work

Most point cloud registration algorithms can be broadly divided into four key steps: feature extraction, correspondence search, outlier filtering, and transformation parameter estimation.

Feature extraction methods

Many algorithms utilize unique feature descriptors to determine point cloud correspondences, resulting in more accurate registration results^{16,20,21,22,23,24,25}. SpinNet²¹voxelizes point clouds into spherical representations and leverages meticulously designed cylindrical convolutions to extract rich local features, demonstrating strong generalization capability in unseen scenarios. However, its voxel representation incurs significant computational overhead. GeoTrans¹⁶encodes rotation-invariant features, such as angles and distances between superpoints, and improves feature representation by capturing global relationships via the Transformer. Nevertheless, these methods fail to account for the fact that rotationally isovariant features retain the orientation information of the point cloud. YOHO²³and RoReg²⁵simultaneously encode both rotationally invariant and isovariant features, enabling fast and robust registration. Recent research on adversarial attacks in 3D point clouds²⁶ has shown that manifold-constrained methods can enhance robustness to local geometric deformations by limiting perturbations in the feature space.

Correspondence search methods

In the presence of noise interference and partial overlap, constructing robust point cloud correspondences poses significant challenges. Reference²⁷introduces the concept of hardening soft-assignment, dynamically adjusting the strictness of matching through Gaussian kernels and an annealing strategy. This approach encourages the model to prioritize high-confidence correspondences during inference, effectively suppressing noise and outliers. MCSVR²⁸, building on the coarse-to-fine framework of CoFiNet¹⁵, innovatively employs a region-level Gaussian mixture model to represent the geometric distribution of point clouds. This method quickly filters potential matching regions and establishes precise hard correspondences within local areas by balancing local geometric details and global distribution characteristics. Unlike these existing approaches, the proposed algorithm first establishes hard correspondences between superpoints, forming region-level correspondences through Euclidean neighborhood aggregation. Then, within a constrained search space, soft assignment is applied to allocate multiple matching weights to each point based on feature similarity. This “hard-matching-guided, soft-assignment-refined” mechanism maintains the determinacy of hard matching while leveraging the fault tolerance of soft assignment, thereby enhancing the robustness of point cloud registration.

Outlier filtering methods

Existing learning-based methods^29,30,31first filter initial correspondences using deep feature similarity and then rely on RANSAC or regression networks to estimate transformation parameters. However, these approaches neither fully exploit spatial information in geometric transformations nor consider the overall spatial relationships among inliers. Spatial compatibility-based methods^32,33,34incorporate spatial consistency constraints during feature extraction and outlier filtering. Nevertheless, they still depend on coarse correspondences as input and cannot achieve end-to-end point cloud registration. Notably, SymAttack³⁵ introduces a novel symmetry-aware attack framework that generates perturbations while preserving the symmetry of the point cloud. The outliers produced by such perturbations are highly inconspicuous-not only are they subtle, but they also maintain the original shape’s symmetry. This characteristic makes traditional geometry-based outlier filtering methods ineffective in detecting these perturbations, posing new challenges to the robustness of the registration process.

Transformation parameter estimation methods

The coupling between the rotation matrix and translation vector complicates the estimation of rigid transformation parameters. This occurs because variations in one parameter (either in the rotation matrix or translation vectors) may influence the estimation of the other, potentially causing bias or errors in the final registration result. To address the problem of parameter interference, DetarNet³⁶separates the estimation of rotation and translation into two stages. Once the interference from translation vectors is removed, the rotation parameters are determined using singular value decomposition (SVD). FINet³⁷ employs a two-branch structure to encourage the model to separately extract features for the two parameters and then applies a regression network to predict the final transformation. However, these methods often fail to fully exploit the local geometric structure of the point cloud, leading to a significant number of outliers in the established correspondences.

Methodology

Problem description

Let the source point cloud be $P = \left\{ p _ { 1 } , p _ { 2 } , \ldots , p _ { n } \right\}$ and the reference point cloud be $Q = \left\{ q _ { 1 } , q _ { 2 } , \ldots , q _ { m } \right\}$ representing the point sets of two point clouds to be aligned, where n and m represent the number of points in P and Q, respectively. The goal of the point cloud registration is to find an optimal rigid transformation ${\textrm{T}} = ({\textrm{R}},{\textrm{t}})$ that best aligns the source point cloud P with the reference point cloud Q, where $\textrm{R} \in S O ( 3 )$ is the rotation matrix (the special orthogonal group) and $\textrm{t} \in {\mathbb {R}} ^ 3$ is the translation vector. The optimal rigid transformation $\textrm{T}$ is obtained by minimizing the distance between the real corresponding points $( p _ { i } ^ { * } , q _ { j } ^ { * } )$:

$$\begin{aligned} \mathop {\min }\limits _{{\textrm{R}},{\textrm{t}}} \sum {_{\left( {p_i^*,q_j^*} \right) \in {C^*}}||{\textrm{R}} \cdot p_i^* + {\textrm{t}} - q_j^*||_2^2} \end{aligned}$$

(1)

$C ^ { * }$ is the set of real correspondences between the two point clouds. The method proposed in this paper leverages the speed of hard matching and the robustness of soft matching by combining two-stage soft and hard matching, ensuring the entire matching process produces robust correspondences while maintaining efficiency.

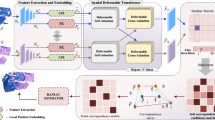
Network architecture

The overall architecture of the proposed method is depicted in Fig. 2. The backbone network performs a downsampling of the input point clouds P and Q while simultaneously extracting their features. The hard matching stage establishes hard correspondences between the superpoints by computing the similarity of superpoint features using the hybrid similarity fusion module. The superpoint correspondences are extended to patch correspondences by combining their neighboring points. The soft matching stage refines these patch correspondences into point correspondences by computing and adjusting the similarity matrix of the patches. Finally, all local point correspondences are pooled into global correspondences, and the final transformation parameters are computed using the weighted SVD algorithm.

Fig. 2

HarSoNet network architecture.

Point cloud preprocessing

Point clouds typically contain a large number of points, and high point cloud density can lead to significant computational costs when calculating distances or performing feature matching. Reducing the number of points through downsampling effectively reduces computational complexity, thereby improving registration efficiency. In this paper, we use the KPConv-FPN backbone network^38,39 to downsample the original point clouds P and Q, extracting their corresponding features. Through the first level of downsampling, we derive the dense point sets ${\tilde{P}}$ and ${\tilde{Q}}$, along with their feature representations ${\tilde{F}} ^ { P } \in {\mathbb {R}} ^ { | {\tilde{P}} | \times {\tilde{d}} }$ and ${\tilde{F}} ^ { Q } \in {\mathbb {R}} ^ { | {\tilde{Q}} | \times {\tilde{d}} }$. At the final level of downsampling, we obtain the superpoint sets ${\hat{P}}$ and ${\hat{Q}}$, as well as their feature representations ${\hat{F}} ^ { P } \in {\mathbb {R}} ^ { | {\hat{P}} | \times {\hat{d}} }$ and ${\hat{F}} ^ { Q } \in {\mathbb {R}} ^ { | {\hat{Q}} | \times {\hat{d}} }$. Here, $| {\tilde{P}} |$ and $| {\tilde{Q}} |$ denote the number of dense points, while ${\tilde{d}}$ represents the dimensionality of the dense point features. Similarly, $| {\hat{P}} |$ and $| {\hat{Q}} |$ indicate the number of superpoints, with ${\hat{d}}$ denoting the dimensionality of the superpoint features. Each point ${\tilde{p}}$ in the dense point ${\tilde{P}}$ is mapped to the nearest superpoint in geometric space, forming a local patch $M _ { i } ^ { P }$:

$$\begin{aligned} M_i^P = \left\{ {{{\tilde{p}}} \in {{\tilde{P}}}\left| {i = \arg {{\min }_j}\left( {{{\left\| {{{\tilde{p}}} - {{{{\hat{p}}}}_j}} \right\| }_2}} \right) } \right. ,{{{{\hat{p}}}}_j} \in {{\hat{P}}}} \right\} \end{aligned}$$

(2)

The feature $F _ { i } ^ { P }$ of patch $M _ { i } ^ { P }$ is composed of the features ${{\tilde{F}}} ^ {{\tilde{p}}}$ of the points ${\tilde{p}}$ within $M _ { i } ^ { P }$ :

$$\begin{aligned} F_i^P = \left\{ {{{{{\tilde{F}}}}^{{{\tilde{p}}}}} \in {{{{\tilde{F}}}}^P}\left| {i = \arg {{\min }_j}\left( {{{\left\| {{{\tilde{p}}} - {{{{\hat{p}}}}_j}} \right\| }_2}} \right) } \right. ,{{{{\hat{p}}}}_j} \in {{\hat{P}}}} \right\} \end{aligned}$$

(3)

Similarly, the local patch $M _ { i } ^ { Q }$ of point cloud Q and its corresponding feature $F _ { i } ^ { Q }$ are computed using Eq. (2) and Eq. (3).

Hard matching stage

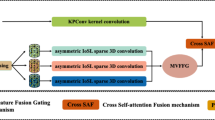
In this paper, we establish hard correspondences between superpoints by encoding their rotation invariant embedding and applying the proposed hybrid similarity fusion module. The framework of the hard matching stage is illustrated in Fig. 3. First, rotation invariant embedding are encoded for superpoints ${\hat{P}}$ and ${\hat{Q}}$, respectively. Next, these features, along with those extracted by the backbone network ${\hat{F}} ^ { P }$ and ${\hat{F}} ^ { Q }$, are fed into the Transformer. This process, comprising rotation invariant embedding and Transformer, is defined as the Rotation Invariant Transformer Embedding. Finally, hard correspondences between superpoints are obtained using the hybrid similarity fusion module.

Fig. 3

Hard matching stage.

Rotation invariant transformer embedding

Most previous directly input the features extracted by neural networks into the Transformer, where some information may be redundant or unnecessary, reducing the geometric distinctiveness of the model. Studies^13,16,40 have shown that incorporating geometric features, such as point cloud rotational invariance, into the Transformer enhances its focus on critical alignment features, thereby reducing ambiguities, mitigating outlier matches, and improving registration efficiency and performance.

In this paper, we apply pair-wise distance embedding and triplet-wise angular embedding¹⁶ for superpoints. The core idea is to extract rotation-invariant embedding (angles and distances), which remain constant under rigid transformations. Theoretically, these features ensure a stable representation of the same spatial entity’s geometric properties across different viewpoints.

Given two superpoints ${\hat{p}} _ { i } , {\hat{p}} _ { j } \in {\hat{P}}$, the pair-wise distance embedding $r _ { i , j } ^ { D } \in {\mathbb {R}} ^ { f }$ between them, with even-dimensional feature $r _ { i , j , 2 r } ^ { D }$ and odd-dimensional feature $r _ { i , j , 2 r + 1 } ^ { D } ,$ can be expressed as:

$$\begin{aligned} \left\{ {\begin{array}{cc} {r_{i,j,2r}^D = \sin \left( {\frac{{{{{d_{i,j}}} \big / {{\sigma _d}}}}}{{{{10}^{{{4 \cdot 2r} / f}}}}}} \right) }\\ {r_{i,j,2r + 1}^D = \cos \left( {\frac{{{{{d_{i,j}}} \big / {{\sigma _d}}}}}{{{{10}^{{{4 \cdot 2r} / f}}}}}} \right) } \end{array}} \right. \end{aligned}$$

(4)

where r denotes the index of the current dimension, f is the dimension of the feature, ${d_{i,j}} = ||{{{\hat{p}}}_i} - {{{\hat{p}}}_j}|{|_2}$ is the Euclidean distance between the superpoints ${\hat{p}} _ { i }$ and ${\hat{p}} _ { j }$. ${\sigma _d}$ is a hyperparameter that adjusts distance scaling. Eq. (4) represents the spatial distribution pattern of superpoints. As the dimension r increases, different frequency encodings are generated using sine and cosine functions. High-frequency components capture subtle distance variations, while low-frequency components encode large-scale distance patterns, enabling adaptive perception of multi-scale geometric structures.

Assuming ${\hat{p}} _ { c } ( 1 \le c \le k )$ represents the k nearest points in the neighbourhood of superpoint ${\hat{p}} _ { i }$, we define $\Delta _ { i , j } = {\hat{p}} _ { i } - {\hat{p}} _ { j }$. For each ${\hat{p}} _ { c }$, $\alpha _{i,j,c}^A = \angle ({\Delta _{c,j}},{\Delta _{j,i}})$, which denotes the angle between vector $\Delta _ { c , j }$ and $\Delta _ { j , i }$. The triplet-wise angular embedding $r _ { i , j , c } ^ { A }$ between superpoint ${\hat{p}} _ { i }$, its neighbourhood point ${\hat{p}} _ { c }$, and superpoint ${\hat{p}} _ { j }$ can be represented by the even-dimensional feature $r_{i,j,c,2l}^A$ and the odd-dimensional feature $r_{i,j,c,2l+1}^A$:

$$\begin{aligned} \left\{ {\begin{array}{cc} {r_{i,j,c,2l}^A = \sin \left( {\frac{{{{\alpha _{i,j,c}^A} \big / {{\sigma _a}}}}}{{{{10}^{4 \cdot {{2l} / f}}}}}} \right) }\\ {r_{i,j,c,2l + 1}^A = \cos \left( {\frac{{{{\alpha _{i,j,c}^A} \big / {{\sigma _a}}}}}{{{{10}^{4 \cdot {{2l} / f}}}}}} \right) } \end{array}} \right. \end{aligned}$$

(5)

l denotes the index of the current dimension, and ${\sigma _d}$ is a hyperparameter that adjusts for angular changes. Eq. (5) captures the local geometric morphology of superpoints. Similar to pair-wise distance embedding, it employs sine and cosine functions to generate multi-frequency scale coverage as the dimension l increases. High-frequency components distinguish subtle angular variations, while low-frequency components encode macroscopic geometric patterns. Compared to traditional linear projection methods, the nonlinear mapping of sine and cosine functions better adapts to complex geometric structures.

Finally, the rotation invariant embedding between the superpoint ${\hat{p}} _ { i }$ and ${\hat{p}} _ { j }$ can be expressed as:

$$\begin{aligned} {r_{i,j}} = r_{i,j}^D{{\textrm{W}}^D} + {\textrm{max}_c}\left\{ {r_{i,j,c}^A{{\textrm{W}}^A}} \right\} \end{aligned}$$

(6)

Here, $r _ { i , j } \in R ^ { {\hat{P}} }$, ${{\textrm{W}}^D}$ and ${{\textrm{W}}^A} \in {{\mathbb {R}}^{f\times f}}$, are projection matrices for distance and angle encoding, f is the feature dimension, and $\textrm{max}_c$ denotes the largest ternary angular embedding $r _ { i , j , c } ^ { A }$ in the neighbourhood of the superpoint ${\hat{p}} _ { i }$. Pair-wise distance embedding characterizes the proximity between point pairs, while triplet-wise angular embedding captures local shape information. By employing a learnable projection matrix, these distinct geometric features are mapped into a unified space, providing a comprehensive representation of the superpoint’s geometric structure. This unified representation also facilitates subsequent processing by attention mechanisms.

In point cloud P, the rotation invariant embedding between each superpoint and other superpoints is denoted as $R ^ { {\hat{P}} }$. Then, $R ^ { {\hat{P}} }$ is concatenated with the superpoint feature ${\hat{F}} ^ { P }$ extracted by the backbone network:

$$\begin{aligned} {F^{{{\hat{P}}}}} = {{\textrm{R}}^{{{\hat{P}}}}} \oplus {{{\hat{F}}}^P} \end{aligned}$$

(7)

where $\oplus$ denotes concatenation along the feature dimension. The same operation is applied to point cloud Q. The concatenated features $F^{{\hat{P}}} \in {\mathbb {R}}^{|{\hat{P}}| \times d}$ and $F^{{\hat{Q}}} \in {\mathbb {R}}^{|{\hat{Q}}| \times d}$ are then fed into a Transformer composed of self-attention and cross-attention layers for further encoding. In the Transformer, the attention mechanism is defined as:

$$\begin{aligned} {\textrm{MHAtten}}\left( {{\textrm{Q}},{\textrm{K}},{\textrm{V}}} \right) = \left( {{\textrm{hea}}{{\textrm{d}}_1} \oplus \ldots \oplus {\textrm{hea}}{{\textrm{d}}_H}} \right) {{\textrm{W}}^O} \end{aligned}$$

(8)

$$\begin{aligned} {\textrm{hea}}{{\textrm{d}}_h} = {\textrm{Atten}}\left( {{\textrm{QW}}_h^Q,{\textrm{KW}}_h^K,{\textrm{VW}}_h^V} \right) \end{aligned}$$

(9)

where $\oplus$ denotes concatenation along the channel dimension, and ${\textrm{W}}_h^Q,{\textrm{W}}_h^K,{\textrm{W}}_h^V \in {\mathbb {R}}{^{d \times {d_{{\textrm{head}}}}}}$ as well as ${{\textrm{W}}^O} \in {\mathbb {R}}{^{H{d_{{\textrm{head}}}} \times d}}$ are learnable projection matrices. The number of attention heads is set to $H=4$, with ${d_{{\textrm{head}}}} = {d \big / H}$. The feature interaction in each projection space is computed using the scaled dot-product attention:

$$\begin{aligned} {\textrm{Atten}}\left( {{\textrm{Q}},{\textrm{K}},{\textrm{V}}} \right) = {\textrm{softmax}}\left( {\frac{{{\textrm{Q}}{{\textrm{K}}^{\textrm{T}}}}}{{\sqrt{{d_{head}}} }}} \right) {\textrm{V}} \end{aligned}$$

(10)

In the self-attention layer, the query, key, and value matrices are set as ${\mathrm{Q = K = V = }}{F^{{{\hat{P}}}}}$. Each superpoint updates its feature representation based on its relationship with other superpoints, enabling intra-superpoint feature interaction and information propagation. In the cross-attention layer, the query is set as ${\mathrm{Q = }}{F^{{{\hat{P}}}}}$, ${\mathrm{K = V = }}{F^{{{\hat{Q}}}}}$. This cross-attention mechanism facilitates feature interaction between the two point clouds, thereby enhancing their alignment and registration. Finally, the features of the two point clouds after the self-attention and cross-attention layers of the Transformer are represented as $\phi ^ { {\hat{P}} } \in {\mathbb {R}} ^ { | {\hat{P}} | \times { d } }$ and $\phi ^ { {\hat{Q}} } \in {\mathbb {R}} ^ { | {\hat{Q}} | \times { d } }$, respectively.

Hybrid similarity fusion module

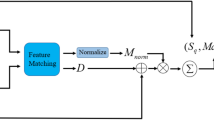
Previous methods for calculating similarity often fail to consider interactions between features or overlook similarity within local regions of the point cloud. The HarSoNet network architecture evaluates the similarity between superpoint features using the proposed hybrid similarity fusion module. As shown in Fig. 4, the similarity between two superpoint features is initially calculated using Scaled Dot-Product Similarity (SDPS) and Pairwise Distance Similarity (PDS). The two similarity results are then combined using a $1\times 1$ convolution. Scaled Dot-Product Similarity captures the global structure and feature interactions within the point cloud, while Pairwise Distance Similarity effectively describes spatial distribution and local feature similarities. Combining both methods provides a holistic understanding of the point cloud, enabling a more comprehensive assessment of feature similarity from local to global levels.

Fig. 4

Hybrid similarity fusion module.

${\textrm{SDPS}} \in {\mathbb {R}}^{|{{\hat{P}}}|\times |{{\hat{Q}}}|}$ can be expressed as follows:

$$\begin{aligned} {\textrm{SDPS}} = {{\textrm{e}}^{\left( { - \frac{{{\phi ^{{{\hat{P}}}}} \cdot {{\left( {{\phi ^{{{\hat{Q}}}}}} \right) }^{\mathrm{\top }}}}}{{\sqrt{d} }}} \right) }} \end{aligned}$$

(11)

where $\top$ denotes the transpose of the matrix. Similar to the attention mechanism in Transformer, SDPS computes the dot product between two feature vectors. The denominator $\sqrt{d}$ is used to scale the dot product, preventing similarity values from becoming excessively large when dealing with high-dimensional feature vectors. Since SDPS is based on the dot product operation, it effectively captures the global structure of the point cloud and facilitates feature interactions, enhancing the overall registration process. $\textrm{PDS} \in {\mathbb {R}}^{|{{\hat{P}}}|\times |{{\hat{Q}}}|}$ can be expressed as follows:

$$\begin{aligned} {\textrm{PDS}} = {{\textrm{e}}^{\left( { - \left\| {{\phi ^{{{\hat{P}}}}} - {\phi ^{{{\hat{Q}}}}}} \right\| _2^2} \right) }} \end{aligned}$$

(12)

PDS computes the squared Euclidean distance between two feature vectors and transforms it into a similarity measure using an exponential function. This approach effectively captures the spatial distribution of features, emphasizing how features are positioned relative to each other in the embedding space. By leveraging Euclidean distance, PDS provides a more geometrically intuitive similarity measure compared to SDPS. After stacking the two similarity results, a hybrid similarity matrix $C_{i,:,:}\in {\mathbb {R}}^{2\times |{{\hat{P}}}|\times |{{\hat{Q}}}|}$ can be expressed as:

$$\begin{aligned} {C_{i,:,:}} = \left\{ {\begin{array}{c} {\!\!\!{\textrm{SDPS,}}i = {\textrm{0}}}\\ {\!\!\!{\textrm{PDS}},i = 1} \end{array}} \right. \end{aligned}$$

(13)

The similarity matrices from different channels of $C_{i,:,:}$ are fused using a convolutional neural network, resulting in the final output $\textrm{S u p e r M} \in {\mathbb {R}} ^ { | {\hat{P}} | \times | {\hat{Q}} | }$:

$$\begin{aligned} {\textrm{SuperM}} = {\mu _\theta }\left( {{C_{i,:,:}}} \right) \end{aligned}$$

(14)

where $\mu _ { \theta }$ denotes a two-dimensional convolutional layer. The combined similarity result leverages the advantages of SDPS, which is sensitive to the global structure of the point cloud, and PDS, which captures distance relationships. By integrating these two complementary measures, the final similarity computation becomes more robust, effectively balancing structural awareness and spatial sensitivity to improve matching accuracy in point cloud registration. Then, we apply double normalization to the $\textrm{SuperM}$matrix¹⁹ for suppressing anomalous matching:

$$\begin{aligned} {\overline{{\textrm{SuperM}}} _{i,j}} = \frac{{{\textrm{Super}}{{\textrm{M}}_{i,j}}}}{{\sum \nolimits _{k = 1}^{\left| {{{\hat{Q}}}} \right| } {{\textrm{Super}}{{\textrm{M}}_{i,k}}} }} \cdot \frac{{{\textrm{Super}}{{\textrm{M}}_{i,j}}}}{{\sum \nolimits _{k = 1}^{\left| {{{\hat{P}}}} \right| } {{\textrm{Super}}{{\textrm{M}}_{k,j}}} }} \end{aligned}$$

(15)

where ${\textrm{S u p e r M }}_{i,j}$ is an element of the $\textrm{SuperM}$ matrix. By applying dual normalization, ambiguous matches are suppressed, and mutually consistent reliable correspondences are selected, enhancing the distinctiveness of the matching process. The top $N _ { c }$ elements ${\overline{ {\textrm{S u p e r M}}} _ { x , y } }$ in the normalized matrix $\overline{\textrm{SuperM}}$ are selected as the hard matching correspondences between the superpoints:

$$\begin{aligned} {{\hat{C}}} = \left\{ {\left( {{{{{\hat{p}}}}_{{x_i}}},{{{{\hat{q}}}}_{{y_i}}}} \right) |\left( {{x_i},{y_i}} \right) \in {{{\mathop {\textrm{topk}}\nolimits } }_{x,y}}({{\overline{{\textrm{SuperM}}} }_{x,y}})} \right\} \end{aligned}$$

(16)

Using Eq. (16), we obtain the set of correspondences between superpoints, denoted as ${{\hat{C}}}$. Each correspondence $\left( {{{{{\hat{p}}}}_{{x_i}}},{{{{\hat{q}}}}_{{y_i}}}} \right)$ represents a matched pair of superpoints, while $( x _ { i } , y _ { i } )$ denote the indices of ${\overline{ {\textrm{S u p e r M}}} _ { x , y } }.$

Soft matching stage

The superpoint correspondences established in the hard matching stage provide crucial initial information and constraints for the soft matching stage. This enables the soft matching process to focus its search within a targeted region rather than the entire point cloud space, resulting in faster and more robust matching.

As shown in Fig. 5, each superpoint corresponds $\hat{ C _ { i } } = ( {\hat{p}} _ { x _ { i } } , {\hat{q}} _ { y _ { i } } )$ aggregates nearby dense points using Eq. (2) and Eq. (3) to form the patch correspondences $(M_{{x_i}}^P,M_{{y_i}}^Q)$ and their corresponding features $(F_{{x_i}}^P,F_{{y_i}}^Q)$. The similarity matrix for each patch correspondence, denoted as ${\textrm{P o i n t M}} _ { i }$, can be expressed as:

$$\begin{aligned} {\textrm{Point}}{{\textrm{M}}_i}{\mathrm{= }}{{{\textrm{F}}_{{x_i}}^P{{\left( {{\textrm{F}}_{{y_i}}^Q} \right) }^{\mathrm{\top }}}} \Big / {\sqrt{{\widetilde{d}}} }} \end{aligned}$$

(17)

Here, $\top$ denotes the matrix transpose, and ${\tilde{d}}$ represents the feature dimension of the patch. Each element in ${\textrm{P o i n t M}} _ { i }$ represents the similarity between each dense point ${\tilde{p}}$ in the local patch $M_{{x_i}}^P$ and each dense point ${\tilde{q}}$ in the local patch $M_{{y_i}}^Q$.

Fig. 5

Soft matching stage.

Sort-regenerate

Next, adjustments are made to ${\textrm{P o i n t M}} _ { i }$ and $M_{{x_i}}^P$. Each row of the similarity matrix ${\textrm{P o i n t M}} _ { i }$ represents the similarity between each dense point ${\tilde{p}}$ in the patch $M_{{x_i}}^P$ and each dense point ${\tilde{q}}$ in the patch $M_{{y_i}}^Q$. First, the maximum value in each row is selected, representing the similarity of each ${\tilde{p}}$ to its most similar ${\tilde{q}}$. Based on these results, the order of ${\textrm{P o i n t M}} _ { i }$ and $M_{{x_i}}^P$ is adjusted to obtain the new similarity matrix ${\textrm{S o r t P o i n t M}} _ { i }$ and the reordered source point cloud matrix $SortM_{{x_i}}^P$, facilitating optimal correspondence matching with the target point cloud:

$$\begin{aligned} {\text{SortPoint}}{{{M}}_i}{\mathrm{= }}{{\mathop{\text{Point}M}\nolimits } _i}\left[ {{\mathop {\textrm{argsort}}\nolimits } (\mathop {\max }\limits _k {{({{{\mathop {\textrm{PointM}}\nolimits } }_i})}_{j,k}})} \right] \end{aligned}$$

(18)

$$\begin{aligned} SortM_{{x_i}}^P = M_{{x_i}}^P\left[ {{\mathop {argsort}\nolimits } (\mathop {\max }\limits _k {{({{{\mathop {\text{PointM}}\nolimits } }_i})}_{j,k}})} \right] \end{aligned}$$

(19)

Corr-point computing

Finally, for each reordered source point cloud matrix $SortM_{{x_i}}^P$, the corresponding reference point cloud matrix ${\bar{M}}_{{y_i}}^Q$ can be expressed as:

$$\begin{aligned} {\bar{M}}_{{y_i}}^Q = {\left( {SortM_{{x_i}}^P} \right) ^{\mathrm{\top }}}\textrm{SortPoint}{\textrm{M}_i} \end{aligned}$$

(20)

The top-k correspondences with the highest confidence scores from $(SortM_{{x_i}}^P,{\bar{M}}_{{y_i}}^Q)$ are chosen as the final selected point correspondences ${\tilde{C}} _ { i }$:

$$\begin{aligned} {{\widetilde{C}}_i} = {\textrm{topk}}\left( {SortM_{{x_i}}^P,{\bar{M}}_{{y_i}}^Q} \right) \end{aligned}$$

(21)

Estimation of transformation parameters

All local point correspondences ${\tilde{C}} _ { i }$ are aggregated into the global point correspondences ${\tilde{C}}$ using (17), where $N _ { c }$ represents the number of patch correspondences. The rigid transformation T is computed using (18), where the similarity scores from each soft matching correspondence $( {\tilde{p}} _ { x _ { j } } , {\tilde{q}} _ { y _ { j } } )$ serve as the weights $w_j$:

$$\begin{aligned} {{\tilde{C}}} = {\mathop {\textrm{Concat}}\nolimits } ({{\widetilde{C}}_i},i = 1,2, \cdots ,{N_c}) \end{aligned}$$

(22)

$$\begin{aligned} {\textrm{R,t}} = \mathop {\min }\limits _{\mathrm{{R,t}}} \sum \nolimits _{\left( {{{{{\tilde{p}}}}_{{x_j}}},{{{{\tilde{q}}}}_{{y_j}}}} \right) \in {{\tilde{C}}}} {{w_j}\left\| {{\textrm{R}} \cdot {{{{\tilde{p}}}}_{{x_j}}} + {\textrm{t}} - {{{{\tilde{q}}}}_{{y_j}}}} \right\| } _2^2 \end{aligned}$$

(23)

Loss function

The loss function $L = L _ { o a } + L _ { r t }$ in this paper comprises two components: the superpoint matching loss $L _ { o a }$ and the transformation parameters loss $L _ { r t }$.

The superpoint matching process is supervised using the overlapping perceptual circle loss. A set of anchor patches $\Lambda$ is defined with the local patch $M _ { i } ^ { P }$ of the source point cloud P and $M _ { i } ^ { Q }$ of the reference point cloud Q. Patches are categorised as positive pairs if they are repeatable; otherwise, they are classified as negative pairs. For each $M _ { i } ^ { P } \in \Lambda$, the sets of positive and negative patches in Q are denoted as $\omega _ { t } ^ { i }$ and $\omega _ { f } ^ { i }$, respectively. The overlapping perceptual circle loss on the source point cloud P is expressed as:

$$\begin{aligned} L_{oa}^P = \frac{1}{{\left| \Lambda \right| }}\!\!\sum \limits _{M_i^P \in \Lambda } \!\!\!{\log \!\!\left[ {1 +\!\!\!\!\!\!\sum \limits _{M_j^Q \in \omega _t^i} \!\!\!\!{{{\textrm{e}}^{\lambda _i^j\delta _t^{i,j}(d_i^j - {\Delta _t})}}} \cdot \!\!\!\!\!\!\sum \limits _{M_k^Q \in \omega _f^i} \!\!\!\!{{{\textrm{e}}^{\delta _f^{i,k}({\Delta _f} - d_i^k)}}} } \right] } \end{aligned}$$

(24)

where $d _ { i } ^ { j } = | | \phi _ { i } ^ { {\hat{P}} } - \phi _ { j } ^ { {\hat{Q}} } | | _ { 2 }$ is the Euclidean distance between the superpoint features, and $\lambda _ { i } ^ { j } = ( o _ { i } ^ { j } ) ^ { 1 / 2 }$ represents the overlap rate between the patches $M _ { i } ^ { P }$ and $M _ { j } ^ { Q }$; futher details are provided in¹⁶. The hyperparameters $\Delta _ { t } = 0 . 1$, $\Delta _ { f } = 1 . 4$, and the weights of the positive and negative patch sets are defined as $\delta _ { t } ^ { i , j } = \gamma ( d _ { i } ^ { j } - \Delta _ { t } )$ and $\delta _ { f } ^ { i , k } = \gamma ( \Delta _ { f } - d _ { i } ^ { k } )$, representing the non-negative results of $( d _ { i } ^ { j } - \Delta _ { t } )$ and $( \Delta _ { f } - d _ { i } ^ { k } )$. The total superpoint matching loss is the average of the losses from point clouds P and Q: $L _ { o a } = ( L _ { o a } ^ { P } + L _ { o a } ^ { Q } ) / 2$.

To optimize rotation and translation parameters, reducing registration errors, the following loss function calculates the deviation between predicted and true transformation parameters:

$$\begin{aligned} {L_{rt}} = \lambda ({\left\| {{{\textrm{R}}^{\mathrm{{\textrm{T}}}}} \cdot {\mathrm{{{\hat{R}}}}} - I} \right\| ^2} + {\left\| {{\textrm{t}} - {\mathrm{{{\hat{t}}}}}} \right\| ^2}) \end{aligned}$$

(25)

where $\mathrm{{\hat{R}}}$ and $\mathrm{{\hat{t}}}$ are the true transformation parameters, $\textrm{R}$ and $\textrm{t}$ are the predicted transformation parameters, and $\lambda$ is a balancing weight for the loss components.

Experiments

Implementation details

The experiments in this study were conducted on a system equipped with a 12-vCPU Intel$\phantom{0}^\circledR$ Xeon$\phantom{0}^\circledR$ Platinum 8352 V CPU running at 2.10 GHz and an NVIDIA RTX 3090 GPU. The computation framework is implemented using PyTorch, with 200 training rounds on the ModelNet40 dataset and 60 rounds on the 3DMatch dataset. The Adam optimizer is used for parameter updates. The batch size was set to 1. The initial learning rate was 0.0001, with a decay rate of 0.000001. During training, $N_g=128$ real superpoint correspondences were used. In the testing phase, $N_c=256$ estimated superpoint correspondences were employed.

ModelNet40 dataset

ModelNet40 comprises 40 categories of 3D CAD models. Eight symmetric categories (e.g., cups, vases) were excluded from both training and testing. The remaining categories were split into training (4,194 models), validation (1,002 models), and test (1,146 models) sets. Following¹², all points were randomly projected, and 70% ($p = 0.7$) were retained to create partially overlapping source and reference point clouds. The source point cloud was subjected to a rotational transformation within the range $[0,r=45]$ and a translational transformation within $[-0.5,0.5]$. The point cloud was then sampled twice: data from the first sampling was denoted as OS, and data from the second as TS.

To validate the performance of the proposed algorithm, we compare it with traditional methods, including ICP (point-to-point) and RANSAC, as well as learning-based methods such as DCP¹⁰, RPM-NET¹², OMNet⁴¹, and GeoTrans¹⁶on Unseen Shape, Unseen Categories and Gaussian Noises. We employ the implementations of ICP and RANSAC from Intel Open3D⁴²and utilize (Fast Point Feature Histogram)FPFH⁴³ for feature matching. Three metrics were used to evaluate the transformation parameters: root mean square error (RMSE), mean absolute error (MAE), and isotropic error (Error).

Unseen shapes

In this study, we initially trained the model using full-class data and tested it on unseen OS and TS datasets. The results in Table 1 indicate that traditional algorithms perform worse across all metrics compared to learning-based methods, demonstrating the strong generalization ability and adaptability of learning-based approaches. The proposed HarSoNet outperforms other methods across all metrics. The Error(R) and Error(t) values are 0.846 and 0.007 for OS, and 1.575 and 0.011 for TS, respectively. Fig. 6 presents a qualitative comparison of learning-based methods on OS, where HarSoNet achieves the most accurate registration results, closely matching the ground truth.

Fig. 6

Qualitative examples of different network models on Unseen Shapes. (a) input. (b) Ground-truth(GT). (c)-(g) The qualitative examples with different network models.

Table 1 Comparison of registration results on Unseen Shapes. Boldfaced numbers highlight the best and the second best are underlined.

Unseen categories

To assess the model’s generalization ability, we trained it on the first 14 categories and tested it on the remaining unseen categories. The results are presented in Table 2. In this part of the experiment, the results of learning-based methods were generally inferior to their performance on Unseen Shape. Traditional algorithms demonstrated a certain level of robustness. HarSoNet achieved the best results on all OS data, with RMSE(R) and MAE(R) reaching 0.751 and 0.637, respectively. On TSdata, its performance was second only to GeoTrans¹⁶. HarSoNet demonstrated strong robustness on unseen categories point cloud data. Fig. 7 presents a qualitative comparison of learning-based methods on OS.

Fig. 7

Qualitative examples of different network models on Unseen Categories. (a) input. (b) Ground-truth(GT). (c)-(g) The qualitative examples with different network models.

Table 2 Comparison of registration results on Unseen Categories. Boldfaced numbers highlight the best and the second best are underlined.

Gaussian noise

To assess the models’ robustness to noise, Gaussian noise of ${ N ( 0 , 0 . 0 1 ^ { 2 } ) }$ was added to the Unseen Categories, and each point was clipped to the range $[-0.05, 0.05]$. The experimental results, presented in Table 3, indicate that after adding Gaussian noise, all models exhibited some robustness. The proposed method achieved the best results across all OS metrics, with Error(R) reaching 1.376 and Error(t) 0.015, demonstrating strong noise resilience. Fig. 8 presents a qualitative comparison of learning-based methods on OS.

Fig. 8

Qualitative examples of different network models on Gaussian Noise. (a) input. (b) Ground-truth(GT). (c)-(g) The qualitative examples with different network models.

Table 3 Comparison of registration results on Gaussian Noise. Boldfaced numbers highlight the best and the second best are underlined.

Large rotation

In this part of the experiment, OS samples in the Gaussian Noise experiment were set to ModelNet with $p=0.7$ and ModelLoNet with $p=0.5$. The maximum rotation angle r between the two point clouds was set to $1 8 0 ^ { \circ }$. Due to this setup, algorithms such as ICP and DCP¹⁰did not produce reasonable results; therefore, their outcomes are omitted from this paper. Meanwhile, Predator¹⁴and CoFiNet¹⁵, which use similar correspondence-based methods, were included in the comparison experiments. The results of Predator¹⁴and CoFiNet¹⁵were refined using RANSAC estimation. To clearly and intuitively evaluate differences in transformation parameters, the relative rotation error (RRE), the relative translation error (RTE), and corrected Chamfer Distance (CD)¹² were used. Table 4 presents the experimental results. The performance of all methods decreases when the initial poses of the two point clouds differ significantly. Performance further declines when dealing with point clouds that have low overlap. However, because hard-to-soft matching enhances the soft matching search space and establishes accurate correspondences, the proposed method outperforms others on most metrics.

Table 4 Comparison of registration results on Large Rotation. Boldfaced numbers highlight the best and the second best are underlined.

3DMatch dataset

The 3DMatch dataset, comprising 62 3D scans of indoor scenes, is widely used for research in point cloud alignment, scene reconstruction, and robot navigation. The dataset includes 46 scenes for training, 8 for validation, and 8 for testing. Following the pre-processing protocol of Predator¹⁴, the data are categorized into 3DMatch (overlap>30%) and 3DLoMatch (overlap between 10% and 30%).

To validate the performance of the proposed algorithms, comparisons were conducted with D3 Feat¹¹, SpinNet²¹, Predator¹⁴, YOHO²³, GeoTrans¹⁶, and REGTR⁴⁰on the 3DMatch and 3DLoMatch datasets. Registration Recall (RR) was used as the evaluation metric, and the inference time of all methods was recorded. Given the limited point correspondences generated by soft matching, the proposed algorithms were evaluated directly on all points, following the sparse matching approach of REGTR⁴⁰. As shown in Table 5, the proposed algorithm achieves a RR of 91.8% on the 3DMatch dataset, ranking second only to GEGTR⁴⁰. On the 3DLoMatch dataset, which has a low overlap rate, the algorithm attains a 67.5% RR, second only to GeoTrans¹⁶. Notably, the algorithm demonstrates the fastest runtime among all methods while maintaining sub-optimal RR, highlighting the efficiency of the two-stage combined soft and hard matching approach. Fig. 9 illustrates the registration results achieved by the proposed algorithm on the 3DMatch and 3DLoMatch datasets.

Fig. 9

Registration visualization on 3DMatch and 3DLoMatch.

Table 5 RR for each method across different numbers of correspondences. Boldfaced numbers highlight the best and the second best are underlined.

Private data

Fig. 10 presents the point cloud data for a launch vehicle engine diaphragm featuring a pressure-sensitive structure. The data contains approximately 200 million points. The point distributions are as follows: X-axis: [1.855, 82.325], Y-axis: [0.005, 89.995], and Z-axis: [0.355, 2.046].

In this part of the experiment, the original point cloud data is first scaled by a factor of 0.05. Following¹², all points are randomly projected, and points with a retention probability of $p=1.0$ are kept to generate FullData, which represents the fully overlapping source and reference point clouds. Points with a retention probability of $p=0.7$ are kept to generate LoData, representing partially overlapping source and reference point clouds. Then, FullData and LoData are randomly downsampled to retain approximately 35,000 points. Finally, rotation transformations within the range of $[0,r=45]$ and translation transformations within the range of $[-0.5,0.5]$ are applied to the reference point cloud in both experimental settings.

To evaluate the efficacy of our method, comparative benchmarking was conducted against conventional approaches, including ICP and RANSAC, as well as learning-based end-to-end methods such as RPM-NET¹²and GeoTrans¹⁶, with experimental validation performed on FullData and LoData. All methods used training weights from the ModelNet40 dataset. Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Isotropic Error (Error) served as evaluation metrics. The results, shown in Table 6 and visualized in Fig. 11, indicate that the proposed algorithm outperforms others across all metrics. The suboptimal performance of conventional point cloud registration approaches can be primarily attributed to the computational challenges posed by the sheer volume of data requiring alignment. A secondary contributing factor emerges in RANSAC-based implementations, where the absence of surface normal information in raw point clouds necessitates normal estimation during FPFH computation, introducing additional computational uncertainties that may propagate through subsequent registration stages. The visualization results show that the proposed algorithm aligns the diaphragm incision accurately, highlighting the method’s effectiveness. Overall, these results highlight the algorithm’s strong generalization ability on unseen data.

Fig. 10

Point cloud data of the original diaphragm.

Fig. 11

Registration visualization on FullData and LoData. The left shows the visualization results of FullData, and the right shows the visualization results of LoData.

Table 6 Comparison of registration results on FullData and LoData. Boldfaced numbers highlight the best and the second best are underlined.

Ablation studies

To assess the effectiveness of each module in the proposed model, we conducted experiments to evaluate different configurations, as summarized in Table 7. The experiment was conducted on the ModelNet40 dataset, following the data settings in Gaussian Noise, and using isotropic errors Error(R) and Error(t) for evaluation.

Calculation of similarity

This paper verifies the effectiveness of the proposed hybrid similarity fusion module. As shown in rows 1) and 2) of Table 7, using only scaled dot product similarity or pairwise distance similarity results in the worst registration performance. In contrast, combining both methods, as demonstrated in rows 3) and 4) of Table 7, achieves the best performance. Specifically, under the two-stage Hard-to-Hard (HTH) structure, Error(R) reaches 1.736 and Error(t) 0.019. In the Hard-to-Soft (HTS) structure, Error(R) improves to 1.376, and Error(t) reduces to 0.015.

Two-stage network structure

The hard-to-soft matching method forms the core structure of the proposed model. When compared with the two-stage hard matching method used in CoFiNet¹⁵and GeoTrans¹⁶, results in rows 3) and 4) of Table 7 show that the HTS structure yields the lowest error. This indicates that the proposed hard and soft matching approach effectively reduces anomalous matches, thereby enhancing matching accuracy.

Table 7 Ablation of different modules on ModelNet40 dataset. Boldfaced numbers highlight the best.

Conclusion

This paper proposes an end-to-end point cloud registration model that integrates two-stage hard and soft matching. In the hard matching phase, initial correspondences are quickly established through localization and coarse matching, while the hybrid similarity fusion module reduces anomalous matches and enhances reliability. The soft matching phase refines these correspondences, optimizing the coarse matches into more accurate point registrations and improving overall stability. By leveraging the speed of hard matching and the robustness of soft matching, the combined approach ensures efficient and reliable correspondences. Experimental results demonstrate that the proposed method is noise-robust and generalizes well to point clouds with unknown categories and shapes.