Introduction

The Campi Flegrei eruptive history started 39000 years ago with the Campanian Ignimbrite eruption and was marked by the Tufo Giallo Napoletano eruption 15000 years ago1,2. Since then, at least, 70 intracalderic eruptions1 signed the topographic aspect of the caldera. The history ended with the 1538 AD Monte Nuovo eruption.

Since 1950, the Campi Flegrei caldera has undergone four bradiseismic crises (1950–1952, 1970–1972, 1982–1984 and 2005–now day) with a total uplift of 4.3 m3,4.

During the 1950 unrest, the sensitivity of the monitoring system was not sufficient to produce significant results and literature. The 1970 unrest resulted in an uplift of 150 cm accompanied by low magnitude seismicity, with only a few events felt by the population3,4.

The two subsequent crises were characterized by the occurrence of a large number of earthquakes accompanying the ground uplift.

The 1982–84 unrest started with a swarm of 17 earthquakes that occurred on 2 November 1982. The seismicity rate greatly increased from May 1983 reaching about 16000 events at the end of the unrest (December 1984)5. Ground uplift started in mid-1982 and ended in December 1984 with an average rate of 1.4 mm per day for a total uplift of 1.8 m5. The seismic activity was characterized by frequent swarms mainly located in the areas of Solfatara and Pozzuoli at shallow depth (above 3 km), whereas deeper seismicity was recorded offshore inside the caldera5,6. Focal mechanisms’ solutions indicated an extensional stress regime in agreement with the inferred stress field in the area7. The ground uplift, estimated by leveling surveys and gravimetric data has been modeled following different approaches8. However, the difficulty of providing a simple mechanical model has been evidenced since the late ’609. Indeed, in order to reproduce the observed very localised ground deformation pattern, many models have suggested ranging from a very shallow and highly over-pressured source, the presence of more than one source, lens-shaped magmatic body to the effect of the caldera boundaries (see Bonafede et al.10 for a comprehensive review).

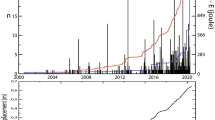
The present unrest started in 2005 and is still ongoing. The average velocity of the soil uplift is 10–20 mm/month measured at the GNSS station RITE located in the area of the highest deformation. The soil uplift increased with a small velocity (\(\simeq\)2.5 cm/y from 2005 to 2013). Then the velocity increased to \(\simeq\)6.5 cm/y in the period 2014–2020 and reached more than \(\simeq\)30 cm/y in the last period11,12. In addition to the seismicity, the current uplift is accompanied by a degassing that amounts to about 5000 tons of \(\hbox {CO}_2\) per day. A comprehensive analysis of the correlation between the geophysical and geochemical parameters is described in Tramelli et al.13. Since 2005 the number of recorded earthquakes with magnitude larger than 0.0 is 7738 with depth confined in the first 6 km.

In both the two last bradiseismic crises the unrest has been interpreted as due to direct magmatic intrusions or to magmatic gas transfer from a deep source (>7–8km) to the shallow hydrothermal system by a large number of authors (see among the others Trasatti et al.8, De Siena et al.14, Petrosino and De Siena15, and Astort et al.16)

Aside from the nature of the source driving the two unrests, the spatial distribution of the seismicity evidences that either the 1982–1984 and the current unrest have activated the same main structures of the caldera both on-land and off-shore17. However, the largest earthquake recorded during the present unrest is larger than the largest one that occurred during the 1982–1984 unrest (\(M_d=4.4\) and \(M_d=4\), respectively).

A crucial ingredient in the interpretation of our results is the presence of a concrete layer firstly observed close to the surface of the Solfatara by18 and named caprock.

In this study, we focus on a comparative analysis of the 1982–1984 and 2005–2024 unrest periods at Campi Flegrei, using b value estimation as a key observable. The b value is a critical indicator of the stress regime in the crust and is sensitive to changes in the volcanic system allowing us to uncover underlying differences in the processes driving these two crises. Our approach, leveraging the b more positive method, provides an enhanced framework for identifying changes in the strain distribution without the need to estimate the completeness magnitude, thus allowing for a more robust interpretation of the data (Fig. 1).

Data

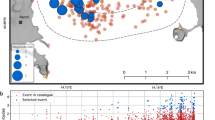
Here we used two catalogues of the Campi Flegrei seismic activity. The first spans from 04 February 1982 to 12 December 1984 and contains 5575 events with duration magnitude in the range [0, 4]. The first event recorded in the second catalogue occurred on 22 August 2000 and the last one on 25 June 2024. The catalogue contains 11166 events with a duration magnitude in the range [−0.2, 4.2]. The epicentral distribution and the hypocenters of the events contained in the two catalogues are shown in Fig. 2.

The cumulative magnitude distributions are shown in Fig. 1 using different \(m_c\) for the two periods (upper panel) and the same \(m_c\) (lower panel).

Fig. 1
figure 1

The cumulative magnitude distributions for periods 1 and 2 using different magnitude of completeness. The upper panel shows the results when \(m_c=0.5\) is used for the period and \(m_c=1\) for the second period. The lower panel refers to the case in which the same \(m_c=1\) is used for both the two periods. The completeness magnitude has been estimated using the method of19. In both cases the two cumulative distributions have to be considered different at a confidence level reported in the legends. The insets show the probability density function of the magnitude.

Full size image

The difference in the cumulative distributions in the upper panel (verified through the Kolmogorov-Smirnov statistical test) has to be attributed to the increased sensitivity of the present seismic network. Conversely, the difference in the lower panel has to be attributed to the different b values (\(b=1.1\) at present time and \(b=1\) in 1982–84).

Results

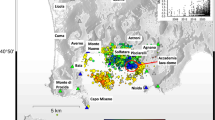
When applying the CUBITm+ code “Dividing the catalogue in cells” section we obtained 11 cells, for the 1982–1984 catalogue, with a b in the range [0.74, 1.2] and a \(\sigma _b\) in the range [1.5E−02, 2.5E−02] (Fig. 3). Whereas the 2005–2024 catalogue is divided into 21 cells exhibiting very similar ranges of b [0.65, 1.2] and \(\sigma _b\) [1.5E−02, 2.6E−02] (Fig. 4). The maps of the b standard deviation are shown in Supplemental Information for both cases.

Fig. 2
figure 2

Location of the seismicity recorded in 1982–1984 (black dots) in comparison with the one recorded during the current unrest (red dots). The coordinates are expressed in UTM Zone 33T and are reported in meters, where X represents the eastward direction and Y represents the northward direction; the depth is in meters referred to the sea level. The yellow triangle indicates the position of the GPS station RITE.

Full size image
Fig. 3
figure 3

The map of the b value in 1982–1984 with the two vertical projection from South and from East. The coordinates are expressed in UTM Zone 33T and are reported in meters, where X represents the eastward direction and Y represents the northward direction; the depth is in meters referred to the sea level.

Full size image
Fig. 4
figure 4

The map of the b value in 2000–2024 with the two vertical projection from South and from East. The coordinates are expressed in UTM Zone 33T and are reported in meters, where X represents the eastward direction and Y represents the northward direction; the depth is in meters referred to the sea level.

Full size image

To enlighten the differences between the two maps (Figs. 3 and 4) we adopt the method presented in “Comparison of the b maps” section obtaining the map of Fig. 5. For the great part of the shallower events, the difference (\(b_{1982-1984}\) – \(b_{2000-2024}\)) is negative. This implies that, there, the b value increased suggesting that the stress distribution in the interested volume is decreased in the 2000–2024 catalogue with respect to the 1982–1984 one. However, four areas exhibit a positive \(\Delta b\) indicating an increase of the stress: the Accademia lava dome, Pisciarelli, a zone NW of the Solfatara and the deeper part of the Pozzuoli harbor. The increased stress indicated by the low b-value in the Accademia dome could be explained by the activation of fractures in more concrete and cold rocks. If we exclude the events closely located to this lava dome, both data with \(\Delta b>0\) and \(\Delta b<0\) exhibit very similar average depth (2 km for the first one and 1.7 km for the second one) and a standard deviation equal to 0.6 km for both the data sets. This implies that the great part of the events reported in Fig. 5 are earthquakes occurring within the caprock, which has been located at 1.5–2.0 km by18,20. However, the difference of 0.3 km of the average depth causes the dominant blue (negative \(\Delta b\)) in the horizontal projection of the map. Conversely, positive \(\Delta b\) are evident for shallower seismicity at the NW of Solfatara zone and at Pisciarelli.

Fig. 5
figure 5

The surface projection of the \(\Delta b\) value for four different depths. Here \(\Delta b\) is defined as \(b_1 - b_2\) where \(b_1\) is the b value of the events occurred in 1982–1984 and \(b_2\) is the b value of the events occurred in 2000–2024. The whole 3D map is shown in the supplemental information.

Full size image

For both the two catalogues we observe a very similar decrease of the b value with depth (Fig. 6) confirming a result already obtained in many tectonic areas21,22,23,24,25,26,27,28,29 and generally interpreted as related to the average stress gradient in the crust (see among the others30). Interestingly, the same results showing a large scatter suggest an anisotropic distribution of the b value in the volume.

Fig. 6
figure 6

The b value as a function of the depth being \(\langle z\rangle\) the average depth in the cell.

Full size image

The time dependence of the b value has been investigated using the method described in “Evaluating the b value as a function of time” section. Moreover, we evaluate b(t) for two different classes of events: those occurring at a depth smaller than 2 km and the ones occurring at a depth larger than 2 km. The choice of such a depth value derives by two different observations: (1) the cap-rock bottom, separating two volumes with different rheological behaviour, is located at about 2 km20; (2) the two volumes are characterized by different seismic clustering properties31. Figures 7 and 8 enlighten similarities and differences between 1982–1984 and 2000–2024 catalogues.

In the following, we will refer to the 1982–1984 catalogue as case 1 and to the 2000–2024 catalogue as case 2.

In case 1 we observe large fluctuations of the b value [0.7,1.1] for the whole data set. Conversely, they are smaller [0.7,0.8] for the deeper events 7. Interestingly, the latter exhibit a tendency to decrease during the first 0.9 years and then stabilize with small fluctuations around the value of 0.75.

In case 2 the whole data set exhibits smaller fluctuations of the b value [0.8,1.2] compared to the shallower events [0.8,1.6] 8. Moreover, for the shallower events the b value tends to increase since 2018, then it assumes, on average the value 1.2 but with large fluctuations. Conversely, deeper seismicity tends to decrease up to approximately June 2023, then it slightly increases with larger fluctuations.

Fig. 7
figure 7

Upper panel: The b value as a function of time for the 1982–1984 catalogue. Time starts at 01/01/1982. The whole data set is plotted without error bars for graphical reasons. However, its size is comparable to the other two sets. Lower panel: The daily rate of occurrence.

Full size image
Fig. 8
figure 8

Upper panel: The b value as a function of time for the 2000–2024 catalogue. The time starts on 01/01/2000. The whole data set is plotted without error bars for graphical reasons. However, its size is comparable to the other two sets. Lower panel: The daily rate of occurrence.

Full size image

In case 1 we observe 500 earthquakes approximately five months after the beginning of the catalogue and, after one more month, the number of events with \(z \ge 2\) km also reaches the value 500. Conversely, in case 2, the number of 500 earthquakes is reached only after 17 years from the beginning of the catalogue and after 12 years of the starting time of the current unrest. The number of events with \(z\ge\)2 km is 500 only in 2022. However, 2028 events occurred at depths larger than 2 km in the following 2 years. In both case 1 and case 2, shallower seismicity exhibits a larger b value and larger fluctuations in respect with the deeper one. However, in case 1, the largest b value fluctuations are observed for the whole data set. Conversely, in case 2, the entire data set fluctuations are similar to those of shallower seismicity even in the period (\(t>22\) years) of overlapping of the two series.

For both cases, the daily rate of occurrence is plotted for comparison.

Discussion

Interpreting the b-value in terms of stress, the \(\Delta b\) maps suggest that the stress distribution in space is different in case 1 and case 2 (see  “Results” section). This could imply that, assuming the same source of deformation, the caprock18,32 breaks in different points in the two cases. However, the delay between the occurrence of deeper earthquakes in respect to the shallower ones suggests that the caprock fracturing and the consequent intrusion of fluids in the upper part of the crust (\(z<\)2 km) induces an increase of the stress in this region leaving the zone beneath the caprock at a stress level not yet sufficient to trigger earthquakes. In fact, the seismicity is more abundant in the shallower region in the first time windows. We hypothesize that the shallower seismicity could be caused by the heating of the hydrothermal system due to the passage of hot and pressurized gases through the fractures of the caprock. Then (after a few months in case 1 and some years in case 2) the increase of the stress generates new seismicity beneath the caprock where the temperature is higher and the rocks can sustain higher stress33.

There are two main differences between the 1982–1984 unrest and the 2005–2024 one. The first one concerns the velocity of the phenomenon in terms of deformation and seismicity rate that was higher in case 1. The other difference concerns the b value temporal fluctuations. In case 1 the observed temporal fluctuations are caused by the alternation of deep and shallow seismicity occurrence in the different sliding windows. Indeed, both shallow and deep data sets exhibit smaller fluctuations. In other words, when the dominant seismicity, in the window, is the deeper one, b assumes smaller values whereas it increases when the shallow seismicity become dominant in the window. Conversely, in case 2, the b fluctuations of the whole data set are dominated by the shallower seismicity. This is because of the relative abundance of shallower events observed in this catalogue. There are \(\simeq\)3500 shallow earthquakes and \(\simeq\)2200 deep ones in the case 1 catalogue and \(\simeq\)8000 shallow earthquakes and \(\simeq\)3000 deep ones in the case 2 catalogue including both off-shore and on-shore earthquakes. The large fluctuation (reflecting fluctuation of the stress) observed from the end of 2020 up to present time for the shallower data set could be interpreted as due to fluctuations of the temperature and gas flux in the hydrothermal system. These fluctuations do not reflect on the soil uplift because of their high frequency. In both cases (1 and 2), the tendency to increase of the b value for the deeper data sets is a consequence of the delay with which the deeper structures react to the increased stress exhibiting a visco-elastic behaviour. In other words, the deeper on-land structures are activated (the number of events is larger than or equal to 500) only when the stress, caused by the heating of the hydrothermal system, reaches a given threshold. Then the b value tends to decrease reflecting into an increase of the stress. When the stress become more constant also the b value appears to be almost stationary, even if there are significant fluctuations, for shallow earthquakes, especially in case 2.

Conclusions

Based on the above discussion the scenario that we can depict is: the caprock breaks allowing the passage of the volcanic gases in the hydrothermal system34. This one is warmed by the hotter gases causing the increase of the volume and the uplift of the soil35. At the same time the earthquakes start to occur at shallower depth. When the stress reaches a higher level the deeper structures are activated causing the occurrence of larger earthquakes and, consequently, the decrease of the b value for the deeper seismicity. Here we hypothesize two possible mechanisms to explain the delay of the deeper structures activation. In the first one, the rising of the magma16,36 causes an increase of the stress, but the deeper rocks are more resistant and the stress has to reach a higher value in order to generate earthquakes. The second one views the heating, caused by the fluid passage through the caprock, of the shallower hydrothermal system as being itself the cause of the increased stress on the deeper structures. More precisely, the warmed fluids induce, as expected, a soil deformation not only in the upward direction, but also in the downward direction causing the activation of the deeper structures with a time delay.

In this scenario, the smaller uplift velocity observed in case 2 could be ascribed to several mechanisms among which:

  1. 1.

    A smaller temperature diffusivity in case 2 in respect to case 1 making slower the warming of the shallow hydrothermal system

  2. 2.

    An increased fracture density allowing a more efficient degassing of the shallow hydrothermal system and a less efficient deformation rate (unfortunately no information about the gases flux is available for the period 1982–1984)

  3. 3.

    The increased \(\hbox {CO}_2/\hbox {H}_2\hbox {O}\) ratio35, which reflects the rise in gas fluxes, reduces the efficiency of the temperature-pressure relationship, as part of the energy is consumed in generating higher fluxes rather than contributing to deformation.

Methods

Dividing the catalogue in cells

Here we use the unstruCtUred B mappIng Tool CUBITm+ code for the evaluation of b value maps. The method, firstly introduced by Godano et al.37, selects the largest event in the catalogue not yet assigned to a cell and includes in the cell, around the chosen earthquake, \(n\pm n_{tol}\) events (here \(n=500\) and \(n_{tol}=30\)) (see Supplemental Information for a detailed description of the algorithm). It has been applied for mapping the b value on the Antakia earthquake fault38 and on the major \((m>7)\) Californian earthquakes faults39 and at Campi Flegrei volcanic area32 in the period 2000–2024. The main difference with respect to the previous applications of CUBITm+ is that, here, we use a different method for the estimation of the b value.

Estimation of the b value

The b positive method is based on the observation that the distribution of the difference between the magnitude of two successive earthquakes \(\delta m\) follows a Laplace distribution independently of the completeness magnitude \(m_c\)40. This makes the b value maximum likelihood estimation more easy and reliable. The b positive method has been futherly improved by the b more positive method: given a certain event it looks for the next larger earthquake and evaluates \(\delta m\). Then the \(\delta m\) distribution is evaluated. This strategy allows a more robust estimation of the b value41. In the present study we have adopted the b more positive method41. The distribution of \(\delta m\) in the different cells and for the two catalogues here analysed are shown in the Supplemental Information.

Even if the \(\delta m\) distribution is independent of the completeness magnitude, it presents a small curvature at small \(\delta m\). As a consequence the correct asymptotic b value can be obtained only for \(\delta m\) larger than \(\simeq\)0.541. This is particularly true for large areas catalogues, whereas for smaller regions (as Campi Flegrei) the curvature disappears (see figures in Supplemental Information). Such an aspect deserves deeper analyses and will be investigated in a fore coming paper.

Comparison of the b maps

The comparison of the maps has been performed on the basis of the b value differences. Namely, for each earthquake occurred in 1982–1984 we look for the closest event occurred in 2000–2024. If the closest event occurs within a distance of 0.2 km, we evaluate the difference \(\Delta b=b_1-b_2\) where \(b_1\) is the b value associated with the event occurred in 1982–1984 and \(b_2\) is the b value associated with the event occurred in 2000–2024. If the closest event occurs at a distance larger than 0.2 km the earthquake is discarded. Then \(\Delta b\) is plotted using the coordinates of the 1982–1984 earthquake only when the difference is significant at the 95% level (t-test).

The choice of 0.2 km corresponds to the radius of the smallest cell avoiding cells superposition. Moreover, this value is the average location error in the central part of the caldera for both the analised catalogues. It is noteworthy that this choice does not allow the comparison of the two catalogues in the off-shore area.

Evaluating the b value as a function of time

The b value time variation has been investigated estimating its value by using the b more positive method41 in samples of 500 events sliding of an event per time. The estimated b value is plotted as a function of the occurrence time of the last earthquake in the window. We have checked that using sliding of 125, 250, 375 and 500 events does not changes significantly our results. Indeed the only significant effect is the reduction of the number of points in the plot.

Moreover, we checked that the b value estimates obtained in a previous paper32 are very similar to the ones here obtained. There we used the variation coefficient \(c_v\) method19,42 for estimating the completeness magnitude. The estimation of the b value was obtained using the maximum likelihood method43. Its standard deviation \(\sigma _b\) was obtained following Shi and Bolt44). The only significant difference is represented by the number of obtained cells. This because, in the previous version, we discarded the cells with \(m_{max}-m_c<1.5\). In the present paper the b value estimation are \(m_c\) independent.