Introduction

Nonlinear partial differential equations (NLPDEs) are used to model precise physical processes across several scientific fields, including plasma physics, plasma waves, fluid dynamics, and solid-state physics1,2,3,4,5. Owing to their extensive variety of applications in science and social fields of expertise, such as ecology, physics, engineering, social dynamics, and mathematics for finance3, chemical physics, fiber optics4,5, quantum mechanics6, Neuro-physics7, and many more, The assessment of NLPDEs is an increasingly important area of research. Each day, more scientists and researchers are drawn to analyze physical events, utilizing various techniques and instruments to understand their underlying principles. Currently, nonlinear partial differential equations (NLPDEs) serve as valuable tools for gaining insights into the structure of these nonlinear processes5. They enable analysts to assess the structure of a phenomenon involving multiple variables simultaneously, making them highly effective for conveying clear and accurate information about physical phenomena8. In recent decades, several researchers have developed, expanded, and effectively utilized many innovative approaches. Among these are various stimulating methods and mathematical tools, including Bernoulli sub-equation function method9, the (G′/G)-expansion extended method 10, Sardar subsection equation method11, Riccati-Bernoulli Sub-equation method12, Kudryashov method13, variational principle method14, Hamiltonian-based method15, improved modified extended tanh-function method16, simplest equation method17, \(\Phi^{6}\)- expansion method18, Hirota bilinear method19 and many more.

Another intriguing wave phenomenon is the soliton, often referred to as a solitary wave. A soliton is a self-sustaining wave that maintains its shape and steady speed, even after interacting with other waves, without changing its amplitude9. Solitons are stable, localized structures that play a significant role in the optical transmission of signals, attracting the attention of both physicists and mathematicians5. John Scott Russell’s discovery of the wave of translation marks the beginning of the history of solitons. Many prominent scientists and philosophers praised Russell’s work, which was ultimately confirmed in the 1870s, highlighting its significance for the progress of science20. Boussinesq’s work from 1872 was influential and anticipated key concepts still utilized by modern scientists and scholars21,22,23. The generation and analysis of soliton solutions is increasingly important in the study of electromagnetic, optical, and telecommunication fibers, as well as other fields in engineering and the physical sciences12,22,24.

The Higgs equation concept began in 1960, when British theoretical physicist Peter Higgs and his colleagues sought to explain how particles acquire mass. In 1964, the Higgs mechanism was introduced, clarifying how elementary particles acquire mass. This mechanism involves a scalar field that permeates space and is associated with the Higgs boson25. In the Standard Model of particle physics, the Higgs field interacts with particles through spontaneous symmetry breaking. This scenario can be visualized as a ball rolling into a circular valley. Initially, the system shows rotational symmetry; however, as the ball rolls, it ultimately comes to rest at a specific point, disrupting that symmetry. The Higgs field has a constant, non-zero value throughout space, which breaks electroweak symmetry and gives particles their mass. The strength of a particle’s interaction with the Higgs field determines its mass, providing a clear explanation for the wide range of particle masses observed in nature26. In 2012, scientists at CERN confirmed the discovery of the Higgs boson. This was a major achievement for the Standard Model of particle physics, as it validated key predictions and enhanced our understanding of how mass is generated in the universe through both experimental research and theoretical advancements27. The classical Higgs equation written by Refs.28,29.

$$u_{tt} - u_{xx} - \beta u + \alpha \left| u \right|^{2} u = 0,$$
(1)

\(u(x,t)\) is a function of complex scalar nucleon field, \(\alpha\) and \(\beta\) are arbitrary real constants. The Partial differentiations are indicated by the subscripts, \(x\) and \(t\) avariables are both spatial and temporal, respectively.The Higgs field’s connection to gauge fields, leading to the creation of mass and the unification of electromagnetic and weak nuclear forces, is described by the coupled Higgs field equations (CHFE)30.

Equation for the Higgs field:

$$u_{tt} - u_{xx} - \beta u + \alpha \left| u \right|^{2} u - 2uv = 0.$$
(2a)

Equation for the Gauge field:

$$v_{tt} + v_{xx} - \alpha \left( {\left| u \right|^{2} } \right)_{xx} = 0.$$
(2b)

Equation (2a) and (2b) above explains how neutral scalar mesons and conserved scalar nucleons interact in the physics of particle. The \(v(x,t)\) function is a real scalar meson field. In Eq. (2a) and (2b) for \(\alpha < 0\)\(\beta < 0\), the composition is the nonlinear coupled Klein–Gordon equation and it becomes coupled nonlinear Higgs equation for \(\alpha > 0\) and \(\beta > 0\)31. Equation (1) and Eq. (2a) and (2b) makes up the system: one governs the background field’s evolution and the other illustrates the soliton amplitude and phase changes over time. These equations represent the dynamics of the Higgs field, a scalar field that is responsible for giving mass to fundamental particles through spontaneous symmetry breaking. Analyzing the coupled Higgs field equations is crucial for understanding the dynamics of fields in particle physics, cosmology, and condensed matter systems.This framework encompasses various physical phenomena, including the mass mechanism for gauge bosons, the fragmentation mechanism in low-energy antiproton-induced nuclear reactions, and heavy-ion collisions etc32. In Eq. (1), there is only a single soliton solution, while Eq. (2a) and (2b) contains both two-soliton and N-soliton solutions33.

Soliton solutions for CHF equations have been identified using various techniques. Given their significance and numerous applications, researchers have thoroughly explored the solutions of this model through multiple strategies5. Solitons are stable localized structures that significantly impact particle interactions, attracting the interest of both mathematicians and physicists5. Various effective methods have been developed for constructing soliton solutions. The equations were first investigated by Tajiri34 who obtained N-soliton by employing the Hirota bilinear method. Zhao35 developed a more comprehensive travelling wave solution through the anstaz of an extended algebraic approach. Mann36 analyzed the solutions of CHFE using the auxiliary equation method and extended the Sinh-Gordon expansion approach. Kaplan37 built more extensive exact solutions for the coupled Higgs equation by using \(\left( {{{G^{\prime}} \mathord{\left/ {\vphantom {{G^{\prime}} {G,{1 \mathord{\left/ {\vphantom {1 G}} \right. \kern-0pt} G}}}} \right. \kern-0pt} {G,{1 \mathord{\left/ {\vphantom {1 G}} \right. \kern-0pt} G}}}} \right)\) and \(\left( {1/G^{\prime}} \right)\) expansion methods. Abbas38 obtained solutions of CHFE using Jacobi elliptic function techniques. Marwan39 obtained a solution of coupled Hihhs equation using sine–cosine and modified rational sinh-cosh methos. Alam40 solve CHFE by employing travelling wave solution .Akbari41 find the travelling wave solution using a modified simplest method. Khajeh et al.42, analyzed CHF equations expoliting the Exp-function method. Jabbari43, established the exact solution of the CHFE using He’s semi-inverse method and \(\left( {{{G^{\prime}} \mathord{\left/ {\vphantom {{G^{\prime}} G}} \right. \kern-0pt} G}} \right) -\) expansion method. Singh44 investigates CHF equations using the trial equation method. Wen45 used the Riccati-Bernoulli subsidiary ordinary differential equation method to solve soliton solution of CHFE. Ali et al.14, explore some wave solutions of CHFE via rational exp \((-\varphi \left(\eta \right))\)-expansion method. Atas et al.46 construct the optical solutions of CHFE through the generalized rational function method. Ozisik47 explain the analytical solutions of CHFE using the enhanced modified extended tanh expansion method. Drawing from the extensive literature on the CHFE, it is noted that the generalized Riccati equation and the enhanced Sardar sub-equation techniques have yet to be utilized in finding solutions for the CHFE. This study aims to develop new and accurate solutions for the CHFE by utilizing both the generalized Riccati method (GRM) and the Enhanced Sardar sub-equation Method (ESSM). In comparison to other methods, this approach stands out as comprehensive, robust, and efficient. It offers a distinct advantage due to its inherent simplicity in all computational processes, making it notably user-friendly. This simplicity facilitates the development of more comprehensive, accurate, and reliable solutions, which are easier to interpret than those produced by established methodologies. It is particularly effective in deriving general solutions involving hyperbolic, trigonometric, rational, and exponential functions.

The remaining parts of this paper are organized as follows: In Sect.  “An overview of the ESSM and the GRM”, we describe the enhanced Sardar sub-equation method and the generalized Riccati method. Section  “The CHFE solutions utilizing ESSM” discusses the solution to the CHFE using the ESSM. In Sect.  “The generalised Riccati equation method’s solutions”, we present the solution obtained through the GRM. Section  “Graphical illustration and discussion” focuses on graphical visualization by assigning appropriate parameters to the applied techniques. Finally, Sect. “Conclusion” offers the conclusion of the article.

An overview of the ESSM and the GRM

This section describes the methodology of the ESSM and GRM in deriving new solutions to the CHFE. One of the primary advantages of these methods is their capability to generate a wide variety of soliton solutions, including those derived from hyperbolic, trigonometric, and exponential functions. These solutions exhibit different soliton structures, such as periodic, singular, bright, and dark soliton waves. Additionally, further details about these methods can be found in Refs.48,49,. Therefore, we are considering the NLPDE.

$$H^{NLPDE} \left( {\varphi ,\varphi_{t} ,\varphi_{tt} ,\varphi_{xx} ,\varphi_{xxx} ...} \right) = 0,$$
(3)

where \(\varphi = \varphi \left( {x,t} \right)\) is an unknown function, \(H\) is a polynomial in \(\varphi \left( {x,t} \right)\) and its derivatives. The subscripts remain for the partial derivatives. Next, we convert the NLPDE (3) into the nonlinear differential equation (NLODE) with the wave transformation applied as:

$$\varphi (x,t) = Q(\xi )e^{{i\left( {bx - \eta t} \right)}} ,\,\xi = x - kt,$$
(4)

where \(Q\) is a real-valued function, parameter \(k\) is a constant, while parameters \(b\) and \(\eta\) denote the wave number and the circular frequency, respectively.

The transformation (4) is incorporated into Eq. (3), resulting in the following

$$Z^{NLODE} \left( {Q,Q^{\prime},Q^{\prime\prime},Q^{\prime\prime\prime},...} \right) = 0,$$
(5)

where \(Z\) is the polynomial of \(Q\) and its derivatives. Regarding the superscript \(\left( ^{\prime} \right)\) denote the ordinary derivative with respect to \(\xi\).

The solution of ISSM of Eq. (5) above is defined as follows:

$$Q\left( \xi \right) = b_{0} + \sum\limits_{i = 1}^{m} {b_{i} Z(\xi )^{i} } ,b_{m} \ne 0,$$
(6)

where,\(b_{i}\), \(\left( {i = 0,1,2,...,m} \right)\) are parameters that will be acquired subsequently and the homogenous equillibrium method decides the value of \(m\) amongst the nonlinear terms and the maximum derivative terms in Eq. (5). Furthermore, for ISSM the function \(Z(\xi )\) in Eq. (6) completes the following equation.:

$$\left( {Z^{\prime}(\xi )} \right)^{2} = \delta_{2} Z(\xi )^{4} + \delta_{1} Z(\xi )^{2} + \delta_{o} ,$$
(7a)

where \(\delta_{0} ,\delta_{1}\) and \(\delta_{2}\) are constant and will ultimately be determined later.

While regarding the GRM function \(Z(\xi )\) in Eq. (6) satisfies the following equation:

$$Z^{\prime}(\xi ) = r_{2} Z(\xi )^{2} + r_{1} Z(\xi ) + r_{o} ,$$
(7b)

where \(r_{2} ,r_{1}\) and \(r_{0}\) are constants to determined later. The Eq. (7a) and Eq. (7b) have many solutions that are omitted here to avoid repetition, we refer readers to Ref.48.

The CHFE solutions utilizing ESSM

In this section, the ESSM49 is employed to address the CHFE, resulting in various solutions for solitary waves including exponential, trigonometric, and hyperbolic forms. The wave transformation will be conducted as follows:

$$u(x,t) = U(\xi )e^{i\vartheta } \,\,\,{\text{and }}\,v(x,t) = V(\xi ),$$
(8)

where \(\vartheta = bx - \eta t,\) \(\xi = x - rt\). Now substitute Eq. (2a) and (2b) into the system (2a) and (2b) to obtain the following NLODE

$$\left. \begin{gathered} (k^{2} - 1)U^{\prime\prime}\left( \xi \right) + (\eta^{2} - b^{2} + \alpha )U\left( \xi \right) + \beta U^{3} \left( \xi \right) - 2U\left( \xi \right)V\left( \xi \right) = 0, \hfill \\ (k^{2} + 1)V^{\prime\prime}\left( \xi \right) - \beta (U^{2} )^{\prime\prime}\left( \xi \right) = 0, \hfill \\ \end{gathered} \right\}$$
(9)

where \(\left( ^{\prime} \right) = \frac{d}{d\xi }\).Taking into account the zero constant of integration, we integrate the Eq. (9) above, to obtain

$$V\left( \xi \right) = \frac{{\beta U^{2} \left( \xi \right)}}{{k^{2} + 1}}.$$
(10)

Substitution Eq. (10) into Eq. (9) to have

$$(k^{2} - 1)U^{\prime\prime}\left( \xi \right) + (\eta^{2} - b^{2} + \alpha )U\left( \xi \right) + \frac{{\beta (k^{2} - 1)}}{{k^{2} + 1}}U^{3} \left( \xi \right) = 0.$$
(11)

Simplifying Eq. (11) to get

$$(k^{2} + 1)(k^{2} - 1)U^{\prime\prime}\left( \xi \right) + (k^{2} + 1)(\eta^{2} - b^{2} + \alpha )U\left( \xi \right) + \beta (k^{2} - 1)U^{3} \left( \xi \right) = 0.$$
(12)

From Eq. (12) above, we apply the homogenous balancing principle to derive a unique value of by balancing the highest order nonlinear term \(\left( {U^{3} } \right)\) and highest order derivative term \(\left( {U^{\prime\prime}} \right)\) to obtain

$$\begin{gathered} 3m = m + 2, \hfill \\ m = 1. \hfill \\ \end{gathered}$$
(13)

thus, the solution of Eq. (13) takes the following form for \(m = 1,\)

$$U\left( \xi \right) = b_{o} + b_{1} Z(\xi ).$$
(14)

Now, substituting Eq. (14) into Eq. (12) by incorporating Eq. (7a) and inserting the coefficient of the powers of \(Z(\xi )^{i}\) to zero to obtained a series of algebraic equations. Solving algebraic equations yields:

$$b_{o} = 0,b_{1} = b_{1} ,\delta_{o} = \delta_{o} ,\delta_{1} = \frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} + 1}},\delta_{2} = - \frac{1}{2}\frac{{\beta b_{1}^{2} }}{{k^{2} + 1}}.$$
(15)

Therefore, substituting Eq. (15) into Eq. (14) using different solutions \(Z(\xi )\) of Eq. (7) as stated in 48 to derived the following for the system of NLODE Eq. (9) for \(\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}} > 0\):

$$u_{1,1} (\xi ) = \left( {\frac{{4b_{1} e^{{\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)}} (\eta^{2} - b^{2} + \alpha )}}{{\left( {k^{2} - 1} \right)\left( {e^{{2\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)}} + \frac{{2(\eta^{2} - b^{2} + \alpha )\beta b_{1}^{2} }}{{\left( {k^{2} - 1} \right)\left( {k^{2} + 1} \right)}}} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(16)
$$v_{1,1} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{4b_{1} e^{{\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)}} (\eta^{2} - b^{2} + \alpha )}}{{\left( {k^{2} - 1} \right)\left( {e^{{2\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)}} + \frac{{2(\eta^{2} - b^{2} + \alpha )\beta b_{1}^{2} }}{{\left( {k^{2} - 1} \right)\left( {k^{2} + 1} \right)}}} \right)}}} \right)^{2} .$$
(17)
$$u_{1,2} (\xi ) = \left( {\frac{{4e^{{\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)}} \left( {\eta^{2} - b^{2} + \alpha } \right)b_{1} }}{{\left( {k^{2} - 1} \right)\left( {1 + \frac{{2b_{1}^{2} \beta e^{{\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)}} \left( {\eta^{2} - b^{2} + \alpha } \right)}}{{\left( {k^{2} - 1} \right)\left( {k^{2} + 1} \right)}}} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(18)
$$v_{1,2} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{4e^{{\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)}} \left( {\eta^{2} - b^{2} + \alpha } \right)b_{1} }}{{\left( {k^{2} - 1} \right)\left( {1 + \frac{{2b_{1}^{2} \beta e^{{\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)}} \left( {\eta^{2} - b^{2} + \alpha } \right)}}{{\left( {k^{2} - 1} \right)\left( {k^{2} + 1} \right)}}} \right)}}} \right)^{2} .$$
(19)
$$u_{1,3} (\xi ) = \left( {\sqrt 2 \sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} {\text{sech}} \left( {\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)b_{1} } \right) \times e^{{i\left( {bx - \eta t} \right)}} ,$$
(20)
$$v_{1,3} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\sqrt 2 \sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} {\text{sech}} \left( {\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)b_{1} } \right)^{2} .$$
(21)
$$u_{1,4} (\xi ) = \left( {\sqrt { - \frac{{\left( {2\eta^{2} - 2b^{2} + 2\alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} {\text{csch}} \left( {\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)b_{1} } \right) \times e^{{i\left( {bx - \eta t} \right)}} ,$$
(22)
$$v_{1,4} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\sqrt { - \frac{{\left( {2\eta^{2} - 2b^{2} + 2\alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} {\text{csch}} \left( {\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)b_{1} } \right)^{2} .$$
(23)
$$u_{1,5} (\xi ) = \left( {\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \tanh \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right) \times e^{i(bx - \eta t)} ,$$
(24)
$$v_{1,5} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \tanh \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right)^{2} .$$
(25)
$$u_{1,6} (\xi ) = \left( {\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \coth \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right) \times e^{i(bx - \eta t)} ,$$
(26)
$$v_{1,6} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \coth \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right)^{2} .$$
(27)
$$u_{1,7} (\xi ) = \left( {\frac{{\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right),}}} \right) \times e^{i(bx - \eta t)} ,$$
(28)
$$v_{1,7} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right),}}} \right)^{2} .$$
(29)
$$u_{1,8} (\xi ) = \left( {\frac{{\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {\cosh \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(30)
$$v_{1,8} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {\cosh \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(31)
$$u_{1,9} (\xi ) = \left( {\frac{1}{2}\frac{{\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {2\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right)}}{{\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(32)
$$v_{1,9} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{1}{2}\frac{{\sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {2\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right)}}{{\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(33)

For \(\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}} < 0:\)

$$u_{2,0} (\xi ) = \left( {\sqrt 2 \sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \cos \left( {\sqrt { - \frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right) \times e^{i(bx - \eta t)} ,$$
(34)
$$v_{2,0} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\sqrt 2 \sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \cos \left( {\sqrt { - \frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right)^{2} .$$
(35)
$$u_{2,1} (\xi ) = \left( {\sqrt 2 \sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \csc \left( {\sqrt { - \frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right) \times e^{i(bx - \eta t)} ,$$
(36)
$$v_{2,1} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\sqrt 2 \sqrt {\frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \csc \left( {\sqrt { - \frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right)^{2} .$$
(37)
$$u_{2,2} (\xi ) = \left( {\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \tan \left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right) \times e^{i(bx - \eta t)} ,$$
(38)
$$v_{2,2} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \tan \left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right)^{2} .$$
(39)
$$u_{2,3} (\xi ) = \left( {\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \cot \left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right) \times e^{i(bx - \eta t)} ,$$
(40)
$$v_{2,3} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} \cot \left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)b_{1} } \right)^{2} .$$
(41)
$$u_{2,4} (\xi ) = \left( {\frac{{\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {\sin \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\cos \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(42)
$$v_{2,4} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {\sin \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\cos \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(43)
$$u_{2,5} (\xi ) = \left( {\frac{{\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {\cos \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\sin \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(44)
$$v_{2,5} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {\cos \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\sin \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(45)
$$u_{2,6} (\xi ) = \left( { - \frac{1}{2}\frac{{\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {2\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right)}}{{\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)\sin \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(46)
$$v_{2,6} \left( \xi \right) = \frac{\beta }{{k^{2} + 1}}\left( { - \frac{1}{2}\frac{{\sqrt { - \frac{{\left( {\eta^{2} - b^{2} + \alpha } \right)\left( {k^{2} + 1} \right)}}{{\left( {k^{2} - 1} \right)\beta b_{1}^{2} }}} b_{1} \left( {2\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right)}}{{\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)\sin \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{\left( {k^{2} - 1} \right)}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(47)

The generalised Riccati equation method’s solutions

This section presents various trigonometric and hyperbolic solitary wave solutions derived from the CHF equations using the generalized Riccati equation method. According to the methodology outlined in Sect. 2, the solution assumes the following form:

$$U\left( \xi \right) = A_{o} + A_{1} Z(\xi ).$$
(48)

Now, substituting Eq. (48) into Eq. (12) by incorporating Eq. (7b) and allowing the coefficient of the powers of \(Z(\xi )^{i}\) to zero to get a set of algebraic equations. The following set of solutions can be obtained by solving the algebraic equations:

Set 1

$$A_{0} = 0,A_{1} = \sqrt { - \frac{{2k^{2} + 2}}{\beta }} ,r_{0} = \frac{1}{2}\frac{{\eta^{2} - b^{2} + \alpha }}{{r_{2} \left( {k - 1} \right)\left( {k + 1} \right)}},r_{1} = 0$$
(49)

Set 2

$$A_{0} = - \frac{{\left( {k^{2} + 1} \right)r_{1} }}{{\beta \sqrt { - \frac{{2k^{2} + 2}}{\beta }} }},A_{1} = \sqrt { - \frac{{2k^{2} + 2}}{\beta }} r_{2} ,r_{0} = \frac{1}{4}\frac{{k^{2} r_{1}^{2} + 2\eta^{2} - 2b^{2} - r_{1}^{2} + 2\alpha }}{{r_{2} \left( {k^{2} - 1} \right)}}$$
(50)

Family 1

We have reached the following solutions for the first set of solution for \(\frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k - 1} \right)\left( {k + 1} \right)}} < 0\):

$$u_{2,7} (\xi ) = \left( { - \frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k - 1} \right)\left( {k + 1} \right)}}} \tanh \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k - 1} \right)\left( {k + 1} \right)}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} } \right) \times e^{i(bx - \eta t)} ,$$
(51)
$$v_{2,7} (\xi ) = \frac{\beta }{k + 1}\left( { - \frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k - 1} \right)\left( {k + 1} \right)}}} \tanh \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{\left( {k - 1} \right)\left( {k + 1} \right)}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} } \right)^{2} .$$
(52)

For \(\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}} > 0:\)

$$u_{2,8} (\xi ) = \left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \tan \left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} } \right) \times e^{i(bx - \eta t)} ,$$
(53)
$$v_{2,8} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \tan \left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} } \right)^{2} .$$
(54)
$$u_{2,9} (\xi ) = \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \coth \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} } \right) \times e^{i(bx - \eta t)} ,$$
(55)
$$v_{2,9} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \coth \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} } \right)^{2} .$$
(56)
$$u_{3,0} (\xi ) = \left( { - \frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \cot \left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} } \right) \times e^{i(bx - \eta t)} ,$$
(57)
$$v_{3,0} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( { - \frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \cot \left( {\frac{1}{2}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} } \right)^{2} .$$
(58)
$$u_{3,1} (\xi ) = \left( {\frac{1}{2}\frac{{\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(59)
$$\begin{gathered} v_{3,1} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{1}{2}\frac{{\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} . \hfill \\ . \hfill \\ \end{gathered}$$
(60)
$$u_{3,2} (\xi ) = \left( {\frac{1}{2}\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {\sin \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\cos \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(61)
$$v_{3,2} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{1}{2}\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {\sin \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\cos \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(62)
$$u_{3,3} (\xi ) = \left( { - \frac{1}{2}\frac{{\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(63)
$$v_{3,3} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( { - \frac{1}{2}\frac{{\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(64)
$$u_{3,4} (\xi ) = \left( { - \frac{1}{2}\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {\cos \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\sin \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(65)
$$v_{3,4} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( { - \frac{1}{2}\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {\cos \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + 1} \right)}}{{\sin \left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(66)
$$u_{3,5} (\xi ) = \left( { - \frac{1}{4}\frac{{\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {2\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right)}}{{\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sinh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(67)
$$v_{3,5} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( { - \frac{1}{4}\frac{{\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {2\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right)}}{{\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sinh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(66)
$$u_{3,6} (\xi ) = \left( { - \frac{1}{4}\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {2\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right)}}{{\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sin \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right) \times e^{i(bx - \eta t)} ,$$
(67)
$$v_{3,6} \left( \xi \right) = \frac{\beta }{{k^{2} + 1}}\left( { - \frac{1}{4}\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \sqrt { - \frac{{2k^{2} + 2}}{\beta }} \left( {2\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right)}}{{\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sin \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}} \right)^{2} .$$
(68)

Family 2

We developed the following answers for the second set of solutions for \(\frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}} < 0\):

$$u_{3,7} (\xi ) = \left( {\frac{{\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \tanh \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\left( {k^{2} + 1} \right)}}{{\beta \sqrt { - \frac{{2k^{2} + 2}}{\beta }} }}} \right) \times e^{i(bx - \eta t)} ,$$
(69)
$$v_{3,7} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \tanh \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\left( {k^{2} + 1} \right)}}{{\beta \sqrt { - \frac{{2k^{2} + 2}}{\beta }} }}} \right)^{2} .$$
(70)

For \(\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}} > 0:\)

$$u_{3,8} (\xi ) = \left( {\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \tan \left( {\frac{1}{2}\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\left( {k^{2} + 1} \right)}}{{\beta \sqrt { - \frac{{2k^{2} + 2}}{\beta }} }}} \right) \times e^{i(bx - \eta t)} ,$$
(71)
$$v\left( \xi \right) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \tan \left( {\frac{1}{2}\sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\left( {k^{2} + 1} \right)}}{{\beta \sqrt { - \frac{{2k^{2} + 2}}{\beta }} }}} \right)^{2} .$$
(72)
$$u_{3,9} (\xi ) = \left( { - \frac{{\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \coth \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\left( {k^{2} + 1} \right)}}{{\beta \sqrt { - \frac{{2k^{2} + 2}}{\beta }} }}} \right) \times e^{i(bx - \eta t)} ,$$
(73)
$$v_{3,9} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( { - \frac{{\left( {k^{2} + 1} \right)\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \coth \left( {\frac{1}{2}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)}}{{\beta \sqrt { - \frac{{2k^{2} + 2}}{\beta }} }}} \right)^{2} .$$
(74)
$$u_{4,0} (\xi ) = \left( {\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \cot \left( {\frac{1}{2}\sqrt { - \frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\left( {k^{2} + 1} \right)}}{{\beta \sqrt { - \frac{{2k^{2} + 2}}{\beta }} }}} \right) \times e^{i(bx - \eta t)} ,$$
(75)
$$v_{4,0} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \cot \left( {\frac{1}{2}\sqrt { - \frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\left( {k^{2} + 1} \right)}}{{\beta \sqrt { - \frac{{2k^{2} + 2}}{\beta }} }}} \right)^{2}$$
(76)
$$u_{4,1} (\xi ) = \left( {\frac{{\left( {k^{2} + 1} \right)\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta }}} \right) \times e^{i(bx - \eta t)} ,$$
(77)
$$v_{4,1} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\left( {k^{2} + 1} \right)\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} }}} \right)^{2} .$$
(78)
$$u_{4,2} (\xi ) = \left( {\frac{{\left( {k^{2} + 1} \right)\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\sin \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\cos \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta }}} \right) \times e^{i(bx - \eta t)} ,$$
(79)
$$v_{4,2} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\left( {k^{2} + 1} \right)\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\sin \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\cos \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta }}} \right)^{2} .$$
(80)
$$u_{4,3} (\xi ) = \left( {\frac{{\left( {k^{2} + 1} \right)\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta }}} \right) \times e^{i(bx - \eta t)} ,$$
(81)
$$v_{4,3} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\left( {k^{2} + 1} \right)\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\cosh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\sinh \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta }}} \right)^{2} .$$
(82)
$$u_{4,4} (\xi ) = \left( {\frac{{\left( {k^{2} + 1} \right)\sqrt 2 \sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\cos \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\sin \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta }}} \right) \times e^{i(bx - \eta t)} ,$$
(83)
$$v_{4,4} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\left( {k^{2} + 1} \right)\sqrt 2 \sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\cos \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right) + I} \right)}}{{\sin \left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta }}} \right)^{2} .$$
(84)
$$u_{4,5} (\xi ) = \frac{{\frac{1}{2}\left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {k^{2} + 1} \right)\left\{ {2\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right\}} \right)}}{{\left( {\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sinh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta } \right)}} \times e^{i(bx - \eta t)} ,$$
(85)
$$v_{4,5} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\frac{1}{2}\left( {\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {k^{2} + 1} \right)\left\{ {2\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right\}} \right)}}{{\left( {\cosh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sinh \left( {\frac{1}{4}\sqrt { - \frac{{2\eta^{2} - 2b^{2} + 2\alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta } \right)}}} \right)^{2} .$$
(86)
$$u_{4,6} (\xi ) = \frac{{\frac{1}{2}\left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {k^{2} + 1} \right)\left\{ {2\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right\}} \right)}}{{\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sin \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta }} \times e^{i(bx - \eta t)} ,$$
(87)
$$v_{4,6} (\xi ) = \frac{\beta }{{k^{2} + 1}}\left( {\frac{{\frac{1}{2}\left( {\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {k^{2} + 1} \right)\left\{ {2\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)^{2} - 1} \right\}} \right)}}{{\cos \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sin \left( {\frac{1}{4}\sqrt 2 \sqrt {\frac{{\eta^{2} - b^{2} + \alpha }}{{k^{2} - 1}}} \left( {\xi + C} \right)} \right)\sqrt { - \frac{{2k^{2} + 2}}{\beta }} \beta }}} \right)^{2} .$$
(88)

Graphical illustration and discussion

To underscore the importance of the CHFE, we meticulously choose pertinent elements concerning its physical characteristics. Our aim in choosing these parameters is to raise awareness about the significance of this issue. The ESSM and GRM provide various solutions, including trigonometric, hyperbolic, and exponential functions, due to the balanced interaction between linear and nonlinear effects. Additionally, We have also included a series of graphs to searve as visual aids to illustrate the practical significance of the solutions obtained. These graphical representations clarify the physical implications of the equations and highlight the characteristics that enable the novel solitary wave solutions shown in the 2D and 3D graphs. Below are some of the solutions discussed:

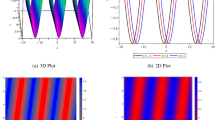
Figure 1 The graph of modulus plot of solutions (16) and (17) with parameters \(\beta = - 0.5\), \(\alpha = - 0.5\),\(b = - 0.2\), \(k = 5\),\(b_{1} = 0.8\), \(\eta = - 0.2\) and \(C = - 0.2\) portrayed periodic solution, periodic solitary waves are essential to many physical processes, Like self-reinforcing systems, reaction–diffusion-advection systems, and impulsive systems etc.

Fig. 1
figure 1

Profile for solution \(\left| {u_{1,1} (x,t)} \right|\) and \(\left| {v_{1,1} (x,t)} \right|\) with selected parameters.

Full size image

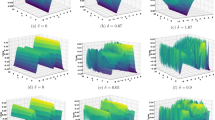
Figure 2 Reveal bell shape for (20) and kinky-bright soliton for (21) with selected parameters \(\beta = 2\), \(\alpha = - 2\),\(b = 2\), \(k = 5\), \(\eta = 2\), \(C = 5\). bright soliton in CHFE can model topological defects in the early universe, such as domain walls and cosmic strings. These soliton can described the behavior of Higgs bosons in high-energy collisions and providing insight into fundamental forces of nature as well as providing a mathematical framework for studying nonlinear dynamics.

Fig. 2
figure 2

Profile for solution \(\left| {u_{1,3} (x,t)} \right|\) and \(\left| {v_{1,3} (x,t)} \right|\) with selected parameters.

Full size image

Figure 3 The behavior of the modulus solution of (26) and (27) with parameters \(\beta = 2.5\), \(\alpha = 2.2\),\(b = 2.5\), \(k = 5\), \(\eta = - 2.5\) and \(C = 0.2\) characterise singular-periodic solution.

Fig. 3
figure 3

Profile for solution \(\left| {u_{1,6} (x,t)} \right|\) and \(\left| {v_{1,6} (x,t)} \right|\) with selected parameters.

Full size image

Figure 4 Displayed the configuration anti-bell shape for (51) and dark soliton for (52) with specific parameters \(\beta = 2.5\), \(\alpha = - 0.2\),\(b = 0.5\), \(k = 5\),\(\eta = 0.5\) and \(C = - 0.5\). Anti-bell soliton can model exotic state of matter, such as superconducting vortices, magnetic skyrmions and provide a rich mathematical framework for studying nonlinear dynamics, symmetry breaking and interactions.

Fig. 4
figure 4

Profile for solution \(\left| {u_{2,7} (x,t)} \right|\) and \(\left| {v_{2,7} (x,t)} \right|\) with selected parameters.

Full size image

Figure 5 The behavior of the modulus solutions of (69) and (70) with appropriate values \(\beta = 5.0\), \(\alpha = 8.0\),\(b = - 9.0\), \(k = 5\), \(\eta = - 7.5\) and \(C = 5.2\) portrayed dark soliton, The finding of dark soliton, which suggests the existence of coherent structures that withstand dispersion and preserve their integrity during propagation, advances our knowledge of the dynamics of the system. The stability and resilience of localised structures within systems are affected by the bright sun’s manifestations in applications like linear optics and plasma physics.

Fig. 5
figure 5

Profile for solution \(\left| {u_{3,7} (x,t)} \right|\) and \(\left| {v_{3,7} (x,t)} \right|\) with selected parameters.

Full size image

Conclusion

The ESSM and GRM were successfully used in this study to create new soliton solutions for CHFE. The techniques produced a number of novel soliton solutions, which were expressed as exponential, trigonometric, and hyperbolic functions. Using 2D and 3D graphs generated with Maple 18 version 18.01 (www.maplesoft.com), we effectively demonstrated the dynamic characteristics and practical significance of these solutions. The graphs illustrated different types of solitons which includes periodic, dark, dark-bell, bright, and anti-bell solitons. The solutions were proved to be more convenient to interpret the model in simple and straightforward manner. The results obtained were new and very auspicious for further investigation and stances on a strong basis for the solution of NLEEs. Compared to the methodologies employed in Refs.38,47, the solutions contained hyperbolic functions but did not include trigonometric and exponential functions, Therefore, the solutions constructed in this article were more diverse and the methods were more adaptable and straightforward, leading to more general solutions. The uniqueness of our study lies in the methods we employed, which have enabled us to discover a variety of new exact solutions and solitons. Our findings revealed promising opportunities for advancing in optical communications and associated technologies. The methods demonstrated in our research were versatile and can be applied to a broader range of differential equations beyond those specific to optical fibers. Furthermore, the techniques used have the potential to enhance our understanding and application of wave solitons across various scientific fields, including quantum mechanics, fluid dynamics, and marine engineering. As a result, this may lead to new research initiatives, technological innovations and an extension of the proposed methods for fractional model in future work.