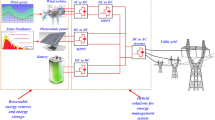
Abstract
Microgrid (MG) is basically composed of different distribution generators (DGs) connected in parallel for supplying a specific set of loads managed by an Energy management system (EMS). EMS is a control system integrated within MGs for managing the operations of these DGs effectively to fulfill a power balance between power production and load demand in the most optimal way, especially in island MGs. In this paper, an EMS based on Multiple Adaptive Neuro-Fuzzy Inference System optimized by Genetic Algorithm (MANFIS-GA) is proposed for PV/Wind/Diesel Generator/Battery (PWDB) island MG system, to optimize the output power of diesel generator, manage charging-discharging operation of MG Battery Storage keeping its State of Charge (SOC) in acceptable limits, and improve the MG system reliability and stability by mitigating the effects of sudden changes in the electrical loading and Renewable energy sources (RES) Power. The prediction system is implemented by using 8760 samples based on an hourly meteorological data of a whole year. GA is used as an optimization technique for training MANFIS to accomplish the desired objects of EMS. For evaluation purpose, a real case study of a day-ahead data is tested and discussed in details. Experiments show that the proposed smart system provides accurate results for the expected outputs and achieves a good performance.
Similar content being viewed by others
Introduction
Due to the projected growth in world population, global demand of electricity is largely increasing1, which led to increase the power production capacity from fossil fuels, resulted in an energy crisis and environmental pollution2. Hence the world went to a clean, economic, unlimited energy resources to cover that demand of electricity3,4. Renewable energy sources (RES) are currently being deployed on a large scale, and used as primary energy sources in the power grid system5.However, the intermittence and sudden change in sun irradiance and wind speed effects the power quality of electrical grid system significantly6. Therefore, a new form of electrical grid was used. It’s more flexible, reliable and smart. Where it can increase the efficiency and resiliency of electrical networks, and provide a viable utilization for different RES into distribution networks7, which is called MG. Relevant literature on MG is increasing day by day, introduce the concept, benefits and features of it8,9,10,11,12. MG is electrically bounded area that can involve a wide range of energy sources which is known as Distributed Generators (DGs), which are controlled by the power electronics technology. However, these DGs can include microturbines, gas turbines, diesel generators, photovoltaic arrays, fuel cells and wind generators, are equipped with an Energy Storage System (ESS) like a battery and supercapacitor, for supplying different electrical loads: controllable loads and uncontrollable (critical) loads forming a self-sufficient energy system. ESS play an important role in the power balancing between DG produced power and loads consumed power for a duration of time by supporting the RES deficit when necessary, and storing the excess energy when it possible13.The MG scheme is depicted in Fig. 1. MGs can be classified to AC-MG, DC-MG , and HybridMG according to the main Busbar (B.B) voltage of MG. Due to difference between DGs and ESS output voltage, and frequency values in MG, the DGs and ESS are commonly interfaced to the main B.B by the means of power-electronic devices like Voltage Source Inverters (VSI) and Current Source Inverters (CSI)14 as shown in Fig. 2. However, these inverters are controlled by Micro-source Controllers (MC), which are managed by MG Central Controller (MGCC) forming a single controllable entity. Where it can absorb/inject power from/to the main grid in grid connected mode15, and during large disturbances (voltage collapse, faults and poor power quality) at the main grid, it separates from the main grid and transfers to island mode, and the MG loads are supplied by local DGs only16. MGCC is like a brain of MG17, that has the most important role for satisfactory automated operation and control of microgrid while working in two modes18, by issuing commands to MCs and Load Controllers (LCs) of MG aiming to coordinate and manage the DGs produced power according to the load demand, and shed the loads for demand reduction when the demand exceeds the produced power for achieving the power balance in MG19. Furthermore it regulates and synchronizes the output voltage and frequency values of different DGs that connected on the same AC bus20, and synchronizes with main grid in grid concocted mode, and determines the operation mode of MG according to the power quality of the main grid and load demand21, etc.
All objectives and operations of processing, sensing and adjusting, monitoring and supervising, maintenance and optimization, that were done by MGCC, MCs, and LCs. It can be described through three layers of control: primary, secondary and territory, respectively22,23,24,25,26,27,28 ; according to its time frame which were accomplished in and speed of response, in addition to its infrastructure requirements29, these layers are accomplished in parallel, arranged in a control structure that called a hierarchical control, which is offering high efficiency and more degree of freedom energy management. The hierarchical Control layers of MGs is illustrated in Fig. 3.
-
(1)
First layer (Primary Control): Active and reactive power-sharing control, primary frequency and voltage adjustment of DGs, and controlling the performance of energy storage systems; in this layer, these operations is done instinctually within milliseconds as well as its more sensitive to any variation in the source or demand of the system in order to maintain the power stability and reliability.
-
(2)
Second level (Secondary Control): Power flow monitoring and controlling, voltage and frequency compensation and synchronization within the allowed limits regardless of source and load changes and disturbances, also synchronization to main grid, control operations in this layer is slower than primary control. It is accomplished within few milliseconds to minute, in order to justify the dynamic between both levels.
-
(3)
Third level (Territory Control): The operations and functions of energy Management System (EMS) involves dayahead power scheduling and real-time energy management based on distributed generation availability30,31,32,33, load forecasting, the purchasing/selling electricity price, this layer it has the slowest response to the MG devices variation compared with the first and second layers, that are usually deployed from every few minutes to 1 h.
EMS is usually integrated within MGs due to the requirement of a control system that manages the operations of the DGs effectively, and to fulfill these control operation, many advanced and smart control methods have been proposed recently, such as Fuzzy Logic Control (FLC), Adaptive Neuro Fuzzy Interference System (ANFIS), which work independently from the mathematical model of controlled system plant, unlike classical control methods such as Proportional Integral (PI) control. ANFIS has appeared as an attractive solution for handling the EMS control operations, due to its fast dynamic response, robustness, and accuracy that achieved by integrating both neural networks and fuzzy logic principles. ANFIS based EMS is developed to manage the available energy in different MGs, The ANFIS method is used to generate the input/output relationship according to the input/output data and the human experience, and EMS decisions are determined according to these relations of ANFIS34,35.
In recent years, many studies have discussed different designs EMS that achieve different control operations in MG, such as:33, used ANFIS for designing an EMS for hybrid MG, that recognizes the changes of transient behavior of the load current and the power of the fuel cell (PFC) for maintaining the DC bus voltage in constant ranges.Another study34 proposed energy management system for AC-MG Based on ANFIS, the suggested MG composed from two renewable DGs (wind and solar) connected with ESS feeding different loads, ANFIS controllers taking the produced power of RES, consumed power of load and battery of SOC as inputs for optimizing the energy of DGs. In35 research, The ANFIS EMS is proposed for intelligent redistribution of the prosumer energy balance between the ESS and the connected grid in order to maximize the profit generated by the energy exchange with the main grid. In36 paper, introduces (ANFIS) for AC MG consisting of a diesel-based generator connected in parallel with a double fed induction generator (DFIG) driven by RES (wind and solar systems), ANFIS system is taking the wind speed, solar radiation and temperature data as input for achieving the power balance between produced power and consumed power, decreasing DG fossil fuel to minimum consumption, keep the MG voltage stability. In37 research, the ANFIS controller is designed to control the hybrid energy storage system HESS of a PV microgrid. HESS combined which combines the battery and super-capacitor (SC), and the performance of the ANFIS controller is compared with other existing controllers such as Q-leaning PI controller.
This paper proposes a novel smart EMS for DGs in island AC-MG based on MANFIS optimized by GA, and the main contributions are :
-
1.
a design of island MG combined from WT, PV, ESS and DGS is presented in details, controlled by EMS which is developed to manage the available energy of these sources efficiently according to variable load profile and available RES power, while The EMS decisions are updated by MANFIS technique.
-
2.
A design of MANFIS technique is implemented and trained by using dataset of 8760 samples that describes the proposed EMS behavior according to different values of (available RES power, demand power, and SOC). Where RES power values are calculated based on hourly meteorological data of MG location’s weather. Furthermore, the proposed MANFIS is also optimized by GA algorithm for achieving most optimum energy management in MG.
-
3.
The proposed system is implemented and simulated by using MATLAB-Simulink 2021 environment, and comparison is held between the accuracy results of system before-after using GA. Additionally, the proposed system is validated by applying Day-ahead case study on it.
The rest of this paper is organized as follows: section “Design of microgrid (MG)” presents the design of considered MG. A brief description of developed EMS is provided in section “MANFIS based energy management system (EMS)”, followed by simulation results and discussion in section “Results and discussion” the paper. Finally, concluding remarks appear in section “Conclusion” .
Design of microgrid (MG)
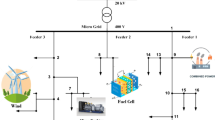
In this work, Gaza strip was selected to be a location for MG installation. The proposed AC MG works in island mode only, where its combined from Renewable Energy Sources (RES) based DG (wind and solar), and connected with 5 diesel-based generator units controlled by generator switching logic (GSL) within Diesel Generators System (DGS). MG is equipped with an Energy Storage System (ESS). ESS and DGS work in parallel as a backup system for MG loads at peak hours demand and low RES power production. The overall structure of MG is summarized in Fig. 4.
Renewable energy sources (RES) plants
In this work, the suggested MG integrates the power plants driven by renewable energy sources, the components of these plants were built in MATLAB Simulink environment including its equivalent circuits, mathematical models and efficiency curves of it’s power components.
Solar power plant (PV)
One of the most common renewable sources is solar energy, capable of meeting most of the challenges that confront the world38. It provides people with a safe and environmentally friendly energy source. Solar power systems capture the sunlight, converting it to electrical energy, and distributing it to the user in two operation modes: on-grid, and off grid39. Generally, solar power systems consist of photovoltaic (PV) panels connected to DC-AC inverter through DC-DC converter (on-grid), can be connected with a battery storage through bidirectional DCDC converter (off-grid)40.
The hourly values of solar output power in the suggested MG including the main expected system losses during generation and transmission are calculated by using a mathematical model of solar power plant (Fig. 5). It is based on a structural approach including solar array, DC cabling , PV inverters, and AC cabling between the inverter devices and main B.B of MG. The mathematical model takes solar radiation and ambient temperature as an input parameters, and produces the expected power that injected in grid as an output parameter41.
As shown in Fig. 5, the mathematical model of solar power plant components are:
(1) Solar array: its formed by photovoltaic (PV) panels connected in series and parallel. PV panel is a collection of PV cells, which can be used to absorb the sun’s rays and convert them into DC power through photovoltaic effect42.The hourly Maximum Power Point (MPP) voltage and current values of solar array are calculated by using the equivalent circuit of PV cell43, which is combined from light-generated current source (\(I_{ph}\)) connected in parallel with diode and resistance (\(R_p\)), and connected is series with resistance (\(R_s\)) as shown in Fig. 6.
\(I_{ph}\) is flowing and distributed through diode, \(R_p\), and \(R_s\), Diode I-V characteristics for a single module are defined by Eqs. (1) and (2)42:
where \(I_{D}\), and \(V_{D}\) are the diode current and voltage, respectively; \(I_{0}\) is the diode saturation current. nl is the ideality percent of diode; k is Boltzman constant = 1.3806e−23 J.K\(^{-}1\); q is the electron charge = \(1.6022^{-19} C\); T is the cell temperature (K); and \(N_{cell}\) is the number of cells connected in series in a module.
The suggested solar array in MG is combined from 1400 solar panels, distributed into 70 solar strings, where each string combined from 20 solar panels connected in series. The used solar panel is combined from 154 solar cells, there specifications illustrated in Table 1.
The hourly voltage and current values of solar array are measured according to the to the recorded data of solar irradiance and ambient temperature of Gaza Strip between 1995–202144, The hourly Maximum Power Point (MPP) voltage and current values are illustrated in Fig. 7.
According to array MPP voltage and current values, MPP power values of the suggested solar array are illustrated in Fig. 8.
(2) DC Cables: Its equivalent scheme consists of an active electrical resistor that represents the losses of DC cabling and connections. The current flow through this resistor results voltage drop and active losses. The cable equivalent resistance is determined by Eq. (3)45.
where R is the resistance in ohms; \(\rho\) is the resistivity of wire material in ohms per meter; L is the wire length in meter; and A is the conductor cross section area in square meter. The active losses of DC connection are determined by Eq. (4)46.
where P is the power loses in W; I is the current value.
(3) Solar inverter: Its a power electronic device that transforms the DC power output from solar panels (solar array) into AC power which is injected into the AC grid47. The conversion from DC power value (after passing the DC cables) to AC power including conversion losses is done by using efficiency curve which is given by the inverter factory (Fig. 9). Where efficiency curve is the relation between inverter power and its efficiency that describes the behavior of PV inverter43. It can be defined by Eq. (5).
where a–\(a_{n}\) are the efficiency coefficients. According to the proposed solar array size, 7 units of 100 kVA solar inverter are used.
Wind power plant (WT)
Solar power systems are sunlight dependent for gathering solar energy, therefore, solar power is unavailable in the night hours, as well as, in a cloudy and rainy days, which can have a noticeable effect on the efficiency of solar generated power. on the other hand, wind speed increases in winter days, and in night hours. The stronger wind, the more electricity is generated, so that solar and wind energy can complement each other48.
Wind turbines work on a simple principle, wind potential turns turbine blades which are connected to a rotor that spins the electrical generator, producing electricity injected in power grid. The wind power that passing perpendicularly through a circular area (turbine’s swept) is calculated by Eq. (6)49.
where \(P_{in}\) is the entered wind power to the turbine; \(\rho\) is the air density constant = to 1.225 \(kg/m^{3}\); A is the swept area; and v denotes the magnitude of the horizontal velocity.
The amount of produced electrical power from wind turbine is directly proportional with the swept area according to Eq. (7)48:
where \(P_{out}\) is the generated power from turbine; \(C_{p}\) is the turbine power coefficient, which can be calculated by Eq. (8)50.
where \(\eta _{b}\), \(\eta _{m}\); and \(\eta _{e}\) denote the blade aerodynamic, mechanical, electrical efficiencies, respectively.
In the current paper, the amount of produced electrical power by wind turbine is calculated at maximum value of \(C_{p}\) = 0.593 which is determined by Betz limit51. The suggested wind turbine specifications are illustrated in Table 2.
The produced wind power is also can be calculated from the efficiency curve of the suggested wind turbine (Fig. 10) by using MATLAB curve fitting tool51, then, an average is taken between the calculated values from the two methods. The efficiency curve equation of wind turbine is illustrated in Eq. (9).
where \(a_1\)–\(a_n\) and \(q_1\)–\(q_n\) are the efficiency curve coefficients. In the provided MG, 30 wind turbines are suggested , and the produced power by these turbines is calculated according to the wind speed forecasts, the wind speed and direction data at 10m above the ground is provided for a typical meteorological year, which are compilations of measured hourly data time series from 1998–2021, the data is measured by satellites for Gaza Strip location46. The harvested wind power of February month is illustrated in Fig. 11.
Backup system (BS)
BS have an important and diverse role in the proposed MG, it keeps the stability against uncontrollable components of MG system52. It combined from:
Energy storage system (ESS)
ESS is implemented to achieve the power balance between DGs produced power and loads consumed power by storing the surplus energy of RES at off-peak hours, and supply it at peak hours. it keeps the MG system stability against the main frequency and voltage fluctuations that can be caused due to the intermittent nature of RES (RES smoothing) and variable load profiles. Furthermore, it is used as a grid forming source in order to synchronize the DGs technology of MG53. ESS of the suggested MG combined from Lithium battery storage interfaced with the main B.B of MG through bidirectional inverter as shown in Fig. 12.
(1) Lithium Battery Storage: its the main component of ESS, consist of individual cells connected into modules and then into packs. the battery storage can be presented by an open circuit model54, which composes from an ideal voltage source (\(E_a\)) connected in series with a variable internal resistance (R) as shown in Fig. 13. Where the charge of the battery storage is determined by the SOC, which is the ratio of the real time capacity to the nominal capacity of the battery55, SOC can be determined by Eq. (10).
where SOC(t) is the soc of battery at time t; \(E_{Batt}(t)\) is the real time charge of battery; \(E_{Batt}^{Total}\) is the total charge capacity of battery. Lithium battery is also equipped with BMS, which works as a monitor device for battery status, monitors its SOC, ensuring its protection from over-charge/over-discharge, run within its capability and provides the best performance56.
The suggested battery of MG is combined from 10 modules of 100 kWH Lithium battery, forming a 1 MWH battery storage source.
(2) Bidirectional Inverter: It is a device that is used to regulate and monitor the power flow between a DC bus and an AC grid56. Worked for dual mode: when PV generation is higher than the load requirement, the inverter transfers the power from the connected AC grid to the DC. On the contrary, the inverter draws power from the AC grid to compensate the load requirement57. The conversion from DC power value of batteries to AC power including conversion losses is done by using efficiency curve which is given by the inverter factory as shown in Fig. 14. In the provided ESS, 5 devices of 250 kW bidirectional inverter connected to the battery set.
(3) DC Cables: Calculations of DC cables power losses are treated the same as AC and DC cables of solar power plant.
Diesels generator system (DGS)
DGS provides reliability for MG system by providing a steady source that supports electrical loads when RES and ESS cannot work. DGS can work in conjunction with ESS for supplying MG loads at peak hours.
In the considered MG, 5 units of diesel generator, have the same specifications, are connected in parallel forming a large capacity source, each generator has a power rating 312 kVA, 250 kW at 0.8 power factor (PF), voltage rating: 400 V, and 50 Hz frequency. Using multiple units of same rating diesel generators is suggested to increase the reliability of MG system and keep the stability of voltage and frequency of the system against large load changes. furthermore the future expansion of MG will be more flexible. The proposed unit commitment (UC) for Diesel generation systems (DGS) will determine the optimal start and stop times for each unit, as well as the power output of each unit to meet the required power value specified by the ED (MANFIS) system at the lowest possible cost. In other words, the UC will use the value of power requirement determined by the ED system to decide which units to operate, when to operate them, and at what level, taking into account various constraints and unit types. Figure 15 illustrates the schematic of the UC system.
Elements of the unit-commitment problem include a set of generating units with their cost/emission curves, a load profile to be satisfied, reliability constraints, financial constraints and time horizon along which decisions have to be made. The constraints that the decisions must meet include system requirements such as load balance and spinning reserve and unit limitations including generation and ramp-rate limits. To perform the optimization model of UC, there is need to transform the description of the problem as given above into a model that can be interpreted and solved by optimization engines. The goal of unit commitment is to find the optimal scheduling of generating units that minimizes the overall cost of operating the power system while meeting the load demand and satisfying the operational constraints. This is typically done using mathematical optimization techniques such as dynamic programming, mixed-integer linear programming, or other advanced optimization algorithms. There is a significant amount of research on unit commitment based on MILP formulations. MILP is a widely used optimization technique that can solve complex unit commitment problems by considering binary variables to represent the on/off status of generating units over a specified time horizon.
MANFIS based energy management system (EMS)
The main aim of the proposed EMS is to manage the available energy in MG system efficiently. It monitors the status of MG in real time, and optimizes the output power of DGS and ESS considering the load demand and available RES power. EMS achieves the power balance in MG as expressed below:
where \(P_{Load}(t)\) is the load demand power at time t; \(P_{RES}(t)\) is the available RES power at time t; and \(P_{BS}(t)\) is the power supplied by backup system at time t. \(P_{RES}(t)\) can be defined by the following equation:
where \(P_{pv}(t)\) is the available solar power at time t; and \(P_{wt}(t)\) is the available wind power at time t.
While, \(P_{BS}(t)\) can be defined by the following equation:
where \(P_{Batt}(t)\) is the power supplied by the battery storage; and \(P_{Gen}(t)\) denotes the power supplied by diesel generator.
In the proposed EMS, RES is used as a main source for covering the total power demand in MG. If the amount of total power demand exceeds RES power, EMS will supply the remaining power demand from a BS in parallel according to its sources constraints. While BS is combined from ESS and/or DGS . On the other hand, if the available RES power exceeds the total load consumption, EMS will store the surplus power of RES in Lithium batteries through bidirectional inverters considering its constraints.
According to system inputs, EMS arranges charging-discharging operation considering the following constraints:
-
1.
SOC should be remained within acceptable limits (Eq. (14))?, ensuring the battery’s life protection.
$$\begin{aligned}&SOC_{Batt}^{min}\le SOC(t)\le SOC_{Batt}^{max} \end{aligned}$$(14)where \(SOC_{Batt}^{min}\) is the minimum SOC limit of battery; and \(SOC_{Batt}^{min}\) is the maximum SOC limit of battery.
-
2.
Charging-Discharging operation is performed within charging-discharging limits (Eqs. (15, 16)) of the battery at off peak and on peak hours, respectively. Meanwhile, charging-discharging efficiency should be satisfied (Eq.(17)).
$$\begin{aligned}&P_{Charge}^{min}\le P_{Charge}(t)\le P_{Charge}^{max} \end{aligned}$$(15)$$\begin{aligned}&P_{Discharge}^{min}\le P_{Discharge}(t)\le P_{Discharge}^{max} \end{aligned}$$(16)$$\begin{aligned}&E_{Batt}^{t+1}=E_{Batt}(t)+P_{Charge}(t)\cdot \eta _{Charge}\cdot \Delta t+P_{Discharge}(t)/ \eta _{Discharge}\cdot \Delta t \end{aligned}$$(17)where \(P_{Charge}(t)\) and \(P_{Discharge}(t)\) are the charging and discharging power at time t, receptively; While \(P_{charge}^{min}\) and \(P_{charge}^{max}\) are the minimum and maximum charging power, receptively; \(P_{Discharge}^{min}\) and \(P_{Discharge}^{max}\) are the minimum and maximum discharging power, receptively; and \(\eta _{Charge}\) , \(\eta _{Discharge}\) are charging and discharging efficiency, respectively.
-
3.
It is not possible to charge and discharge the lithium battery at same operational time interval (Eq. (18))16.
where \(U_{charge}(t)\) and \(U_{discharge}(t)\) are the binary variable of battery charging and discharging, respectively. At low limits of lithium battery’s SOC (Eq. (14)), or at high ranges of load demand that exceed charging-discharging power rates in ESS (Eqs. (15, 16)); The diesel generator system is called for power supplying in parallel with lithium battery to heal MG system against the variable load demand, (achieving power balance and guarantee MG system stability). (in addition to guarantee the battery life time).
The required power value that supplied by DGS is determined by EMS, considering its low operating load power. according to that value (\(P_Gen\)), the GSL determines the number of diesel generator units to be turned on, considering its power operating rates, if the required power of the generator \(P_Gen\) system exceeds 70 of the first generator unit rating, the second unit is started and \(P_Gen\) is divided on them58. And When the \(P_Gen\) drops to 70 of the first generator rating, the auxiliary unit is shut down, in the other hand, if the \(P_Gen\) exceeds 70 of two generator units rating the third unit is started and \(P_Gen\) is divided on three generators, and so on. Generators can work interchangeably, The proposed EMS flowchart is summarized in Fig. 16.
Multiple ANFIS (MANFIS) deals with nonlinear systems effectively, without using the mathematical model of the controlled system plant. In this work, MANFIS is considered for implementing the proposed EMS scheme, it has three inputs and three outputs. MANFIS inputs are defined by \(P_{RES}(t)\), \(P_{Load}(t)\), and SOC(t). Whereas the outputs are defined by \(P_{Gen}(t)\), \(P_{charge}(t)\), and \(P_{discharge}(t)\).
MANFIS
MANFIS is an extension of the ANFIS (Adaptive Neuro-Fussy Inference System). However, ANFIS is a common and one of the prominent neuro-fuzzy systems. It is introduced by Jang in 1993, and based on Sugeno fuzzy model where Rk rule is formulated as:
where k is the rules number; \(\mu _{Ai}\) and \(\mu _{Bi}\) are the fuzzy membership functions; x1 and x2 are the system inputs; while, \(p_k\), \(q_k\), and \(r_k\) are linear parameters of consequent part of the kth rule. The basic architecture of ANFIS is illustrated in Fig. 17. It includes five main layers :
-
1.
Layer one performs the fuzzification operation; each node i is an adaptive node with a membership function such as triangular, gaussian, etc.
$$\begin{aligned}&\begin{array}{l} O_i^1 = \mu _{Ai}(x1) \\ O_i^1 = \mu _{Bi}(x2), \quad \forall i = 1,2,\ldots \end{array} \end{aligned}$$(20)where \(O_i^1\) is node i output result for layer one.
-
2.
Layer two obtains the firing strength (weight) for each rule using the following equation :
$$\begin{aligned}&O_i^2 = w_i = \mu _{Ai}(x1) \times \mu _{Bi}(x2), \quad \forall i = 1,2,\ldots \end{aligned}$$(21)where \(O_i^2\) is node i weight result for layer two.
-
3.
Layer three normalizes each rule weight from the previous layer, as shown below:
$$\begin{aligned}&O_i^3 = \overline{w_i} = \frac{w_i}{\sum w_i}, \quad \forall i = 1,2,\ldots \end{aligned}$$(22)where \(\overline{w_i}\) is the normalised weight, and \(O_i^3\) is the output result of layer three.
-
4.
Layer four represents the consequent part of fuzzy logic rule:
$$\begin{aligned}&O_i^4 = \overline{w_i} \times f_i = \overline{w_i} \times (p_k x1 + q_k x2 + r_k), \quad \forall i = 1,2,\ldots \end{aligned}$$(23)where \(p_k\), \(q_k\) and \(r_k\) are the trainable linear parameters; and \(O_i^3\) is the layer four output.
-
5.
Layer five performs the defuzzification operation; it sums up all outputs rules.
$$\begin{aligned}&O_i^5 = = \sum \overline{w_i} \times (p_k x1 + q_k x2 + r_k), \quad \forall i = 1,2,\ldots \end{aligned}$$(24)where \(O_i^5\) is the layer five output.
ANFIS gets its strength from combining between neural network learning capability and fuzzy logic representation ability together?. In other words, it overcomes the learning weakness of fuzzy logic and transparency lack of neural networks. In fact, although ANFIS is considered as a powerful tool, it suffers from the obvious Multiple Input Single Output (MISO) problem which limits ANFIS to be used in only single output applications. As a solution, MANFIS approach is proposed in Multiple Input Multiple Output (MIMO) applications as illustrated in Fig. 18; its architecture comprises multiple ANFIS structures which are concatenated together to produce all system outputs.
Results and discussion
The proposed system has been implemented by using Simulink 2021. Its input/output relationships and rules were performed according to the input/output training dataset. The data set is composed of 8760 samples, which is hourly data that can be occurred in one year. However, the dataset samples were divided randomly using a five-fold cross-validation strategy into training and testing sets, 70% training samples and 30% testing samples. All inputs and outputs values were normalized using the 0–1 range.
The design of the system went through three steps. Where the first step is designing EMS with a standard fuzzy interference system (FIS), with five linear membership functions. However, the results of FIS predictions were very poor through the whole three outputs of the system as shown in Fig. 19.
After that, The implanted fuzzy system was optimized using the ANN algorithm and formed the MANFIS system. While, the MANFIS settings were adjusted with hybrid optimization method, an error tolerance of zero. However, The MANFIS system provided high accuracy in the predicted values of DGS power as shown in Fig. 20. While the performance of MANFIS through the charging-discharging outputs still has lower accuracy in comparison with the predicted values of DGS power, and that related to the nature of DGS power values, which is more computable with the MANFIS algorithm.
And that led to go through the last step: MANFIS-GA, to increase the accuracy of the EMS system. The MANFIS was incorporated with a genetic algorithm for optimizing the prediction operation of MANFIS. The used GA parameters are illustrated in the Table 3.
MANFIS-GA provided a significant accuracy as shown in Fig. 21, resulting in the predicted values of the three outputs: Generator power, charging and discharging power, with very low errors. Furthermore, achieve the goals of EMS system effectively.
The accuracy percent was calculated through the testing samples at every step of design and illustrated in the Table 4. the proposed MANFIS-GA system have a highest accuracy value in comparing with FIS and ANFIS. Which referred to the MANFIS structure that Incorporated with GA algorithm, as well as, the used database that covers the hourly cases in a whole one year.
Once MANFIS-GA implementation has been completed, it has been used for implementing the desired structure of EMS control strategy. In order to examine the validity of our proposed model, the simulation of day-head (24 hours) case study is carried out. According to the weather meteorological data of proposed case study. The available RES power is illustrated in Fig. 22, and the power demand of MG is illustrated in Fig. 23.
As shown in Fig. 24. The proposed MANFIS determines the charging-discharging power within ESS constraints, and maintains the SOC of Lithium battery within healthy charge limits as shown in Fig. 25. When the load demand exceeds RES power (2:00–3:00) period, battery is used for supplying the load in parallel with RES. On the other hand, at low load, and high available RES power hours (8:00–16:00), EMS is completely dependent on RES for covering the load demand at these hours, and storing the surplus power considering charging constraints.
However, when the load demand exceeds RES power and battery SOC in period (4:00–7:00) or battery discharging rates in period (17:00–21:00), DGS incorporates with ESS for supplying the loads in parallel with RES. The use of ESS reduces the effects of loads and RES power variability The amount of DGS supplied power (\(P_Gen\)) is illustrated in Fig. 26. According to the amount of \(P_Gen\), DGS is switching the generator units by GSL as shown in Fig. 27.
Conclusion
In this work, a smart EMS is proposed for controlling the operation of the different DGs (WT, PV, ESS and DGS) of island MG including generation power in DGS and charging-discharging in ESS according to the variation of the power demand and RES power. Furthermore, improving MG system stability and reliability. While EMS is controlled by MANFIS technique with three inputs and three outputs, its rules are defined by 8760 samples, which summarize the proposed EMS scenario in a whole year.//
System modeling is performed by using MATLAB-Simulink, furthermore it tested with day-ahead case study for system validation. The simulation results demonstrates that the proposed MANFIS based EMS optimizes the usage of each energy source of the MG effectively considering its constraints and balance the consumed power with produced power. The proposed BS in MG plays a good role for minimizing the uncertainties related weather-dependent sources (RES) and variable loads. MANFIS technique control the multi-input multi-output EMS plant effectively, without using mathematical models of the proposed system, which decreases the system complexity that reduces computation time.
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Zohuri, B. Nuclear fuel cycle and decommissioning. In Nuclear Reactor Technology Development and Utilization 61–120 (Woodhead Publishing, 2020).
Krishnan, S. K., Kandasamy, S. & Subbiah, K. Fabrication of microbial fuel cells with nanoelectrodes for enhanced bioenergy production. In Nanomaterials 677–687 (Academic Press, 2021).
Aryal, N., Ottosen, L. D. M., Bentien, A., Pant, D. & Kofoed, M. V. W. Bioelectrochemical systems for biogas upgrading and biomethane production. In Emerging Technologies and Biological Systems for Biogas Upgrading 363–382 (Academic Press, 2021).
Moorthy, K., Patwa, N. & Gupta, Y. Breaking barriers in deployment of renewable energy. Heliyon 5(1) (2019).
Ganesan, S., Subramaniam, U., Ghodke, A. A., Elavarasan, R. M., Raju, K. & Bhaskar, M. S. Investigation on sizing of voltage source for a battery energy storage system in microgrid with renewable energy sources. IEEE Access 8. https://doi.org/10.1109/ACCESS.2020.3030729 (2020).
Bhattar, C. L. & Chaudhari, M. A. Energy management scheme for renewable energy source based DC microgrid with energy storage. In 2021 5th International Conference on Green Energy and Applications (ICGEA) 97–102. https://doi.org/10.1109/ICGEA51694.2021.9487610 (2022).
Hirsch, A., Parag, Y. & Guerrero, J. Microgrids: A review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 90, 402–411. https://doi.org/10.1016/j.rser.2018.03.0402018 (2018).
Elsayed, A. T., Mohamed, A. A. & Mohammed, O. A. DC microgrids and distribution systems: An overview. Electr. Power Syst. Res. 119, 407–417. https://doi.org/10.1016/j.epsr.2014.10.017 (2015).
Debouza, M., Al-Durra, A., EL-Fouly, T. H. & Zeineldin, H. H. Survey on microgrids with flexible boundaries: Strategies, applications, and future trends. Electr. Power Syst. Res. 205, 107765. https://doi.org/10.1016/j.epsr.2021.107765 (2022).
Bolurian, A., Akbari, H. & Mousavi, S. Day-ahead optimal scheduling of microgrid with considering demand side management under uncertainty. Electr. Power Syst. Res. 209, 107965. https://doi.org/10.1016/j.epsr.2022.107965 (2022).
Sami, M. S. et al. Energy management of microgrids for smart cities: A review. Energies 14(18), 5976. https://doi.org/10.3390/en14185976 (2021).
Cagnano, A. E. D. T., De Tuglie, E. & Mancarella, P. Microgrids: Overview and guidelines for practical implementations and operation. Appl. Energy 258, 114039. https://doi.org/10.1016/j.apenergy.2019.114039 (2020).
Bhavsar, Y. S., Joshi, P. V. & Akolkar, S. M. Simulation of microgrid with energy management system. In 2015 International Conference on Energy Systems and Applications 592–596 (IEEE, 2015). https://doi.org/10.1109/ICESA.2015.7503418
Saeed, M. H., Fangzong, W., Kalwar, B. A. & Iqbal, S. A review on microgrids’ challenges and perspectives. IEEE Access 9, 166502–166517. https://doi.org/10.1109/ACCESS.2021.3135083 (2021).
Topa Gavilema, Á. O., Álvarez, J. D., Torres Moreno, J. L. & García, M. P. Towards optimal management in microgrids: An overview. Energies 14(16), 5202. https://doi.org/10.3390/en14165202 (2021).
Elmouatamid, A. et al. Review of control and energy management approaches in micro-grid systems. Energies 14(1), 168. https://doi.org/10.3390/en14010168 (2020).
Jiang, T., Costa, L. M., Siebert, N. & Tordjman, P. Automated microgrid control systems. IET Cired Open Access Proc. J., 961–964. https://doi.org/10.1049/oap-cired.2017.1220 (2017).
Kaur, A., Kaushal, J. & Basak, P. A review on microgrid central controller. Renew. Sustain. Energy Rev. 55, 338–345. https://doi.org/10.1016/j.rser.2015.10.141 (2016).
Pourghasem, P., Seyedi, H. & Zare, K. A new optimal under-voltage load shedding scheme for voltage collapse prevention in a multi-microgrid system. Electr. Power Syst. Res. 203, 107629. https://doi.org/10.1016/j.epsr.2021.107629 (2022).
Sajadi, A., Kenyon, R. W. & Hodge, B. M. Synchronization in electric power networks with inherent heterogeneity up to 100% inverter-based renewable generation. Nat. Commun. 13(1), 2490. https://doi.org/10.1038/s41467-022-30164-3 (2022).
Rasheduzzaman, M., Bhaskara, S. N. & Chowdhury, B. H. Implementation of a microgrid central controller in a laboratory microgrid network. In 2012 North American Power Symposium (NAPS) 1–6 (IEEE, 2012). https://doi.org/10.1109/NAPS.2012.6336332
Dragičević, T. Model predictive control of power converters for robust and fast operation of AC microgrids. IEEE Trans. Power Electron. 33(7), 6304–6317. https://doi.org/10.1109/TPEL.2017.2744986 (2017).
Cheng, J., Duan, D., Cheng, X., Yang, L. & Cui, S. Probabilistic microgrid energy management with interval predictions. Energies 13(12), 3116. https://doi.org/10.3390/en13123116 (2020).
Alam, M. N., Chakrabarti, S. & Ghosh, A. Networked microgrids: State-of-the-art and future perspectives. IEEE Trans. Ind. Inform. 15(3), 1238–1250. https://doi.org/10.1109/TII.2018.2881540 (2018).
Al-Tameemi, Z. H. A., Lie, T. T., Foo, G. & Blaabjerg, F. Control strategies of DC microgrids cluster: A comprehensive review. Energies 14(22), 7569. https://doi.org/10.3390/en14227569 (2021).
Palizban, O. & Kauhaniemi, K. Hierarchical control structure in microgrids with distributed generation: Island and grid-connected mode. Renew. Sustain. Energy Rev. 44, 797–813. https://doi.org/10.1016/j.rser.2015.01.008 (2015).
Zhang, B., Dou, C. X., Yue, D., Zhang, Z. Q. & Ma, K. Distributed control strategy of microgrid based on the concept of cyber physical system. Electr. Power Compon. Syst. 47(1–2), 55–76. https://doi.org/10.1080/15325008.2018.1564227 (2019).
Zheng, L. & Weiye, D. A hierarchical control strategy for isolated microgrid with energy storage. In 2021 IEEE 1st International Power Electronics and Application Symposium (PEAS) 1–4 (IEEE, 2021). https://doi.org/10.1109/PEAS53589.2021.9628397
Villalón, A. et al. Predictive control for microgrid applications: A review study. Energies 13(10), 2454. https://doi.org/10.3390/en13102454 (2020).
Soshinskaya, M., Crijns-Graus, W. H., Guerrero, J. M. & Vasquez, J. C. Microgrids: Experiences, barriers and success factors. Renew. Sustain. Energy Rev. 40, 659–672. https://doi.org/10.1016/j.rser.2014.07.198 (2014).
Kong, X., Bai, L., Hu, Q., Li, F. & Wang, C. Day-ahead optimal scheduling method for grid-connected microgrid based on energy storage control strategy. J. Mod. Power Syst. Clean Energy 4(4), 648–658. https://doi.org/10.1007/s40565-016-0245-0 (2016).
Mehrdad, A. & Seyed, M. Locating and sizing of capacitor banks and multiple DGs in distribution system to improve reliability indexes and reduce loss using ABC algorithm. Bull. Electr. Eng. Inform. 10(2), 559–568. https://doi.org/10.11591/eei.v10i2.2641 (2021).
Salman, H., Mehrdad, A., Hassan, S., Ilhami, C. & El, M. Economic dispatch optimization considering operation cost and environmental constraints using the HBMO method. Energy Rep. 10, 1718–1725. https://doi.org/10.1016/j.egyr (2023).
Sayyaadi, H. Modeling, assessment, and optimization of energy systems-Chapter 8. In Real-time Optimization of Energy Systems Using the Soft-computing Approaches (Academic Press, 2021). https://doi.org/10.1016/B978-0-12-816656-7.00008-7
Elkerdany, M. S., Safwat, I. M., Yossef, A. M. M. & Elkhatib, M. M. Hybrid fuel cell/battery intelligent energy management system for UAV. In 2020 16th International Computer Engineering Conference (ICENCO) 88–91 (IEEE, 2020). https://doi.org/10.1109/ICENCO49778.2020.9357393
Bayhan, S. & Abu-Rub, H. Smart energy management system for distributed generations in AC microgrid. In 2019 IEEE 13th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG) 1–5 (IEEE, 2019). https://doi.org/10.1109/CPE.2019.8862356
Leonori, S., Martino, A., Mascioli, F. M. F. & Rizzi, A. ANFIS microgrid energy management system synthesis by hyperplane clustering supported by neurofuzzy min-max classifier. IEEE Trans. Emerg. Top. Comput. Intell. 3(3), 193–204. https://doi.org/10.1109/TETCI.2018.2880815 (2019).
Fekry, H. M., Eldesouky, A. A., Kassem, A. M. & Abdelaziz, A. Y. Power management strategy based on adaptive neuro fuzzy inference system for AC microgrid. IEEE Access 8(192087–192100), 2020. https://doi.org/10.1109/access.2020.3032705 (2020).
Tu, Y. et al. Research on lightning overvoltages of solar arrays in a rooftop photovoltaic power system. Electr. Power Syst. Res. 94, 10–15. https://doi.org/10.1016/j.epsr.2012.06.012 (2013).
Kumar, N. M., Subathra, M. P. & Moses, J. E. On-grid solar photovoltaic system: components, design considerations, and case study. In 2018 4th International Conference on Electrical Energy Systems (ICEES) 616–619 (IEEE, 2018). https://doi.org/10.1109/icees
Stanev, R. & Tanev, T. Mathematical model of photovoltaic power plant. In 2018 20th International Symposium on Electrical Apparatus and Technologies (SIELA) 1–4 (IEEE, 2018). https://doi.org/10.1109/siela.2018.8447173
Ibrahim, O., Yahaya, N. Z., Saad, N. & Umar, M. W. Matlab/Simulink model of solar PV array with perturb and observe MPPT for maximising PV array efficiency. In 2015 IEEE Conference on Energy Conversion (CENCON) 254–258 (IEEE, 2015). https://doi.org/10.1109/CENCON.2015.7409549
Dewangan, D., Mudliar, A., Deb, S., Banik, A. & Bhusnur, S. Fuzzy logic control for energy management in distributed generation paradigm. In 2021 International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT) 1–5 (IEEE, 2021). https://doi.org/10.1109/ICAECT49130.2021.9392448
Noda, T., Nakamatsu, T. & Mekaru, T. Measurement of cable resistance at high frequencies. IEEJ Trans. Electr. Electron. Eng. 10(1), 112–113. https://doi.org/10.1002/tee.22069 (2015).
Rozegnał, B., Albrechtowicz, P., Mamcarz, D., Rerak, M. & Skaza, M. The power losses in cable lines supplying nonlinear loads. Energies 14(5), 1374. https://doi.org/10.3390/en14051374 (2021).
Bourogaoui, M., Houari, A., Sethom, H. B. A. & Machmoum, M. A novel technique for online resonance frequencies monitoring based on wavelet transform for grid-connected solar inverters. Electr. Power Syst. Res. 199, 107417. https://doi.org/10.1016/j.epsr.2021.107417 (2021).
Rashid, S., Rana, S., Shezan, S. K. A., AB Karim, S. & Anower, S. Optimized design of a hybrid PV-wind-diesel energy system for sustainable development at coastal areas in Bangladesh. Environ. Prog. Sustain. Energy 36(1), 297–304. https://doi.org/10.1002/ep.12496 (2017).
Elnaggar, M., Edwan, E. & Ritter, M. Wind energy potential of Gaza using small wind turbines: A feasibility study. Energies 10(8), 1229. https://doi.org/10.3390/en10081229 (2017).
Xiong, B. et al. Short-term wind power forecasting based on attention mechanism and deep learning. Electr. Power Syst. Res. 206, 107776. https://doi.org/10.1016/j.epsr.2022.107776 (2022).
curvefitting/www.mathworks.com
Firas, M., Ayman, A., Ahmad, A.,, Hani At. Ahmed, A., Mehrdad, A. & Phatiphat, T. Optimal management of energy storage systems for peak shaving in a smart grid. Comput. Mater. Contin. 75(2), 3317–3337. https://doi.org/10.32604/cmc.2023.035690 (2023).
Anttila, S., Döhler, J. S., Oliveira, J. G. & Boström, C. Grid forming inverters: A review of the state of the art of key elements for microgrid operation. Energies 15(15), 5517. https://doi.org/10.3390/en15155517 (2022).
Wang, J. et al. Precise equivalent circuit model for Li-ion battery by experimental improvement and parameter optimization. J. Energy Storage 52, 104980. https://doi.org/10.1016/j.est.2022.104980 (2022).
Choudhury, S. Review of energy storage system technologies integration to microgrid: Types, control strategies, issues, and future prospects. J. Energy Storage 48, 103966. https://doi.org/10.1016/j.est.2022.103966 (2022).
Hajian, A., Styles, P. & Zomorrodian, H. Depth estimation of cavities from microgravity data through multi adaptive neuro fuzzy interference system. In Near Surface 2011-17th EAGE European Meeting of Environmental and Engineering Geophysics cp-253 (European Association of Geoscientists and Engineers, 2011). https://doi.org/10.3997/2214-4609.20144374
Şahin, M. & Erol, R. A comparative study of neural networks and ANFIS for forecasting attendance rate of soccer games. Math. Comput. Appl. 22(4), 43. https://doi.org/10.3390/mca22040043 (2017).
Peter, A. & Akshay, K. Impact of incorporating disturbance prediction on the performance of energy management systems in micro-grid. IEEE Access 10, 1109 (2020).
Acknowledgements
The paper was supported by the Jilin Provincial Department of Science and Technology under grant 20250102141JC, the Department of Education of Jilin Province under grants JJKH20230064KJ and JJKH20240084KJ, the Jilin Provincial Development and Reform Commission under grant 2022C045-11, the Beihua University Research and Innovation Project under grants [2023]009 and [2024]016.
Author information
Authors and Affiliations
Contributions
Y.M.C. and D.J.L. wrote the main manuscript text, M.A.S. and J.Q.Z. did modeling and simulation; Y.L.Z., J.N. and C.D. prepared equations and figures. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Cheng, Y., Zhang, J., Al Shurafa, M. et al. An improved multiple adaptive neuro fuzzy inference system based on genetic algorithm for energy management system of island microgrid. Sci Rep 15, 17988 (2025). https://doi.org/10.1038/s41598-025-98665-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-98665-x