Generation driven understanding of localized 3D scenes with 3D diffusion model

Abstract

In recent years, diffusion models have been widely used in 3D scenes-related work. However, the existing diffusion models primarily focus on the global structure and are constrained by predefined dataset categories, which are unable to accurately resolve the detailed structure of complex 3D scenes. This study therefore integrates Denoising Diffusion Probabilistic Models (DDPM) with Learning Dense Volumetric Segmentation from Sparse Annotation (3D U-Net) architecture fusion, a novel approach to local 3D scenes generation-driven understanding is proposed, namely a customized 3D diffusion model (3D-UDDPM) for local cubes. In contrast to conventional global or local single-structure analysis techniques, the 3D-UDDPM framework is designed to prioritize the capture and recovery of local details during the generation of localized 3D scenes. In addition to accurately predicting the distribution of the noise tensor, the framework significantly enhances the understanding of localized scenes by effectively integrating spatial context information. Specifically, 3D-UDDPM combines Markov chain Monte Carlo (MCMC) sampling and variational inference methods to reconstruct clear structural details in a stepwise backward inference manner, thereby driving the generation and understanding of local 3D scenes by internalizing geometric features as a priori knowledge. The innovative diffusion process enables the model to recover fine local details while maintaining global structural coherence during the gradual denoising process. When combined with the spatial convolutional properties of the 3D U-Net architecture, the modelling accuracy and generation quality of complex 3D shapes are further enhanced, ensuring excellent performance in complex environments. The results demonstrate superior performance on two benchmark datasets in comparison to existing methodologies.

Introduction

In the field of computer vision, accurately resolving the detailed structure of complex 3D scenes is consistently presented as a central challenge. Existing methods for 3D scene understanding mainly focus on the global structure and are restricted to predefined dataset categories^1,2. Such methods tend to ignore the richness and diversity of local details, as well as the flexibility and universality of local features in different scenes^3,4. Concurrently, the substantial data volume and computational resource constraints that may be imposed by processing 3D data from a global perspective render the focus on the understanding of local structural information particularly crucial^5,6.

In recent years, the development of deep learning techniques, especially the application of diffusion models, has led to the discovery of novel methods for learning the local 3D structure of complex scenes from limited data⁷. The Denoising Diffusion Probabilistic Models (DDPM)⁸ framework is a generative model with stable performance that contains both diffusion and denoising processes. It simulates a Markov chain that is gradually transformed from a Gaussian noise to a data distribution, thereby enabling the direct learning of the data distribution. This process is capable of generating rich structural details in a delicate way. However, when dealing with complex 3D data, the DDPM⁸ framework often lacks sufficient spatial context information to guide high-quality reconstruction⁹. To address this issue, this study incorporates the Learning Dense Volumetric Segmentation from Sparse Annotation (3D U-Net)¹⁰ architecture into the iterative denoising process of the DDPM⁸ framework. The 3D U-Net¹⁰ is a deep learning network designed for processing 3D images, which has excellent feature extraction and spatial context information capabilities to reconstruct accurate 3D morphology more efficiently.

The objective of this study is to mine and generate 3D structural information and prior knowledge in order to gain a deeper understanding of local scenes¹¹. To this end, a customized 3D diffusion model (3D-UDDPM) for local cubes has been developed, which allows for generation-driven understanding of local 3D scenes. This model is based on the DDPM⁸ framework and the 3D U-Net¹⁰ architecture. The model is capable of gradually recovering noiseless and clear 3D structures from the noise-added data. After deep iterative learning and data training, the internalized geometric features are used as a priori knowledge bridges¹² to complete the task of generating and understanding the local 3D scene. In the initial stage of model training, in order to enhance data diversity, enhance model generalization ability, and enhance model robustness¹³, we randomly extract multiple local cubes¹⁴ with sizes varying from 5% to 25% of the object boundary volume along the surface of the 3D object and voxelize¹⁵ them after selecting a random mesh of data from the ShapeNetCore.v2¹⁶ dataset. In particular, some of the randomly extracted local cubes may contain outliers that do not form a coherent structure of individual voxels. These outliers do not represent the real features of the local cubes, which are moderately optimized in the methodology and experiments to ensure the data quality¹⁷.

Experimental evidence indicates that this research method is highly effective in the deep mining of local 3D scenes, the generation-driven understanding of scene structure and semantic information, and the comprehensive grasp of complex scenes.

The principal findings of this study are as follows:

• In the case of voxelized local cubes, the framework is based on DDPM and incorporates an enhanced and optimized 3D U-Net architecture that focuses on local details as well as more accurate noise distribution learning capabilities.

• The DDPM framework is deeply integrated with the 3D U-Net architecture to leverage the stepwise backward inference mechanism of the diffusion process in conjunction with the spatial convolutional property of 3D U-Net, thereby facilitating the efficient processing and generation of local 3D object data.

• The framework not only enhances the quality and precision of localized 3D object generation but also offers a novel perspective for comprehending and constructing localized 3D scenes. This paves the way for a multitude of prospective applications in 3D scene generation and associated research domains.

Related work

3D datasets and global scenario analysis

Initial research concentrated on the utilisation of 3D datasets for the comprehension and analysis of global structures. Data-related works, such as the ShapeNetCore¹⁶ dataset initially proposed by Chang et al., comprise approximately 51,300 distinctive 3D models encompassing 55 common object classes, thereby furnishing a substantial resource for 3D object classification and recognition. Furthermore, Song et al.’s SUNCG dataset¹⁸ and Dai et al.’s ScanNet¹⁹ provide a substantial quantity of labeled data for indoor 3D scenes. Recently, the full-object 3D dataset OmniObject3D²⁰ has been proposed. It contains 6,000 scanned high-quality textured meshes with 190 categories, exhibiting accurate shape and geometric details, as well as realistic appearance. In the context of scene understanding models, particularly convolutional neural networks (CNN)²¹ and generative adversarial networks (GAN)²², there is evidence that they are capable of learning intricate feature representations from unprocessed 3D data. This enables their utilisation in a range of scene understanding tasks^2,23. For instance, research works such as PointNet¹, Habitat²⁴, and VLPrompt²⁵ demonstrate the effectiveness of learning useful features directly from point cloud or voxel data for the classification and semantic segmentation of 3D objects. However, these models primarily concentrate on global scene analysis²⁶, and the comprehension capacity of the various models is constrained by the training dataset⁶.

Localized scene understanding

The objective of localized 3D scene understanding is to achieve a high level of detail in the resolution of specific regions or objects within the scene. In order to enhance the generalisation capacity and resilience of the models, researchers have been investigating novel methodologies and model architectures to optimise the capture and utilisation of local details and contextual information within 3D data. For instance, the Dynamic Graph Convolutional Neural Network (DGCNN)³ and PointWeb⁹ have demonstrably enhanced the performance of models in 3D scene understanding tasks by improving the representation of local features. In the same year, DeepSDF²⁷, proposed by Park et al., and Occupancy Networks²⁸, proposed by Mescheder et al., accurately capture the details of complex 3D structures by learning continuous symbolic distance functions and implicit surface representations, respectively. Subsequently, Maturana and Scherer proposed VoxNet²⁹, a real-time object recognition system based on 3D convolutional neural networks that learns the features of objects directly from 3D point cloud data. This demonstrated the potential of deep learning for local 3D scene understanding. DeepPoint3D³⁰ focuses on processing unstructured 3D point clouds directly. Through deep metric learning, AutoSDF³¹ is able to learn 3D local descriptors and understand the distribution of 3D scenes. This is achieved by capturing complex patterns and structural transformations in 3D data using autoregressive transformers. OpenScene³² is capable of predicting the dense features of 3D reconstructed points independently of annotated 3D datasets. This enables the efficient identification of details in complex scenes. While these methods mitigate the limitations of datasets and computational resources to some extent⁶, there are still challenges in reconstructing and understanding complex scenes with high quality³³. StegaNERF³⁴ is a neural radiation field model for embedding invisible information, which is primarily employed for embedding invisible data in the three-dimensional generation process. This technique involves concealing the data within the generated 3D scene while maintaining the visibility of the scene. Pan et al.³⁵ proposed a method for 6-degree-of-freedom (6DoF) pose estimation from RGB images. This method was trained using a small amount of data and demonstrated strong generalization ability.

Deep learning in 3D scenes

The 3D U-Net¹⁰ architecture, proposed in 2016, represents an advanced deep learning framework designed for the purpose of volumetric medical image segmentation. The architecture represents a significant advancement over the classical U-Net³⁶ model, incorporating a 3D convolutional layer that enables the model to adapt to volumetric data of varying sizes and resolutions. This layer facilitates the efficient capture and utilization of spatial information throughout the volume, a capability that is essential for the effective segmentation of medical images. Prior work on 3D scenes has employed Generative Adversarial Networks (GAN)^22,37 or Variational Auto-Encoders (VAE)³⁸ to learn 3D shape representation distributions, including voxel meshes, point clouds, grids, and implicit neural representations. However, these methods demonstrate limited efficacy in complex scenes¹⁷. In recent years, diffusion modeling⁵ has emerged as a powerful generative model that significantly improves the performance of 3D data generation and reconstruction. As evidenced by studies such as Diffusionerf³⁹, HoloDiffusion⁴⁰, and Dit-3d⁴¹, diffusion models are capable of efficiently estimating scene-optimized gradient orientations and generating local 3D structures while maintaining data quality. Denoising diffusion probabilistic models (DDPM)⁸ have been extensively investigated in deep learning frameworks such as DiffRF⁴² and Diffuscene⁴³ due to their robust representation capabilities. DDPM models reconstruct the original data by simulating the backward diffusion process through incremental noise addition and subsequent denoising⁴⁴. This distinctive training strategy enables the model to capture the intrinsic distributional complexity and nuances of the data, while being applicable to 3D scenes⁴⁵. GaussianStego⁴⁶ proposes a steganography method based on generating 3D Gaussian point clouds to embed steganographic information in 3D scenes through the generated point clouds. The method utilizes a Gaussian distribution to encode 3D data and is able to embed information without altering the visibility of the scene.

Method

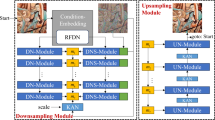
This study represents a novel approach to global and local single-structure analysis. It fuses the DDPM⁸ model with the 3D U-Net¹⁰ architecture to propose a customized 3D diffusion model specifically for voxelized local cubes. This model is capable of accurately estimating the noise tensor, correcting outliers, internalizing the generative understanding of local geometric features, and forming a priori knowledge to capture local structural details in complex 3D scenes in a more refined and comprehensive way. Furthermore, this method incorporates data enhancement and diversification strategies in the pre-data stage, which further enhances the model’s generalizability and generative understanding. The overall process block diagram is depicted in Fig. 1.

Fig. 1

Overview of 3D-UDDPM. In this research method, the ShapeNetCore.v2¹⁶ dataset is selected for analysis. The dataset is then randomly sampled and subjected to data enhancement operations, including voxelization, before being fed into the 3D-UDDPM. The 3D-UDDPM model incorporates non-uniform Gaussian noise into 3D objects within a Markov Chain framework. Subsequently, a bespoke 3D U-Net architecture is employed to predict the noise distribution, thereby facilitating precise denoising. This methodology enables the generation and comprehension of 3D localized scenes.

Preparation of data

Dataset selection

In this study, the ShapeNetCore.v2¹⁶ dataset is selected as the object of study. A Randomized Grid Sampling (RGS)^1,2,47 strategy is employed to extract different subsets of 3D objects from the dataset. This is done in order to ensure the diversity of data samples and to reduce the computational load. First, the 3D bounding box $\Omega$ of the ShapeNetCore dataset (with a spatial extent of $\Omega \subseteq \mathbb {R}^3$) is established, and $\Omega$ is uniformly divided into $\Delta x,\Delta y,\Delta z$ grid cells of size $\Delta x\times \Delta y\times \Delta z$ in their corresponding dimensions. Then, random grid sampling is performed to obtain the subset of 3D objects used for training, as follows:

$$\begin{aligned} & S=\{p_i| p_i\text { is randomly selected from }\Omega _{ijk},\forall \Omega _{ijk}\in \textrm{Grid}(\Omega ,\Delta x,\Delta y,\Delta z),\mathrm {~with~}P(\Omega _{ijk})=\rho \} \end{aligned}$$

(1)

where $\text {S}$ denotes the subset of 3D objects extracted, $p_{i}$ is a point extracted from grid cell $\Omega _{ijk}$, $Grid(\Omega ,\Delta x,\Delta y,\Delta z)$ is an operation that splits $\Omega$ into smaller grids, $P(\Omega _{ijk})$ is the probability that a grid cell is extracted as a subset. Given the substantial collection of 3D objects represented by the ShapeNetCore dataset, it is essential to calibrate the sampling rate, denoted by $\rho$, in order to optimize the trade-off between geometric complexity and computational resources. This calibration process enables the attainment of an optimal balanced value for $\rho$ , which exhibits a range from 0.28 to 0.72 floating.

Local cube extraction

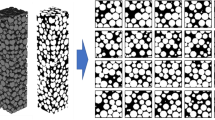
For the selected subset of 3D objects, multiple local cubes with sizes varying from 5% to 25% of the object boundary volume are randomly extracted along their surfaces, as illustrated in Fig. 2. This volume range is verified by considering the complexity of the object and the level of detail of the local scene understanding. It is important to note that too small local cubes voxelized with insufficient features and increased sparsity will increase the model learning effectiveness. Once a 3D object $\text {O}$ and its boundary volume $V_{O}$ have been defined, the volume $V_{cube}$ of the local cube can be calculated as follows:

$$\begin{aligned} & V_{cube}=l_{cube}^{3}=\lambda \cdot V_{o} ,\quad \lambda \in [\lambda _{\min }=0.05,\lambda _{\max }=0.25] \end{aligned}$$

(2)

where $l_{cube}$ is the local cube side length and $\lambda$ is a randomly selected volume factor.

Fig. 2

Local cube. As illustrated in the accompanying figure, a number of local cubes with a volume size of 5%-25% of the original object boundary volume are randomly selected on the 3D object.

Subsequently, a randomly selected sampling point on the surface $S_{o}$ of the 3D object $\text {O}$ is used as the local cube center $\text {c}$, and an octree collision checking mechanism^48,49 $\textrm{Insert}(\textit{cube})$ is introduced, viz:

$$\begin{aligned}&p_c\sim \mathcal {P}_{\mathcal {S}_o}, \end{aligned}$$

(3)

$$\begin{aligned}&\quad \text {Insert}(cube)={\left\{ \begin{array}{ll}\text {true}& \text {if OctreeIntersect}(cube,\\ & \text {Octree})=\text {false}\\ \text {false}& \text {otherwise}\end{array}\right. }. \end{aligned}$$

(4)

in this context, $p_{c}$ is a function that obeys a probability distribution function $\mathcal {P}_{\mathcal {S}_0}$. This ensures that the selection probability is proportional to the local density of the surface region. $\text {Insert(cube)}$ is a Boolean function that returns a value indicating whether the local cube is successfully inserted into the octree. OctreeIntersect(cube, Octree) is a function that checks whether the cube intersects with all the cubes that already exist in the octree. Consequently, these local cubes are capable of representing disparate local geometric characteristics of the model, thereby capturing local geometric information across a range of scales. This approach ensures inter-sample independence and the quality of local structure samples.

Voxelization and data enhancement

In consideration of the intrinsic characteristics of the 3D U-Net¹⁰ architecture, random rotation and dilation transformations are performed subsequent to the conversion of the local cubes into voxel cubes with a resolution of 32x32x32. This step facilitates a transition from a continuous geometric space to a discrete voxel cube representation, which enhances the model’s generalizability and resilience when confronted with intricate 3D scenarios.

Rendering depth and normals

It is necessary to render depth and normal maps of localized cubes at multiple viewpoints^50,51. The rendering of the parallax map from the viewpoints as illustrated in Fig. 3 simultaneously performs the computation of the piecewise normals, resolves the surface properties of the local cube, quantifies the surface details, understands its geometrical complexity, and evaluates the geometrical fidelity of the voxelization and data enhancement.

Fig. 3

A depth map and a normal map are two essential components of the 3D rendering process. The rendering of localized cubes at multiple angles serves to ensure the geometric fidelity of the localized cubes.

The preceding steps result in the acquisition of a voxelized local cube for training purposes. This data will henceforth be referred to as the local cube, and will be utilized in subsequent sections of this study.

3D-UDDPM

The 3D diffusion model, based on the DDPM⁸ framework and incorporating the properties of the 3D U-Net¹⁰ architecture, employs an iterative denoising process to recover a clear local 3D structural model, as illustrated in Fig. 4. Thereafter, the model utilises the internalised geometric laws to analyse the local structure and achieve an accurate generative understanding of the local 3D scene.

Fig. 4

The 3D-UDDPM. The Markov chain is complete, beginning with a local cube devoid of noise and subsequently injecting inhomogeneous Gaussian noise while embedding the time step $\text {t}$ until the entire chain is completely injected with noise. Reverse inference is then performed to estimate the noise $\varepsilon _{\theta }(x_{t},t)$ at a time step using the learned noise distribution, gradually recovering normal, clearly localized three-dimensional objects.

In particular, due to the possibility that the local cube may contain some outlier points^48,52,53, the local cube is now subjected to dynamic 26-neighborhood connectivity detection⁵⁴ and marked with initial outlier points $O_{\textrm{initial}}$. This facilitates the subsequent denoising penalties and improves the data purity, i.e.:

$$\begin{aligned}&{\left\{ \begin{array}{ll}\mid R(\nu _s)\mid =\sum _{r\in R(\nu _s)}1\\ O_{\textrm{initial}}=\{\nu _s\mid \mid R(\nu _s)\mid <\tau \cdot \mid R(\nu _s)\mid \}\end{array}\right. } \end{aligned}$$

(5)

where, $\text {R}$ represents the total number of voxels present within the specified local cube. Similarly, $\nu _{s}$ denotes the No. s voxel, $|R(\nu _s)|$ signifies the number of voxels within the neighborhood of $\nu _{s}$, and $\tau \approx 0.1$ serves as the dynamic scaling factor.

The process of diffusion

In this research project, given the potential for uniform noise to obscure crucial structural details and the considerable computational resources required, a non-uniform noise distribution strategy based on spatial location is presented as a means of introducing varying noise levels at the edges of the localized cube in comparison to the interior^55,56.

Firstly, in order to account for the spatial location and local structural features of different voxels, a spatial adjustment function $c_{t}$ is employed to control the noise weighting factor of each voxel, while a local feature-dependent covariance function $\Sigma$ is introduced to adjust the noise sensitivity:

$$\begin{aligned}&c_{t}(i,j,k)=1-\alpha \cdot e^{-\lambda d(i,j,k)},\Sigma (x_{t-1},\phi )=\beta _{t}\cdot I+\gamma \cdot F(x_{t-1}). \end{aligned}$$

(6)

where, d(i, j, k) represents the distance of a voxel to the nearest surface or localized cube edge. $\alpha$ and $\lambda$ are moderating parameters that influence the impact of distance on the noise level. $F(x_{t-1})$ denotes the value of the contribution to the variance, which is calculated based on the local features of the voxel $x_{t-1}$. $\gamma$ is the weight factor, which is moderated by the parameter $\varvec{\phi }$. $\varvec{I}$ is the unit matrix, and $\varvec{\beta }_t$ represents the noise factor. Furthermore, a series of experiments were conducted to ascertain the most effective combinations of empirical values for the 3D reconstruction task. In these experiments, the parameter $\alpha$ was varied from 0.1 to 0.7, while the parameter $\lambda$ was set from 0.1 to 1.0. The optimal parameter values that achieved the optimal balance between local feature preservation and noise control were determined to be $\alpha$ = 0.6 and $\lambda$ = 0.55.

Once more, $\varvec{\beta }_t$ is a smooth increment, there:

$$\begin{aligned}&\beta _t=\beta _{\min }+(\beta _{\max }-\beta _{\min })\cdot \frac{(e^{(t/T\cdot \log (\frac{\beta _{\max }}{\beta _{\min }}))}-1)}{e^{\log (\frac{\beta _{\max }}{\beta _{\min }})}-1)} \end{aligned}$$

(7)

where, the starting value of the noise growth sequence, denoted by $\beta _{\min }\approx 0.0001$, represents the initial level of noise in the system. The maximum value of the noise growth sequence, represented by $\beta _{\max }\approx 0.02$, is the highest level of noise observed during the diffusion process. The total number of diffusion steps, represented by $\text {T}$, is the cumulative number of steps taken by the noise. The current step, represented by $\text {t}$, is the step in the diffusion process that is currently being considered. The variance retention rate, represented by $\alpha _{t}=1-\beta _{t}$, is the proportion of noise variance retained in the system.

The rapid introduction of noise early in the diffusion process and its gradual stabilization in the later stages of the iteration allows the model to handle the denoising step in a more detailed manner. This is because the model can observe the noise at different stages of its evolution, allowing it to identify patterns and trends in the noise.

In the event that $x_0[i,j,k]$ represents the original, noise-free voxel data of the local cube, the voxelized local cube is defined by the addition of noise at time step $\text {t}$, i.e.:

$$\begin{aligned} x_{t}[i,j,k]=\sqrt{1-\beta _{t}}\cdot x_{t-1}[i,j,k]+c_{t}(i,j,k)\cdot \varepsilon _{t}[i,j,k]\cdot \sqrt{\Sigma (x_{t-1}[i,j,k],\phi )} \end{aligned}$$

(8)

in this context, $\varepsilon _{t}[i,j,k]\sim \mathcal {N}(0,1)$ represents the noise sampled at time step $\text {t}$ under a Gaussian distribution. It should be noted that due to the three-dimensionality of the voxel data and the large number of parameters in Eq. (8), $x_{0}[i,j,k],x_{t}[i,j,k],x_{t-1}[i,j,k],\varepsilon _{t}[i,j,k]$ is denoted as $x_{0},x_{t},x_{t-1},\varepsilon _{t}$, respectively, to simplify the representation.

Accordingly, the diffusion process of a localized cube is described as follows:

$$\begin{aligned} q(x_{1:T}\mid x_0)=\prod _{t=1}^Tq(x_t\mid x_{t-1}), \end{aligned}$$

(9)

where, $x_{1:T}$ represents the sequence of all data points from time step 1 to T, whereas $q(x_t\mid x_{t-1})$ denotes the conditional probability distribution of the localized cube state $x_{t}$, conditioned on the localized cube state $x_{t-1}$, at time step $\text {t-1}$. This distribution is defined as follows:

$$\begin{aligned} q(x_t\mid x_{t-1})=\mathcal {N}(x_t;\mu (x_{t-1},\phi ),\Sigma (x_{t-1},\phi )). \end{aligned}$$

(10)

in this context, $\mathcal {N}$ represents a Gaussian distribution, while $\mu$ denotes a mean value function that is controlled by the voxel $x_{t-1}$ position, local features, and parameter $\varvec{\phi }$.

The entire process can be described as a Markov chain, whereby the data is initially clear but subsequently becomes completely noisy.

Denoising processes

In regard to the denoising process, the DDPM⁸ framework offers a robust foundation for the generation of 3D structural models. However, it is still constrained in its ability to accurately recover fine local cubic details. For this reason, this study introduces a customized 3D U-Net¹⁰ architecture, which utilizes its unique “U-shaped” multiresolution network architecture to receive the noisy voxel cubes and their noise levels in each denoising step to achieve accurate denoising. The training and sampling process is shown in Algorithm 1. In our model, the 3D U-Net serves not only as a noise predictor but also as a conduit for conveying crucial spatial data regarding the local structure in each iteration. It eliminates some outliers from the model, thereby assisting the DDPM⁸ framework in more accurately predicting the state of each voxel in the denoising step. The conditional probability distribution of the denoising process is Gaussian, i.e.:

$$\begin{aligned} p_{\theta }(x_{t-1}\mid x_{t})=\mathcal {N}(x_{t-1};\mu _{\theta }(x_{t},t),\sigma _{\theta }^{2}(x_{t},t)I) \end{aligned}$$

(11)

where, in order to reduce the prediction error, the variance $\sigma _{\theta }^{2}(x_{t},t)$ is generated by 3D U-Net as a constant. The product of cumulative variance retention $\bar{\alpha }_t=\Pi _{s=1}^t\alpha _s$ and the mean $\mu _\theta (x_t,t)$ is generated by the following equation:

$$\begin{aligned} \mu _\theta (x_t,t)=x_t-\sqrt{1-\bar{\alpha }_t}\varepsilon _\theta (x_t,t) \end{aligned}$$

(12)

where, the computing method employs a multilayer 3D convolution, coupled with bulk normalization and ReLU activation functions, to process high-dimensional features and predict noise. This enables the model to meticulously predict the dynamics of the denoising process at each iteration step.

And there’s more:

$$\begin{aligned} x_{t-1}=\frac{1}{\sqrt{\alpha _{t}}}\Bigg (x_{t}-\frac{1-\alpha _{t}}{\sqrt{1-\bar{\alpha }_{t}}}\varepsilon _{\theta }(x_{t},t)\Bigg ) \end{aligned}$$

(13)

In this context, $\alpha _{t}$ represents the diffusion coefficient associated with time step $\text {t}$. Similarly, $\bar{\alpha }_t$ denotes the cumulative product of all noise levels up to the current time step, while $\varepsilon _{\theta }(x_{t},t)$ signifies the prediction of the noise by 3D U-Net $f_{\theta }$ at time step $\text {t}$.

Algorithm 1

3D-UDDPM reverse process

Figure 5 illustrates the customized 3D U-Net architecture for predicting the local cube noise $\varepsilon _\theta (x_t,t)$ and optimizing the data, comprising a total of approximately 4.75 million voxels. First, the voxel data $\text {x}$ and time step $\text {t}$ of the local cube with added noise are input for normalization. The voxel data features are then extracted using operations such as a 3x3x3 convolution kernel with step 1, 3x3x3 max pooling with step 2, batch normalization, and ReLU activation in the encoding phase. Subsequently, a dropout layer is added after the convolution of the bottleneck layer. The dropout process randomly turns off some of the neurons in the network, as the bottleneck layer contains the most abstract representation of the features in the network, i.e.:

$$\begin{aligned} {\left\{ \begin{array}{ll}H=\operatorname {Re}LU(BN(Con\nu 3D(X)))\\ H'=H\odot M\end{array}\right. } \end{aligned}$$

(14)

where, $\text {H}$ represents the voxel feature mapping output derived from the bottleneck layer. $\text {M}$ is a randomized binary mask matrix that is isomorphic to $\text {H}$ and determines whether the elements are retained or discarded. Finally, $\odot$ denotes the element multiplication. This approach effectively reduces overfitting, thereby enhancing the network’s robustness. The decoding stage is then initiated, utilising a 2x2x2 transposed convolutional kernel with a step size of 2. The jump connection combines context and spatial information layer by layer. Following this, the noise penalty function is fused with outlier processing after three layers of convolutional block, i.e.:

$$\begin{aligned} L_{\textrm{noise}}=\sum _{s=1}^Rw_s\cdot \max (0,\hat{V}_s-V)\cdot (1-y_s)\cdot \textbf{1}_{\{\nu _s\in O_{\textrm{initial}}\}} \end{aligned}$$

(15)

in this context, $\hat{V}_s$ represents the probability that the predicted numbered voxel, designated $\text {s}$, is noise. Similarly, $\mathcal {Y}_{s}$ denotes the true label of voxel $\text {s}$, while $\text {V}$ signifies the noise probability threshold. Additionally, $w_{i}$ represents the structural weight coefficient, and $\textbf{1}_{\{\nu _s\in O_{\textrm{initial}}\}}$ serves as the indicator function. A value of 1 is assigned when voxel $v_{s}$ is identified as an initial set of outlier points $O_{\textrm{initial}}$, and a value of 0 is assigned when it is not. To ensure data integrity, the intersection of outlier points from the 26 neighborhood detection⁵⁴ results and the noise penalty function results is selected for effective penalty, i.e.:

$$\begin{aligned} O_{\textrm{final}}=O_{\textrm{initial}}\cap \{v_{s}| L_{\textrm{noise}}(v_{s})>\theta \} \end{aligned}$$

(16)

where, $\theta$ is the noise penalty threshold. Given the model’s emphasis on localized regions, a cross-validation procedure during training is employed to determine the optimal threshold value of 0.12, with the objective of enhancing the precision of noise identification.

Ultimately, the voxel data features are recovered by combining the Sigmoid activation function with other elements to obtain a prediction noise tensor with the same dimensions, as follows:

$$\begin{aligned} \varepsilon _\theta (x_t,t)=W*H+\text {g} \end{aligned}$$

(17)

In this context, the variables $\text {W}$, $\text {g}$, and $\text {*}$ represent the convolutional layer weight matrix, the bias vector, and the convolution operation, respectively, which accomplishes the conversion of each voxel feature to the prediction noise $\varepsilon _\theta (x_t,t)$.

Fig. 5

Customized 3D U-Net. The Markov chain is complete, beginning with a local cube devoid of noise and subsequently injecting inhomogeneous Gaussian noise while embedding the time step $\text {t}$ until the entire chain is completely injected with noise. Reverse inference is then performed to estimate the noise $\varepsilon _{\theta }(x_{t},t)$ at a time step using the learned noise distribution, gradually recovering normal, clearly localized three-dimensional objects.

The objective of the denoising process is to reverse the effects of the diffusion process. This involves predicting the noise introduced during the diffusion process at each time step and then removing this noise from the noisy data. To achieve this, a denoising loss function, $L_{denoise}(\theta )$, is required to reduce the discrepancy between the predicted noise, $\varepsilon _\theta (x_t,t)$, and the true noise, $\varepsilon _{t}$, as follows:

$$\begin{aligned} \begin{aligned}&L_{denoise}(\theta ) \\ &=\mathbb {E}_{q}\Bigg [\frac{1}{2\sigma _{t}^{2}}\parallel \tilde{\mu }_{t}(x_{t},x_{0})-\mu _{\theta }(x_{t},t)\parallel ^{2}\Bigg ]+C \\&=\mathbb {E}_{t,x_{0},\varepsilon }\left[ \frac{1}{2\sigma _{t}^{2}}\parallel \tilde{\mu }_{t}\left( x_{t}(x_{0},\varepsilon ),\frac{1}{\sqrt{\alpha _{t}}}(x_{t}(x_{0},\varepsilon )-\sqrt{1-\alpha _{t}}\varepsilon )\right) -\mu _{\theta }(x_{t}(x_{0},\varepsilon ),t)\parallel ^{2}\right] +C \\&=\mathbb {E}_{t,x_{0},\varepsilon }\left\lceil \frac{1}{2\sigma _{t}^{2}}\parallel \frac{1}{\sqrt{\alpha _{t}}}x_{t}(x_{0},\varepsilon )-\frac{\beta _{t}}{\sqrt{1-\alpha _{t}}\varepsilon }-\mu _{\theta }(x_{t}(x_{0},\varepsilon ),t)\parallel ^{2}\right\rceil +C \end{aligned} \end{aligned}$$

(18)

where, the predicted mean, denoted by $\tilde{\mu }_{t}$, represents the expected value of the dependent variable. The constant term, denoted by $\text {C}$, is a parameter that is independent of the independent variable, $\theta$. This term gradually recovers the original, unadulterated data.

Data-driven 3D a priori internalization

With training, 3D-UDDPM learns iteratively from a substantial corpus of localized cube data, completing the Markov chain process from the injection of noise to the comprehension of the noise distribution $\varepsilon _\theta (x_t,t)$. Over time, it gradually builds up an in-depth generative understanding of potential 3D feature bodies in the real world. This generative understanding translates into a priori knowledge within the model, enabling the model to predict and generate new localized cube structures that conform to real-world geometric laws.

Experiments

At the outset of this study, given the distinctive attributes of the dataset and the necessity of transforming from 2D pixels to 3D voxels for the baseline model DDPM, as well as the importance of 3D reconstruction in the subsequent phase, the methodology was devised following a comprehensive array of experimental evaluations^8,57,58. To ensure the stability and accuracy of the experimental data, an epoch of 1000 is set and saved every 10 rounds of training. The Adam optimizer is introduced for adaptive learning to ensure that the optimal weight parameters are obtained. Subsequently, a series of ablation experiments and comparison experiments were conducted, and the training and running were all based on the PyTorch method on an NVIDIA RTX 3060 graphics card.

The evaluation metrics included are as follows:

• Peak Signal-to-Noise Ratio (PSNR)⁵⁹: This metric quantifies the discrepancy between the shape of the generated local 3D scene and the ground truth by calculating the peak signal-to-noise ratio. The larger the value, the more detailed the generated effect.

• Structural Similarity (SSIM)⁶⁰ is a metric that assesses the visual similarity between the generated local 3D scene and the ground truth. It is calculated by combining brightness, contrast, and structural information. A higher value indicates a greater degree of visual similarity.

• Learned perceptual image patch similarity (LPIPS)⁶¹ is a deep learning-based perceptual image similarity index. A smaller value indicates a greater degree of similarity between the generated local 3D scene and the ground truth.

• Intersection over Union (IoU)⁶² is a measure of occupancy similarity between the shape of the generated local 3D scene and the ground truth. In this study, the voxel-level IoU score is employed to calculate the consistency between the samples of the generated local 3D scene and the ground truth.

The results of the 3D-UDDPM generation comprehension task are presented in Fig. 6.

Fig. 6

Visualization results. The experiments conducted for this study, both in terms of visualization results and evaluation metrics, yielded excellent generative understanding outcomes. Additionally, the removal of outliers proved to be highly beneficial for comprehending local 3D scenes.

Verification experiment

In this section, we conduct validation experiments on additional, real datasets. The ShapeNetCore.v2¹⁶ dataset was selected as the dataset before preprocessing for this study due to its large number and inclusion of numerous varieties. While the training and validation process achieved relatively excellent generative comprehension results, further analysis is necessary to demonstrate the feasibility of the methodology of this study. To demonstrate the feasibility of the methodology employed in this study, the dataset was pre-processed using a high-quality, real scanned 3D object from the OmniObject3D²⁰ dataset. Following this, the pre-processing was evaluated further, and a self-comparison of the two datasets is presented in Table 1.

Table 1 Comparison of ShapeNetCore.v2¹⁶ dataset with OmniObject3D²⁰ dataset in terms of number and categories.

The methodology employed in this study pertains to the preprocessed local cubes; consequently, the validation experimental process does not necessitate differentiation according to categories. The validation experiments continue to employ a random grid to select distinct classes of local cubes among the 6,000 models, thereby ensuring that the experimental outcomes are more compelling. The quantitative analysis results of the 3D-UDDPM model under different datasets are presented in Fig. 7. It can be observed that high-quality differences and precise generation performance are achieved on both the noisy real dataset and the corrupted synthetic dataset. Also, ablation experiments were conducted for the noise addition strategy by comparing the uniform noise with the non-uniform noise in this method, the results are shown in Table 2, which verifies the superiority of the non-uniform noise strategy.

Table 2 Comparing uniform vs. non-uniform noise schedules.

Fig. 7

Results of evaluation indicators. In order to enhance the visual representation of the results, the SSIM outcomes are multiplied by 10, the LPIPS outcomes are multiplied by $10^2$, and the IoU outcomes are multiplied by 10.

Ablation experiment

The advantages of this method are demonstrated by a comparison of the results of experiments conducted using the 3D-UDDPM model, which has been customized for the method employed in the present study, with the results obtained from a model of the native 3D U-Net¹⁰ architecture that has been fused with the DDPM⁸ framework. The native 3D U-Net¹⁰ architecture was fused with the DDPM⁸ framework to predict the noise tensor. This resulted in the inclusion of a large number of outliers in the noise, the loss of high-frequency details, and a reduction in the evaluation metrics, specifically the PSNR, which decreased by 3.72, and the SSIM, which decreased by 0.145. The LPIPS metric was elevated by 0.089, the IoU metric was reduced by 3.64, and the qualitative visualization results are shown in Fig. 8, which demonstrated a lack of clarity in the comprehension of the generation of the potential space.

Fig. 8

Experimental results of model visualization with native 3D U-Net architecture combined with DDPM framework. The visualization results demonstrate that there is still considerable scope for improvement in generative understanding. In addition, some of the local cubes exhibit excessive or insufficient denoising processing.

Comparison experiments

In conjunction with this study, the dataset is unified with the preprocessed ShapeNetCore.v2¹⁶ dataset, which enhances the accuracy of the evaluation. Comparison experiments were conducted to assess generative understanding models with 3D objects as inputs, as the comparison of other generative models was not sufficiently convincing.

$\pi$-GAN (Periodic Implicit Generative Adversarial Networks for 3D-Aware Image Synthesis)⁶³ is a generative adversarial network (GAN^22,37) optimized for 3D image synthesis. It is centered on the idea of representing a 3D scene by means of a periodic implicit function, which is capable of generating images with 3D perception. $\pi$-GAN⁶³ employs an Implicit Neural Representation, namely a neural network that implicitly represents the surface of a 3D object. The fundamental concept is to represent the 3D scene through periodic implicit functions, which can facilitate the perception of the 3D scene. $\pi$-GAN⁶³ utilizes an Implicit Neural Representation to map a low-dimensional latent vector into a high-dimensional space, thereby enabling the generation of continuous 3D scene objects.

EG3D (Efficient Geometry-Aware 3D Generative Adversarial Networks)⁶⁴ represents another efficient 3D generative adversarial network that places a particular emphasis on the perception and representation of geometric information. The model optimizes 3D scene details by combining local geometric features and image features. EG3D⁶⁴ employs geometric information from multiple viewpoints to ensure the generated 3D images are consistent across different viewpoints. Additionally, it optimizes both computational resources and generation speed, which is more practical in real 3D scene understanding.

DiffRF (Differentiable Radiance Fields)⁶⁵ represents 3D scenes through the use of differentiable radiance fields. In contrast to traditional implicit representations, DiffRF⁶⁵ employs ray tracing and differentiable rendering techniques to generate realistic 3D scenes. Its highly flexible representation capability allows for the efficient generation of complex scenes and detailed 3D objects.

AutoSDF (Shape Priors for 3D Completion, Reconstruction and Generation)³¹ is a model that has been optimized based on VQ-VAE (Vector Quantized Variational Autoencoder)⁶⁶, which places greater emphasis on 3D shapes within 3D scenes. AutoSDF enhances the precision and variety of 3D shape generation by incorporating Shape Priors. The fundamental principle of AutoSDF³¹ is to leverage the discrete potential space of VQ-VAE to represent the 3D scene, which enables more comprehensive capture of intricate details and complex structures within the 3D scene during the generation process.

The evaluation process entails a comprehensive comparison of $\pi$-GAN⁶³, EG3D⁶⁴, DiffRF⁶⁵, AutoSDF³¹, and the 3D-UDDPM model proposed in this study. These models originate from the mainstream basic framework of generative modeling and are therefore subject to the same inputs, evaluation of their representational capabilities in 3D scenes, and comprehensive comparison of various types of The evaluation metrics (quality of the generated images, 3D consistency, shape accuracy, etc.) demonstrate that the method of this study exhibits superior performance in the generation and understanding of local cubes, as evidenced by the IoU (intersection over union) evaluation of the intersection and merger ratio of the generation results. The temporal requirements of various models are delineated in Table 3, while the outcomes of a comparative assessment of reconstruction quality are exhibited in Table 4. Furthermore, the experiments were executed on a local computer equipped with a NVIDIA RTX 3060 12GB graphics card, a configuration that facilitates the scalability of subsequent research endeavors.

Table 3 Experiments comparing training and inference times for different models.

Table 4 Comparative experiments on reconstruction quality of different models.

Conclusion

This study aims to elucidate the intricacies of a 3D localized scene by discerning the minutiae of a localized cube with the aid of a 3D diffusion model. The 3D object mapping in different dimensions is employed to accurately estimate the noise and realize the entire Markov chain process. Furthermore, the model is capable of accurately capturing minor local changes, thereby enhancing the realism and detail representation of the overall 3D scene with a minimal amount of computational complexity and resource consumption. Ultimately, a comprehensive understanding of the entire 3D scene is achieved. It should be noted that this research method is not without limitations. These include the voxelized objects used as input and output, as well as the global attention given to the complete 3D scene. These aspects require further optimization. Going forward, we intend to refine and enhance the method based on the present approach. We will then apply it to 3D reconstruction-related work. This will facilitate a more comprehensive understanding of the scene in 3D reconstruction. It will also enhance the quality and speed of reconstruction while ensuring lightweight processing.